Compound Fault Diagnosis and Sequential Prognosis for Electric Scooter with Uncertainties
Abstract
1. Introduction
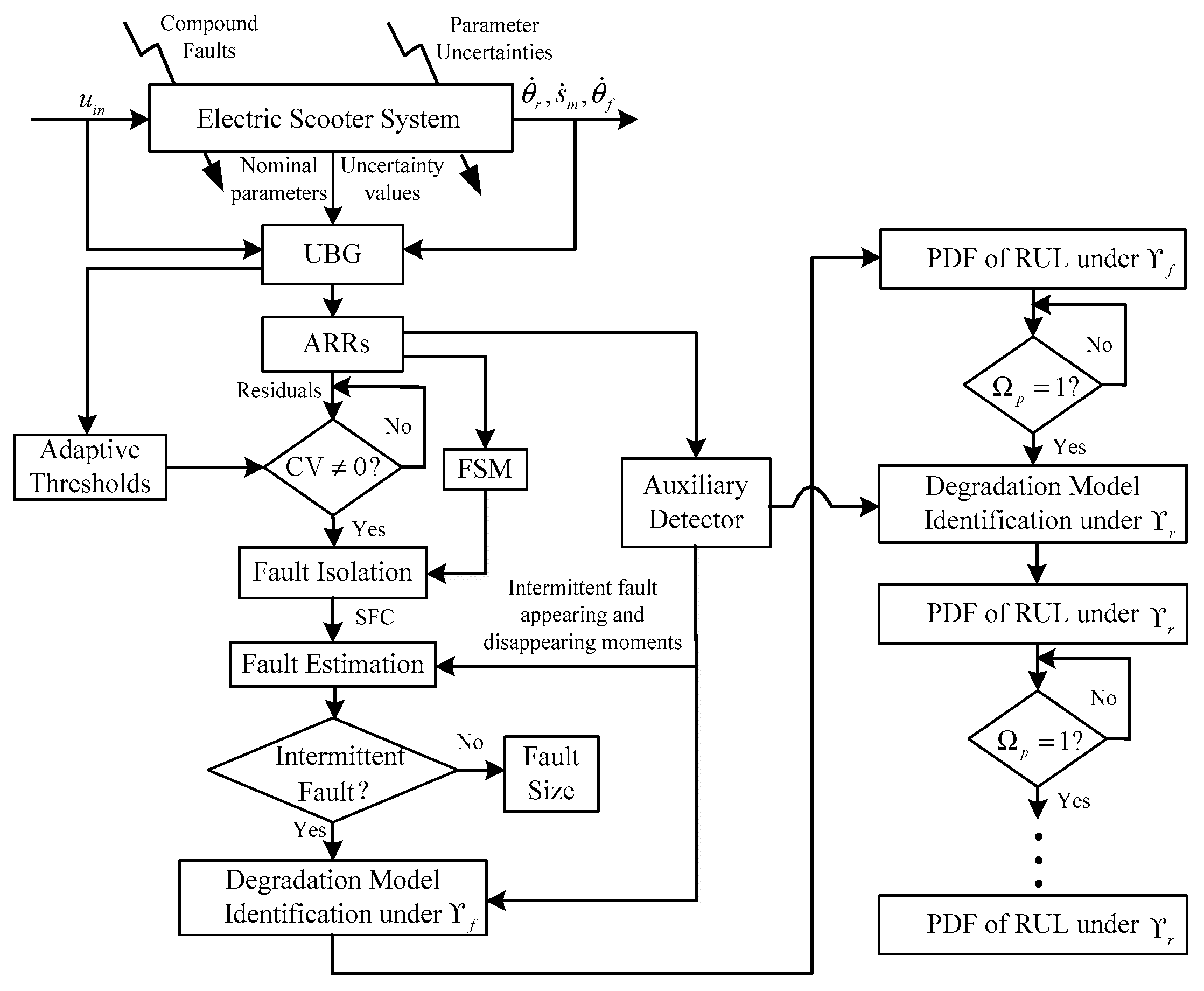
2. UBG Model and FDI of Electric Scooter
2.1. Electric Scooter System Model
2.2. FDI Method
3. Fault Estimation and Sequential Prognosis
3.1. Fault Estimation Scheme
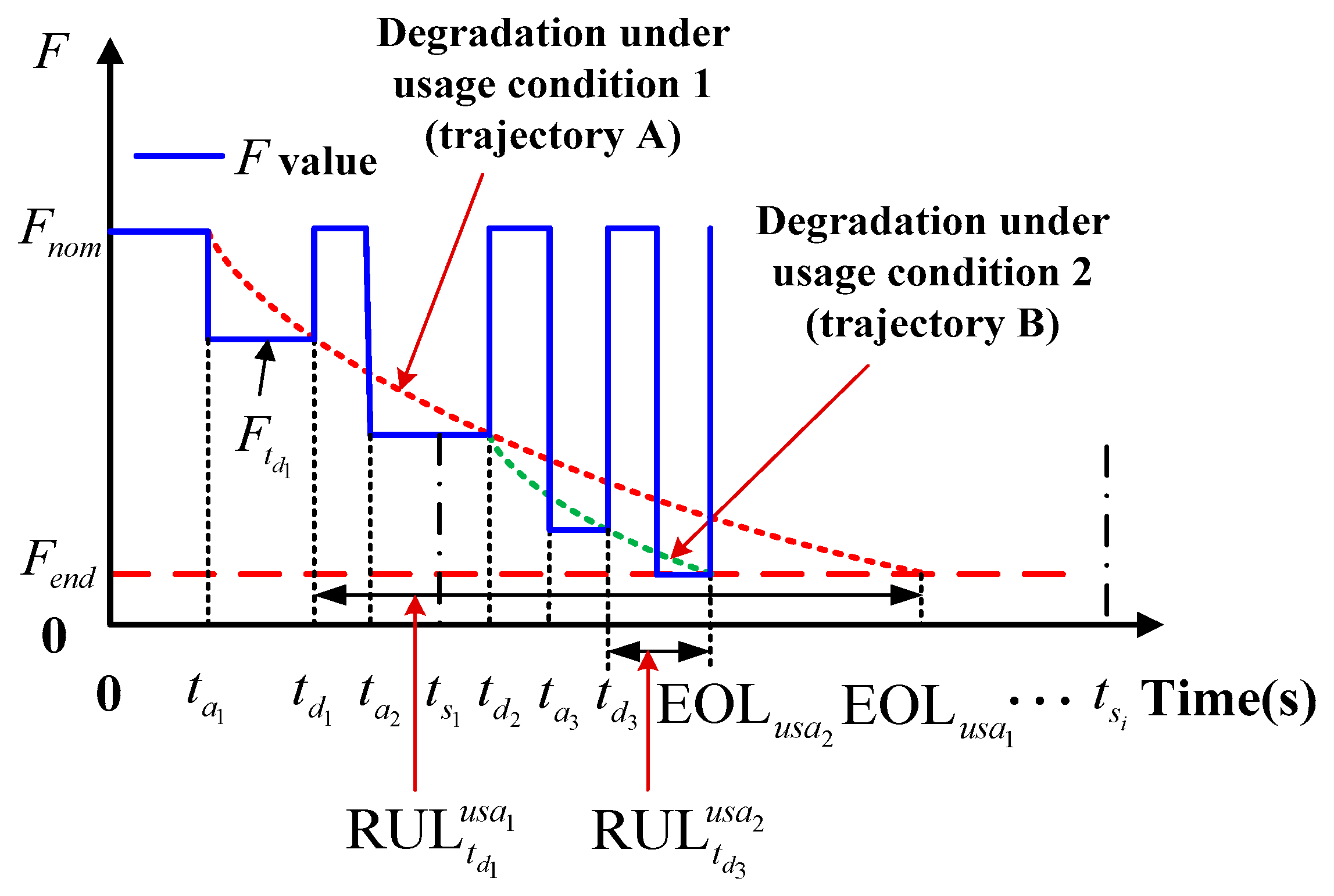
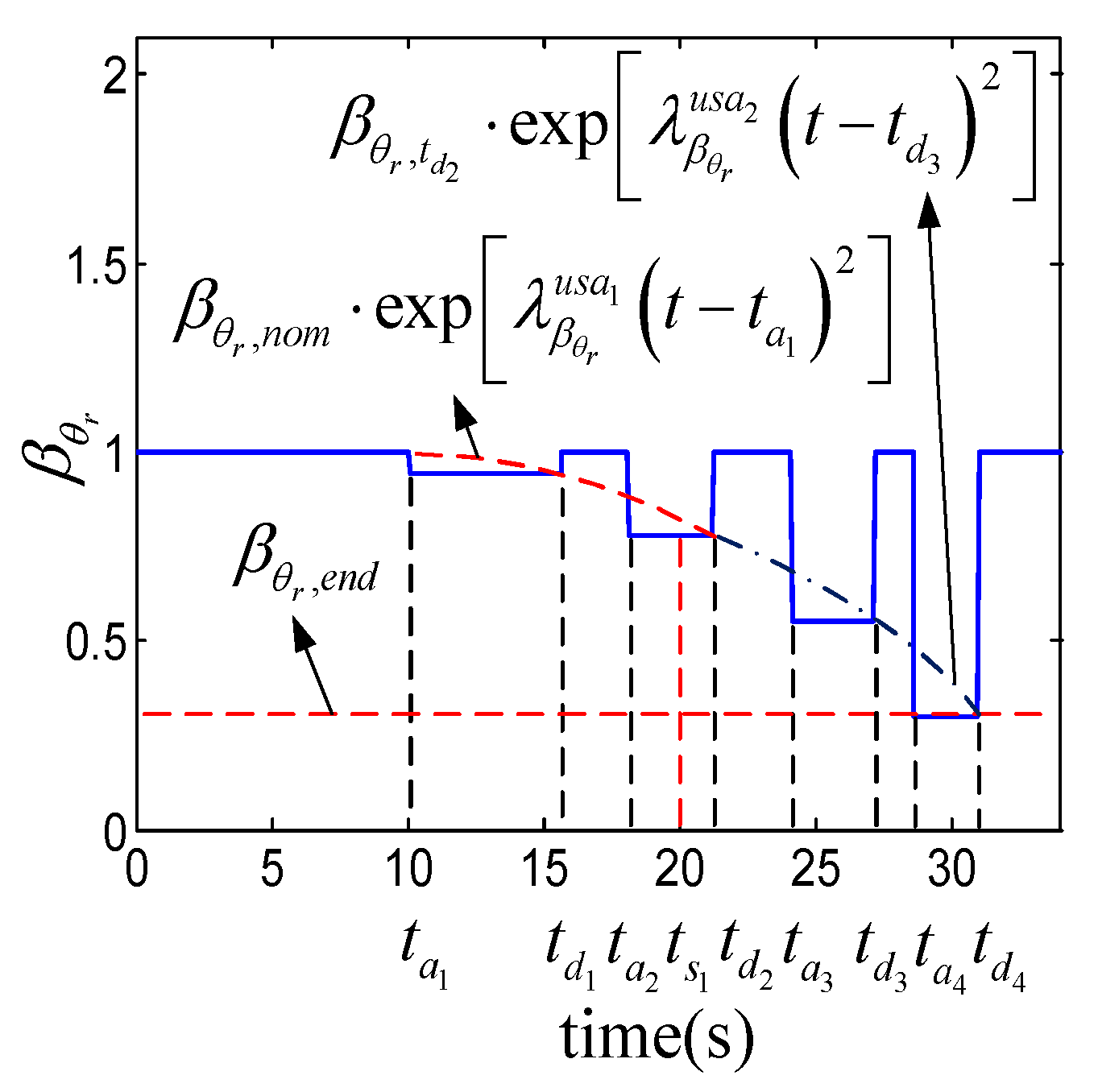
3.2. Sequential Prognosis
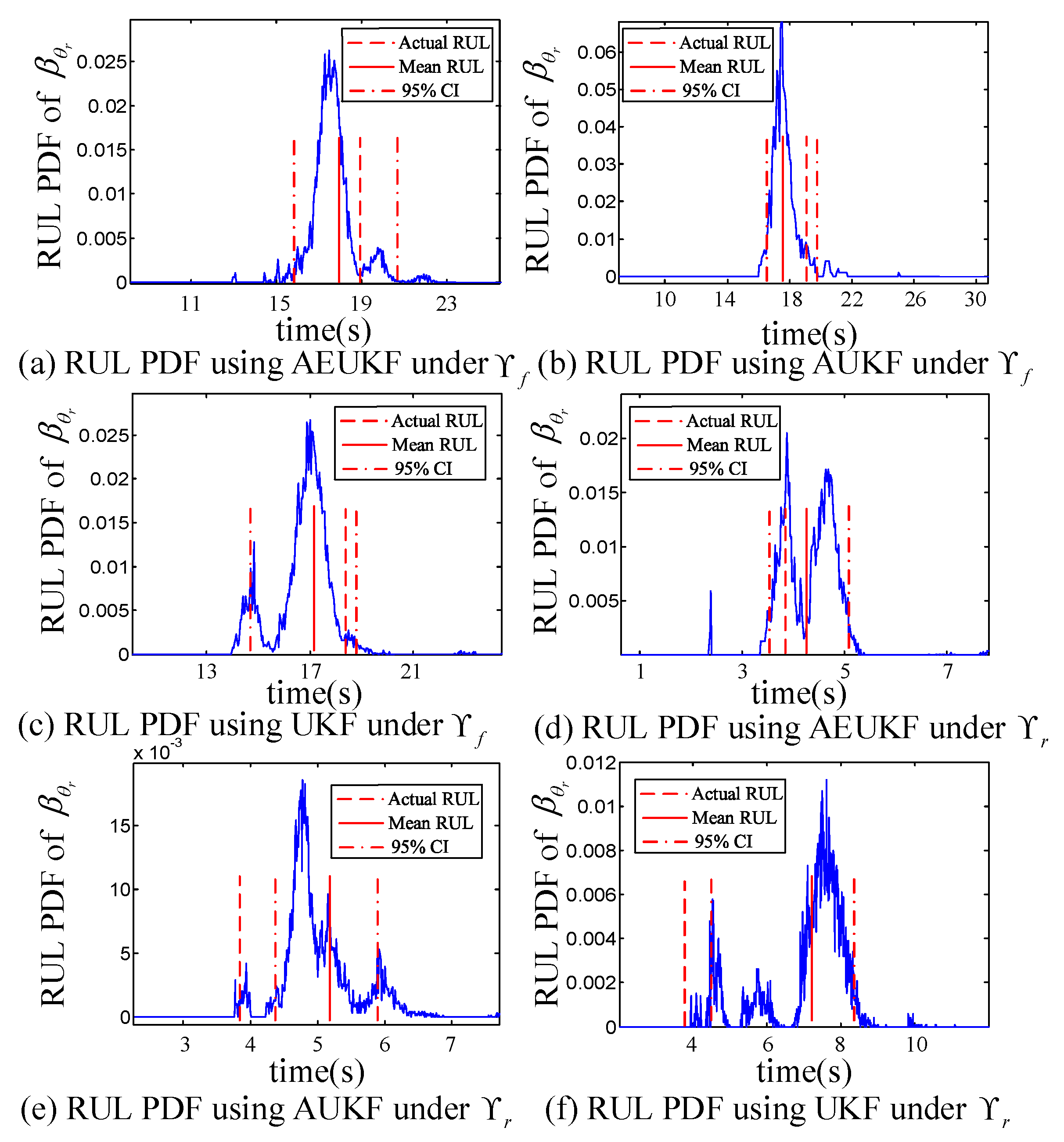
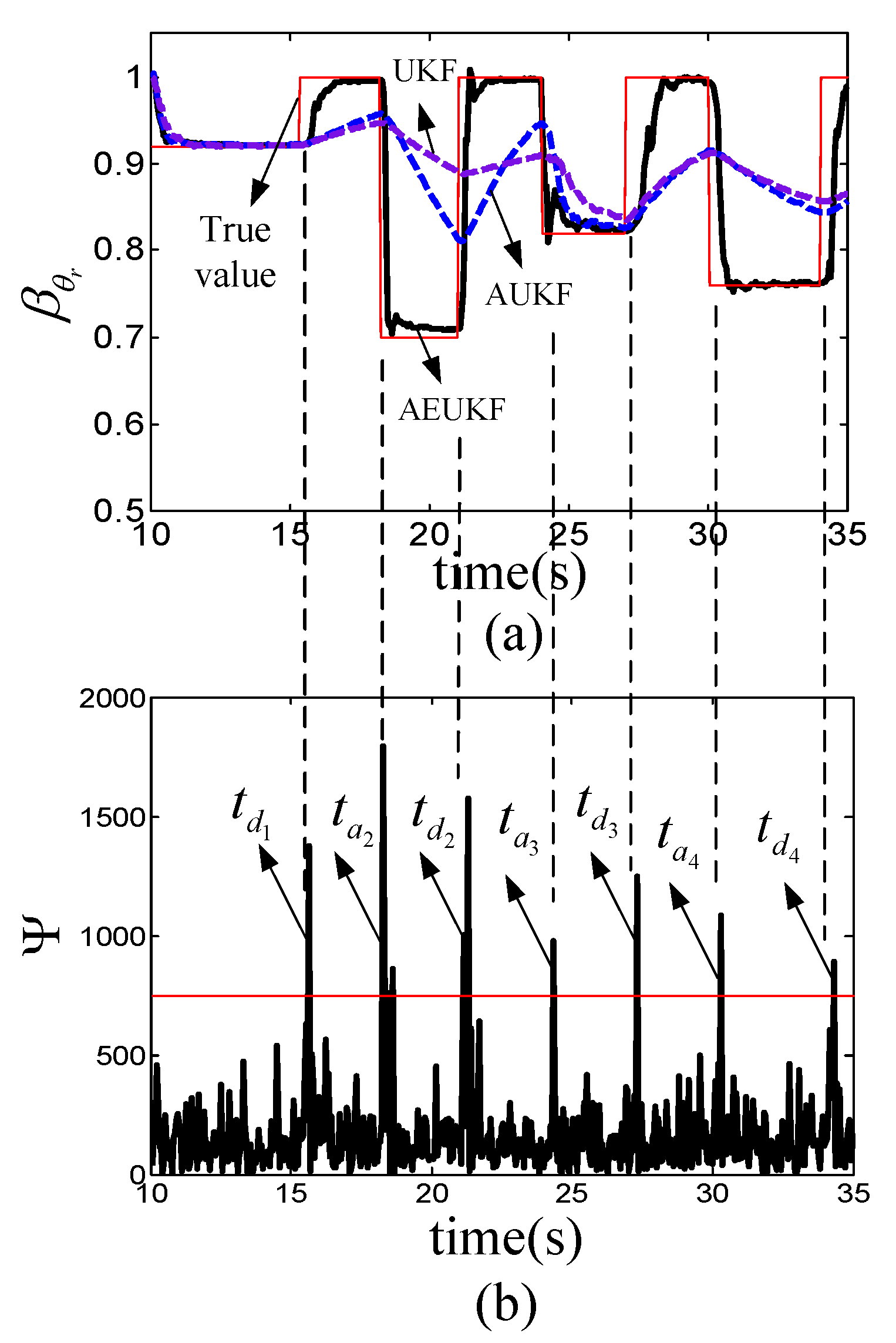
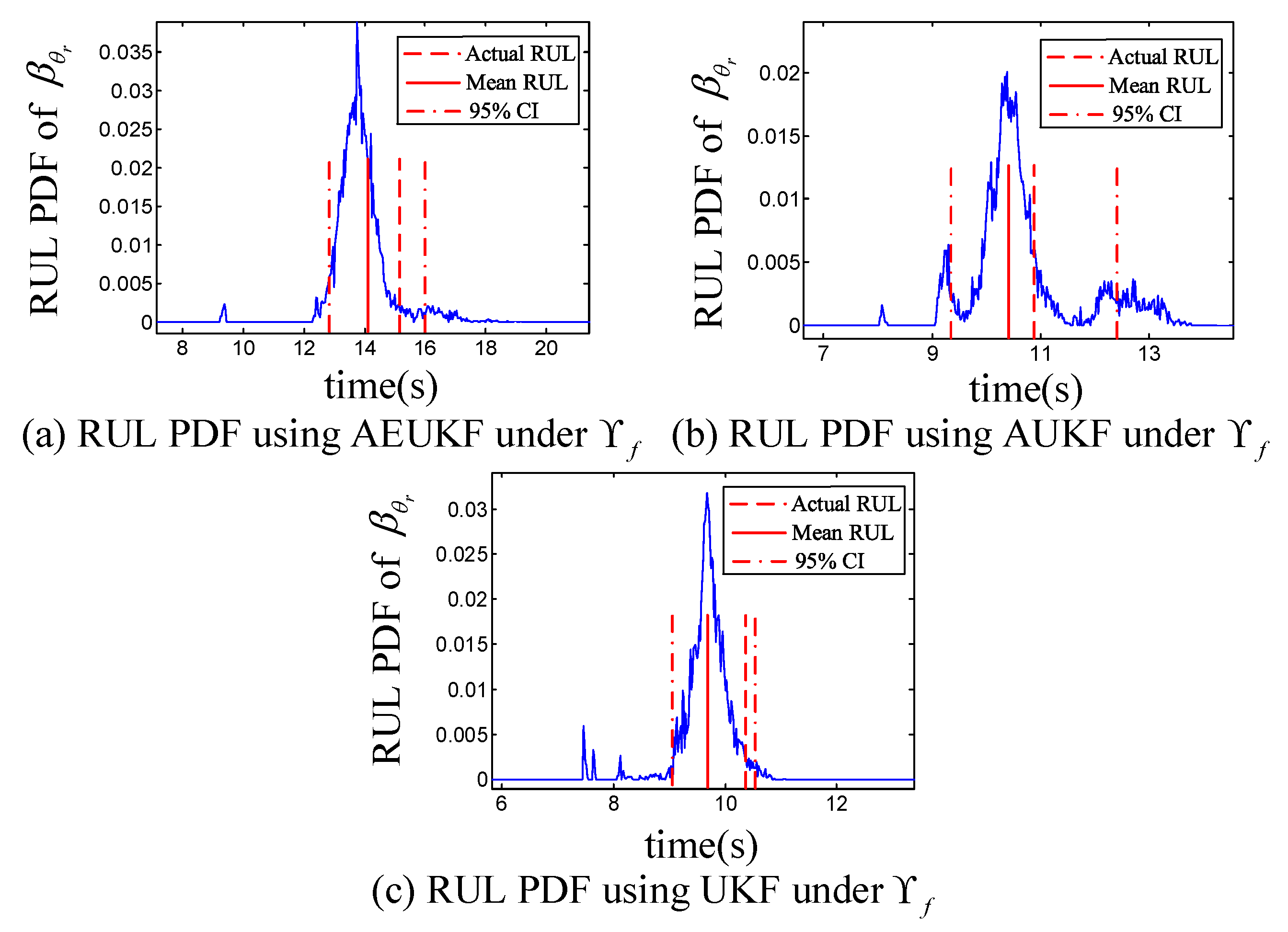
4. Experiment Results
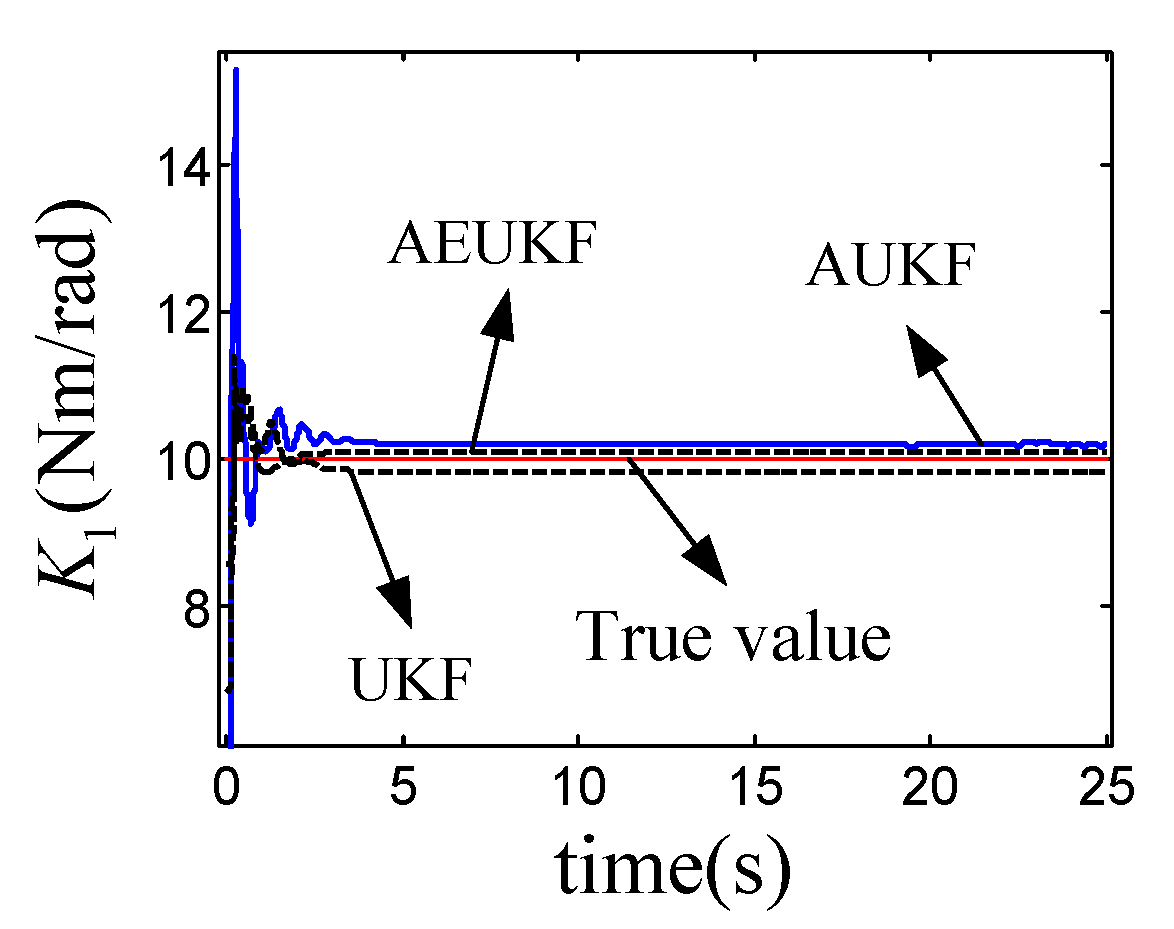
4.1. Parameter Identification and Model Validation
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques-part I: Fault diagnosis with model-based and signal-based approach. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Z.; Chen, M.Z.Q. Takagi-Sugeno fuzzy model based fault estimation and signal compensation with application to wind turbines. IEEE Trans. Ind. Electron. 2017, 64, 5678–5689. [Google Scholar] [CrossRef]
- Blesa, J.; Jiménez, P.; Rotondo, D.; Nejjari, F.; Puig, V. An interval NLPV parity equations approach for fault detection and isolation of a wind farm. IEEE Trans. Ind. Electron. 2015, 62, 3794–3805. [Google Scholar] [CrossRef]
- Verma, N.K.; Sevakula, R.K.; Dixit, S.; Salour, A. Intelligent condition based monitoring using acoustic signals for air compressors. IEEE Trans. Reliab. 2016, 65, 291–309. [Google Scholar] [CrossRef]
- Li, R.; He, D. Rotational machine health monitoring and fault detection using EMD-based acoustic emission feature quantification. IEEE Trans. Instrum. Meas. 2012, 61, 990–1001. [Google Scholar] [CrossRef]
- Benmoussa, S.; Bouamama, B.O.; Merzouki, R. Bond graph approach for plant fault detection and isolation: Application to intelligent autonomous vehicle. IEEE Trans. Autom. Sci. Eng. 2014, 11, 585–593. [Google Scholar] [CrossRef]
- Djeziri, M.A.; Merzouki, R.; Bouamama, B.O.; Dauphin-Tanguy, G. Robust fault diagnosis by using bond graph approach. IEEE/ASME Trans. Mechatron. 2007, 12, 599–611. [Google Scholar] [CrossRef]
- Zhang, X.; Polycarpou, M.M.; Parisini, T. A robust detection and isolation scheme for abrupt and incipient faults in nonlinear systems. IEEE Trans. Automat. Control. 2002, 47, 576–593. [Google Scholar] [CrossRef]
- Zhang, X.; Parisini, T.; Polycarpou, M.M. Adaptive fault-tolerant control of nonlinear uncertain systems: An information-based diagnostic approach. IEEE Trans. Automat. Control. 2004, 49, 1259–1274. [Google Scholar] [CrossRef]
- Kolar, D.; Lisjak, D.; Pająk, M.; Pavković, D. Fault diagnosis of rotary machines using deep convolutional neural network with wide three axis vibration signal input. Sensors 2020, 20, 4017. [Google Scholar] [CrossRef]
- Pająk, M.; Muślewski, Ł.; Landowski, B.; Grządziela, A. Fuzzy identification of the reliability state of the mine detecting ship propulsion system. Pol. Marit. Res. 2019, 26, 55–64. [Google Scholar] [CrossRef]
- Nguyen, V.; Seshadrinath, J.; Wang, D.; Nadarajan, S.; Vaiyapuri, V. Model-based diagnosis and RUL estimation of induction machines under interturn fault. IEEE Trans. Ind. Appl. 2017, 53, 2690–2701. [Google Scholar] [CrossRef]
- Yu, M.; Wang, D.; Luo, M. An integrated approach to prognosis of hybrid systems with unknown mode changes. IEEE Trans. Ind. Electron. 2015, 62, 503–515. [Google Scholar] [CrossRef]
- Pająk, M. Fuzzy identification of a threat of the inability state occurrence. J. Intell. Fuzzy Syst. 2018, 35, 3593–3604. [Google Scholar] [CrossRef]
- Pająk, M. Fuzzy model of the operational potential consumption process of a complex technical system. Facta Univ. Ser. Mech. Eng. 2020, 18, 453–472. [Google Scholar]
- Daigle, M.; Bregon, A.; Roychoudhury, I. Distributed prognostics based on structural model decomposition. IEEE Trans. Reliab. 2016, 63, 495–510. [Google Scholar] [CrossRef]
- Hu, X.; Jiang, J.; Cao, D.; Egardt, B. Battery health prognosis for electric vehicles using sample entropy and sparse Bayesian predictive modeling. IEEE Trans. Ind. Electron. 2016, 63, 2645–2655. [Google Scholar] [CrossRef]
- Climente-Alarcon, V.; Antonino-Daviu, J.A.; Strangas, E.G.; Riera-Guasp, M. Rotor-bar breakage mechanism and prognosis in an induction motor. IEEE Trans. Ind. Electron. 2015, 62, 1814–1825. [Google Scholar] [CrossRef]
- Gucik-Derigny, D.; Outbib, R.; Ouladsine, M. A comparative study of unknown-input observers for prognosis applied to an electromechanical system. IEEE Trans. Reliab. 2016, 65, 704–717. [Google Scholar] [CrossRef]
- Ompusunggu, A.P.; Papy, J.; Vandenplas, S. Kalman-filtering-based prognostics for automatic transmission clutches. IEEE/ASME Trans. Mechatron. 2016, 21, 419–430. [Google Scholar] [CrossRef]
- Lei, Y.; Xie, H.; Yuan, Y.; Chang, Q. Fault location for the intermittent connection problems on CAN networks. IEEE Trans. Ind. Electron. 2015, 62, 7203–7213. [Google Scholar] [CrossRef]
- Obeid, N.H.; Battiston, A.; Boileau, T.; Nahid-Mobarakeh, B. Early intermittent interturn fault detection and localization for a permanent magnet synchronous motor of electrical vehicles using wavelet transform. IEEE Trans. Transp. Electrif. 2017, 3, 694–702. [Google Scholar] [CrossRef]
- Yan, R.; He, X.; Wang, Z.; Zhou, D. Detection, isolation and diagnosability analysis of intermittent faults in stochastic systems. Int. J. Control 2018, 91, 480–494. [Google Scholar] [CrossRef]
- Hu, S.; Wang, L.; Mao, J.; Gao, C.; Zhang, B.; Yang, S. Synchronous online diagnosis of multiple cable intermittent faults based on chaotic spread spectrum sequence. IEEE Trans. Ind. Electron. 2019, 66, 3217–3226. [Google Scholar] [CrossRef]
- Auzanneau, F. Detection and characterization of microsecond intermittent faults in wired networks. IEEE Trans. Instrum. Meas. 2018, 67, 2256–2258. [Google Scholar] [CrossRef]
- Syed, W.; Perinpanayagam, S.; Samie, M.; Jennions, I. A novel intermittent fault detection algorithm and health monitoring for electronic interconnections. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 400–406. [Google Scholar] [CrossRef]
- Borutzky, W. Bond graph model-based system mode identification and mode-dependent fault thresholds for hybrid systems. Math. Comput. Model. Dyn. Syst. 2014, 20, 584–615. [Google Scholar] [CrossRef]
- Partovibakhsh, M.; Liu, G. An adaptive unscented Kalman filtering approach for online estimation of model parameters and state-of-charge of lithium-ion batteries for autonomous mobile robots. IEEE Trans. Control Syst. Technol. 2015, 23, 357–363. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Gao, F. Lithium polymer battery state-of-charge estimation based on adaptive unscented Kalman filter and support vector machine. IEEE Trans. Power Electron. 2016, 31, 2226–2238. [Google Scholar] [CrossRef]
- Arogeti, S.; Wang, D.; Low, C.B.; Yu, M. Fault detection isolation and estimation in a vehicle steering system. IEEE Trans. Ind. Electron. 2012, 59, 4810–4820. [Google Scholar] [CrossRef]









| Variable | Nomenclature | Variable | Nomenclature |
|---|---|---|---|
| Input signal | Motor viscous friction | ||
| Electrical resistance of the motor | Motor Coulomb friction | ||
| Voltage-to-current constant | Rear wheel viscous friction | ||
| Current-to-torque ratio | Rear wheel Coulomb friction | ||
| Reduction ratio | Front wheel viscous friction | ||
| Wheel radius | Front wheel Coulomb friction | ||
| Motor inertia | Longitudinal displacement | ||
| Motor mechanical friction | Angular position of front wheel | ||
| Front wheel friction | Angular position of rear wheel | ||
| Rear wheel friction | Adaptive threshold | ||
| Transmission axis rigidity | Analytical redundancy relation | ||
| Longitudinal speed | Front wheel inertial | ||
| Angular velocity of front wheel | Multiplicative uncertainty | ||
| Angular velocity of rear wheel | Efficiency factor | ||
| Rear wheel inertial | Additional effort source |
| 1 | 0 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 0 | 1 | ||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||
| 0 | 1 | 1 | ||
| 0 | 1 | 1 |
| Nominal Value | Uncertainty Value | Nominal Value | Uncertainty Value | ||
|---|---|---|---|---|---|
| 3 A/V | / | 4.87 | 2.84% | ||
| 0.0666 Nm/A | / | 6.97 | 2.76% | ||
| 1/18 | / | 3.545 Nms/rad | 5.12% | ||
| 0.115 m | / | 5.955 Nm | 1.89% | ||
| 1.03 | 2.61% | 1.02 Nms/rad | 2.79% | ||
| 1.725 Nms/rad | 2.98% | 1.857 Nm | 2.91% | ||
| 5.635 Nm | 5.86% | 10.02 Nm/rad | 2.29% | ||
| 5.03 | 8.12% | 10.07 Nm/rad | 1.13% | ||
| 20.7 kg | 2.06% |
| Actual value | 0.94 | 0.78 | 0.55 | 0.469 | 10.02 | |
| Mean | AEUKF | 0.95 | 0.79 | 0.56 | 0.463 | 10.05 |
| AUKF | 0.96 | 0.85 | 0.62 | 0.477 | 10.09 | |
| UKF | 0.96 | 0.91 | 0.70 | 0.487 | 9.88 | |
| St.dev | AEUKF | 0.0011 | 0.0012 | 0.0011 | 0.0012 | 0.06 |
| AUKF | 0.0016 | 0.0016 | 0.0017 | 0.0015 | 0.11 | |
| UKF | 0.0022 | 0.0021 | 0.0022 | 0.0023 | 0.14 | |
| RA | RSD | |||
|---|---|---|---|---|
| Experiment1 | Usage1 | UKF | 90.57 | 9.57 |
| AUKF | 93.94 | 9.06 | ||
| AEUKF | 94.15 | 9.32 | ||
| Usage2 | UKF | |||
| AUKF | ||||
| AEUKF | 90.71 | 11.59 | ||
| Experiment2 | Usage1 | UKF | 90.68 | 8.31 |
| AUKF | 93.51 | 8.25 | ||
| AEUKF | 95.07 | 8.28 |
| Actual value | 0.92 | 0.70 | 0.82 | 0.76 | 0.469 | 10.02 | |
| AEUKF | 0.92 | 0.72 | 0.83 | 0.76 | 0.462 | 9.98 | |
| Mean | AUKF | 0.92 | 0.81 | 0.83 | 0.85 | 0.448 | 9.93 |
| UKF | 0.93 | 0.89 | 0.84 | 0.86 | 0.443 | 10.12 | |
| AEUKF | 0.0011 | 0.0013 | 0.0011 | 0.0012 | 0.0013 | 0.06 | |
| St.dev | AUKF | 0.0016 | 0.0017 | 0.0015 | 0.0017 | 0.0019 | 0.12 |
| UKF | 0.0022 | 0.0022 | 0.0023 | 0.0021 | 0.0023 | 0.13 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, M.; Lu, H.; Wang, H.; Xiao, C.; Lan, D. Compound Fault Diagnosis and Sequential Prognosis for Electric Scooter with Uncertainties. Actuators 2020, 9, 128. https://doi.org/10.3390/act9040128
Yu M, Lu H, Wang H, Xiao C, Lan D. Compound Fault Diagnosis and Sequential Prognosis for Electric Scooter with Uncertainties. Actuators. 2020; 9(4):128. https://doi.org/10.3390/act9040128
Chicago/Turabian StyleYu, Ming, Haotian Lu, Hai Wang, Chenyu Xiao, and Dun Lan. 2020. "Compound Fault Diagnosis and Sequential Prognosis for Electric Scooter with Uncertainties" Actuators 9, no. 4: 128. https://doi.org/10.3390/act9040128
APA StyleYu, M., Lu, H., Wang, H., Xiao, C., & Lan, D. (2020). Compound Fault Diagnosis and Sequential Prognosis for Electric Scooter with Uncertainties. Actuators, 9(4), 128. https://doi.org/10.3390/act9040128






