Electrothermal Phenomena in Ferroelectrics
Abstract
:1. Background
2. Review of Phenomenology in Ferroelectrics
2.1. Static/Equilibrium Ferroelectric Phenomenology
2.1.1. Thermodynamical Functions
≦ TdS + Xdx + EdD
2.1.2. Linear Energy Handling
2.1.3. Nonlinear Energy Handling
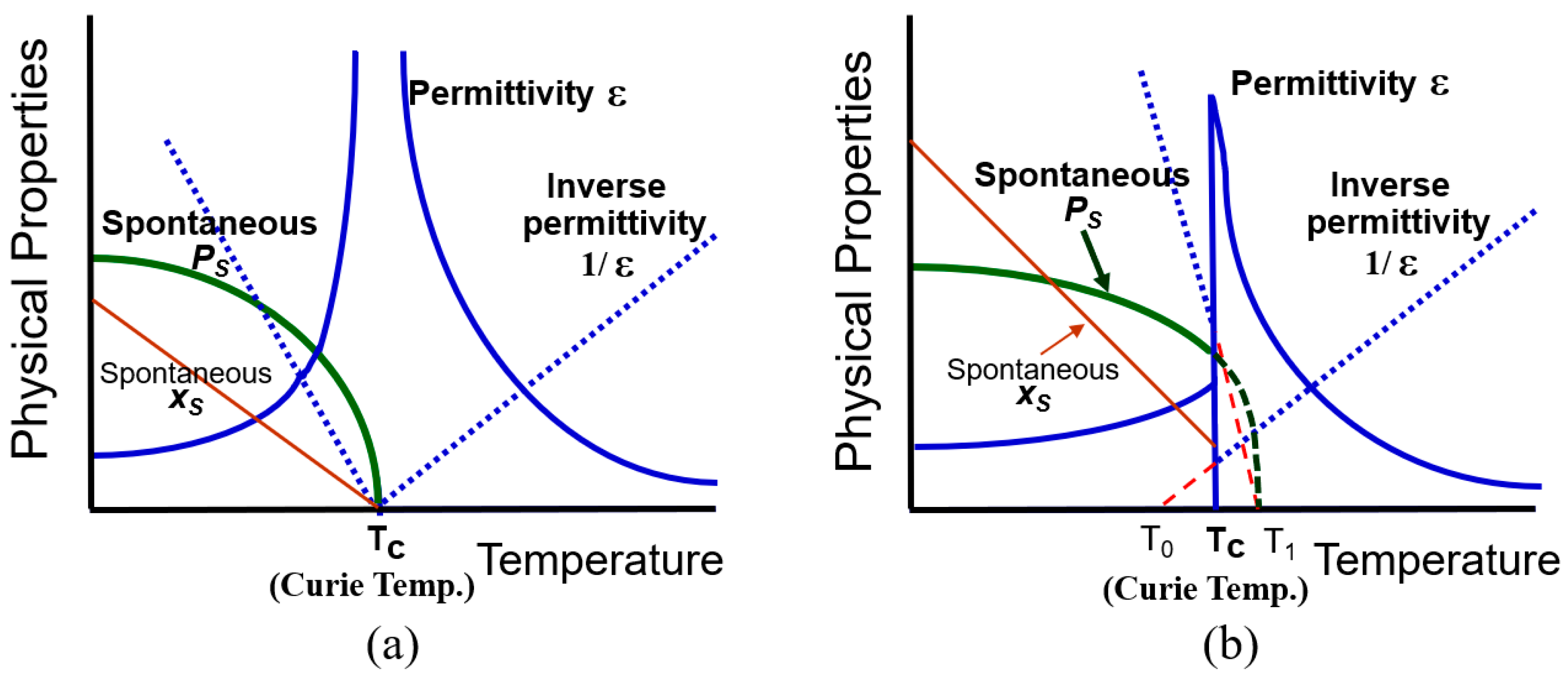
2.1.3.1. Second-Order Phase Transition
2.1.3.2. First-Order Phase Transition
− (1/2)s X2 − Q P2X, (α = (T − T0)/ε0 C)
2.1.4. Isothermal Process—Piezoelectric Coupling
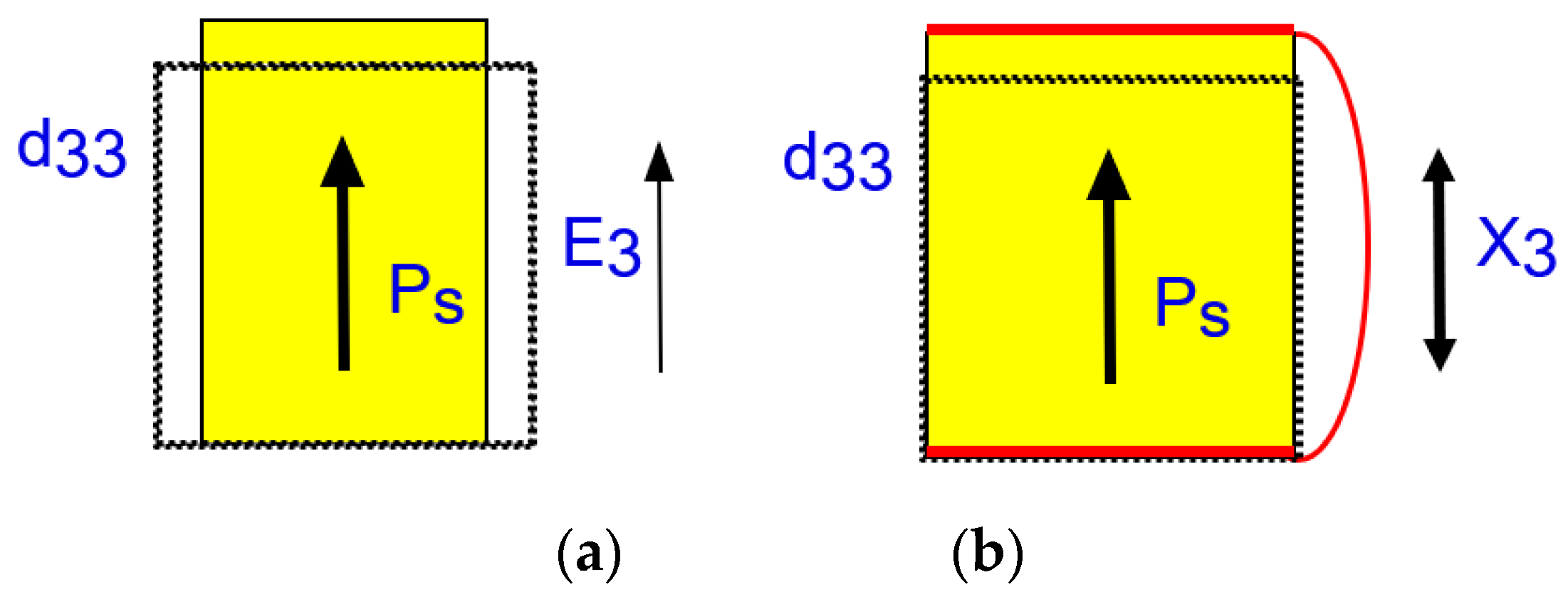
2.1.4.1. Thermodynamical Meaning of Piezoelectric Constant
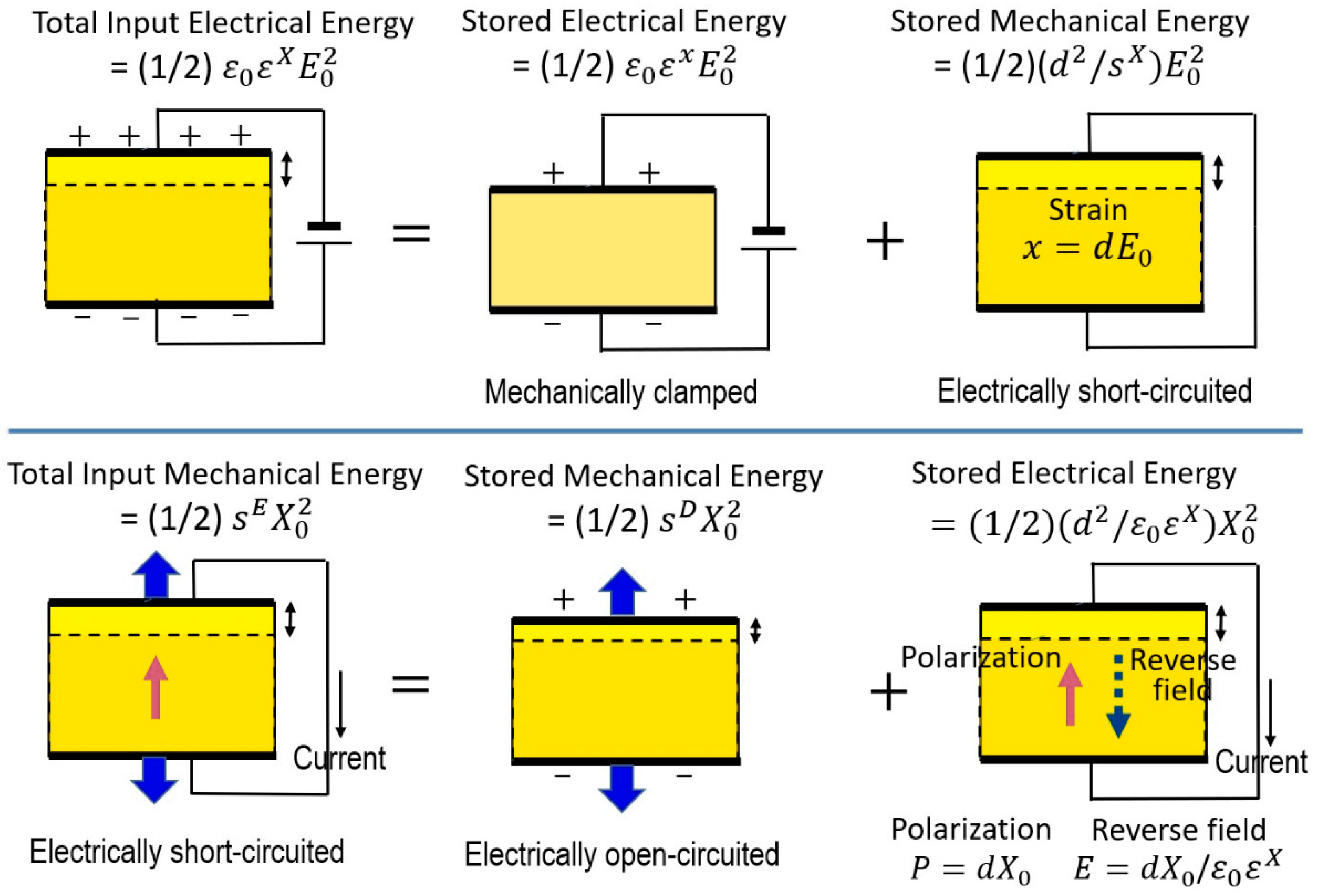
2.1.4.2. Electromechanical Coupling Factor
= d332/ε0ε3X∙s33E
= d332/ε0ε3X∙s33E
2.1.4.3. Constraint Physical Parameters
2.1.5. Adiabatic Process 1—Piezothermal Effect
2.1.6. Adiabatic Process 2—Electrothermal Effect
2.1.6.1. Constraint Specific Heat Capacity
2.1.6.2. Constraint (Adiabatic) Permittivity
2.1.6.3. Electrocaloric Effect
- (a)
- Specific Heat Capacity
- (b)
- Pyroelectric CoefficientNoting here , the pyroelectric coefficient is obtained as
- (c)
- Figure of Merit of Electrocaloric Effect
2.1.6.4. “Electrothermal Coupling Factor”
- Permittivity
2.2. Time-Dependent Ferroelectric Phenomenology
2.2.1. Polarization Relaxation
- Time constant is proportional to “permittivity” .
- t → gives P → PS.
- With approaching T → T0, → . The recovery time of P is very slow around TC = T0.
2.2.2. Temperature Relaxation
- In a uniform (no space gradient) specimen, temperature change follows an exponential trend with time: .
- t → gives → . corresponds to the temperature change by the electrocaloric effect.
- Time constant is proportional to temperature, and inversely proportional to the specific heat capacity . The larger the specific heat capacity , and the lower the temperature, the lower the time constant . The recovery time of θ is quicker. This τ is roughly a suitable rise time period of an applying pseudo-step electric field.
3. Thermal Diffusivity and Conductivity
3.1. 1D Heat Conduction Model
- q—Heat flux = quantity of heat passing through cross section of rod per unit area per unit time. The unit of heat quantity is calorie (cal), and 1 cal corresponds to 4.186 Joule in energy.
- λ—Thermal conductivity = thermal or heat conductance per unit length of material. The inverse 1/λ is the resistance which measures the temperature drop per unit length when heat flux is unity.
- C—Heat capacitance of material = specific heat capacity cp (, ) density ρ, number of heat units to raise block of unit area and unit length (i.e., per unit volume) 1 °C in temperature. Note that the specific heat capacity [J/(kg·K)] is determined per unit mass (kg), which must be multiplied by density (kg/m3) to obtain the heat capacitance per unit volume [J/(m3·K)].
- Thermal conductivity — [W/(m·K)]
- Specific heat capacity — [J/(kg·K)]
- Mass density —7600 [kg/m3]
- Thermal diffusivity — [m2/s]
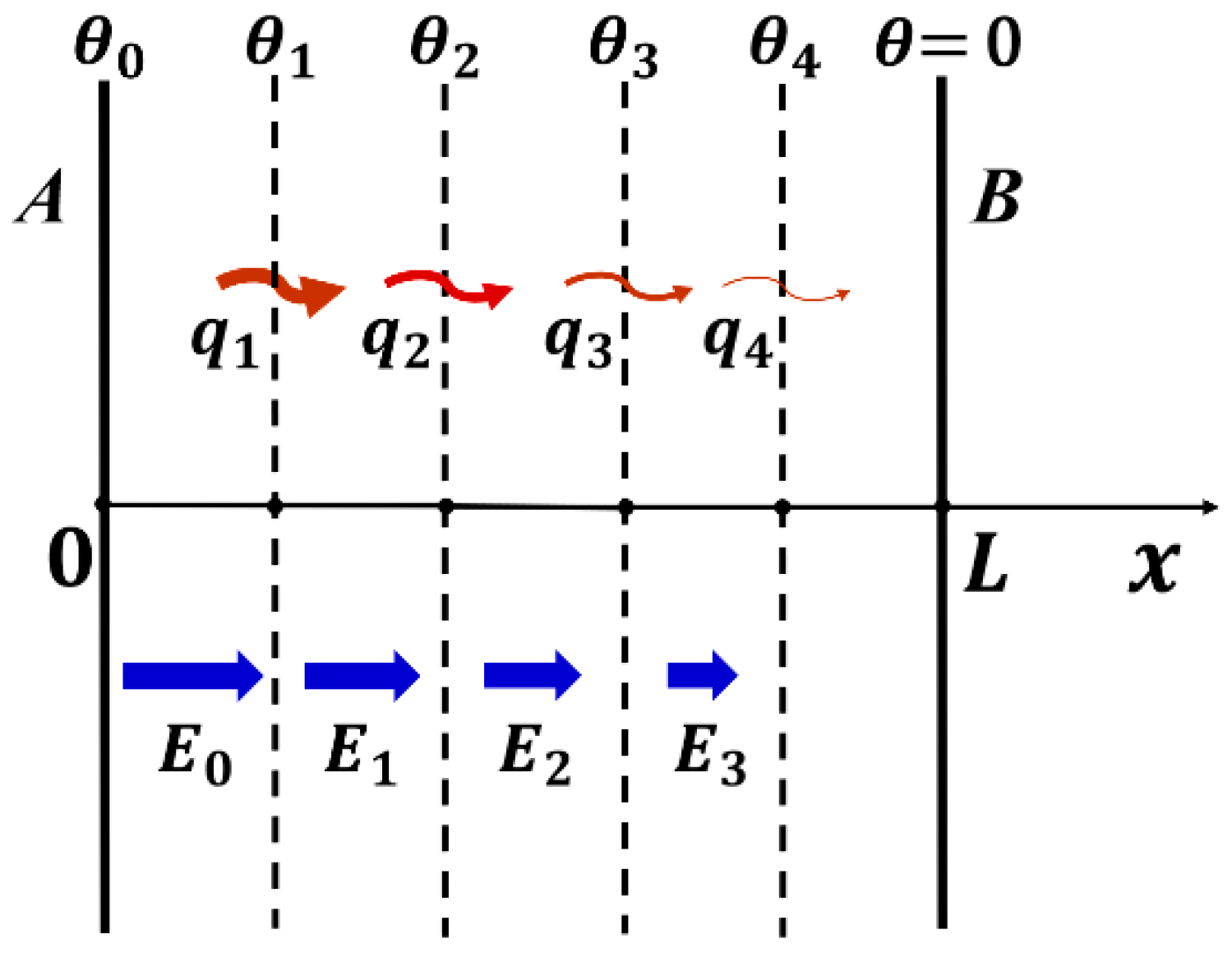
3.2. Solution of 1D Heat Transfer Equation
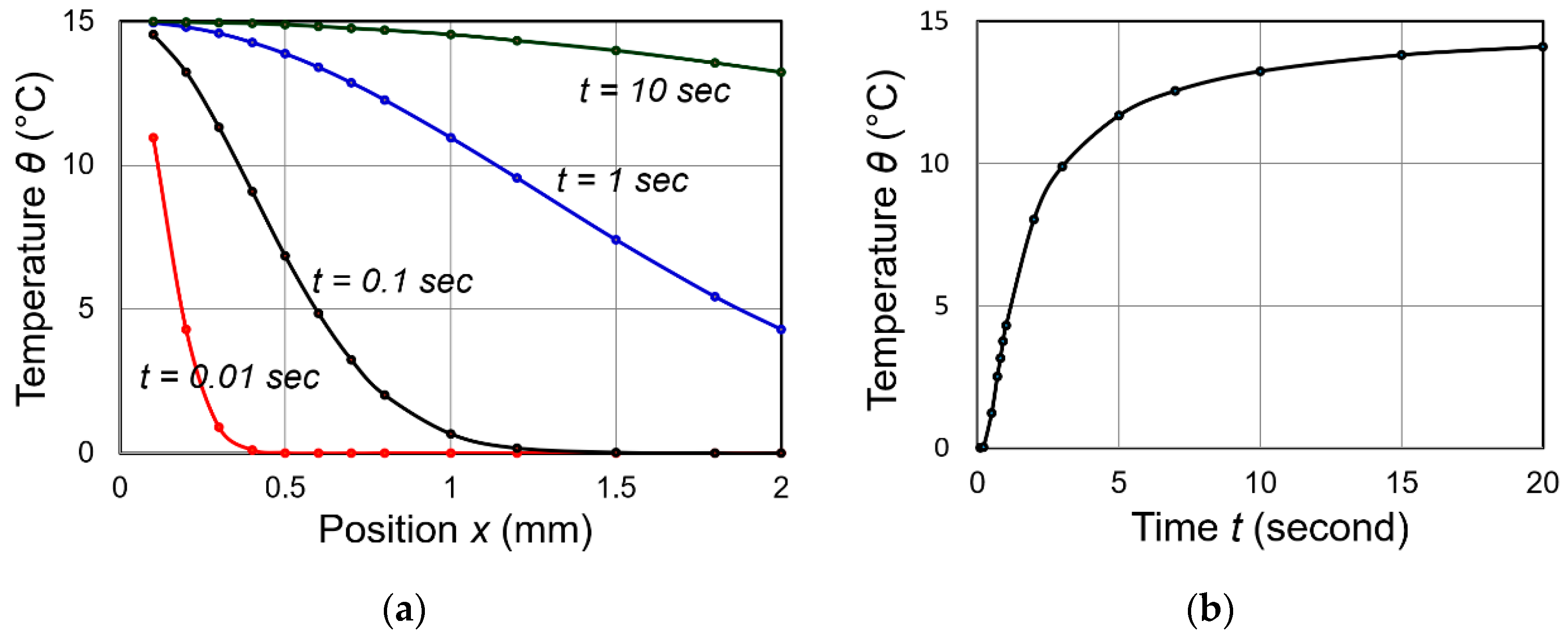
- At x = 0, —Temperature is constant at , irrelevant to time after attaching to heat source.
- At x = L, —By measuring temperature change with t at x = L, we can obtain the thermal diffusivity .
3.3. Thermal Diffusivity Measurements
3.4. Thermal Diffusivity under Different Electrical Constraints
3.4.1. Specific Heat Capacity—Scalar Parameter
3.4.2. Thermal Conductivity—Tensor Parameter
3.5. Thermal Conductivity in Pb-Free Piezoelectrics
4. Nonlinear Elastic Performances and “Phonons”
4.1. Electrostriction and Thermal Expansion
4.2. Lattice Vibration and Phonon
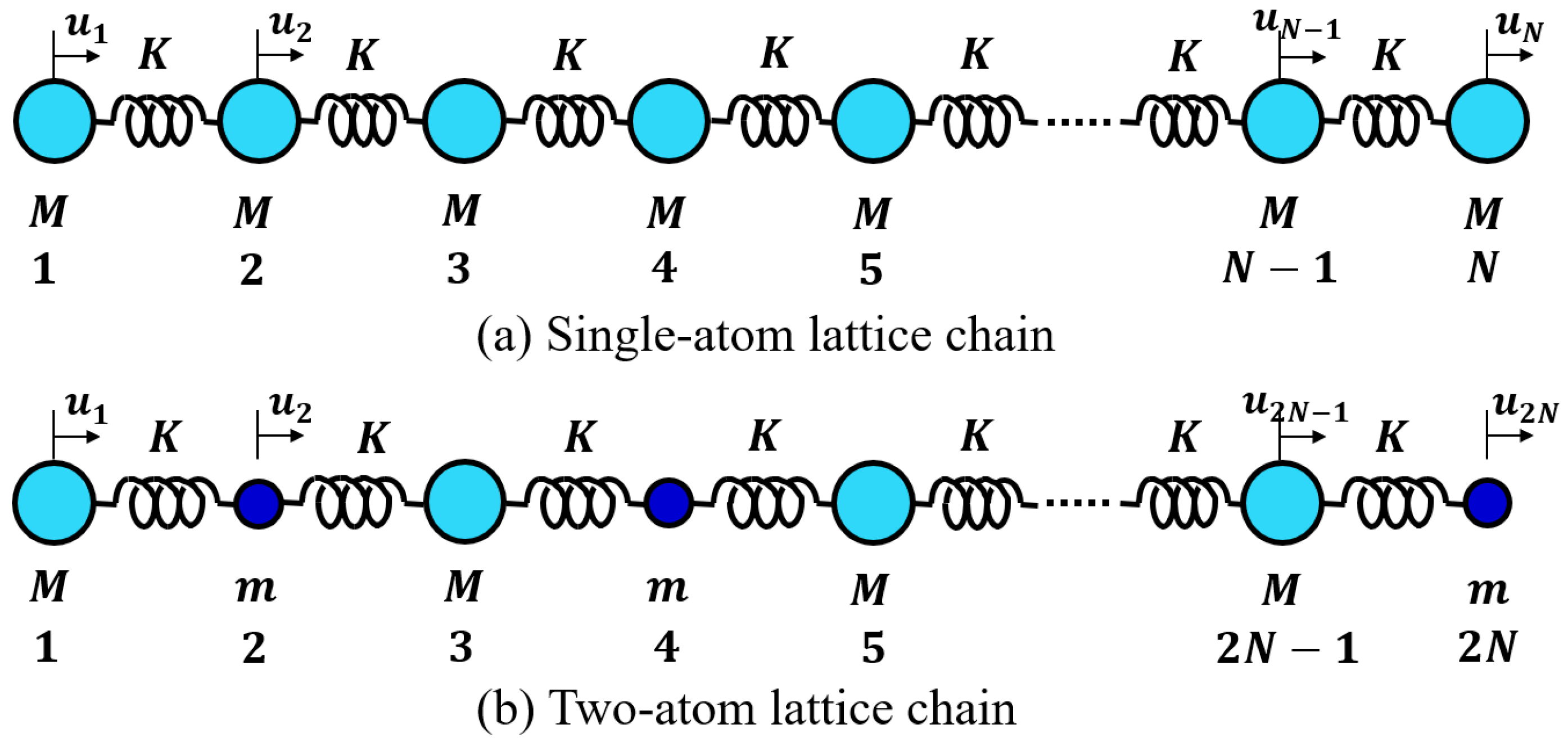
4.2.1. Lattice Vibration—One-Atom Chain Model
4.2.2. Lattice Vibration—Two-Atom Chain Model
4.2.3. Phonon Spectral Density
4.3. Anharmonic Phonon Modes and Electrothermal Coupling
4.3.1. Anharmonic Phonon Modes and Wave Packet
4.3.2. Heat Flow and Electrothermal Coupling
5. Thermal Analysis on Piezoelectric Transducers
5.1. Pseudo-DC Piezoelectric Actuators
5.1.1. Heat Generation from Multilayer Actuators
5.1.2. Thermal Analysis on ML Actuators
5.2. Resonance Drive Piezoelectric Transducers
5.2.1. Heat Generation from a Resonating Piezoelectric Specimen
5.2.2. Heat Generation at the Antiresonance Mode
5.2.3. Thermal Analysis on the Resonance Mode
5.2.3.1. Heat Transfer Modeling
- (1)
- 1D heat conduction in the specimen.
- (2)
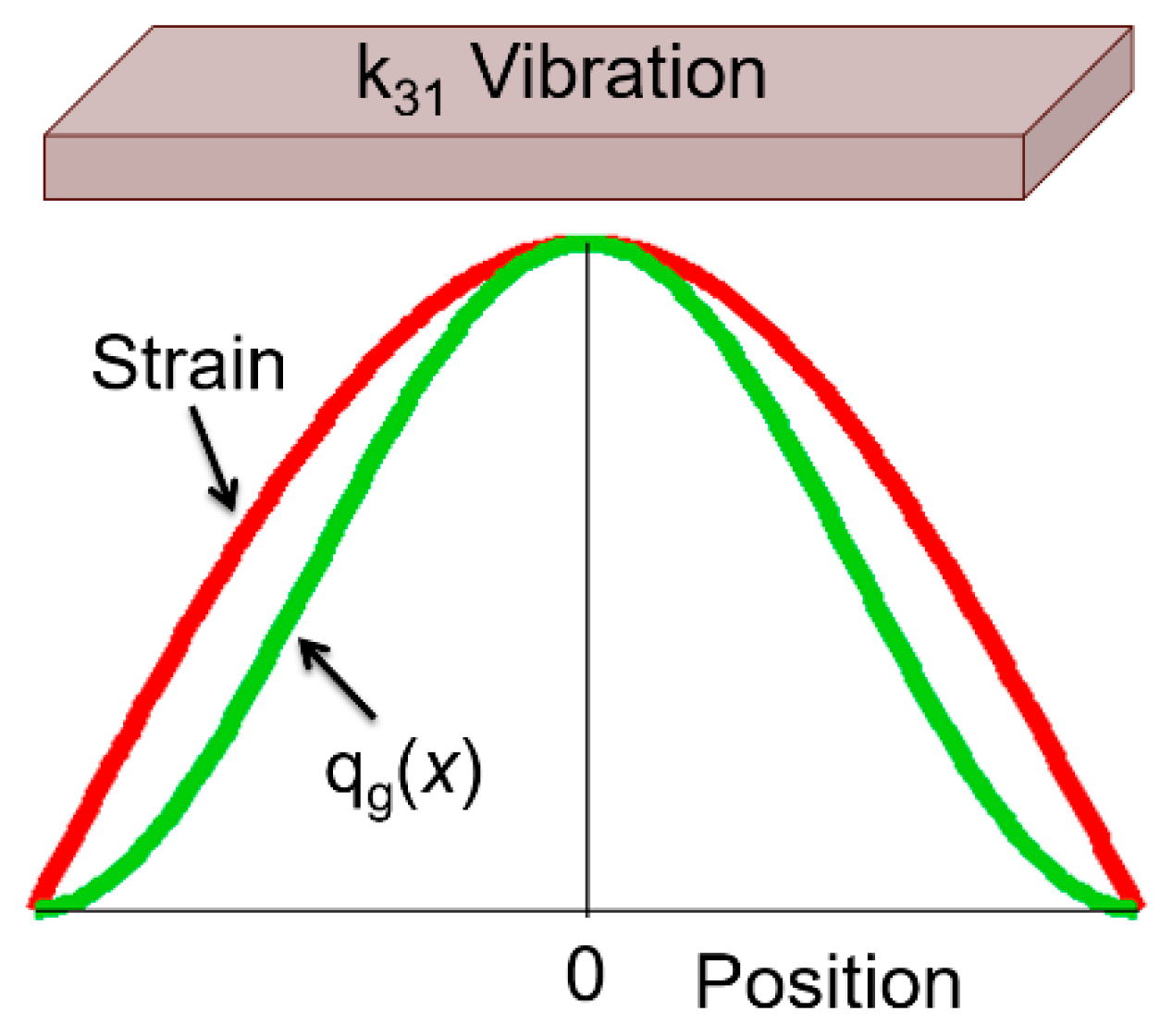
- Heat generation is proportional to strain squared (i.e., elastic energy), distributed on the specimen.
- (3)
- Heat dissipation via convection (to air) and radiation. Conduction is neglected.
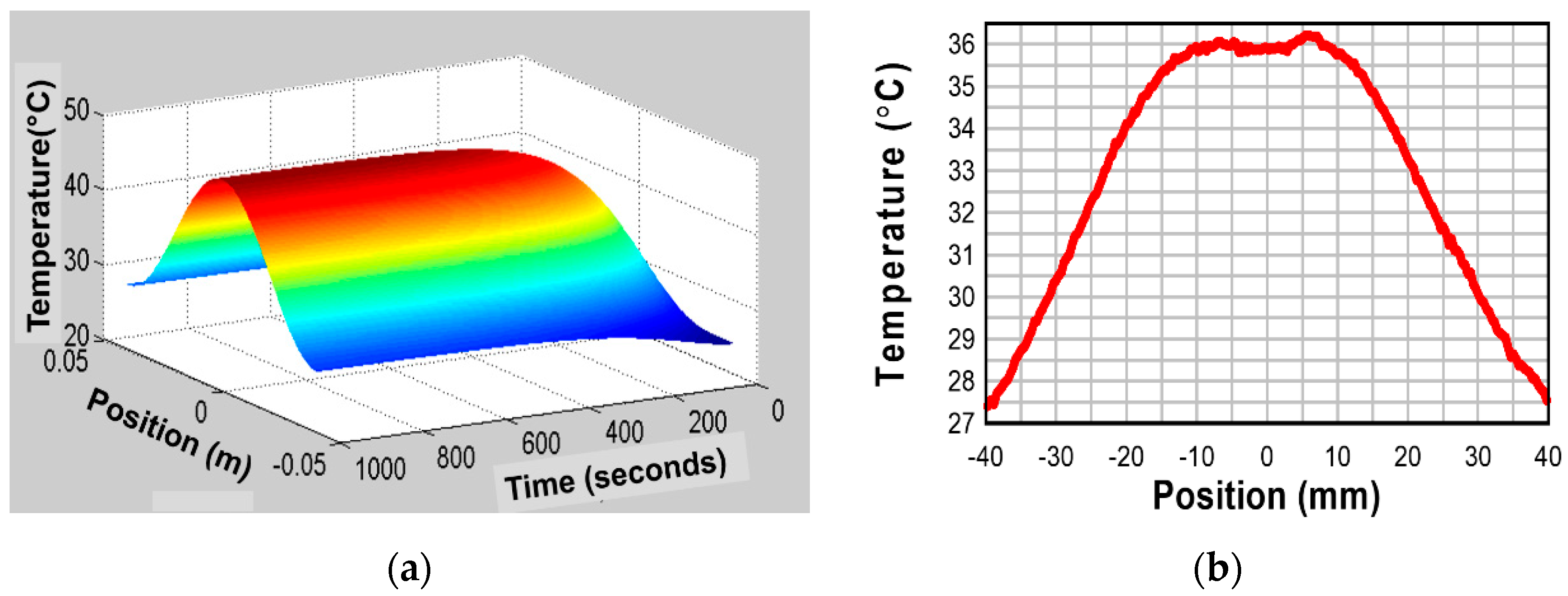
5.2.3.2. Temperature Distribution Profile Change with Time
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Priya, S.; Uchino, K. Estimation of Polarocaloric Contribution to Dielectric Loss in Oriented 0.92PZN-0.08PT Single Crystals. Jpn. J. Appl. Phys. 2003, 42, 5158–5164. [Google Scholar] [CrossRef]
- Mischenko, A.S.; Zhang, Q.; Scott, J.F.; Whatmore, W.R.; Mathur, N.D. Giant Electrocaloric Effect in Thin-Film PbZr0.95Ti0.05O3. Science 2006, 311, 1270–1271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neese, B.; Chu, B.; Lu, S.-G.; Wang, Y.; Furman, E.; Zhang, Q.M. Large Electrocaloric Effect in Ferroelectric Polymers Near Room Temperature. Science 2008, 321, 821–823. [Google Scholar] [CrossRef] [PubMed]
- Uchino, K. High. Power Piezoelectrics and Loss Mechanisms; CRC Press: Boca Ratton, FL, USA, 2020; ISBN 978-0-367-54069-2. [Google Scholar]
- Uchino, K.; Hirose, S. Loss Mechanisms in Piezoelectrics: How to Measure Different Losses Separately. IEEE-UFFC Trans. 2001, 48, 307–321. [Google Scholar] [CrossRef] [PubMed]
- Ural, S.; Park, S.; Priya, S.; Uchino, K. High Power Piezoelectric Transformers with Cofired Copper Electrodes—Part I. In Proceedings of the 10th International Conference New Actuators, Bremen, Germany, 14–16 June 2006; pp. 556–558. [Google Scholar]
- Shekhani, H.N.; Uchino, K. Characterization of Mechanical Loss in Piezoelectric Materials Using Temperature and Vibration Measurements. J. Am. Ceram. Soc. 2014, 97, 2810–2814. [Google Scholar] [CrossRef]
- Uchino, K. High Power Piezoelectric Materials. In Proceedings of the IEEE UFFC Distinguished Lectures, University of Mexico, Morelia, Mexico, 29 April–3 May 2019. [Google Scholar]
- Shekhani, H.N.; Gurdal, E.A.; Ganapatibhotla, L.; Maranas, J.K.; Staut, R.; Uchino, K. Thermal Conductivities of PZT Piezoelectric Ceramics under Different Electrical Boundary Conditions. J. Insight Mat. Sci. 2020, 3, 10–14. [Google Scholar] [CrossRef]
- Mitsui, T.; Tatsuzaki, T.; Nakamura, E. Ferroelectrics. In Related Substances, b)(LANDOLT-BORNSTEIN Numerical Data and Functional Relationships in Science and Technology, IIV16b; Springer: Berlin/Heidelberg, Germany, 1982; p. 1969. [Google Scholar]
- Devonshire, A.F. Theory of Barium Titanate. Philos. Mag. 1949, 40, 1040–1063. [Google Scholar] [CrossRef]
- Devonshire, A.F. Theory of Ferroelectrics. Adv. Phys. 1954, 3, 85–130. [Google Scholar] [CrossRef]
- Kay, H.F. Electrostriction. Rep. Prog. Phys. 1955, 43, 230. [Google Scholar] [CrossRef]
- Uchino, K. Ferroelectric Devices, 2nd ed.; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- Cooks, W.R., Jr.; Berlincourt, D.A.; Scholz, F.J. Thermal Expansion and Pyroelectricity in Lead Titanate Zirconate and Barium Titanate. J. Appl. Phys. 1963, 34, 1392. [Google Scholar] [CrossRef]
- Lang, S.B. Pyroelectric Thermometer for Use at Low Temperatures. Rev. Sci. Instr. 1969, 40, 274. [Google Scholar] [CrossRef]
- Lane, R.; Luff, D.; Brown, K.R.; Marshallsay, H.J. The variation of the pyroelectric coefficient with composition and phase structure for lead zirconate titanate ceramics. Trans. J. Br. Ceram. Soc. 1973, 72, 39. [Google Scholar]
- Lines, M.E.; Glass, A.M. Principles and Applications of Ferroelectrics and Related Materials; Clarendon Press: Oxford, UK, 1977. [Google Scholar]
- Physical and Piezoelectric Properties of APC Materials. Available online: https://www.americanpiezo.com/apc-materials/physical-piezoelectric-properties.html (accessed on 18 September 2011).
- Landau, L.D.; Khalatnikov, I.M. Collected Papers of Landau, L.D.; Haar, D.T., Ed.; Gordon & Breach: New York, NY, USA, 1965. [Google Scholar]
- Landau, L.D.; Khalatnikov, I.M. On the anomalous absorption of sound near a second order phase transition point. Dokladii Academii Nauk 1954, 96, 469–472. [Google Scholar]
- Pipes, L.A. Applied Mathematics for Engineers and Physicists, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1958. [Google Scholar]
- Yarlagadda, S.; Chan, M.; Lee, H.; Lesieutre, G.A.; Jensen, D.W.; Messer, R.S. Low temperature thermal conductivity, heat capacity, and heat generation of PZT. J. Intell. Mater. Syst. Struct. 1995, 6, 757–764. [Google Scholar] [CrossRef]
- Kallaev, S.N.; Gadzhiev, G.G.; Kamilov, I.K.; Omarov, Z.M.; Sadykov, S.A.; Reznichenko, L.A. Thermal properties of PZT-based ferroelectric ceramics. Phys. Solid State 2006, 48, 1169–1170. [Google Scholar] [CrossRef]
- Shekhani, H.N.; Uchino, K. Thermal diffusivity measurements using insulating and isothermal boundary conditions. Rev. Sci. Instrum. 2014, 85, 015117. [Google Scholar] [CrossRef]
- Gurdal, E.A.; Ural, S.O.; Park, H.Y.; Nahm, S.; Uchino, K. High Power Characterization Of (Na0.5K0.5)NbO3 Based Lead-Free Piezoelectric Ceramics. Sens. Actuators A Phys. 2013, 200, 44–46. [Google Scholar] [CrossRef]
- Hejazi, M.; Taghaddos, E.; Gurdal, E.; Uchino, K.; Safari, A. High Power Performance of Manganese-Doped BNT-Based Pb-Free Piezoelectric Ceramics. J. Am. Ceram. Soc. 2014, 97, 3192–3196. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; W.B. Saunders Co.: Orlando, FL, USA, 1976; ISBN 0-03-083993-9. [Google Scholar]
- Uchino, K.; Cross, L.E. Electrostriction and its Interrelation with Other Anharmonic Properties of Materials. Jpn. J. Appl. Phys. 1980, 19, L171–L173. [Google Scholar] [CrossRef]
- Born, M.; Göppert-Mayer, M. Handbuch der Physik; Springer: Berlin/Heidelberg, Germany, 1933; Volume 24, p. 623. [Google Scholar]
- Zhang, H.; Shang, S.L.; Wang, Y.; Saengdeejing, A.; Chen, L.Q.; Liu, Z.K. First-principles calculations of the elastic, phonon and thermodynamic properties of Al12Mg17. Acta Mater. 2010, 58, 4012–4018. [Google Scholar] [CrossRef]
- Ishii, K. Vibration and Eigenvalue Problem. Mod. Math. 1972, 5, 24–32. [Google Scholar]
- Pichanusakorn, P.; Bandaru, P. Nanostructured thermoelectrics. Mat. Sci. Eng. R. Rep. 2009, 67, 19–63. [Google Scholar] [CrossRef]
- Zheng, J.; Takahashi, S.; Yoshikawa, S.; Uchino, K.; de Vries, J.W.C. Heat Generation in Multilayer Piezoelectric Actuators. J. Am. Ceram. Soc. 1996, 79, 3193–3198. [Google Scholar] [CrossRef]
- Uchino, K.; Zheng, J.; Joshi, A.; Chen, Y.H.; Yoshikawa, S.; Hirose, S.; Takahashi, S.; de Vries, J.W.C. High Power Characterization of Piezoelectric Materials. J. Electroceram. 1998, 2, 33–40. [Google Scholar] [CrossRef]
- Tashiro, S.; Ikehiro, M.; Igarashi, H. Influence of temperature rise and vibration level on electromechanical properties of high-power piezoelectric ceramics. Jpn. J. Appl. Phys. 1997, 36, 3004–3009. [Google Scholar] [CrossRef]
- Uchino, K. Micromechatronics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2019; ISBN-13: 978-0-367-20231-6. [Google Scholar]
- Yuan, T.; Dong, X.; Shekhani, H.; Li, C.; Maida, Y.; Tou, T.; Uchino, K. Driving an inductive piezoelectric transducer with class E inverter. Sens. Actuators A Phys. 2017, A261, 219–227. [Google Scholar] [CrossRef]













| Hard PZT | Thermal Diffusivity (10−7 m2/s) | +/− | Specific Heat Capacity cp (J/kg K) | Thermal Conductivity (W/m K) | +/− |
|---|---|---|---|---|---|
| Unpoled | 4.32 | 0.34 | = 279 | 0.91 | 0.10 |
| Open Circuit | 5.02 | 0.23 | = 320 | 1.22 | 0.06 |
| Short Circuit | 8.25 | 0.78 | = 340 | 2.13 | 0.23 |
| Thermal Properties | cp (J/kg K) | λ (W/m/K) |
|---|---|---|
| Hard-PZT | 420 | 1.25 |
| NKN-Cu | 580 | 3.10 |
| Actuator | 4.5 × 3.5 × 2.0 mm3 | 7.0 × 7.0 × 2.0 mm3 | 17 × 3.5 × 1.0 mm3 |
|---|---|---|---|
| wT (kJ/m3) [] | 19.2 | 19.9 | 19.7 |
| P-E hysteresis loss (kJ/m3) | 18.5 | 17.8 | 17.4 |
| k(T) (W/m2 K) | 38.4 | 39.2 | 34.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uchino, K. Electrothermal Phenomena in Ferroelectrics. Actuators 2020, 9, 93. https://doi.org/10.3390/act9040093
Uchino K. Electrothermal Phenomena in Ferroelectrics. Actuators. 2020; 9(4):93. https://doi.org/10.3390/act9040093
Chicago/Turabian StyleUchino, Kenji. 2020. "Electrothermal Phenomena in Ferroelectrics" Actuators 9, no. 4: 93. https://doi.org/10.3390/act9040093
APA StyleUchino, K. (2020). Electrothermal Phenomena in Ferroelectrics. Actuators, 9(4), 93. https://doi.org/10.3390/act9040093





