Hierarchies and Dominance Behaviors in European Pond Turtle (Emys orbicularis galloitalica) Hatchlings in a Controlled Environment
Abstract
:Simple Summary
Abstract
1. Introduction
- Do hierarchies exist in same-age groups of European Pond Turtle hatchlings? Which are the most effective behaviors individuals adopt to establish and maintain hierarchies?
- If hierarchies are present in juvenile turtles, when does a group of individuals establishes such a hierarchy? Is this hierarchy stable over time? How steady is it?
- Is the rank of individuals related to one or more biometric parameters (e.g., size, weight)?
2. Materials and Methods
2.1. Rearing Set-Up
2.2. Biometric and Behavioral Data
2.3. Data Analyses
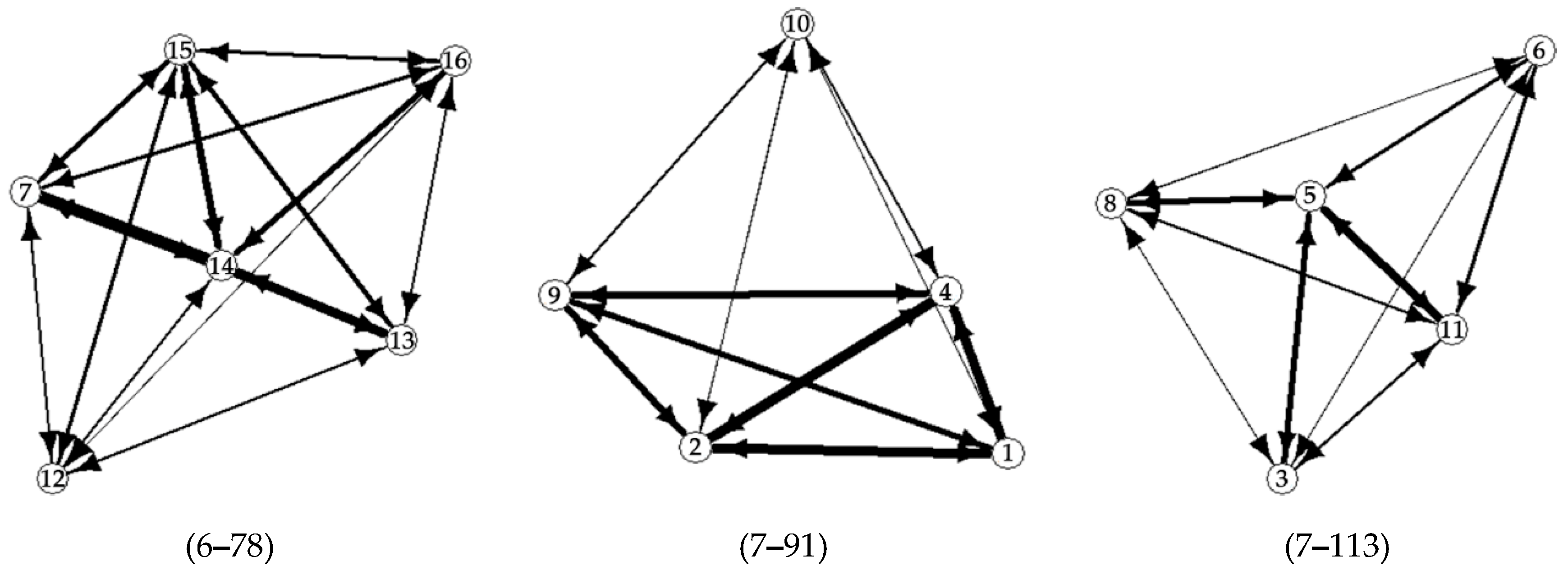
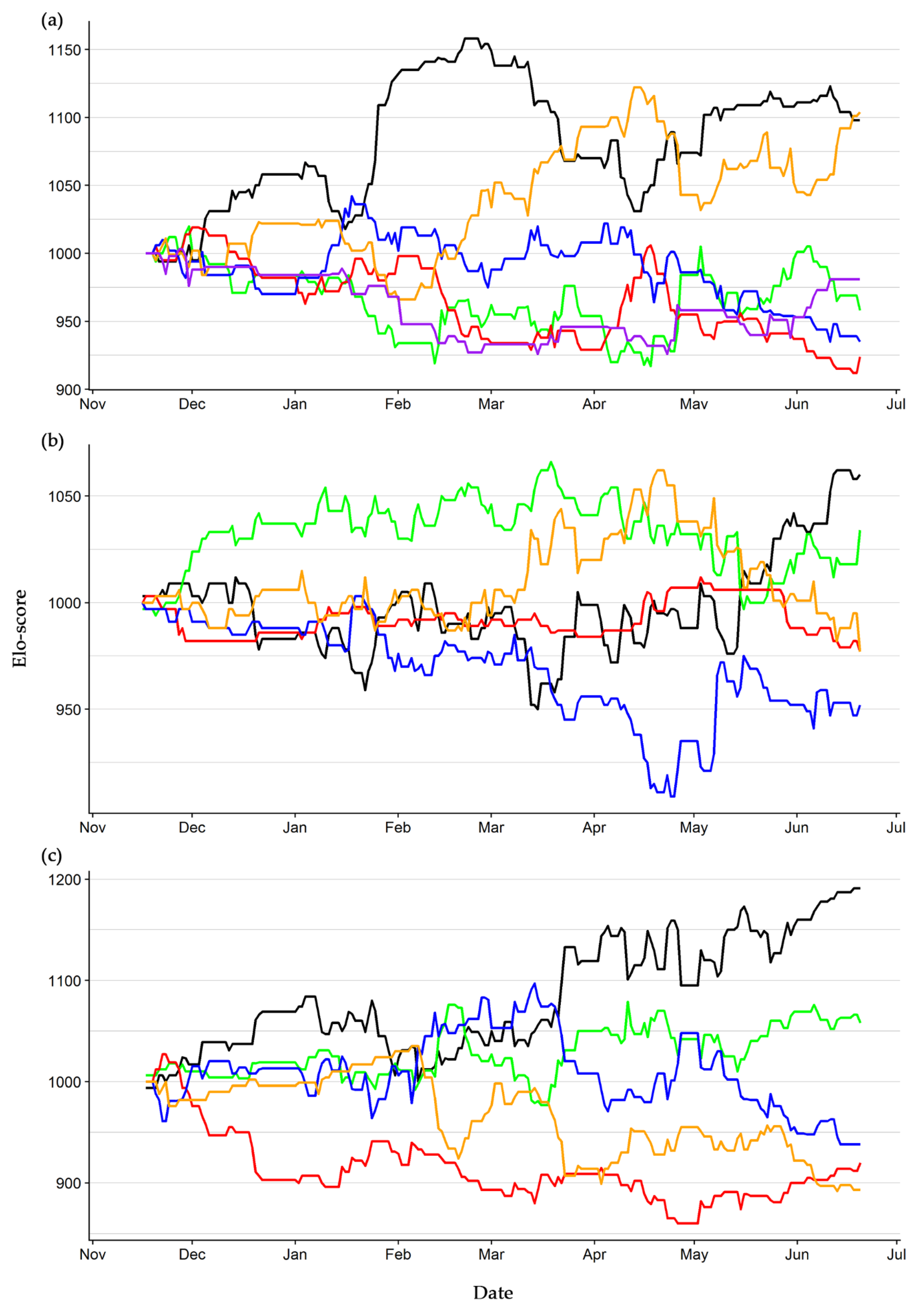
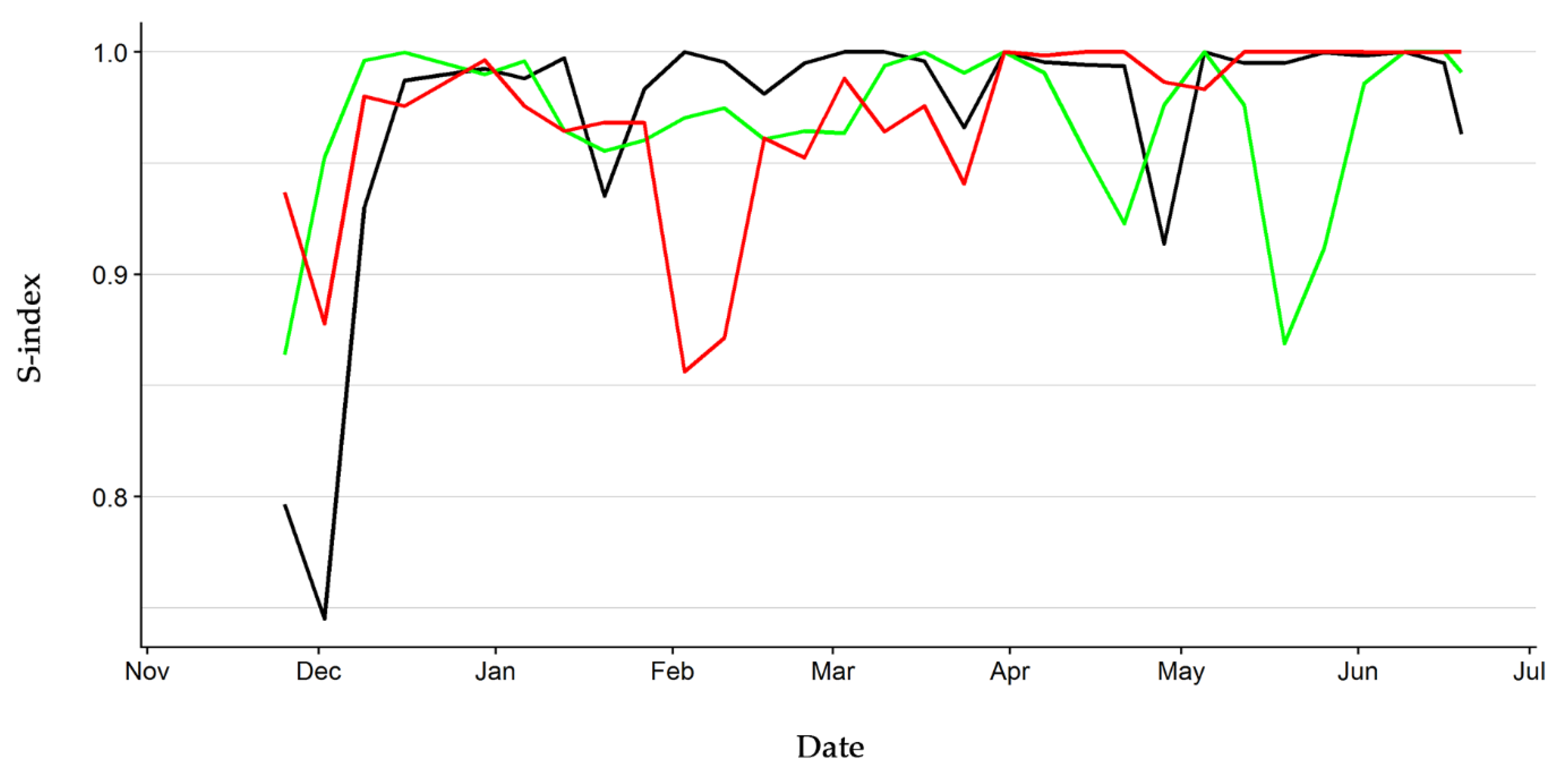
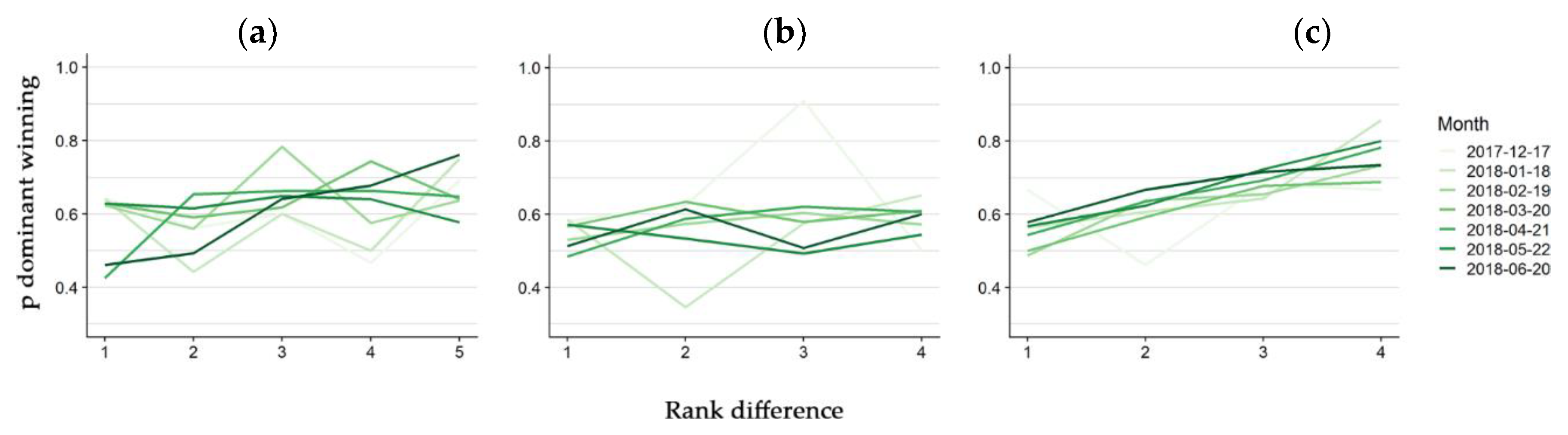
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doody, J.S.; Burghardt, G.M.; Dinets, V. Breaking the social-non-social dichotomy: A role for reptiles in vertebrate social behavior research? Ethology 2013, 119, 95–103. [Google Scholar] [CrossRef]
- Gardner, M.G.; Pearson, S.K.; Johnston, G.R.; Schwarz, M.P. Group living in squamate reptiles: A review of evidence for stable aggregations. Biol. Rev. 2015, 91, 925–936. [Google Scholar] [CrossRef] [PubMed]
- Burghardt, G.M.; Greene, H.W.; Rand, A.S. Social behavior in hatchling green iguanas-life at a reptile rookery. Science 1977, 195, 689–691. [Google Scholar] [CrossRef] [PubMed]
- Barker, D.G.; Murphy, J.B.; Smith, K.W. Social Behavior in a Captive Group of Indian Pythons, Python molurus (Serpentes, Boidae) with Formation of a Linear Social Hierarchy. Copeia 1979, 3, 466–471. [Google Scholar] [CrossRef]
- Gillingham, J.C.; Carpenter, C.C.; Murphy, J.B. Courtship, Male Combat and Dominance in the Western Diamondback Rattlesnake, Crotalus atrox. J. Herpetol. 1983, 17, 265–270. [Google Scholar] [CrossRef]
- Sinervo, B.; Lively, C.M. The rock-paper-scissors game and the evolution of alternative male strategies. Nature 1996, 380, 240–243. [Google Scholar] [CrossRef]
- Gilman, C.A.; Corl, A.; Sinervo, B.; Irschick, D.J. Genital Morphology associated with mating strategy in the polimorphic lizard, Uta stansburiana. J. Morphol. 2019, 280, 184–192. [Google Scholar] [CrossRef]
- Lardie, R.L. Aggressive interactions and territoriality in the yellow mud turtle, Kinosternon flavescens flavescens (Agassiz). Bull. Okla. Herpretol. Soc. 1983, 8, 68–81. [Google Scholar]
- Rovero, F.; Lebboroni, M.; Chelazzi, G. Aggressive interactions and mating in wild populations of the European pond turtle, Emys orbicularis. J. Herpetol. 1999, 33, 258–263. [Google Scholar] [CrossRef]
- Rodrigues, J.F.M.; Liu, Y. An overview of same-sex mounting in turtles and tortoises. J. Ethol. 2016, 34, 133–137. [Google Scholar] [CrossRef]
- Cox, N.A.; Temple, H.J. European Red List of Reptiles; Office for Official Publications of the European Communities: Luxembourg, 2009. [Google Scholar]
- Rondinini, C.; Battistoni, A.; Peronace, V.; Teofili, C. Lista Rossa IUCN dei Vertebrati Italiani; Comitato Italiano IUCN e Ministero dell’Ambiente e della Tutela del Territorio e del Mare: Roma, Italy, 2013. [Google Scholar]
- Sánchez-Tójar, A.; Schroeder, J.; Farine, D.R. A practical guide for inferring reliable dominance hierarchies and estimating their uncertainty. J. Anim. Ecol. 2018, 87, 594–608. [Google Scholar] [CrossRef] [PubMed]
- Neumann, C.; McDonald, D.B.; Shizuka, D. Dominance ranks, dominance ratings and linear hierarchies: A critique. Anim. Behav. 2018, 144, e1–e16. [Google Scholar] [CrossRef]
- Strauss, E.D.; Holekamp, K.E. Inferring longitudinal hierarchies: Framework and methods for studying the dynamics of dominance. J. Anim. Ecol. 2019, 88, 521–536. [Google Scholar] [CrossRef] [PubMed]
- Albers, P.C.H.; de Vries, H. Elo-rating as a tool in the sequential estimation of dominance strengths. Anim. Behav. 2001, 61, 489–495. [Google Scholar] [CrossRef] [Green Version]
- Lemoine, S.; Preis, A.; Samuni, L.; Boesch, C.; Crockford, C.; Wittig, R.M. Between-Group Competition Impacts Reproductive Success in Wild Chimpanzees. Curr. Biol. 2020, 30, 312–318. [Google Scholar] [CrossRef] [Green Version]
- Moyers, S.C.; Adelman, J.S.; Farine, D.R.; Moore, I.T.; Hawley, D.M. Exploratory behavior is linked to stress physiology and social network centrality in free-living house finches (Haemorhous mexicanus). Horm. Behav. 2018, 102, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Carvalho, R.R.; Palme, R.; da Vasconcellos, A.S. An integrated analysis of social stress in laying hens: The interaction between physiology, behaviour, and hierarchy. Behav. Process. 2018, 149, 43–51. [Google Scholar] [CrossRef]
- Tong, X.; Shen, C.; Chen, R.; Gao, S.; Liu, X.; Schinckel, A.P.; Zhou, B. Reestablishment of Social Hierarchies in Weaned Pigs after Mixing. Animals 2020, 10, 36. [Google Scholar] [CrossRef] [Green Version]
- Neumann, C.; Duboscq, J.; Dubuc, C.; Ginting, A.; Irwan, A.M.; Agil, M.; Widdig, A.; Engelhardt, A. Assessing dominance hierarchies: Validation and advantages of progressive evaluation with Elo-rating. Anim. Behav. 2011, 82, 911–921. [Google Scholar] [CrossRef]
- Franz, M.; McLean, E.; Tung, J.; Altmann, J.; Alberts, S.C. Self-Organizing Dominance Hierarchies in a Wild Primate Population. Proc. R. Soc. B Biol. Sci. 2015, 282, 20151512. [Google Scholar] [CrossRef]
- Neumann, C.; Kulik, L. EloRating: Animal Dominance Hierarchies by Elo Rating, R Package Version 0.46.10. 2019. Available online: https://CRAN.R-project.org/package=EloRating (accessed on 25 August 2020).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- McDonald, D.B.; Shizuka, D. Comparative Transitive and Temporal Orderliness in Dominance Networks. Behav. Ecol. 2013, 24, 511–520. [Google Scholar] [CrossRef] [Green Version]
- Farine, D.R.; Sánchez-Tójar, A. aniDom: Inferring Dominance Hierarchies and Estimating Uncertainty, R Package Version 0.1.3. 2018. Available online: https://CRAN.R-project.org/package=aniDom (accessed on 25 August 2020).
- Halliday, T.R.; Verrell, P.A. Body Size and Age in Amphibians and Reptiles. J. Herpetol. 1988, 22, 253–265. [Google Scholar] [CrossRef]
- Scott, R.; Marsh, R.; Hays, G.C. Life in the really slow lane: Loggerhead sea turtles mature late relative to other reptiles. Funct. Ecol. 2012, 26, 227–235. [Google Scholar] [CrossRef]
- Patnaik, B.K. Ageing in reptiles. Gerontology 1994, 40, 200–220. [Google Scholar] [CrossRef] [PubMed]
- Massot, M.; Clobert, J.; Montes-Poloni, L.; Haussy, C.; Cubo, J.; Meylan, S. An integrative study of ageing in a wild population of common lizards. Funct. Ecol. 2011, 25, 848–858. [Google Scholar] [CrossRef]
- Bjorndal, K.A.; Parsons, J.; Mustin, W.; Bolten, A.B. Threshold to maturity in a long-lived reptile: Interactions of age, size, and growth. Mar. Biol. 2013, 160, 607–616. [Google Scholar] [CrossRef]
- Sacerdote-Velat, A.B.; Earnhardt, J.M.; Mulkerin, D.; Boehm, D.; Glowacki, G. Evaluation of headstarting and release techniques for population augmentation and reintroduction of the smooth green snake. Anim. Conserv. 2014, 17, 65–73. [Google Scholar] [CrossRef]
- Kuznetsova, A.; Brockhoff, P.B.; Christensen, R.H.B. lmerTest Package: Tests in Linear Mixed Effects Models. J. Stat. Softw. 2017, 82, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Boice, R. Competitive feeding behaviours in captive Terrapene c. carolina. Anim. Behav. 1970, 18, 703–710. [Google Scholar] [CrossRef]
- Froese, A.D.; Burghardt, G.M. Food competition in captive juvenile snapping turtles, Chelydra serpentine. Anim. Behav. 1974, 22, 735–740. [Google Scholar] [CrossRef]
- Rogers, L.J.; Astiningsih, K. Social hierarchies in very young chicks. Br. Poult. Sci. 1991, 32, 47–56. [Google Scholar] [CrossRef] [PubMed]
- Rajecki, D.W.; Nerenz, D.R.; Hoff, S.J.; Newman, E.R.; Volbrecht, V.J. Early development of aggression in chickens: The relative importance of pecking and leaping. Behav. Process. 1981, 6, 239–248. [Google Scholar] [CrossRef]
- Mench, J.A. The development of aggressive behavior in male broiler chicks: A comparison with laying-type males and the effects of feed restriction. Appl. Anim. Behav. Sci. 1988, 21, 233–242. [Google Scholar] [CrossRef]
- Chase, I.D.; Tovey, C.; Spangler-Martin, D.; Manfredonia, M. Individual differences versus social dynamics in the formation of animal dominance hierarchies. Proc. Natl. Acad. Sci. USA 2002, 99, 5744–5749. [Google Scholar] [CrossRef] [Green Version]
- Bush, J.M.; Quinn, M.M.; Balreira, E.C.; Johnson, M.A. How do lizards determine dominance? Applying ranking algorithms to animal social behavior. Anim. Behav. 2016, 118, 65–74. [Google Scholar] [CrossRef] [Green Version]
- Mitrus, S.; Najbar, B.; Kotowicz, A.; Najbar, A. The body size of headstarted and wild juvenile European pond turtles (Emys orbicularis). Russ. J. Herpetol. 2018, 25, 161–164. [Google Scholar] [CrossRef]
- Mitrus, S. Headstarting in European pond turtles (Emys orbicularis): Does it work? Amphib. Reptil. 2005, 26, 333–341. [Google Scholar] [CrossRef]
- Goffe, A.S.; Fischer, J.; Sennhenn-Reulen, H. Bayesian inference and simulation approaches improve the assessment of Elo-ratings in the analysis of social behaviour. Methods Ecol. Evol. 2018, 9, 2131–2144. [Google Scholar] [CrossRef]
- Burke, R.L. Head-starting turtles: Learning from experience. Herpetol. Conserv. Biol. 2015, 10, 299–308. [Google Scholar]
- Bennett, A.M.; Steiner, J.; Carstairs, S.; Gielens, A.; Davy, C.M. A question of scale: Replication and the effective evaluation of conservation interventions. Facets 2017, 2, 892–909. [Google Scholar] [CrossRef] [Green Version]
- Cadi, A.; Joly, P. Competition for basking places between the endangered European pond turtle (Emys orbicularis galloitalica) and the introduced red-eared slider (Trachemys scripta elegans). Can. J. Zool. 2003, 81, 1392–1398. [Google Scholar] [CrossRef] [Green Version]
- Polo-Cavia, N.; López, P.; Martín, J. Competitive interactions during basking between native and invasive freshwater turtle species. Biol. Invasions 2010, 12, 2141–2152. [Google Scholar] [CrossRef]
- Polo-Cavia, N.; López, P.; Martín, J. Aggressive interactions during feeding between native and invasive freshwater turtles. Biol. Invasions 2011, 13, 1387–1396. [Google Scholar] [CrossRef]

| Group | Intercept | SCL Difference | SD of Random Effect | |||||
|---|---|---|---|---|---|---|---|---|
| Value | SE | p-Value | β | SE | p-Value | Intercept | SCL Difference | |
| 1 | −1.70 | 21.77 | 0.941 | −26.92 | 3.49 | <0.001 | 52.95 | 1.48 |
| 2 | 7.61 | 16.41 | 0.667 | 31.72 | 12.89 | 0.068 | 36.34 | 26.95 |
| 3 | −10.36 | 36.96 | 0.793 | −97.94 | 10.22 | <0.001 | 82.27 | 5.12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masin, S.; Bani, L.; Vardanega, D.; Chiodini, N.; Orioli, V. Hierarchies and Dominance Behaviors in European Pond Turtle (Emys orbicularis galloitalica) Hatchlings in a Controlled Environment. Animals 2020, 10, 1510. https://doi.org/10.3390/ani10091510
Masin S, Bani L, Vardanega D, Chiodini N, Orioli V. Hierarchies and Dominance Behaviors in European Pond Turtle (Emys orbicularis galloitalica) Hatchlings in a Controlled Environment. Animals. 2020; 10(9):1510. https://doi.org/10.3390/ani10091510
Chicago/Turabian StyleMasin, Simone, Luciano Bani, Davide Vardanega, Norberto Chiodini, and Valerio Orioli. 2020. "Hierarchies and Dominance Behaviors in European Pond Turtle (Emys orbicularis galloitalica) Hatchlings in a Controlled Environment" Animals 10, no. 9: 1510. https://doi.org/10.3390/ani10091510
APA StyleMasin, S., Bani, L., Vardanega, D., Chiodini, N., & Orioli, V. (2020). Hierarchies and Dominance Behaviors in European Pond Turtle (Emys orbicularis galloitalica) Hatchlings in a Controlled Environment. Animals, 10(9), 1510. https://doi.org/10.3390/ani10091510






