An Illustrative Analysis of Atypical Gas Production Profiles Obtained from In Vitro Digestibility Studies Using Fecal Inoculum
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets and Gas Production Technique
2.2. Curve Smoothing
2.3. Mathematical Considerations
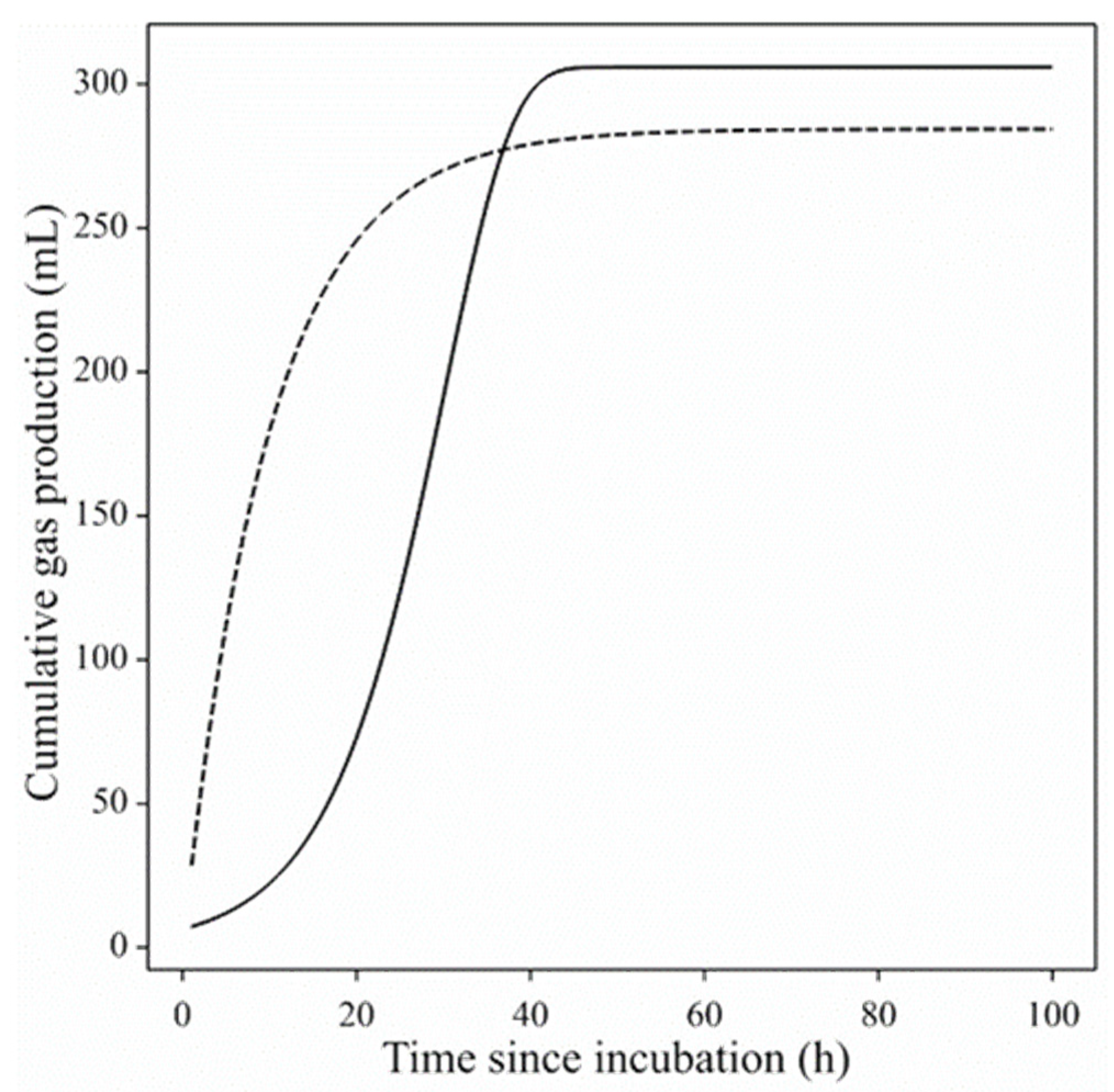
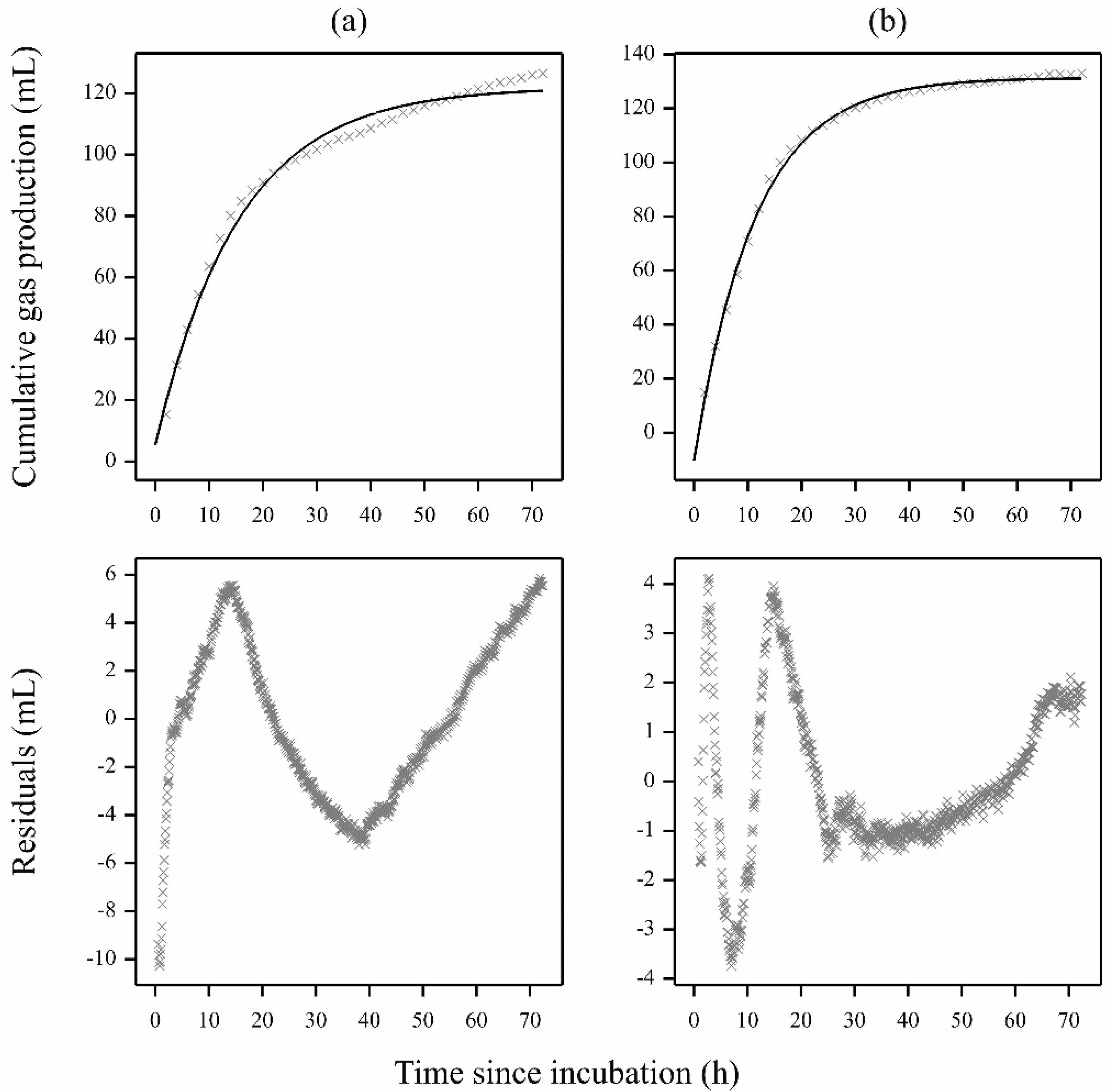
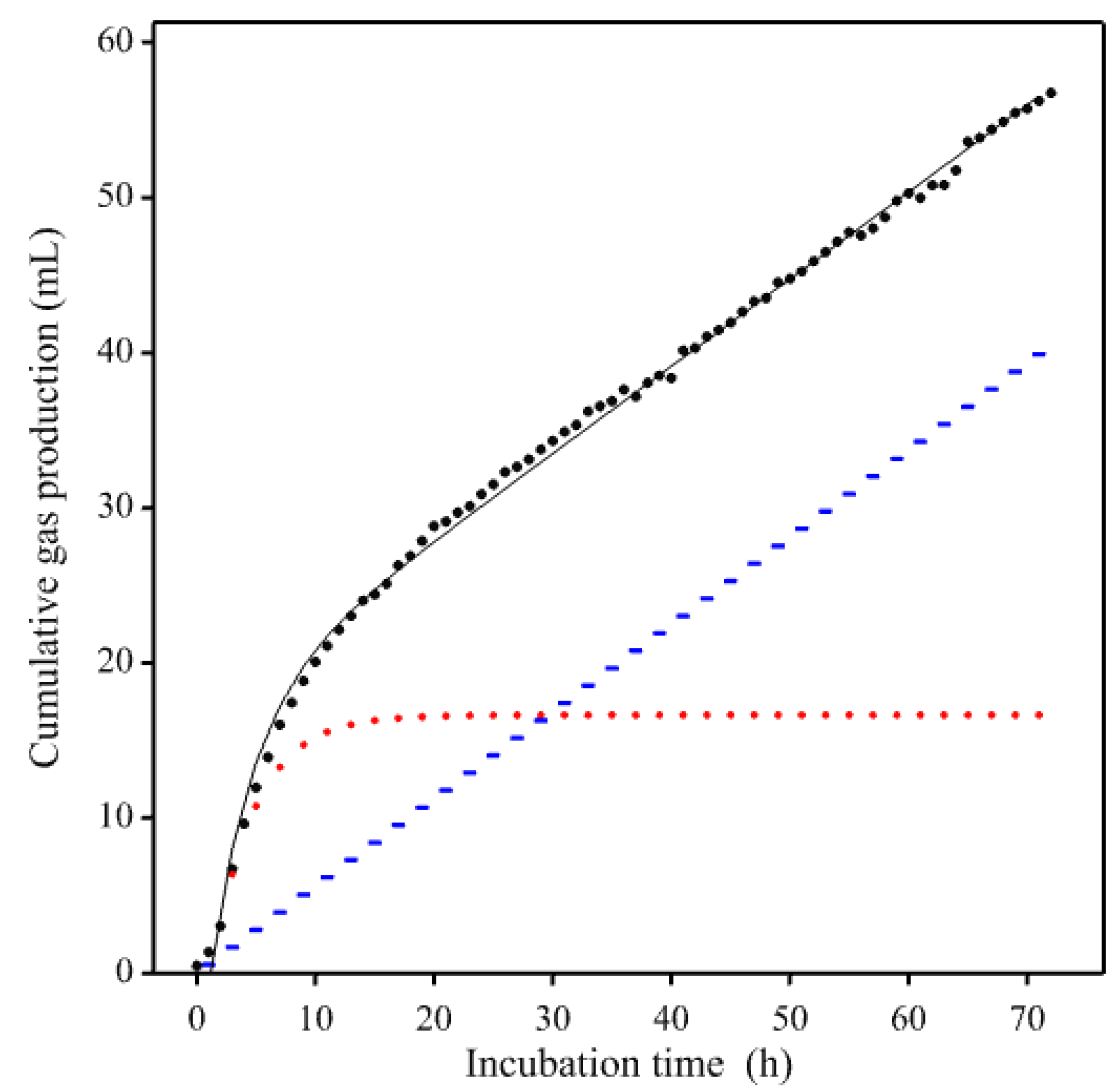
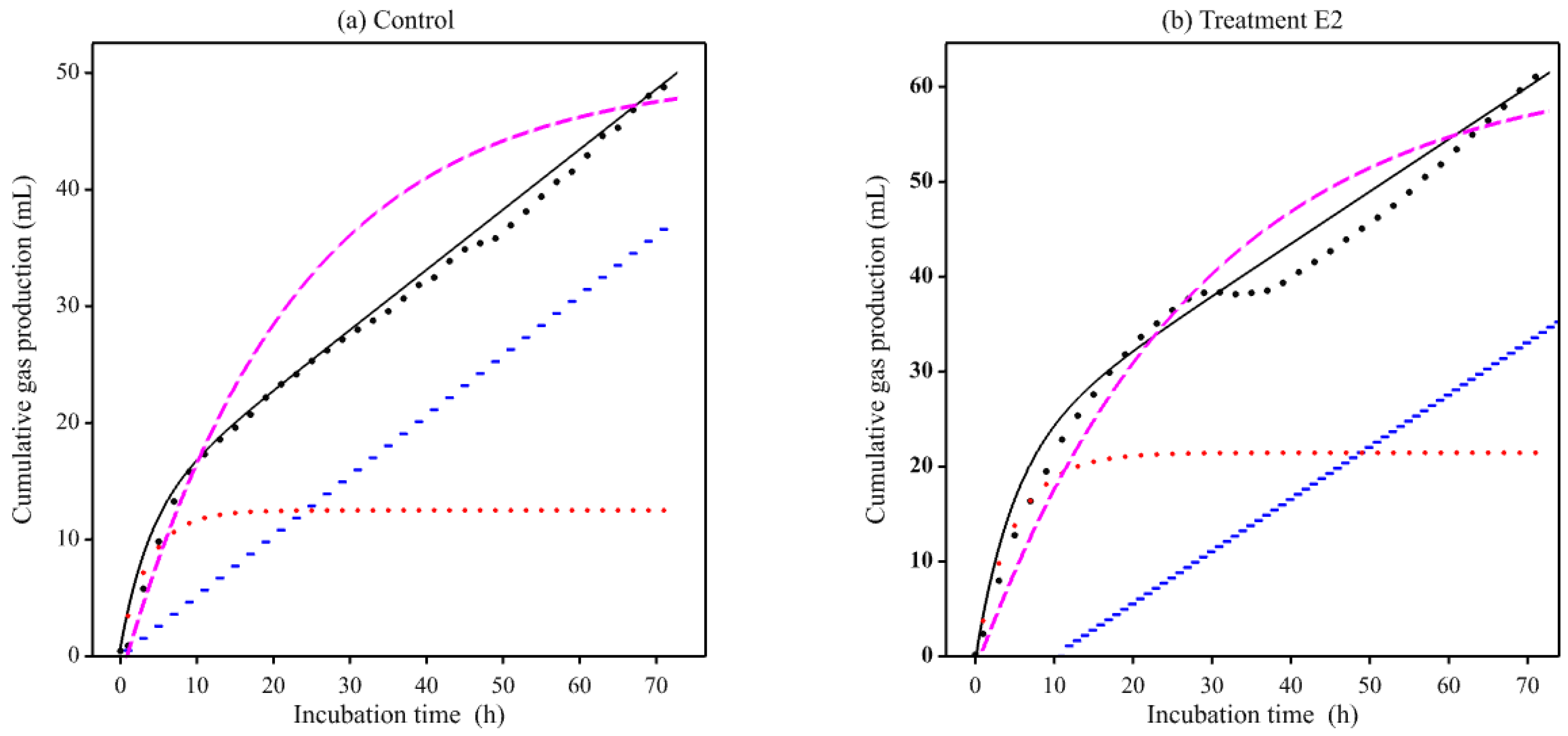
3. Results
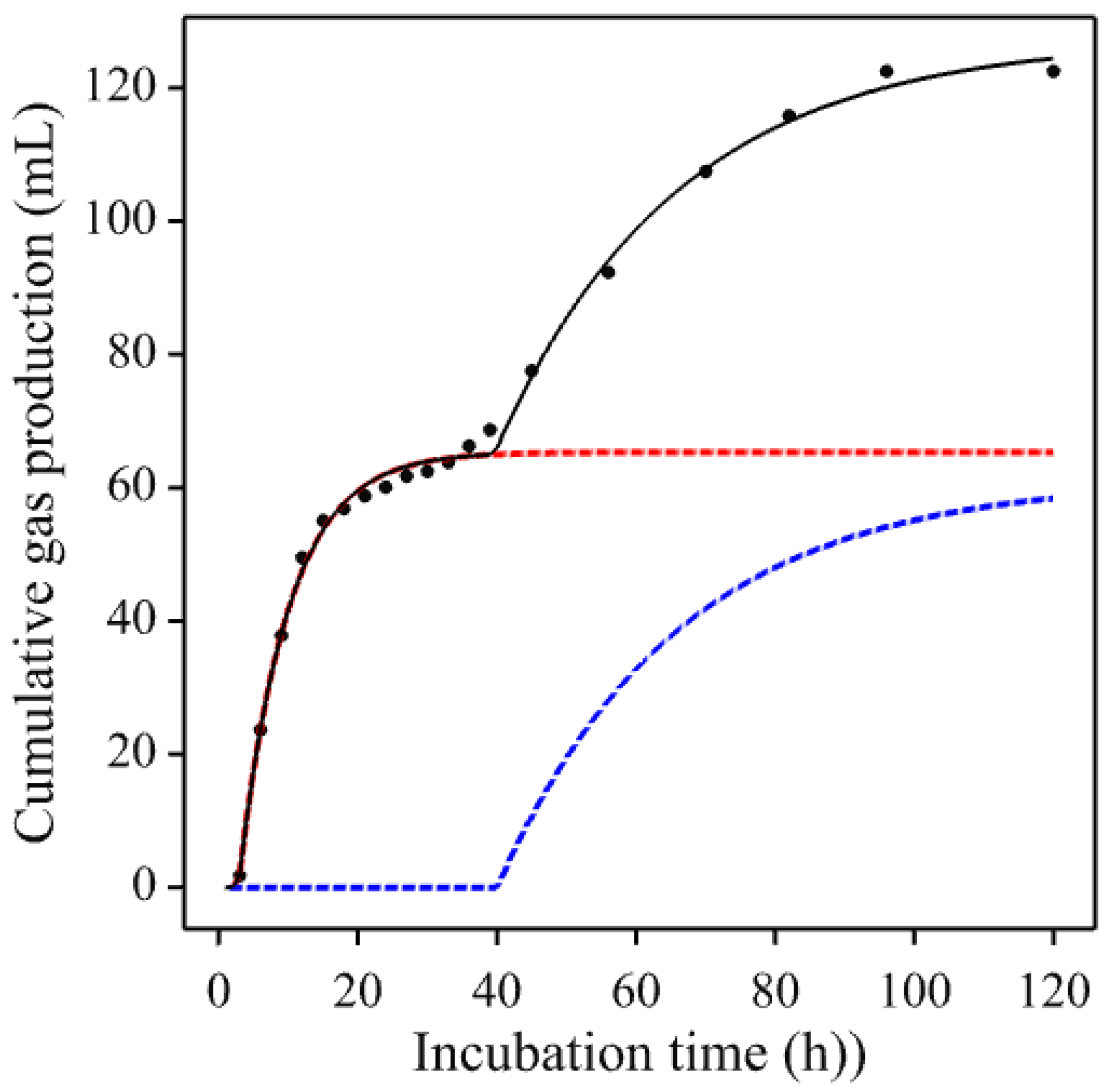
3.1. Gas Production Curves Using Porcine Fecal Inocula
3.2. Gas Production Curves Using Equine Fecal Inocula
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Williams, B.A.; Bosch, M.W.; Boer, H.; Verstegen, M.W.A.; Tamminga, S. An in vitro batch culture method to assess potential fermentability of feed ingredients for monogastric diets. Anim. Feed Sci. Technol. 2005, 123–124, 445–462. [Google Scholar] [CrossRef]
- Dhanoa, M.S.; France, J.; Crompton, L.A.; Mauricio, R.M.; Kebreab, E.; Mills, J.A.N.; Sanderson, R.; Dijkstra, J.; López, S. Technical note: A proposed method to determine the extent of degradation of a feed in the rumen from the degradation profile obtained with the in vitro gas production technique using feces as the inoculum. J. Anim. Sci. 2004, 82, 733–746. [Google Scholar] [CrossRef]
- El-Meadaway, A.; Mir, Z.; Mir, P.S.; Zaman, M.S.; Yanke, L.J. Relative efficacy of inocula from rumen fluid or faecal solution for determining in vitro digestibility and gas production. Can. J. Anim. Sci. 1998, 78, 673–679. [Google Scholar] [CrossRef]
- Mauricio, R.M.; Owen, E.; Mould, F.L.; Givens, I.; Theodorou, M.K.; France, J.; Davies, D.R.; Dhanoa, M.S. Comparison of bovine rumen liquor and bovine faeces as inoculum for an in vitro gas production technique for evaluating forages. Anim. Feed Sci. Technol. 2001, 89, 33–48. [Google Scholar] [CrossRef]
- Groot, J.C.J.; Cone, J.W.; Williams, B.A.; Debersaques, F.M.A.; Lantinga, E.A. Multiphasic analysis of gas production kinetics for in vitro fermentation of ruminant feeds. Anim. Feed Sci. Technol. 1996, 64, 77–89. [Google Scholar] [CrossRef]
- Cone, J.W.; Van Gelder, A.H.; Driehuis, F. Description of gas production profiles with a three-phasic model. Anim. Feed Sci. Technol. 1997, 66, 31–45. [Google Scholar] [CrossRef]
- López, S.; Dijkstra, J.; Dhanoa, M.S.; Bannink, A.; Kebreab, E.; France, J. A generic multi-stage compartmental model for interpreting gas production profiles. In Modelling Nutrient Digestion and Utilisation in Farm Animals; Sauvant, D., Van Milgen, J., Faverdin, P., Friggens, N., Eds.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2011; pp. 139–147. [Google Scholar]
- Powell, C.D.; Dhanoa, M.S.; Garber, A.; Murray, J.-A.M.D.; López, S.; Ellis, J.L.; France, J. Models based on the Mitscherlich equation for describing typical and atypical gas production profiles obtained from in vitro digestibility studies using equine faecal inoculum. Animals 2020, 10, 308. [Google Scholar] [CrossRef] [Green Version]
- Menke, K.; Steingass, H. Estimation of the energetic feed value obtained from chemical analysis and in vitro gas production using rumen fluid. Anim. Res. Dev. 1988, 28, 7–55. [Google Scholar]
- Mauricio, R.M.; Mould, F.L.; Dhanoa, M.S.; Owen, E.; Channa, K.S.; Theodorou, M.K. A semi-automated in vitro gas production technique for ruminant feedstuff evaluation. Anim. Feed Sci. Technol. 1999, 79, 321–330. [Google Scholar] [CrossRef]
- Theodorou, M.K.; Williams, B.A.; Dhanoa, M.S.; McAllan, A.B.; France, J. A simple gas production method using a pressure transducer to determine the fermentation kinetics of ruminant feeds. Anim. Feed Sci. Technol. 1994, 48, 185–197. [Google Scholar] [CrossRef]
- ANKOM. Gas Production System–Operator’s Manual; Ankom Technology: Macedon, NY, USA, 2015. [Google Scholar]
- Mould, F.L.; Mauricio, R.M.; Owen, E. Cumulative and rate of gas release profiles of pure carbohydrates fermented in vitro using the Reading Pressure Technique. In Gas Production: Fermentation Kinetics for Feed Evaluation and to Assess Microbial Activity; Deaville, E.R., Williams, B.A., Cone, J., Eds.; British Society for Animal Science: Edinburgh, Scotland, 2000; pp. 27–28. [Google Scholar]
- France, J.; Dhanoa, M.S.; Theodorou, M.K.; Lister, S.J.; Davies, D.R.; Isac, D. A model to interpret gas accumulation profiles asssociated with in vitro degradation of ruminant feeds. J. Theor. Biol. 1993, 163, 99–111. [Google Scholar] [CrossRef]
- Widaningrum; Flanagan, B.M.; Williams, B.A.; Sonni, F.; Mikkelsen, D.; Gidley, M.J. Fruit and vegetable insoluble dietary fibre in vitro fermentation characteristics depend on cell wall type. Bioact. Carbohydr. Diet. Fibre 2020, 23, 100223. [Google Scholar] [CrossRef]
- Widaningrum; Flanagan, B.M.; Williams, B.A.; Sonni, F.; Chen, P.; Mikkelsen, D.; Gidley, M.J. Fermentation profiles of undigested fractions from legumes and nuts are distinctly affected by plant cell wall architecture. Unpublished work. 2021. [Google Scholar]
- Yang, H.J.; Zhuang, H.; Meng, X.K.; Zhang, D.F.; Cao, B.H. Effect of melamine on in vitro r+umen microbial growth, methane production and fermentation of Chinese wild rye hay and maize meal in binary mixtures. J. Agric. Sci. 2014, 152, 686–696. [Google Scholar] [CrossRef]
- Murray, J.-A.M.D.; Scott, B.; Hastie, P.M. Fermentative capacity of equine faecal inocula obtained from clinically normal horses and those predisposed to laminitis. Anim. Feed Sci. Technol. 2009, 151, 306–311. [Google Scholar] [CrossRef]
- Garber, A.; Hastie, P.M.; Farci, V.; Bulmer, L.; Alzahal, O.; Murray, J.M.D. The effect of supplementing pony diets with yeast on 1. In vivo and in vitro digestibility, faecal pH and particle size. Animal 2020, 14, 2481–2492. [Google Scholar] [CrossRef] [PubMed]
- Ramsay, J.O. Monotone regression splines in action. Stat. Sci. 1988, 3, 425–441. [Google Scholar] [CrossRef]
- Thornley, J.H.M.; France, J. Mathematical Models in Agriculture: Quantitative Methods for the Plant, Animal and Ecological Sciences; CAB International: Wallingford, UK, 2007; ISBN 9780851990101. [Google Scholar]
- Mitscherlich, E.A. Das gesetz des minimums und das gesetz des abnehmenden bodenertrages. Landwirtsch. Jahrbücher 1909, 38, 537–552. [Google Scholar]
- VSN International. Genstat for Windows, 18th ed.; VSN International: Hemel Hempstead, UK, 2015. [Google Scholar]
- Dunne, A. An iterative curve stripping technique for pharmacokinetic parameter estimation. J. Pharm. Pharmacol. 1986, 38, 97–101. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.I.-K. A concordance correlation coefficient to evaluate reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef]
- Davies, O.L. Statistical Methods in Research and Production; Oliver and Boyd: Edinburgh, Scotland; London, UK, 1967. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- López, S.; Dhanoa, M.S.; Dijkstra, J.; Bannink, A.; Kebreab, E.; France, J. Some methodological and analytical considerations regarding application of the gas production technique. Anim. Feed Sci. Technol. 2007, 135, 139–156. [Google Scholar] [CrossRef]
- López, S. In vitro and in situ techniques for estimating digestibility. In Quantitative Aspects of Ruminant Digestion and Metabolism; Dijkstra, J., Forbes, J.M., France, J., Eds.; CAB International: Wallingford, UK, 2005; pp. 87–212. [Google Scholar]
- Rymer, C.; Huntington, J.A.; Williams, B.A.; Givens, D.I. In vitro cumulative gas production techniques: History, methodological considerations and challenges. Anim. Feed Sci. Technol. 2005, 123–124, 9–30. [Google Scholar] [CrossRef]
- Mould, F.L.; Kliem, K.E.; Morgan, R.; Mauricio, R.M. In vitro microbial inoculum: A review of its function and properties. Anim. Feed Sci. Technol. 2005, 123–124, 31–50. [Google Scholar] [CrossRef]
- Nielsen, B.B.; Zhu, W.-Y.; Dhanoa, M.S.; Trinci, A.P.; Theodorou, M.K. Comparison of the growth kinetics of anaerobic gut fungi on wheat straw in batch culture. Anaerobe 2002, 8, 216–222. [Google Scholar] [CrossRef] [Green Version]
- Lowman, R.S.; Theodorou, M.K.; Hyslop, J.J.; Dhanoa, M.S.; Cuddeford, D. Evaluation of an in vitro batch culture technique for estimating the in vivo digestibility and digestible energy content of equine feeds using equine faeces as the source of microbial inoculum. Anim. Feed Sci. Technol. 1999, 80, 11–27. [Google Scholar] [CrossRef]
- Holter, P. Concentration of oxygen, carbon dioxide and methane in the air within dung pats. Pedobiologia 1991, 35, 381–386. [Google Scholar]
- Van Weyenberg, S.; Sales, J.; Janssens, G.P.J. Passage rate of digesta through the equine gastrointestinal tract: A review. Livest. Sci. 2006, 99, 3–12. [Google Scholar] [CrossRef]
- Dhanoa, M.S.; Siddons, R.C.; France, J.; Gale, D.L. A multicompartmental model to describe marker excretion patterns in ruminant faeces. Br. J. Nutr. 1985, 53, 663–671. [Google Scholar] [CrossRef] [Green Version]
- Santos, A.S.; Rodrigues, M.; Bessa, R.; Ferreira, L.M.; Martin-rosset, W. Understanding the equine cecum-colon ecosystem: Current knowledge and future perspectives. Animal 2011, 5, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Garber, A.; Hastie, P.M.; Farci, V.; McGuinness, D.; Bulmer, L.; Alzahal, O.; Murray, J.M.D. The effect of supplementing pony diets with yeast on 2. The faecal microbiome. Animal 2020, 14, 2493–2502. [Google Scholar] [CrossRef]
- Schofield, P. Gas production methods. In Farm Animal Metabolism and Nutrition; D’Mello, J.P.F., Ed.; CABI Publishing: Wallingford, UK, 2000; pp. 209–232. [Google Scholar]
- France, J.; Dijkstra, J.; Dhanoa, M.S.S.; López, S.; Bannink, A. Estimating the extent of degradation of ruminant feeds from a description of their gas production profiles observed in vitro: Derivation of models and other mathematical considerations. Br. J. Nutr. 2000, 83, 143–150. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Residual SD § | (%) § | Runs Test | Concordance * | SD Ratio † | |
|---|---|---|---|---|---|
| (a) Equation (7) | |||||
| Mean | 5.94 | 96.1 | 7.7 | 0.989 | 2.294 |
| Median | 4.93 | 96.7 | 7 | 0.991 | 1.754 |
| Minimum | 3.15 | 85.7 | 6 | 0.955 | 1.152 |
| Range | 16.95 | 13.1 | 5 | 0.041 | 6.459 |
| q1§ | 3.59 | 96.1 | 7 | 0.987 | 1.443 |
| q3§ | 6.03 | 98.1 | 8.25 | 0.995 | 2.888 |
| SEM § | 0.864 | 0.688 | 0.326 | 0.002 | 0.318 |
| (b) Equation (8) | |||||
| Mean | 2.75 | 99.0 | 8.7 | 0.997 | 0.542 |
| Median | 2.33 | 99.4 | 8 | 0.998 | 0.570 |
| Minimum | 1.80 | 97.2 | 7 | 0.990 | 0.131 |
| Range | 4.11 | 2.70 | 5 | 0.0096 | 0.737 |
| q1§ | 1.99 | 98.3 | 7 | 0.995 | 0.347 |
| q3§ | 3.06 | 99.6 | 10.25 | 0.998 | 0.693 |
| SEM § | 0.237 | 0.164 | 0.380 | 0.0006 | 0.045 |
| Equation (2) | Equation (4) | Equation (5) | Equation (6) | Equation (7) | Equation (8) | ||
|---|---|---|---|---|---|---|---|
| Parameters | 4 | 3 | 6 | 5 | 6 | 5 | |
| RMSE § | |||||||
| Mean | 5.97 | 6.35 | 4.80 | 4.59 | 1.92 | 4.13 | |
| Median | 6.34 | 6.96 | 4.64 | 4.94 | 2.06 | 4.46 | |
| Minimum | 1.73 | 2.18 | 2.33 | 0.76 | 0.43 | 0.95 | |
| Maximum | 10.74 | 9.10 | 8.37 | 6.70 | 3.64 | 7.09 | |
| § | |||||||
| Mean | 94.6 | 94.0 | 96.3 | 97.0 | 99.3 | 97.5 | |
| Median | 95.4 | 94.6 | 97.1 | 97.0 | 99.6 | 97.4 | |
| Minimum | 83.8 | 86.7 | 90.2 | 94.0 | 97.3 | 93.0 | |
| Maximum | 99.0 | 98.3 | 98.5 | 99.8 | 99.9 | 99.7 | |
| AIC § | |||||||
| Mean | 70.6 | 72.8 | 66.8 | 55.0 | 20.0 | 51.7 | |
| Median | 72.4 | 75.3 | 63.9 | 63.5 | 30.8 | 59.6 | |
| Minimum | 36.5 | 50.0 | 49.1 | −13.8 | −47.8 | −0.15 | |
| Maximum | 92.4 | 85.4 | 98.0 | 75.1 | 52.3 | 77.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhanoa, M.S.; López, S.; Powell, C.D.; Sanderson, R.; Ellis, J.L.; Murray, J.-A.M.D.; Garber, A.; Williams, B.A.; France, J. An Illustrative Analysis of Atypical Gas Production Profiles Obtained from In Vitro Digestibility Studies Using Fecal Inoculum. Animals 2021, 11, 1069. https://doi.org/10.3390/ani11041069
Dhanoa MS, López S, Powell CD, Sanderson R, Ellis JL, Murray J-AMD, Garber A, Williams BA, France J. An Illustrative Analysis of Atypical Gas Production Profiles Obtained from In Vitro Digestibility Studies Using Fecal Inoculum. Animals. 2021; 11(4):1069. https://doi.org/10.3390/ani11041069
Chicago/Turabian StyleDhanoa, Mewa S., Secundino López, Christopher D. Powell, Ruth Sanderson, Jennifer L. Ellis, Jo-Anne M. D. Murray, Anna Garber, Barbara A. Williams, and James France. 2021. "An Illustrative Analysis of Atypical Gas Production Profiles Obtained from In Vitro Digestibility Studies Using Fecal Inoculum" Animals 11, no. 4: 1069. https://doi.org/10.3390/ani11041069
APA StyleDhanoa, M. S., López, S., Powell, C. D., Sanderson, R., Ellis, J. L., Murray, J.-A. M. D., Garber, A., Williams, B. A., & France, J. (2021). An Illustrative Analysis of Atypical Gas Production Profiles Obtained from In Vitro Digestibility Studies Using Fecal Inoculum. Animals, 11(4), 1069. https://doi.org/10.3390/ani11041069







