Comparison of Single-Breed and Multi-Breed Training Populations for Infrared Predictions of Novel Phenotypes in Holstein Cows
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics Approval
2.2. Data
2.3. Infrared Milk Spectra
2.4. Design of the Cross-Validation (CV) Populations
2.5. Statistical Method
2.6. Assessment of Model Performance
3. Results
3.1. Phenotypic and FTIR Spectra Information
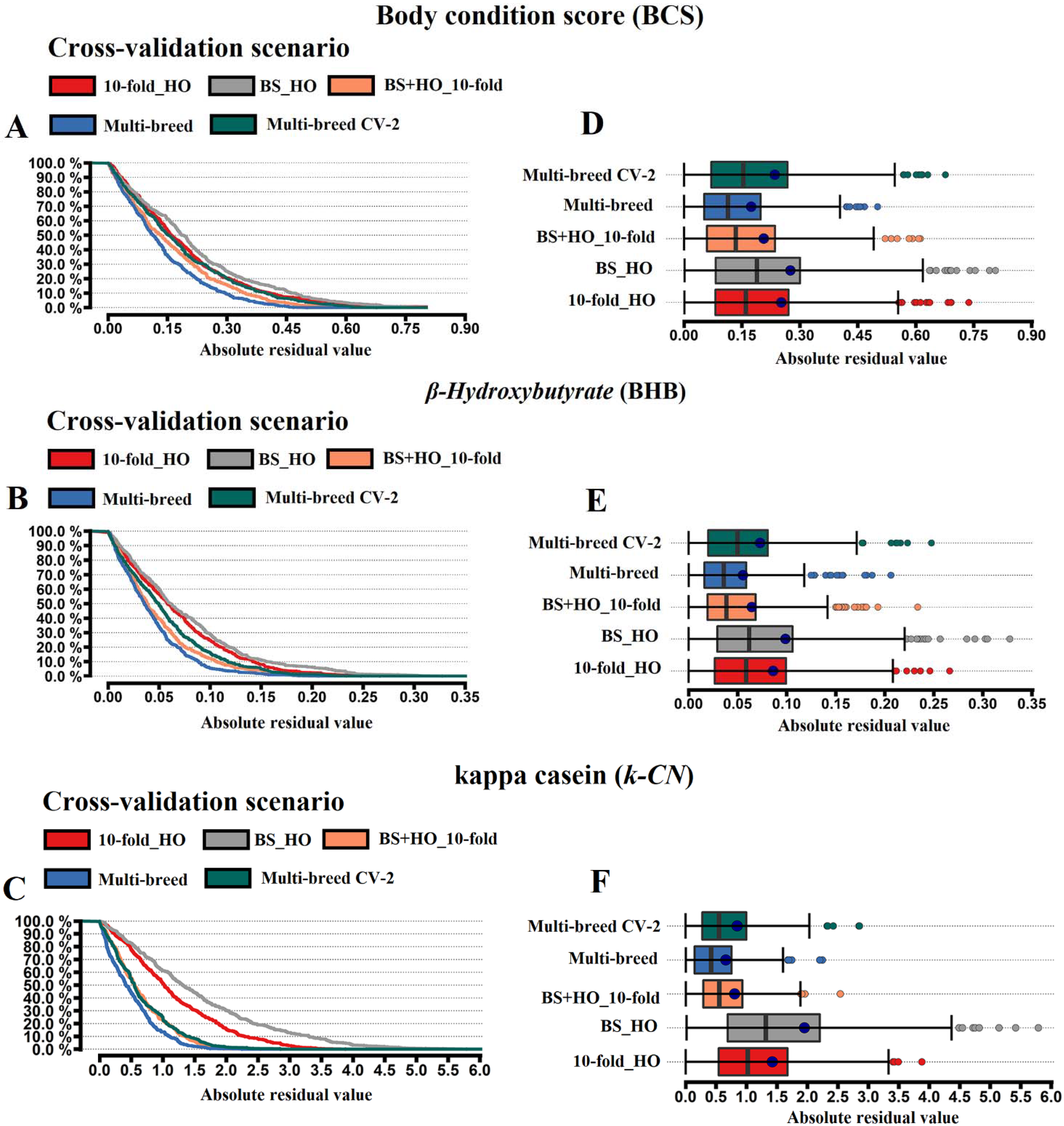
3.2. Cross-Validation Scenarios
3.3. Bias and Predictive Error Parameters of the Cross-Validation Scenarios
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Faghihzadeh, F.; Anaya, N.M.; Schifman, L.A.; Oyanedel-Craver, V. Fourier transform infrared spectroscopy to assess molecular-level changes in microorganisms exposed to nanoparticles. Nanotechnol. Environ. Eng. 2016, 1, 1–16. [Google Scholar] [CrossRef]
- Soyeurt, H.; Dehareng, F.; Gengler, N.; McParland, S.; Wall, E.; Berry, D.P.; Coffey, M.; Dardenne, P. Mid-infrared prediction of bovine milk fatty acids across multiple breeds, production systems, and countries. J. Dairy Sci. 2011, 94, 1657–1667. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonfatti, V.; Degano, L.; Menegoz, A.; Carnier, P. Mid-infrared spectroscopy prediction of fine milk composition and technological properties in Italian Simmental. J. Dairy Sci. 2016, 99, 8216–8221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Bovenhuis, H. Validation strategy can result in an overoptimistic view of the ability of milk infrared spectra to predict methane emission of dairy cattle. J. Dairy Sci. 2019, 102, 6288–6295. [Google Scholar] [CrossRef] [PubMed]
- McParland, S.; Berry, D. The potential of Fourier transform infrared spectroscopy of milk samples to predict energy intake and efficiency in dairy cows. J. Dairy Sci. 2016, 99, 4056–4070. [Google Scholar] [CrossRef]
- Tiplady, K.M.; Lopdell, T.J.; Littlejohn, M.D.; Garrick, D.J. The evolving role of Fourier-transform mid-infrared spectroscopy in genetic improvement of dairy cattle. J. Anim. Sci. Biotechnol. 2020, 11, 39. [Google Scholar] [CrossRef] [PubMed]
- Iheshiulor, O.O.M.; Woolliams, J.A.; Yu, X.; Wellmann, R.; Meuwissen, T.H.E. Within- and across-breed genomic prediction using whole-genome sequence and single nucleotide polymorphism panels. Genet. Sel. Evol. 2016, 48, 15. [Google Scholar] [CrossRef] [Green Version]
- Van den Berg, I.; Meuwissen, T.; MacLeod, I.; Goddard, M. Predicting the effect of reference population on the accuracy of within, across, and multibreed genomic prediction. J. Dairy Sci. 2019, 102, 3155–3174. [Google Scholar] [CrossRef] [Green Version]
- Hozé, C.; Fritz, S.; Phocas, F.; Boichard, D.; Ducrocq, V.; Croiseau, P. Efficiency of multi-breed genomic selection for dairy cattle breeds with different sizes of reference population. J. Dairy Sci. 2014, 97, 3918–3929. [Google Scholar] [CrossRef] [Green Version]
- Jónás, D.; Ducrocq, V.; Fritz, S.; Baur, A.; Sanchez, M.P.; Croiseau, P. Genomic evaluation of regional dairy cattle breeds in single-breed and multibreed contexts. J. Anim. Breed. Genet. 2017, 134, 3–13. [Google Scholar] [CrossRef]
- Cecchinato, A.; Bobbo, T.; Ruegg, P.L.; Gallo, L.; Bittante, G.; Pegolo, S. Genetic variation in serum protein pattern and blood β-hydroxybutyrate and their relationships with udder health traits, protein profile, and cheese-making properties in Holstein cows. J. Dairy Sci. 2018, 101, 11108–11119. [Google Scholar] [CrossRef] [Green Version]
- Stocco, G.; Cipolat-Gotet, C.; Bobbo, T.; Cecchinato, A.; Bittante, G. Breed of cow and herd productivity affect milk composition and modeling of coagulation, curd firming, and syneresis. J. Dairy Sci. 2017, 100, 129–145. [Google Scholar] [CrossRef]
- Edmonson, A.J.; Lean, I.J.; Weaver, L.D.; Farver, T.; Webster, G. A Body Condition Scoring Chart for Holstein Dairy Cows. J. Dairy Sci. 1989, 72, 68–78. [Google Scholar] [CrossRef]
- Maurmayr, A.; Cecchinato, A.; Grigoletto, L.; Bittante, G. Detection and quantification of αS1-, αS2-, β-, κ-casein, α-lactalbumin, β-lactoglobulin and lactoferrin in bovine milk by reverse-phase high- performance liquid chromatography. Agric. Conspec. Sci. 2013, 78, 201–205. [Google Scholar]
- D’Amico, A.; Natale, C.D.; Castro, F.L.; Iarossi, S.; Catini, A.; Martinelli, E. Volatile compounds detection by IR acousto-optic detectors. NATO Sci. Peace Secur. Ser. B Phys. Biophys. 2009, 21–59. [Google Scholar]
- Shah, N.K.; Gemperline, P.J. A program for calculating Mahalanobis distances using principal component analysis. Trends Anal. Chem. 1989, 8, 357–361. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference and Prediction; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 1–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mota, L.F.M.; Pegolo, S.; Baba, T.; Peñagaricano, F.; Morota, G.; Bittante, G.; Cecchinato, A. Evaluating the performance of machine learning methods and variable selection methods for predicting difficult-to-measure traits in Holstein dairy cattle using milk infrared spectral data. J. Dairy Sci. 2021, 104, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting. Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Montesinos-López, A.; Pérez-Rodríguez, P.; Barrón-López, J.A.; Martini, J.W.R.; Fajardo-Flores, S.B.; Gaytan-Lugo, L.S.; Santana-Mancilla, P.C.; Crossa, J. A review of deep learning applications for genomic selection. BMC Genomics 2021, 22, 19. [Google Scholar] [CrossRef]
- Dunn, O.J.; Clark, V. Comparison of Tests of the Equality of Dependent Correlation Coefficients. J. Am. Stat. Assoc. 1971, 66, 904. [Google Scholar] [CrossRef]
- Zou, G.Y. Toward Using Confidence Intervals to Compare Correlations. Psychol. Methods 2007, 12, 399–413. [Google Scholar] [CrossRef]
- Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 89, 225–247. [Google Scholar] [CrossRef]
- Cecchinato, A.; de Marchi, M.; Gallo, L.; Bittante, G.; Carnier, P. Mid-infrared spectroscopy predictions as indicator traits in breeding programs for enhanced coagulation properties of milk. J. Dairy Sci. 2009, 92, 5304–5313. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McParland, S.; Banos, G.; McCarthy, B.; Lewis, E.; Coffey, M.P.; O’Neill, B.; O’Donovan, M.; Wall, E.; Berry, D.P. Validation of mid-infrared spectrometry in milk for predicting body energy status in Holstein-Friesian cows. J. Dairy Sci. 2012, 95, 7225–7235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maurice-Van Eijndhoven, M.H.T.; Soyeurt, H.; Dehareng, F.; Calus, M.P.L. Validation of fatty acid predictions in milk using mid-infrared spectrometry across cattle breeds. Animal 2013, 7, 348–354. [Google Scholar] [CrossRef] [Green Version]
- Roberts, D.R.; Bahn, V.; Ciuti, S.; Boyce, M.S.; Elith, J.; Guillera-Arroita, G.; Hauenstein, S.; Lahoz-Monfort, J.J.; Schröder, B.; Thuiller, W.; et al. Cross-validation strategies for data with temporal, spatial, hierarchical, or phylogenetic structure. Ecography 2017, 40, 913–929. [Google Scholar] [CrossRef]
- Rutten, M.J.M.; Bovenhuis, H.; van Arendonk, J.A.M. The effect of the number of observations used for Fourier transform infrared model calibration for bovine milk fat composition on the estimated genetic parameters of the predicted data. J. Dairy Sci. 2010, 93, 4872–4882. [Google Scholar] [CrossRef] [Green Version]
- Cecchinato, A.; Toledo-Alvarado, H.; Pegolo, S.; Rossoni, A.; Santus, E.; Maltecca, C.; Bittante, G.; Tiezzi, F. Integration of Wet-Lab Measures, Milk Infrared Spectra, and Genomics to Improve Difficult-to-Measure Traits in Dairy Cattle Populations. Front. Genet. 2020, 11. [Google Scholar] [CrossRef] [PubMed]


| Breed | N | Mean 1 | SD | Min | Max |
|---|---|---|---|---|---|
| BCS | |||||
| Holstein | 460 | 2.81 c | 0.324 | 2.00 | 3.75 |
| Brown Swiss | 646 | 2.96 b | 0.339 | 2.00 | 4.00 |
| Simmental | 154 | 3.06 a | 0.342 | 2.50 | 4.00 |
| Rendena | 99 | 2.97 ab | 0.346 | 2.00 | 3.75 |
| Alpine Grey | 73 | 3.07 ab | 0.342 | 2.50 | 4.00 |
| β-hydroxybutyrate (BHB, mmol/L) | |||||
| Holstein | 449 | 0.55 bc | 0.163 | 0.22 | 1.01 |
| Brown Swiss | 620 | 0.58 b | 0.136 | 0.32 | 1.03 |
| Simmental | 155 | 0.62 a | 0.146 | 0.34 | 1.01 |
| Rendena | 97 | 0.53 c | 0.112 | 0.32 | 0.90 |
| Alpine Grey | 73 | 0.56 bc | 0.109 | 0.33 | 0.87 |
| Kappa casein (k-CN, % N) | |||||
| Holstein | 392 | 13.73 c | 2.151 | 8.27 | 20.15 |
| Brown Swiss | 520 | 16.13 a | 1.632 | 11.31 | 21.40 |
| Simmental | 93 | 14.25 b | 1.386 | 9.83 | 17.80 |
| Rendena | 95 | 14.53 b | 2.219 | 8.89 | 19.55 |
| Alpine Grey | 68 | 15.34 b | 1.882 | 10.60 | 20.18 |
| Trait | Model Fit 1 | Validation Strategies for Holstein Prediction 2 | ||||
|---|---|---|---|---|---|---|
| 10-fold_HO | BS_HO | BS+HO_10-fold | Multi-Breed | Multi-Breed CV2 | ||
| BCS | 0.63 (0.023) b | 0.57 c | 0.66 (0.025) ab | 0.68 (0.022) a | 0.63 (0.036) b | |
| RD (%) | − | −9.52 | 4.76 (0.025) | 7.94 (0.022) | −0.47 (0.036) | |
| MPE | −1.54 (0.882) | −3.33 | 0.84 (0.869) | 0.70 (0.664) | −1.05 (0.904) | |
| RMSE | 0.25 (0.017) | 0.28 | 0.25 (0.019) | 0.23 (0.015) | 0.27 (0.031) | |
| slope | 1.07 (0.030) | 1.15 | 0.97 (0.029) | 0.99 (0.023) | 1.10 (0.093) | |
| BHB | 0.80 (0.023) bc | 0.75 c | 0.85 (0.027) ab | 0.87 (0.025) a | 0.79 (0.035) bc | |
| RD (%) | − | −7.41 | 4.94 (0.027) | 7.41 (0.025) | −1.23 (0.035) | |
| MPE | −0.96 (2.085) | 2.29 | −0.62 (2.033) | −0.39 (0.851) | 0.89 (1.046) | |
| RMSE | 0.09 (0.009) | 0.10 | 0.08 (0.009) | 0.07 (0.006) | 0.09 (0.010) | |
| slope | 1.03 (0.026) | 0.94 | 1.05 (0.028) | 1.00 (0.021) | 0.97 (0.033) | |
| k-CN | 0.81 (0.025) b | 0.76 c | 0.87 (0.022) ab | 0.88 (0.023) a | 0.82 (0.076) b | |
| RD (%) | − | −11.25 | 8.75 (0.022) | 9.99 (0.023) | 2.47 (0.076) | |
| MPE | −6.82 (3.356) | −21.09 | −5.33 (3.061) | −2.94 (1.983) | 3.56 (2.851) | |
| RMSE | 1.08 (0.052) | 1.42 | 0.96 (0.036) | 0.84 (0.027) | 1.01 (0.107) | |
| slope | 1.06 (0.034) | 1.21 | 1.08 (0.039) | 1.00 (0.029) | 0.95 (0.059) | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mota, L.F.M.; Pegolo, S.; Baba, T.; Morota, G.; Peñagaricano, F.; Bittante, G.; Cecchinato, A. Comparison of Single-Breed and Multi-Breed Training Populations for Infrared Predictions of Novel Phenotypes in Holstein Cows. Animals 2021, 11, 1993. https://doi.org/10.3390/ani11071993
Mota LFM, Pegolo S, Baba T, Morota G, Peñagaricano F, Bittante G, Cecchinato A. Comparison of Single-Breed and Multi-Breed Training Populations for Infrared Predictions of Novel Phenotypes in Holstein Cows. Animals. 2021; 11(7):1993. https://doi.org/10.3390/ani11071993
Chicago/Turabian StyleMota, Lucio Flavio Macedo, Sara Pegolo, Toshimi Baba, Gota Morota, Francisco Peñagaricano, Giovanni Bittante, and Alessio Cecchinato. 2021. "Comparison of Single-Breed and Multi-Breed Training Populations for Infrared Predictions of Novel Phenotypes in Holstein Cows" Animals 11, no. 7: 1993. https://doi.org/10.3390/ani11071993
APA StyleMota, L. F. M., Pegolo, S., Baba, T., Morota, G., Peñagaricano, F., Bittante, G., & Cecchinato, A. (2021). Comparison of Single-Breed and Multi-Breed Training Populations for Infrared Predictions of Novel Phenotypes in Holstein Cows. Animals, 11(7), 1993. https://doi.org/10.3390/ani11071993








