Assessing Population Trends of Species with Imperfect Detection: Double Count Analyses and Simulations Confirm Reliable Estimates in Brown Frogs
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
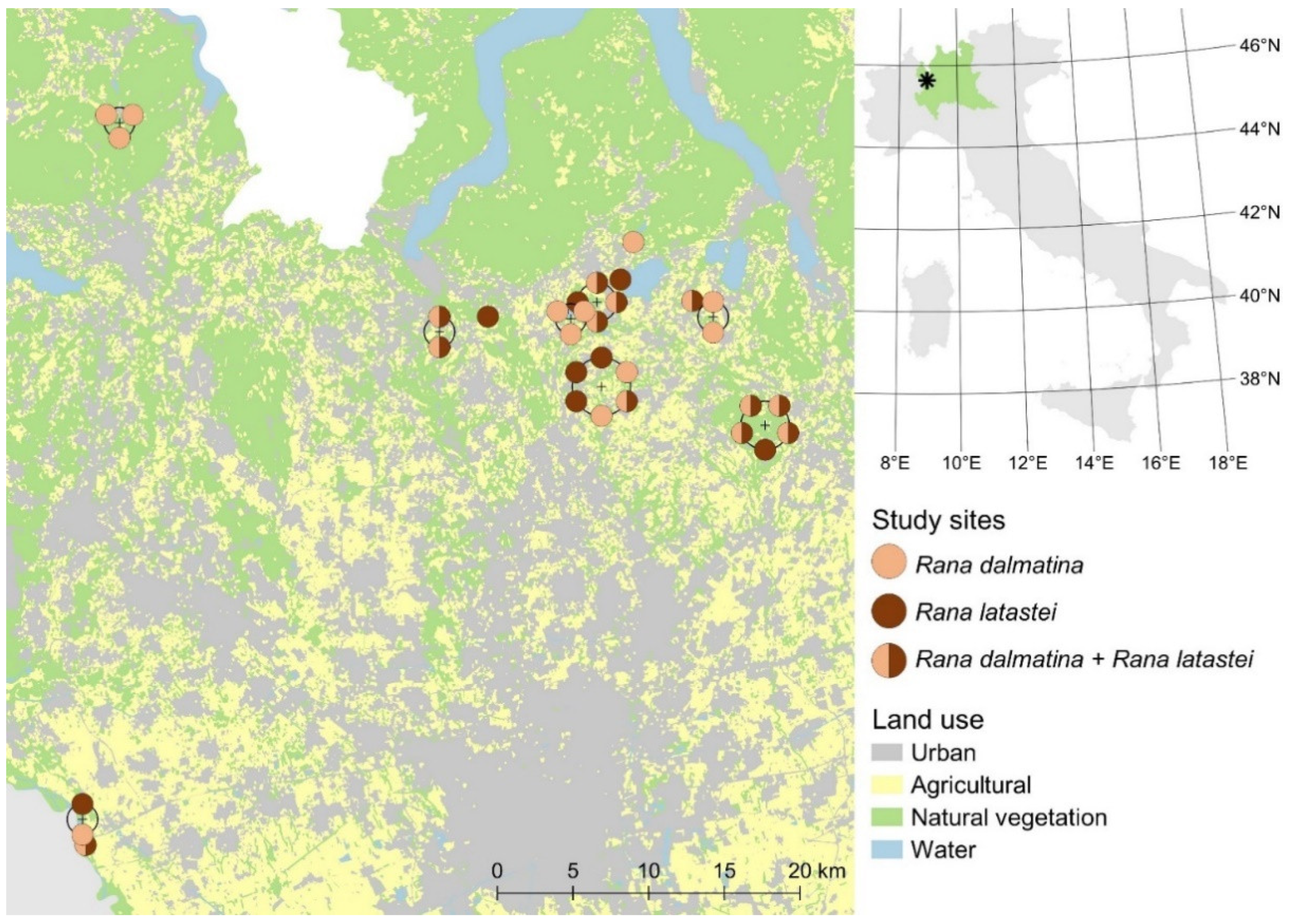
2.1. Study System
2.2. Estimating Detection Probability of Egg Clutches
2.3. Simulation of Population Declines
3. Results
3.1. Detection Probability of Egg Clutches
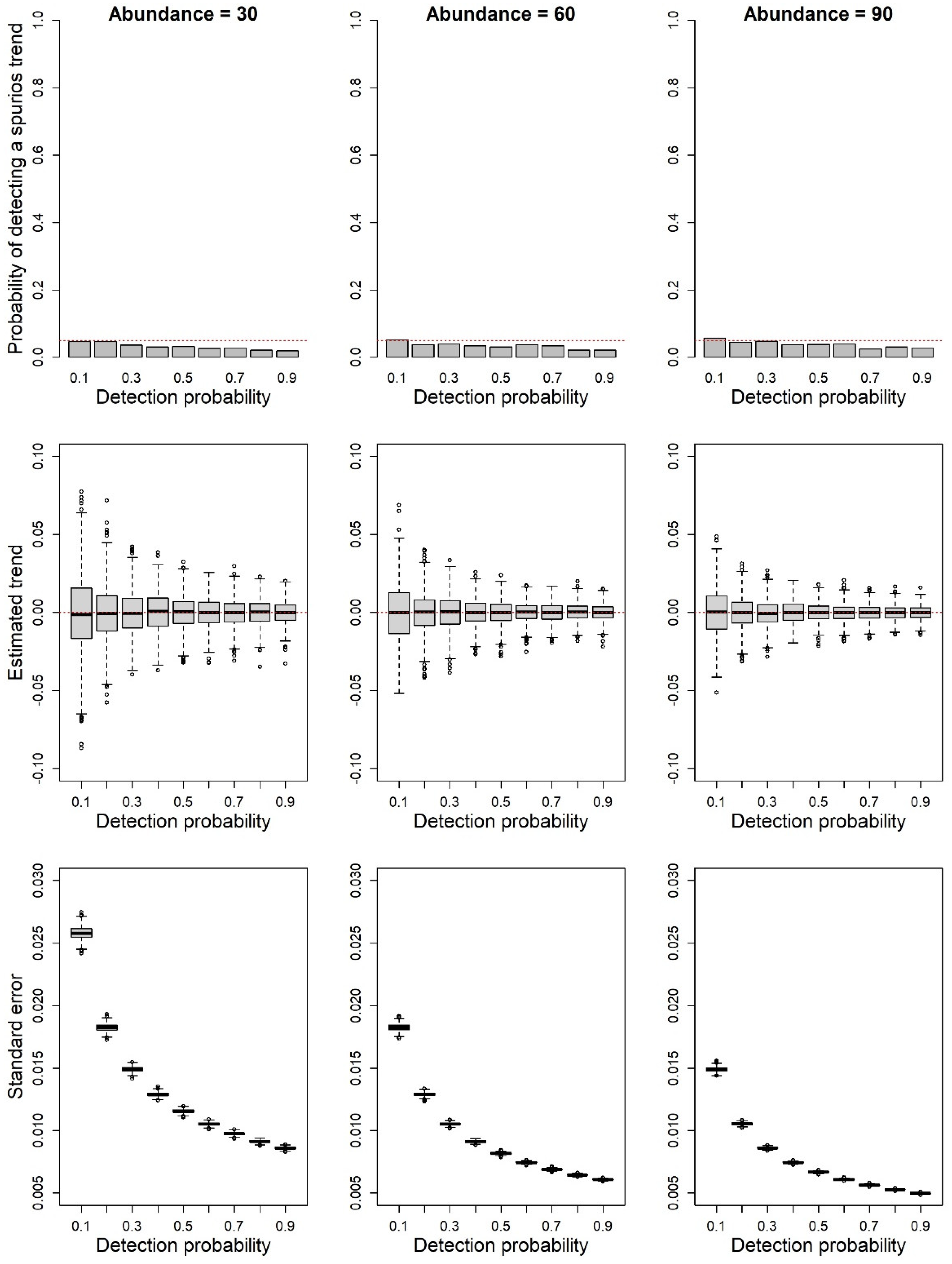
3.2. Analyses of Simulated Population Trend Data at Different Levels of Detection Probability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Site | Randal1 | Randal2 | Ranlat1 | Ranlat2 |
|---|---|---|---|---|
| 1 | 0 | 1 | ||
| 2 | 1 | 0 | ||
| 3 | 13 | 2 | 3 | 0 |
| 4 | 2 | 0 | ||
| 5 | 5 | 1 | ||
| 6 | 1 | 0 | ||
| 7 | 2 | 0 | ||
| 8 | 8 | 0 | ||
| 9 | 5 | 0 | 1 | 1 |
| 10 | 74 | 8 | ||
| 11 | 40 | 2 | ||
| 12 | 3 | 0 | ||
| 13 | 4 | 0 | 9 | 0 |
| 14 | 3 | 1 | 1 | 0 |
| 15 | 14 | 0 | ||
| 16 | 4 | 0 | ||
| 17 | 273 | 24 | ||
| 18 | 11 | 3 | 44 | 0 |
| 19 | 1 | 0 | 7 | 0 |
| 20 | 6 | 0 | ||
| 21 | 2 | 0 | 4 | 0 |
| 22 | 8 | 0 | 50 | 3 |
| 23 | 3 | 0 | 67 | 3 |
| 24 | 7 | 1 | 51 | 1 |
| 25 | 106 | 0 | 18 | 0 |
| 26 | 79 | 1 | ||
| 27 | 3 | 1 | ||
| 28 | 3 | 0 | 2 | 0 |
| 29 | 2 | 0 | ||
| 30 | 12 | 0 | ||
| 31 | 54 | 0 | ||
| 32 | 7 | 1 |
References
- Kéry, M. Towards the Modelling of True Species Distributions. J. Biogeogr. 2011, 38, 617–618. [Google Scholar] [CrossRef]
- Kellner, K.F.; Swihart, R.K. Accounting for Imperfect Detection in Ecology: A Quantitative Review. PLoS ONE 2014, 9, e111436. [Google Scholar] [CrossRef] [PubMed]
- Romano, A.; Roner, L.; Costa, A.; Salvidio, S.; Pedrini, P.; Romano, A.; Roner, L.; Costa, A.; Salvidio, S.; Romano, A.; et al. When No Color Pattern Is Available: Application of Double Observer Methods to Estimate Population Size of the Alpine Salamander Estimate Population Size of the Alpine Salamander. Arct. Antarct. Alp. Res. 2021, 53, 300–308. [Google Scholar] [CrossRef]
- Falaschi, M. Phenology and Temperature Are the Main Drivers Shaping the Detection Probability of the Common Wall Lizard. Amphib. Reptil. 2021, 42, 297–303. [Google Scholar] [CrossRef]
- Schmidt, J.H.; McIntyre, C.L.; MacCluskie, M.C. Accounting for Incomplete Detection: What Are We Estimating and How Might It Affect Long-Term Passerine Monitoring Programs? Biol. Conserv. 2013, 160, 130–139. [Google Scholar] [CrossRef]
- Kéry, M.; Schaub, M. Bayesian Population Analysis Using WinBUGS: A Hierarchical Perspective; Academic Press: Cambridge, MA, USA, 2012; ISBN 9780123870209. [Google Scholar]
- Falaschi, M.; Manenti, R.; Thuiller, W.; Ficetola, G.F. Continental-Scale Determinants of Population Trends in European Amphibians and Reptiles. Glob. Chang. Biol. 2019, 25, 3504–3515. [Google Scholar] [CrossRef]
- van Klink, R.; Bowler, D.E.; Gongalsky, K.B.; Swengel, A.B.; Gentile, A.; Chase, J.M. Meta-Analysis Reveals Declines in Terrestrial but Increases in Freshwater Insect Abundances. Science 2020, 420, 417–420. [Google Scholar] [CrossRef]
- Gaston, K.J.; Fuller, R.A. Commonness, Population Depletion and Conservation Biology. Trends Ecol. Evol. 2008, 23, 14–19. [Google Scholar] [CrossRef]
- Ficetola, G.F.; Romano, A.; Salvidio, S.; Sindaco, R. Optimizing Monitoring Schemes to Detect Trends in Abundance over Broad Scales. Anim. Conserv. 2018, 21, 221–231. [Google Scholar] [CrossRef]
- MacKenzie, D.I.; Kendall, W.L. How Should Detection Probability Be Incorporated into Estimates of Relative Abundance? Ecology 2002, 83, 2387–2393. [Google Scholar] [CrossRef]
- Gervasi, V.; Brøseth, H.; Gimenez, O.; Nilsen, E.B.; Linnell, J.D.C. The Risks of Learning: Confounding Detection and Demographic Trend When Using Count-Based Indices for Population Monitoring. Ecol. Evol. 2014, 4, 4637–4648. [Google Scholar] [CrossRef]
- Collier, B.A.; Ditchkoff, S.S.; Raglin, J.B.; Smith, J.M. Detection Probability and Sources of Variation in White-Tailed Deer Spotlight Surveys. J. Wildl. Manag. 2007, 71, 277–281. [Google Scholar] [CrossRef]
- Campbell Grant, E.H.; Jung, R.E.; Nichols, J.D.; Hines, J.E. Double-Observer Approach to Estimating Egg Mass Abundance of Pool-Breeding Amphibians. Wetl. Ecol. Manag. 2005, 13, 305–320. [Google Scholar] [CrossRef]
- Dalpasso, A.; Ficetola, G.F.; Giachello, S.; Lo Parrino, E.; Manenti, R.; Muraro, M.; Falaschi, M. Similar Species, Different Fates: Abundance Dynamics in Spatially Structured Populations of Common and Threatened Frogs. Divers. Distrib. 2022, 28, 770–781. [Google Scholar] [CrossRef]
- Muraro, M.; Romagnoli, S.; Barzaghi, B.; Falaschi, M.; Manenti, R.; Ficetola, G.F. Invasive Predators Induce Plastic and Adaptive Responses during Embryo Development in a Threatened Frog. NeoBiota 2021, 70, 69–86. [Google Scholar] [CrossRef]
- Loman, J. Breeding Phenology in Rana Temporaria. Local Variation Is Due to Pond Temperature and Population Size. Ecol. Evol. 2016, 6, 6202–6209. [Google Scholar] [CrossRef]
- Băncilă, R.I.; Ozgul, A.; Hartel, T.; Sos, T.; Schmidt, B.R. Direct Negative Density-Dependence in a Pond-Breeding Frog Population. Ecography 2016, 39, 449–455. [Google Scholar] [CrossRef]
- Manenti, R.; Falaschi, M.; Monache, D.D.; Marta, S.; Ficetola, G.F. Network-Scale Effects of Invasive Species on Spatially-Structured Amphibian Populations. Ecography 2020, 43, 119–127. [Google Scholar] [CrossRef]
- Bernini, F.; Gentilli, A.; Merli, E.; Razzetti, E. Rana Dalmatina and R. Latastei: Habitat Selection, Fluctuation in Egg Clutch Deposition and Response to Exceptional Floods in Northern Italy. Ital. J. Zool. 2010, 71, 147–149. [Google Scholar] [CrossRef]
- Lanza, B.; Andreone, F.; Bologna, M.A.; Corti, C.; Razzetti, E. Fauna d’Italia Vol. XLII—Amphibia; Calderini: Bologna, Italy, 2007; ISBN 9788850652563. [Google Scholar]
- Lodé, T.; Holveck, M.J.; Lesbarrères, D. Asynchronous Arrival Pattern, Operational Sex Ratio and Occurrence of Multiple Paternities in a Territorial Breeding Anuran, Rana Dalmatina. Biol. J. Linn. Soc. 2005, 86, 191–200. [Google Scholar] [CrossRef]
- Nichols, J.D.; Hines, J.E.; Sauer, J.R.; Fallon, F.W.; Fallon, J.E.; Heglund, P.J. A Double-Observer Approach for Estimating Detection Probability and Abundance from Point Counts. Auk 2000, 117, 393–408. [Google Scholar] [CrossRef]
- Fiske, I.J.; Chandler, R.B. Unmarked: An R Package for Fitting Hierarchical Models of Wildlife Occurrence and Abundance. J. Stat. Softw. 2011, 43, 1–23. [Google Scholar] [CrossRef]
- Falaschi, M.; Giachello, S.; Lo Parrino, E.; Muraro, M.; Manenti, R.; Ficetola, G.F. Long-Term Drivers of Persistence and Colonization Dynamics in Spatially Structured Amphibian Populations. Conserv. Biol. 2021, 35, 1530–1539. [Google Scholar] [CrossRef]
- Falaschi, M.; Muraro, M.; Gibertini, C.; Delle Monache, D.; Lo Parrino, E.; Faraci, F.; Belluardo, F.; Di Nicola, M.R.; Manenti, R.; Ficetola, G.F. Explaining Declines of Newt Abundance in Northern Italy. Freshw. Biol. 2022, 67, 1174–1187. [Google Scholar] [CrossRef]
- Brooks, G.C.; Smith, J.A.; Gorman, T.A.; Haas, C.A. Discerning the Environmental Drivers of Annual Migrations in an Endangered Amphibian. Copeia 2019, 107, 270–276. [Google Scholar] [CrossRef]
- Cayuela, H.; Valenzuela-Sánchez, A.; Teulier, L.; Martínez-Solano, Í.; Léna, J.-P.; Merilä, J.; Muths, E.; Shine, R.; Quay, L.; Denoël, M.; et al. Determinants and Consequences of Dispersal in Vertebrates with Complex Life Cycles: A Review of Pond-Breeding Amphibians. Quartely Rev. Biol. 2020, 95, 1–36. [Google Scholar] [CrossRef]
- Miller, D.A.W.; Grant, E.H.C.; Muths, E.; Amburgey, S.M.; Adams, M.J.; Joseph, M.B.; Waddle, J.H.; Johnson, P.T.J.; Ryan, M.E.; Schmidt, B.R.; et al. Quantifying Climate Sensitivity and Climate-Driven Change in North American Amphibian Communities. Nat. Commun. 2018, 9, 3626. [Google Scholar] [CrossRef]
- Ambrogio, A.; Mezzadri, S. Brown Frogs of Italy; Gavia Edizioni: Piacenza, Italy, 2018. [Google Scholar]
- Bailey, L.L.; Simons, T.R.; Pollock, K.H. Estimating Site Occupancy and Species Detection Probability Paramters for Terrestrial Salamanders. Ecol. Appl. 2004, 14, 692–702. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falaschi, M.; Gibertini, C.; Lo Parrino, E.; Muraro, M.; Barzaghi, B.; Manenti, R.; Ficetola, G.F. Assessing Population Trends of Species with Imperfect Detection: Double Count Analyses and Simulations Confirm Reliable Estimates in Brown Frogs. Animals 2022, 12, 2085. https://doi.org/10.3390/ani12162085
Falaschi M, Gibertini C, Lo Parrino E, Muraro M, Barzaghi B, Manenti R, Ficetola GF. Assessing Population Trends of Species with Imperfect Detection: Double Count Analyses and Simulations Confirm Reliable Estimates in Brown Frogs. Animals. 2022; 12(16):2085. https://doi.org/10.3390/ani12162085
Chicago/Turabian StyleFalaschi, Mattia, Chiara Gibertini, Elia Lo Parrino, Martina Muraro, Benedetta Barzaghi, Raoul Manenti, and Gentile Francesco Ficetola. 2022. "Assessing Population Trends of Species with Imperfect Detection: Double Count Analyses and Simulations Confirm Reliable Estimates in Brown Frogs" Animals 12, no. 16: 2085. https://doi.org/10.3390/ani12162085
APA StyleFalaschi, M., Gibertini, C., Lo Parrino, E., Muraro, M., Barzaghi, B., Manenti, R., & Ficetola, G. F. (2022). Assessing Population Trends of Species with Imperfect Detection: Double Count Analyses and Simulations Confirm Reliable Estimates in Brown Frogs. Animals, 12(16), 2085. https://doi.org/10.3390/ani12162085








