Evaluation of Four Thermal Comfort Indices and Their Relationship with Physiological Variables in Feedlot Cattle
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Micrometeorological Data Collection and Thermal Indices Estimation
2.2. Physiological Data Collection
2.3. Statistical Analysis
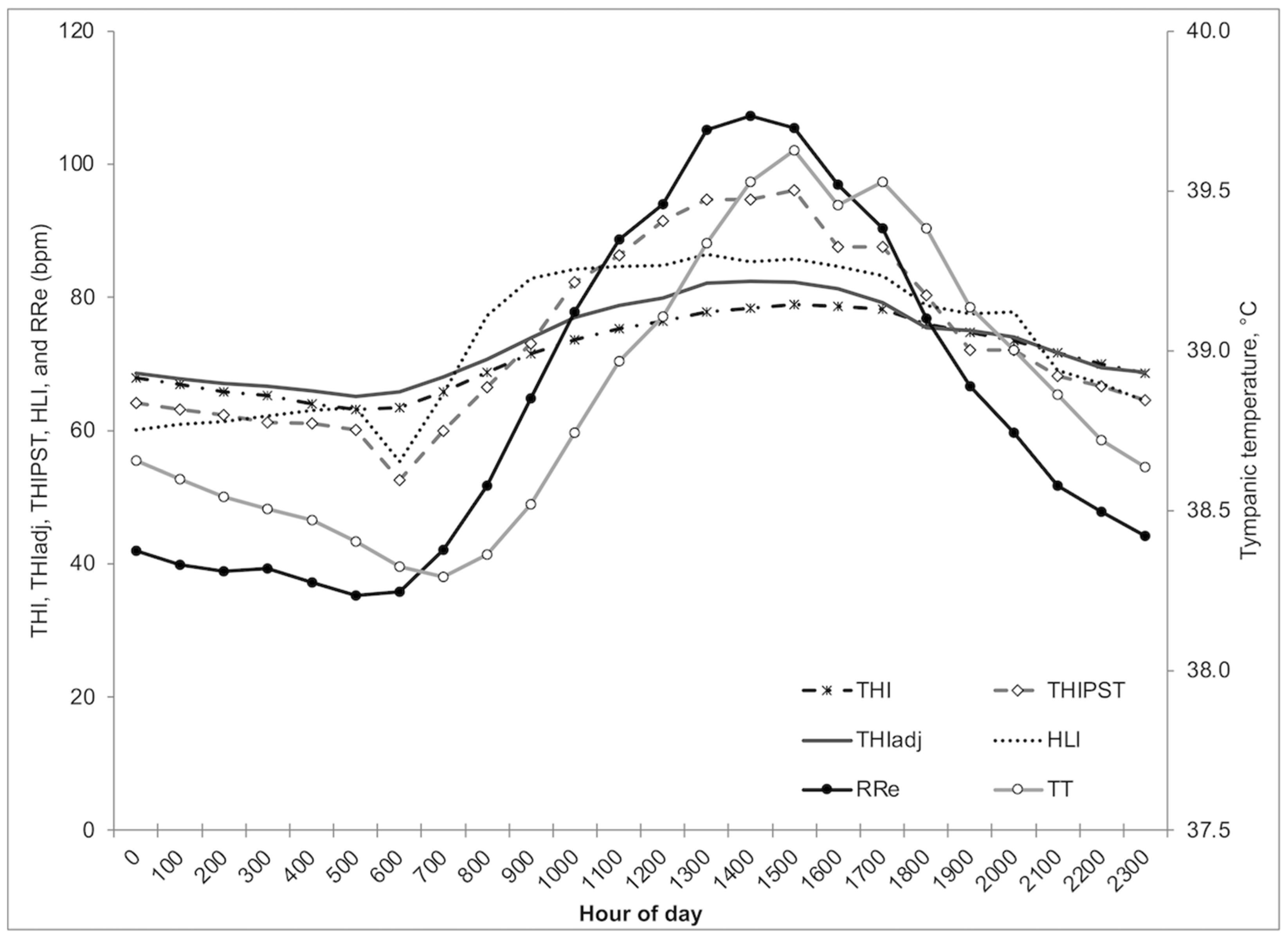
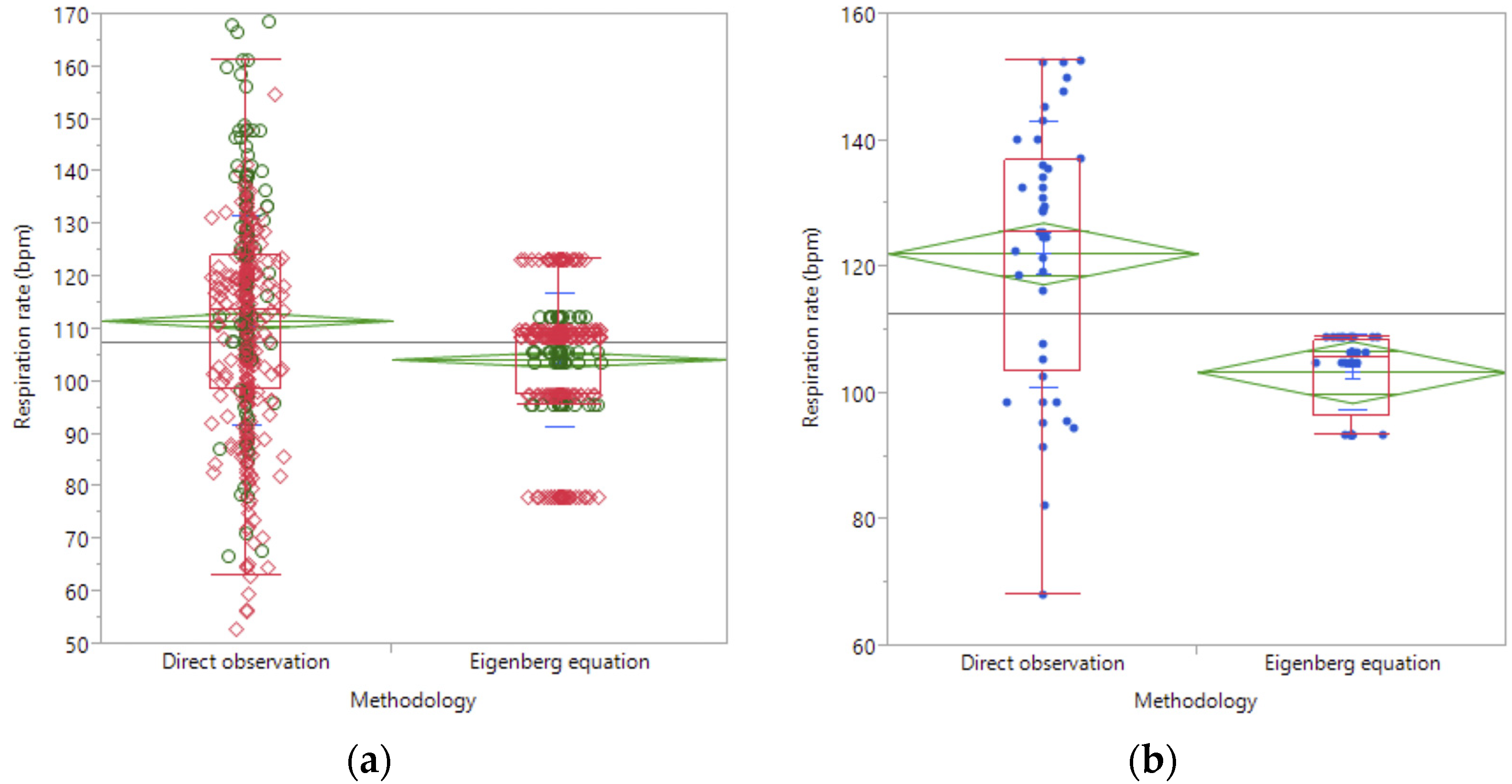
3. Results
Climate Conditions
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mader, T.L. Environmental Stress in Confined Beef Cattle. J. Anim. Sci. 2003, 81, E110–E119. [Google Scholar]
- Hahn, G.L. Dynamic Response of Cattle to Thermal Heat Loads. J. Anim. Sci. 1999, 77, 10–20. [Google Scholar] [CrossRef]
- Hubbard, K.G.; Stooksbury, D.E.; Hahn, G.L.; Mader, T.L. A Climatological Perspective on Feedlot Cattle Performance and Mortality Related to the Temperature-Humidity Index. J. Prod. Agric. 1999, 12, 650–653. [Google Scholar] [CrossRef]
- Ryan, P. The Microclimate of Australian Cattle Feedlots. Master’s Thesis, University of Southern Queensland, Darling Heights, QLD, Australia, 2007. [Google Scholar]
- Hahn, G.L.; Mader, T.L.; Eigenberg, R.A. Perspective on Development of Thermal Indices for Animal Studies and Management. In Interactions between Climate and Animal Production; Lacetera, N., Bernabucci, U., Khalifa, H.H., Ronchi, B., Nardone, A., Eds.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2003; pp. 31–44. [Google Scholar]
- Davis, S.; Mader, T.L. Adjustments for Wind Speed and Solar Radiation to the Temperature Humidity Index; Nebraska Beef Cattle Reports; University of Nebraska-Lincoln: Lincoln, NE, USA, 2003; pp. 49–51. [Google Scholar]
- Mader, T.L.; Davis, M.S.; Brown-Brandl, T. Environmental Factors Influencing Heat Stress in Feedlot Cattle. J. Anim. Sci. 2006, 84, 712–719. [Google Scholar] [CrossRef] [PubMed]
- Brown-Brandl, T.M.; Eigenberg, R.A.; Nienaber, J.A.; Hahn, G.L. Dynamic Response Indicators of Heat Stress in Shaded and Non-Shaded Feedlot Cattle, Part 1: Analyses of Indicators. Biosyst. Eng. 2005, 90, 451–462. [Google Scholar] [CrossRef]
- Eigenberg, R.A.; Brown-Brandl, T.M.; Nienaber, J.A.; Hahn, G.L. Dynamic Response Indicators of Heat Stress in Shaded and Non-Shaded Feedlot Cattle, Part 2: Predictive Relationships. Biosyst. Eng. 2005, 91, 111–118. [Google Scholar] [CrossRef]
- Finch, V.A. Body Temperature in Beef Cattle: Its Control and Relevance to Production in the Tropics. J. Anim. Sci. 1986, 62, 531–542. [Google Scholar] [CrossRef]
- Lees, A.M.; Sejian, V.; Wallage, A.L.; Steel, C.C.; Mader, T.L.; Lees, J.C.; Gaughan, J.B. The Impact of Heat Load on Cattle. Animals 2019, 9, 322. [Google Scholar] [CrossRef] [PubMed]
- St-Pierre, N.R.; Cobanov, B.; Schnitkey, G. Economic Losses from Heat Stress by Us Livestock Industries. J. Dairy Sci. 2003, 86, E52–E77. [Google Scholar] [CrossRef]
- Mader, T.L.; Gaughan, J.B. Effects of Climate Variability on Domestic Livestock. In Handook on Climate Change and Agriculture; Dinar, A., Mendelsohn, R., Eds.; Edward Elgar Publishing Limited: Northampton, MA, USA, 2011; pp. 32–48. [Google Scholar]
- Thom, E.C. The Discomfort Index. Weatherwise 1959, 12, 57–59. [Google Scholar] [CrossRef]
- Arias, R.A. Modeling the Effects of Environmental Factors on Finished Cattle. Ph.D. Thesis, University of Nebraska, Lincoln, NE, USA, 2008. [Google Scholar]
- Arias, R.A.; Mader, T.L.; Escobar, P.C. Climatic Factors Affecting Cattle Performance in Dairy and Beef Farms. Arch. Med. Vet. 2008, 40, 7–22. [Google Scholar]
- Gaughan, J.B.; Mader, T.L.; Holt, S.M.; Lisle, A. A New Heat Load Index for Feedlot Cattle. J. Anim. Sci. 2008, 86, 226–234. [Google Scholar] [CrossRef]
- Johnson, J.S. Heat Stress: Impact on Livestock Well-Being and Productivity and Mitigation Strategies to Alleviate the Negative Effects. Anim. Prod. Sci. 2018, 58, 1404–1413. [Google Scholar] [CrossRef]
- Mellor, D.J. Updating Animal Welfare Thinking: Moving Beyond the “Five Freedoms” Towards “a Life Worth Living”. Animals 2016, 6, 21. [Google Scholar] [CrossRef] [PubMed]
- Webster, J. Animal Welfare: Freedoms, Dominions and “a Life Worth Living”. Animals 2016, 6, 35. [Google Scholar] [CrossRef]
- LCI. Patterns of Transient Losses; Livestock Conservation Incorporated: Omaha, NE, USA, 1970. [Google Scholar]
- Brown-Brandl, T.M.; Jones, D.D.; Woldt, W.E. Evaluating Modelling Techniques for Cattle Heat Stress Prediction. Biosys. Eng. 2005, 91, 513–524. [Google Scholar] [CrossRef]
- Brown-Brandl, T.M.; Nienaber, J.A.; Eigenberg, R.A.; Mader, T.L.; Morrow, J.L.; Dailey, J.W. Comparison of Heat Tolerance of Feedlot Heifers of Different Breeds. Livest. Sci. 2006, 105, 19–26. [Google Scholar] [CrossRef]
- Collier, R.J.; Zimbelman, R.B. Heat Stress Effect on Cattle: What We Know and What We Don’t Know. In Proceedings of the 22nd Annual Southwest Nutrition & Management Conference, Tempe, AZ, USA, 22–23 February 2007. [Google Scholar]
- Buffington, D.E.; Collazo-Arocho, A.; Canton, G.H.; Pitt, D.; Thatcher, W.W.; Collier, R.J. Black Globe-Humidity Index (Bghi) as Comfort Equation for Dairy Cows. Trans. ASABE 1981, 24, 711–714. [Google Scholar] [CrossRef]
- Mader, T.L.; Dahlquist, J.M.; Gaughan, J.B. Wind Protection Effects and Airflow Patterns in Outside Feedlots. J. Anim. Sci. 1997, 75, 26–36. [Google Scholar] [CrossRef]
- Mader, T.L.; Davis, M.S.; Gaughan, J.B.; Brown-Brandl, T.M. Wind Speed and Solar Radiation Adjustments for the Temperature-Humidity Index. In Proceedings of the 26th Agricultural and Forest Meteorology/13th Air Pollution/5th Urban Environment/16th Biometeorology and Aerobiology, Vancouver, BC, Canada, 22–26 August 2004. [Google Scholar]
- da Silva, R.G.; Morais, D.A.E.F.; Guilhermino, M.M. Evaluation of Thermal Stress Indexes for Dairy Cows in Tropical Regions. Rev. Bras. Zootec. 2007, 36, 1192–1198. [Google Scholar] [CrossRef]
- Arias, R.A.; Mader, T.L.; Parkhurst, A.M. Effects of Diet Type and Metabolizable Energy Intake on Tympanic Temperature of Steers Fed During Summer and Winter Seasons. J. Anim. Sci. 2011, 89, 1574–1580. [Google Scholar] [CrossRef] [PubMed]
- Epstein, Y.; Moran, D.S. Thermal Comfort and Health Stress Indices. Ind. Health 2006, 44, 388–398. [Google Scholar] [CrossRef] [PubMed]
- Nienaber, J.A.; Hahn, G.L.; Eigenberg, R.A. Quantifying Livestock Responses for Heat Stress Management: A Review. Int. J. Biometeorol. 1999, 42, 183–188. [Google Scholar] [CrossRef] [PubMed]
- Baeta, F.C.; Meador, N.F.; Shanklin, M.D.; Johnson, H.D. Equivalent Temperature Index at Temperatures above Thermoneutral for Lactating Dairy Cows. In Proceedings of the ASAE Summer Meeting Paper 87-4015, Baltimore, MD, USA, 28 June–1 July 1987. [Google Scholar]
- NRC. Effect of Environment on Nutrient Requirements of Domestic Animals; National Academy Press: Washington, DC, USA, 1981. [Google Scholar]
- Gaughan, J.B.; Holt, S.M.; Hahn, G.L.; Mader, T.L.; Eigenberg, R.A. Respiration Rate—Is It a Good Measure of Heat Stress in Cattle? Asian-Aust. J. Anim. Sci. 2000, 13, 329–332. [Google Scholar]
- Kabuga, J.D. The Influence of Thermal Conditions on Rectal Temperature, Respiration Rate and Pulse Rate of Lactating Holstein-Friesian Cows in the Humid Tropics. Int. J. Biometeorol. 1992, 36, 146–150. [Google Scholar] [CrossRef]
- Brown-Brandl, T. Understanding Heat Stress in Beef Cattle. Rev. Bras. Zootec. 2018, 47, 9. [Google Scholar] [CrossRef]

| Score | Description |
|---|---|
| 0 | Normal respiration |
| 1 | Elevated respiration |
| 2 | Moderate panting and/or presence of drool or small amount of saliva |
| 3 | Heavy open-mouthed panting; saliva usually present. |
| 4 | Severe open-mouthed panting accompanied by protruding tongue and excessive salivation; usually with neck extended forward |
| Year and Location | RH (%) | WS (m/s) | THI | THIadj | THIPST | HLI | ST | PST | Ta | BG | TT | SWin | SWout | LWin | LWout |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (°C) | (W/m−2) | ||||||||||||||
| 2007, Concord | |||||||||||||||
| Mean Max Min SEM 2 | 67.1 94.4 35.1 1.6 | 2.4 7.3 0.5 0.1 | 72.0 83.7 52.2 0.6 | 73.9 88.3 53.3 0.6 | 77.7 102.3 52.6 1.0 | 70.5 95.4 45.4 1.2 | 28.2 32.6 23.1 0.5 | 28.8 47.8 11.3 0.8 | 24.5 35.3 11.0 0.5 | 27.2 42.3 8.8 0.8 | 39.1 40.5 38.4 0.05 | 305.3 991.0 −8.4 30.1 | 56.3 187.0 −1.1 5.4 | 372.9 446,7 296.3 3.0 | 448.6 529.2 364.0 3.7 |
| 2008, Concord | |||||||||||||||
| Mean Max Min SEM | 79.8 100.0 35.8 1.6 | 2.5 4.5 0.7 0.1 | 74.1 83.0 61.5 0.6 | 75.7 86.9 61.5 0.7 | 70.9 98.4 55.6 1.1 | 80.1 171.1 52.5 2.4 | 26.2 28.0 24.3 0.4 | 23.9 43.1 13.0 0.9 | 24.8 32.2 16.5 0.4 | 30.5 80.1 15.4 1.3 | 38.7 40.4 37.8 0.06 | 298.8 958.2 −5.7 36.7 | 50.6 167.4 −0.4 6.2 | 405.3 456.3 350.7 2.8 | 483.7 630.1 404.5 6.8 |
| 2008, Scottsbluff | |||||||||||||||
| Mean Max Min SEM | 66.1 99.6 28 2.2 | 2.3 7.2 0.5 0.1 | 70.0 80.4 57.1 0.7 | 71.8 86.6 59.1 0.8 | 74.3 120.9 39.8 2.2 | 72.9 99.8 50.0 1.3 | 27.4 34.1 21.7 0.6 | 27.3 61.2 4.2 1.7 | 23.4 33.4 13.9 0.6 | 28.4 99.8 10.9 0.9 | 38.8 40.3 37.2 0.07 | 281.8 989.8 −4.1 37.1 | 28.5 132.7 −0.2 3.8 | 389.8 441.8 336.3 3.1 | 454.1 629.3 388.0 6.3 |
| Pooled locations | |||||||||||||||
| Mean Max Min SEM | 70.3 100.0 28.0 1.1 | 2.4 7.3 0.5 0.1 | 72.0 83.7 52.2 0.4 | 73.8 88.3 53.3 0.4 | 74.8 120.9 39.8 0.8 | 73.9 171.1 45.4 1.0 | 27.4 34.1 21.7 0.2 | 27.0 61.2 4.2 0.6 | 24.3 35.3 11.0 0.4 | 28.5 80.8 8.8 0.5 | 38.9 40.5 37.2 0.03 | 296.5 991.0 −8.4 19.7 | 46.4 187.0 −1.0 3.2 | 286.9 456.3 296.3 1.9 | 459.9 630.1 364.0 3.2 |
| TT | THI | THIadj | THIPST | HLI | RRe | |
|---|---|---|---|---|---|---|
| TT | 1.00 | |||||
| THI | 0.68 | 1.00 | ||||
| THIadj | 0.70 | 0.93 | 1.00 | |||
| THIPST | 0.75 | 0.77 | 0.82 | 1.00 | ||
| HLI | 0.63 | 0.51 | 0.57 | 0.43 | 1.00 | |
| RRe | 0.68 | 0.93 | 0.96 | 0.85 | 0.59 | 1.00 |
| TT | THI | THIadj | THIPST | HLI | RRe | |
|---|---|---|---|---|---|---|
| TT | 1.00 | |||||
| THI | 0.68 | 1.00 | ||||
| THIadj | 0.70 | 0.93 | 1.00 | |||
| THIPST | 0.80 | 0.79 | 0.84 | 1.00 | ||
| HLI | 0.22 | 0.45 | 0.53 | 0.42 | 1.00 | |
| RRe | 0.94 | 0.94 | 0.95 | 0.87 | 0.55 | 1.00 |
| TT | THI | THIadj | THIPST | HLI | RRe | |
|---|---|---|---|---|---|---|
| TT | 1.00 | |||||
| THI | 0.63 | 1.00 | ||||
| THIadj | 0.63 | 0.93 | 1.00 | |||
| THIPST | 0.70 | 0.79 | 0.84 | 1.00 | ||
| HLI | 0.52 | 0.73 | 0.76 | 0.61 | 1.00 | |
| RRe | 0.69 | 0.91 | 0.97 | 0.88 | 0.75 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arias, R.A.; Mader, T.L. Evaluation of Four Thermal Comfort Indices and Their Relationship with Physiological Variables in Feedlot Cattle. Animals 2023, 13, 1169. https://doi.org/10.3390/ani13071169
Arias RA, Mader TL. Evaluation of Four Thermal Comfort Indices and Their Relationship with Physiological Variables in Feedlot Cattle. Animals. 2023; 13(7):1169. https://doi.org/10.3390/ani13071169
Chicago/Turabian StyleArias, Rodrigo A., and Terry L. Mader. 2023. "Evaluation of Four Thermal Comfort Indices and Their Relationship with Physiological Variables in Feedlot Cattle" Animals 13, no. 7: 1169. https://doi.org/10.3390/ani13071169
APA StyleArias, R. A., & Mader, T. L. (2023). Evaluation of Four Thermal Comfort Indices and Their Relationship with Physiological Variables in Feedlot Cattle. Animals, 13(7), 1169. https://doi.org/10.3390/ani13071169





