Development of a Feed Conversion Ratio Prediction Model for Yorkshire Boars Using Cumulative Feed Intake
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Animals
2.2. Data Collection and Quality Control
2.3. Statistical Analysis
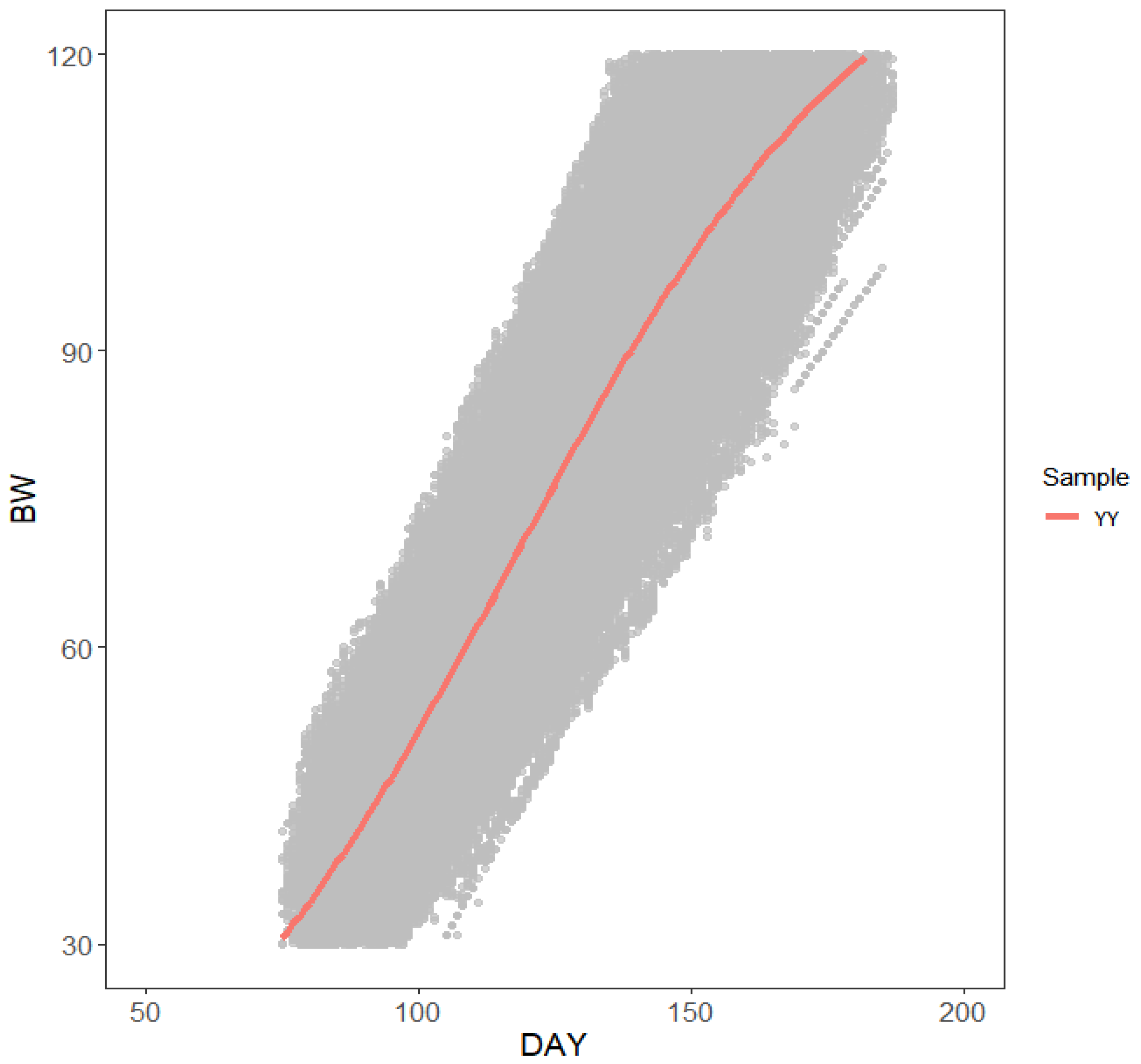
2.4. Construction of the Correction Formula for the Cumulative Feed Intake of Pigs with Body Weight from 30 Kg to 120 Kg
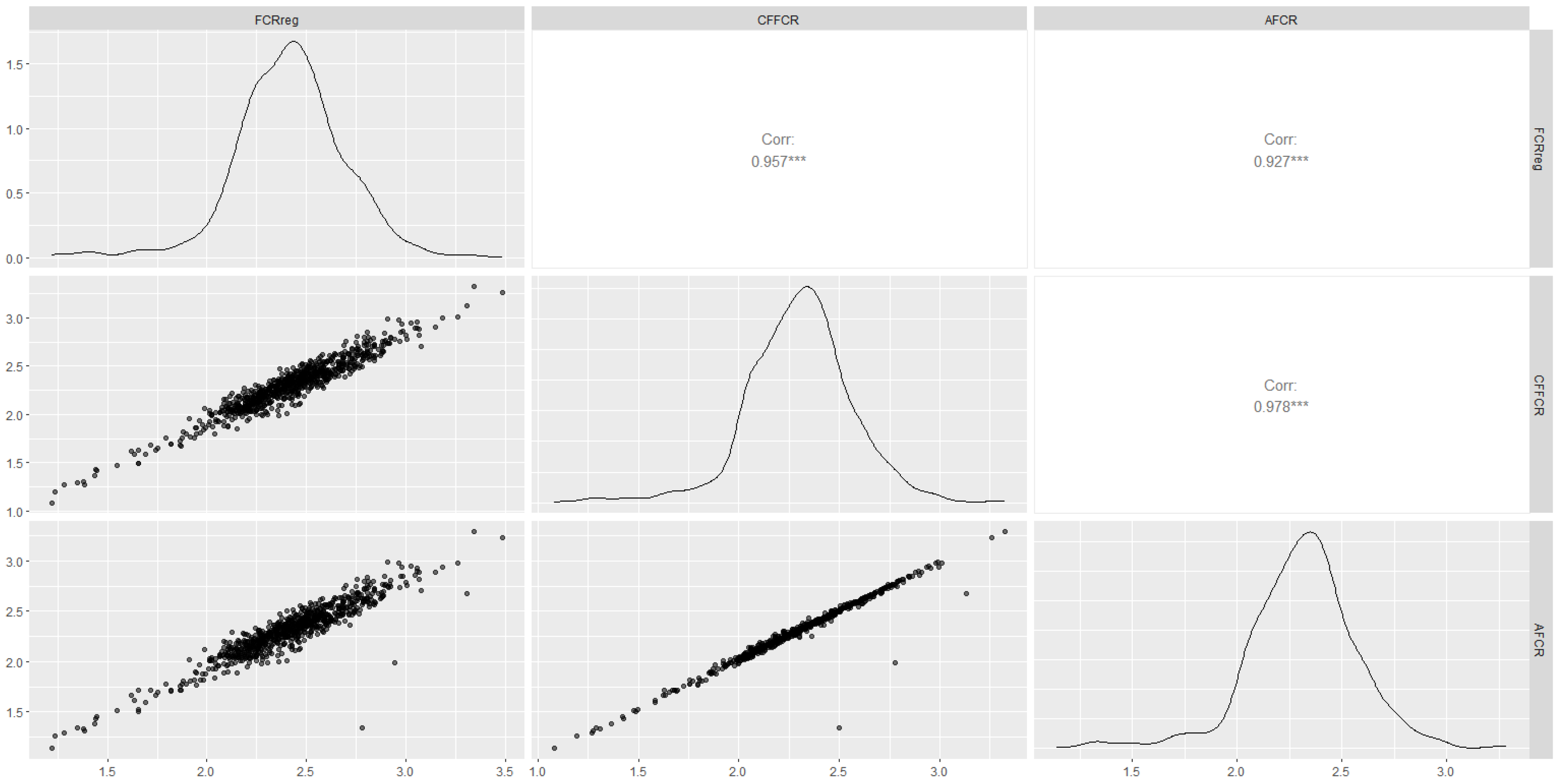
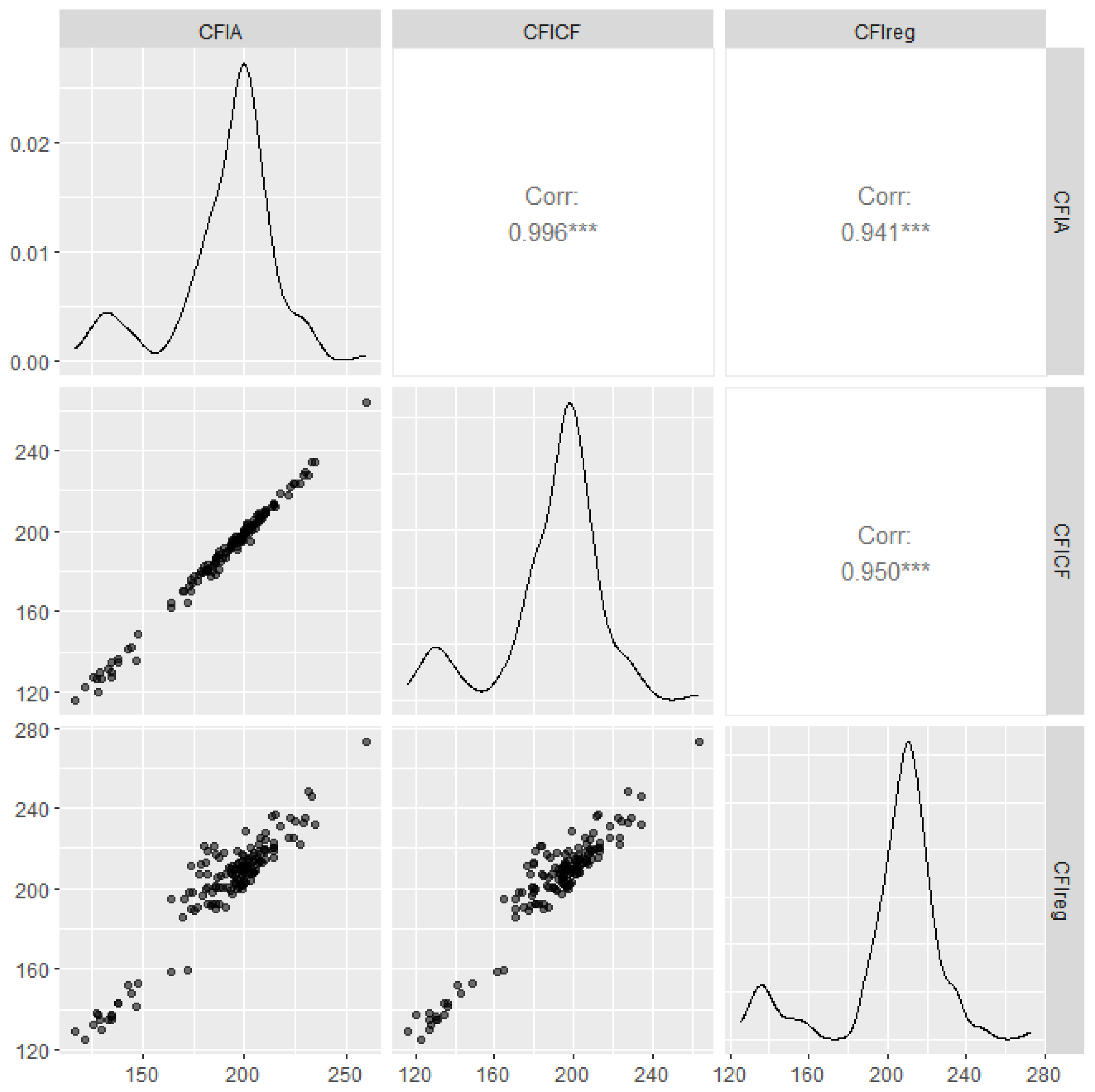
2.5. Construction of the Prediction Model
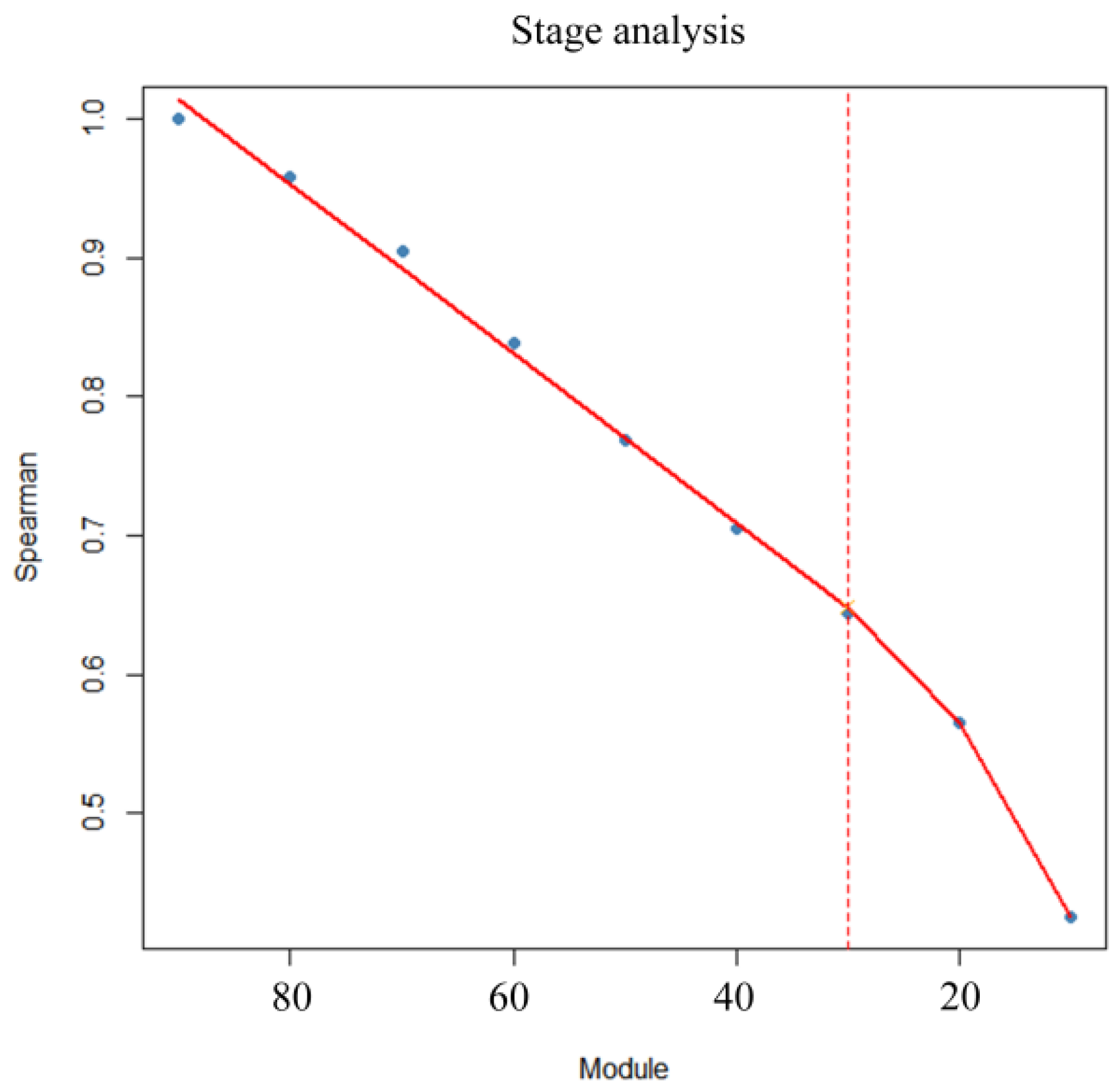
2.6. Grouped Validation
3. Results
3.1. Descriptive Statistics
3.2. Results of the Correction Formula Construction for 30–120 Kg
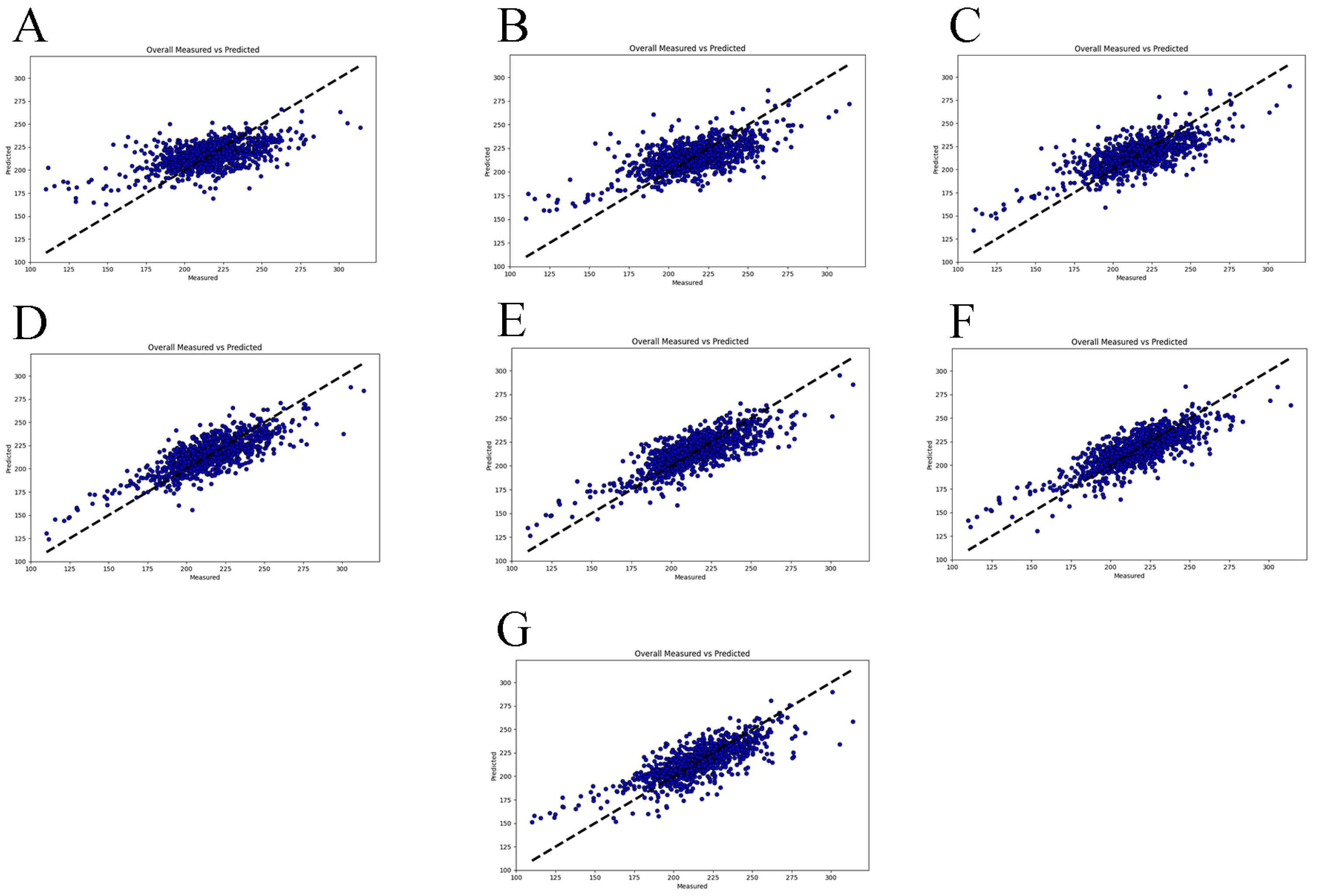
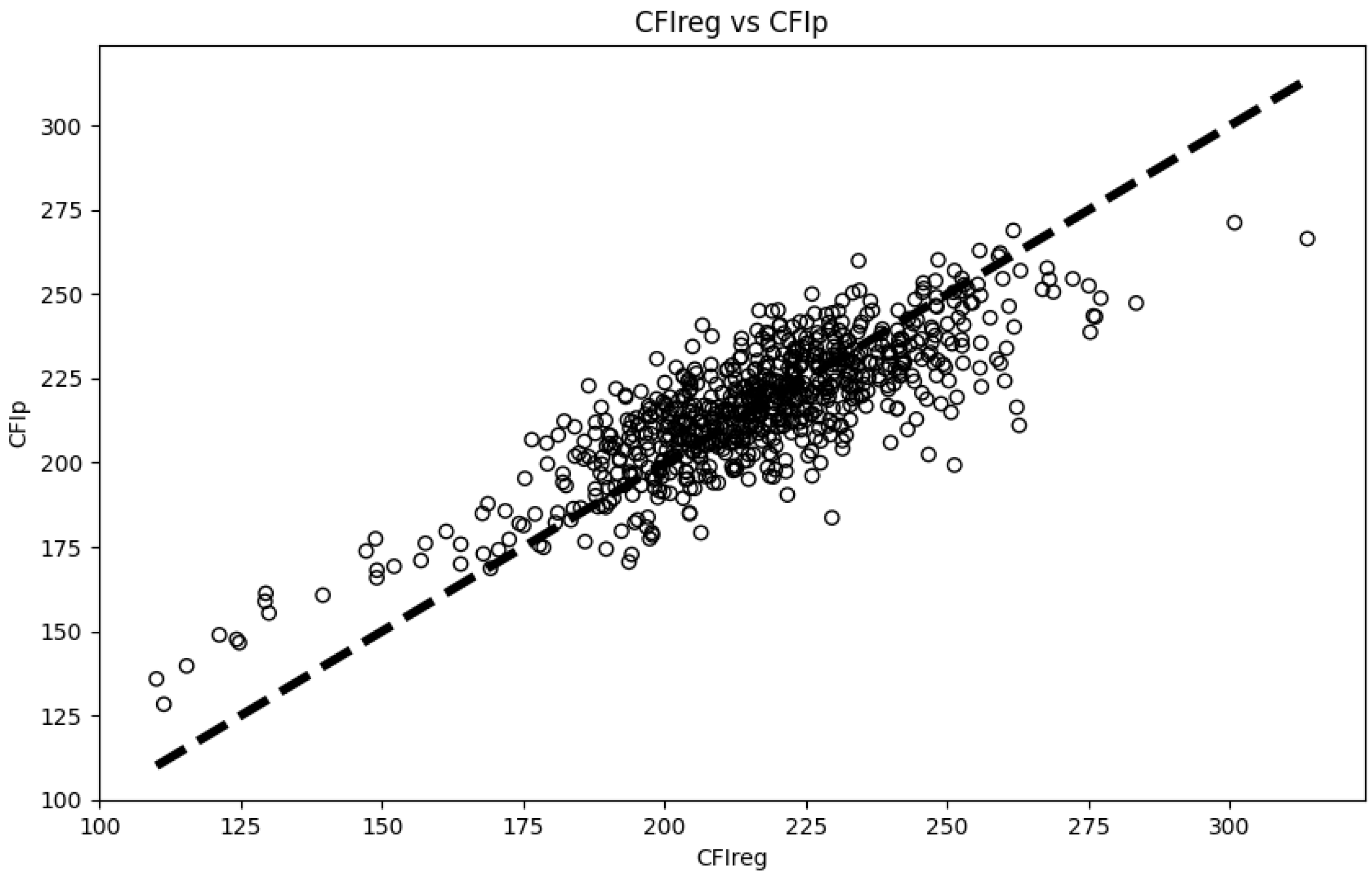
3.3. Predictive Model for Cumulative Feed Intake in the 80–110 Kg Range
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Zhang, D.; Guo, S.; Wang, Y.; Wei, X. The World Trends and Patterns of Grain Loss and Waste Research and Their Implications. ACS Agric. Sci. Technol. 2024, 4, 82–91. [Google Scholar] [CrossRef]
- Jiang, H.; Fang, S.; Yang, H.; Chen, C. Identification of the relationship between the gut microbiome and feed efficiency in a commercial pig cohort. J. Anim. Sci. 2021, 99, skab045. [Google Scholar] [CrossRef] [PubMed]
- Silva, É.F.; Lopes, M.S.; Lopes, P.S.; Gasparino, E. A genome-wide association study for feed efficiency-related traits in a crossbred pig population. Animal 2019, 13, 2447–2456. [Google Scholar] [CrossRef] [PubMed]
- Homma, C.; Hirose, K.; Ito, T.; Kamikawa, M.; Toma, S.; Nikaido, S.; Satoh, M.; Uemoto, Y. Estimation of genetic parameter for feed efficiency and resilience traits in three pig breeds. Animal 2021, 15, 100384. [Google Scholar] [CrossRef]
- Pierozan, C.R.; Agostini, P.S.; Gasa, J.; Novais, A.K.; Dias, C.P.; Santos, R.S.K.; Pereira, M., Jr.; Nagi, J.G.; Alves, J.B.; Silva, C.A. Factors affecting the daily feed intake and feed conversion ratio of pigs in grow-finishing units: The case of a company. Porc. Health Manag 2016, 2, 7. [Google Scholar] [CrossRef][Green Version]
- Lv, Y.; Zheng, Z.; Zeng, J.; Chen, Y.; Abdeen, M.A.; Qiu, W.; Wu, W.; Luo, Y. Transportation Machinery and Feeding Systems for Pigs in Multi-Storey Buildings: A Review. Processes 2024, 12, 1427. [Google Scholar] [CrossRef]
- Dambaulova, G.K.; Madin, V.A.; Utebayeva, Z.A.; Baimyrzaeva, M.K.; Shora, L.Z. Benefits of automated pig feeding system: A simplified cost-benefit analysis in the context of Kazakhstan. Vet. World 2023, 16, 2205–2209. [Google Scholar] [CrossRef]
- Poullet, N.; Rauw, W.M.; Renaudeau, D.; Riquet, J.; Giorgi, M.; Billon, Y.; Gilbert, H.; Gourdine, J.L. Plasticity of feeding behaviour traits in response to production environment (temperate vs. tropical) in group-housed growing pigs. Sci. Rep. 2022, 12, 847. [Google Scholar] [CrossRef]
- Lenoir, G.; Flatres-Grall, L.; Muñoz-Tamayo, R.; David, I.; Friggens, N.C. Disentangling the dynamics of energy allocation to develop a proxy for robustness of fattening pigs. Genet. Sel. Evol. 2023, 55, 77. [Google Scholar] [CrossRef]
- Jiao, S.; Tiezzi, F.; Huang, Y.; Gray, K.A.; Maltecca, C. The use of multiple imputation for the accurate measurements of individual feed intake by electronic feeders. J. Anim. Sci. 2016, 94, 824–832. [Google Scholar] [CrossRef][Green Version]
- Ding, R.; Yang, M.; Wang, X.; Quan, J.; Zhuang, Z.; Zhou, S.; Li, S.; Xu, Z.; Zheng, E.; Cai, G.; et al. Genetic Architecture of Feeding Behavior and Feed Efficiency in a Duroc Pig Population. Front. Genet. 2018, 9, 220. [Google Scholar] [CrossRef] [PubMed]
- Ito, T.; Fukawa, K.; Kamikawa, M.; Nikaidou, S.; Taniguchi, M.; Arakawa, A.; Tanaka, G.; Mikawa, S.; Furukawa, T.; Hirose, K. Effects of correcting missing daily feed intake values on the genetic parameters and estimated breeding values for feeding traits in pigs. Anim. Sci. J. 2018, 89, 12–20. [Google Scholar] [CrossRef]
- Crampton, E.W.; Bell, J.M. The Effect of Fineness of Grinding on the Utilization of Oats by Market Hogs. J. Anim. Sci. 1946, 5, 200–210. [Google Scholar] [CrossRef]
- Verschuren, L.M.G.; Schokker, D.; Bergsma, R.; van Milgen, J.; Molist, F.; Calus, M.P.L.; Jansman, A.J.M. Variation in faecal digestibility values related to feed efficiency traits of grower-finisher pigs. Animal 2021, 15, 100211. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Li, C.; He, Z.; Liu, H.; Wang, M.; He, J. Metabolomics Profiling of Serum and Urine from Chuanzang Black Pigs with Different Residual Feed Intake. Animals 2024, 14, 2323. [Google Scholar] [CrossRef]
- Wang, Z.; Nkrumah, J.D.; Li, C.; Basarab, J.A.; Goonewardene, L.A.; Okine, E.K.; Crews, D.H., Jr.; Moore, S.S. Test duration for growth, feed intake, and feed efficiency in beef cattle using the GrowSafe System. J. Anim. Sci. 2006, 84, 2289–2298. [Google Scholar] [CrossRef]
- Zou, Y.; Pan, S.; Zhao, P.; Han, L.; Wang, X.; Hemerik, L.; Knops, J.; van der Werf, W. Outbreak analysis with a logistic growth model shows COVID-19 suppression dynamics in China. PLoS ONE 2020, 15, e0235247. [Google Scholar] [CrossRef]
- Ding, R.; Qiu, Y.; Zhuang, Z.; Ruan, D.; Wu, J.; Zhou, S.; Ye, J.; Cao, L.; Hong, L.; Xu, Z.; et al. Genome-wide association studies reveals polygenic genetic architecture of litter traits in Duroc pigs. Theriogenology 2021, 173, 269–278. [Google Scholar] [CrossRef]
- Aliakbari, A.; Zemb, O.; Cauquil, L.; Barilly, C.; Billon, Y.; Gilbert, H. Microbiability and microbiome-wide association analyses of feed efficiency and performance traits in pigs. Genet. Sel. Evol. 2022, 54, 29. [Google Scholar] [CrossRef]
- Bouquet, A.; Déru, V.; Blanchet, B.; Ganier, P.; Flatrès-Grall, L.; Ligonesche, B.; Carillier-Jacquin, C.; Labussière, E.; Gilbert, H. Digestive efficiency traits in growing pigs are genetically correlated with sow litter traits in the Large White breed. Animal 2022, 16, 100447. [Google Scholar] [CrossRef]
- Lenoir, G.; Flatres-Grall, L.; Friggens, N.C.; David, I. Robustness scores in fattening pigs based on routinely collected phenotypes: Determination and genetic parameters. J. Anim. Sci. 2022, 100, skac157. [Google Scholar] [CrossRef] [PubMed]
- Losinger, W.C. Feed-conversion ratio of finisher pigs in the USA. Prev. Vet. Med. 1998, 36, 287–305. [Google Scholar] [CrossRef] [PubMed]
- Zumbach, B.; Misztal, I.; Chen, C.Y.; Tsuruta, S.; Łukaszewicz, M.; Herring, W.O.; Culbertson, M. Use of serial pig body weights for genetic evaluation of daily gain. J. Anim. Breed Genet. 2010, 127, 93–99. [Google Scholar] [CrossRef]
- Veylit, L.; Sæther, B.E.; Gaillard, J.M.; Baubet, E.; Gamelon, M. Many lifetime growth trajectories for a single mammal. Ecol. Evol. 2021, 11, 14789–14804. [Google Scholar] [CrossRef] [PubMed]
- Nguyen-Ba, H.; van Milgen, J.; Taghipoor, M. A procedure to quantify the feed intake response of growing pigs to perturbations. Animal 2020, 14, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Tu, J.-m.; Xiong, X.-p.; Zhang, Z.-k.; Li, L.-y.; Huang, L.-b.; Huang, Z.-y.; Xiao, S.-j.; Guo, Y.-m. Estimating the correction coefficient of days to 100 kg in Licha black pig and its intercross with Berkshire. Sci. Agric. Sin. 2020, 53, 2493–2501. [Google Scholar]
- Cui, D.-S.; Xiong, S.-Y.; Zheng, H.; Li, L.-Y.; Yu, N.-B.; Huang, Z.-Y.; Xiao, S.-J.; Guo, Y.-M. Comparing methods for correcting days to 100 kg of sows in Licha black pig and its intercross with Berkshire. Sci. Agric. Sin. 2023, 65, 1177–1188. [Google Scholar]
- Costa, A.; Sneddon, N.W.; Goi, A.; Visentin, G.; Mammi, L.M.E.; Savarino, E.V.; Zingone, F.; Formigoni, A.; Penasa, M.; De Marchi, M. Invited review: Bovine colostrum, a promising ingredient for humans and animals-Properties, processing technologies, and uses. J. Dairy Sci. 2023, 106, 5197–5217. [Google Scholar] [CrossRef]
- Agostini, P.S.; Fahey, A.G.; Manzanilla, E.G.; O’Doherty, J.V.; de Blas, C.; Gasa, J. Management factors affecting mortality, feed intake and feed conversion ratio of grow-finishing pigs. Animal 2014, 8, 1312–1318. [Google Scholar] [CrossRef]
- Davison, C.; Michie, C.; Tachtatzis, C.; Andonovic, I.; Bowen, J.; Duthie, C.A. Feed Conversion Ratio (FCR) and Performance Group Estimation Based on Predicted Feed Intake for the Optimisation of Beef Production. Sensors 2023, 23, 4621. [Google Scholar] [CrossRef]
- Mostafa, S.M.; Eladimy, A.S.; Hamad, S.; Amano, H. CBRG: A novel algorithm for handling missing data using Bayesian ridge regression and feature selection based on gain ratio. IEEE Access 2020, 8, 216969–216985. [Google Scholar] [CrossRef]
- Kaplan, D. On the Quantification of Model Uncertainty: A Bayesian Perspective. Psychometrika 2021, 86, 215–238. [Google Scholar] [CrossRef] [PubMed]
- Massaoudi, M.; Refaat, S.S.; Abu-Rub, H.; Chihi, I.; Wesleti, F.S. A hybrid Bayesian ridge regression-CWT-catboost model for PV power forecasting. In Proceedings of the 2020 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 13–14 July 2020; pp. 1–5. [Google Scholar]
- Stuke, H.; Priebe, K.; Weilnhammer, V.A.; Stuke, H.; Schoofs, N. Sparse models for predicting psychosocial impairments in patients with PTSD: An empirical Bayes approach. Psychol. Trauma 2023, 15, 80–87. [Google Scholar] [CrossRef]
- Schneeweiss, S.; Eddings, W.; Glynn, R.J.; Patorno, E.; Rassen, J.; Franklin, J.M. Variable Selection for Confounding Adjustment in High-dimensional Covariate Spaces When Analyzing Healthcare Databases. Epidemiology 2017, 28, 237–248. [Google Scholar] [CrossRef] [PubMed]
- Ferragina, A.; de los Campos, G.; Vazquez, A.I.; Cecchinato, A.; Bittante, G. Bayesian regression models outperform partial least squares methods for predicting milk components and technological properties using infrared spectral data. J. Dairy Sci. 2015, 98, 8133–8151. [Google Scholar] [CrossRef]
- Schoepfer, A.A.; Laplaza, R.; Wodrich, M.D.; Waser, J.; Corminboeuf, C. Reaction-Agnostic Featurization of Bidentate Ligands for Bayesian Ridge Regression of Enantioselectivity. ACS Catal. 2024, 14, 9302–9312. [Google Scholar] [CrossRef]
- Rauseo, E.; Salih, A.; Raisi-Estabragh, Z.; Aung, N.; Khanderia, N.; Slabaugh, G.G.; Marshall, C.R.; Neubauer, S.; Radeva, P.; Galazzo, I.B.; et al. Ischemic Heart Disease and Vascular Risk Factors Are Associated With Accelerated Brain Aging. JACC Cardiovasc. Imaging 2023, 16, 905–915. [Google Scholar] [CrossRef]
- Saqib, M. Forecasting COVID-19 outbreak progression using hybrid polynomial-Bayesian ridge regression model. Appl. Intell. 2021, 51, 2703–2713. [Google Scholar] [CrossRef]
- Effrosynidis, D.; Spiliotis, E.; Sylaios, G.; Arampatzis, A. Time series and regression methods for univariate environmental forecasting: An empirical evaluation. Sci. Total Environ. 2023, 875, 162580. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Pal, S.; Mitra, R.; Rai, S. Applications of Bayesian shrinkage prior models in clinical research with categorical responses. BMC Med. Res. Methodol. 2022, 22, 126. [Google Scholar] [CrossRef]
- Muggeo, V.M. Segmented: An R package to fit regression models with broken-line relationships. R News 2008, 8, 20–25. [Google Scholar]

| Growth Stage | 25–50 kg | 50–75 kg | 75-Marketed |
|---|---|---|---|
| Corn 8.2 (1) | 653.4 | 652.6 | 668.1 |
| Wheat bran | 70 | 70 | 132.9 |
| Soybean meal | 139.9 | 223.4 | 160 |
| Extruded full fat soybeans | 80 | / | / |
| Soybean oil | 12.7 | 10 | / |
| Kim Tsai Fook (2) | 40 | / | / |
| King Jin Yu (2) | / | 40 | 35 |
| Premix Small Feed A (3) | 4 | 4 | 4 |
| Error Index | Error Type | Error Definition |
|---|---|---|
| 1 | FIV (1)-low | FIV < −0 g for all visits |
| 2 | FIV-high | FIV > 2000 g for all visits |
| 3 | FIV-0 | FIV > 20 g or FIV < −20 g for visits with OTV = 0 s |
| 4 | OTV (2)-low | OTV < 0 s for all visits |
| 5 | OTV-high | OTV > 3600 s for all visits |
| 6 | FRV (3)-high-FIV-low | FRV > 500 g/min for visits with 0 < FIV < 50 g |
| 7 | FRV-high | FRV > 350 g/min for visits with FIV > 50 g |
| 8 | FRV-0 | FRV = 0 g/min for visits with OTV > 500 s |
| Traits | Abbreviations | Units | Yorkshire | ||
|---|---|---|---|---|---|
| N (1) | Mean | SD (2) | |||
| Average daily gain from 30 to 120 kg | ADG | kg | 987 | 1.02 | 0.12 |
| Average daily feed intake | ADFI | kg | 987 | 2.35 | 0.32 |
| Average occupation time in feeder per day | AOC | min | 987 | 53.99 | 10.49 |
| Average number of visits to feeder per day | AVT | counts | 987 | 7.93 | 3.07 |
| Average feed intake per visit | FPV | kg | 987 | 0.25 | 0.25 |
| Average occupation time in feeder per visit | OPV | min | 987 | 5.67 | 5.26 |
| Feed intake rate | FR | g/min | 987 | 45.65 | 23.94 |
| Feed conversion ratio | FCR | kg/kg | 987 | 2.31 | 0.27 |
| Type | N (1) | Mean | SD (2) | Min | Max |
|---|---|---|---|---|---|
| CF | 815 | 1.03 | 0.04 | 0.87 | 1.20 |
| A | −103.52 | 26.46 | −301.02 | −49.70 |
| Module | Average MSE | Average RMSE | Average R2 | Spearman | Pearson |
|---|---|---|---|---|---|
| 30–60 | 338.71 ± 39.01 | 18.37 ± 1.07 | 0.43 ± 0.04 | 0.49 | 0.56 |
| 40–70 | 271.19 ± 17.18 | 16.46 ± 0.53 | 0.54 ± 0.05 | 0.57 | 0.66 |
| 50–80 | 256.47 ± 16.68 | 16.01 ± 0.51 | 0.56 ± 0.06 | 0.64 | 0.71 |
| 60–90 | 230.59 ± 39.59 | 15.13 ± 1.27 | 0.61 ± 0.07 | 0.72 | 0.78 |
| 70–100 | 223.78 ± 21.67 | 14.94 ± 0.70 | 0.62 ± 0.07 | 0.74 | 0.80 |
| 80–110 | 204.44 ± 30.67 | 14.26 ± 1.09 | 0.65 ± 0.06 | 0.80 | 0.83 |
| 90–120 | 223.68 ± 33.33 | 14.91 ± 1.11 | 0.62 ± 0.03 | 0.76 | 0.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Cheng, H.; Wang, Y.; Duan, D.; Han, J.; Zhou, S.; Xin, W.; Li, X. Development of a Feed Conversion Ratio Prediction Model for Yorkshire Boars Using Cumulative Feed Intake. Animals 2025, 15, 507. https://doi.org/10.3390/ani15040507
Zhou H, Cheng H, Wang Y, Duan D, Han J, Zhou S, Xin W, Li X. Development of a Feed Conversion Ratio Prediction Model for Yorkshire Boars Using Cumulative Feed Intake. Animals. 2025; 15(4):507. https://doi.org/10.3390/ani15040507
Chicago/Turabian StyleZhou, Hao, Haoshi Cheng, Yuyang Wang, Dongdong Duan, Jinyi Han, Shenping Zhou, Wenshui Xin, and Xinjian Li. 2025. "Development of a Feed Conversion Ratio Prediction Model for Yorkshire Boars Using Cumulative Feed Intake" Animals 15, no. 4: 507. https://doi.org/10.3390/ani15040507
APA StyleZhou, H., Cheng, H., Wang, Y., Duan, D., Han, J., Zhou, S., Xin, W., & Li, X. (2025). Development of a Feed Conversion Ratio Prediction Model for Yorkshire Boars Using Cumulative Feed Intake. Animals, 15(4), 507. https://doi.org/10.3390/ani15040507






