Granger Causality Analysis of Geophysical, Geodetic and Geochemical Observations during Volcanic Unrest: A Case Study in the Campi Flegrei Caldera (Italy)

Abstract

The recent signs of reawakening at Campi Flegrei caldera (Southern Italy) received a great deal of attention due to the issues related to the volcanic risk management in a densely populated area. This paper explores relations between ground deformations, seismicity and geochemical time series in the time span 2004–2016. The aim is to unravel primary processes of unrest and the related indicators which may change in time. Data structure and interactions among variables were examined applying the clustering analysis, the correlations and the Granger causality test. The hierarchical agglomerative clustering detected two sub-periods which were further investigated. In both sub-period causal links were observed between variables while correlations did not appear and vice versa. Thus, well established formal approaches are required to study causal relations. Granger test results indicate that during 2004–2011 the awakening unrest could be mainly ascribed to hydrothermal system pressure fluctuations, probably induced by deep-rooted fluids injection, and that ground deformation together with CO₂/H₂O appears the most suitable geo-indicators. The 2011–2016 sub-period is characterized by enhanced dynamical connectivity. Granger test results suggest that the unrest is driven by a more localized and shallower thermohydromechanical engine. CO/CO₂, He/CH₄ and ground deformation velocity are mutually interacting appearing the most suitable geo-indicators.

1. Introduction

Accurate knowledge of volcanic structures and behavior needs the definition and the understanding of several major processes, an ongoing task that can be undertaken via physical and mathematical parametrization (modeling) or via purely statistical approaches [1,2]. Despite the progressive improvements made by the scientific community, some issues are still unresolved. A major challenge concerns the study of unrest processes aimed to forecast.

It has long been recognized that deformation, seismicity and degassing are the main indicators of volcanic unrest [3]. However, these direct observations are all the expression of endogenous processes on Earth’s surface. How driving forces influence external manifestations requires the study of complex temporal interactions meanwhile competitive (e.g., fracturing and sealing processes) and/or synergic (e.g., pressurization in a spatially correlated heat source and tectonically week zones) processes may occur. This is just the case of magmatic-hydrothermal systems. Temperature/pressure changes within the magmatic reservoir and hydro-mechanical changes within the hydrothermal system can both drive to unrest. Critical factors to this kind of study are the time dependence of the studied variables on the state of the system, which may generate spurious correlations [4,5]. Thus, retrieving the relative contribution of primary processes from the behavior of indirect observations, implicitly requires the study of causality. This task can be faced via statistical approaches, which use predictability to identify causation between time series variables.

Statistical short-term forecasting, dynamic behavior of time series and causality may be assessed performing the vector autoregressive (VAR) model [6], which is a multi-equation system where all the variables are treated as endogenous (dependent). In this work, we address the uncertainty issues related to the understanding of volcanic unrest exploring hypotheses about statistical order applying the Granger causality test [7,8]. A time series variable X is said to “Granger-cause” variable Y if past values of X helps to predict Y, better than just the past values of Y do. The method, originating in econometrics, has enjoyed increasing popularity in many other fields of sciences. Applications to climatic [9,10,11,12] environmental/ecological [13,14,15,16], hydrogeological [17] and neurobiological [18,19,20,21] measures both in time and frequency domain are reported. However, as far as we know, the Granger causality test has never been applied in volcanological contexts.

Data availability for the Campi Flegrei caldera (CFc), a semiplugged felsic caldera located in Southern Italy, provides a great opportunity to investigate the volcanic-hydrothermal forcing with the Granger causality test. The current unrest phase at CFc began in 2005 and it is still ongoing [22,23,24]. Compared to the past ones, this unrest period is characterized by a progressive uplift, the occurrence of shallow (<4 km) microseismicity and the increase in the flux of the magmatic gases. Both volcanic and non-magmatic hydrothermal unrest are plausible mechanisms responsible for the recent CFc crisis [3,25].

In the current study, we used ground deformations, seismicity and geochemical (CO₂/H₂O, He/CH₄, CO/CO₂) time series variables recorded by the volcanic monitoring networks at CFc in the time span 2004–2016. Our aim is to understand their behavior looking for causal relations to unravel the primary process of unrest and the related indicators.

2. Study Area

The CFc is a volcanic complex located in the Campanian Plain, Southern Italy (Figure 1). During its history, the caldera has experienced notably large explosive events. The eruptions of the Campanian Ignimbrite and the Neapolitan Yellow Tuff [26,27,28] led to the formation of its primary structure. It consists of a subcircular depression composed of two nested collapses (Figure 1) infilled by Plio-Quaternary continental and marine sediments and by volcanic deposits [29]. The more recent Agnano Monte Spina and Astroni explosive eruptions modified the caldera structure, as did the numerous successive eruptions, thereby generating pyroclastic deposits spread over an extremely large area [30]. The last eruption in CFc occurred in AD 1538 [31], which demonstrates that the caldera magmatic system is still active. The Solfatara-Agnano area (Figure 1) hosts fumaroles, mud pools and hot springs which testify to intense hydrothermal activity. The dynamic of this volcanic structure was strongly sensed by the bradyseismic episodes that occurred in 1969–1972 and 1982–1984, which generated a rapid uplift of 3.5 m around the town of Pozzuoli [32,33]. Notably, the 1982–1984 crisis was accompanied by more than 15,000 shallow earthquakes [34]. Successively, ground subsided until 2005, when a new uplift process began, and it is still ongoing. This new phase of unrest, different from the previous ones, is characterized by a smaller number of shallow earthquakes of low magnitude and an increase of fumaroles emissions rates and temperatures [35] which caused great concern. Despite numerous studies being carried out for the understanding of the CFc structures and related dynamics, several issues are still under debate. Here, we report some key features, derived by geophysical studies, of the deep to shallow structure of the caldera: (i) a low velocity zone interpreted as magmatic source at 7.5 km depth overlined by a limestones basement whose top locates at about 4 km depth [36,37]; (ii) a low Vp/Vs anomaly likely related to a fractured supercritical gas-bearing formation at about 4 km depth beneath the city of Pozzuoli [38,39]; (iii) a 1 km wide aseismic area of high attenuation located SE of Pozzuoli at 4–4.5 km depth maybe related to an intrusion occurred during the 1984 bradyseismic crisis, and a seismic high attenuation zone at about 3–4 km of depth interpreted as fractured over-pressured gas-bearing formations [40,41]; (iv) a low Vp/Vs and high Qp and Qs seismic layer at 2 km depth underneath the CFc caldera with its central most permeable part (a low Vp/Vs and low Qp and Qs) in correspondence of the Pozzuoli area interpreted as a structure responsible of the magmatic fluids migration from the deep magma reservoir to the shallow Pozzuoli geothermal reservoir [42]; (v) a resistive plume underneath the Solfatara crater down to 2–3 km depth associable to steam/gas within the hydrothermal system [43,44]; (vi) a conductive layer related to a fractured clay cap confined in the first 500 m of depth below the Solfatara–Pisciarelli area [43]; (vii) a resistive unit interpreted as a gas dominated reservoir located 60 m beneath the Bocca Grande fumarole and connected to the vent [45]. Besides, geochemical studies greatly contributed to the knowledge of the CFc volcanic processes and of the ground displacement source, suggesting conceptual models [22,35,46,47] accounting for fumarolic gas chemistry changes, diffuse CO₂ soil degassing and temperature increase, physical simulations and geophysical observations. The recent unrest was interpreted as driven by batches of injected fluids, released at shallow depth (about 4 km) by decompressing magmas at a critical degassing pressure and entering the hydrothermal system [35]. Consistently, background seismicity and soil degassing of CO₂ fluctuations result are controlled by the temperature and pressure increase of the hydrothermal system [23,48]. On the contrary, other authors argue that the ongoing unrest is not related to the activity of a shallow evolving degassing magma, but rather due to magmatic fluids, ascending directly from the deep (8 km) regional magmatic reservoir [47]. Summing up, a debate is still open about the nature of the source, and its relative depth, of the CFc unrest processes. With the present study, we aim to contribute to a better understanding of the processes temporal sequence, using a statistical approach applied to geochemical and geophysical time series. By means of the Granger causality relationship, we look for insights into the most suitable geo-indicators of unrest processes.

3. Materials and Methods

3.1. Dataset

The geodetic (GPS) dataset is composed of monthly averaged elevation changes (Figure 2a) from January 2004 to December 2016 recorded at the RITE station [50,51] (Figure 1). Ground deformation data are recorded at a 30 s sampling rate [50] allowing for an accurate estimate of the associated errors. Here, we use monthly data for which the associated mean error is about ± 0.2 cm. Note that in Figure 2a the dots are thicker than 0.5 cm. During the studied period, the minimum value is found in March 2005, and afterwards, an uplift period starts. The uplift period is characterized by a fastening increasing rate and by the superimposition of small-scale episodes of faster uplift (2006 and 2012–2013). Hereafter, this time series will be referred to as GD.

The second dataset consists of volcano-tectonic (VT) monthly number of earthquakes located in the CFc area (Figure 1) and taken from the catalog of Osservatorio Vesuviano, Istituto Nazionale di Geofisica e Vulcanologia [52]. This public catalog reports the space-time events’ occurrence with a quality factor based on 3-D ellipsoid location error integrated with the azimuthal coverage of the hypocenter location. The average value of the location error is of the order of some hundred meters. In the period 2004–2016, 570 VT seismic events were located in the Pozzuoli area (Figure 1). The Gutenberg-Richter distribution fit the data with magnitude Md > −0.5. With this cutoff, the number of earthquakes reduces to 507 obtaining the catalog completeness. For the scope of the present work, we are interested in the number of VT events rather than to their magnitude, thus we used the whole dataset composed of 570 events. Preserving the size of the statistical sample should not bias our analysis. Indeed, comparing the data vectors of monthly occurrences obtained with the cutoff at 507 earthquakes (Md > −0.5) with the original one (570 events) we obtained a correlation coefficient of about 0.96. This very high correlation is explicable if the distribution (respect to time) of earthquakes with Md > −0.5 is the same for the earthquakes catalog without cutoff. This time series (hereafter EQ; Figure 2b) appears to have an episodic character and only in the time span 2014–2016 an increasing trend appears. It is worth noting that in the considered time period seismic events are mainly concentrated between the Solfatara crater and the Agnano plain (Figure 1). Moreover, observations are distributed at depths from 0 to 5 km although mainly clustered in the range of 1–2 km (Figure 2c).

Finally, the multivariate dataset includes a monthly averaged time series of fluids compositions discharged at the main fumarolic vent in Solfatara, Bocca Grande ([35,53]; in Figure 1). The geochemical data sampling rate is mainly monthly. The analytical (laboratory data analysis) error is very small with respect to the measured data. Since the geochemical variables are compositional data [54,55], they all were transformed into ratios. Among the available species, CO₂/H₂O, He/CH₄, CO/CO₂ were selected since they are representative of specific volcanic processes. CO₂/H₂O ratio is a useful indicator of magma degassing, He/CH₄ provides information of magmatic fluid contribution in the hydrothermal system and CO/CO₂ is considered the best gas-geothermometer in the hydrothermal system [22,56,57]. He/CH₄ has a quite stable behavior with low variance and a mean value around 0.1 up to 2007 where a first clear peak around June 2007 seems to change the variables dynamic, whereupon a fluctuating trend is observable (Figure 2d). Both CO₂/H₂O and CO/CO₂ (respectively, Figure 2e,f) have an increasing trend in the whole period; these two latter ratios seem to have a more stable behavior showing minor variance.

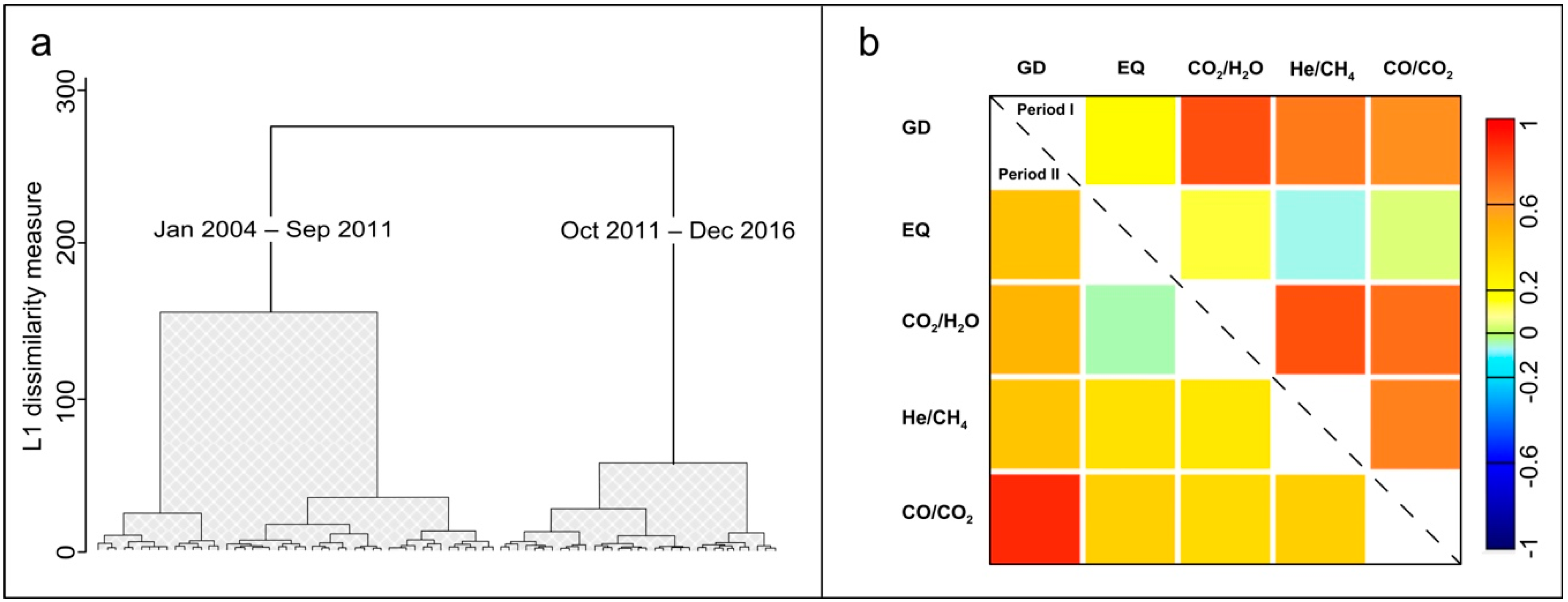
3.2. Hierarchical Agglomerative Clustering, Correlation and Granger Causality Analysis

The inter-relation structure of the multivariate time series was explored using three statistical approaches: clustering analysis, simple correlations and Granger causality test. These statistical methods analyze different and complementary aspects of the observed data variability to capture data structure and relationships. Moreover, the single time series and their causal relationships are expected to change due to the dynamic nature of the system. Since clustering and correlation analysis have to satisfy the normal distribution, while stationarity is required for Granger analysis, row data were analyzed following the method proposed by [58] to test for normal data distribution. All time series do not validate the Shapiro-Wilk normality test for a confidence level of 95% [59,60]. Thus, row data were logarithmically transformed to reduce variance, skewness and kurtosis [58] and standardized in the whole period to make time series comparable before data mining. A hierarchical agglomerative clustering analysis, based on Ward’s method [61,62], was performed to investigate time series similarity among different time periods. Once detected the time grouping based on similarity, Spearman’s correlation [63] and Granger causality tests were performed within the detected time groupings.

A vector autoregressive (VAR) model was estimated to perform the Granger causality tests (Appendix A). VAR is an analytic technique used to explain causal relationships among multivariate time series over time, as well as predict future observations. The VAR model [6], fits a multivariate time series regression of each dependent variable on lags of itself and on lags of all other dependent variables. Therefore, each variable is a linear function of past lags of itself and past lags of the other variables. Under appropriate assumptions, the VAR coefficients can be estimated consistently by applying the Ordinary Least Squares (OLS) method to each equation. The distribution of the estimates thus obtained is approximated by a normal distribution.

The effectiveness of a VAR model, and in turn of the Granger test results, depends on the correct postulation of the VAR model and estimation of its parameters [6]. We built the VAR model performing the following steps: data trend test [64,65]; stationarity test of the individual time series within each period with Augmented Dickey-Fuller test [66]; determination of the number of lags based on lag-length selection criteria using AIC (Akaike’s information criterion) [67], HQIC (Hannan-Quinn information criterion) [68] and FPE (final prediction error) [69,70]; evaluation of residual autocorrelation by means of the Lagrange Multiplier (LM) test and assessment of stability with the autoregressive (AR) roots graph [6,71].

Given a VAR model, we may want to know if one variable X “Granger-cause” another variable Y. A method for testing Granger’s causality is the regression of Y on the delayed values of Y and X then testing the null hypothesis that the coefficients estimated on the delayed values of X are jointly zero. Failure to reject the null hypothesis is equivalent to failure to reject the hypothesis that X is not Granger’s cause Y. The null hypothesis is rejected when the p-value is less than 0.05. The Granger’s causality does not indicate whether the effect is positive or negative, how long it lasts and whether it derives from another (indirect) variable. Four possible outcomes regarding causal relationships between X and Y exist: (i) absence of any causal relationship (X and Y are independent); (ii) unidirectional causality, X causes Y but Y does not cause X; (iii) unidirectional causality, Y causes X but X does not cause Y; (iv) bidirectional causality between the two variables, X and Y are in feedback.

4. Result

Hereafter are reported the results from the statistical multivariate analysis performed on GD, EQ, CO₂/H₂O, He/CH₄ and CO/CO₂ time series.

The hierarchical agglomerative clustering analysis result is reported in Figure 3a. In the Dendrogram, each leaf (vertex) represents the classified temporal unit and the different heights of the branches (edges) represent the existing ultrametric distance with another branch. The groups differ based on the height of the branches until the next knot of the chart. A suitable choice of the ultrametric distance, at which to make the cut, leads to the identification of groups that have homogeneity within them. According to these criteria, two or three mains groups can be recognized.

In this regard, it should be reminded that the cluster analysis was performed to detect time windows for which changes on correlations and causal relationships may be revealed. We have chosen to divide the time series into two sub-periods constituted by 93 samples in the time windows January 2004–September 2011 and 63 samples in the time window October 2011–December 2016. This choice seemed the best compromise between reducing potential bias which may derive from the significantly small series length and the resolution loss due to too large series length. Within the two sub-periods, the logarithmically transformed time series results in less dispersion compared to the raw data in the whole period, showing quite a low variance, skewness, and kurtosis (

Table A1. Statistics of time series in the whole period and in the two sub-periods.

Time Series	Mean	Median	st.dev.	Variance	Skewness	Kurtosis
GD (Jan 2004–Dec 2016)	12.40	5.72	12.33	152.09	0.93	2.56
ln GD (Jan 2004–Sep 2011)	2.71	2.72	0.16	0.02	−0.00	2.14
ln GD (Oct 2011–Dec 2016)	3.58	3.55	0.26	0.06	−0.34	2.34
EQ (Jan 2004–Dec 2016)	3.65	1.00	7.05	49.77	3.23	15.55
ln EQ (Jan 2004–Dec 2016)	0.43	0.00	0.72	0.52	1.75	5.6
ln EQ (Oct 2011–Dec 2016)	1.55	1.61	1.08	1.17	0.10	2.08
He/CH4 (Jan 2004–Dec 2016)	0.15	0.16	0.04	0.00	0.47	4.27
ln He/CH4 (Jan 2004–Sep 2011)	−1.95	−1.88	0.30	0.09	0.09	2.12
ln He/CH4 (Oct 2011–Dec 2016)	−1.84	−1.84	0.09	0.01	−0.12	2.03
CO/CO2 (Jan 2004–Dec 2016)	4.34 × 10−6	4.18 × 10−6	1.02 × 10−6	1.03 × 10−12	0.45	2.06
ln CO/CO2 (Jan 2004–Sep 2011)	−12.53	−12.53	0.13	0.02	−0.04	2.61
ln CO/CO2 (Oct 2011–Dec 2016)	−12.14	−12.13	0.12	0.01	−0.49	2.89
CO2/H2O (Jan 2004–Dec 2016)	0.29	0.30	0.04	0.00	−0.58	2.26
ln CO2/H2O (Jan 2004–Sep 2011)	−1.31	−1.25	0.13	0.02	−0.41	1.61
ln CO2/H2O (Oct 2011–Dec 2016)	−1.11	−1.12	0.05	0.00	−0.25	2.40

in Appendix B).

Correlation analysis results, obtained within the sub-periods January 2004–September 2011 and October 2011–December 2016, are reported in Figure 3b. In the first sub-period, significant, from strong to moderate, correlations exist between: GD and CO₂/H₂O (0.78); CO₂/H₂O and He/CH₄ (0.77); CO₂/H₂O and CO/CO₂ (0.70); GD and He/CH₄ (0.68); He/CH₄ and CO/CO₂ (0.66); GD and CO/CO₂ (0.62). In the second sub-period, fewer correlations appear. Significant correlations are found between GD and CO/CO₂ (0.86) and between GD and CO₂/H₂O (0.50).

In the two sub-periods, all the time series showed trends that were removed. Then, standardization with respect to the mean and the standard deviation within the distinct sub-periods was carried out. Results, based on AIC, HQIC and FPE information criteria, indicate 3–4 lags for the first sub-period (2004–2011) and two lags for the second one (2011–2016). Thus, for the first sub-period, we used three lags, while in the second period residual autocorrelations were detected using two lags. Since the existence of autocorrelation in the residuals may be due to insufficient lags [12,21], three lags were used in the second sub-period, together with the GD first derivative. For this reason, for the second sub-period, we will refer to the velocity of GD (vGD).

Granger test results are reported in

Table 1. Granger causality analysis in two different periods with null hypothesis that X does not Granger causes Y ((*) results obtained by differentiating GD).

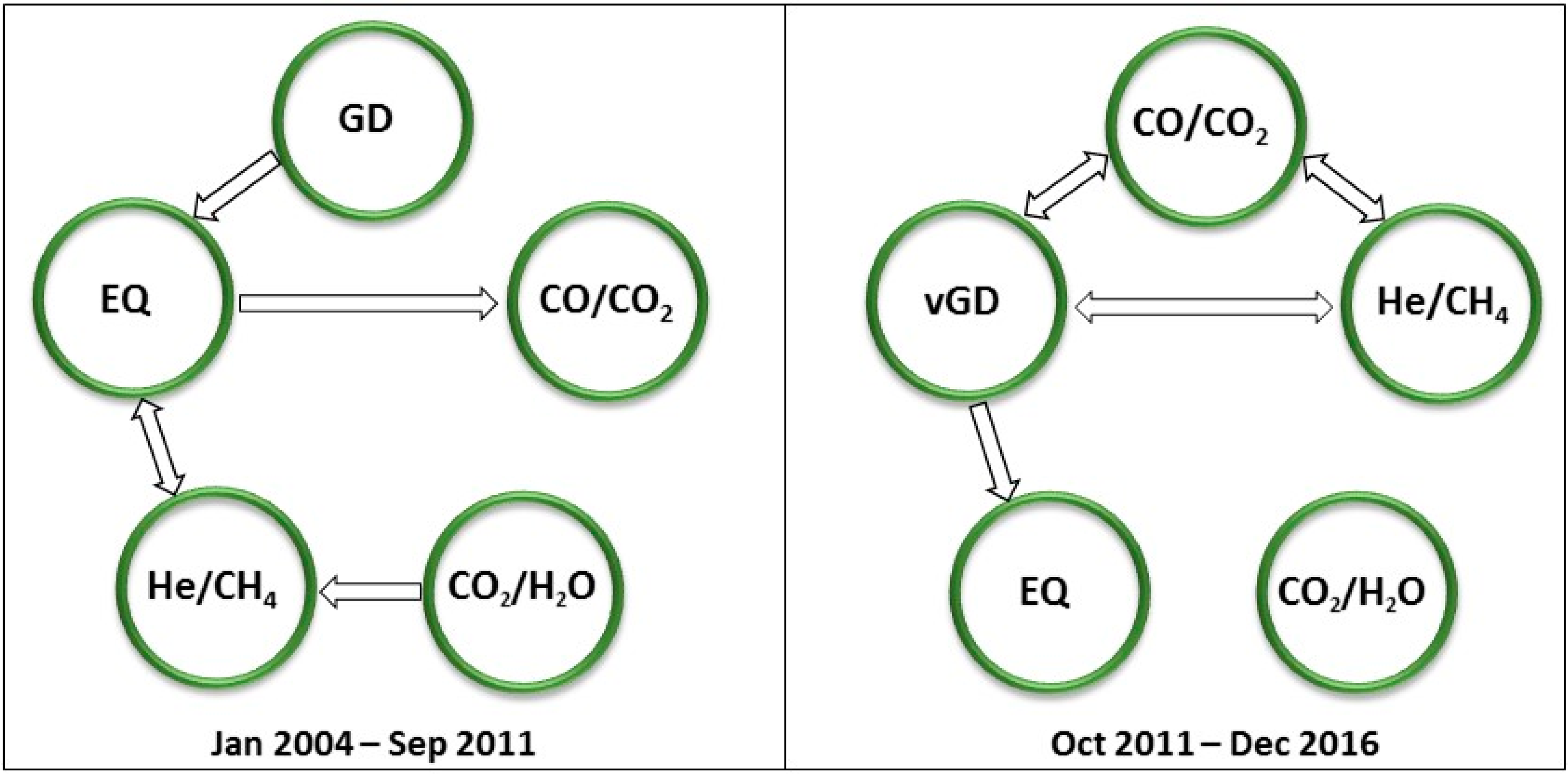
Granger Causality Wald Test		Jan 2004–Sep 2011	Oct 2011–Dec 2016
Variable Y	Variable X	F (P-value)	F (P-value) (*)
GD	EQ	0.586 (0.6260)	1.212 (0.3167)
GD	He/CH4	1.394 (0.2525)	2.174 (0.0910)
GD	CO2/H2O	0.280 (0.8391)	0.158 (0.9234)
GD	CO/CO2	1.453 (0.2356)	2.761 (0.0535)
EQ	GD	5.200 (0.0028)	2.721 (0.0561)
EQ	He/CH4	2.709 (0.0524)	0.399 (0.7544)
EQ	CO2/H2O	1.513 (0.2196)	1.179 (0.3290)
EQ	CO/CO2	1.559 (0.2079)	0.528 (0.6654)
He/CH4	GD	0.637 (0.5936)	4.219 (0.0065)
He/CH4	EQ	3.688 (0.0163)	0.269 (0.8473)
He/CH4	CO2/H2O	3.172 (0.0301)	0.579 (0.6317)
He/CH4	CO/CO2	1.281 (0.2883)	3.165 (0.0339)
CO2/H2O	GD	1.009 (0.3944)	1.810 (0.1596)
CO2/H2O	EQ	0.985 (0.4053)	1.456 (0.2398)
CO2/H2O	He/CH4	0.241 (0.8676)	0.679 (0.5696)
CO2/H2O	CO/CO2	0.870 (0.4614)	0.117 (0.9496)
CO/CO2	GD	0.312 (0.8166)	2.272 (0.0937)
CO/CO2	EQ	3.543 (0.0194)	0.666 (0.5772)
CO/CO2	He/CH4	1.379 (0.2570)	2.634 (0.0619)
CO/CO2	CO2/H2O	1.075 (0.3660)	0.547 (0.6530)

and we show the unidirectional and bidirectional causality relationships in Figure 4. In the first sub-period GD and CO₂/H₂O, respectively, Granger-cause EQ and He/CH_4. The latter variables are in feedback. EQ Granger-cause CO/CO₂. In the second sub-period, He/CH₄ and CO/CO₂ are in feedback. Weaker feedback appears also between He/CH₄ and vGD as well as between CO/CO₂ and vGD. Moreover, vGD Granger-cause EQ and CO₂/H₂O results to be independent.

Before discussing the obtained results, it is worth noting to remember that Granger causality is not intended as strictly causality but indicates that one thing happens before something else.

5. Discussion

The present work is the first attempt to disclose Granger causal relationships among geo-indicator variables monitored at CFc. Thus, results will be discussed and interpreted at the light of previous studies based on different approaches. The two different explored sub-periods will be firstly discussed separately and finally together.

In the first sub-period, the results of correlation analysis agree with those from the Granger test only as regards the existence of a relation between CO₂/H₂O and He/CH₄, reporting evidence of the interaction between exsolved hot magmatic gases (CO₂-rich) and the hydrothermal system. Since CO₂/H₂O anticipate He/CH₄, we can argue that the injection of deep-rooted CO₂/H₂O at the base of the hydrothermal system drives the increase of magmatic species such as He/CH₄ within the hydrothermal system that feeds the Bocca Grande fumarole. This result is in agreement with observations reported in [22]. The unidirectional causalities found from GD to EQ and from EQ to CO/CO₂ and the bidirectional causality found between EQ and He/CH₄ highlight relations that did not appear from the correlation analysis. In calderas hosting hydrothermal systems, GD and EQ can be associated to magmatic (magmatic bodies/fluids injection or removal) or to non-magmatic processes (groundwater properties fluctuations, poro-elastic transients in the hydrothermal system, regional stress field variations) as well as to their combined action [3,24,72,73,74]. Both magma intrusion and crystallization can act as a source for pressure–volume changes, and thus provide enough energy for crustal deformation and for rock failure in the brittle domain; rock failure likely provides fractures for fluids transport triggering earthquake swarms. Moreover, short-term oscillations linked to thermohydromechanical disturbances of the hydrothermal system have also been recorded [75]. Fluid migration in both scenarios, magmatic and hydrothermal sources, plays a key role. For CFc, a mechanism involving ground deformation, magmatic fluid migration and earthquakes generated through brittle shear failure processes, has already been proposed by other authors [76,77]. Here, the precedence of GD on EQ, both responding to pressure changes, indicates that deformation fluctuations generate elastic stress acting on rocks which ultimate response is represented by the occurrence of EQ. The precedence of the GD with respect to EQ is probably due to the time necessary for the crustal fluids to ascend through the brittle domain. Since EQ is in feedback with He/CH₄, we can argue that the changes in the volume of magmatic species in the hydrothermal system evolve together with EQ occurrences due to the pore pressure acting on rocks. Indeed, while fluid migration along faults or fractures may promote earthquakes, these last may enhance permeability facilitating fluid migration [78]. In this framework, EQ anticipates CO/CO₂ which is considered the most sensitive reactive species to temperature [57]. Maybe, CO-rich species reach the surface with a delay which depends on the earthquakes’ effectiveness in generating escape routes (cracks and fissures) toward the surface. In this regard, numerical simulations have shown that fumaroles’ fluid composition also depends on the rock’s properties, like permeability, which controls the timing and the amplitude of their changes through time [79].

In the second sub-period, significant correlations only appear between GD and CO₂/H₂O and between GD and CO/CO₂. Contrastingly, the Granger test, which now accounts for ground displacement velocity (vGD), reveals a denser network of relationships among the variables. Notably, a more complex model with mutually interacting variables points to increased dynamical connectivity. Particularly interesting are the new interactions found for CO/CO₂, which in the first sub-period was only staggered in time by EQ. Here, CO/CO₂ is in feedback with He/CH₄ and with vGD; moreover, He/CH₄ is in feedback with vGD which, in turn, anticipates EQ. As already reported CO/CO₂ is sensitive to temperature variations [57], thus we may derive that temperature fluctuations are evolving together with fluctuations of magmatic species such as He/CH₄ and with deformations. Under hydrothermal conditions, the permeability of fractured rocks depends significantly on the temperature [80]. A laboratory study on representative materials from CFc showed that the Neapolitan Yellow Tuff permeability increases with increasing thermal stressing temperature [81]. Our results indicate a cyclic behavior driven by pressure and thermal stress fluctuations involving sealing and fracturing processes. The pressure and fluid volume increase provoke inflation and temperature growth. Afterwards, the augmented fracturing processes induce pressure dissipation and ground subsidence, by means of the upwards release of fluids. As the pressure dissipates, the fluid flux and temperature both lower with consequent fractures sealing, which in turn determines the pressure increase. The fluid pressure cycling recorded by changes in vGD is finally followed by EQ, as already observed in the first period. Overall, the temperature of the shallow hydrothermal system seems to play a key role along with pressure, thus making thermohydromechanical changes the driving forces. vGD and EQ could represent the mechanical response to the shallow volume–pressure–temperature induced stress. The enhanced connectivity dynamic reasonably reflects an increased velocity of interactions among the variables in this second sub-period.

As just seen, the results of the Granger test are often different from the results of the correlations in terms of relationships found between the variables. The appearance of some relationships in the correlation analysis was not confirmed in terms of Granger causal relationships and vice versa. For example, in the first sub-period, significant correlations exist among GD and geochemical species, especially between GD and CO₂/H₂O and between GD and He/CH₄ but no causal relations are found between GD and CO₂/H₂O and between GD and He/CH₄. This type of discordance may be due to spurious correlations which generate when variables share a common trend or to correlations with an indirect (latent) variable [82]. In complex systems, as the present case, it is not uncommon to come across circumstances in which two variables depend on a third latent variable omitted in the VAR model. For CFc, the relation between ground deformation and fumarolic gas chemistry changes has been linked to different and/or interconnected processes. Hydrothermal and magmatic sources have been proposed [47,83], invoking over-pressured fluids produced by magma crystallization, overpressure of the hydrothermal system due to the emplacement of magma at shallow depths, increase in pore pressures within the hydrothermal system due to active degassing. These different interpretations share a common element which is the pressure changes occurring within the system. In this context, it is immediate to invoke the pressure as a latent variable. However, it cannot be excluded that the failure to reject the null hypothesis may be due to the number of lags or the blanketing effect deriving from the combination of different casual links [82]. Whatsoever, the interesting point here is that during this first sub-period, the only variables that are not preceded by the others are GD and CO₂/H₂O, notably two pressure-driven variables. As for the second sub-period, we note that CO₂/H₂O results independently. As already stated, this result may depend on the number of the used lags which cannot capture longer-term fluctuations of deep-rooted processes.

Conversely, both in the first and in the second investigated periods, several links not revealed by the correlation analysis were disclosed by the Granger test. This type of discordance is quite common because correlation does not mean causation and unconventional approaches, like Granger test, are generally used to reveal hidden relationships.

This work differs from most existing studies in that it is based on a purely statistical approach to explore the data structure and causal relationships between volcanological variables of interest. Open issues, which could be explored using different geochemical ratios, exogenous data [84] or cross-mapping techniques [13], still remain. However, within the limits (number and type of variables, order model) of the estimated VAR model, the Granger test allowed to reveal the existence of a number of delayed relationships with causalities that are hopefully in certain agreement with studies performed in a similar context [85,86,87].

6. Conclusions

Ground deformations, seismicity and geochemical time series recorded at CFc were analyzed via a purely statistical approach. Our most striking result derives from the exploration of causal relations made within two distinct sub-periods detected by the cluster analysis. Granger causality results in the first and in second sub-periods are different, reflecting the distinctive features of the volcano driving forces at different unrest stages. Basically, we recognize the contribution of different processes that drive these stages. During 2004–2011, we infer that the unrest awakening could be ascribed by hydrothermal system pressure fluctuations, likely generated by a magmatic process. GD and CO₂/H₂O seem to be the most suitable geo-indicators in revealing the unrest awakening. During the end of 2011 till the end of 2016, the unrest evolution could be ascribed to the thermohydromechanical engine. CO/CO₂, He/CH₄ and vGD seem to be the most suitable geo-indicators of unrest characterized by a higher dynamism. The temporal evolution of the observed seismicity in this period (increase of earthquakes at a depth of < 1 km), suggests a more localized and shallower dynamic. Our results capture interesting features of the recent CFc unrest with a method never applied in volcanic contexts. The proposed analysis is not in competition with the methods traditionally used to study volcanic environments. Conversely, considering that for complex environments any method implies and returns simplifications, we believe that new approaches deserve interest and exploration. Additional information may be further investigated by analyzing other data or using a complementary approach. Identifying causal networks or performing frequency domain analysis could be used to improve our knowledge and forecasting ability in active calderas.