Assessment of Geotechnical Seismic Isolation (GSI) as a Mitigation Technique for Seismic Hazard Events
Abstract
1. Background
2. Case Study
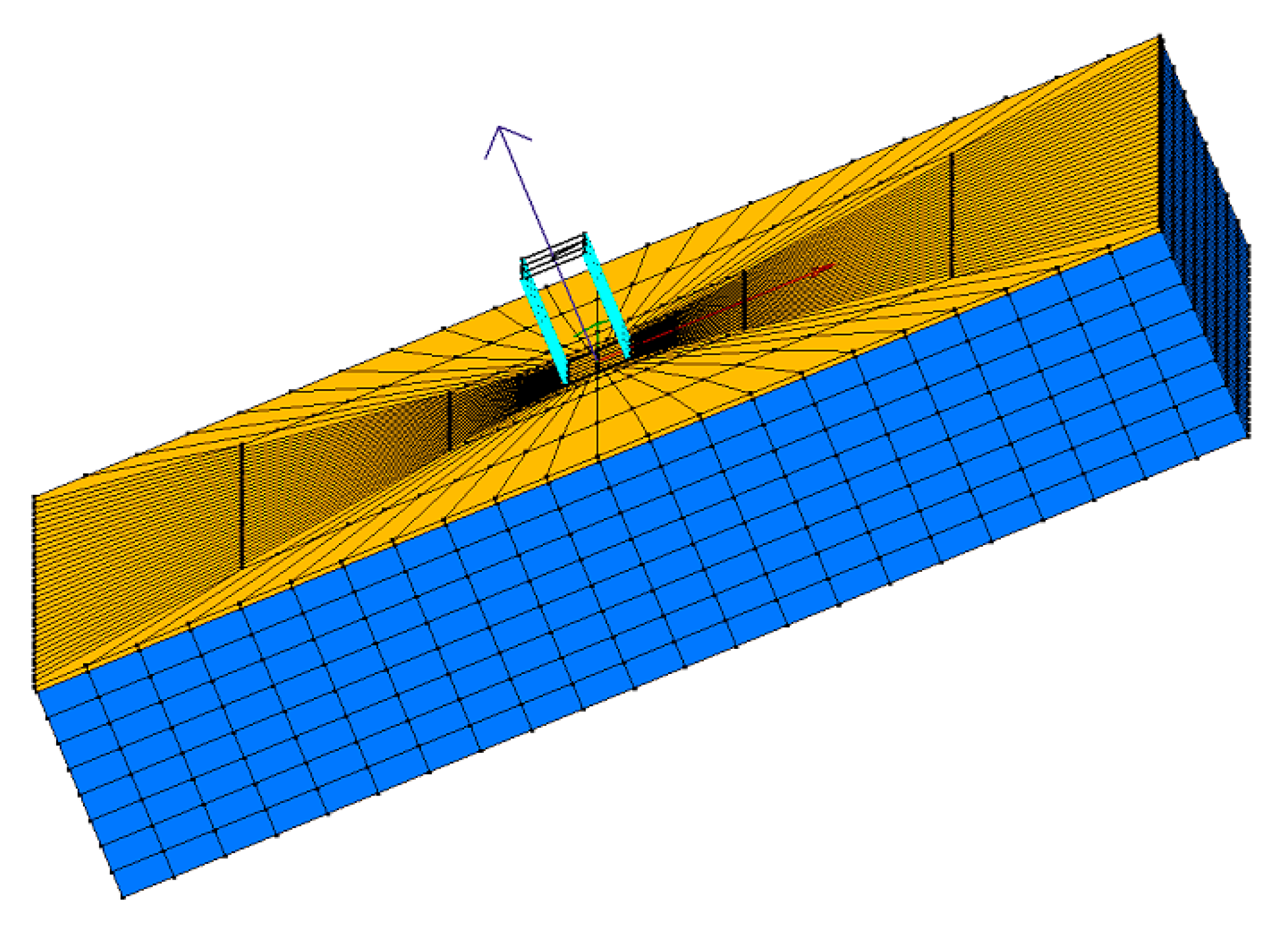
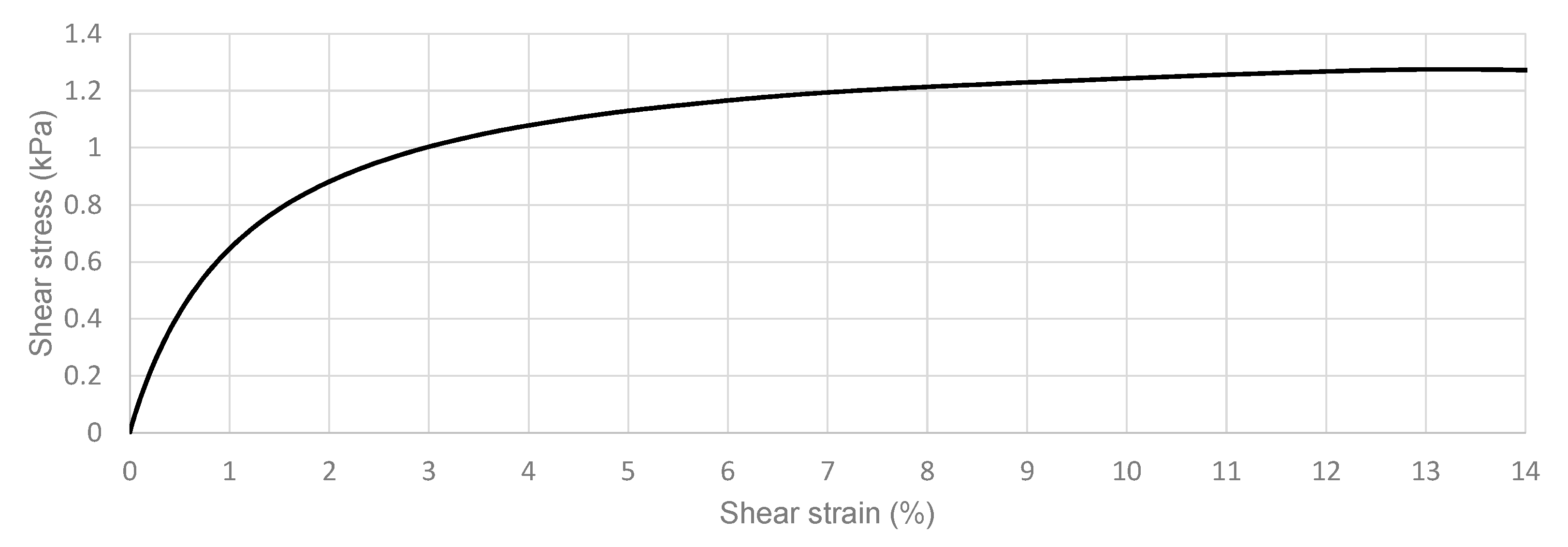
3. Finite Element Models
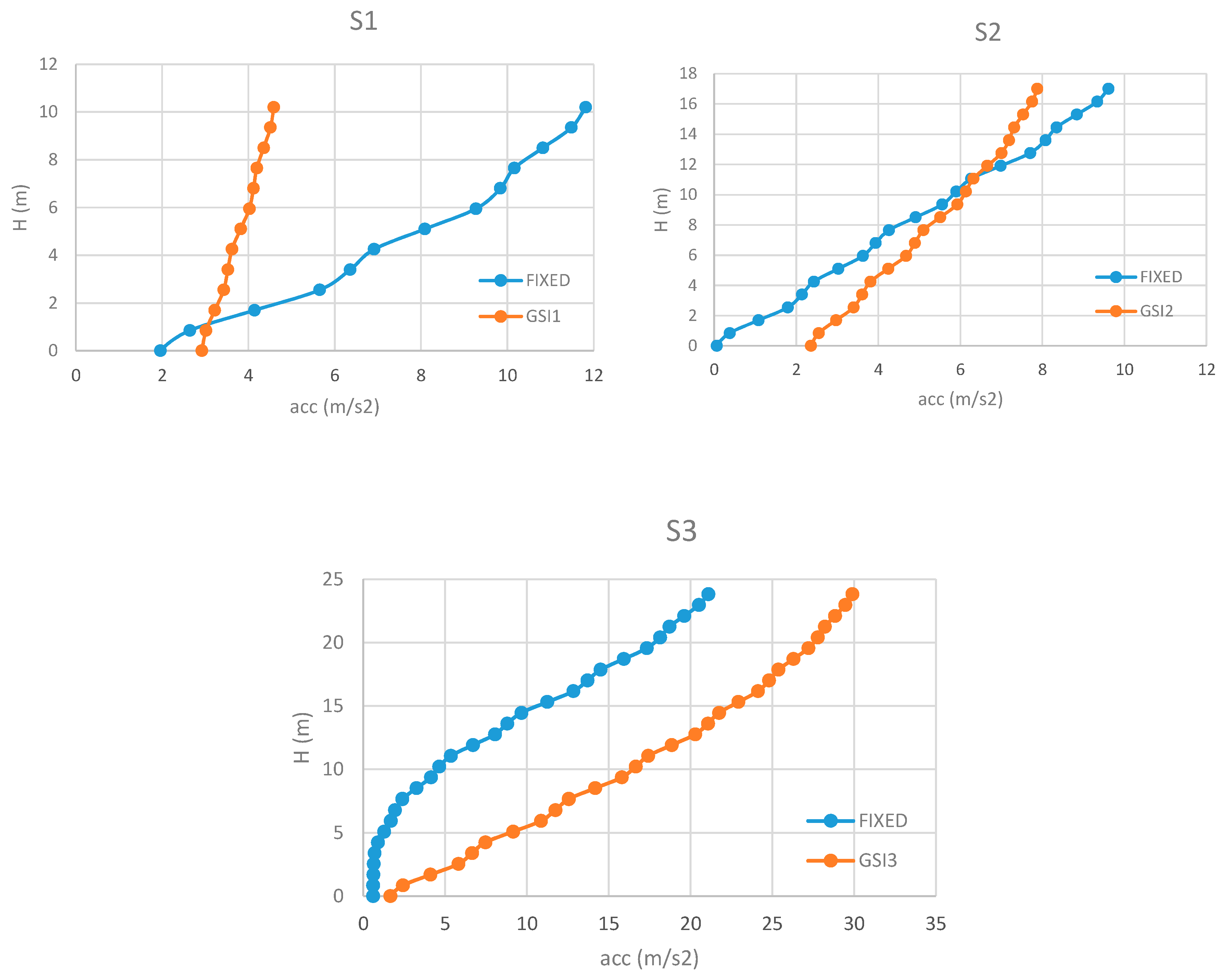
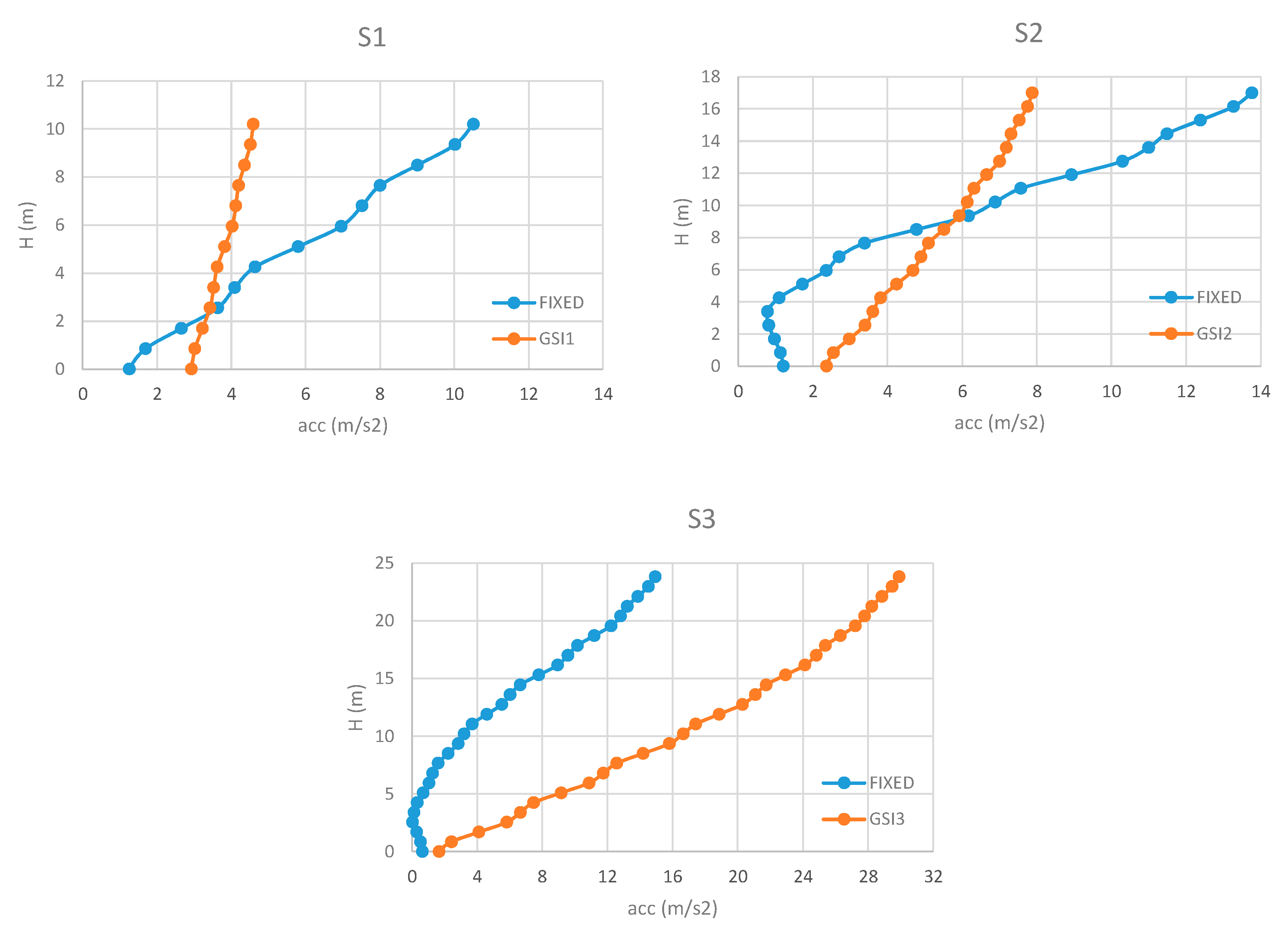
4. Results
5. Conclusions
Funding
Conflicts of Interest
References
- Przewłócki, J.; Dardzinska, I.; Swinianski, J. Review of historical buildings’ foundations. Géotechnique 2005, 55, 363–372. [Google Scholar]
- Carpani, B. Base isolation from a historical perspective. In Proceedings of the 16th World Conference on Earthquake, Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Kulukčija, S.; Humo, M.; Mandžić, E.; Mandžić, K.; Selimović, M. Existing historical foundation system of two old bridges from the Ottoman period in Bosnia and Herzegovina. In Proceedings of the Third International Congress on Construction, Cottbus, Germany, 20–24 May 2009. [Google Scholar]
- Tsiavos, A.; Alexander, N.; Diambra, A.; Ibraim, E.; Vardanega, P.J.; Gonzalez-Buelga, A.; Sextos, A.G. A sand-rubber deformable granular layer as a low-cost seismic isolation strategy in developing countries: Experimental investigation. Soil Dyn. Earthq. Eng. 2019, 125, 105731. [Google Scholar] [CrossRef]
- Tsang, H.H. Seismic isolation by rubber-soil mixtures for developing countries. Earthq. Eng. Struct. Dyn. 2007, 37, 283–303. [Google Scholar] [CrossRef]
- Pecker, A.; Prevost, J.H.; Dormieux, L. Analysis of pore pressure generation and dissipation in cohesionless materials during seismic loading. J. Earth. Eng. 2001, 5, 441–464. [Google Scholar] [CrossRef]
- Pecker, A. Aseismic foundation design process, lessons learned from two major projects: The Vasco de Gama and the Rion Antirion bridges. In Proceedings of the ACI International Conference on Seismic Bridge Design and Retrofit, La Jolla, CA, USA, 8–9 December 2003. [Google Scholar]
- Steenfelt, J.S.; Foged, B.; Augustesen, A.H. Izmit Bay bridge-geotechnical challenges and innovative solutions. Int. J. Brid. Eng. 2015, 3, 53–68. [Google Scholar]
- Azinović, B.; Koren, D.; Kilar, V. The seismic response of low-energy buildings founded on a thermal insulation layer—A parametric study. Eng. Struct. 2014, 81, 398–411. [Google Scholar] [CrossRef]
- Azinović, B.; Kilar, V.; Koren, D. Energy-efficient solution for the foundation of passive houses in earthquake-prone regions. Eng. Struct. 2016, 112, 133–145. [Google Scholar] [CrossRef]
- Azzam, W.; Ayeldeen, M.; El Siragy, M. Improving the structural stability during earthquakes using in-filled trench with EPS geofoam—Numerical study. Arab. J. Geosci. 2018, 11, 395. [Google Scholar] [CrossRef]
- Hadad, H.A.; Calabrese, A.; Strano, S.; Serino, G. A Base Isolation System for Developing Countries Using Discarded Tyres Filled with Elastomeric Recycled Materials. J. Earthq. Eng. 2016, 21, 246–266. [Google Scholar] [CrossRef]
- Karatzia, X.; Mylonakis, G. Geotechnical seismic isolation using eps geofoam around piles. In Proceedings of the 6th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Rhodes Island, Greece, 15–17 June 2017. [Google Scholar]
- Doudoumis, I.; Papadopoulos, P.; Papaliangas, T. Low-cost base isolation system on artificial soil layers with low shearing resistance. In Proceedings of the 12th European Conference on Earthquake Engineering, London, UK, 9–13 September 2002. [Google Scholar]
- Yegian, M.K.; Catan, M. Soil Isolation for Seismic Protection Using a Smooth Synthetic Liner. J. Geotech. Geoenviron. Eng. 2004, 130, 1131–1139. [Google Scholar]
- Yegian, M.K.; Kadakal, U. Foundation Isolation for Seismic Protection Using a Smooth Synthetic Liner. J. Geotech. Geoenviron. Eng. 2004, 130, 1121–1130. [Google Scholar]
- Nanda, R.P.; Shrikhande, M.; Agarwal, P. Effect of ground motion characteristics on the pure friction isolation system. Earthq. Struct. 2012, 3, 169–180. [Google Scholar] [CrossRef]
- Kalpakci, V.; Bonab, A.T.; Özkan, M.Y.; Gulerce, Z. Experimental evaluation of geomembrane/geotextile interface as base isolating system. Geosynth. Int. 2018, 25, 1–11. [Google Scholar] [CrossRef]
- Makris, N. A half-century of rocking isolation. Earthq. Struct. 2014, 7, 1187–1221. [Google Scholar] [CrossRef]
- Chung, Y.L.; Du, L.J.; Pan, H.H. Performance evaluation of a rocking steel column base equipped with asymmetrical resistance friction damper. Earthqu. Struct. 2019, 17, 49–61. [Google Scholar]
- Feng, R.; Chen, Y.; Cui, G. Dynamic response of post-tensioned rocking wall-moment frames under near-fault ground excitation. Earthqu. Struct. 2018, 15, 243–251. [Google Scholar]
- Wang, J.; He, J.X.; Yang, Q.; Yang, N. Study on mechanical behaviors of column foot joint in traditional timber structure. Earthqu. Struct. 2018, 66, 1–14. [Google Scholar]
- Banović, I.; Radnić, J.; Grgić, N. Geotechnical Seismic Isolation System Based on Sliding Mechanism Using Stone Pebble Layer: Shake-Table Experiments. Shock. Vib. 2019, 2019, 9346232. [Google Scholar] [CrossRef]
- Banović, I.; Radnić, J.; Grgić, N.; Matesan, D. The Use of Limestone Sand for the Seismic Base Isolation of Structures. Adv. Civ. Eng. 2018, 2018, 9734283. [Google Scholar] [CrossRef]
- Spizzuoco, M.; Calabrese, A.; Serino, G. Innovative low-cost recycled rubber–fiber reinforced isolator: Experimental tests and Finite Element Analyses. Eng. Struct. 2014, 76, 99–111. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Loli, M.; Georgarakos, T.; Drosos, V. Shaking Table Testing of Rocking—Isolated Bridge Pier on Sand. J. Earthq. Eng. 2012, 17, 1–32. [Google Scholar] [CrossRef]
- Xiong, W.; Li, Y. Seismic isolation using granulated tire-soil mixtures for less-developed regions: Experimental validation. Earthq. Eng. Struct. Dyn. 2013, 42. [Google Scholar] [CrossRef]
- Xiong, W.; Yan, M.R.; Li, Y.Z. Geotechnical Seismic Isolation System—Further Experimental Study. Appl. Mech. Mater. 2014, 580, 1490–1493. [Google Scholar] [CrossRef]
- Patil, S.J.; Reddy, G.; Shivshankar, R.; Babu, R.; Jayalekshmi, B.; Kumar, B. Seismic base isolation for structures using river sand. Earthq. Struct. 2016, 10, 829–847. [Google Scholar] [CrossRef]
- Radnić, J.; Grgić, N.; Matešan, D.; Baloević, G. Shake table testing of reinforced concrete columns with different layout size of foundation. Mater. Werkst. 2015, 46, 348–367. [Google Scholar] [CrossRef]
- Tehrani, F.M.; Hasani, A. Behaviour of Iranian low rise buildings on sliding base to earthquake excitation. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996; p. 1433. [Google Scholar]
- Mavronicola, E.; Komodromos, P.; Charmpis, D.C. Numerical Investigation of Potential Usage of Rubber-Soil Mixtures as a Distributed Seismic Isolation Approach. In Proceedings of the Tenth International Conference on Computational Structures Technology, Valencia, Spain, 14–17 September 2010. [Google Scholar]
- Panjamani, A.; Ramegowda, M.D.; Divyesh, R. Low cost damping scheme for low to medium rise buildings using rubber soil mixtures. Jpn. Geotech. Soc. Spec. Publ. 2015, 3, 24–28. [Google Scholar] [CrossRef][Green Version]
- Xiao, H.; Butterworth, J.W.; Larkin, T. Low technology techniques for seismic isolation. In Proceedings of the 2004 NZSEE Conference, Rototua, New Zealand, 19–21 March 2004. [Google Scholar]
- Bandyopadhyay, S.; Sengupta, A.; Reddy, G.R. Performance of sand and shredded rubber tire mixture as a natural base isolator for earthquake protection. Earthq. Eng. Eng. Vib. 2015, 14, 683–693. [Google Scholar] [CrossRef]
- Brunet, S.; De La Llera, J.; Kausel, E. Non-linear modeling of seismic isolation systems made of recycled tire-rubber. Soil Dyn. Earthq. Eng. 2016, 85, 134–145. [Google Scholar] [CrossRef]
- Tsang, H.-H.; Pitilakis, K. Mechanism of geotechnical seismic isolation system: Analytical modeling. Soil Dyn. Earthq. Eng. 2019, 122, 171–184. [Google Scholar] [CrossRef]
- Tsang, H.-H.; Lo, S.H.; Xu, X.; Sheikh, M.N. Seismic isolation for low-to-medium-rise buildings using granulated rubber-soil mixtures: Numerical study. Earthq. Eng. Struct. Dyn. 2012, 41, 2009–2024. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, Q.; Zhang, Q.; He, J. Numerical study on seismic isolation effect of gravel cushion. In Proceedings of the 7th International Conference on Discrete Element Methods, Dalian, China, 1–4 August 2016. [Google Scholar]
- Forcellini, D. Assessment on geotechnical seismic isolation (GSI) on bridge configurations. Innov. Infrastruct. Solutions 2017, 2, 760. [Google Scholar] [CrossRef]
- Pitilakis, K.; Karapetrou, S.; Tsagdi, K. Numerical investigation of the seismic response of RC buildings on soil replaced with rubber–sand mixtures. Soil Dyn. Earthq. Eng. 2015, 79, 237–252. [Google Scholar] [CrossRef]
- Van Engelen, N.C.; Osgooei, P.M.; Tait, M.J.; Konstantinidis, D. Experimental and finite element study on the compression properties of Modified Rectangular Fiber-Reinforced Elastomeric Isolators (MR-FREIs). Eng. Struct. 2014, 74, 52–64. [Google Scholar] [CrossRef]
- Rossi, E.; Sebastiani, M.; Gigliotti, R.; D’Amato, M. An Innovative Procedure for the In-situ Characterization of Elastomeric Bearings by Using Nanoindentation Test. Int. J. Arch. Herit. 2020, 1–13. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G. Nanoindentation in materials research: Past, present, and future. MRS Bull. 2010, 35, 897–907. [Google Scholar] [CrossRef]
- Habieb, A.B.; Valente, M.; Milani, G. Hybrid seismic base isolation of a historical masonry church using unbonded fiber reinforced elastomeric isolators and shape memory alloy wires. Eng. Struct. 2019, 196, 109281. [Google Scholar] [CrossRef]
- Dhanya, J.S.; Boominathan, A.; Banerjee, S. Response of low-rise building with geotechnical seismic isolation system. Soil Dyn. Earthquake Eng. 2020, 136, 106187. [Google Scholar] [CrossRef]
- Lu, J.; Elgamal, A.; Yang, Z. OpenSeesPL: 3D Lateral Pile-Ground Interaction, User Manual, Beta 1.0. Available online: http://soilquake.net/openseespl/ (accessed on 5 June 2020).
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. Open System for Earthquake Engineering Simulation User Command-Language Manual. Available online: http://opensees.berkeley.edu/OpenSees/manuals/usermanual (accessed on 5 June 2020).
- Forcellini, D. Seismic assessment of a benchmark based isolated ordinary building with soil structure interaction. Bull. Earthq. Eng. 2017, 16, 2021–2042. [Google Scholar] [CrossRef]
- Forcellini, D. Cost assessment of isolation technique applied to a benchmark bridge with soil structure interaction. Bull. Earthq. Eng. 2016, 15, 51–69. [Google Scholar] [CrossRef]
- Forcellini, D. Numerical simulations of liquefaction on an ordinary building during Italian (20 May 2012) earthquake. Bull. Earthq. Eng. 2019, 17, 4797–4823. [Google Scholar] [CrossRef]
- Forcellini, D. Soil-structure interaction analyses of shallow-founded structures on a potential-liquefiable soil deposit. Soil Dyn. Earthq. Eng. 2020, 133, 106108. [Google Scholar] [CrossRef]
- Mina, D.; Forcellini, D. Soil–structure interaction assessment of the 23 November 1980 Irpinia-Basilicata earthquake. Geosciences 2020, 10, 152. [Google Scholar] [CrossRef]
- Skinner, R.I.; Robinson, W.H.; McVerry, G.H. An Introduction to Seismic Isolation; John Willey & Sons: New York, NY, USA, 1994. [Google Scholar]








| Structure | S1 | S2 | S3 |
|---|---|---|---|
| Number of floor | 3 | 5 | 7 |
| H [m] | 10.20 | 17.00 | 23.80 |
| H/B | 1.38 | 2.30 | 3.22 |
| T1 [s] | 0.301 | 0.484 | 0.685 |
| T2 [s] | 0.107 | 0.165 | 0.229 |
| T3 [s] | 0.073 | 0.101 | 0.134 |
| T4 [s] | — | 0.078 | 0.100 |
| T5 [s] | — | 0.069 | 0.082 |
| T6 [s] | — | — | 0.072 |
| T7 [s] | — | — | 0.053 |
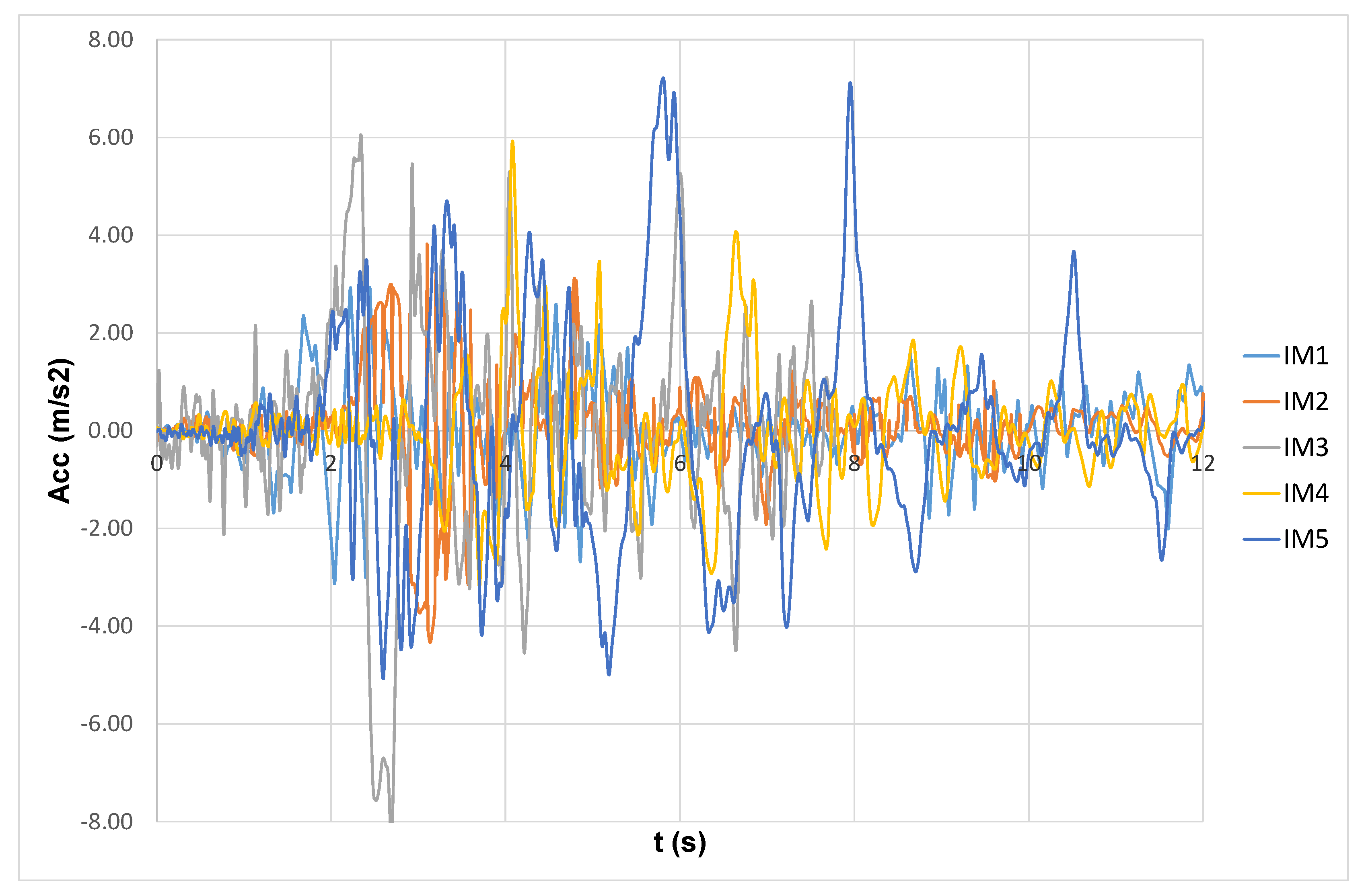
| Input | Station | PGA [g] | PGV [m/s] | PGD [cm] |
|---|---|---|---|---|
| IM1) Northridge (1994) | Rinaldi receiving | 0.89 | 185.08 | 60.07 |
| IM2) ElCentro (1940) | Caltech IIA001 | 0.35 | 38.47 | 82.44 |
| IM3) Northridge (1994) | Sylmar Converter | 0.70 | 135.82 | 58.20 |
| IM4) Erzincan (1992) | Erzincan | 0.44 | 125.80 | 53.30 |
| IM5) Hyogo-Ken (1995) | Takatori | 0.74 | 155.44 | 44.95 |
| Parameters | Value |
|---|---|
| Density [Mg/m3] | 2.4 |
| Young Modulus [kPa] | 3.50 × 107 |
| Shear Modulus [kPa] | 1.73 × 107 |
| Cross section [m2] | 0.12 |
| Inertial moment [m4] | 9.0 × 10−4 |
| Parameters | Concrete |
|---|---|
| Density [Mg/m3] | 2.4 |
| Reference Shear Modulus [kPa] | 1.25 × 107 |
| Reference Bulk Modulus [kPa] | 1.67 × 107 |
| Soil | GSI | Soil |
|---|---|---|
| Density [Mg/m3] | 1.2 | 2.2 |
| Reference Shear Modulus [kPa] | 120 | 5.60 × 107 |
| Reference Bulk Modulus [kPa] | 390 | 7.50 × 107 |
| Shear wave velocity [m/s] | 10 | 1600 |
| Cohesion [kPa] | 40 | 10,000 |
| Input | S1 [m] | S2 [m] | S3 [m] |
|---|---|---|---|
| IM1) Northridge (1994) | 0.493 | 0.498 | 0.503 |
| IM2) ElCentro (1940) | 0.076 | 0.083 | 0.091 |
| IM3) Northridge (1994) | 0.938 | 0.945 | 0.956 |
| IM4) Erzincan (1992) | 0.341 | 0.349 | 0.356 |
| IM5) Hyogo-Ken (1995) | 0.774 | 0.781 | 0.792 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forcellini, D. Assessment of Geotechnical Seismic Isolation (GSI) as a Mitigation Technique for Seismic Hazard Events. Geosciences 2020, 10, 222. https://doi.org/10.3390/geosciences10060222
Forcellini D. Assessment of Geotechnical Seismic Isolation (GSI) as a Mitigation Technique for Seismic Hazard Events. Geosciences. 2020; 10(6):222. https://doi.org/10.3390/geosciences10060222
Chicago/Turabian StyleForcellini, Davide. 2020. "Assessment of Geotechnical Seismic Isolation (GSI) as a Mitigation Technique for Seismic Hazard Events" Geosciences 10, no. 6: 222. https://doi.org/10.3390/geosciences10060222
APA StyleForcellini, D. (2020). Assessment of Geotechnical Seismic Isolation (GSI) as a Mitigation Technique for Seismic Hazard Events. Geosciences, 10(6), 222. https://doi.org/10.3390/geosciences10060222




