Fracture Spacing Variability and the Distribution of Fracture Patterns in Granitic Geothermal Reservoir: A Case Study in the Noble Hills Range (Death Valley, CA, USA)
Abstract
:1. Introduction
- Pervasive alteration of the NH granite;
- Ubiquitous argillic alteration affecting plagioclase and biotite is present;
- Unaltered K-feldspar;
- Porosity is enhanced by the alteration and microfracturing;
- Evidence of the hydrothermal fluid percolation, as identified in an exploited geothermal reservoirs;
- Fluid circulation in open system such as in EGS systems (input of potassium and carbonates).
- Through a description of the fracture system using orientation, density, spacing and aperture parameters;
- By highlighting the role of the proximity to the regional major faults on the fracture patterns;
- By highlighting the role of the deformation gradient and structural heritage at outcrop scale.
2. Geological Setting
3. Methodology
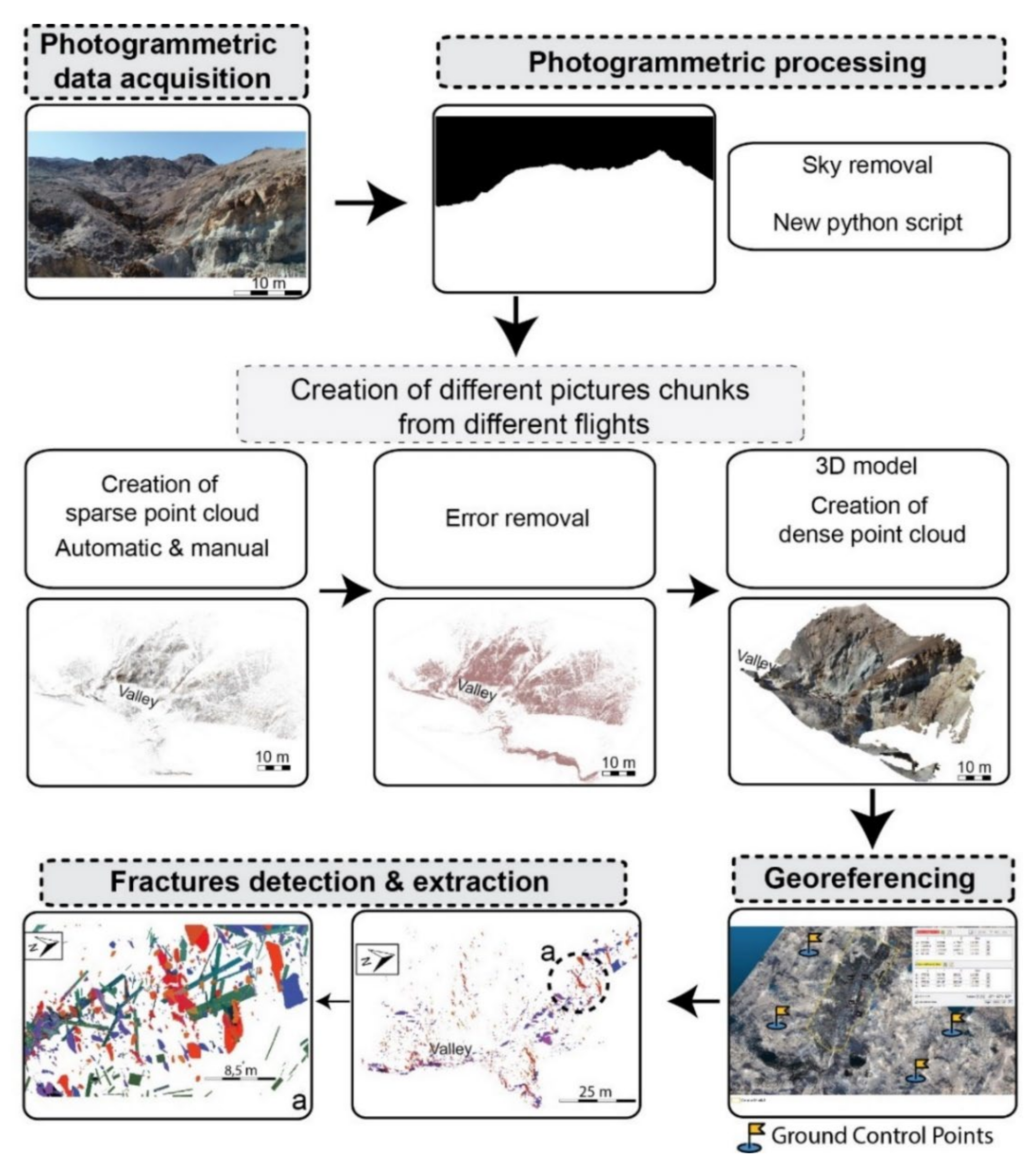
3.1. Scanline Data Acquisition
- Digitized fractures are loaded in shapefile format (e.g., shp format);
- Virtual lines are traced along the georeferenced outcrop, and the intersection between the digitized fractures and the virtual line are collected. Note that, the intersection point ID must be the same as that of digitized fractures;
- X and Y coordinates are added to the intersection points file, computed directly in QGIS®;
- Values are classified according to X coordinate in Excel software, to ensure the right position of each intersected fracture;
- Spacings are computed following [17]:
3.2. Fracture Orientation Analysis
3.3. Analysis of Spacing
3.4. Fracture Density P10
3.5. Cumulative Frequency Diagrams
4. Results
4.1. Description of Fracture Systems Acquired from NH Range
4.1.1. Fieldwork Scanlines
4.1.2. Virtual Scanlines
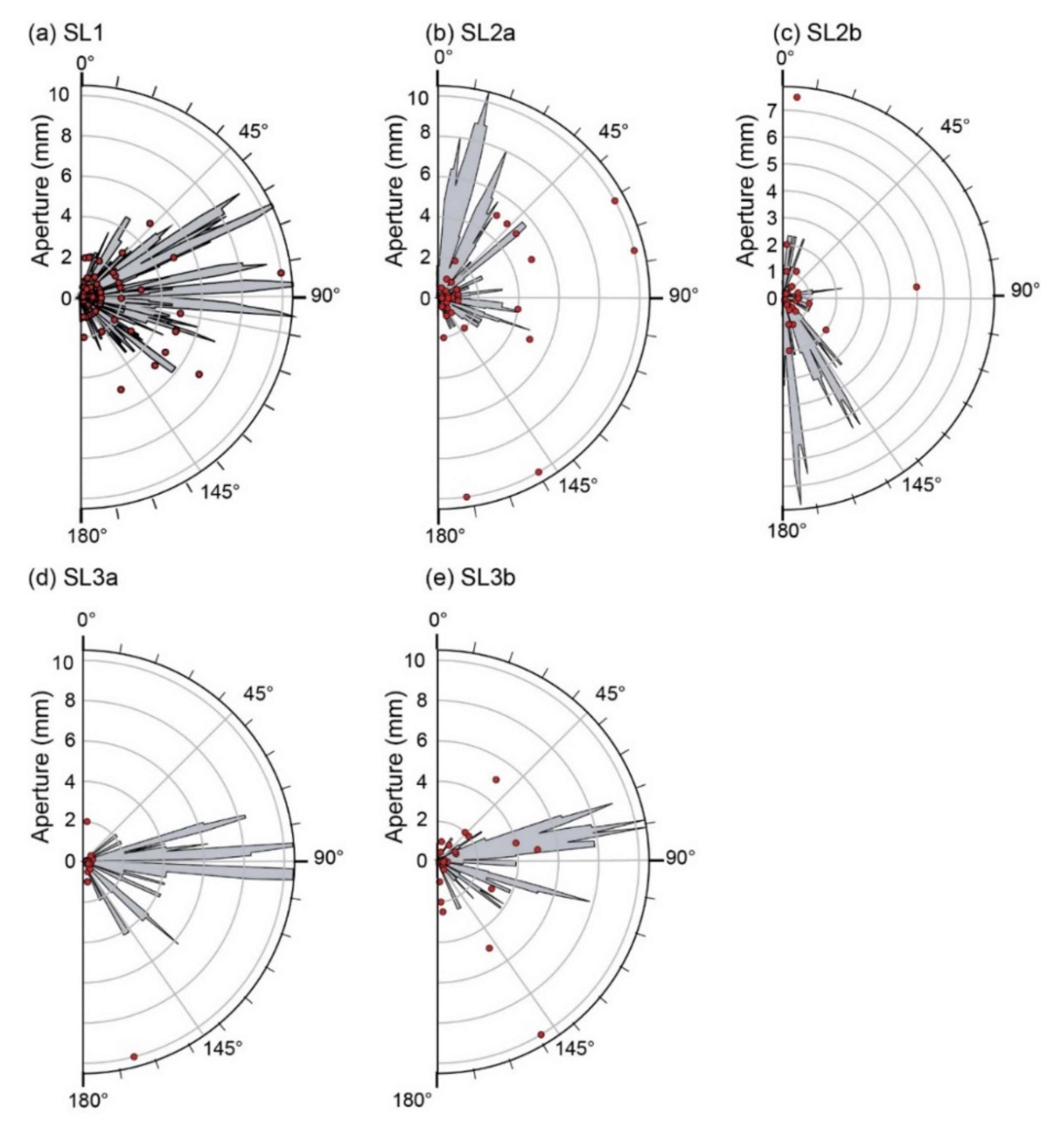
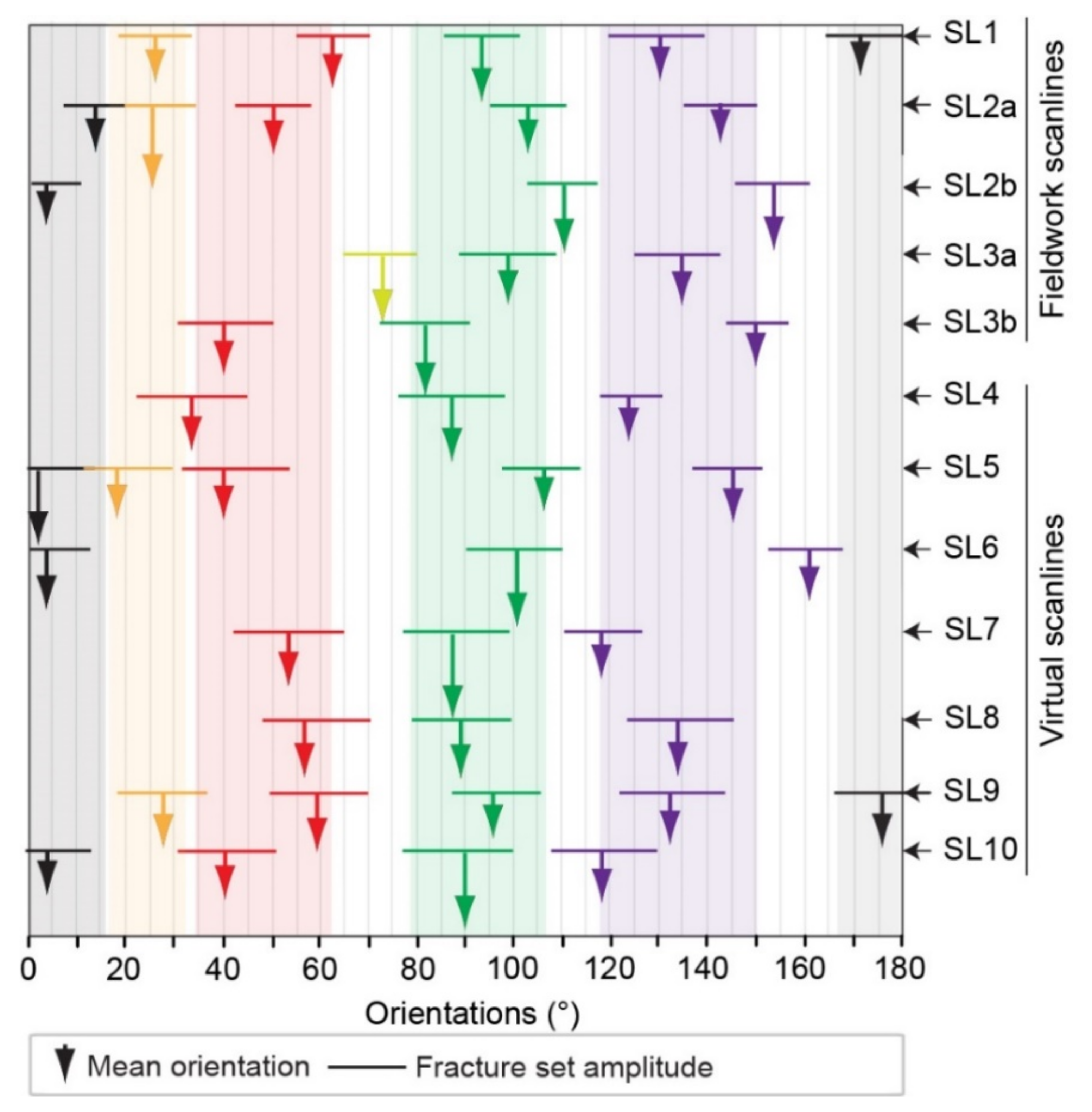
4.2. Fracture Orientation Distributions
4.3. Spatial Distribution of Fractures
- Fractures distributed randomly in fracture set N026 with Cv = 1.03;
- Fractures uniformly spaced in fracture set N062 with Cv = 0.53;
- Fractures more irregularly spaced or clustered in fracture sets N092, N0130, and N171 with, respectively, Cv = 1.44, 1.43, and 1.37.
- N029 fracture set with one fracture cluster identified around 20 m;
- N060 fracture set with four fracture clusters characterized around 20, 42, 47, and 80 m;
- N096 fracture set with one fracture cluster identified around 15–20 m;
- N132 fracture set with five fracture clusters identified around 15–20, 35, 40–45, 55, and 80 m;
- N176 fracture set with four fracture clusters identified around 20, 25, 35–40, and 55 m.
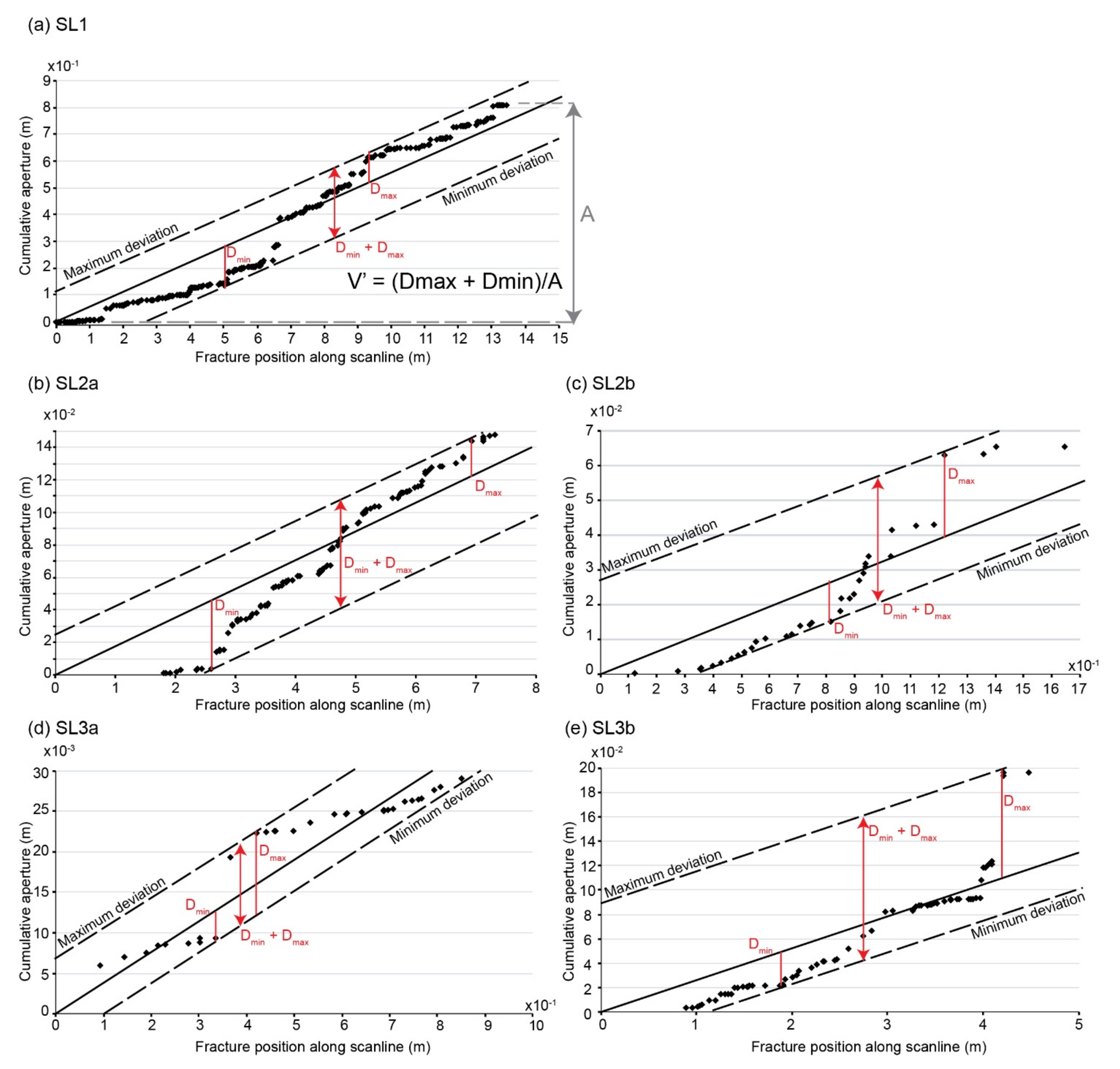
4.4. Fracture Aperture Distribution
5. Discussion
5.1. Representativness of the Fieldwork and Virtual Scanlines
5.2. Consistency of the Recorded Fracture Sets
5.3. Clustering of Fractures in Central Part of NH
- Crosscutting or location close to major faults segments: This observation is supported essentially by OT1, OT6, OT7 and OT8 fracture distribution, in which SDVFZ and a thrust fault proximity enhance the considerably clustering and fracture density of each fracture set.
- The deformation gradient: Based on fieldwork observations, the most deformed zone is located close to OT6 and OT7 and strongly impacts the fracture distribution. Indeed, the fracture density is much higher in these areas, and the fracture patterns is arranged into clusters following E/W and NW/SE directions.
5.4. Conceptual Model of NH Paleo Geothermal Analogue
6. Conclusions
- Three configurations (uniform, random and clustered distribution) were shown for SL1 spacing fractures: Regular distribution within N062, uniform distribution within N026, and clustered distribution within N092, N130, and N171 fracture sets;
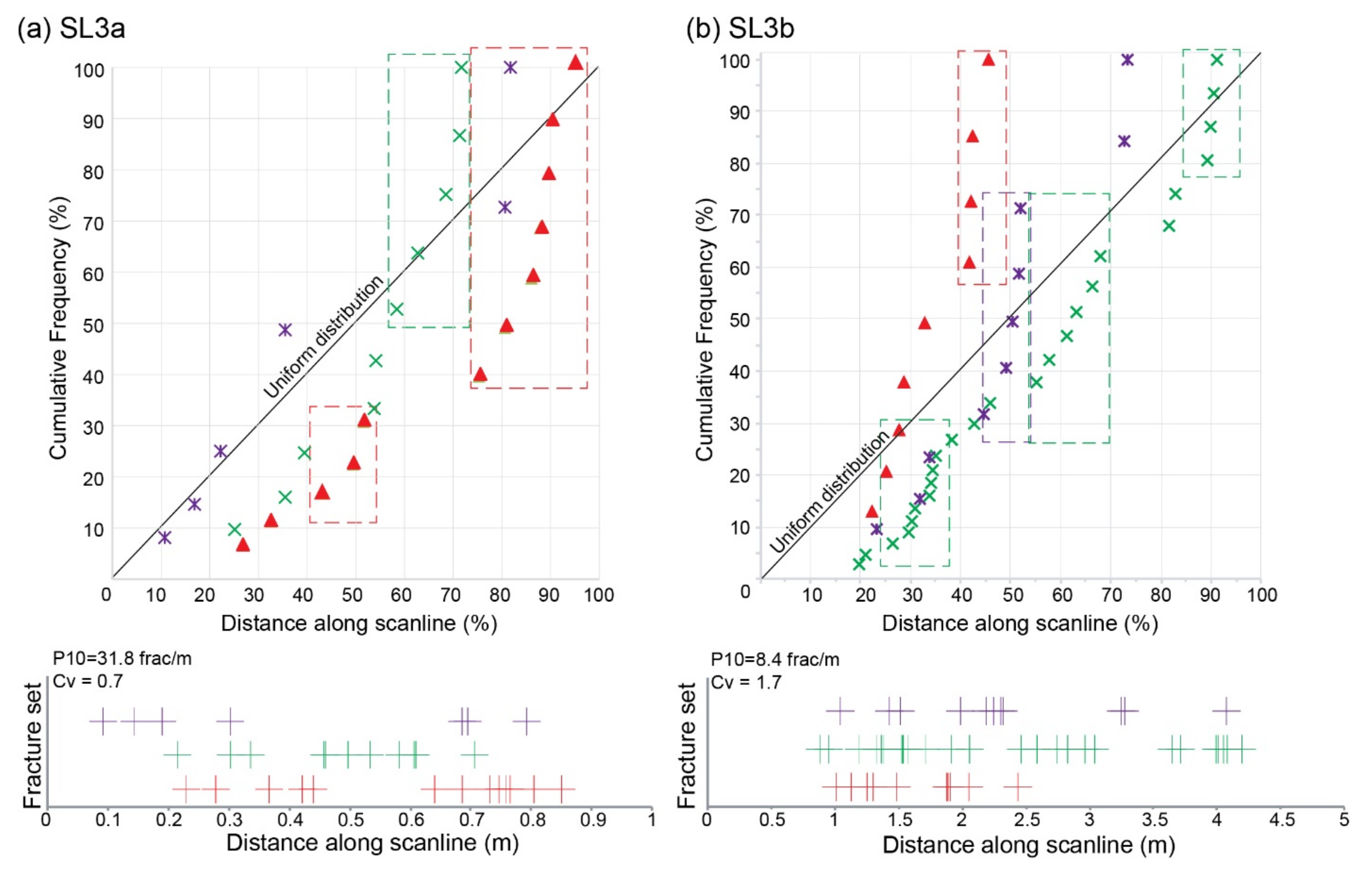
- For SL3a and SL6, two configurations were identified: Uniform distribution within respectively N077 and N100 trends, clustered distribution within N098 and N135 for SL3a, and N004 and N161 fracture sets for SL6;
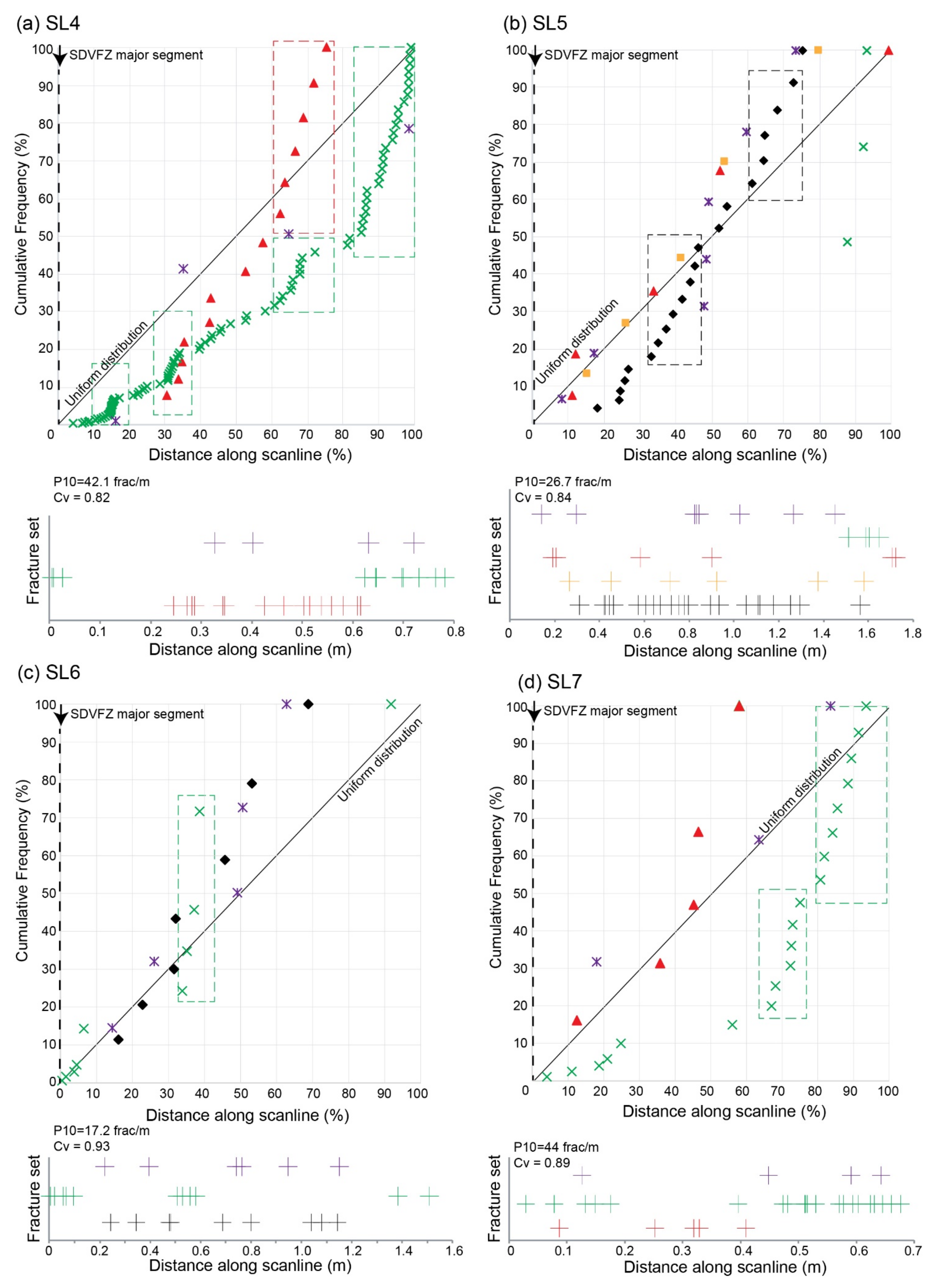
- SL2b, SL4, SL5, and SL7 profiles showed only one configuration, which consists in uniform distribution, not dependent on the direction;
- SL2a and SL3b, SL8, SL9, and SL10 showed a high Cv whatever the direction, which indicates a stronger clustering in the fracture system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Torabi, A.; Ellingsen, T.S.S.; Johannessen, M.U.; Alaei, B.; Rotevatn, A.; Chiarella, D. Fault Zone Architecture and Its Scaling Laws: Where Does the Damage Zone Start and Stop? Geol. Soc. Lond. Spec. Publ. 2020, 496, 99–124. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Nixon, C.W. The Use of Topology in Fracture Network Characterization. J. Struct. Geol. 2015, 72, 55–66. [Google Scholar] [CrossRef]
- Dezayes, C.; Lerouge, C.; Innocent, C.; Lach, P. Structural Control on Fluid Circulation in a Graben System: Constraints from the Saint Pierre Bois Quarry (Vosges, France). J. Struct. Geol. 2021, 146, 104323. [Google Scholar] [CrossRef]
- Barton, C.A.; Zoback, M.D. Self-Similar Distribution and Properties of Macroscopic Fractures at Depth in Crystalline Rock in the Cajon Pass Scientific Drill Hole. J. Geophys. Res. Solid Earth 1992, 97, 5181–5200. [Google Scholar] [CrossRef]
- Caine, J.S.; Evans, J.P.; Forster, C.B. Fault Zone Architecture and Permeability Structure. Geology 1996, 24, 1025–1028. [Google Scholar] [CrossRef]
- Callahan, O.A.; Eichhubl, P.; Olson, J.E.; Davatzes, N.C. Fracture Mechanical Properties of Damaged and Hydrothermally Altered Rocks, Dixie Valley-Stillwater Fault Zone, Nevada, USA. J. Geophys. Res. Solid Earth 2019, 124, 4069–4090. [Google Scholar] [CrossRef] [Green Version]
- Laubach, S.E.; Lamarche, J.; Gauthier, B.D.M.; Dunne, W.M.; Sanderson, D.J. Spatial Arrangement of Faults and Opening-Mode Fractures. J. Struct. Geol. 2018, 108, 2–15. [Google Scholar] [CrossRef]
- Klee, J.; Chabani, A.; Ledésert, B.A.; Potel, S.; Hébert, R.L.; Trullenque, G. Fluid-Rock Interactions in a Paleo-Geothermal Reservoir (Noble Hills Granite, California, USA). Part 2: The Influence of Fracturing on Granite Alteration Processes and Fluid Circulation at Low to Moderate Regional Strain. Geosciences 2021, 11, 433. [Google Scholar] [CrossRef]
- Bour, O.; Davy, P. Connectivity of Random Fault Networks Following a Power Law Fault Length Distribution. Water Resour. Res. 1997, 33, 1567–1583. [Google Scholar] [CrossRef]
- Genter, A.; Traineau, H.; Ledésert, B.; Bourgine, B.; Gentier, S. Over 10 Years of Geological Investigations within the HDR Soultz Project, France; International Geothermal Association: Reykjavik, Iceland, 2000; pp. 3707–3712. [Google Scholar]
- Renshaw, C.E. Influence of Subcritical Fracture Growth on the Connectivity of Fracture Networks. Water Resour. Res. 1996, 32, 1519–1530. [Google Scholar] [CrossRef]
- Laubach, S.E.; Lander, R.H.; Criscenti, L.J.; Anovitz, L.M.; Urai, J.L.; Pollyea, R.M.; Hooker, J.N.; Narr, W.; Evans, M.A.; Kerisit, S.N.; et al. The Role of Chemistry in Fracture Pattern Development and Opportunities to Advance Interpretations of Geological Materials. Rev. Geophys. 2019, 57, 1065–1111. [Google Scholar] [CrossRef] [Green Version]
- Lamarche, J.; Chabani, A.; Gauthier, B.D. Dimensional Threshold for Fracture Linkage and Hooking. J. Struct. Geol. 2018, 108, 171–179. [Google Scholar] [CrossRef]
- Bour, O.; Davy, P. On the Connectivity of Three-dimensional Fault Networks. Water Resour. Res. 1998, 34, 2611–2622. [Google Scholar] [CrossRef]
- Darcel, C.; Bour, O.; Davy, P.; de Dreuzy, J.R. Connectivity Properties of Two-Dimensional Fracture Networks with Stochastic Fractal Correlation: Connectivity of 2D fractal fracture networks. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Odling, N.E. Scaling and Connectivity of Joint Systems in Sandstones from Western Norway. J. Struct. Geol. 1997, 19, 1257–1271. [Google Scholar] [CrossRef]
- Chabani, A. Analyse Méthodologique et Caractérisation Multi-Échelle Des Systèmes de Fractures à l’interface Socle/Couverture Sédimentaire–Application à La Géothermie (Bassin de Valence, SE France). These de doctorat, Paris Sciences et Lettres (ComUE). 2019. Available online: http://www.theses.fr/2019PSLEM046 (accessed on 21 September 2021).
- Narr, W. Estimating Average Fracture Spacing in Subsurface Rock. AAPG Bull. 1996, 80, 1565–1585. [Google Scholar] [CrossRef]
- Haffen, S.; Géraud, Y.; Diraison, M.; Dezayes, C. Determination of Fluid-Flow Zones in a Geothermal Sandstone Reservoir Using Thermal Conductivity and Temperature Logs. Geothermics 2013, 46, 32–41. [Google Scholar] [CrossRef] [Green Version]
- Sanderson, D.J.; Peacock, D.C. Line Sampling of Fracture Swarms and Corridors. J. Struct. Geol. 2019, 122, 27–37. [Google Scholar] [CrossRef]
- Fossen, H.; Cavalcante, G.C.G. Shear Zones–A Review. Earth Sci. Rev. 2017, 171, 434–455. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Peacock, D.C.P.; Sanderson, D.J. Mesoscale Strike-Slip Faults and Damage Zones at Marsalforn, Gozo Island, Malta. J. Struct. Geol. 2003, 25, 793–812. [Google Scholar] [CrossRef]
- Ostermeijer, G.A.; Mitchell, T.M.; Aben, F.M.; Dorsey, M.T.; Browning, J.; Rockwell, T.K.; Fletcher, J.M.; Ostermeijer, F. Damage Zone Heterogeneity on Seismogenic Faults in Crystalline Rock; a Field Study of the Borrego Fault, Baja California. J. Struct. Geol. 2020, 137, 104016. [Google Scholar] [CrossRef]
- Marrett, R.; Gale, J.F.W.; Gómez, L.A.; Laubach, S.E. Correlation Analysis of Fracture Arrangement in Space. J. Struct. Geol. 2018, 108, 16–33. [Google Scholar] [CrossRef]
- Chabani, A.; Trullenque, G.; Ledésert, B.A.; Klee, J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), Application to Geothermal Reservoirs. Geosciences 2021, 11, 280. [Google Scholar] [CrossRef]
- Gillespie, P.A.; Howard, C.B.; Walsh, J.J.; Watterson, J. Measurement and Characterisation of Spatial Distributions of Fractures. Tectonophysics 1993, 226, 113–141. [Google Scholar] [CrossRef]
- Wang, Q.; Laubach, S.E.; Gale, J.F.W.; Ramos, M.J. Quantified Fracture (Joint) Clustering in Archean Basement, Wyoming: Application of the Normalized Correlation Count Method. Pet. Geosci. 2019, 25, 415–428. [Google Scholar] [CrossRef]
- Pavičić, I.; Dragičević, I.; Vlahović, T.; Grgasović, T. Fractal Analysis of Fracture Systems in Upper Triassic Dolomites in Žumberak Mountain, Croatia. Rud. Geološko-Naft. Zb. 2017, 32, 1–13. Available online: https://hrcak.srce.hr/ojs/index.php/rgn/article/view/4894/pdf (accessed on 21 September 2021). [CrossRef]
- Shiri, Y.; Hassani, H. Two-Component Fluid Front Tracking in Fault Zone and Discontinuity with Permeability Heterogeneity. Rud. Geol. Naft. Zb. 2021, 36, 19–30. [Google Scholar] [CrossRef]
- Hooker, J.N.; Laubach, S.E.; Marrett, R. Microfracture Spacing Distributions and the Evolution of Fracture Patterns in Sandstones. J. Struct. Geol. 2018, 108, 66–79. [Google Scholar] [CrossRef]
- Putz-Perrier, M.W.; Sanderson, D.J. Spatial Distribution of Brittle Strain in Layered Sequences. J. Struct. Geol. 2008, 30, 50–64. [Google Scholar] [CrossRef]
- Bourbiaux, B.; Basquet, R.; Daniel, J.M.; Hu, L.Y.; Jenni, S.; Lange, G.; Rasolofosaon, P. Fractured Reservoirs Modelling: A Review of the Challenges and Some Recent Solutions. First Break 2005, 23, 33–40. [Google Scholar] [CrossRef]
- Trullenque, G.; Genter, A.; Leiss, B.; Wagner, B.; Bouchet, R.; Léoutre, E.; Malnar, B.; Bär, K.; Rajšl, I. Upscaling of EGS in Different Geological Conditions: A European Perspective. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018; p. SGP-TR-213. [Google Scholar]
- Klee, J.; Trullenque, G.; Ledésert, B.; Potel, S.; Hébert, R.; Chabani, A.; Genter, A. Petrographic Analyzes of Fractured Granites Used as An Analogue of the Soultz-Sous-Forêts Geothermal Reservoir: Noble Hills, CA, USA. In Proceedings of the Extended Abstract, Reykjavik, Island, 26 May 2021. [Google Scholar]
- Chabani, A.; Trullenque, G.; Rishi, P.; Pomart, A.; Attali, R.; Sass, I. Modelling of Fractured Granitic Geothermal Reservoirs: Use of Deterministic and Stochastic Methods in Discrete Fracture Networks and a Coupled Processes Modeling Framework. In Proceedings of the Extended Abstract, Reykjavik, Island, 2 May 2021. [Google Scholar]
- Pavlis, T.L.; Trullenque, G. Evidence for 40–41 Km of Dextral Slip on the Southern Death Valley Fault: Implications for the Eastern California Shear Zone and Extensional Tectonics. Geology 2021, 49, 767–772. [Google Scholar] [CrossRef]
- Klee, J.; Potel, S.; Ledésert, B.A.; Hébert, R.L.; Chabani, A.; Barrier, P.; Trullenque, G. Fluid-Rock Interactions in a Paleo-Geothermal Reservoir (Noble Hills Granite, California, USA). Part 1: Granite Pervasive Alteration Processes Away from Fracture Zones. Geosciences 2021, 11, 325. [Google Scholar] [CrossRef]
- Brady III, R.H. Neogene Stratigraphy of the Avawatz Mountains between the Garlock and Death Valley Fault Zones, Southern Death Valley, California: Implications as to Late Cenozoic Tectonism. Sediment. Geol. 1984, 38, 127–157. [Google Scholar] [CrossRef]
- Pavlis, T.L.; Rutkofske, J.; Guerrero, F.; Serpa, L.F. Structural Overprinting of Mesozoic Thrust Systems in Eastern California and Its Importance to Reconstruction of Neogene Extension in the Southern Basin and Range. Geosphere 2014, 10, 732–756. [Google Scholar] [CrossRef] [Green Version]
- Miller, M.; Pavlis, T. The Black Mountains Turtlebacks: Rosetta Stones of Death Valley Tectonics. Earth-Sci. Rev. 2005, 73, 115–138. [Google Scholar] [CrossRef]
- Snow, J.K. Cenozoic Tectonism in the Central Basin and Range; Magnitude, Rate, and Distribution of Upper Crustal Strain. Am. J. Sci. 2000, 300, 659–719. [Google Scholar] [CrossRef]
- Calzia, J.; Rämö, O. Late Cenozoic Crustal Extension and Magmatism, Southern Death Valley Region, California. GSA Field Guides 2000, 2, 135–164. [Google Scholar] [CrossRef]
- Calzia, J.; Ramo, O. Miocene Rapakivi Granites in the Southern Death Valley Region, California, USA. Earth-Sci. Rev. 2005, 73, 221–243. [Google Scholar] [CrossRef]
- Brady, R. Cenozoic Geology of the Northern Avawatz Mountains in Relation to the Intersection of the Garlock and Death Valley Fault Zones, San Bernardino County, California. Ph.D. Thesis, University of California, Davis, CA, USA, 1987. [Google Scholar]
- Norton, I. Two-Stage Formation of Death Valley. Geosphere 2011, 7, 171–182. [Google Scholar] [CrossRef]
- Burchfiel, B.C.; Stewart, J.H. “Pull-Apart” Origin of the Central Segment of Death Valley, California. Geol. Soc. Am. Bull. 1966, 77, 439–442. [Google Scholar] [CrossRef]
- Niles, J.H. Post-Middle Pliocene Tectonic Development of the Noble Hills, Southern Death Valley, California. Ph.D. Thesis, San Francisco State University, San Francisco, CA, USA, 2016. [Google Scholar]
- Reinert, E. Low Temperature Thermochronometry of the Avawatz Mountians, California: Implications for the Inception of the Eastern California Shear Zone. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2004. Available online: https://www.ess.washington.edu/content/people/student_publications_files/reinert--erik/Reinert_2004.pdf (accessed on 21 September 2021).
- Spencer, J.E. Late Cenozoic Extensional and Compressional Tectonism in the Southern and Western Avawatz Mountains, Southeastern California. In Basin and Range Extensional Tectonics Near the Latitude of Las Vegas, Nevada: Geological Society of America Memoir; Geological Society of America: Boulder, CO, USA, 1990; Volume 176, pp. 317–333. [Google Scholar] [CrossRef]
- Mahon, R.C.; Dehler, C.M.; Link, P.K.; Karlstrom, K.E.; Gehrels, G.E. Geochronologic and Stratigraphic Constraints on the Mesoproterozoic and Neoproterozoic Pahrump Group, Death Valley, California: A Record of the Assembly, Stability, and Breakup of Rodinia. Bulletin 2014, 126, 652–664. [Google Scholar] [CrossRef] [Green Version]
- Pickering, G.; Bull, J.M.; Sanderson, D.J. Sampling Power-Law Distributions. Tectonophysics 1995, 248, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Odling, N.E.; Gillespie, P.; Bourgine, B.; Castaing, C.; Chiles, J.P.; Christensen, N.P.; Fillion, E.; Genter, A.; Olsen, C.; Thrane, L.; et al. Variations in Fracture System Geometry and Their Implications for Fluid Flow in Fractured Hydrocarbon Reservoirs. Pet. Geosci. 1999, 5, 373–384. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of Fracture Systems in Geological Media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Priest, S.D. Discontinuity Analysis for Rock Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Ledésert, B.A.; Hébert, R.L. How Can Deep Geothermal Projects Provide Information on the Temperature Distribution in the Upper Rhine Graben? The Example of the Soultz-Sous-Forêts-Enhanced Geothermal System. Geosciences 2020, 10, 459. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Estimation of Discontinuity Spacing and Trace Length Using Scanline Surveys; Elsevier: Amsterdam, The Netherlands, 1981; Volume 18, pp. 183–197. [Google Scholar] [CrossRef]
- Hardebol, N.J.; Maier, C.; Nick, H.; Geiger, S.; Bertotti, G.; Boro, H. Multiscale Fracture Network Characterization and Impact on Flow: A Case Study on the Latemar Carbonate Platform. J. Geophys. Res. Solid Earth 2015, 120, 8197–8222. [Google Scholar] [CrossRef]
- Bisdom, K.; Gauthier, B.D.M.; Bertotti, G.; Hardebol, N.J. Calibrating Discrete Fracture-Network Models with a Carbonate Threedimensional Outcrop Fracture Network: Mplications for Naturally Fractured Reservoir Modeling. AAPG Bull. 2014, 98, 13511376. [Google Scholar] [CrossRef]
- Bertrand, L.; Géraud, Y.; Le Garzic, E.; Place, J.; Diraison, M.; Walter, B.; Haffen, S. A Multiscale Analysis of a Fracture Pattern in Granite: A Case Study of the Tamariu Granite, Catalunya, Spain. J. Struct. Geol. 2015, 78, 52–66. [Google Scholar] [CrossRef]
- Terzaghi, R.D. Sources of Error in Joint Surveys. In Geotechnique; Road Research Laboratory: Crowthorne, UK, 1965; Volume 15, pp. 287–304. Available online: http://worldcat.org/issn/00168505 (accessed on 21 September 2021).
- Delvaux, D.; Sperner, B. Stress Tensor Inversion from Fault Kinematic Indicators and Focal Mechanism Data: The TENSOR Program. New Insights Struct. Interpret. Model. 2003, 212, 75–100. [Google Scholar] [CrossRef] [Green Version]
- Cardozo, N.; Allmendinger, R.W. Spherical projections with OSXStereonet. Comput. Geosci. 2013, 51, 193–205. [Google Scholar] [CrossRef]
- Hardebol, N.J.; Bertotti, G. DigiFract: A Software and Data Model Implementation for Flexible Acquisition and Processing of Fracture Data from Outcrops. Comput. Geosci. 2013, 54, 326–336. [Google Scholar] [CrossRef]
- Fisher, R. Dispersion on a Sphere. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1953, 217, 295–305. Available online: http://palaeo.spb.ru/pmlibrary/pmpapers/fisher_1953.pdf (accessed on 21 September 2021). [CrossRef]
- Kent, J.T. The Fisher-Bingham Distribution on the Sphere. J. R. Stat. Soc. Ser. B 1982, 44, 71–80. Available online: http://www.jstor.org/stable/2984712 (accessed on 21 September 2021). [CrossRef]
- Von Mises, R. Uber Die “Ganzzahligkeit” Der Atomgewicht Und Verwandte Fragen. Physikal. Z 1918, 19, 490–500. [Google Scholar]
- Lark, R.M.; Clifford, D.; Waters, C.N. Modelling Complex Geological Circular Data with the Projected Normal Distribution and Mixtures of von Mises Distributions. Solid Earth 2014, 5, 631–639. [Google Scholar] [CrossRef] [Green Version]
- Chabani, A.; Mehl, C.; Cojan, I.; Alais, R.; Bruel, D. Semi-Automated Component Identification of a Complex Fracture Network Using a Mixture of von Mises Distributions: Application to the Ardeche Margin (South-East France). Comput. Geosci. 2020, 137, 104435. [Google Scholar] [CrossRef]
- Gillespie, D.T. Approximate Accelerated Stochastic Simulation of Chemically Reacting Systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Kuiper, N.H. Tests Concerning Random Points on a Circle. In Proceedings of the Koninklijke; Nederlandse Akademie van Wetenschappen: Amsterdam, The Netherlands, 1960; Volume 63, pp. 38–47. [Google Scholar] [CrossRef] [Green Version]
- Sanderson, D.J.; Roberts, S.; Gumiel, P.; Greenfield, C. Quantitative Analysis of Tin-and Tungsten-Bearing Sheeted Vein Systems. Econ. Geol. 2008, 103, 1043–1056. [Google Scholar] [CrossRef]
- Ortega, O.J.; Marrett, R.A.; Laubach, S.E. A Scale-Independent Approach to Fracture Intensity and Average Spacing Measurement. AAPG Bull. 2006, 90, 193–208. [Google Scholar] [CrossRef]
- Chinn, L.D. Low-Temperature Thermochronometry of the Avawatz Mountains; Implications for the Eastern Terminus and Inception of the Garlock Fault Zone. 2013. Available online: https://www.ess.washington.edu/content/people/student_publications_files/chinn--logan/chinn--logan_ms_2013.pdf (accessed on 21 September 2021).
- Franklin, B. Characterising Fracture Systems within Upfaulted Basement Highs in the Hebridean Islands: An Onshore Analogue for the Clair Field. Ph.D. Thesis, Durham University, Durham, UK, 2013. Available online: http://etheses.dur.ac.uk/7765/ (accessed on 21 September 2021).
- Bourbiaux, B.; Basquet, R.; Cacas, M.-C.; Daniel, J.-M.; Sarda, S. An Integrated Workflow to Account for Multi-Scale Fractures in Reservoir Simulation Models: Implementation and Benefits. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 13–16 October 2002. [Google Scholar]
- Ledésert, B.; Hebert, R.; Genter, A.; Bartier, D.; Clauer, N.; Grall, C. Fractures, Hydrothermal Alterations and Permeability in the Soultz Enhanced Geothermal System. Comptes Rendus Geosci. 2010, 342, 607–615. [Google Scholar] [CrossRef]
- Dorbath, L.; Cuenot, N.; Genter, A.; Frogneux, M. Seismic Response of the Fractured and Faulted Granite of Soultz-Sous-Forêts (France) to 5 Km Deep Massive Water Injections. Geophys. J. Int. 2009, 177, 653–675. [Google Scholar] [CrossRef] [Green Version]
- Morellato, C.; Redini, F.; Doglioni, C. On the Number and Spacing of Faults. Terra Nova 2003, 15, 315–321. [Google Scholar] [CrossRef]






| Outcrop | SL | Number of Fractures | Proximity to Major Fault Segments | SL Orientation | Length (m) | Mean Spacing (m) | Density (frac/m) | Cv | V′ (95%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | SL1 | 261 | 10 m to SDVFZ sgmt | N010 | 13.45 | 0.04 | 19.4 | 1.2 | 0.29 |
| 2 | SL2a | 80 | Crosscut by SDVFZ sgmt | N160 | 7.50 | 0.07 | 10.6 | 14.4 | 0.42 |
| SL2b | 32 | Crosscut by SDVFZ sgmt | N070 | 1.64 | 0.04 | 19.5 | 1.1 | 0.50 | |
| 3 | SL3a | 27 | 40 m to SDVFZ sgmt | N055 | 0.85 | 0.03 | 31.8 | 0.7 | 0.32 |
| SL3b | 38 | 42 m to SDVFZ sgmt | N160 | 4.50 | 0.06 | 8.4 | 1.7 | 0.57 | |
| 4 * | SL4 | 28 | 6 m to SDVFZ sgmt | N163 | 0.80 | 0.02 | 42.1 | 0.82 | / |
| SL5 | 46 | 6 m to SDVFZ sgmt | N073 | 1.72 | 0.04 | 26.7 | 0.84 | / | |
| 5 * | SL6 | 26 | 4 m to SDVFZ sgmt | N074 | 1.50 | 0.05 | 17.2 | 0.93 | / |
| SL7 | 31 | 4 m to SDVFZ sgmt | N157 | 0.70 | 0.02 | 44 | 0.89 | / | |
| 6 * | SL8 | 171 | Crosscut by SDVFZ sgmt and thrust fault | N020 | 109 | 0.64 | 1.55 | 3.22 | / |
| 7 * | SL9 | 188 | Crosscut by SDVFZ sgmt | N132 | 82.22 | 0.5 | 2 | 3.26 | / |
| 8 * | SL10 | 258 | Crosscut by SDVFZ sgmt and thrust fault | N154 | 97.50 | 0.4 | 2.66 | 1.67 | / |
| Number of Fractures in Each Set | Parameters | Number of Fractures in Each Set | Parameters | ||||||
|---|---|---|---|---|---|---|---|---|---|
| µ (°) | ĸ | ω (%) | Cv | µ (°) | ĸ | ω (%) | Cv | ||
| SL1 | SL5 | ||||||||
| 44 | N026 | 5.07 | 17 | 1.03 | 18 | N001 | 44.83 | 39 | 0.79 |
| 55 | N062 | 11.30 | 21 | 0.53 | 6 | N018 | 57.7 | 13 | 0.79 |
| 97 | N092 | 5.73 | 37 | 1.44 | 6 | N040 | 31.58 | 13 | 0.86 |
| 39 | N130 | 6.77 | 15 | 1.43 | 4 | N113 | 4.95 | 9 | 0.74 |
| 26 | N171 | 5.11 | 10 | 1.37 | 12 | N144 | 15.13 | 26 | 0.95 |
| SL2a | SL6 | ||||||||
| 14 35 8 18 5 | N014 N025 N050 N102 N143 | 27.98 1.19 29.67 4.21 8.91 | 18 46 8 27 1 | 1.97 1.67 1.26 1.12 1.35 | 10 13 4 | N004 N100 N161 | 23 6.91 29.66 | 35 49 16 | 0.54 1.35 0.83 |
| SL2b | SL7 | ||||||||
| 10 10 12 | N003 N112 N152 | 11.4 0.09 18 | 31 31 38 | 1.05 1 0.9 | 4 22 5 | N053 N087 N116 | 3.54 46.2 33.5 | 13 81 6 | 0.88 0.83 0.84 |
| SL3a | SL8 | ||||||||
| 13 6 8 | N077 N098 N135 | 12.06 14.22 14.1 | 49 25 26 | 1.07 0.6 0.8 | 54 61 54 | N058 N090 N132 | 10.09 21.05 3.1 | 32 36 32 | 1.3 3.45 2.82 |
| SL3b | SL9 | ||||||||
| 9 25 4 | N040 N081 N150 | 4.57 5.05 1.47 | 24 65 11 | 1.23 1.23 1.04 | 34 46 15 38 38 | N029 N060 N096 N132 N176 | 7.17 10.45 6.25 9.85 5.38 | 20 27 9 22 22 | 2.97 1.93 3.83 2.31 2.62 |
| SL4 | SL10 | ||||||||
| 11 18 5 | N034 N086 N123 | 2.18 11.4 11 | 34 53 13 | 0.82 0.85 0.7 | 8 18 189 44 | N004 N040 N091 N118 | 75 75 43.23 35.3 | 3 7 73 17 | 0.81 1.68 1.7 1.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chabani, A.; Trullenque, G.; Klee, J.; Ledésert, B.A. Fracture Spacing Variability and the Distribution of Fracture Patterns in Granitic Geothermal Reservoir: A Case Study in the Noble Hills Range (Death Valley, CA, USA). Geosciences 2021, 11, 520. https://doi.org/10.3390/geosciences11120520
Chabani A, Trullenque G, Klee J, Ledésert BA. Fracture Spacing Variability and the Distribution of Fracture Patterns in Granitic Geothermal Reservoir: A Case Study in the Noble Hills Range (Death Valley, CA, USA). Geosciences. 2021; 11(12):520. https://doi.org/10.3390/geosciences11120520
Chicago/Turabian StyleChabani, Arezki, Ghislain Trullenque, Johanne Klee, and Béatrice A. Ledésert. 2021. "Fracture Spacing Variability and the Distribution of Fracture Patterns in Granitic Geothermal Reservoir: A Case Study in the Noble Hills Range (Death Valley, CA, USA)" Geosciences 11, no. 12: 520. https://doi.org/10.3390/geosciences11120520
APA StyleChabani, A., Trullenque, G., Klee, J., & Ledésert, B. A. (2021). Fracture Spacing Variability and the Distribution of Fracture Patterns in Granitic Geothermal Reservoir: A Case Study in the Noble Hills Range (Death Valley, CA, USA). Geosciences, 11(12), 520. https://doi.org/10.3390/geosciences11120520








