Influence of Tsunami Aspect Ratio on Near and Far-Field Tsunami Amplitude
Abstract
1. Introduction
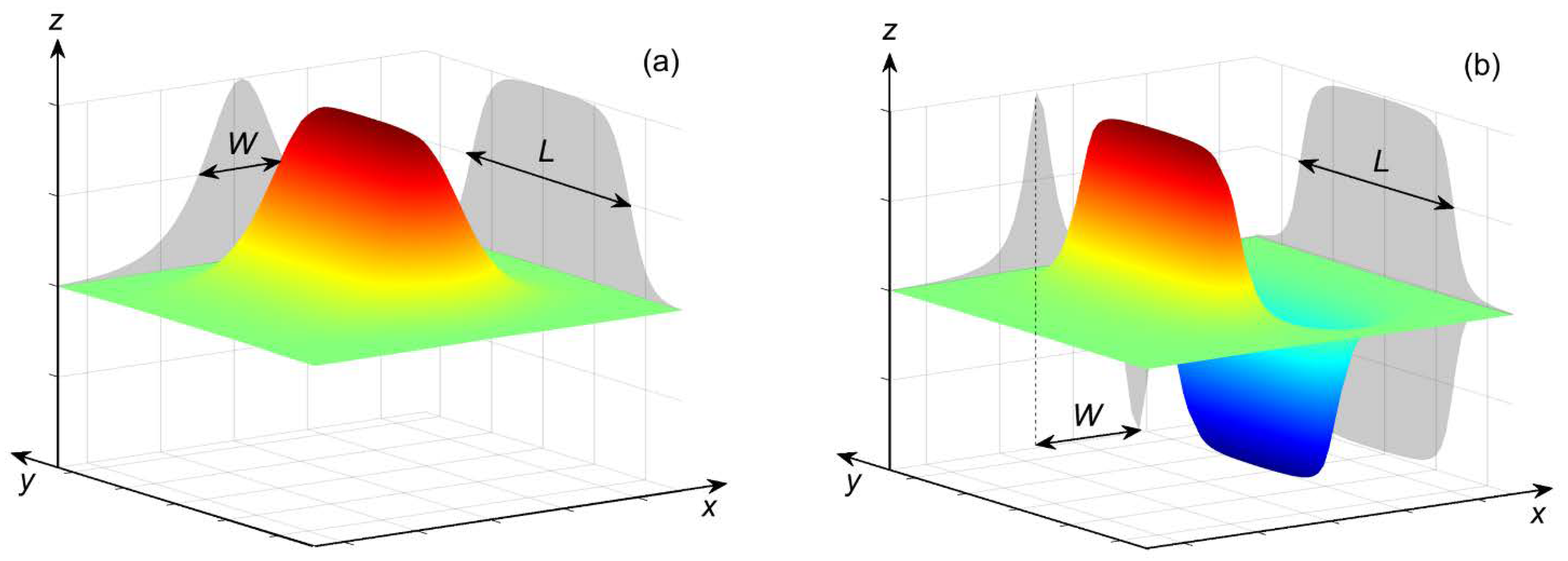
2. Methodology
3. Results and Discussions
3.1. Idealized Scenarios in the Basin with Constant Depth
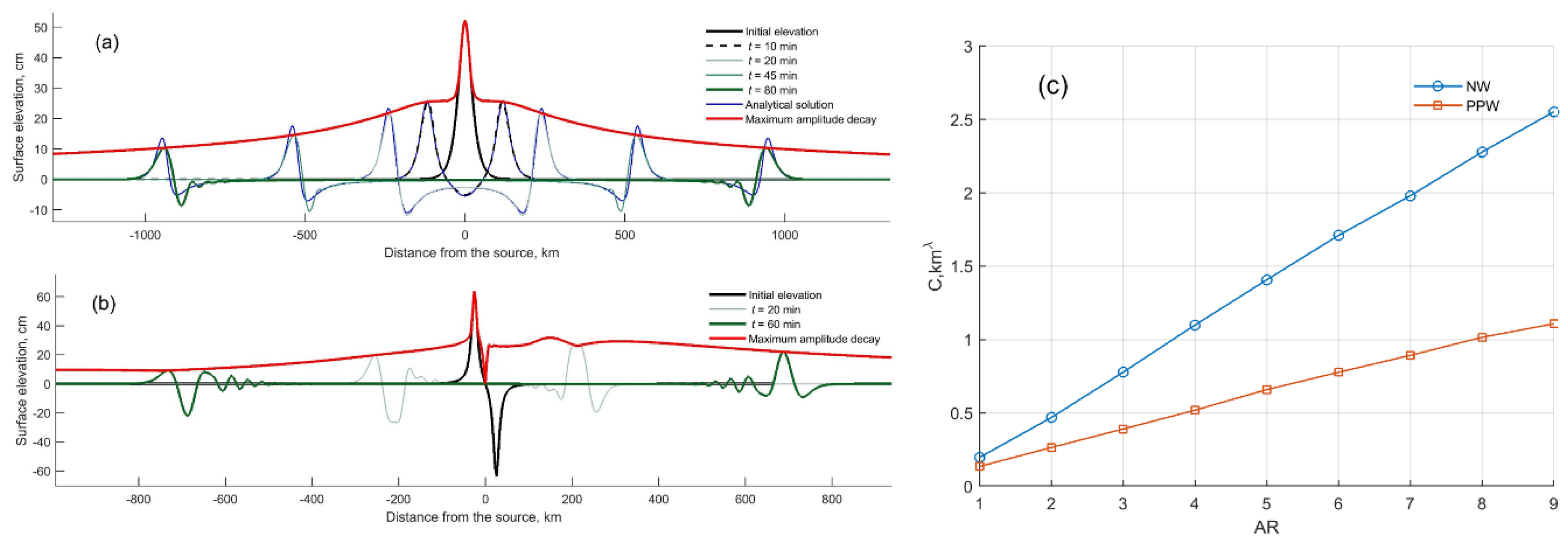
3.1.1. Comparison with Analytical Solution
3.1.2. Wave Decay
3.1.3. Cross-Over Point
3.2. Idealized Sources in the Pacific Ocean
3.2.1. Source AR and Damaging Potential in the Near- and Far-field
3.2.2. Real Events in the Pacific Ocean
4. Short Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arcas, D.; Segur, H. Seismically generated tsunamis. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 1505–1542. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ben-Menahem, A.; Rosenman, M. Amplitude patterns of tsunami waves from submarine earthquakes. J. Geophys. Res. Space Phys. 1972, 77, 3097–3128. [Google Scholar] [CrossRef]
- Davies, G.; Griffin, J. Sensitivity of Probabilistic Tsunami Hazard Assessment to Far-Field Earthquake Slip Complexity and Rigidity Depth-Dependence: Case Study of Australia. Pure Appl. Geophys. 2020, 177, 1521–1548. [Google Scholar] [CrossRef]
- Fritz, H.M.; Borrero, J.C. Somalia Field Survey after the December 2004 Indian Ocean Tsunami. Earthq. Spectra 2006, 22, 219–233. [Google Scholar] [CrossRef]
- Okal, E.A. Tsunamigenic Earthquakes: Past and Present Milestones. Pure Appl. Geophys. 2010, 168, 969–995. [Google Scholar] [CrossRef]
- Okal, E.A.; Synolakis, C.E.; Fryer, G.J.; Heinrich, P.; Borrero, J.C.; Ruscher, C.; Arcas, D.; Guille, G.; Rousseau, D. A Field Survey of the 1946 Aleutian Tsunami in the Far Field. Seism. Res. Lett. 2002, 73, 490–503. [Google Scholar] [CrossRef]
- Kowalik, Z.; Horrillo, J.; Knight, W.; Logan, T. Kuril Islands tsunami of November 2006: Impact at Crescent City by distant scattering. J. Geophys. Res. Space Phys. 2008, 113, 01020. [Google Scholar] [CrossRef]
- Mofjeld, H.O.; Gonzalez, F.I.; Titov, V.V.; Newman, J.C. Tsunami scattering provinces in the Pacific Ocean. Geophys. Res. Lett. 2001, 28, 335–337. [Google Scholar] [CrossRef]
- Gica, E.; Teng, M.H.; Liu, P.L.-F.; Titov, V.; Zhou, H. Sensitivity Analysis of Source Parameters for Earthquake-Generated Distant Tsunamis. J. Waterw. Port Coastal Ocean Eng. 2007, 133, 429–441. [Google Scholar] [CrossRef]
- Synolakis, C.; Roush, W. SEISMOLOGY: Enhanced: Tsunamigenic Sea-Floor Deformations. Science 1997, 278, 598–600. [Google Scholar] [CrossRef]
- Fukutani, Y.; Anawat, S.; Imamura, F. Uncertainty in tsunami wave heights and arrival times caused by the rupture velocity in the strike direction of large earthquakes. Nat. Hazards 2016, 80, 1749–1782. [Google Scholar] [CrossRef]
- Williamson, A.; Melgar, D.; Rim, D. The Effect of Earthquake Kinematics on Tsunami Propagation. J. Geophys. Res. Solid Earth 2019, 124, 11639–11650. [Google Scholar] [CrossRef]
- Kawata, Y.; Okumura, Y.; Koshimura, S. Influence of dynamic fault rupture effects on tsunami generation. Proc. Coast. Eng. Conf. Jpn. Soc. Civ. Eng. 2006, 53, 291–295. (In Japanese) [Google Scholar]
- Suppasri, A.; Imamura, F.; Koshimura, S. Effects of the Rupture Velocity of Fault Motion, Ocean Current and Initial Sea Level on the Transoceanic Propagation of Tsunami. Coast. Eng. J. 2010, 52, 107–132. [Google Scholar] [CrossRef]
- Kajiura, K. Tsunami source, energy and the directivity of wave radiation. Bull. Earthq. Res Inst. 1970, 48, 835–869. [Google Scholar]
- Le Gal, M.; Violeau, D.; Benoit, M. Influence of timescales on the generation of seismic tsunamis. Eur. J. Mech. B Fluids 2017, 65, 257–273. [Google Scholar] [CrossRef]
- Geist, E.L. Local Tsunamis and Earthquake Source Parameters. Adv. Geophys. 1998, 39, 117–209. [Google Scholar] [CrossRef]
- Geist, E.L. Rapid tsunami models and earthquake source parameters: Far-field and local applications. ISET J. Earthq. Technol. 2005, 42, 127–136. [Google Scholar]
- Gica, E.; Spillane, M.C.; Titov, V.V.; Chamberlin, C.D.; Newman, J.C. Development of the Forecast Propagation Database for NOAA’s Short-Term Inundation Forecasting for Tsunamis (SIFT); U.S. Department of Commerce, National Oceanic and Atmospheric Administration, Office of Oceanic and Atmospheric Research, Pacific Marine Environmental Laboratory: Seattle, WA, USA, 2008.
- Goda, K.; Mai, P.M.; Yasuda, T.; Mori, N. Sensitivity of tsunami wave profiles and inundation simulations to earthquake slip and fault geometry for the 2011 Tohoku earthquake. Earth Planets Space 2014, 66, 105. [Google Scholar] [CrossRef]
- Ioualalen, M. Sensitivity tests on relations between tsunami signal and seismic rupture characteristics: The 26 December 2004 Indian Ocean event case study. Environ. Model. Softw. 2009, 24, 1354–1362. [Google Scholar] [CrossRef]
- Levin, B.W.; Nosov, M. Physics of Tsunamis. Metzler, J.B., Ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Necmioglu, O.; Ozel, N. An Earthquake Source Sensitivity Analysis for Tsunami Propagation in the Eastern Mediterranean. Oceanogr. 2014, 27, 76–85. [Google Scholar] [CrossRef]
- Okal, E.A. Seismic parameters controlling far-field tsunami amplitudes: A review. Nat. Hazards 1988, 1, 67–96. [Google Scholar] [CrossRef]
- Okal, E.A.; Synolakis, C.E. Source discriminants for near-field tsunamis. Geophys. J. Int. 2004, 158, 899–912. [Google Scholar] [CrossRef]
- Pires, C.; Miranda, P.M.A. Sensitivity of the adjoint method in the inversion of tsunami source parameters. Nat. Hazards Earth Syst. Sci. 2003, 3, 341–351. [Google Scholar] [CrossRef]
- Satake, K.; Tanioka, Y. Tsunami generation of the 1993 Hokkaido Nansei-Oki earthquake. Pure Appl. Geophys. PAGEOPH 1995, 144, 803–821. [Google Scholar] [CrossRef]
- Titov, V.V.; Gonzales, F.I.; Mofjeld, H.O.; Newman, J.C. Offshore Forecasting of Alaska-Aleutian Subduction Zone Tsunamis in Hawaii; NOAA Technical Memorandum ERL PMEL-U.S. Government Publishing Office: Seattle, WA, USA, 1999.
- Carrier, G.F.; Yeh, H. Tsunami propagation from a finite source. Comput. Model. Eng. Sci. 2005, 10, 113–121. [Google Scholar] [CrossRef]
- Takahashi, R.; Hatori, T. A model experiment on the tsunami generation from a bottom deformation area of elliptic shape. Bull. Earthq. Res. Inst. 1962, 40, 873–883. [Google Scholar]
- Okal, E.A. Normal Mode Energetics for Far-field Tsunamis Generated by Dislocations and Landslides. Pure Appl. Geophys. 2003, 160, 2189–2221. [Google Scholar] [CrossRef]
- Okal, E.A.; Synolakis, C.E. Far-field tsunami hazard from mega-thrust earthquakes in the Indian Ocean. Geophys. J. Int. 2008, 172, 995–1015. [Google Scholar] [CrossRef]
- Yolsal, S.; Taymaz, T. Sensitivity analysis on relations between earthquake source rupture parameters and far-field tsunami waves: Case studies in the Eastern Mediterranean region. Turk. J. Earth Sci. 2010, 19, 313–349. [Google Scholar] [CrossRef]
- Synolakis, C.E.; Bernard, E.N.; Titov, V.V.; Kânoğlu, U.; González, F.I. Validation and Verification of Tsunami Numerical Models. Pure Appl. Geophys. 2008, 165, 2197–2228. [Google Scholar] [CrossRef]
- Titov, V.V.; Synolakis, C.E. Numerical Modeling of Tidal Wave Runup. J. Waterw. Port Coastal Ocean Eng. 1998, 124, 157–171. [Google Scholar] [CrossRef]
- Titov, V.V.; Gonzalez, F.I. Implementation and Testing of the Method of Splitting Tsunami (MOST) Model; NOAA Technical Memorandum ERL PMEL-U.S. Government Publishing Office: Seattle, WA, USA, 1997.
- Okada, Y. Surface deformation due to shear and tensile faults in a half space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global Bathymetry and Topography at 15 Arc Sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Polyanin, A.D. Linear partial differential equations for Engineers and Scientists; Chapman and Hall/CRC: London, UK; New York, NY, USA; Washington, DC, USA, 2002; pp. 354–356. [Google Scholar]
- Wells, D.; Coppersmith, K. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Tang, L.; Titov, V.V.; Bernard, E.N.; Wei, Y.; Chamberlin, C.D.; Newman, J.C.; Mofjeld, H.O.; Arcas, D.; Eble, M.C.; Moore, C.; et al. Direct energy estimation of the 2011 Japan tsunami using deep-ocean pressure measurements. J. Geophys. Res. Space Phys. 2012, 117, 08008. [Google Scholar] [CrossRef]
- Gusiakov, V.K. Static displacement on the surface of an elastic space. In Ill-Posed Problems of Mathematical Physics and Interpretation of Geophysical Data; Computer Center of Soviet Academy of Sciences: Novosibirsk, Russia, 1978; pp. 23–51. [Google Scholar]
- Omira, R.; Baptista, M.A.C.V.; Lisboa, F. Tsunami Characteristics Along the Peru–Chile Trench: Analysis of the 2015 Mw8.3 Illapel, the 2014 Mw8.2 Iquique and the 2010 Mw8.8 Maule Tsunamis in the Near-field. Pure Appl. Geophys. 2016, 173, 1063–1077. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sannikova, N.K.; Segur, H.; Arcas, D. Influence of Tsunami Aspect Ratio on Near and Far-Field Tsunami Amplitude. Geosciences 2021, 11, 178. https://doi.org/10.3390/geosciences11040178
Sannikova NK, Segur H, Arcas D. Influence of Tsunami Aspect Ratio on Near and Far-Field Tsunami Amplitude. Geosciences. 2021; 11(4):178. https://doi.org/10.3390/geosciences11040178
Chicago/Turabian StyleSannikova, Natalia K., Harvey Segur, and Diego Arcas. 2021. "Influence of Tsunami Aspect Ratio on Near and Far-Field Tsunami Amplitude" Geosciences 11, no. 4: 178. https://doi.org/10.3390/geosciences11040178
APA StyleSannikova, N. K., Segur, H., & Arcas, D. (2021). Influence of Tsunami Aspect Ratio on Near and Far-Field Tsunami Amplitude. Geosciences, 11(4), 178. https://doi.org/10.3390/geosciences11040178




