Next Article in Journal
Lateral Constrained Inversion of DC-Resistivity Data Observed at the Area North of Tenth of Ramadan City, Egypt for Groundwater Exploration
Previous Article in Journal
SyPEAH: The WebAPP System for Protection and Education to Archaeological Heritage in the Parco Archeologico del Colosseo
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 11
Issue 6
10.3390/geosciences11060247
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Technical Note

Reappraisal of the ASTM/AASHTO Standard Rolling Device Method for Plastic Limit Determination of Fine-Grained Soils

by
Amin Soltani
1,2,* and
Brendan C. O’Kelly
3
1
School of Engineering, IT and Physical Sciences, Federation University, Churchill, VIC 3842, Australia
2
Department of Infrastructure Engineering, The University of Melbourne, Parkville, VIC 3010, Australia
3
Department of Civil, Structural and Environmental Engineering, Trinity College Dublin, D02 PN40 Dublin, Ireland
*
Author to whom correspondence should be addressed.
Geosciences 2021, 11(6), 247; https://doi.org/10.3390/geosciences11060247
Submission received: 21 May 2021 / Revised: 3 June 2021 / Accepted: 4 June 2021 / Published: 6 June 2021
(This article belongs to the Section Geomechanics)
Browse Figures
Versions Notes

Abstract

:
Given its apparent limitations, various attempts have been made to develop alternative testing approaches to the standardized rolling-thread plastic limit (PLRT) method (for fine-grained soils), targeting higher degrees of repeatability and reproducibility. Among these, device-rolling techniques, including the method described in ASTM D4318/AASHTO T90 standards, based on original work by Bobrowski and Griekspoor (BG) and which follows the same basic principles as the standard thread-rolling (by hand) test, have been highly underrated by some researchers. To better understand the true potentials and/or limitations of the BG method for soil plasticity determination (i.e., PLBG), this paper presents a critical reappraisal of the PLRT–PLBG relationship using a comprehensive statistical analysis performed on a large and diverse database of 60 PLRT–PLBG test pairs. It is demonstrated that for a given fine-grained soil, the BG and RT methods produce essentially similar PL values. The 95% lower and upper (water content) statistical agreement limits between PLBG and PLRT were, respectively, obtained as −5.03% and +4.51%, and both deemed “statistically insignificant” when compared to the inductively-defined reference limit of ±8% (i.e., the highest possible difference in PLRT based on its repeatability, as reported in the literature). Furthermore, the likelihoods of PLBG underestimating and overestimating PLRT were 50% and 40%, respectively; debunking the notion presented by some researchers that the BG method generally tends to greatly underestimate PLRT. It is also shown that the degree of underestimation/overestimation does not systematically change with changes in basic soil properties; suggesting that the differences between PLBG and PLRT are most likely random in nature. Compared to PLRT, the likelihood of achieving consistent soil classifications employing PLBG (along with the liquid limit) was shown to be 98%, with the identified discrepancies being cases that plot relatively close to the A-Line. As such, PLBG can be used with confidence for soil classification purposes.

1. Introduction

Since their inception in the early 1910s, the liquid limit (LL) and plastic limit (PL) remain among the most commonly specified soil parameters in geotechnical engineering practice. These limits, originally introduced by Atterberg [1,2] and later standardized for use in geoengineering applications by Terzaghi [3,4] and Casagrande [5,6], describe changes in the consistency states (and hence mechanical behavior) of fine-grained soils with respect to variations in water content. The LL and PL, together with their arithmetic difference, the plasticity index (PI), have been successfully incorporated into the soil mechanics framework, serving a variety of useful purposes, including their adoption for routine soil classification purposes [7,8,9,10], as well as their widespread applications for predicting useful soil properties (e.g., compactability, permeability, compressibility, and shear strength) for performing preliminary geotechnical designs [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. Both the LL and PL tests are conventionally performed on the soil fraction passing the 425-μm sieve size.
The LL is conceptually defined as the water content at which fine-grained soil transitions from the liquid state to the plastic state. The LL magnitude is strongly dependent on the soil gradation, composition, mineralogical properties (of the clay fraction), and the quantity of interlayer water in the case of expanding clay minerals such as montmorillonite [26,27,28]. The Casagrande percussion-cup (PC) and the fall-cone (FC) tests are standard methods conventionally employed for LL determinations of fine-grained soils; the former being the preferred method in the USA [29,30], while the latter is favored in the UK [31,32], the Eurocodes, and elsewhere, including Australia [33]. Since no sudden definite change in behavior can be associated with the transition from liquid to plastic consistency states, the LL is determined as the water content corresponding to an arbitrarily chosen (low) shear strength on a continuum of ever-weakening behavior with increasing water content [34]. As such, the designation of the LL for a given fine-grained soil is somewhat arbitrary, with its value also dependent on the measurement technique (PC or FC apparatus), the definition for LL determination, and the testing standard employed [34]. For instance, the standard PC test (ASTM D4318 [30]) involves manipulating the water content of a soil specimen such that 25 blows of the specimen cup would be required for the closure of a standard groove (formed by drawing a standard grooving tool through the soil paste specimen on a line joining the highest point to the lowest point on the rim of the cup) over a length of 13 mm. As it is almost impossible to achieve the required groove-closure condition at exactly 25 blows, several trials at varying water contents w and corresponding numbers of blows Nb (for groove-closure) are performed, and the results are plotted in the semi-logarithmic space of w:log10Nb, from which the water content corresponding to Nb = 25, defined as the LLPC, can be determined from the fitted best-fit line. Following the British Standard (BS) FC test (BS 1377–2 [31]), the LL is defined as the water content for which an 80 g–30° cone, with its tip just contacting the top surface of the soil paste specimen, is able to penetrate into the specimen to a depth of d = 20 mm before coming to rest; this state equating to an undrained shear strength value of approximately 1.7 kPa [14,34,35]. Data from several trials for a range of water contents covering d = 15–25 mm are plotted in the arithmetic space of w:d, from which the water content corresponding to d = 20 mm, defined as the LLFC following the BS, can be established.
The PL of a fine-grained soil material is recognized as the water content at which it transitions from plastic (or ductile) to brittle consistency. The rolling-thread (RT) method is conventionally employed for PL determination of fine-grained soils. Following the RT test, the water content at which a uniform thread formed from the soil, with a starting diameter of about 6 mm, first begins to crumble (likely due to air entry or cavitation within the soil thread [36]) when manually rolled out (by hand) on a glass plate to about 3.0 mm [31,32,37] or 3.2 mm [30,38] in diameter is defined as the PLRT. Unlike the LL, which can be determined with confidence (with the FC test arguably producing higher degrees of repeatability and reproducibility), the standard (hand rolling) RT test can be associated with high degrees of subjective variability—that is, measuring the PLRT (by hand-rolling) can be overly dependent on operator performance and judgments [39,40,41,42,43,44].
Given its apparent limitations, various attempts have been made to develop alternative testing approaches to the standard hand-rolling PLRT method, targeting higher degrees of repeatability and reproducibility. Most suggestions in this context are essentially strength-based methods, executed using FC or reverse-extrusion devices, which mainly work on the premise of associating the PLRT with a set value of undrained shear strength (a more detailed review of these methods is given in O’Kelly et al. [34], Vardanega and Haigh [45] and O’Kelly [46,47]). However, several studies have demonstrated that when considering a range of different fine-grained soils, the PLRT (onset of brittleness) does not correspond to a fixed value of undrained shear strength [22,34,36,37,48,49,50]. In other words, while strength-based “PL” determination methods arguably benefit from higher degrees of repeatability and reproducibility, they cannot replicate the standard PLRT testing condition, which assesses soil plasticity (toughness) behavior/properties. Attempts to improve on the standard hand-rolling PL test itself, particularly in terms of reproducibility by minimizing the uncertainties associated with the rolling out (by hand) procedure (i.e., rate of rolling, the hand pressure and/or the initial and final thread diameter criteria), include various device-rolling techniques [51,52,53,54,55,56,57,58]. These methods mainly follow the same basic principles as the standard (hand-rolling) RT test. In particular, the device-rolling technique proposed by Bobrowski and Griekspoor (BG) [52] (a thread-rolling device consisting of two acrylic flat plates covered with unglazed paper), which was subsequently adopted as an alternate PLRT determination method in the USA (by ASTM D4318 [30] and AASHTO T90 [38]; see Figure 1), appears to be highly underrated and hence demands further attention. In performing the ASTM/AASHTO rolling device method for PL determination (i.e., PLBG), downward force is simultaneously applied (via the rigid top plate) to the soil thread with the back and forth rolling motion, until the top plate comes into contact with the 3.2-mm-deep side rails. Apart from this standardized method, none of the other proposed device-rolling techniques have been adopted more widely. Note that, in addition to device-rolling techniques, other methods developed based on the “onset of brittleness” concept for improved PL determination include the likes of the indentation test [59] and the thread-bending technique [60,61,62].
Further, there seems to exist a general belief among some researchers that the PL deduced using the BG-type rolling device (i.e., PLBG) generally tends to (greatly) underestimate the PLRT; possibly due to heterogeneity of the soil thread caused by the contacting paper during the rolling out procedure (i.e., the outside of the soil thread becoming drier than its core) [58,63,64]. Although the published results to support this claim (i.e., typically PLBG < PLRT) are limited, and mainly derived from statistical analyses performed on small (and rather uniform) datasets, this preconception appears to have hindered the more widespread acceptance of the PLBG testing approach (as presented in ASTM D4318 [30] and AASHTO T90 [38] standards), as well as its adoption in other PL determination standards; this alone highlighting the need for further investigations.
To better understand the true potentials and/or limitations of the ASTM/AASHTO device-rolling technique for soil plasticity determination, this study presents a critical statistical appraisal of the PLRT–PLBG relationship (employing the largest and most diverse PLRT–PLBG database compared to those previously investigated in the literature). The validity of the PLBG parameter is investigated by quantifying and critically examining its statistical level of agreement with the standard PLRT. An attempt, for the first time, is also made to assess the accuracy of PLBG in the context of soil classification (based on the BS soil plasticity-chart framework).

2. Database of PLRT–PLBG Tests

A large and diverse database of 60 PLRT–PLBG test results, conducted on 60 fine-grained soils (obtained from natural deposits, as well as commercially produced kaolinite- and bentonite-based blends), was assembled to examine the level of agreement between the PLRT and PLBG measurements. A detailed description of the assembled database is presented in Table 1. The database consisted of 51 PLRT–PLBG data pairs sourced from the research literature (designated by Test IDs S1–S51) [52,63,64,65], as well as original test results of nine fine-grained soils investigated by the authors (Test IDs S52–S60). As demonstrated in Table 1, the database soils, in addition to their geographical diversity, cover reasonably wide ranges of surface texture, plasticity and mineralogical properties—that is, fclay (<2 μm) = 8.9–59.5%, fsilt (2–75 μm) = 7.0–72.7%, LLFC = 24.6–141.1%, PLRT = 11.9–53.4%, PIFC-RT = LLFC − PLRT = 8.1–101.6%, and AFC = PIFC-RT/fclay = 0.49–1.85 (where fclay, fsilt, LLFC, PLRT, PIFC-RT and AFC denote clay content, silt content, BS fall-cone liquid limit, standard rolling-thread plastic limit, plasticity index deduced from the FC and RT test results, and soil activity index, respectively). Since the assembled database employed in this investigation is, to date, the largest and most diverse of its kind, it provides a solid basis for a critical statistical appraisal of the PLRT–PLBG relationship.
Figure 2 illustrates the database soils, with the exception of S18–S22 (for which the LLPC or LLFC values were not reported), plotted on the BS soil plasticity chart. As demonstrated in this figure, all of the investigated soil materials plot below the U-Line, indicating that the assembled database conforms to the general correlation framework proposed by Casagrande [66]. Following the BS soil plasticity-chart classification framework, employing their LLPC or LLFC and PLRT values, the database soils consisted of 46 clays and 9 silts (note that soils S18–S22 could not be classified since their LLPC or LLFC values were not reported), covering all of the five soil plasticity level classes defined in BS 5930 [9].

3. Results and Discussion

3.1. Statistical Appraisal of the PLRT–PLBG Relationship

Figure 3a illustrates the variations of PLRT against PLBG for the compiled database of N = 60 fine-grained soils. As is evident from this figure, the two PL measurement methods are strongly correlated with each other, exhibiting a linear relationship in the form of PLRT = 1.01 PLBG − 4.66 × 10−2 (with R2 = 0.943), essentially suggesting that PLRT ≈ PLBG. The average error associated with the PLRT ≈ PLBG trendline shown in Figure 3a was quantified by the mean absolute percentage error (MAPE calculated by Equation (1) [67]) and the normalized root-mean-squared error (NRMSE calculated by Equation (2,3) [68]), which resulted in MAPE = 6.5% and NRMSE = 5.9% (note that MAPE and NRMSE are both dimensionless quantities expressed in %). These values, which are lower than the usual 5–10% reference limit, indicate an average variation of 5.9–6.5% between the PLRT and PLBG measurements.
MAPE = 1 N ∑ n = 1 N | PL RT ( n ) − PL BG ( n ) PL RT ( n ) | × 100 %
NRMSE = RMSE PL RT ( max ) − PL RT ( min ) × 100 %
RMSE = 1 N ∑ n = 1 N ( PL RT ( n ) − PL BG ( n ) ) 2
where RMSE = root-mean-squared error (in % water content); PLRT(max) and PLRT(min) = maximum and minimum of PLRT data, respectively; n = index of summation; and N = number of investigated PLRT–PLBG test pairs (N = 60).
The excellent graphical correlation (high R2) and low MAPE or NRMSE values obtained for the PLRT ≈ PLBG trendline outlined in Figure 3a would normally lead to accepting the PLBG as a suitable replacement for the PLRT. However, the statistical “limits of agreement” between these two PL measurement methods should also be quantified (and critically examined) to better perceive the true implications of the PLBG parameter for routine geoengineering applications, including its potential use in the many well-established empirical correlations reported between the PLRT or the PLRT-deduced PI and other geomechanical parameters (e.g., shear strength, compressibility, permeability, and compactability). This was achieved by performing the Bland–Altman (BA) analysis [69], which involves developing an x:y scatter plot, with the y-axis representing the difference between the two measurement techniques (i.e., DBA = PLBG − PLRT) and the x-axis showing the average of these measurements (i.e., MBA = [PLBG + PLRT]/2). Following the BA framework, the 95% lower and upper agreement limits between the PLBG and PLRT can be, respectively, defined as LAL = μD − 1.96 σD and UAL = μD + 1.96 σD (where μD and σD denote the arithmetic mean and standard deviation of the DBA = PLBG − PLRT data, respectively). Note that the calculated LAL and UAL must be examined against an inductively-defined limit, often selected as the highest possible (water content) difference/variation in the standard measurement method (i.e., PLRT) based on its repeatability [65]. A review of the research literature indicates that the maximum variation in the PLRT for a given fine-grained soil (accounting for measurement variations across multiple operators) can be conservatively taken as ±8% [34]. Accordingly, this water content limit was considered as a point of reference to examine the LAL and UAL obtained in the present investigation.
The BA plot for the N = 60 pairs of PLBG–PLRT data is provided in Figure 3b. The mean of differences between PLBG and PLRT was shown to be μD = −0.26%, implying that the PLBG is on average 0.26% (water content) lower than the PLRT. The 95% agreement limits between PLBG and PLRT were calculated as LAL = −5.03% and UAL = +4.51%, indicating that 95% of the differences between these two PL measurement methods lie between these lower and upper water content limits, both of which are less than (in terms of magnitude) the chosen reference limit (for the present investigation) of ±8%. This implies that the BG-based and RT methods are expected to produce similar PL values for a given fine-grained soil investigated under identical testing conditions—that is, the ASTM/AASHTO rolling device method can be deemed as a reliable PL determination technique capable of alleviating the labor, time and possibly also some of the variability associated with the conventional RT test. Referring to Figure 3b; those data pairs that plot above/below the 95% agreement limits (which may count as potential outliers) were associated with DBA = PLBG − PLRT = −6.1%, −7.2% and +10.1% (for S15–S17, respectively), the magnitudes of which are still less than (or on par with) the reference water content limit of ±8%.
Referring to Figure 3b; the likelihoods of underestimating (i.e., PLBG < PLRT) and overestimating (i.e., PLBG > PLRT) the PLRT can be calculated as 50% and 40%, respectively; allowing one to simply debunk the notion presented by some researchers that the BG method generally tends to greatly underestimate the PLRT [58,63,64]. To further examine this critical aspect, and to investigate whether the degree of underestimation or overestimation is systematically related to fundamental soil properties (i.e., plasticity level class, clay and silt contents, and soil mineralogy), the PLBG-to-PLRT ratio is plotted against LLPC or LLFC, fclay, fsilt, and APC or AFC (see Figure 4). As is evident from this figure, the PLBG/PLRT ratio does not systematically increase or decrease with changes in soil type (or behavior); suggesting that the differences between the PLBG and PLRT measurements are most likely random in nature.
In view of the potential outlier DBA (= PLBG − PLRT) values obtained for S15–S17 (all classified as silt with very high plasticity, MV, as per BS 5930 [9]), one may postulate that the BG-based method is potentially less workable for less-cohesive soils (or silts). However, given that the bulk of the compiled database consisted of clays, and the fact that other silts within the database (i.e., S1, S10, S13, S27, S28 and S51) produced acceptable DBA values (i.e., |DBA| < 8%), this early postulation should be taken with caution, demanding further investigation.

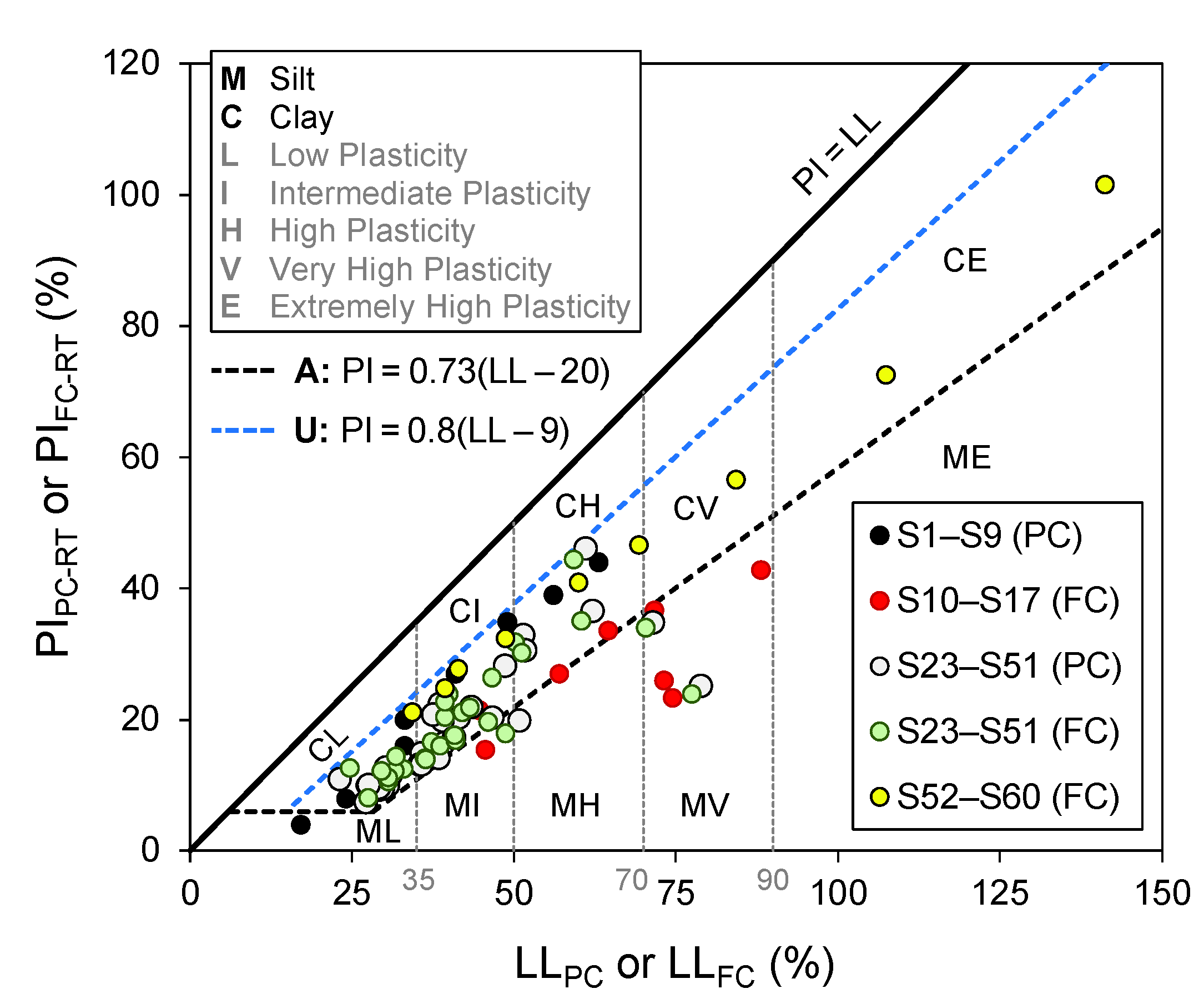
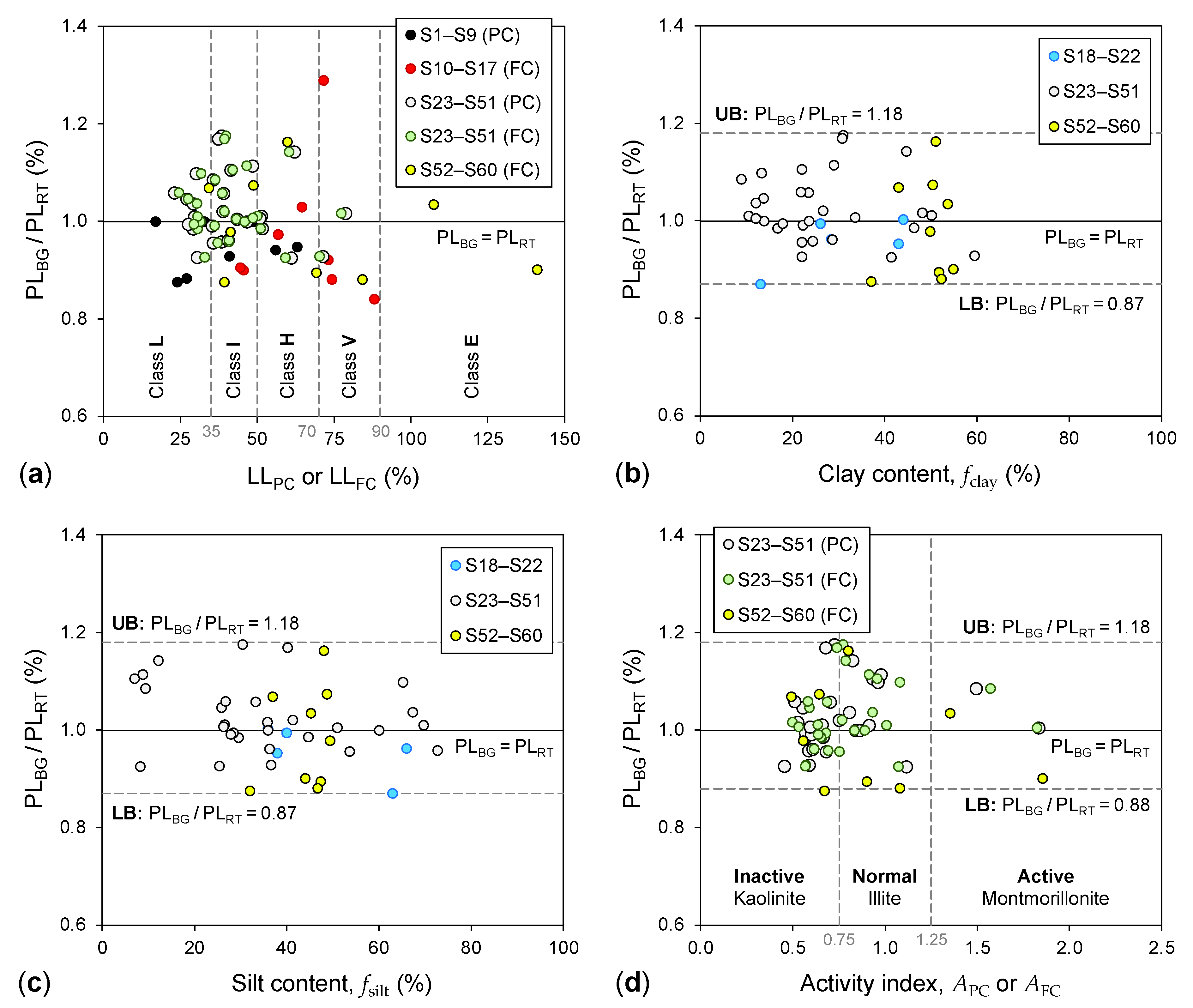
3.2. Use of PLBG for Soil Classification

The LL (i.e., LLPC or LLFC), together with the PI (i.e., PIPC-RT = LLPC − PLRT or PIFC-RT = LLFC − PLRT), are commonly employed with the Casagrande-style plasticity chart for classifying fine-grained soils [7,8,9,10]. Accordingly, any alternate PLRT measurement technique, such as the BG-based method, is expected to produce reliable soil classifications. To the authors’ knowledge, this critical requirement has not yet been examined (nor discussed) for the PLBG parameter. Herein, an attempt is made to examine the validity of the PLBG parameter in the context of soil classification using the BS soil plasticity-chart framework, as per BS 5930 [9].
Figure 5 illustrates the variations of the RT-deduced PI (PIPC-RT or PIFC-RT, written as PIPC/FC-RT for simplicity) against the BG-deduced PI (PIPC-BG or PIFC-BG; i.e., PIPC/FC-BG) for the compiled database (excluding S18–S22 for which the LLPC or LLFC values were nor reported). As expected, the two PI parameters are strongly correlated, exhibiting a linear relationship in the form of PIPC/FC-RT = 0.96 PIPC/FC-BG + 1.01 (with R2 = 0.980), implying that the RT- and BG-deduced PI parameters are approximately equal. Note that the MAPE and NRMSE associated with PIPC/FC-RT ≈ PIPC/FC-BG were shown to be 6.6% and 2.3%, respectively.
Making use of the LLPC and/or LLFC, together with the BG-deduced PI, only two cases (out of 84 examined)—namely, S16 employing LLFC and S28 employing LLPC—were shown to produce classifications different from those obtained based on the RT-deduced PI; that is, in terms of deducing clay instead of silt when plotted on the BS soil plasticity chart (see Table 2). Overall, this implies that compared to PLRT, the likelihood of achieving consistent soil classifications employing the PLBG parameter stands at 98%. Quite clearly, if the potential errors/variations associated with the PLRT measurements are also considered in the analysis, the two classification discrepancies can be deemed acceptable; especially when considering the small actual vertical distance for S16 and S28 from the A-Line, which can be calculated as DA = PIPC/FC-RT − 0.73 (LLPC/FC − 20) = −6.81% and −2.45%, respectively. In view of these results, it is concluded that the PLBG parameter can be used with confidence for routine soil classification purposes.

4. Summary and Conclusions

In view of its apparent shortcomings, several attempts have been made to devise alternative testing approaches to the standard hand-rolling PLRT method, targeting higher degrees of repeatability and reproducibility. Among these, device-rolling techniques, which mainly follow the same basic principles as the standard thread-rolling (by hand) test (i.e., PLRT), have been highly underrated by some researchers and hence demand further attention. Furthermore, there seems to exist a general belief among them that the “PL” deduced from such devices, including the well-established PLBG parameter obtained from the ASTM D4318/AASHTO T90 rolling device method, which is based on the original work by Bobrowski and Griekspoor [52], generally tends to greatly underestimate the PLRT. To examine this point, and to better understand the true potentials and/or limitations of the BG-based device-rolling technique for soil plasticity determination, this study investigated the validity of the PLBG parameter by quantifying and critically examining its statistical level of agreement with the standard PLRT. The following conclusions can be drawn from this study:
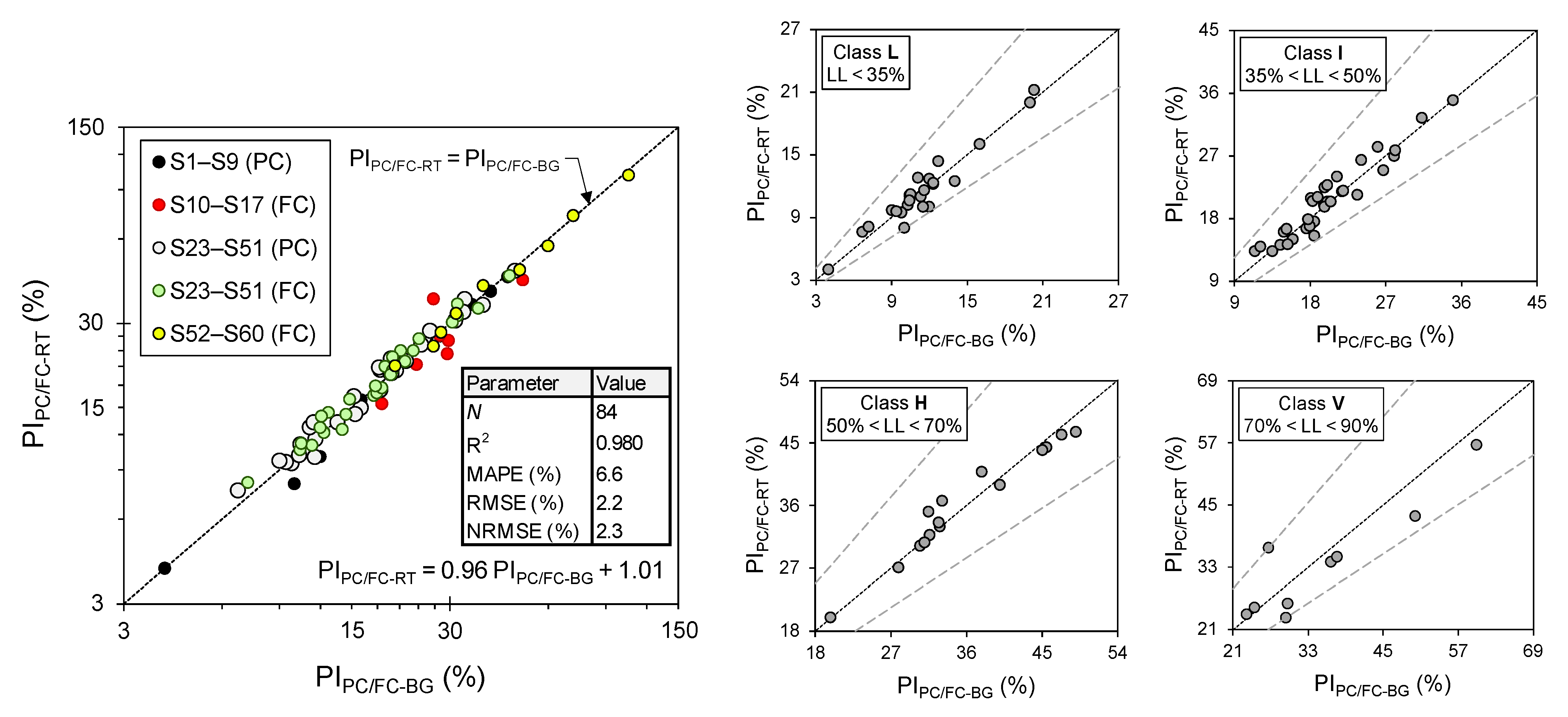
  • Following a comprehensive statistical analysis performed on a large and diverse database of 60 PLRT–PLBG test pairs, it was demonstrated that, under identical testing conditions, the BG-based and RT methods produce essentially similar PL values (i.e., PLRT ≈ PLBG). The 95% lower and upper agreement limits between PLBG and PLRT were obtained as −5.03% and +4.51%, respectively; implying that 95% of the differences between the two PL measurement methods lie between these two small water content limits, both of which can be deemed “statistically insignificant” when compared to the inductively-defined reference limit of ±8% (i.e., the highest possible difference/variation in the PLRT based on its repeatability, as reported in the research literature).
  • Further, the likelihoods of underestimating (i.e., PLBG < PLRT) and overestimating (i.e., PLBG > PLRT) the PLRT were obtained as 50% and 40%, respectively; thereby, debunking the notion presented by some researchers that the BG method generally tends to greatly underestimate the PLRT. It was also demonstrated that the degree of underestimation or overestimation does not systematically increase or decrease with changes in fundamental soil properties (i.e., plasticity level class, clay and silt contents, and soil mineralogy); suggesting that the differences between PLBG and PLRT are most likely random in nature.
  • Finally, making use of the BS soil plasticity-chart framework, an attempt, for the first time, was made to examine the validity of the PLBG parameter in the context of fine-grained soil classification. Compared to PLRT, the likelihood of achieving consistent soil classifications employing the PLBG (in conjunction with LLPC and/or LLFC) was shown to be 98%, with the classification discrepancies (only two cases out of 84 examined) being soil materials that plot relatively close to the A-Line. This implies that the PLBG parameter, as determined using the ASTM D4318/AASHTO T90 rolling device method, can be used with confidence for routine soil classification purposes.

Author Contributions

Conceptualization, A.S. and B.C.O.; Methodology, A.S. and B.C.O.; Validation, A.S. and B.C.O.; Formal analysis, A.S.; Investigation, A.S. and B.C.O.; Writing—original draft preparation, A.S.; Writing—review and editing, A.S. and B.C.O.; Visualization, A.S.; Funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The authors declare that the data supporting the findings of this study are available within the article.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

AASHTOAmerican Association of State Highway and Transportation Officials
ASTMAmerican Society for Testing and Materials
BABland–Altman (analysis/plot)
BGBobrowski and Griekspoor (method/device)
BSBritish Standard
CEClay with extremely high plasticity
CHClay with high plasticity
CIClay with intermediate plasticity
CLClay with low plasticity
CVClay with very high plasticity
FCFall-cone (method)
MESilt with extremely high plasticity
MHSilt with high plasticity
MISilt with intermediate plasticity
MLSilt with low plasticity
MVSilt with very high plasticity
PCPercussion-cup (method)
RTRolling-thread (method)
USCSUnified Soil Classification System

Notations

AFCSoil activity index (=PIFC-RT/fclay)
APCSoil activity index (=PIPC-RT/fclay)
dCone penetration depth (FC test) [mm]
DBAPlastic limit difference, defined as DBA = PLBG − PLRT [%]
DAActual vertical distance from the A-Line [%]
fclayClay content [%]
fsiltSilt content [%]
LALLower (water content) agreement limit [%]
LBLower (PLBG-to-PLRT variation) boundary
LLFCFall-cone liquid limit [%]
LLPCPercussion-cup liquid limit [%]
MBAPlastic limit average, defined as MBA = (PLBG + PLRT)/2 [%]
MAPEMean absolute percentage error [%]
nIndex of summation
NNumber of tests/observations
NbNumber of blows (PC test)
NRMSENormalized root-mean-squared error [%]
PIFC-BGPlasticity index (= LLFC − PLBG) [%]
PIFC-RTPlasticity index (= LLFC − PLRT) [%]
PIPC-BGPlasticity index (= LLPC − PLBG) [%]
PIPC-RTPlasticity index (= LLPC − PLRT) [%]
PLBGDevice-rolling plastic limit [%]
PLRTThread-rolling (by hand) plastic limit [%]
PLRT(max)Maximum of PLRT data [%]
PLRT(min)Minimum of PLRT data [%]
R2Coefficient of determination
RMSERoot-mean-squared error [% water content]
UALUpper (water content) agreement limit [%]
UBUpper (PLBG-to-PLRT variation) boundary
wGravimetric water content [%]
μDArithmetic mean of DBA (=PLBG − PLRT) data [%]
σDStandard deviation of DBA (=PLBG − PLRT) data [%]

References

  1. Atterberg, A. Lerornas forhållande till vatten, deras plasticitetsgränser och plasticitetsgrader. K. Lantbr. Handl. Och Tidskr. 1911, 50, 132–158. (In Swedish) [Google Scholar]
  2. Atterberg, A. Die plastizität der tone. Int. Mitt. Der Bodenkd. 1911, 1, 4–37. (In German) [Google Scholar]
  3. Terzaghi, K. Simplified soil tests for subgrades and their physical significance. Public Roads 1926, 7, 153–170. [Google Scholar]
  4. Terzaghi, K. Principles of final soil classification. Public Roads 1926, 8, 41–53. [Google Scholar]
  5. Casagrande, A. Research on the Atterberg limits of soils. Public Roads 1932, 13, 121–136. [Google Scholar]
  6. Casagrande, A. Notes on the design of the liquid limit device. Géotechnique 1958, 8, 84–91. [Google Scholar] [CrossRef]
  7. AASHTO M145. Standard Specification for Classification of Soils and Soil–Aggregate Mixtures for Highway Construction Purposes; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 1995. [Google Scholar]
  8. ASTM D3282. Standard Practice for Classification of Soils and Soil–Aggregate Mixtures for Highway Construction Purposes; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
  9. BS 5930. Code of Practice for Ground Investigations; British Standards Institution (BSI): London, UK, 2015; ISBN 9780539081350. [Google Scholar]
  10. ASTM D2487. Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System); ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar] [CrossRef]
  11. Skemption, A.W.; Northey, R.D. The sensitivity of clays. Géotechnique 1952, 3, 30–53. [Google Scholar] [CrossRef]
  12. Seed, H.B.; Woodward, R.J.; Lundgren, R. Prediction of swelling potential for compacted clays. J. Soil Mech. Found. Div. 1962, 88, 53–87. [Google Scholar] [CrossRef]
  13. Nayak, N.V.; Christensen, R.W. Swelling characteristics of compacted, expansive soils. Clays Clay Miner. 1971, 19, 251–261. [Google Scholar] [CrossRef]
  14. Wroth, C.P.; Wood, D.M. Correlation of index properties with some basic engineering properties of soils. Can. Geotech. J. 1978, 15, 137–145. [Google Scholar] [CrossRef]
  15. Carrier, W.D. Consolidation parameters derived from index tests. Géotechnique 1985, 35, 211–213. [Google Scholar] [CrossRef]
  16. Nakase, A.; Kamei, T.; Kusakabe, O. Constitutive parameters estimated by plasticity index. J. Geotech. Eng. 1988, 114, 844–858. [Google Scholar] [CrossRef]
  17. Nagaraj, T.S.; Pandian, N.S.; Narashimha Raju, P.S.R. Stress state–permeability relationships for fine-grained soils. Géotechnique 1993, 43, 333–336. [Google Scholar] [CrossRef]
  18. Gurtug, Y.; Sridharan, A. Compaction behaviour and prediction of its characteristics of fine grained soils with particular reference to compaction energy. Soils Found. 2004, 44, 27–36. [Google Scholar] [CrossRef] [Green Version]
  19. Erzin, Y.; Erol, O. Swell pressure prediction by suction methods. Eng. Geol. 2007, 92, 133–145. [Google Scholar] [CrossRef]
  20. Dolinar, B. Predicting the hydraulic conductivity of saturated clays using plasticity-value correlations. Appl. Clay Sci. 2009, 45, 90–94. [Google Scholar] [CrossRef]
  21. Dolinar, B. Predicting the normalized, undrained shear strength of saturated fine-grained soils using plasticity-value correlations. Appl. Clay Sci. 2010, 47, 428–432. [Google Scholar] [CrossRef]
  22. O’Kelly, B.C. Atterberg limits and remolded shear strength–water content relationships. Geotech. Test. J. 2013, 36, 939–947. [Google Scholar] [CrossRef]
  23. Vardanega, P.J.; Haigh, S.K. The undrained strength–liquidity index relationship. Can. Geotech. J. 2014, 51, 1073–1086. [Google Scholar] [CrossRef] [Green Version]
  24. Kootahi, K.; Mayne, P.W. Index test method for estimating the effective preconsolidation stress in clay deposits. J. Geotech. Geoenviron. Eng. 2016, 142, 04016049. [Google Scholar] [CrossRef]
  25. Soltani, A.; Deng, A.; Taheri, A.; Sridharan, A. Consistency limits and compaction characteristics of clay soils containing rubber waste. Proc. Inst. Civ. Eng. Geotech. Eng. 2019, 172, 174–188. [Google Scholar] [CrossRef] [Green Version]
  26. Wood, D.M. Soil Behaviour and Critical State Soil Mechanics, 1st ed.; Cambridge University Press: Cambridge, UK, 1991; ISBN 9780521337823. [Google Scholar]
  27. Dolinar, B.; Trauner, L. Liquid limit and specific surface of clay particles. Geotech. Test. J. 2004, 27, 580–584. [Google Scholar] [CrossRef]
  28. Trauner, L.; Dolinar, B.; Mišič, M. Relationship between the undrained shear strength, water content, and mineralogical properties of fine-grained soils. Int. J. Geomech. 2005, 5, 350–355. [Google Scholar] [CrossRef]
  29. AASHTO T89. Standard Method of Test. for Determining the Liquid Limit of Soils; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2013. [Google Scholar]
  30. ASTM D4318. Standard Test. Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar] [CrossRef]
  31. BS 1377–2. Methods of Test. for Soils for Civil. Engineering Purposes—Part. 2: Classification Tests; British Standards Institution (BSI): London, UK, 1990; ISBN 0580178676. [Google Scholar]
  32. BS EN 1997–2. Eurocode 7—Geotechnical Design—Part. 2: Ground Investigation and Testing; British Standards Institution (BSI): London, UK, 2007; ISBN 9780580718724. [Google Scholar]
  33. AS 1289.3.9.1. Methods of Testing Soils for Engineering Purposes: Soil Classification Tests—Determination of the Cone Liquid Limit of a Soil; Standards Australia (SA): Sydney, Australia, 2015; ISBN 9781760352974. [Google Scholar]
  34. O’Kelly, B.C.; Vardanega, P.J.; Haigh, S.K. Use of fall cones to determine Atterberg limits: A review. Géotechnique 2018, 68, 843–856. [Google Scholar] [CrossRef] [Green Version]
  35. Wood, D.M.; Wroth, C.P. The use of the cone penetrometer to determine the plastic limit of soils. Gr. Eng. 1978, 11, 37. [Google Scholar]
  36. Haigh, S.K.; Vardanega, P.J.; Bolton, M.D. The plastic limit of clays. Géotechnique 2013, 63, 435–440. [Google Scholar] [CrossRef] [Green Version]
  37. AS 1289.3.2.1. Methods of Testing Soils for Engineering Purposes: Soil Classification Tests—Determination of the Plastic Limit of a Soil —Standard Method; Standards Australia (SA): Sydney, Australia, 2009; ISBN 0733790054. [Google Scholar]
  38. AASHTO T90. Standard Method of Test. for Determining the Plastic Limit and Plasticity Index of Soils; American Association of State Highway and Transportation Officials (AASHTO): Washington, DC, USA, 2020. [Google Scholar]
  39. Sherwood, P.T.; Ryley, M.D. An investigation of a cone-penetrometer method for the determination of the liquid limit. Géotechnique 1970, 20, 203–208. [Google Scholar] [CrossRef]
  40. Belviso, R.; Ciampoli, S.; Cotecchia, V.; Federico, A. Use of cone penetrometer to determine consistency limits. Gr. Eng. 1985, 18, 21–22. [Google Scholar]
  41. Sridharan, A.; Nagaraj, H.B.; Prakash, K. Determination of the plasticity index from flow index. Geotech. Test. J. 1999, 22, 175–181. [Google Scholar] [CrossRef]
  42. Feng, T.W. Using a small ring and a fall-cone to determine the plastic limit. J. Geotech. Geoenviron. Eng. 2004, 130, 630–635. [Google Scholar] [CrossRef]
  43. Sivakumar, V.; Glynn, D.; Cairns, P.; Black, J.A. A new method of measuring plastic limit of fine materials. Géotechnique 2009, 59, 813–823. [Google Scholar] [CrossRef]
  44. Sivakumar, V.; O’Kelly, B.C.; Henderson, L.; Moorhead, C.; Chow, S.H. Measuring the plastic limit of fine soils: An experimental study. Proc. Inst. Civ. Eng. Geotech. Eng. 2015, 168, 53–64. [Google Scholar] [CrossRef]
  45. Vardanega, P.J.; Haigh, S.K. Some recent developments in the determination of the Atterberg limits. In Advances in Transportation Geotechnics and Materials for Sustainable Infrastructure (GSP 250); Bulut, R., Hsu, S.C., Eds.; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2014; pp. 48–55. ISBN 9780784478509. [Google Scholar] [CrossRef] [Green Version]
  46. O’Kelly, B.C. Reappraisal of soil extrusion for geomechanical characterisation. Geotech. Res. 2019, 6, 265–287. [Google Scholar] [CrossRef] [Green Version]
  47. O’Kelly, B.C. Review of recent developments and understanding of Atterberg limits determinations. Geotechnics 2021, 1, 59–75. [Google Scholar] [CrossRef]
  48. Prakash, K. Discussion of “Plastic limit, liquid limit, and undrained shear strength of soil—reappraisal” by Binu Sharma and Padma K. Bora. J. Geotech. Geoenviron. Eng. 2005, 131, 402. [Google Scholar] [CrossRef]
  49. Nagaraj, H.B.; Sridharan, A.; Mallikarjuna, H.M. Re-examination of undrained strength at Atterberg limits water contents. Geotech. Geol. Eng. 2012, 30, 727–736. [Google Scholar] [CrossRef]
  50. O’Kelly, B.C.; Vardanega, P.J.; Haigh, S.K.; Barnes, G.E. Discussion: Use of fall cones to determine Atterberg limits: A review. Géotechnique 2020, 70, 647–651. [Google Scholar] [CrossRef] [Green Version]
  51. Gay, G.C.W.; Kaiser, W. Mechanization for remolding fine grained soils and for the plastic limit test. J. Test. Eval. 1973, 1, 317–318. [Google Scholar] [CrossRef]
  52. Bobrowski, L.J.; Griekspoor, D.M. Determination of the plastic limit of a soil by means of a rolling device. Geotech. Test. J. 1992, 15, 284–287. [Google Scholar] [CrossRef]
  53. Temyingyong, A.; Chantawarangul, K.; Sudasna-na-Ayudthya, P. Statistical analysis of influenced factors affecting the plastic limit of soils. Kasetsart J. Nat. Sci. 2002, 36, 98–102. [Google Scholar]
  54. Barnes, G.E. An apparatus for the plastic limit and workability of soils. Proc. Inst. Civ. Eng. Geotech. Eng. 2009, 162, 175–185. [Google Scholar] [CrossRef]
  55. Kayabali, K. Determination of consistency limits: A comparison between –#40 and –#200 materials. Electron. J. Geotech. Eng. 2011, 16, 1547–1561. [Google Scholar]
  56. Kayabali, K. An alternative testing tool for plastic limit. Electron. J. Geotech. Eng. 2012, 17, 2107–2114. [Google Scholar]
  57. Barnes, G.E. An apparatus for the determination of the workability and plastic limit of clays. Appl. Clay Sci. 2013, 80–81, 281–290. [Google Scholar] [CrossRef]
  58. Barnes, G.E. The Plastic Limit and Workability of Soils. Ph.D. Thesis, The University of Manchester, Manchester, UK, 2013. [Google Scholar]
  59. De Oliveira Modesto, C.; Bernardin, A.M. Determination of clay plasticity: Indentation method versus Pfefferkorn method. Appl. Clay Sci. 2008, 40, 15–19. [Google Scholar] [CrossRef]
  60. Moreno-Maroto, J.M.; Alonso-Azcárate, J. An accurate, quick and simple method to determine the plastic limit and consistency changes in all types of clay and soil: The thread-bending test. Appl. Clay Sci. 2015, 114, 497–508. [Google Scholar] [CrossRef]
  61. Moreno-Maroto, J.M.; Alonso-Azcárate, J. A bending test for determining the Atterberg plastic limit in soils. J. Vis. Exp. 2016, 112, e54118. [Google Scholar] [CrossRef]
  62. Moreno-Maroto, J.M.; Alonso-Azcárate, J. Plastic limit and other consistency parameters by a bending method and interpretation of plasticity classification in soils. Geotech. Test. J. 2017, 40, 467–482. [Google Scholar] [CrossRef]
  63. Rashid, A.S.A.; Kassim, K.A.; Katimon, A.; Noor, N.M. Determination of plastic limit of soil using modified methods. Malays. J. Civ. Eng. 2008, 20, 295–305. [Google Scholar] [CrossRef]
  64. Ishaque, F.; Hoque, M.N.; Rashid, M.A. Determination of plastic limit of some selected soils using rolling device. Progress. Agric. 2013, 21, 187–194. [Google Scholar] [CrossRef] [Green Version]
  65. Rehman, H.U.; Pouladi, N.; Pulido-Moncada, M.; Arthur, E. Repeatability and agreement between methods for determining the Atterberg limits of fine-grained soils. Soil Sci. Soc. Am. J. 2020, 84, 21–30. [Google Scholar] [CrossRef]
  66. Casagrande, A. Classification and identification of soils. Proc. Am. Soc. Civ. Eng. 1947, 73, 783–810. [Google Scholar]
  67. Soltani, A.; O’Kelly, B.C. Discussion of “The flow index of clays and its relationship with some basic geotechnical properties” by G. Spagnoli, M. Feinendegen, L. Di Matteo, and D. A. Rubinos, published in Geotechnical Testing Journal 42, No. 6 (2019): 1685–1700. Geotech. Test. J. 2021, 44, 216–219. [Google Scholar] [CrossRef]
  68. Soltani, A.; Deng, A.; Taheri, A.; Sridharan, A.; Estabragh, A.R. A framework for interpretation of the compressibility behavior of soils. Geotech. Test. J. 2018, 41. [Google Scholar] [CrossRef]
  69. Bland, J.M.; Altman, D.G. Measuring agreement in method comparison studies. Stat. Methods Med. Res. 1999, 8, 135–160. [Google Scholar] [CrossRef] [PubMed]
Geosciences 11 00247 g001 550
Figure 1. Schematic illustration of the ASTM/AASHTO rolling device for PL determination (modified from [30]).
Figure 1. Schematic illustration of the ASTM/AASHTO rolling device for PL determination (modified from [30]).
Geosciences 11 00247 g001
Geosciences 11 00247 g002 550
Figure 2. The database soils (excluding S18–S22 for which the LLPC or LLFC values were not reported) plotted on the standard soil plasticity chart, as per BS 5930 [9].
Figure 2. The database soils (excluding S18–S22 for which the LLPC or LLFC values were not reported) plotted on the standard soil plasticity chart, as per BS 5930 [9].
Geosciences 11 00247 g002
Geosciences 11 00247 g003 550
Figure 3. Comparison of PLRT and PLBG for the compiled database of N = 60 fine-grained soils: (a) PLRT–PLBG correlation plot; and (b) PLBG–PLRT Bland–Altman plot. Note: LAL and UAL denote lower and upper agreement limits, respectively.
Figure 3. Comparison of PLRT and PLBG for the compiled database of N = 60 fine-grained soils: (a) PLRT–PLBG correlation plot; and (b) PLBG–PLRT Bland–Altman plot. Note: LAL and UAL denote lower and upper agreement limits, respectively.
Geosciences 11 00247 g003
Geosciences 11 00247 g004 550
Figure 4. Variations of the PLBG-to-PLRT ratio against fundamental soil properties for the compiled database: (a) LLPC or LLFC; (b) fclay; (c) fsilt; and (d) APC or AFC. Note: LB and UB denote lower and upper PLBG/PLRT boundaries, respectively; and L, I, H, V and E represent low, intermediate, high, very high and extremely high plasticity level classes, respectively.
Figure 4. Variations of the PLBG-to-PLRT ratio against fundamental soil properties for the compiled database: (a) LLPC or LLFC; (b) fclay; (c) fsilt; and (d) APC or AFC. Note: LB and UB denote lower and upper PLBG/PLRT boundaries, respectively; and L, I, H, V and E represent low, intermediate, high, very high and extremely high plasticity level classes, respectively.
Geosciences 11 00247 g004
Geosciences 11 00247 g005 550
Figure 5. Variations of the RT-deduced PI (PIPC/FC-RT) against the BG-deduced PI (PIPC/FC-BG) for the compiled database (excluding S18–S22 for which the LLPC or LLFC values were nor reported). Note: L, I, H and V represent low, intermediate, high and very high plasticity level classes, respectively.
Figure 5. Variations of the RT-deduced PI (PIPC/FC-RT) against the BG-deduced PI (PIPC/FC-BG) for the compiled database (excluding S18–S22 for which the LLPC or LLFC values were nor reported). Note: L, I, H and V represent low, intermediate, high and very high plasticity level classes, respectively.
Geosciences 11 00247 g005
Table
Table 1. Detailed description of the compiled database of PLRT–PLBG test results.
Table 1. Detailed description of the compiled database of PLRT–PLBG test results.
SourceSource ID/DescriptionNew IDfclay (%)fsilt (%)LLPC (%)LLFC (%)PLRT (%)PLBG (%)PIPC-RT (%)PIFC-RT (%)APCAFC
[52]1S1——17.0—13.013.04.0———
2S2——24.0—16.014.08.0———
3S3——27.0—17.015.010.0———
4S4——33.0—17.017.016.0———
5S5——33.0—13.013.020.0———
6S6——41.0—14.013.027.0———
7S7——49.0—14.014.035.0———
8S8——56.0—17.016.039.0———
9S9——63.0—19.018.044.0———
[63]Sample AS10———73.147.143.4—26.0——
Sample BS11———56.929.829.0—27.1——
Sample CS12———64.530.931.8—33.6——
Sample DS13———45.530.027.0—15.5——
Sample ES14———44.623.221.0—21.4——
Sample FS15———74.451.145.0—23.3——
Sample GS16———88.145.238.0—42.9——
Sample HS17———71.634.945.0—36.7——
[64]Agronomy FarmS1813.063.0——23.020.0————
LalmaiS1926.040.0——21.121.0————
GaghraS2028.466.0——25.324.3————
BhalukaS2143.038.0——27.826.5————
BhoradubaS2244.036.0——29.930.0————
[65]DK2S2322.07.041.442.020.923.120.521.10.930.96
DK3S2428.98.848.546.620.222.528.326.40.980.91
DK4S2544.612.262.060.425.328.936.735.10.820.79
CH1S2622.053.735.637.220.619.715.016.60.680.75
CH2S2748.135.878.777.453.454.325.324.00.530.50
CH3S2859.536.671.370.336.333.735.034.00.590.57
CH4S2916.729.629.130.619.619.39.511.00.570.66
CH5S3026.641.338.939.318.919.320.020.40.750.77
DE1S3122.025.430.432.920.418.910.012.50.450.57
DE2S3213.725.927.027.519.420.37.68.10.550.59
DE3S3350.126.551.350.118.318.533.031.80.660.63
DE4S3423.533.339.038.622.523.816.516.10.700.69
BE1S3513.860.130.931.619.319.311.612.30.840.89
BE2S3613.365.230.131.717.319.012.814.40.961.08
BE3S3710.569.729.630.620.020.29.610.60.911.01
BE4S3812.067.329.030.519.320.09.711.20.810.93
PK1S3917.928.427.529.517.317.210.212.20.570.68
PK2S4024.472.738.340.924.023.014.316.90.590.69
PK3S4146.344.751.651.120.920.630.730.20.660.65
PK4S4221.826.823.024.611.912.611.112.70.510.58
PK5S4331.030.538.439.915.918.722.524.00.730.77
PK6S4430.840.237.439.316.519.320.922.80.680.74
UA1S4522.227.935.336.222.021.813.314.20.600.64
UA2S468.99.435.636.322.324.213.314.01.491.57
GHS4741.48.361.059.214.813.746.244.41.121.07
CN1S4828.636.340.640.823.222.317.417.60.610.62
CN2S4912.051.043.343.221.321.422.021.91.831.83
NOS5023.636.046.645.926.226.220.419.70.860.83
JPS5133.626.350.748.630.730.920.017.90.600.53
Present StudyKilkenny, South AustraliaS5243.037.0—34.313.114.0—21.2—0.49
Inkerman, South AustraliaS5337.032.0—39.314.412.6—24.9—0.67
KaoliniteS5449.849.4—41.413.613.3—27.8—0.56
Kaolinite + 5% BentoniteS5550.448.7—48.716.217.4—32.5—0.64
Kaolinite + 10% BentoniteS5651.048.1—59.919.022.1—40.9—0.80
Kaolinite + 15% BentoniteS5751.747.4—69.322.720.3—46.6—0.90
Kaolinite + 20% BentoniteS5852.346.7—84.327.724.4—56.6—1.08
Kaolinite + 30% BentoniteS5953.645.3—107.434.836.0—72.6—1.35
Kaolinite + 40% BentoniteS6054.844.0—141.139.535.6—101.6—1.85
Note: fclay and fsilt = clay (<2 μm) and silt (2–75 μm) contents, respectively; LLPC and LLFC = percussion-cup and BS fall-cone liquid limits, respectively; PLRT and PLBG = standard thread-rolling (by hand) and device-rolling plastic limits, respectively; PIPC-RT = plasticity index deduced from the PC and RT tests (=LLPC − PLRT); PIFC-RT = plasticity index deduced from the FC and RT tests (=LLFC − PLRT); and APC or AFC = soil activity index (defined as the PI-to-clay content ratio and hence calculated as APC = PIPC-RT/fclay or AFC = PIFC-RT/fclay).
Table
Table 2. Summary of the soil classification results employing PLRT and PLBG for the compiled database (excluding S18–S22 for which the LLPC or LLFC values were not reported).
Table 2. Summary of the soil classification results employing PLRT and PLBG for the compiled database (excluding S18–S22 for which the LLPC or LLFC values were not reported).
IDLLPC (%)LLFC (%)PLRT (%)PLBG (%)PIPC-RT (%)PIFC-RT (%)USCSPC-RTUSCSFC-RTPIPC-BG (%)PIFC-BG (%)USCSPC-BGUSCSFC-BG
S117.0—13.013.04.0—ML—4.0—ML—
S224.0—16.014.08.0—CL—10.0—CL—
S327.0—17.015.010.0—CL—12.0—CL—
S433.0—17.017.016.0—CL—16.0—CL—
S533.0—13.013.020.0—CL—20.0—CL—
S641.0—14.013.027.0—CI—28.0—CI—
S749.0—14.014.035.0—CI—35.0—CI—
S856.0—17.016.039.0—CH—40.0—CH—
S963.0—19.018.044.0—CH—45.0—CH—
S10—73.147.143.4—26.0—MV—29.7—MV
S11—56.929.829.0—27.1—CH—27.9—CH
S12—64.530.931.8—33.6—CH—32.7—CH
S13—45.530.027.0—15.5—MI—18.5—MI
S14—44.623.221.0—21.4—CI—23.6—CI
S15—74.451.145.0—23.3—MV—29.4—MV
S16—88.145.238.0—42.9—MV—50.1—CV
S17—71.634.945.0—36.7—MV—26.6—MV
S2341.442.020.923.120.521.1CICI18.318.9CICI
S2448.546.620.222.528.326.4CICI26.024.1CICI
S2562.060.425.328.936.735.1CHCH33.131.5CHCH
S2635.637.220.619.715.016.6CICI15.917.5CICI
S2778.777.453.454.325.324.0MVMV24.423.1MVMV
S2871.370.336.333.735.034.0MVMV37.636.6CVMV
S2929.130.619.619.39.511.0CLCL9.811.3CLCL
S3038.939.318.919.320.020.4CICI19.620.0CICI
S3130.432.920.418.910.012.5CLCL11.514.0CLCL
S3227.027.519.420.37.68.1CLCL6.77.2CLCL
S3351.350.118.318.533.031.8CHCH32.831.6CHCH
S3439.038.622.523.816.516.1CICI15.214.8CICI
S3530.931.619.319.311.612.3CLCL11.612.3CLCL
S3630.131.717.319.012.814.4CLCL11.112.7CLCL
S3729.630.620.020.29.610.6CLCL9.410.4CLCL
S3829.030.519.320.09.711.2CLCL9.010.5CLCL
S3927.529.517.317.210.212.2CLCL10.312.3CLCL
S4038.340.924.023.014.316.9CICI15.317.9CICI
S4151.651.120.920.630.730.2CHCH31.030.5CHCH
S4223.024.611.912.611.112.7CLCL10.412.0CLCL
S4338.439.915.918.722.524.0CICI19.721.2CICI
S4437.439.316.519.320.922.8CICI18.120.0CICI
S4535.336.222.021.813.314.2CICI13.514.4CICI
S4635.636.322.324.213.314.0CICI11.412.1CICI
S4761.059.214.813.746.244.4CHCH47.345.5CHCH
S4840.640.823.222.317.417.6CICI18.318.5CICI
S4943.343.221.321.422.021.9CICI21.921.8CICI
S5046.645.926.226.220.419.7CICI20.419.7CICI
S5150.748.630.730.920.017.9MHMI19.817.7MHMI
S52—34.313.114.0—21.2—CL—20.3—CL
S53—39.314.412.6—24.9—CI—26.7—CI
S54—41.413.613.3—27.8—CI—28.1—CI
S55—48.716.217.4—32.5—CI—31.3—CI
S56—59.919.022.1—40.9—CH—37.8—CH
S57—69.322.720.3—46.6—CH—49.0—CH
S58—84.327.724.4—56.6—CV—59.9—CV
S59—107.434.836.0—72.6—CE—71.4—CE
S60—141.139.535.6—101.6—CE—105.5—CE
Note: LLPC and LLFC = percussion-cup and BS fall-cone liquid limits, respectively; PLRT and PLBG = standard thread-rolling (by hand) and device-rolling plastic limits, respectively; PIPC-RT = LLPC − PLRT; PIFC-RT = LLFC − PLRT; PIPC-BG = LLPC − PLBG; PIFC-BG = LLFC − PLBG; and USCS = Unified Soil Classification System, as per BS 5930 [9].
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Soltani, A.; O’Kelly, B.C. Reappraisal of the ASTM/AASHTO Standard Rolling Device Method for Plastic Limit Determination of Fine-Grained Soils. Geosciences 2021, 11, 247. https://doi.org/10.3390/geosciences11060247

AMA Style

Soltani A, O’Kelly BC. Reappraisal of the ASTM/AASHTO Standard Rolling Device Method for Plastic Limit Determination of Fine-Grained Soils. Geosciences. 2021; 11(6):247. https://doi.org/10.3390/geosciences11060247

Chicago/Turabian Style

Soltani, Amin, and Brendan C. O’Kelly. 2021. "Reappraisal of the ASTM/AASHTO Standard Rolling Device Method for Plastic Limit Determination of Fine-Grained Soils" Geosciences 11, no. 6: 247. https://doi.org/10.3390/geosciences11060247

APA Style

Soltani, A., & O’Kelly, B. C. (2021). Reappraisal of the ASTM/AASHTO Standard Rolling Device Method for Plastic Limit Determination of Fine-Grained Soils. Geosciences, 11(6), 247. https://doi.org/10.3390/geosciences11060247

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop