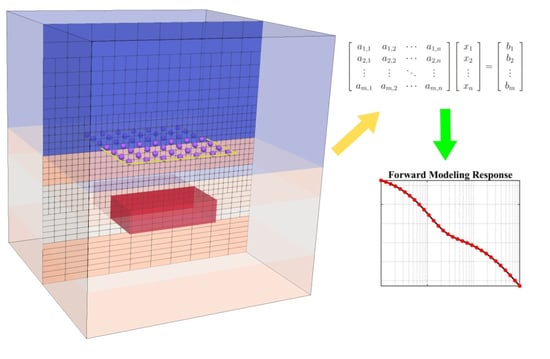
A Comparison Study of Explicit and Implicit 3-D Transient Electromagnetic Forward Modeling Schemes on Multi-Resolution Grid
Abstract
:1. Introduction
2. Methods
2.1. Explicit Scheme in the Modified Version of the Du Fort-Frankel Method
2.2. Implicit Scheme Using the Backward Euler Method
3. Multi-Resolution Grid
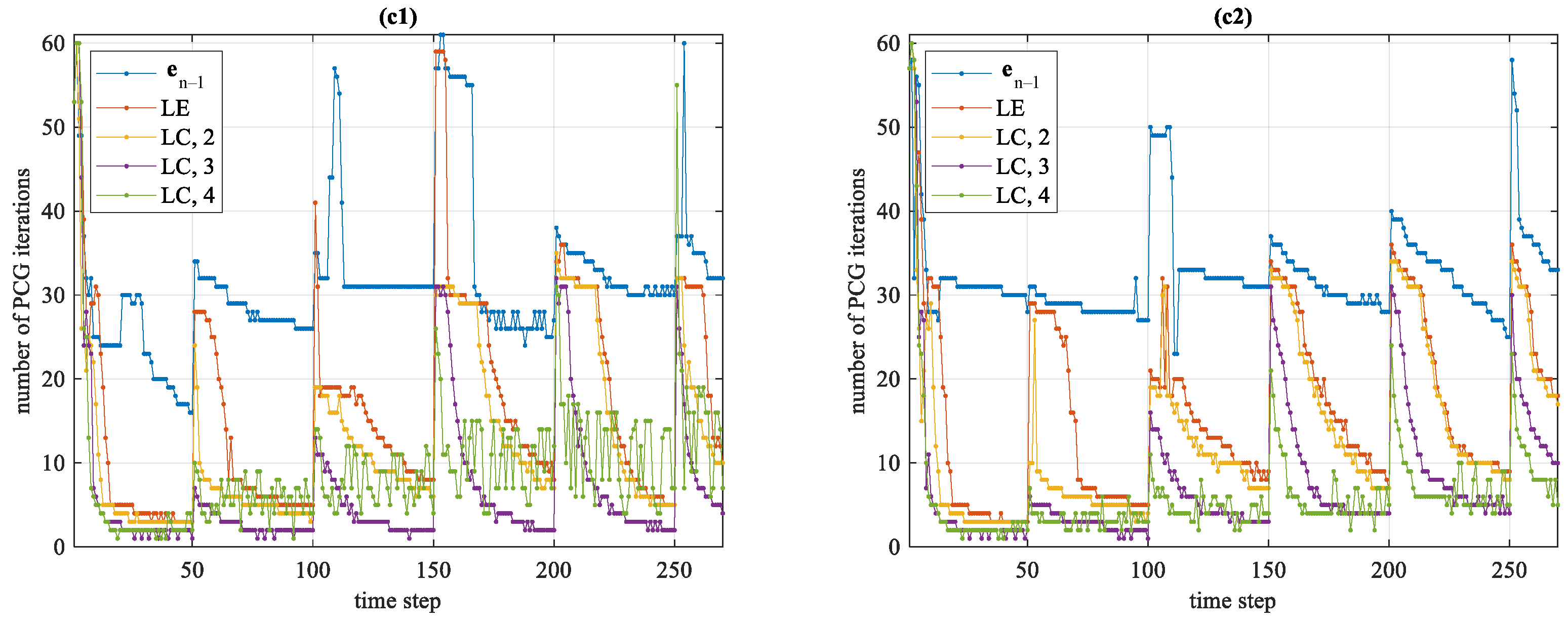
4. Results
4.1. Example 1
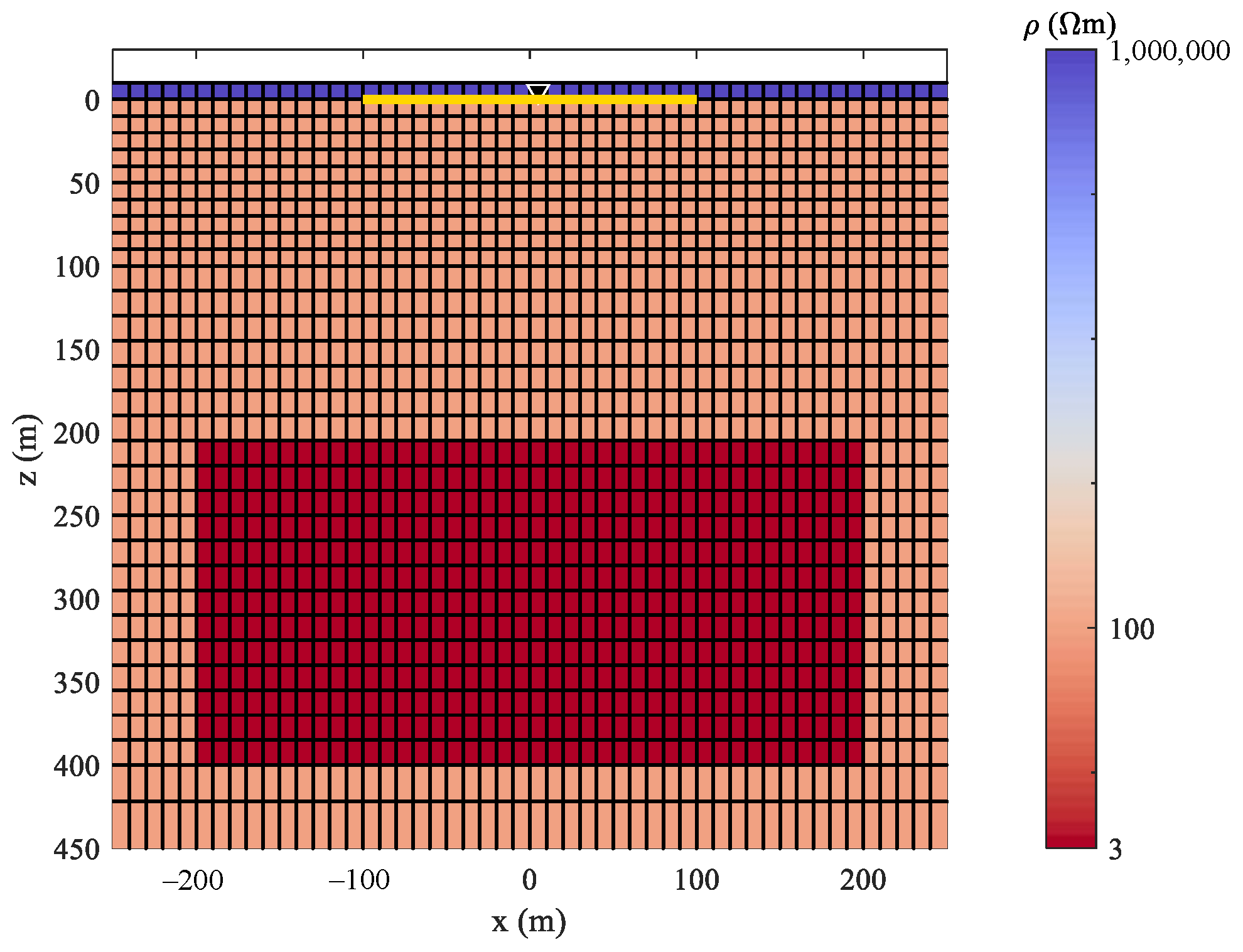
4.2. Example 2
4.3. Example 3
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flores, C.; Peralta-Ortega, S.A. Induced polarization with in-loop transient electromagnetic soundings: A case study of mineral discrimination at El Arco porphyry copper, Mexico. J. Appl. Geophys. 2009, 68, 423–436. [Google Scholar] [CrossRef]
- Swidinsky, A.; Hölz, S.; Jegen, M. On mapping seafloor mineral deposits with central loop transient electromagnetics. Geophysics 2012, 77, E171–E184. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Xue, G.; Liu, J.; Wu, X. Electromagnetic methods for mineral exploration in China: A review. Ore Geol. Rev. 2020, 118, 103357. [Google Scholar] [CrossRef]
- Liu, Y.; Yin, C.; Qiu, C.; Hui, Z.; Zhang, B.; Ren, X.; Weng, A. 3-D Inversion of Transient EM Data with Topography Using Unstructured Tetrahedral Grids. Geophys. J. Int. 2019, 217, 301–318. [Google Scholar] [CrossRef]
- Börner, R.U. Numerical modelling in geo-electromagnetics: Advances and challenges. Surv. Geophys. 2010, 31, 225–245. [Google Scholar] [CrossRef]
- Adhidjaja, J.I.; Hohmann, G.W. A finite-difference algorithm for the transient electromagnetic response of a three-dimensional body. Geophys. J. Int. 1989, 98, 233–242. [Google Scholar] [CrossRef] [Green Version]
- Oristaglio, M.L.; Hohmann, G.W. Diffusion of electromagnetic fields into a two-dimensional earth: A finite-difference approach. Geophysics 1984, 49, 870–894. [Google Scholar] [CrossRef]
- Wang, T.; Hohmann, G.W. A Finite-difference, Time-domain Solution for Three-dimensional Electromagnetic Modeling. Geophysics 1993, 58, 797–809. [Google Scholar] [CrossRef] [Green Version]
- Haber, E.; Ascher, U.; Oldenburg, D.W. 3D forward modelling of time domain electromagnetic data. In SEG Technical Program Expanded Abstracts 2002; Society of Exploration Geophysicists: Tulsa, OK, USA, 2002; pp. 641–644. [Google Scholar]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. 3D time-domain simulation of electromagnetic diffusion phenomena: A finite-element electric-field approach. Geophysics 2010, 75, F115–F126. [Google Scholar] [CrossRef]
- Oldenburg, D.W.; Haber, E.; Shekhtman, R. Three dimensional inversion of multisource time domain electromagnetic data. Geophysics 2013, 78, E47–E57. [Google Scholar] [CrossRef] [Green Version]
- Um, E.S.; Harris, J.M.; Alumbaugh, D.L. An iterative finite element time-domain method for simulating three-dimensional electromagnetic diffusion in earth. Geophys. J. Int. 2012, 190, 871–886. [Google Scholar] [CrossRef] [Green Version]
- Domnikov, P.A. Speedup of three-dimensional finite element geoelectromagnetic fields modelling in time domain. In Proceedings of the 2016 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 3–6 October 2016; Volume 2, pp. 244–246. [Google Scholar]
- Haber, E.; Heldmann, S. An octree multigrid method for quasi-static Maxwell’s equations with highly discontinuous coefficients. J. Comput. Phys. 2007, 223, 783–796. [Google Scholar] [CrossRef]
- Horesh, L.; Haber, E. A second order discretization of Maxwell’s equations in the quasi-static regime on OcTree grids. SIAM J. Sci. Comput. 2011, 33, 2805–2822. [Google Scholar] [CrossRef]
- Cherevatova, M.; Egbert, G.; Smirnov, M.Y. A multi-resolution approach to electromagnetic modelling. Geophys. J. Int. 2018, 214, 656–671. [Google Scholar] [CrossRef]
- Gao, J.; Smirnov, M.; Smirnova, M.; Egbert, G. 3-D DC Resistivity Forward Modeling Using the Multi-resolution Grid. Pure Appl. Geophys. 2020, 117, 2803–2819. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Smirnov, M.; Smirnova, M.; Egbert, G. 3-D time-domain electromagnetic modeling based on multi-resolution grid with application to geomagnetically induced currents. Phys. Earth Planet Inter. 2021, 312, 106651. [Google Scholar] [CrossRef]
- Yee, K. Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef] [Green Version]
- Commer, M.; Newman, G. A Parallel Finite-difference Approach for 3D Transient Electromagnetic Modeling with Galvanic Sources. Geophysics 2004, 69, 1192–1202. [Google Scholar] [CrossRef] [Green Version]
- Farquharson, C.G.; Miensopust, M.P. Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction. J. Appl. Geophys. 2011, 75, 699–710. [Google Scholar] [CrossRef]
- Smith, J.T. Conservative modeling of 3-D electromagnetic fields, Part II: Biconjugate gradient solution and an accelerator. Geophysics 1996, 61, 1319–1324. [Google Scholar] [CrossRef]
- Auken, E.; Christiansen, A.V.; Kirkegaard, C.; Fiandaca, G.; Schamper, C.; Behroozmand, A.A.; Binley, A.; Nielsen, E.; Effersø, F.; Christensen, N.B.; et al. An overview of a highly versatile forward and stable inverse algorithm for airborne, ground-based and borehole electromagnetic and electric data. Explor. Geophys. 2015, 46, 223–235. [Google Scholar] [CrossRef] [Green Version]
- Druskin, V. A spectral semi-discrete method for numerical solution of 3-D non-stationary problems in electrical prospecting. Phys. Sol. Earth 1988, 24, 641–648. [Google Scholar]









| Scheme | Parameter | 100 Model | 1000 Model | 10,000 Model |
|---|---|---|---|---|
| explicit | , | |||
| 3089 | 9724 | |||
| 2-D FFT area () | ||||
| implicit | , | |||
| 270 | 270 | 270 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Smirnov, M.; Smirnova, M.; Egbert, G. A Comparison Study of Explicit and Implicit 3-D Transient Electromagnetic Forward Modeling Schemes on Multi-Resolution Grid. Geosciences 2021, 11, 257. https://doi.org/10.3390/geosciences11060257
Gao J, Smirnov M, Smirnova M, Egbert G. A Comparison Study of Explicit and Implicit 3-D Transient Electromagnetic Forward Modeling Schemes on Multi-Resolution Grid. Geosciences. 2021; 11(6):257. https://doi.org/10.3390/geosciences11060257
Chicago/Turabian StyleGao, Jingyu, Maxim Smirnov, Maria Smirnova, and Gary Egbert. 2021. "A Comparison Study of Explicit and Implicit 3-D Transient Electromagnetic Forward Modeling Schemes on Multi-Resolution Grid" Geosciences 11, no. 6: 257. https://doi.org/10.3390/geosciences11060257