Advanced Determination of Heat Flow Density on an Example of a West Russian Oil Field
Abstract
:1. Introduction
2. Materials and Methods
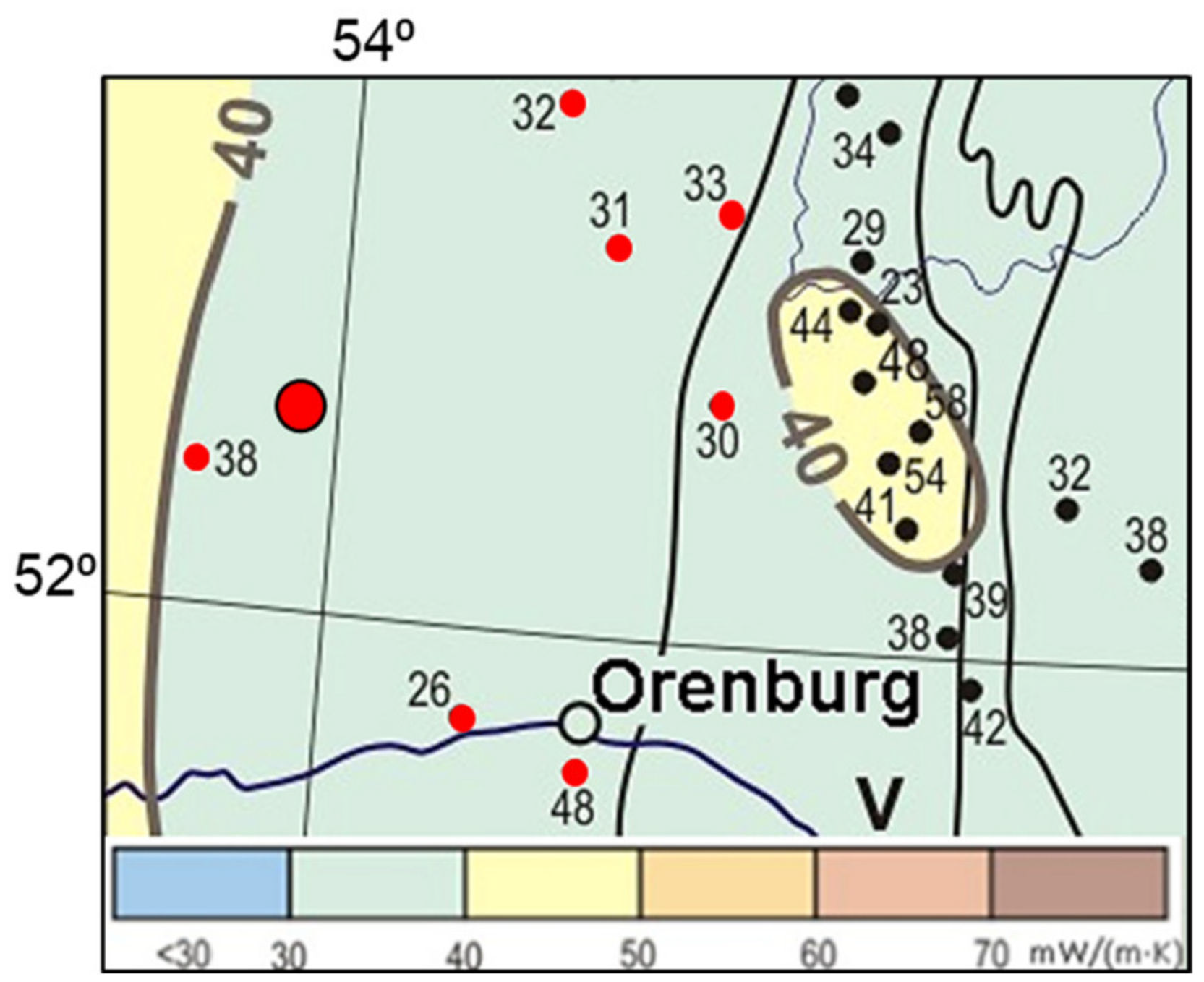
2.1. Object of Study
2.2. Workflow
- Temperature logging in the suspended well is conducted (Section 2.3). Concurrently, the continuous thermal core logging for all available full-sized cores is conducted (Section 2.4.1).
- The continuous thermal core logging of all recovered full-size core samples is conducted at atmospheric pressure and temperature (see Section 2.4.1).
- Based on the results of thermal core logging and the analysis of lithological and stratigraphic data, the reasonable selection of core plugs (see Section 2.4.2) for subsequent measurements of thermal properties at full saturation and elevated pressure and temperature is conducted.
- The investigations of rock thermal properties at elevated temperatures and pressures (Section 2.4.3) and at different saturations are conducted (Section 2.4.2). Based on the obtained results, the nature of thermal anisotropy (textural or technogenic micro-anisotropy) is determined.
- The rock thermal properties are determined within not-cored intervals from well-logging data based on a novel technique (Section 2.5, [26]) accounting for the estimated rock anisotropy.
- The equivalent thermal conductivity is calculated for intervals with experimental and predicted (from well-logging) data on thermal conductivity at atmospheric temperature and pressure (Section 2.6). Concurrently, the temperature gradient is calculated for the intervals with data on rock thermal properties (Section 2.3).
- Based on the results of the measurements of the thermal properties of core plugs from a reasonably selected collection, the corrections for in situ saturation, temperature, and pressure are applied for equivalent thermal conductivities accounting for multiscale rock heterogeneity, the effects of core changes during storage, and textural and micro-anisotropy factors.
- The calculation of heat flow density is performed for intervals with data on rock thermal properties and temperature gradients. The separate method of heat flow determination (when the upper and lower estimates of interval thermal conductivity are used; see Section 2.6) was applied. The calculation of the conductive component of the heat flow density is carried out according to the Fourier equation for the stationary conductive heat transfer [3]:
2.3. Temperature Logging
2.4. Methods for Measuring Thermal Properties of Rocks
- The continuous profiling of thermal properties with an optical scanning technique of all recovered full-sized cores (cores were sawed in half along their axis) from the studied well. During scanning, the parallel and perpendicular components of thermal conductivity were determined, and the assessment of the textural anisotropy and microanisotropy of rocks [10] was performed.
- Determining the effect of the core change on rock thermal conductivity after the extraction of cores from the packing containers via additional measurements on a representative collection of standard core samples with subsequent corrections of the results of thermal core logging.
- Measurements of thermal properties at elevated temperatures on standard core plugs with a combination of measurements with the optical scanning laser setup [26], DTC-300 device (TA instruments), and DSC 214 Polyma (NETZSCH).
- Determining the dependencies of thermal properties on the porosity and type of pore fluid via the measurement of thermal conductivity components for parallel and perpendicular directions to the bedding plane and volumetric heat capacity at different saturations (sequentially dried, saturated with synthetic brine and oil under vacuum conditions) on the collection of standard core plugs using a laser setup for optical scanning.
- Measuring thermal conductivity and volumetric heat capacity on core cuttings at atmospheric and in situ temperatures [26].
- Determining rock thermal properties from well-logging data within intervals that were not cored [28].
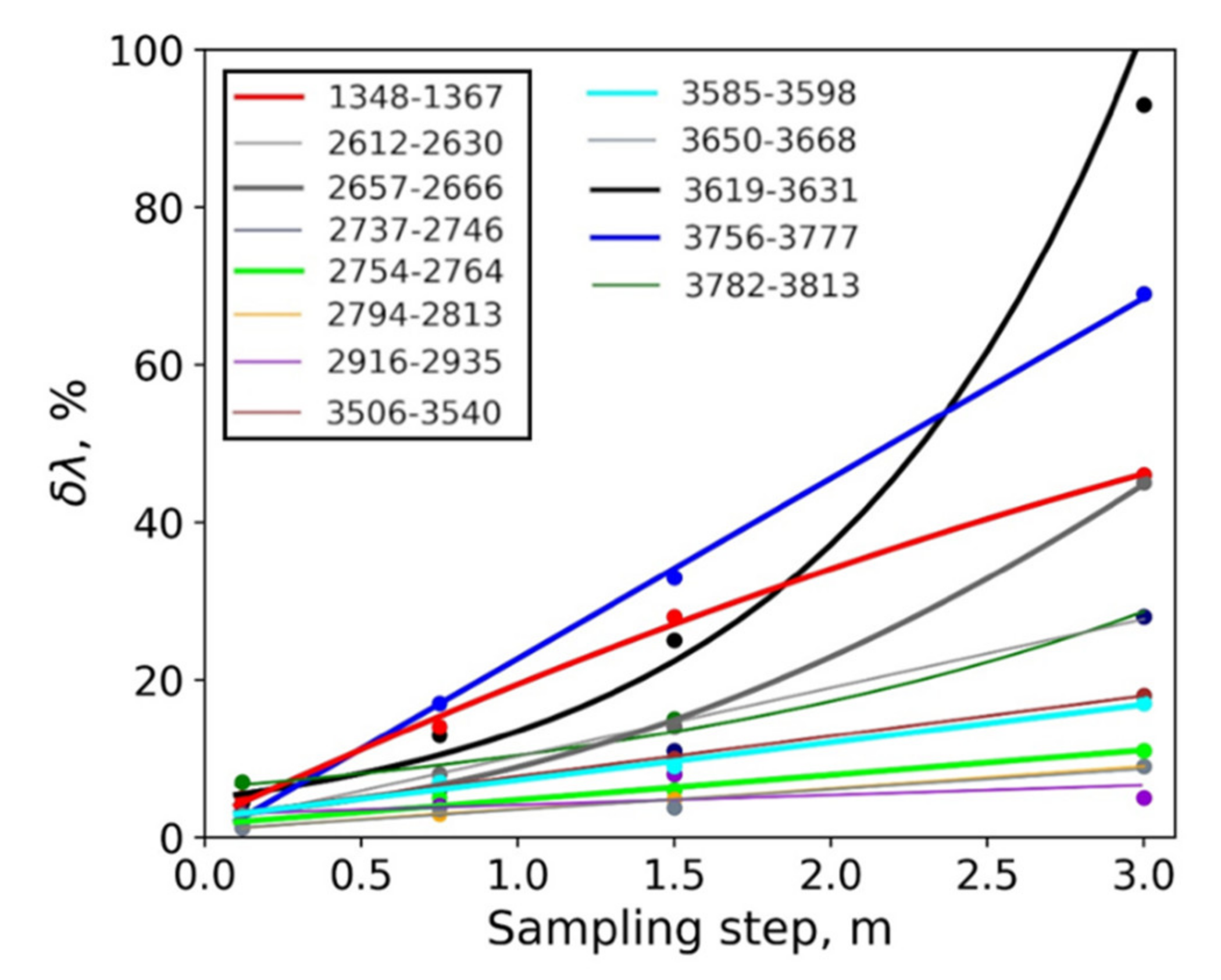
2.4.1. Continuous Thermal Core Logging
- continuous profiles of thermal conductivity, thermal diffusivity, and volumetric heat capacity with a spatial resolution of about 1 mm;
- values of thermal conductivity and thermal diffusivity for parallel and perpendicular directions to the bedding plane and the associated thermal anisotropy coefficient, as well as the rock the volumetric heat capacity;
- the thermal heterogeneity factor of the sample (β), which was as follows:
2.4.2. Measuring Thermal Properties of Rock on Core Plugs
2.4.3. Determining Corrections for Thermal Conductivity at In-Situ Temperature and Pressure
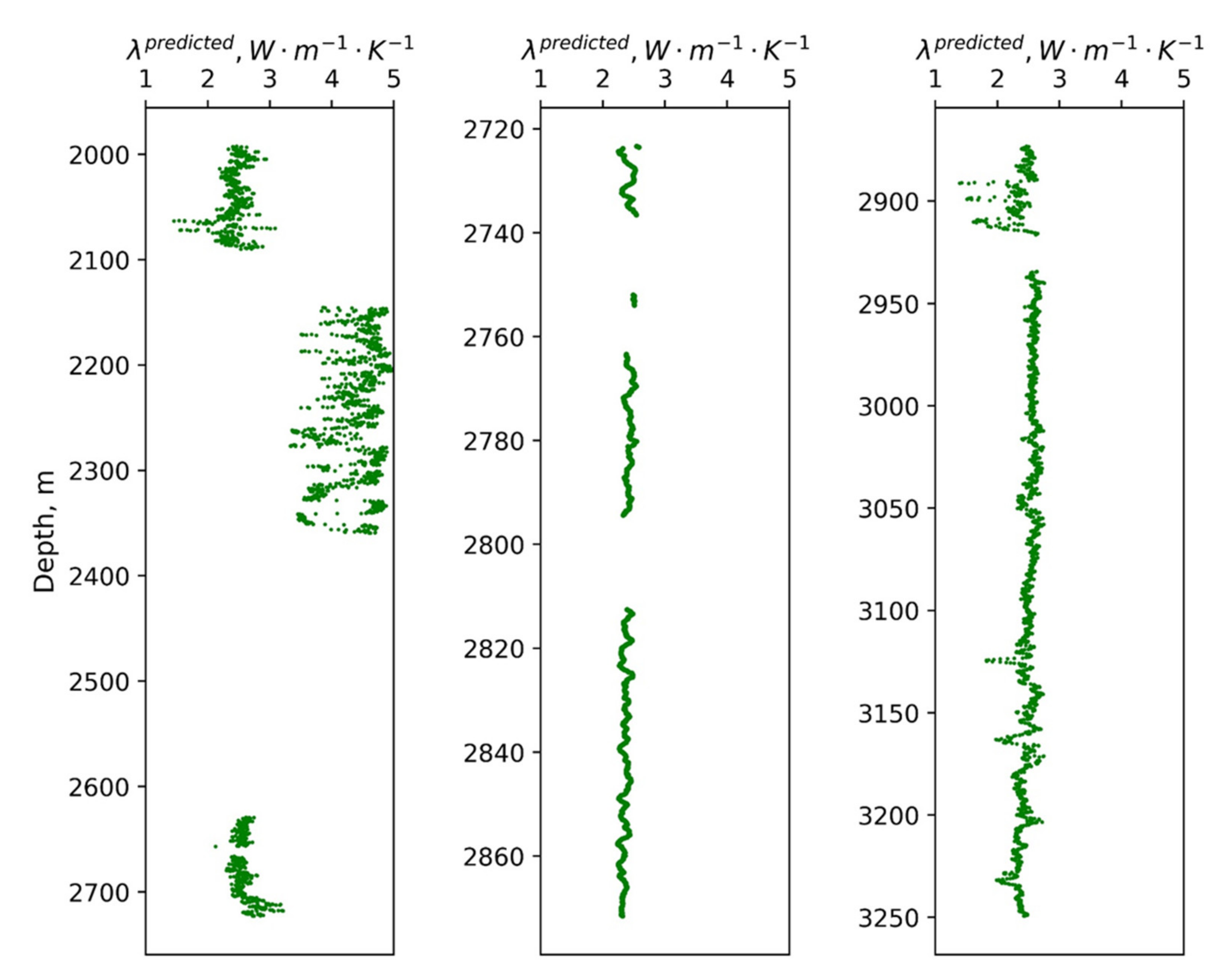
2.5. Well-Log Based Determination of Rock Thermal Conductivity
- The geological and geophysical data from the investigated well are analyzed. In addition, vertical variations of temperature and pressure in the investigating geological profile are analyzed to account for the effect of in situ thermobaric conditions on the thermal properties of rock.
- The directions of the principal axes of thermal conductivity tensors of rock are determined. The directions can be determined via a set of experimental investigations of representative core samples [11] or via well-logging data. After that, a continuous thermal core logging of all recovered core samples is conducted. Thermal core logging is conducted along the established directions of principal axes of the thermal conductivity tensors of the rock. Simultaneously, the reservoir saturation in the reference and target intervals of the investigating wells are inferred from well-logging data.
- A regression analysis of well-logging data and data on the thermal properties of rock is performed, accounting for thermal anisotropy and saturation type. Additionally, the quality of the predictions that can be provided using the established regression model is analyzed via the comparison of the predicted and measured values of thermal properties.
- The rock thermal properties are determined in the target interval using the results of the regression analysis (performed in the third step) from well-logging data.
2.6. Calculating Equivalent Thermal Conductivity
3. Results
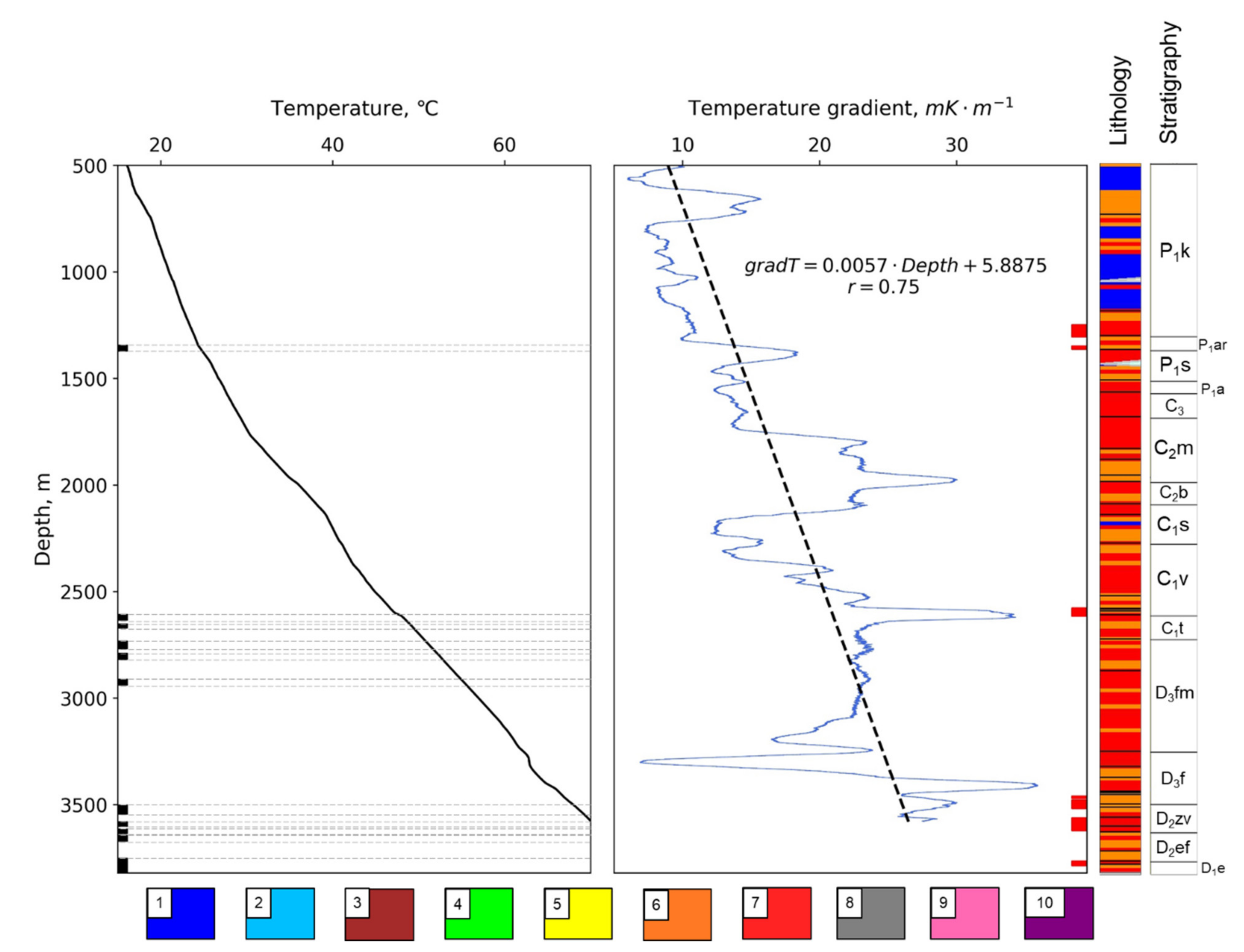
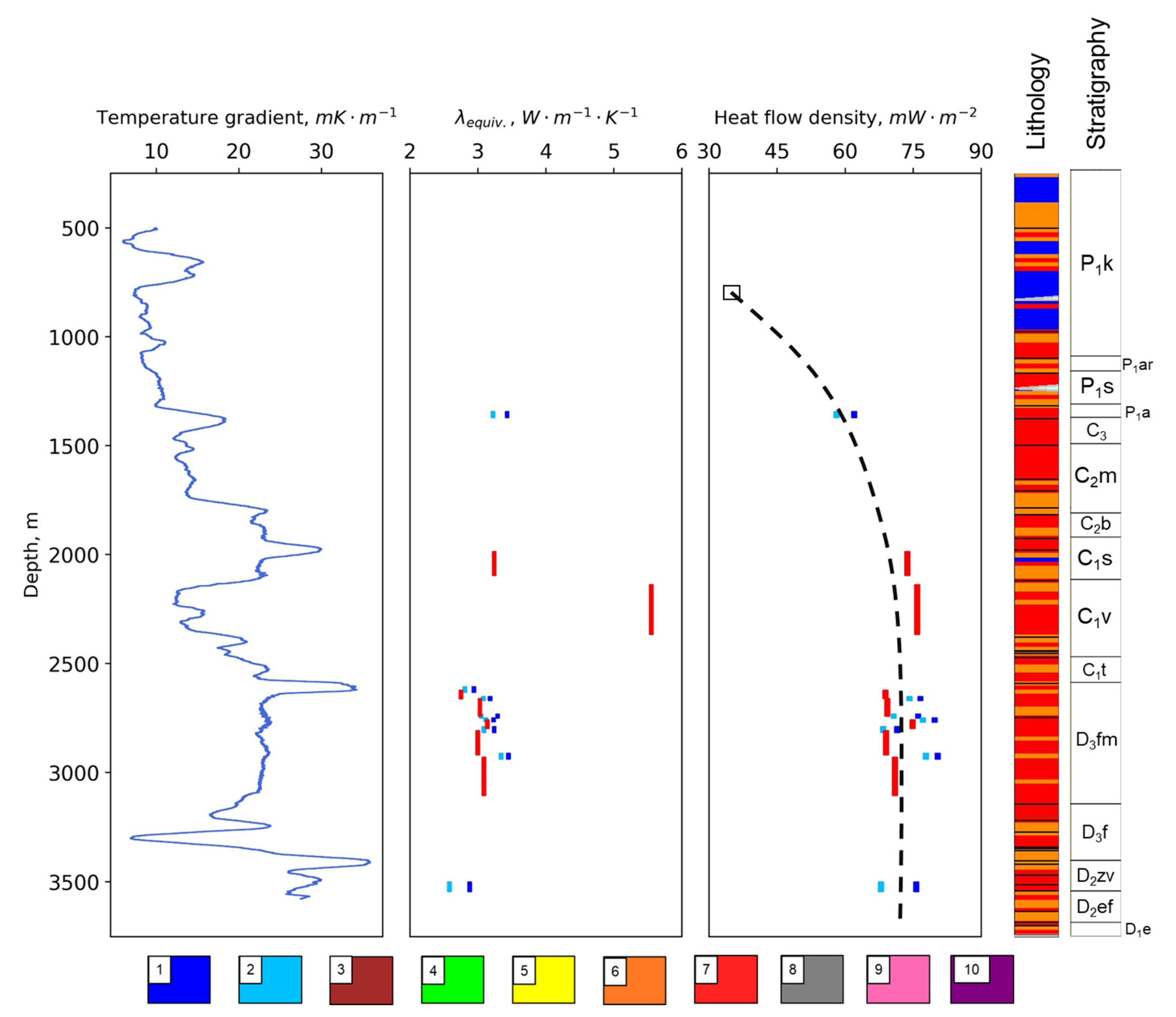
3.1. Results of Temperature Logging and Gradient Determination
3.2. The Results of the Continuous Profiling of the Thermal Properties
3.3. Processing Continuous Thermal Core Logging Data to Determine Heat Flow Density
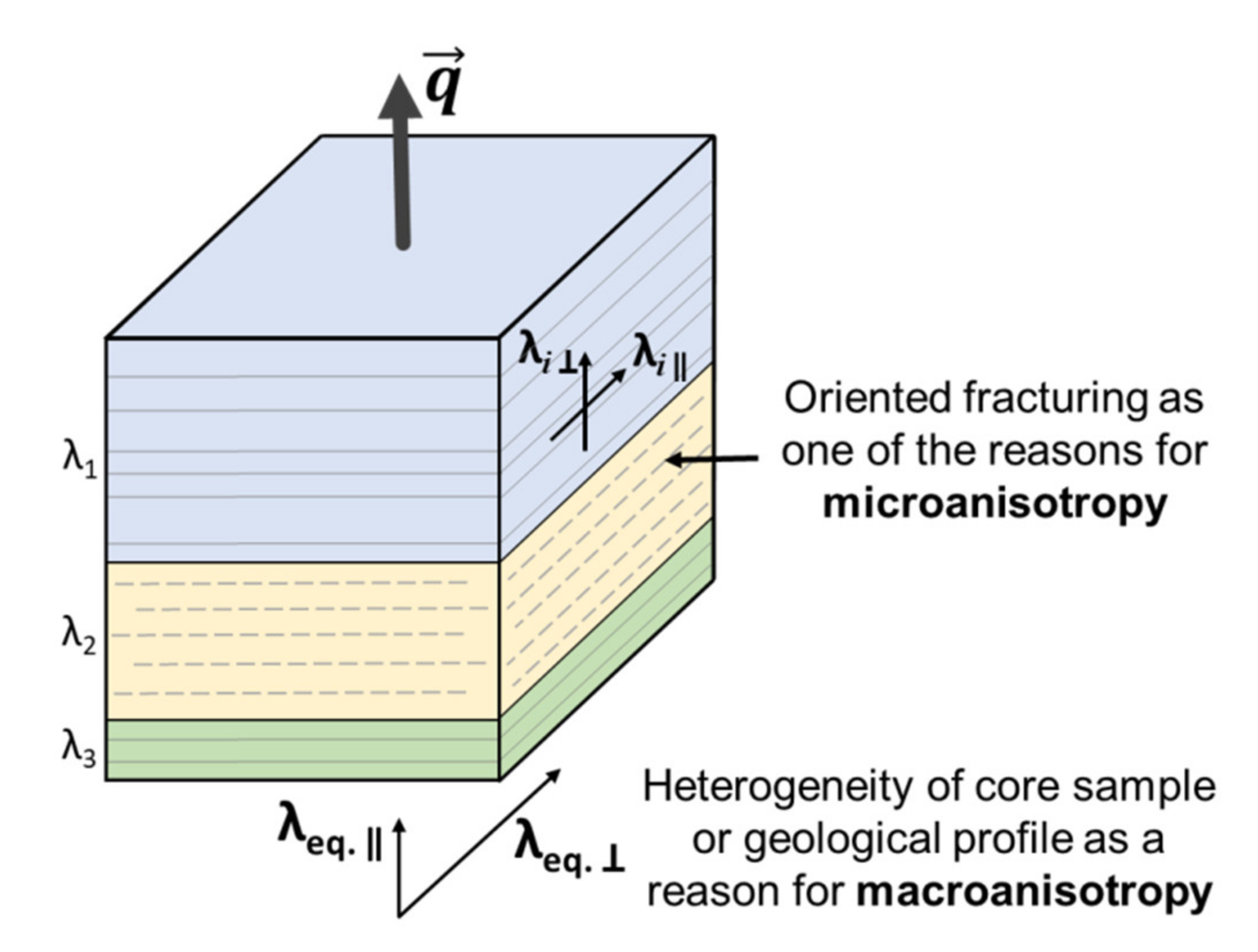
- The thermal macro-anisotropy due to the heterogeneity of rocks on the core sample scale (Figure 4)—a layered texture at the scale of the whole profile conditioned by the alternation of subparallel layers with various thermal conductivities;
- The micro-anisotropy inherent even for homogeneous rocks and caused either by oriented anisotropic mineral grains or oriented microcracks (Figure 4).
- The equivalent thermal conductivity λU was determined according to Formula (5), assuming that the micro-anisotropy was caused by technogenic fractures (directed in most cases parallel to the bedding plane) and has to be excluded from the estimation of the in situ thermal conductivity of the rock mass, and because of that, the thermal conductivity parallel to the bedding plane (λ‖) is a more objective and unbiased characteristic of the core sample compared to the thermal conductivity perpendicular to the bedding plane (λ⊥) affected by micro-cracks (see in [11], Figure 4). For that reason, an upper-bound estimate of rocks’ thermal conductivity was made.
- The equivalent thermal conductivity λL was determined using Equation (4) assuming that the micro-anisotropy is typical for core samples at in situ conditions; i.e., it is caused by natural factors and corresponds to undisturbed rocks. For that reason, a lower-bound estimate of thermal conductivity was made.
3.4. Determining the Equivalent Thermal Conductivity within Non-Coring Intervals
3.5. Estimating the Effect of Core Drying in Core Storage
- measurements of core samples at atmospheric conditions immediately after drilling them out of the full-sized core samples;
- drying samples following the standard procedure in the drying box;
- measurements of the dried core samples at atmospheric conditions;
- vacuum saturation of core samples with mineralized water following the standard procedure;
- measurements on the water-saturated samples at atmospheric conditions;
- measurements of thermal conductivity of rock, volumetric heat capacity, and thermal anisotropy coefficient on water-saturated samples at in situ temperature (the temperature of measurements corresponds to the in situ temperature of the corresponding core sample).
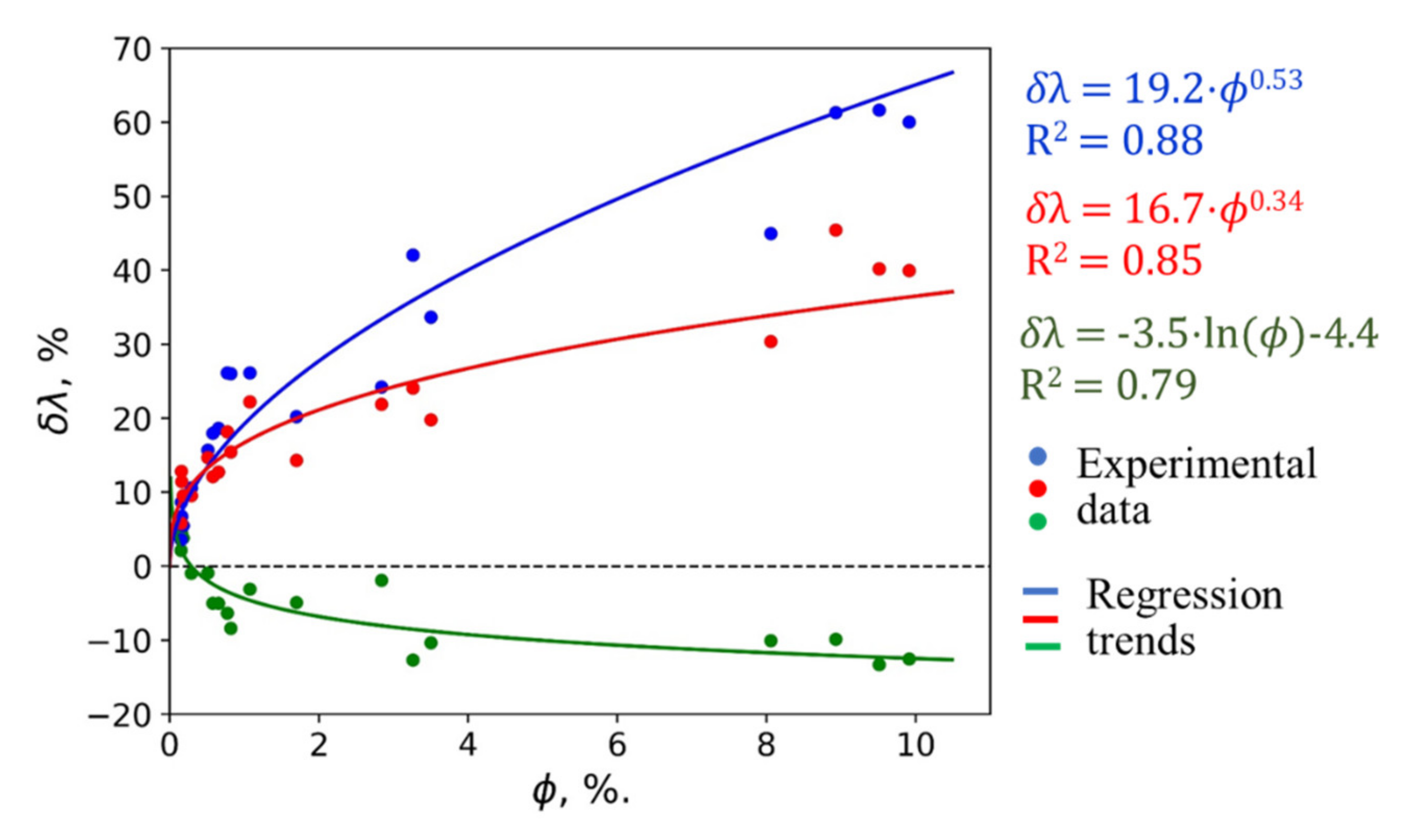
- The degree of thermal conductivity change after both drying and water saturation depended on the core sample porosity.
- The drying of the obtained samples resulted in a very small thermal conductivity decrease. The degree of thermal conductivity reduction depended on the porosity and does not exceed 13%.
- After the water saturation of the dried core samples, a substantial thermal conductivity increase was observed (from 7% to 62%).
- from “as received” state to dried: δλ = −3.5·ln(Φ) − 4.4 with R2 = 0.79;
- from dried to water-saturated: δλ = 19.2·Φ 0.53 with R2 = 0.88;
- from “as received” state to water-saturated: δλ = 16.7·Φ 0.34 with R2 = 0.85.
3.6. Results of Measurements of Thermal Properties at In Situ Temperatures
3.7. Determining Equivalent Thermal Conductivity at In Situ Conditions for Heat Flow Density Estimation
4. Discussion
4.1. Reasons of Vertical Variations in Thermal Properties of Rock
4.2. Analysis of the New Heat Flow Data
4.3. Comparison of the New Heat Flow Estimates with Previous Data
- For 80% of the investigated wells, no measurements of rock thermal conductivity were conducted, whereas the data on rock thermal conductivity were inferred from the literature data for similar rocks [10];
- In the case of experimental measurements of rock thermal conductivity, devices designed for measurements on industrial materials were applied [11]; usually, they do not allow the reliable estimation of the anisotropy and heterogeneity of rock and provide a significantly underestimated thermal conductivity of rock due to the strong effect of thermal contact resistance between the rock sample and the measurement probe [11];
- Most thermal conductivity measurements were conducted without the mandatory water saturation of core samples, which resulted in results for the thermal conductivity measurements for sedimentary and fractured rocks that were underestimates by 20–40% [12] and did not account for the technogenic decompaction of rock samples that can be caused by the decompression effect, drilling equipment impact, and mechanical treatment of core samples required by traditional methods and measurement devices [11];
- The heat flow estimations were conducted for shallow wells (about 70% of wells were less than 1500 m deep) assuming a stable value of heat flow below 300–500 m (considering the negligible effect of radiogenic heat generation);
- In most cases, it was impossible to conduct the temperature logging in wells that reached the thermal equilibrium in rock masses after drilling.
- The thermal property measurements of rock without comprehensive brine saturation results in the underestimation of the measured thermal conductivity by 20–40%, leading to heat flow underestimation by 20–40% [12].
- The influence of thermal resistance between the measuring instrument components and rock sample surfaces in thermal conductivity measurement results leads to heat flow underestimation, usually by 10–30% for crystalline rocks and 15–40% for sedimentary rocks, according to [11] and our long-term experimental experience.
- The temperature measurements in wells that did not reach thermal equilibrium cause an underestimation in temperature gradient that leads to heat flow underestimation (up to 20–30%) according to our long-term temperature measurements in scientific wells.
- Previous practice with averaging temperature gradient causes an underestimation of the temperature gradient that leads to heat flow underestimation;
- The influence of the paleoclimate effect when the measurements are performed in wells with a depth less than 1 km leads to heat flow underestimation, usually by 5–10% [25].
4.4. Estimates of Paleoclimate Effect on Vertical Variations of Temperature Gradient and Heat Flow
4.5. Applying the Updated Geothermal Characteristics for Basin Modeling
5. Conclusions
- The thermal property measurements of rock without comprehensive brine saturation results in the underestimation of the measured thermal conductivity by 20–40%, which leads to heat flow underestimation by 20–40%.
- The influence of thermal resistance between the measuring instrument components and rock sample surface results in thermal conductivity measurement results that usually lead to heat flow underestimation by 10–30% for crystalline rocks and 15–40% for sedimentary rocks.
- The temperature measurements in wells that did not reach thermal equilibrium cause an underestimation of the temperature gradient that leads to heat flow underestimation (up to 20–30%).
- Previous practice with averaging temperature gradient causes an underestimation of the temperature gradient that leads to heat flow underestimation (10–20% for lower horizons).
- The influence of the effect of the paleoclimate when the measurements are performed in wells with a depth less than 1 km leads to heat flow underestimation, usually by 5–10%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hantschel, T.; Kauerauf, A.I. Fundamentals of Basin and Petroleum Systems Modeling, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2009; 476p. [Google Scholar]
- Chekhonin, E.; Popov, Y.; Peshkov, G.; Spasennykh, M.; Popov, E.; Romushkevich, R. On the importance of rock thermal conductivity and heat flow density in basin and petroleum system modelling. Basin Res. 2020, 32, 1261–1276. [Google Scholar] [CrossRef]
- Haenel, R.; Stegena, L.; Rybach, L. Handbook on Terrestrial Heat Flow Density Determination, 1st ed.; Springer: Dordrecht, The Netherlands, 1988; p. 486. [Google Scholar]
- Clauser, C.; Giese, P.; Huenges, E.; Kohl, T.H.; Lehmann, H.; Rybach, L.; Zoth, G. The thermal regime of the crystalline continental crust: Implications from the KTB. J. Geophys. Res. 1997, 102, 18417–18441. [Google Scholar] [CrossRef]
- Emmermann, R.; Lauterjung, J. The German continental deep drilling program KTB: Overview and major results. J. Geophys. Res. 1997, 102, 18179–18201. [Google Scholar] [CrossRef]
- Popov, Y.; Pevzner, S.; Pimenov, V.; Romushkevich, R. New geothermal data from the Kola superdeep well SG-3. Tectonophysics 1999, 306, 343–366. [Google Scholar] [CrossRef]
- Popov, Y.A.; Romushkevich, R.A.; Popov, E.Y.; Bashta, K.G. Results of Drilling and Investigating Super-Deep Ural Well; Nedra Publ.: Yaroslavl, Russia, 1999; pp. 77–88. [Google Scholar]
- Kukkonen, T.; Rath, V.; Kivekas, L.; Šafanda, J.; Čermak, V. Geothermal studies of the Outokumpu Deep Drill Hole, Finland: Vertical variation in heat flow and palaeoclimatic implications. Phys. Earth Planet. Inter. 2011, 188, 9–25. [Google Scholar] [CrossRef]
- Popov, Y.; Huddlestone-Holmes, C.; Gerner, E. Evolution in the reliability of experimental geothermal data. In Proceedings of the 2012 Australian Geothermal Energy Conference, Sydney, Australia, 14–16 November 2012. [Google Scholar]
- Golovanova, I.V. Thermal Field of the Southern Urals; Nedra Publ.: Leningrad, Russia, 2005; 189p. [Google Scholar]
- Popov, Y.; Beardsmore, G.; Clauser, C.; Roy, S. ISRM Suggested methods for determining thermal properties of rocks from laboratory tests at atmospheric pressure. Rock Mech. Rock Eng. 2016, 49, 4179–4207. [Google Scholar] [CrossRef]
- Duchkov, A.D.; Sokolova, L.S.; Ayunov, D.E.; Zlobina, O.N. Thermal conductivity of sediments in high-latitude West Siberia. Russ. Geol. Geophys. 2013, 54, 1952–1960. [Google Scholar] [CrossRef]
- Kukkonen, I.T.; Golovanova, I.V.; Khachay, Y.V.; Druzhinin, V.S.; Kosarev, A.M.; Schapov, V.A. Low geothermal heat flow of the Urals fold belt—Implication of low heat production, fluid circulation or palaeoclimate? Tectonophysics 1997, 276, 63–85. [Google Scholar] [CrossRef]
- Demezhko, D.Y.; Golovanova, I.V. Climatic changes in the Urals over the past millennium—An analysis of geothermal and meteorological data. Clim. Past 2007, 3, 237–242. [Google Scholar] [CrossRef] [Green Version]
- Stein, C.A. Heat Flow of the Earth. In Global Earth Physics: A Handbook of Physical Constants, 3rd ed.; Ahrens, T.J., Ed.; American Geophysical Union: Washington, DC, USA, 1995; pp. 144–158. [Google Scholar] [CrossRef] [Green Version]
- Popov, Y.; Popov, E.; Chekhonin, E.; Spasennykh, M.; Goncharov, A. Evolution in information on crustal geothermal parameters due to application of advanced experimental basis. IOP Conf. Ser. Earth Environ. Sci. 2018, 249, 012042. [Google Scholar] [CrossRef]
- Technically Recoverable Shale Oil and Shale Gas Resources: Russia. U.S. Energy Information Administration Report. Available online: https://www.eia.gov/analysis/studies/worldshalegas/pdf/Russia_2013.pdf (accessed on 25 March 2021).
- Peterson, J.A.; Clarke, J.W. Petroleum Geology and Resources of the Volga-Ural Province, U.S.S.R.; USGS Geological Survey Circular; U.S. Geological Survey: Reston, VA, USA, 1983; 33p. [Google Scholar] [CrossRef]
- Liang, X.; Jin, Z.; Philippov, V.; Obryadchikov, O.; Zhong, D.; Liu, Q.; Uspensky, B.; Morozov, V. Sedimentary characteristics and evolution of Domanik facies from the Devonian–Carboniferous regression in the southern Volga-Ural Basin. Mar. Pet. Geol. 2020, 119, 104438. [Google Scholar] [CrossRef]
- Neruchev, S.G.; Rogozina, E.A.; Parparova, G.M.; Zelichenko, I.A.; Silina, N.P. Oil and Gas Formation in Deposits of the Domanik Type; Nedra Publ.: Leningrad, Russia, 1986; 248p. (In Russian) [Google Scholar]
- Bazhenova, T.K. Hydrocarbon resources estimation of bituminous formations of Russian oil and gas bearing basins. Oil Gas Geol. 2017, 5, 37–50. (In Russian) [Google Scholar]
- Ulmishek, G.F. Petroleum Geology and Resources of the West Siberian Basin, Russia; USGS Bulletin 2201–G; USGS: Denver, CO, USA, 2003; 53p. [Google Scholar]
- Vashkevich, A.A.; Strizhnev, K.V.; Shashel, V.A.; Zakharova, O.A.; Kasyanenko, A.A.; Zagranovskaya, D.E.; Grebenkina, N.Y. Forecast of prospective areas for sediment type Domanic in the Volga-Ural oil and gas Province. Oil Ind. 2018, 12, 14–17. (In Russian) [Google Scholar] [CrossRef]
- Chekhonin, E.; Popov, Y.; Vladimirov, A.; Spasennykh, M.; Zagranovskaya, D.; Zakharova, O. Improving the reliability of basin modeling results by enhancement of determination of geotherml characteristics and their integration into basin model. In Proceedings of the EAGE/SPE Workshop «Shale Science: New Challenges», Moscow, Russia, 5–6 April 2021. [Google Scholar]
- Golovanova, I.V.; Puchkov, V.N.; Sal’manova, R.Y.; Demezhko, D.Y. A New Version of the Heat Flow Map of the Urals with Paleoclimatic corrections. Dokl. Earth Sci. 2008, 422, 1153–1156. (In Russian) [Google Scholar] [CrossRef]
- Popov, E.; Goncharov, A.; Popov, Y.; Spasennykh, M.; Chekhonin, E.; Shakirov, A.; Gabova, A. Advanced techniques for determining thermal properties on rock samples and cuttings and indirect estimating for atmospheric and formation conditions. IOP Conf. Ser. Earth Environ. Sci. 2019, 367, 012017. [Google Scholar] [CrossRef]
- Popov, Y.; Pimenov, V.; Pevzner, L.; Romushkevich, R.; Popov, E. Geothermal characteristics of the Vorotilovo deep borehole drilled into the Puchezh-Katunk impact structure. Tectonophysics 1998, 291, 205–223. [Google Scholar] [CrossRef]
- Shakirov, A.; Chekhonin, E.; Popov, Y.; Popov, E.; Spasennykh, M.; Zagranovskaya, D.; Serkin, M. Rock thermal properties from well-logging data accounting for thermal anisotropy. Geothermics 2021, 92, 102059. [Google Scholar] [CrossRef]
- Popov, E.; Popov, Y.; Chekhonin, E.; Safonov, S.; Savelev, E.; Gurbatova, I.; Ursegov, S.; Shakirov, A. Thermal core profiling as a novel and accurate method for efficient characterization of oil reservoirs. J. Pet. Sci. Eng. 2020, 193, 107384. [Google Scholar] [CrossRef]
- Yakovlev, B.A. Prediction of Hydrocarbon Potential via Geothermal Data; Nedra Publ.: Leningrad, Russia, 1996; 240p. [Google Scholar]
- Kurbanov, A.A. Regularities of Behavior of Thermophysical Properties of Fluid Bearing Reservoirs at In Situ Conditions and Its Applications. Ph.D. Thesis, Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences, Moscow, Russia, October 2007. [Google Scholar]
- Hohne, G.W.; Hemminger, W.F.; Flammersheim, H.J. Differential Scanning Calorimetry, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003; pp. 154–196. ISBN 978-3-662-06710-9. [Google Scholar]
- Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry. Available online: https://www.astm.org/Standards/E1269.htm (accessed on 25 April 2021).
- Popov, Y.; Parshin, A.; Miklashevskiy, D.; Abashkin, V. Instrument for measurements of linear thermal expansion coefficient of rocks. In Proceedings of 46th US Rock Mechanics/Geomechanics Symposium, Chicago, IL, USA, 24 June 2012. [Google Scholar]
- Willis, J. Bounds and self-consistent estimates for the overall properties of anisotropic composites. J. Mech. Phys. Sol. 1977, 25, 185–202. [Google Scholar] [CrossRef]
- Meshalkin, Y.; Shakirov, A.; Popov, E.; Koroteev, D.; Gurbatova, I. Robust well-log based determination of rock thermal conductivity through machine learning. Geophys. J. Int. 2020, 222, 978–988. [Google Scholar] [CrossRef]
- Popov, Y.; Berezin, V.; Soloviov, G.; Romuschkevitch, R.; Korostelev, V.; Kostiurin, A.; Kulikov, A. Thermal conductivity of minerals. Izv. Phys. Solid Earth 1987, 23, 245–253. [Google Scholar]
- Popov, Y.; Pevzner, L.; Romushkevich, R.; Korostelev, V.; Vorobiev, M. Thermophysical and geothermal sections obtained from Kolvinskaya well logging data. Phys. Chem. Earth Part A Solid Earth Geod. 1994, 30, 778–789. [Google Scholar]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics Concomitant Scale Estimates; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; 172p. [Google Scholar]
- Hodyreva, E.Y.; Shchulaev, V.F.; Netkach, A.Y.; Markov, A.I. Initial geothermal field of Orenburg gas-condensate field. Oil Gas Geol. 1985, 3, 43–48. (In Russian) [Google Scholar]
- Gordienko, V.V.; Zavgorodskaya, O.V.; Moiseenko, U.I. Heat Flow Map of the Territory of the USSR. Scale 1:5,000,000. Explanatory Note. Kiev 1987-34 c. (In Russian)
- Mottaghy, D.; Schellschmidt, R.; Popov, Y.A.; Clauser, C.; Romushkevich, R.A.; Kukkonen, I.T.; Nover, G.; Milanovsky, S. New heat flow data from the immediate vicinity of the Kola super-deep borehole: Vertical variation in heat flow confirmed and attributed to advection. Tectonophysics 2005, 401, 119–142. [Google Scholar] [CrossRef]
- Rybach, L. Determination of heat production rate. In Handbook of Terrestrial Heat-Flow Density Determination; Kluwer: Philadelphia, PA, USA, 1988; pp. 125–142. [Google Scholar]
- Sal’nikov, V.E. Geothermal Regime of the Southern Urals; Nedra Publ.: Leningrad, Russia, 1984; 88p. (In Russian) [Google Scholar]
- Demezhko, D.Y.; Ryvkin, D.G.; Outkin, V.I.; Duchkov, A.D.; Balobaev, V.T. Spatial distribution of Pleistocene/Holocene warming amplitudes in Northern Eurasia inferred from geothermal data. Clim. Past 2007, 3, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Golovanova, I.V.; Selezneva, G.V.; Smordov, E.A. Reconstruction of postglacial warming in The Southern Urals using the 1242 temperature logging data. Geol. Sb. 2000, 1, 113–116. (In Russian) [Google Scholar]
- Gallagher, K.; Ramsdale, M.; Lonergan, L.; Morrow, D. The role of thermal conductivity measurements in modelling thermal histories in sedimentary basins. Mar. Pet. Geol. 1997, 14, 201–214. [Google Scholar] [CrossRef]
- Hicks, P.J.; Fraticelli, C.M.; Shosa, J.D.; Hardy, M.J.; Townsley, M.B. Identifying and quantifying significant uncertainties in basin modeling. In Basin Modeling: New Horizons in Research and Applications; Peters, K.E., Curry, D.J., Kacewicz, M., Eds.; AAPG Hedberg Series; AAPG: Tulsa, OK, USA, 2012; Volume 4. [Google Scholar]
- Sekiguchi, K. A method for determining terrestrial heat flow in oil basinal areas. Tectonophysics 1984, 103, 67–79. [Google Scholar] [CrossRef]




| № | Rock Type | Age | Logging Depth, m | N * |
|---|---|---|---|---|
| 1 | In the upper part, anhydrite–dolomite rock, in the middle and lower parts, limestone | P1ar | 1348.50–1366.10 | 135 |
| 2 | Bioclastic limestones with rare inclusions of anhydrite and porous intervals | C1t | 2612.29–2629.20 | 145 |
| 2657.00–2665.74 | 73 | |||
| 3 | Bioclastic limestones that have (1) rare dolomitized intervals and are (2) porous, (3) cavernous, (4) oil-saturated in some intervals, (5) with a rare interbedding of argillites. | D3zv | 2737.30–2746.02 | 78 |
| 2754.90–2763.60 | 65 | |||
| 2794.90–2812.50 | 143 | |||
| 4 | Bioclastic limestones that are porous, fractured, with rare interbedding of argillites. | D3fm | 2916.90–2934.34 | 143 |
| 6 | In the upper part, quartz sandstones and argillites; in the middle part, limestones and argillites; and in the lower part, marlstones. | D3p–D2ml | 3506.40–3539.30 | 272 |
| 7 | Interbedding of quartz sandstones and shaly siltstone. | D2ar | 3585.38–3597.40 | 92 |
| 8 | Bioclastic limestones with oil saturated intervals and thin layers of sandstones. | D2vb–D2af | 3619.20–3630.68 | 89 |
| 9 | Bioclastic limestones that are unevenly oil-saturated. | D2af | 3650.00–3667.08 | 93 |
| 10 | In the upper part, organogenic limestone; in the middle and lower parts, quartz sandstones and argillites. | D2bs–D1kv | 3756.70–3776.31 | 148 |
| 11 | Argillites, sandstones and gravelites. | V–R | 3782.64–3812.12 | 223 |
| № | Interval, m | Temperature Gradient (Via Different Approaches), mK·m−1 | Standard Deviation of Temperature Gradient, mK·m−1 | Uncertainty in Estimates of Temperature Gradient | Difference between the Average Temperature Gradient and Temperature Gradient Determined within 5 m Sliding Window, % | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| By Points | 10 m | 5 m | Corr * | Average | Absolute, mK·m−1 | Relative, % | ||||
| Within core sampling intervals | ||||||||||
| 1 | 1348.50– 1366.10 | 18.07 | 17.97 | 17.99 | 18.44 | 18.12 | 0.219 | 0.350 | 1.93 | −0.704 |
| 2 | 2612.29–2629.20 | 27.87 | 29.40 | 28.30 | 27.02 | 28.15 | 0.990 | 1.579 | 5.61 | 0.526 |
| 3 | 2657.00–2665.74 | 24.25 | 23.67 | 23.83 | 23.29 | 23.76 | 0.397 | 0.634 | 2.67 | 0.293 |
| 4 | 2737.30–2746.02 | 22.72 | 22.76 | 22.78 | 23.08 | 22.84 | 0.165 | 0.264 | 1.15 | −0.242 |
| 5 | 2754.90–2763.60 | 25.57 | 23.65 | 24.53 | 23.74 | 24.37 | 0.891 | 1.421 | 5.83 | 0.638 |
| 6 | 2794.90–2812.50 | 21.99 | 22.01 | 21.83 | 21.49 | 21.83 | 0.241 | 0.384 | 1.76 | 0.000 |
| 7 | 2916.90–2934.34 | 23.22 | 23.29 | 23.21 | 23.31 | 23.26 | 0.050 | 0.080 | 0.34 | −0.207 |
| 8 | 3506.40–3539.30 | 27.17 | 27.37 | 27.24 | 27.18 | 27.24 | 0.092 | 0.147 | 0.54 | 0.000 |
| Within depth intervals with well-log based determinations of rock thermal properties | ||||||||||
| 9 | 1991.00– 2091.00 | 22.95 | 23.00 | 22.96 | 22.67 | 22.90 | 0.152 | 0.242 | 1.06 | 0.285 |
| 10 | 2144.00– 2361.00 | 13.50 | 13.53 | 13.51 | 13.72 | 13.57 | 0.104 | 0.166 | 1.22 | −0.402 |
| 11 | 2628.00– 2658.00 | 25.10 | 24.40 | 24.63 | 24.37 | 24.63 | 0.337 | 0.538 | 2.18 | 0.020 |
| 12 | 2666.00– 2737.00 | 22.72 | 22.76 | 22.76 | 22.73 | 22.74 | 0.021 | 0.033 | 0.14 | 0.077 |
| 13 | 2763.80– 2793.70 | 24.15 | 23.71 | 23.62 | 23.37 | 23.71 | 0.325 | 0.519 | 2.19 | −0.388 |
| 14 | 2813.00– 2915.00 | 22.96 | 22.98 | 22.98 | 22.93 | 22.96 | 0.024 | 0.038 | 0.16 | 0.076 |
| 15 | 2934.90– 3100.00 | 22.75 | 22.73 | 22.75 | 22.72 | 22.74 | 0.015 | 0.024 | 0.11 | 0.055 |
| Mean | 0.140 | 0.22 | 1.01 | −0.04 | ||||||
| № | Age | Thermal Conductivity, W·m−1·K−1 | KT | Thermal Heterogeneity Factor | C, MJ·m−3·K−1 | N | <ϕ>, % | ||
|---|---|---|---|---|---|---|---|---|---|
| λ‖aver | λ⊥aver | β‖ | β⊥ | ||||||
| 1 | P1ar | 2.52 (0.74) (1) 1.74–5.47 (2) | 2.38 (0.73) 1.41–5.15 | 1.07 (0.18) 1.00–2.66 | 0.20 (0.13) 0.04–0.90 | 0.16 (0.11) 0.06–0.85 | 2.17 (0.16) 1.84–2.80 | 135 | 10.9 |
| 2 | C1t | 2.15 (0.37) 1.62–5.54 | 2.07 (0.39) 1.04–5.54 | 1.04 (0.09) 1.00–1.78 | 0.21 (0.16) 0.06–1.32 | 0.16 (0.09) 0.06–0.85 | 2.09 (0.14) 1.72–2.62 | 145 | 9.2 |
| 2.33 (0.26) 1.81–3.03 | 2.25 (0.25) 1.81–2.82 | 1.03 (0.06) 1.00–1.21 | 0.22 (0.10) 0.05–0.52 | 0.21 (0.10) 0.06–0.53 | 2.16 (0.17) 1.83–2.69 | 73 | 8.5 | ||
| 3 | D3zv | 2.54 (0.29) 1.94–3.60 | 2.38 (0.33) 1.32–3.49 | 1.08 (0.18) 1.00–2.30 | 0.22 (0.08) 0.08–0.49 | 0.18 (0.09) 0.06–0.65 | 2.25 (0.17) 1.92–2.94 | 78 | 4.4 |
| 2.44 (0.14) 2.15–2.67 | 2.36 (0.18) 2.00–2.67 | 1.03 (0.05) 1.00–1.17 | 0.19 (0.06) 0.07–0.37 | 0.18 (0.11) 0.07–0.75 | 2.26 (0.12) 1.97–2.61 | 65 | 4.8 | ||
| 2.43 (0.18) 2.07–3.18 | 2.34 (0.23) 1.46–3.18 | 1.04 (0.07) 1.00–1.44 | 0.19 (0.07) 0.06–0.45 | 0.17 (0.07) 0.06–0.43 | 2.23(0.12) 1.97–2.65 | 143 | 5.3 | ||
| 4 | D3fm | 2.54 (0.19) 1.92–2.88 | 2.47 (0.23) 1.68–2.88 | 1.03 (0.07) 1.00–1.39 | 0.16 (0.07) 0.07–0.64 | 0.14 (0.05) 0.05–0.33 | 2.23 (0.14) 1.84–2.51 | 143 | 8.2 |
| 6 | D3p–D2ml | 2.41 (0.60) 1.89–5.44 | 2.19 (0.59) 1.20–5.01 | 1.11 (0.13) 1.00–1.86 | 0.14 (0.07) 0.05–0.57 | 0.14 (0.06) 0.05–0.56 | 2.21 (0.12) 1.69–2.59 | 272 | 3.9 |
| 7 | D2ar | 4.15 (0.53) 2.82–5.65 | 3.53 (0.70) 2.12–5.11 | 1.20 (0.21) 1.00–1.87 | 0.27 (0.14) 0.07–0.67 | 0.23 (0.09) 0.11–0.57 | 1.91 (0.13) 1.67–2.24 | 92 | 7.4 |
| 8 | D2vb–D2af | 2.65 (0.55) 2.06–4.65 | 2.58 (0.59) 1.54–4.65 | 1.03 (0.08) 1.00–1.60 | 0.21 (0.11) 0.08–0.75 | 0.21 (0.09 )0.09–0.60 | 2.21 (0.18) 1.74–2.65 | 89 | 2.4 |
| 9 | D2af | 2.66 (0.16) 2.30–3.12 | 2.48 (0.37) 1.27–3.12 | 1.11 (0.19) 1.00–1.90 | 0.17 (0.09) 0.06–0.58 | 0.18 (0.06) 0.09–0.51 | 2.27 (0.13) 1.81–2.55 | 93 | 7.3 |
| 10 | D2bs–D1kv | 3.25 (0.62) 2.07–4.86 | 2.73 (0.67) 1.23–4.46 | 1.17 (0.26) 1.00–2.42 | 0.31 (0.23) 0.07–1.64 | 0.26 (0.17) 0.07–0.93 | 2.09 (0.27) 1.67–2.67 | 148 | 9.3 |
| 11 | V–R | 2.81 (0.15) 2.04–3.20 | 2.39 (0.30) 1.25–2.98 | 1.20(0.18) 1.00–2.22 | 0.24 (0.09) 0.08–0.59 | 0.19 (0.06) 0.10–0.43 | 1.96 (0.15) 1.68–2.58 | 223 | 8.3 |
| Depth Interval, m | Upper-Bound Estimate λequiv.U, W⋅m−1⋅K−1 | Lower-Bound Estimate λequiv.L, W⋅m−1⋅K−1 | Average and Standard Deviation of λ‖, W⋅m−1⋅K−1 | Average and Standard Deviation of λ⊥,W⋅m−1⋅K−1 | Coefficient of Micro-anisotropy, KT = λ‖·λ⊥−1 | N |
|---|---|---|---|---|---|---|
| 1348.50–1366.10 | 2.38 | 2.24 | 2.52 (0.74) | 2.40 (0.45) | 1.06 | 135 |
| 2612.29–2629.20 | 2.11 | 2.02 | 2.15 (0.37) | 2.07 (0.39) | 1.04 | 145 |
| 2657.00–2665.74 | 2.30 | 2.23 | 2.32 (0.25) | 2.26 (0.28) | 1.03 | 73 |
| 2737.30–2746.02 | 2.51 | 2.33 | 2.54 (0.30) | 2.38 (0.33) | 1.08 | 78 |
| 2754.90–2763.60 | 2.43 | 2.35 | 2.44 (0.14) | 2.36 (0.18) | 1.03 | 65 |
| 2794.90–2812.50 | 2.42 | 2.31 | 2.43 (0.18) | 2.34 (0.33) | 1.04 | 143 |
| 2916.90–2934.34 | 2.52 | 2.44 | 2.54 (0.19) | 2.47 (0.23) | 1.03 | 143 |
| 3506.40–3539.30 | 2.33 | 2.09 | 2.41 (0.60) | 2.19 (0.59) | 1.11 | 272 |
| 3585.38–3597.40 | 4.09 | 3.19 | 4.15 (0.53) | 3.38 (0.76) | 1.28 | 92 |
| 3619.20–3630.68 | 2.57 | 2.46 | 2.65 (0.55) | 2.56 (0.59) | 1.05 | 89 |
| 3650.00–3667.08 | 2.65 | 2.38 | 2.66 (0.16) | 2.46 (0.38) | 1.11 | 93 |
| 3756.70–3776.31 | 3.12 | 2.56 | 3.25 (0.62) | 2.73 (0.67) | 1.24 | 148 |
| 3782.64–3812.12 | 2.80 | 2.30 | 2.81 (0.15) | 2.37 (0.32) | 1.20 | 223 |
| Lithology (Depth Interval) | Regression Equation * | Quality of Prediction Results on the Test Dataset | ||||
|---|---|---|---|---|---|---|
| r | RMSE, W·m−1·K−1 | P, % | A, % | N | ||
| Limestones (2611.76–2665.76) | λ = −2.6·10−4·ΔtP + 0.25·ρ + 0.26·γ + 0.34·NGR + 0.08 | 0.84 | 0.10 | 9.48 | −0.2 | 43 |
| Limestones (2736.96–2812.16) | λ = −3.7·10−4·ΔtP + 0.12·ρ + 0.05·γ + 0.21·NGR + 2.15 | 0.43 | 0.10 | 8.06 | −0.4 | 67 |
| Limestones (2916.56–2934.16) | λ = −1.8·10−4·ΔtP − 0.25·γ + 0.32·NGR + 2.44 | 0.80 | 0.10 | 8.74 | 0.5 | 29 |
| Dolomites (regression equation from the adjacent well) | λ = −0.004·γnormilized + 0.42·NGRnormalized + 4.34 | 93 | 0.17 | 8.18 | 0.2 | 133 |
| Depth Intervals, m | Average λeq, W·m−1·K−1 | Average Porosity, % | Thermal Conductivity Correction for In Situ Saturation, % |
|---|---|---|---|
| For coring depth intervals | |||
| 1348.50–1366.10 | * | 10.9 | 38 |
| 2612.29–2629.20 | * | 9.2 | 36 |
| 2657.00–2665.74 | * | 8.5 | 35 |
| 2737.30–2746.02 | * | 4.4 | 28 |
| 2754.90–2763.60 | * | 4.8 | 28 |
| 2794.90–2812.50 | * | 5.3 | 29 |
| 2916.90–2934.34 | * | 8.2 | 34 |
| 3506.40–3539.30 | * | 2.8 | 23 |
| For intervals with well-log-based predictions of rock thermal conductivity | |||
| 1991–2091 | 2.26 | 11 | 38 |
| 2144–2361 | 4.30 | 3 | 24 |
| 2628–2658 | 1.98 | 9 | 35 |
| 2666–2737 | 2.26 | 6 | 31 |
| 2764–2794 | 2.43 | 3 | 24 |
| 2813–2915 | 2.32 | 3 | 24 |
| 2935–3100 | 2.49 | 2 | 21 |
| Depth Interval, m | The Range of the In Situ Temperature, °C | Temperature Correction for Thermal Conductivity, % | Pressure Correction for Thermal Conductivity, % |
|---|---|---|---|
| For coring depth intervals | |||
| 1348.50–1366.10 | 24.4–24.8 | 0 | 4 |
| 2612.29–2629.20 | 47.9–48.4 | −4 | 6 |
| 2657.00–2665.74 | 49.1–49.3 | −4 | 6 |
| 2737.30–2746.02 | 50.9–51.1 | −4 | 6 |
| 2754.90–2763.60 | 51.3–51.5 | −3.5 | 7 |
| 2794.90–2812.50 | 52.3–52.7 | −3.5 | 7 |
| 2916.90–2934.34 | 55.1–55.5 | −5 | 7 |
| 3506.40–3539.30 | 68.2–69.1 | −7 | 7 |
| For intervals with well-log-based predictions of rock thermal conductivity | |||
| 1991–2091 | 35.84–38.14 | −2 | 5.5 |
| 2144–2361 | 39.27–42.20 | −2.5 | 6 |
| 2628–2658 | 48.35–49.10 | −4 | 6 |
| 2666–2737 | 49.30–50.93 | −4 | 6 |
| 2764–2794 | 51.54–52.26 | −3.5 | 7 |
| 2813–2915 | 52.68–55.02 | −3.5 | 7 |
| 2935–3100 | 55.48–59.24 | −5 | 7 |
| Depth Interval, m | Estimation of Equivalent Thermal Conductivity, W⋅m−1⋅K−1 | Temperature Gradient, mK⋅m−1 | Heat Flow Estimate, mW⋅m−2 | |||
|---|---|---|---|---|---|---|
| Lower | Upper | Lower | Upper | Average | ||
| From results of continuous thermal core logging | ||||||
| 1348.50–1366.10 | 3.21 | 3.42 | 18.05 | 58.0 | 61.7 | 59.8 |
| 2612.29–2629.20 | 2.80 | 2.93 | 28.30 | 79.3 | 82.8 | 81.1 |
| 2657.00–2665.74 | 3.07 | 3.17 | 23.93 | 73.5 | 75.8 | 74.6 |
| 2737.30–2746.02 | 3.04 | 3.28 | 22.72 | 69.1 | 74.5 | 71.8 |
| 2754.90–2763.60 | 3.11 | 3.22 | 24.68 | 76.8 | 79.5 | 78.1 |
| 2794.90–2812.50 | 3.08 | 3.23 | 22.08 | 68.1 | 71.3 | 69.7 |
| 2916.90–2934.34 | 3.33 | 3.44 | 23.00 | 76.7 | 79.2 | 78.0 |
| 3506.40–3539.30 | 2.57 | 2.87 | 27.56 | 70.8 | 79.0 | 74.9 |
| From results of well-log-based predictions of rock thermal conductivity within non-coring intervals (average values of thermal conductivity and heat flow) | ||||||
| 1991–2091 | 3.23 | 22.96 | 74.1 | |||
| 2144–2361 | 5.54 | 13.51 | 74.8 | |||
| 2628–2658 | 2.74 | 24.63 | 67.4 | |||
| 2666–2737 | 3.02 | 22.76 | 68.7 | |||
| 2764–2794 | 3.13 | 23.62 | 73.9 | |||
| 2813–2915 | 2.99 | 22.98 | 68.6 | |||
| 2935–3100 | 3.08 | 22.75 | 70.1 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, Y.; Spasennykh, M.; Shakirov, A.; Chekhonin, E.; Romushkevich, R.; Savelev, E.; Gabova, A.; Zagranovskaya, D.; Valiullin, R.; Yuarullin, R.; et al. Advanced Determination of Heat Flow Density on an Example of a West Russian Oil Field. Geosciences 2021, 11, 346. https://doi.org/10.3390/geosciences11080346
Popov Y, Spasennykh M, Shakirov A, Chekhonin E, Romushkevich R, Savelev E, Gabova A, Zagranovskaya D, Valiullin R, Yuarullin R, et al. Advanced Determination of Heat Flow Density on an Example of a West Russian Oil Field. Geosciences. 2021; 11(8):346. https://doi.org/10.3390/geosciences11080346
Chicago/Turabian StylePopov, Yury, Mikhail Spasennykh, Anuar Shakirov, Evgeny Chekhonin, Raisa Romushkevich, Egor Savelev, Anastasia Gabova, Dzhulia Zagranovskaya, Rim Valiullin, Rashid Yuarullin, and et al. 2021. "Advanced Determination of Heat Flow Density on an Example of a West Russian Oil Field" Geosciences 11, no. 8: 346. https://doi.org/10.3390/geosciences11080346
APA StylePopov, Y., Spasennykh, M., Shakirov, A., Chekhonin, E., Romushkevich, R., Savelev, E., Gabova, A., Zagranovskaya, D., Valiullin, R., Yuarullin, R., Golovanova, I., & Sal’manova, R. (2021). Advanced Determination of Heat Flow Density on an Example of a West Russian Oil Field. Geosciences, 11(8), 346. https://doi.org/10.3390/geosciences11080346







