Identification of Near-Fault Impulsive Signals and Their Initiation and Termination Positions with Convolutional Neural Networks
Abstract
:1. Introduction
- spectral ratios can be locally amplified in the region where the fundamental structural period is closer to the pulse period [9];
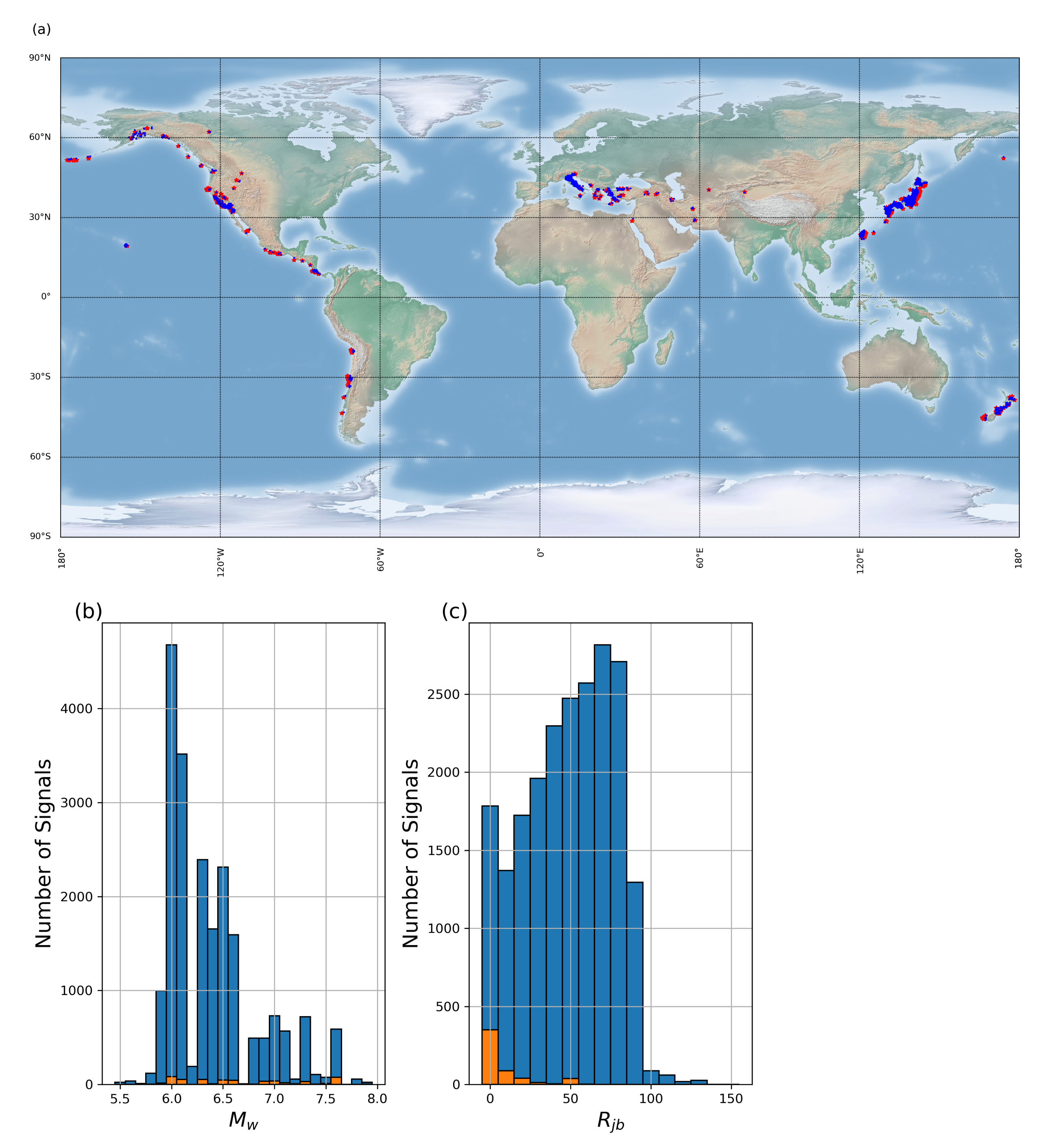
2. Data
3. Method
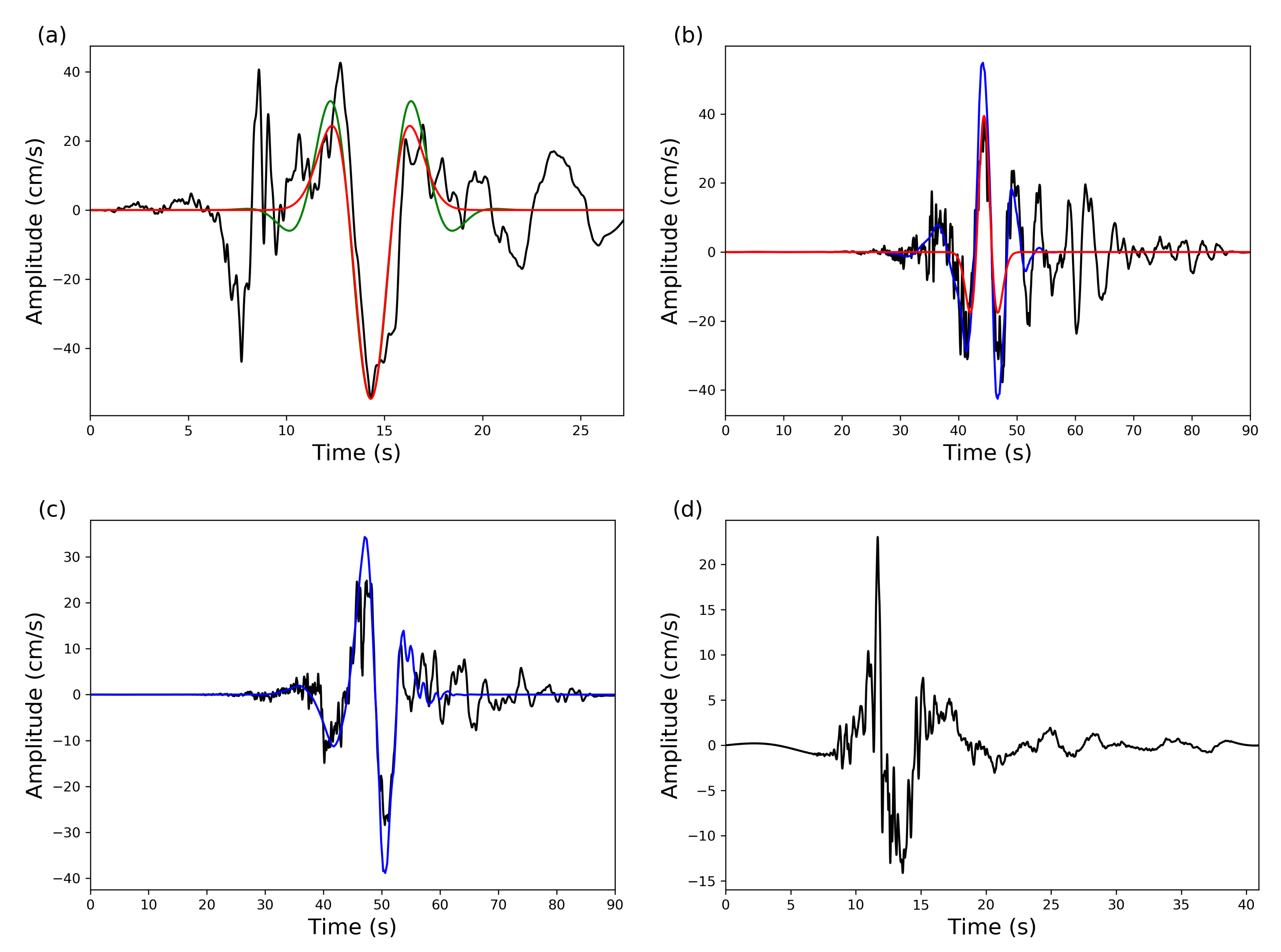
3.1. Identification of Impulsive Signals
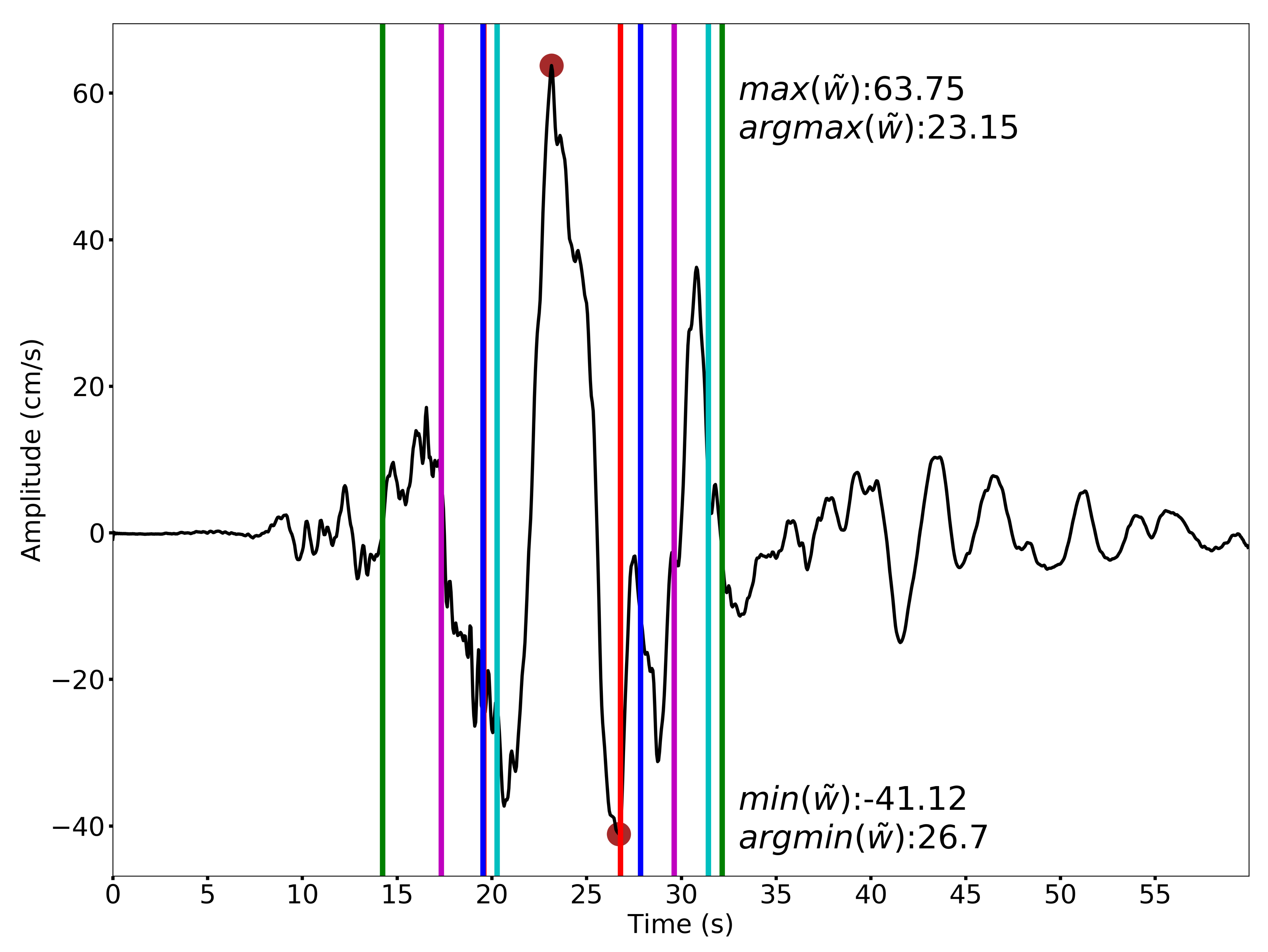
3.2. Determination of Initiation and Termination Positions of Impulsive Signals
4. Results
4.1. Cross-Validation of Identification of Impulsive Signals
4.2. Cross-Validation of Determination of Initiation and Termination Positions of Impulsive Signals
4.3. Comparison of Pulse Periods
4.4. Outliers
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baltzopoulos, G.; Luzi, L.; Iervolino, I. Analysis of Near-Source Ground Motion from the 2019 Ridgecrest Earthquake Sequence. Bull. Seismol. Soc. Am. 2020, 110, 1495–1505. [Google Scholar] [CrossRef]
- Somerville, P.G.; Smith, N.F.; Graves, R.W.; Abrahamson, N.A. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity. Seismol. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Kalkan, E.; Adalier, K.; Pamuk, A. Near source effects and engineering implications of recent earthquakes in Turkey. In International Conference on Case Histories in Geotechnical Engineering; University of Missouri–Rolla: Rolla, MO, USA, 2004; Volume 19. [Google Scholar]
- Kobayashi, H.; Koketsu, K.; Miyake, H. Rupture processes of the 2016 Kumamoto earthquake sequence: Causes for extreme ground motions. Geophys. Res. Lett. 2017, 44, 6002–6010. [Google Scholar] [CrossRef]
- Asano, K.; Iwata, T. Source rupture process of the 2018 Hokkaido Eastern Iburi earthquake deduced from strong-motion data considering seismic wave propagation in three-dimensional velocity structure. Earth Planets Space 2019, 71, 101. [Google Scholar] [CrossRef]
- Kobayashi, H.; Koketsu, K.; Miyake, H. Rupture process of the 2018 Hokkaido Eastern Iburi earthquake derived from strong motion and geodetic data. Earth Planets Space 2019, 71, 63. [Google Scholar] [CrossRef]
- Kalkan, E.; Kunnath, S.K. Effects of fling step and forward directivity on seismic response of buildings. Earthq. Spectra 2006, 22, 367–390. [Google Scholar] [CrossRef]
- Bradley, B.A. Strong ground motion characteristics observed in the 4 September 2010 Darfield, New Zealand earthquake. Soil Dyn. Earthq. Eng. 2012, 42, 32–46. [Google Scholar] [CrossRef]
- Shahi, S.K.; Baker, J.W. An empirically calibrated framework for including the effects of near-fault directivity in probabilistic seismic hazard analysis. Bull. Seismol. Soc. Am. 2011, 101, 742–755. [Google Scholar] [CrossRef]
- Iervolino, I.; Chioccarelli, E.; Baltzopoulos, G. Inelastic displacement ratio of near-source pulse-like ground motions. Earthq. Eng. Struct. Dyn. 2012, 41, 2351–2357. [Google Scholar] [CrossRef]
- Iervolino, I.; Baltzopoulos, G.; Chioccarelli, E.; Suzuki, A. Seismic actions on structures in the near-source region of the 2016 central Italy sequence. Bull. Earthq. Eng. 2017, 17, 5429–5447. [Google Scholar] [CrossRef]
- Li, C.; Kunnath, S.; Zuo, Z.; Peng, W.; Zhai, C. Effects of early-arriving pulse-like ground motions on seismic demands in RC frame structures. Soil Dyn. Earthq. Eng. 2020, 130, 105997. [Google Scholar] [CrossRef]
- Guo, G.; Yang, D.; Liu, Y. Duration effect of near-fault pulse-like ground motions and identification of most suitable duration measure. Bull. Earthq. Eng. 2018, 16, 5095–5119. [Google Scholar] [CrossRef]
- Mazza, F. Seismic demand of base-isolated irregular structures subjected to pulse-type earthquakes. Soil Dyn. Earthq. Eng. 2018, 108, 111–129. [Google Scholar] [CrossRef]
- Antonellis, G.; Panagiotou, M. Seismic response of bridges with rocking foundations compared to fixed-base bridges at a near-fault site. J. Bridge Eng. 2013, 19, 04014007. [Google Scholar] [CrossRef]
- Iervolino, I.; Cornell, C.A. Probability of occurrence of velocity pulses in near-source ground motions. Bull. Seismol. Soc. Am. 2008, 98, 2262–2277. [Google Scholar] [CrossRef]
- Shahi, S.K.; Baker, J.W. An efficient algorithm to identify strong-velocity pulses in multicomponent ground motions. Bull. Seismol. Soc. Am. 2014, 104, 2456–2466. [Google Scholar] [CrossRef]
- Ertuncay, D.; Costa, G. Determination of near-fault impulsive signals with multivariate naïve Bayes method. Nat. Hazards 2021, 108, 1763–1780. [Google Scholar] [CrossRef]
- Chioccarelli, E.; Iervolino, I. Near-source seismic hazard and design scenarios. Earthq. Eng. Struct. Dyn. 2013, 42, 603–622. [Google Scholar] [CrossRef]
- Mavroeidis, G.P.; Papageorgiou, A.S. A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Baker, J.W. Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 2007, 97, 1486–1501. [Google Scholar] [CrossRef]
- Chang, Z.; Sun, X.; Zhai, C.; Zhao, J.X.; Xie, L. An improved energy-based approach for selecting pulse-like ground motions. Earthq. Eng. Struct. Dyn. 2016, 45, 2405–2411. [Google Scholar] [CrossRef]
- Ertuncay, D.; Costa, G. An alternative pulse classification algorithm based on multiple wavelet analysis. J. Seismol. 2019, 23, 929–942. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.; Sheng, Y.; Zhu, W.; Beroza, G.C. STanford EArthquake Dataset (STEAD): A Global Data Set of Seismic Signals for AI. IEEE Access 2019, 7, 179464–179476. [Google Scholar] [CrossRef]
- Meier, M.A.; Ross, Z.E.; Ramachandran, A.; Balakrishna, A.; Nair, S.; Kundzicz, P.; Li, Z.; Andrews, J.; Hauksson, E.; Yue, Y. Reliable real-time seismic signal/noise discrimination with machine learning. J. Geophys. Res. Solid Earth 2019, 124, 788–800. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.M.; Ellsworth, W.L.; Zhu, W.; Chuang, L.Y.; Beroza, G.C. Earthquake transformer—An attentive deep-learning model for simultaneous earthquake detection and phase picking. Nat. Commun. 2020, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Ross, Z.E.; Meier, M.A.; Hauksson, E. P wave arrival picking and first-motion polarity determination with deep learning. J. Geophys. Res. Solid Earth 2018, 123, 5120–5129. [Google Scholar] [CrossRef]
- Ross, Z.E.; Meier, M.A.; Hauksson, E.; Heaton, T.H. Generalized seismic phase detection with deep learning. Bull. Seismol. Soc. Am. 2018, 108, 2894–2901. [Google Scholar] [CrossRef] [Green Version]
- Titos, M.; Bueno, A.; García, L.; Benítez, M.C.; Ibañez, J. Detection and Classification of Continuous Volcano-Seismic Signals with Recurrent Neural Networks. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1936–1948. [Google Scholar] [CrossRef]
- Titos, M.; Bueno, A.; García, L.; Benítez, C. A Deep Neural Networks Approach to Automatic Recognition Systems for Volcano-Seismic Events. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1533–1544. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Beroza, G.C. A machine-learning approach for earthquake magnitude estimation. Geophys. Res. Lett. 2020, 47, e2019GL085976. [Google Scholar] [CrossRef] [Green Version]
- Somerville, P.G. Magnitude scaling of the near fault rupture directivity pulse. Phys. Earth Planet. Inter. 2003, 137, 201–212. [Google Scholar] [CrossRef]
- Bozorgnia, Y.; Abrahamson, N.A.; Atik, L.A.; Ancheta, T.D.; Atkinson, G.M.; Baker, J.W.; Baltay, A.; Boore, D.M.; Campbell, K.W.; Chiou, B.S.J.; et al. NGA-West2 research project. Earthq. Spectra 2014, 30, 973–987. [Google Scholar] [CrossRef] [Green Version]
- Boore, D.M.; Watson-Lamprey, J.; Abrahamson, N.A. Orientation-independent measures of ground motion. Bull. Seismol. Soc. Am. 2006, 96, 1502–1511. [Google Scholar] [CrossRef]
- Sabetta, F.; Pugliese, A. Estimation of response spectra and simulation of nonstationary earthquake ground motions. Bull. Seismol. Soc. Am. 1996, 86, 337–352. [Google Scholar]
- Causse, M.; Chaljub, E.; Cotton, F.; Cornou, C.; Bard, P.Y. New approach for coupling k- 2 and empirical Green’s functions: Application to the blind prediction of broad-band ground motion in the Grenoble basin. Geophys. J. Int. 2009, 179, 1627–1644. [Google Scholar] [CrossRef] [Green Version]
- Bernard, P.; Herrero, A.; Berge, C. Modeling directivity of heterogeneous earthquake ruptures. Bull. Seismol. Soc. Am. 1996, 86, 1149–1160. [Google Scholar]
- Ameri, G.; Gallovič, F.; Pacor, F. Complexity of the Mw 6.3 2009 L’Aquila (central Italy) earthquake: 2. Broadband strong motion modeling. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Coutant, O. Programme de Simulation Numerique AXITRA. Rapport LGIT, Granoble. 1989. Available online: https://github.com/coutanto/axitra (accessed on 20 July 2021).
- Scala, A.; Festa, G.; Del Gaudio, S. Relation Between Near-Fault Ground Motion Impulsive Signals and Source Parameters. J. Geophys. Res. Solid Earth 2018, 123, 7707–7721. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://keras.io (accessed on 25 July 2021).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Cork, T.G.; Kim, J.H.; Mavroeidis, G.P.; Kim, J.K.; Halldorsson, B.; Papageorgiou, A.S. Effects of tectonic regime and soil conditions on the pulse period of near-fault ground motions. Soil Dyn. Earthq. Eng. 2016, 80, 102–118. [Google Scholar] [CrossRef]
- Aristotle University of Thessaloniki Seismological Network. Permanent Regional Seismological Network Operated by the Aristotle University of Thessaloniki. 1981. Available online: http://geophysics.geo.auth.gr/the_seisnet/WEBSITE_2005/station_index_en.html (accessed on 11 September 2021). [CrossRef]
- Boğaziçi University Kandilli Observatory and Earthquake Research Institute. 2001. Available online: http://www.koeri.boun.edu.tr/sismo/2/en/ (accessed on 11 September 2021). [CrossRef]
- Institute of Earth Sciences, Academia Sinica. Broadband Array in Taiwan for Seismology; Institute of Earth Sciences, Academia Sinica: Taipei, Taiwan, 1996. [Google Scholar]
- Geological Survey of Canada. Canadian National Seismograph Network; Geological Survey of Canada: Ottawa, ON, USA, 1989. [Google Scholar] [CrossRef]
- AFAD. AFAD—Turkey Earthquake Data Center System. 2019. Available online: https://tadas.afad.gov.tr/ (accessed on 11 September 2021).
- Van Houtte, C.; Bannister, S.; Holden, C.; Bourguignon, S.; McVerry, G. The New Zealand strong motion database. Bull. New Zeal. Soc. Earthq. Eng. 2017, 50, 1–20. [Google Scholar] [CrossRef]
- National Observatory of Athens. National Observatory of Athens Seismic Network; National Observatory of Athens: Athina, Greece, 1997. [Google Scholar] [CrossRef]
- Institute of Engineering Seimology Earthquake Engineering. ITSAK Strong Motion Network; Institute of Engineering Seimology Earthquake Engineering: Thessaloniki, Greece, 1981. [Google Scholar] [CrossRef]
- Earth Science and Resilience. NIED K-NET, KiK-net. 2019. Available online: https://www.kyoshin.bosai.go.jp/ (accessed on 11 September 2021).
- SSN. Servicio Sismologico Nacional. 2017. Available online: http://www.ssn.unam.mx/ (accessed on 11 September 2021). [CrossRef]
- Universidad De Chile. Red Sismologica Nacional; University of Chile: Metropolitana, Chile, 2013. [Google Scholar] [CrossRef]
- Technological Educational Institute of Crete. Seismological Network of Crete; Technological Educational Institute of Crete: Iraklio, Greece, 2006. [Google Scholar] [CrossRef]
- GEOFON Data Centre. GEOFON Seismic Network; GEOFON Data Centre: Potsdam, Germany, 1993. [Google Scholar] [CrossRef]
- Luzi, L.; Puglia, R.; Russo, E.; D’Amico, M.; Felicetta, C.; Pacor, F.; Lanzano, G.; Çeken, U.; Clinton, J.; Costa, G.; et al. The engineering strong-motion database: A platform to access pan-European accelerometric data. Seismol. Res. Lett. 2016, 87, 987–997. [Google Scholar] [CrossRef] [Green Version]
- Pacor, F.; Paolucci, R.; Luzi, L.; Sabetta, F.; Spinelli, A.; Gorini, A.; Nicoletti, M.; Marcucci, S.; Filippi, L.; Dolce, M. Overview of the Italian strong motion database ITACA 1.0. Bull. Earthq. Eng. 2011, 9, 1723–1739. [Google Scholar] [CrossRef] [Green Version]



| Layer Type | Output Shape |
|---|---|
| Input | 1200 |
| Conv1D | |
| MaxPooling1D | |
| Conv1D | |
| MaxPooling1D | |
| Conv1D | |
| MaxPooling1D | |
| Conv1D | |
| MaxPooling1D | |
| Dropout | |
| Flatten | 960 |
| Input | 2 |
| Concatenate | 962 |
| Dense | 40 |
| Dense | 30 |
| Dense | 1 |
| Activation | 1 |
| Layer Type | Output Shape |
|---|---|
| Input | 1200 |
| Conv1D | |
| MaxPooling1D | |
| Conv1D | |
| MaxPooling1D | |
| Conv1D | |
| MaxPooling1D | |
| Conv1D | |
| MaxPooling1D | |
| Dropout | |
| Flatten | 240 |
| Input | 4 |
| Concatenate | 244 |
| Dense | 40 |
| Dense | 30 |
| Dense | 30 |
| Activation | 1 |
| Method | Noise | FPR | FNR |
|---|---|---|---|
| Shahi & Baker (2014) | 0.003 | 0.279 | |
| Chang et al. (2016) | 0.002 | 0.328 | |
| Ertuncay & Costa (2019) | 0.043 | 0.320 | |
| Mavroeidis Model | Sabetta and Pugliese [35] | 0.206 | 0.360 |
| Mavroeidis Model | 1 std | 0.223 | 0.356 |
| Mavroeidis Model | 2 std | 0.161 | 0.381 |
| Mavroeidis Model | 3 std | 0.187 | 0.386 |
| Model | Sabetta and Pugliese [35] | 0.421 | 0.062 |
| Model | 1 std | 0.223 | 0.356 |
| Model | 2 std | 0.214 | 0.446 |
| Model | 3 std | 0.318 | 0.378 |
| MAE | MSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | s | e | s | e | s | e | |||
| Chang et al. (2016) | 0.95 | 0.97 | 0.96 | 19.60 | 12.85 | 21.40 | 844.41 | 1171.01 | 1007.71 |
| CNN | 0.97 | 0.97 | 0.97 | 17.51 | 22.53 | 20.03 | 610.23 | 1057.47 | 833.85 |
| Ertuncay and Costa (2019) | 0.94 | 0.97 | 0.95 | 24.27 | 25.79 | 25.03 | 1190.31 | 1154.98 | 1172.65 |
| Shahi and Baker (2014) | 0.95 | 0.98 | 0.96 | 22.55 | 20.56 | 21.55 | 978.44 | 812.89 | 895.77 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ertuncay, D.; De Lorenzo, A.; Costa, G. Identification of Near-Fault Impulsive Signals and Their Initiation and Termination Positions with Convolutional Neural Networks. Geosciences 2021, 11, 388. https://doi.org/10.3390/geosciences11090388
Ertuncay D, De Lorenzo A, Costa G. Identification of Near-Fault Impulsive Signals and Their Initiation and Termination Positions with Convolutional Neural Networks. Geosciences. 2021; 11(9):388. https://doi.org/10.3390/geosciences11090388
Chicago/Turabian StyleErtuncay, Deniz, Andrea De Lorenzo, and Giovanni Costa. 2021. "Identification of Near-Fault Impulsive Signals and Their Initiation and Termination Positions with Convolutional Neural Networks" Geosciences 11, no. 9: 388. https://doi.org/10.3390/geosciences11090388
APA StyleErtuncay, D., De Lorenzo, A., & Costa, G. (2021). Identification of Near-Fault Impulsive Signals and Their Initiation and Termination Positions with Convolutional Neural Networks. Geosciences, 11(9), 388. https://doi.org/10.3390/geosciences11090388







