Earthquake-Induced Flow-Type Slope Failure in Weathered Volcanic Deposits—A Case Study: The 16 April 2016 Takanodai Landslide, Japan
Abstract
:1. Introduction
2. The Takanodai Landslide: Characteristics and Field Observations
2.1. Geology of the Mt. Aso Volcanic Caldera
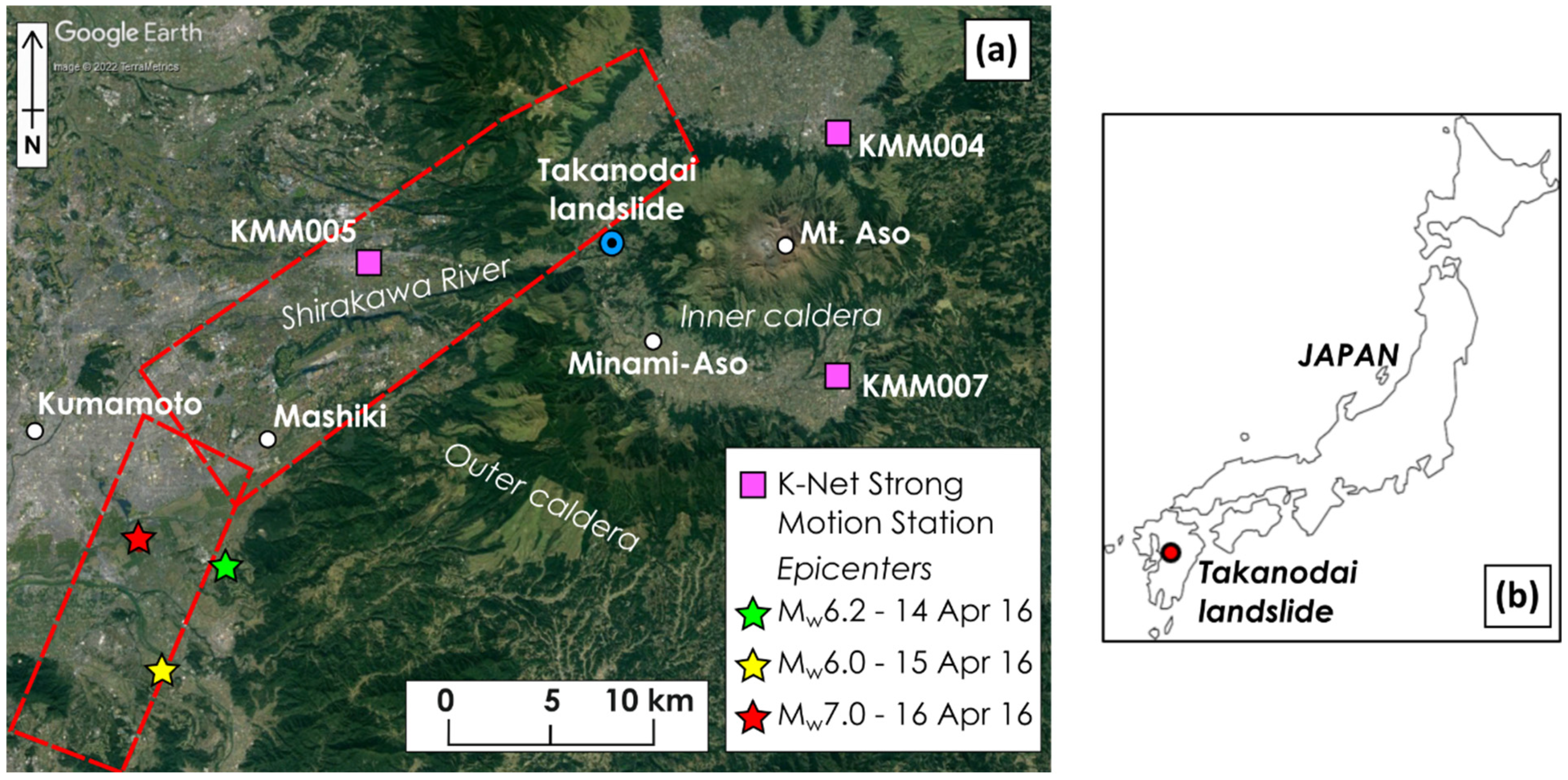
2.2. 2016 Kumamoto Earthquake Sequence
- 14 April 2016 event (foreshock), Mw6.2;
- 15 April 2016 event (foreshock), Mw6.0;
- 16 April 2016 event (main shock), Mw7.0.
2.3. Field Damage Observations at Takanodai Landslide Site
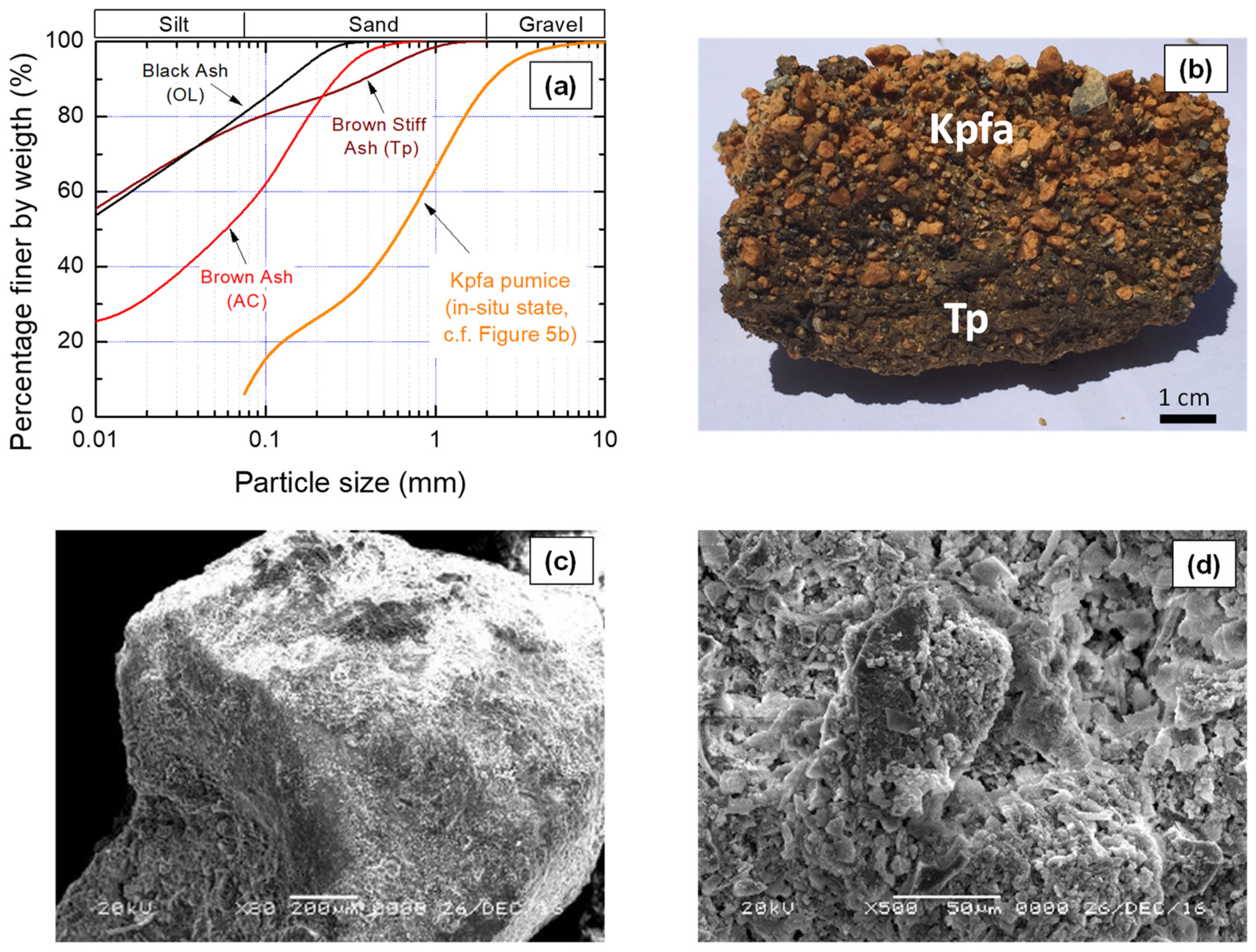
3. Laboratory Testing of Kpfa Pumice
3.1. Test Material
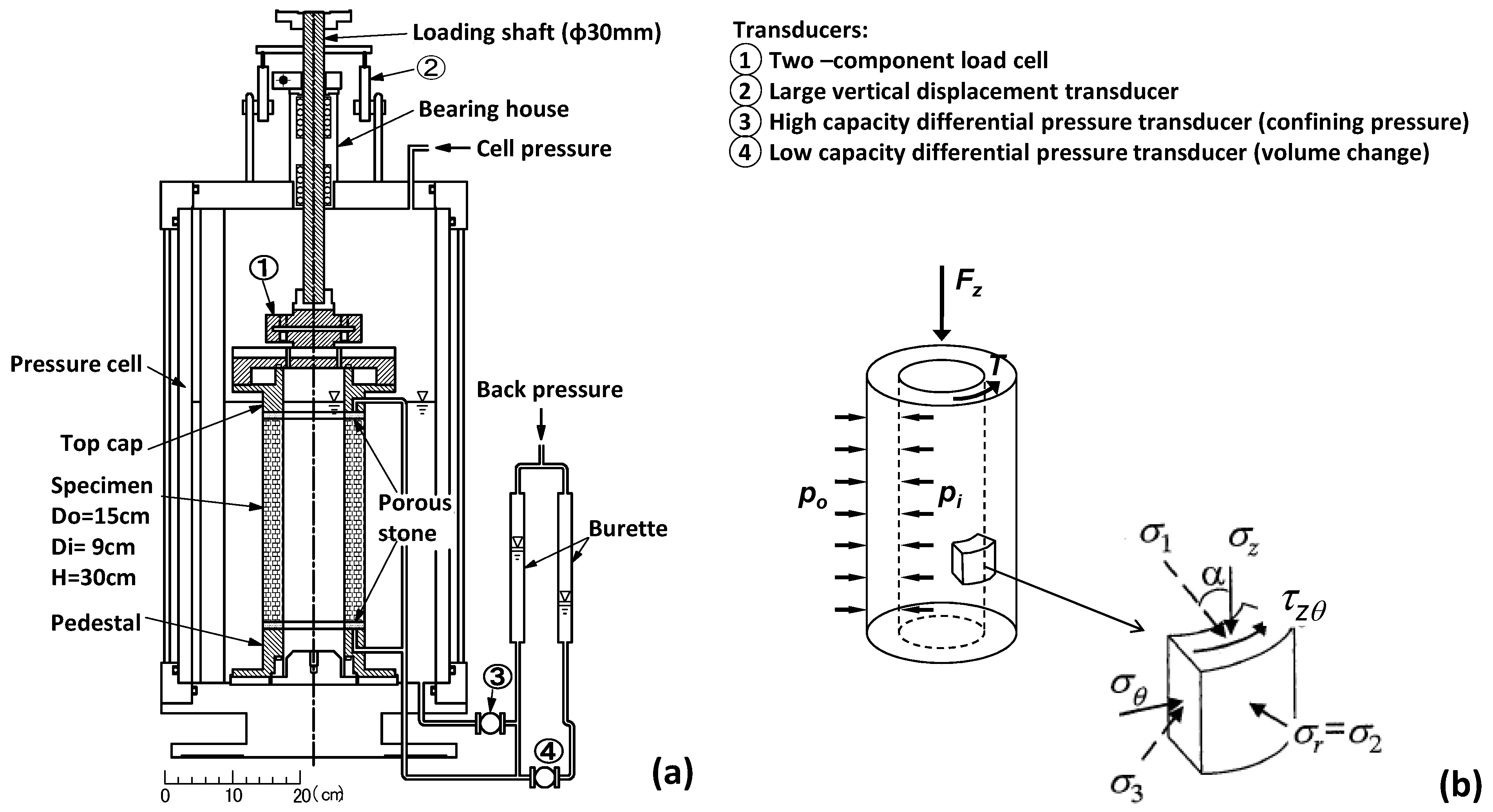
3.2. Test Apparatus
3.3. Test Procedure
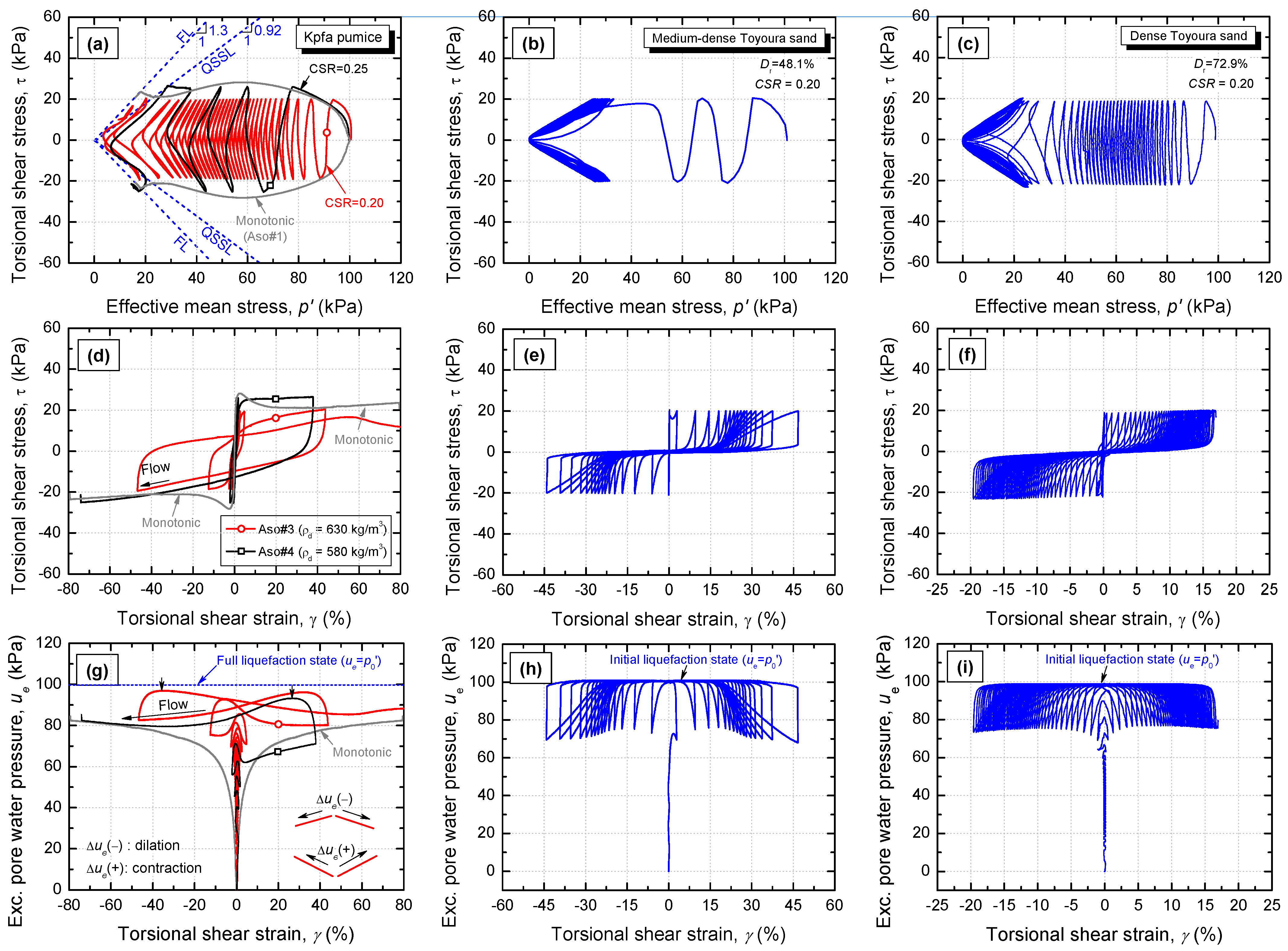
3.4. Test Results
3.4.1. Monotonic Undrained Shear Response
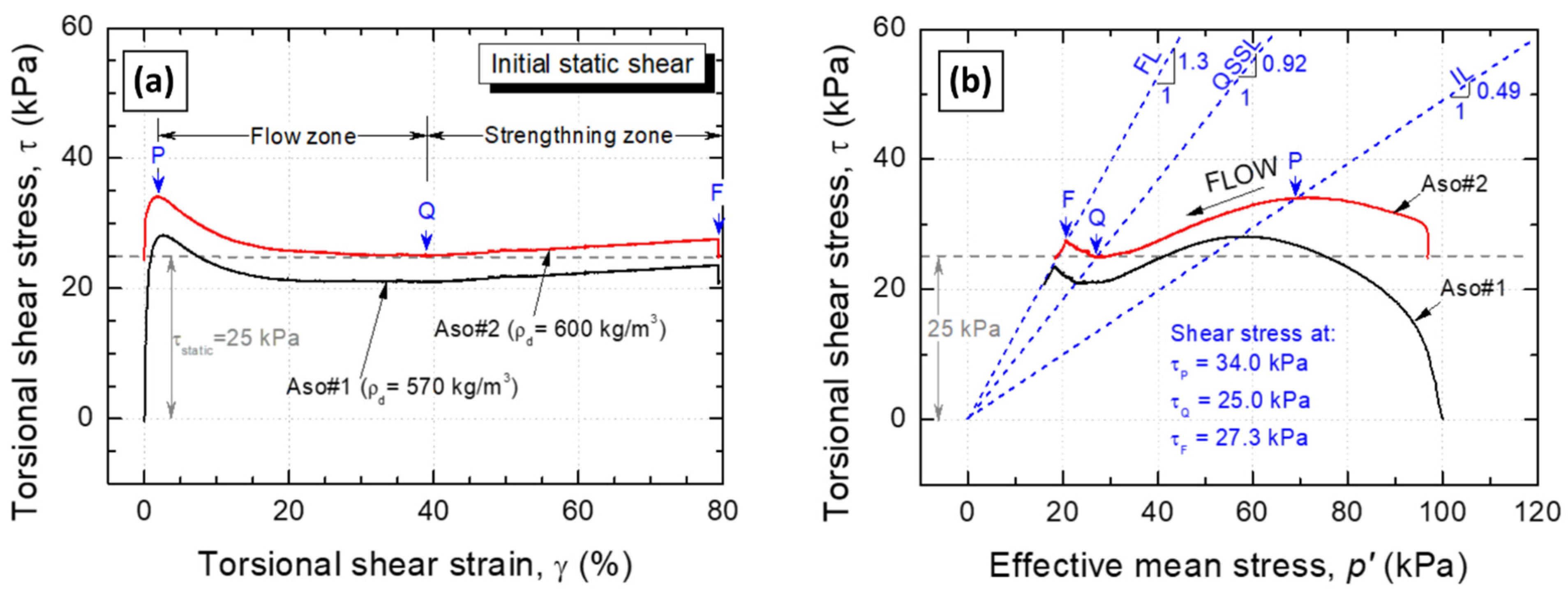
3.4.2. Monotonic Undrained Response under Initial Static Shear
3.4.3. Cyclic Undrained Shear Response
3.4.4. Cyclic Resistance
4. Liquefaction Assessment of the Takanodai Landslide during the Kumamoto Earthquakes
4.1. Outline of the Procedure
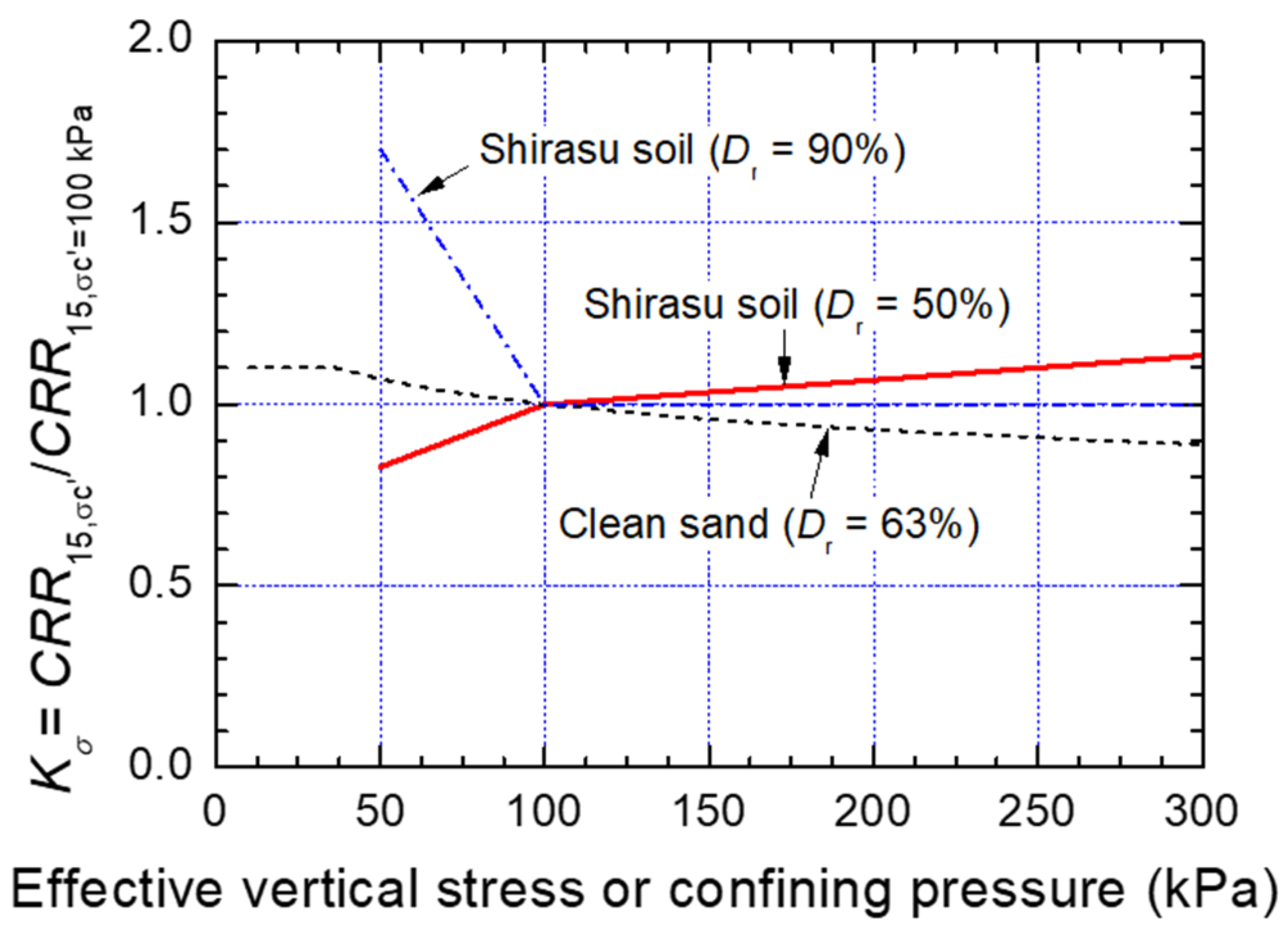
4.2. Evaluation of Kσ for Kpfa Pumice
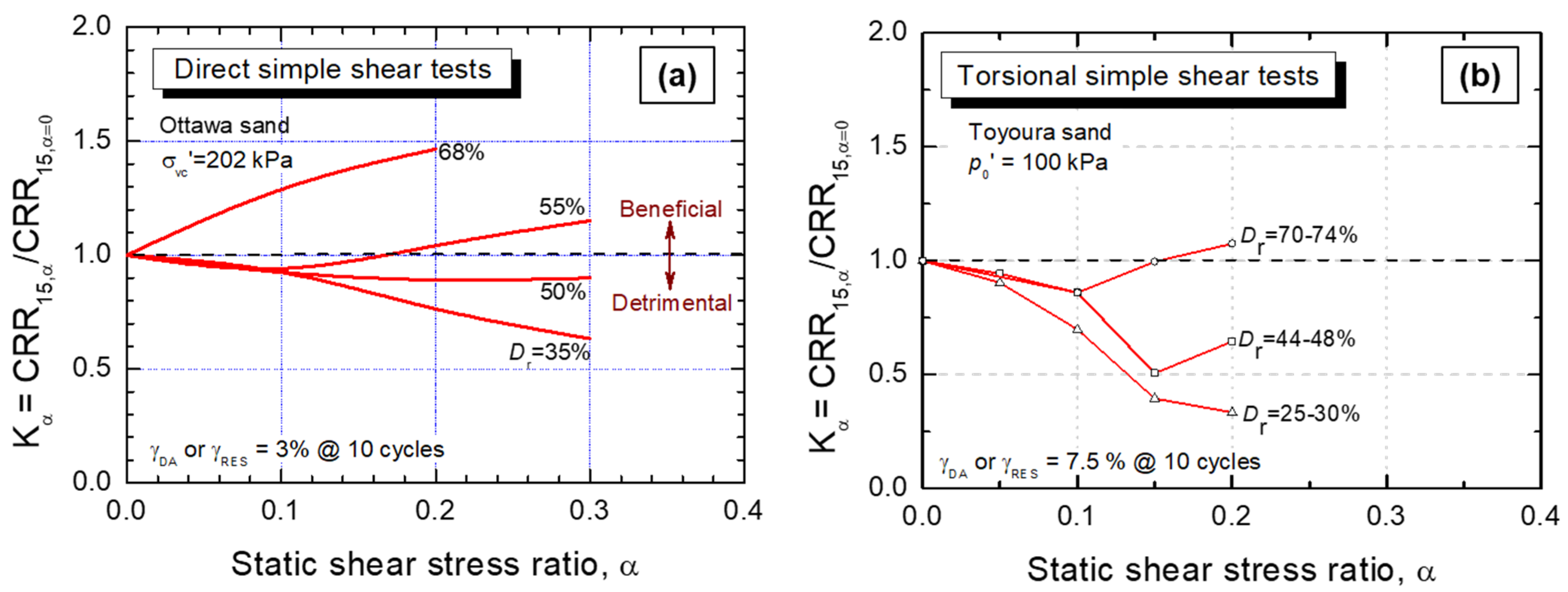
4.3. Evaluation of Kα for Kpfa Pumice
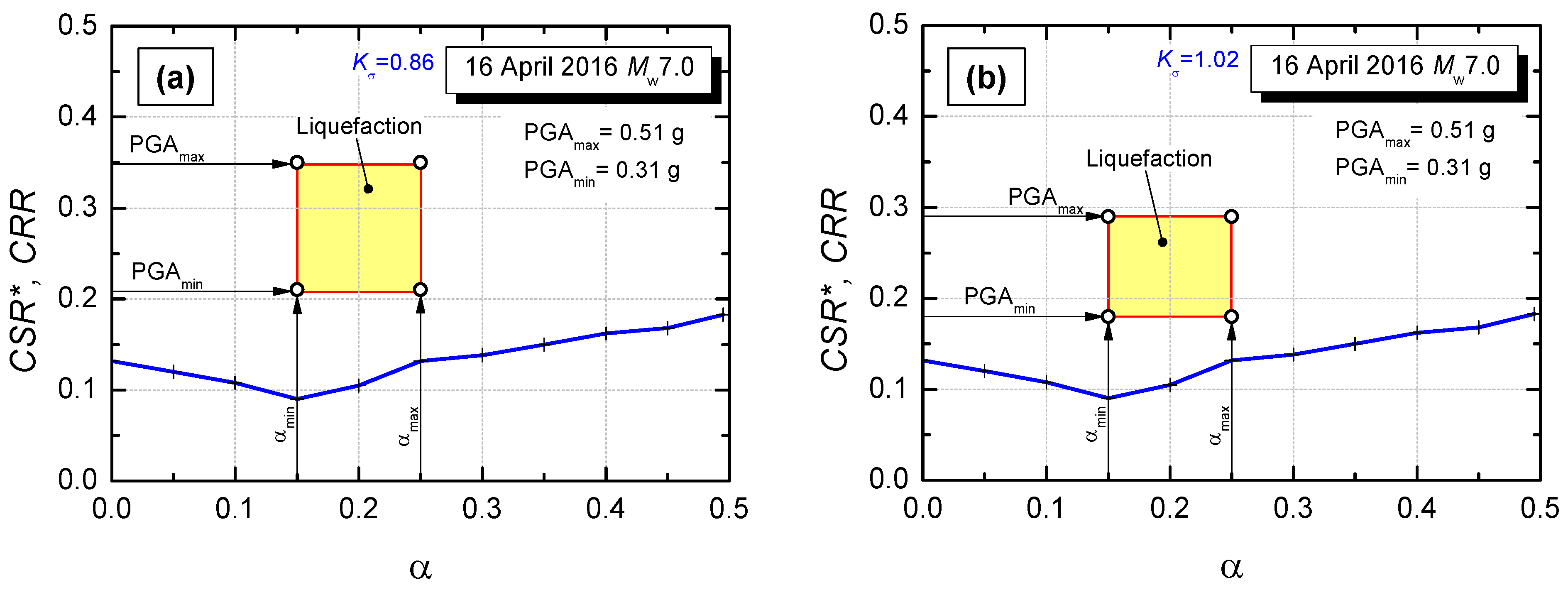
4.4. Liqueafction Assessment: Results and Discussion
5. Conclusions
- Laboratory investigations
- Liquefaction triggering analyses
- Future research needs
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mukunoki, T.; Kasama, T.; Murakami, S.; Ikemi, H.; Ishikura, R.; Fujikawa, T.; Yasufuka, N.; Kitazono, Y. Reconnaissance report on geotechnical damage caused by an earthquake with JMA seismic intensity 7 twice in 28h, Kumamoto, Japan. Soils Found. 2016, 56, 947–964. [Google Scholar] [CrossRef]
- Dang, K.; Sassa, K.; Fukuoka, H.; Sakai, N.; Sato, Y.; Takara, K.; Quang, L.H.; Loi, D.H.; Tien, P.V.; Ha, N.D. Mechanism of two rapid and long runout landslides in the 16 April 2016 Kumamoto earthquake using a ring-shear apparatus and computer simulation (LS-RAPID). Landslides 2016, 13, 1525–1534. [Google Scholar] [CrossRef]
- Kiyota, T.; Ikeda, T.; Konagai, K.; Shiga, M. Geotechnical damage caused by the 2016 Kumamoto Earthquake, Japan. Int. J. Geoeng. Case Hist. 2017, 4, 78–95. [Google Scholar]
- Chiaro, G.; Alexander, G.; Brabhaharan, P.; Massey, C.; Koseki, J.; Yamada, S.; Aoyagi, Y. Reconnaissance report on geotechnical and geological aspects of the 2016 Kumamoto Earthquake, Japan. Bull. N. Z. Soc. Earthq. Eng. 2017, 50, 365–393. [Google Scholar]
- Chigira, M.; Suzuki, T. Prediction of earthquake-induced landslides of pyroclastic fall deposits. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2016; pp. 93–100. [Google Scholar]
- Wang, G. Fluidized landsliding phenomena during earthquakes. In Proceedings of the JTC1 Workshop on Advances in Landslide Understanding, Barcelona, Spain, 24–26 May 2017; p. 4. [Google Scholar]
- Chiaro, G.; Umar, M.; Kiyota, T.; Massey, C. The Takanodai landslide, Kumamoto, Japan: Insights from post-earthquake field observations, laboratory tests and numerical analyses. ASCE Geotech. Spec. Publ. 2018, 293, 98–111. [Google Scholar]
- Chiaro, G.; Chew, K.; Kim, J.S. Numerical analyses of the earthquake-induced Takanodai landslide, Kumamoto, Japan. In Proceedings of the Conference on GIS and Geoinformation Zoning for Disaster Mitigation, Auckland, New Zealand, 23–24 November 2018; pp. 47–54. [Google Scholar]
- Chiaro, G.; Kiyota, T.; Umar, M. Undrained monotonic and cyclic torsional simple shear behavior of the Aso pumiceous soil deposits. In Proceedings of the 7th International Conference on Earthquake Geotechnical Engineering, Rome, Italy, 17–20 June 2019; pp. 1754–1761. [Google Scholar]
- Umar, M.; Chiaro, G.; Takashi, K.; Miyamoto, H. Monotonic and cyclic undrained behavior of Kumamoto-Aso pumice soil by triaxial and torsional shear tests. In Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, 18–21 June 2018; Paper No. 11577. p. 11. [Google Scholar]
- Hazarika, H.; Sumartini, W.O.; Kokusho, T.; Kochi, Y.; Ishibashi, S.; Yamamoto, S.; Matsumoto, D. Investigations on mechanism of landslides during the 2016 Kumamoto Earthquake, Japan. In Proceedings of the 7th International Conference on Earthquake Geotechnical Engineering, Rome, Italy, 17–20 June 2019; pp. 821–832. [Google Scholar]
- Kasama, K.; Furukawa, Z.; Yasufuku, N. Cyclic shear property and seismic runout analysis for pumice fall deposit. Soil Dyn. Earthq. Eng. 2021, 143, 106588. [Google Scholar] [CrossRef]
- Goto, S.; Okada, K. Monotonic and cyclic behavior of tephra layer landslide at Takanodai form the 2016 Kumamoto earthquake. In Understanding and Reducing Landslide Disaster Risk; Tiwari, B., Sassa, K., Bobrowsky, P.T., Takara, K., Eds.; Springer: Cham, Switzerland, 2020; pp. 357–364. [Google Scholar]
- Geological Survey of Japan, AIST Website. Available online: https://gbank.gsj.jp/geonavi/geonavi.php#12,32.87856,130.99942 (accessed on 28 July 2022).
- Geological Survey of Japan. Available online: https://www.gsj.jp/hazards/earthquake/kumamoto2016/geonavi-link.html (accessed on 28 July 2022).
- Asano, K.; Iwata, T. Revisiting the source process of the mainshock of the 2016 Kumamoto earthquake and implications for the generation of near-fault ground motions and forward-directivity pulse. Bull. Seism. Soc. Am. 2021, 111, 2426–2440. [Google Scholar] [CrossRef]
- Kubo, H.; Suzuki, W.; Aoi, S.; Sekiguchi, H. Source rupture process of the 2016 Kumamoto, Japan, earthquakes estimated from strong-motion waveforms. Earth Planets Space 2016, 68, 161. [Google Scholar] [CrossRef] [Green Version]
- Yoshida, K.; Miyakoshi, K.; Somei, K.; Irikura, K. Source process of the 2016 Kumamoto earthquake (Mj7.3) inferred from kinematic inversion of strong-motion records. Earth Planets Space 2017, 69, 64. [Google Scholar] [CrossRef] [Green Version]
- K-net. Available online: https://www.kyoshin.bosai.go.jp/ (accessed on 28 July 2022).
- Paudel, P.; Omura, H.; Kubota, T.; Inoue, T. Spatio-temporal patterns of historical shallow landslides in a volcanic area, Mt. Aso, Japan. Geomorphology 2007, 88, 21–33. [Google Scholar] [CrossRef]
- Kiyota, T.; Sato, T.; Koseki, J.; Mohammad, A. Behavior of liquefied sands under extremely large strain levels in cyclic torsional shear tests. Soils Found. 2008, 48, 727–739. [Google Scholar] [CrossRef] [Green Version]
- Kiyota, T.; Koseki, J.; Sato, T. Comparison of liquefaction-induced ground deformation between results from undrained cyclic torsional shear tests and observations from previous model tests and case studies. Soils Found. 2010, 50, 421–429. [Google Scholar] [CrossRef] [Green Version]
- Vaid, Y.P.; Finn, W.D.L. Static shear and liquefaction potential. J. Geotech. Eng. Div. ASCE 1979, 105, 1233–1246. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Muramatsu, M.; Sasaki, T. Cyclic undrained stress-strain behavior of dense sands by torsional simple shear stress. Soils Found. 1982, 22, 55–70. [Google Scholar] [CrossRef] [Green Version]
- Boulanger, R.W.; Seed, R.B.; Chan, C.K.; Seed, H.B.; Sousa, J.B. Liquefaction Behavior of Saturated and under Uni-Directional and Bi-directional Monotonic and Cyclic Simple Shear Loading; University of California Berkley: Berkeley, CA, USA, 1991. [Google Scholar]
- Cappellaro, C.; Cubrinovski, M.; Bray, D.J.; Chiaro, G.; Riemer, M.; Stringer, M. Liquefaction resistance of Christchurch sandy soils from direct simple shear tests. Soil Dyn. Earthq. Eng. 2021, 141, 106489. [Google Scholar] [CrossRef]
- Yasuda, S.; Nagase, N.; Kiku, H.; Uchida, Y. The mechanisms and a simplified procedure for analyses of permanent ground displacement due to liquefaction. Soils Found. 1992, 32, 149–160. [Google Scholar] [CrossRef] [Green Version]
- Umar, M.; Chiaro, G.; Kiyota, T.; Ullah, N. Deformation and cyclic resistance of sand in large-strain undrained torsional shear tests with initial static shear stress. Soils Found. 2021, 61, 765–781. [Google Scholar] [CrossRef]
- Chiaro, G. Cyclic resistance and large deformation characteristics of sands under sloping ground conditions: Insights from large-strain torsional simple shear tests. In Latest Developments in Geotechnical Earthquake Engineering and Soil Dynamics, Springer Transactions in Civil and Environmental Engineering; Sitharam, T.G., Ed.; Springer: Singapore, 2021; pp. 101–131. [Google Scholar]
- Hight, D.W.; Gens, A.; Symes, M.J. The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils. Geotechnique 1983, 33, 355–383. [Google Scholar] [CrossRef]
- Hyodo, M.; Hyde, A.F.L.; Aramaki, N. Liquefaction of crushable soils. Geotechnique 1998, 48, 527–543. [Google Scholar] [CrossRef]
- Ladd, R. Preparing tests specimens using undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar]
- Pender, M.J.; Wesley, L.D.; Larkin, T.J.; Pranjoto, S. Geotechnical properties of a pumice sand. Soils Found. 2006, 46, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Ampadu, S.I.K. Undrained Behavior of Kaolin in Torsional Simple Shear. PhD Thesis, University of Tokyo, Tokyo, Japan, 1991. [Google Scholar]
- Chiaro, G.; Koseki, J.; Sato, T. Effects of initial static shear on liquefaction and large deformation properties of loose saturated Toyoura sand in undrained cyclic torsional shear. Soils Found. 2012, 52, 498–510. [Google Scholar] [CrossRef] [Green Version]
- Chiaro, G.; Kiyota, T.; Koseki, J. Strain localization characteristics of loose saturated Toyoura sand in undrained cyclic torsional shear tests with initial static shear. Soils Found. 2013, 53, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Seed, H.B.; Lee, K.L. Liquefaction of saturated sands during cyclic loading. J. Soil Mech. Found. Div. 1966, 92, 105–134. [Google Scholar] [CrossRef]
- Finn, W.D.L. Aspects of constant volume cyclic simple shear. In Advances in the Art of Testing Soils Under Cyclic Conditions; Khosla, V., Ed.; ASCE: Reston, VI, USA, 1985; pp. 74–98. [Google Scholar]
- Chiaro, G.; Koseki, J.; De Silva, L.I.N. A density- and stress-dependent elasto-plastic model for sands subjected to monotonic torsional shear loading. Geotech. Eng. J. SEAGS 2013, 44, 18–26. [Google Scholar]
- Chiaro, G.; De Silva, L.I.N.; Koseki, J. Modeling the effects of static shear on the undrained cyclic torsional simple shear behavior of liquefiable sand. Geotech. Eng. J. SEAGS 2017, 48, 1–9. [Google Scholar]
- Chiaro, G.; De Silva, N.L.I.; Koseki, J. Modeling of liquefaction and large-strain response of sand in sloping ground. In Modeling in Geotechnical Engineering; Samui, P., Kumari, S., Makarov, V., Kurup, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 365–391. [Google Scholar]
- Ishihara, K.; Tatsuoka, F.; Yasuda, S. Undrained deformation and liquefaction of sand under cyclic stresses. Soils Found. 1975, 15, 29–44. [Google Scholar] [CrossRef] [Green Version]
- Sladen, J.A.; D’Hollander, R.D.; Krahn, J. The liquefaction of sands, a collapse surface approach. Can. Geotech. J. 1985, 22, 564–578. [Google Scholar] [CrossRef]
- Yoshimine, M.; Ishihara, K. Flow potential of sand during liquefaction. Soils Found. 1998, 38, 189–198. [Google Scholar] [CrossRef] [Green Version]
- Picarelli, L.; Olivares, L.; Lampitiello, S.; Darban, R.; Damiano, E. The undrained behaviour of an air-fall volcanic ash. Geosciences 2020, 10, 60. [Google Scholar] [CrossRef] [Green Version]
- Seed, H.B. Soil liquefaction and cyclic mobility evaluation for level ground during earthquakes. J. Geotech. Eng. Div. 1979, 105, 201–255. [Google Scholar] [CrossRef]
- Ishihara, K. Liquefaction and flow failure during earthquakes. Géotechnique 1993, 4, 351–415. [Google Scholar] [CrossRef]
- Chiaro, G.; Kiyota, T.; Miyamoto, H. Liquefaction potential and large deformation properties of Christchurch liquefied sand subjected to undrained cyclic torsional simple shear loading. In Proceedings of the 19th International Conference on Soil Mechanics and Geotechnical Engineering, Seoul, Korea, 17–22 September 2017; pp. 1497–1500. [Google Scholar]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating soil liquefaction potential. J. Soil Mech. Found. Div. ASCE 1971, 97, 1249–1273. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Soil Liquefaction during earthquakes. In Engineering Monographs on Earthquake Criteria, Structural Design, and Strong motion Records; Earthquake Engineering Research Institute: Oakland, CA, USA, 2008. [Google Scholar]
- Pyke, R.M.; Chan, C.K.; Seed, H.B. Settlement and Liquefaction of Sands under Multi-Directional Shaking; Report No. EERC 74-2; Earthquake Engineering Research Center, University of California at Berkeley: Berkeley, CA, USA, 1974. [Google Scholar]
- Ishihara, K.; Takatsu, H. Effects of overconsolidation and K0, conditions on the liquefaction characteristics of sands. Soils Found. 1979, 19, 59–68. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, K.; Yamazaki, A.; Haga, K. Liquefaction of K0 consolidated sand under cyclic rotation of principal stress direction with lateral constraint. Soils Found. 1985, 5, 63–74. [Google Scholar] [CrossRef] [Green Version]
- Harder, L.F.; Boulanger, R.W. Application of Kσ and Kα correction factors. In Proceedings of the NCEER Workshop on Evaluation of Liquefaction Resistance of Soils, Salt Lake City, UT, USA, 5–6 January 1996; Youd, T.L., Idriss, I.M., Eds.; Technical Report NCEER-97-0022. National Center for Earthquake Engineering Research, SUNY: Buffalo, NY, USA, 1997; pp. 167–190. [Google Scholar]
- Vaid, Y.P.; Sivathayalan, S. Static and cyclic liquefaction potential of Fraser delta sand in simple shear and triaxial tests. Can. Geotech. J. 1996, 33, 281–289. [Google Scholar] [CrossRef]
- Chiaro, G. Deformation Properties of Sand with Initial Static Shear in Undrained Cyclic Torsional Shear Tests and Their Modeling. Ph.D. Thesis, Department of Civil Engineering, University of Tokyo, Tokyo, Japan, 2010; p. 310. [Google Scholar]
- Verdugo, R.; Castillo, P.; Briceño, L. Initial soil structure and steady state strength. In Proceedings of the 1st International Conference on Earthquake Geotechnical Engineering, Tokyo, Japan, 14–16 November 1995. [Google Scholar]
- Mulilis, J.P.; Seed, H.B.; Chan, C.K.; Mitchell, J.K.; Arulanandan, K. Effects of sample preparation on sand liquefaction. J. Geotech. Eng. Div. 1977, 103, 91–108. [Google Scholar] [CrossRef]
- Umehara, Y.; Chiaro, G.; Kiyota, T.; Hosono, Y.; Yaguira, Y.; Chiba, H. Effectiveness of ‘Gel-Push’ sampling technique to retrieve undisturbed sandy specimens for liquefaction test. In Proceedings of the 6th International Conference on Earthquake Geotechnical Engineering, Christchurch, New Zealand, 1–4 November 2015; p. 8. [Google Scholar]
- Mori, K.; Sakai, K. The GP sampler: A new innovation in core sampling. In Proceedings of the 5th International Conference on Geotechnical and Geophysical Site Characterization, Gold Coast, Australia, 5–9 September 2016; pp. 99–124. [Google Scholar]







| Date and Mw of Event | Station | R† (km) | PGA†† (g) | Sa(1 s)†† (g) | Ia†† (m/s) | D5–95†† (s) | CAV†† (m/s) |
|---|---|---|---|---|---|---|---|
| 14 April 2016, 6.2 | KMM004 | 36 | 0.04 | 0.03 | 0.03 | 27.6 | 2.40 |
| KMM005 | 16 | 0.21 | 0.18 | 0.28 | 11.6 | 6.24 | |
| KMM007 | 31 | 0.18 | 0.05 | 0.58 | 15.7 | 8.62 | |
| 15 April 2016, 6.0 | KMM004 | 42 | 0.01 | 0.02 | 0.00 | 41.2 | 1.00 |
| KMM005 | 22 | 0.05 | 0.05 | 0.03 | 12.8 | 1.72 | |
| KMM007 | 35 | 0.08 | 0.02 | 0.10 | 16.2 | 3.40 | |
| 16 April 2016, 7.0 | KMM004 | 7 | 0.31 | 0.53 | 1.84 | 12.0 | 14.83 |
| KMM005 | 0 | 0.51 | 0.41 | 3.79 | 11.7 | 22.47 | |
| KMM007 | 13 | 0.35 | 0.24 | 1.79 | 14.9 | 16.60 |
| Soil Type | Symbol † | Bulk Unit Weight (kN/m3) †† |
|---|---|---|
| Black ash | OL (1) | 11.2 |
| Brown ash | AC (1) | 12.9 |
| Black ash | OL (2) | 11.2 |
| Brown ash | AC (2) | 19.2 |
| Orange pumice | Kpfa | 11.3 |
| Stiff brown ash | Tp | 19.2 |
| Soft rock | --- | 22.0 |
| Test | Loading Conditions | Dry Density ρd (kg/m3) | Cyclic Shear Stress τcyclic (kPa) | Static Shear Stress τstatic (kPa) |
|---|---|---|---|---|
| Aso#1 Aso#2 | Monotonic | 570 600 | --- --- | 0 25 |
| Aso#3 Aso#4 | Cyclic | 630 580 | 20 25 | 0 |
| 0 |
| Test | Peak State (P) | Quasi-Steady State (Q) | Failure State (F) | |||
|---|---|---|---|---|---|---|
| τP (kPa) | ϕP′ (°) | τQ (kPa) | ϕQ′ (°) | τF (kPa) | ϕF′ (°) | |
| Aso#1 | 28.2 | 26.1 | 21.1 | 42.6 | 23.6 | 52.4 |
| Aso#2 | 34.0 | 26.1 | 25.0 | 42.6 | 27.3 | 52.4 |
| Earthquake | Station | PGA (g) | CRR†·Kα | CSR * | FL | CSR * | FL |
|---|---|---|---|---|---|---|---|
| α = 0.15–0.25 | Kσ = 0.86 | Kσ = 1.02 | |||||
| 14 April 2016 Mw6.2 | KMM004 | 0.04 | 0.09–0.13 | 0.02 | 4.5–6.5 | 0.02 | 4.5–6.5 |
| (MSF = 1.41) | KMM005 | 0.21 | 0.09–0.13 | 0.11 | 0.8–1.2 | 0.09 | 1.0–1.4 |
| 16 April 2016 Mw7.0 | KMM004 | 0.31 | 0.09–0.13 | 0.21 | 0.4–0.6 | 0.18 | 0.5–0.7 |
| (MSF = 1.14) | KMM005 | 0.51 | 0.09–0.13 | 0.35 | 0.3–0.4 | 0.29 | 0.3–0.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiaro, G.; Kiyota, T.; Umar, M.; Cappellaro, C. Earthquake-Induced Flow-Type Slope Failure in Weathered Volcanic Deposits—A Case Study: The 16 April 2016 Takanodai Landslide, Japan. Geosciences 2022, 12, 394. https://doi.org/10.3390/geosciences12110394
Chiaro G, Kiyota T, Umar M, Cappellaro C. Earthquake-Induced Flow-Type Slope Failure in Weathered Volcanic Deposits—A Case Study: The 16 April 2016 Takanodai Landslide, Japan. Geosciences. 2022; 12(11):394. https://doi.org/10.3390/geosciences12110394
Chicago/Turabian StyleChiaro, Gabriele, Takashi Kiyota, Muhammad Umar, and Claudio Cappellaro. 2022. "Earthquake-Induced Flow-Type Slope Failure in Weathered Volcanic Deposits—A Case Study: The 16 April 2016 Takanodai Landslide, Japan" Geosciences 12, no. 11: 394. https://doi.org/10.3390/geosciences12110394
APA StyleChiaro, G., Kiyota, T., Umar, M., & Cappellaro, C. (2022). Earthquake-Induced Flow-Type Slope Failure in Weathered Volcanic Deposits—A Case Study: The 16 April 2016 Takanodai Landslide, Japan. Geosciences, 12(11), 394. https://doi.org/10.3390/geosciences12110394









