Ontogenetic Trends of Sutural Complexity in Jurassic Ammonites
Abstract
:1. Introduction
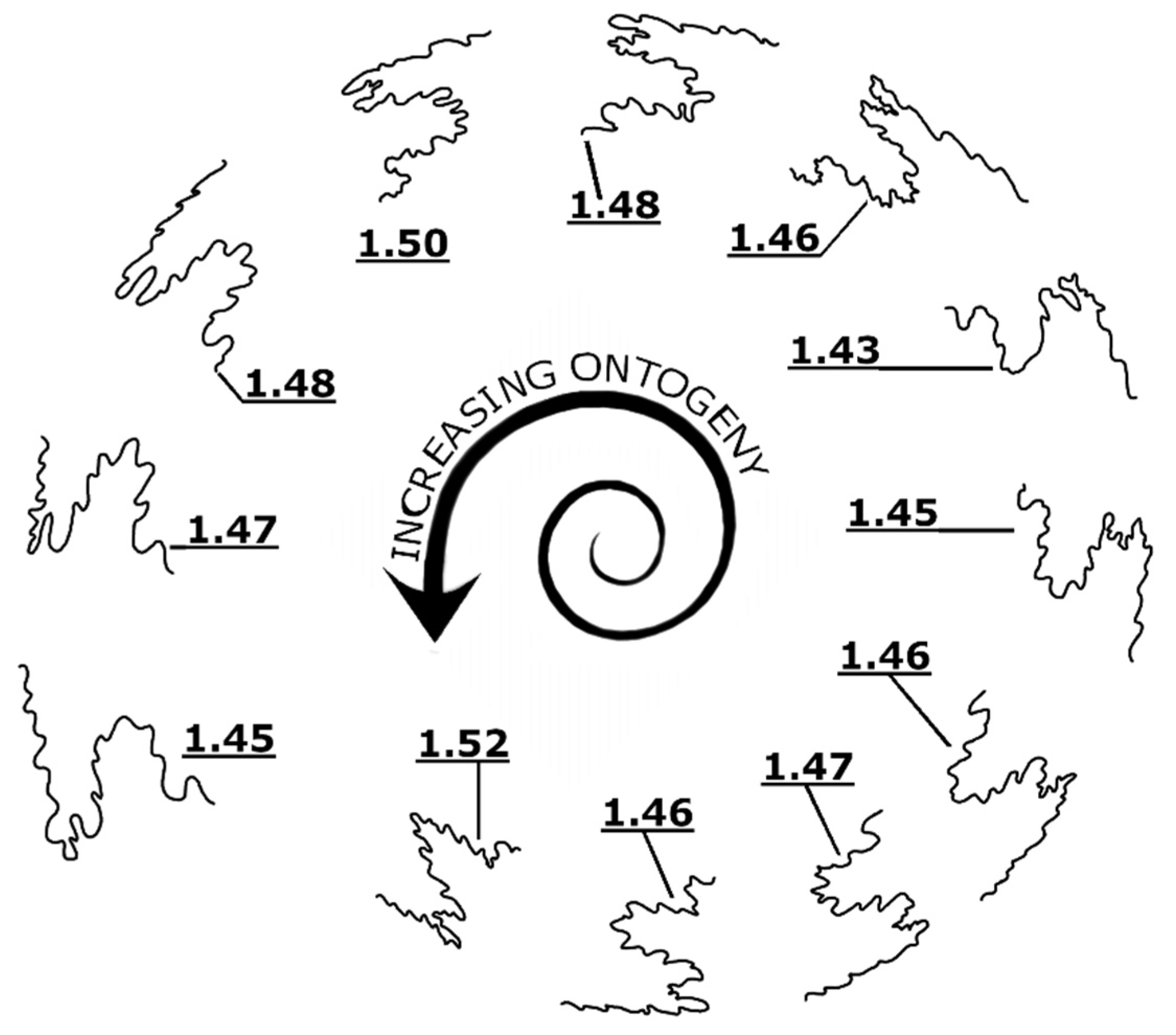
2. Materials and Methods
3. Results
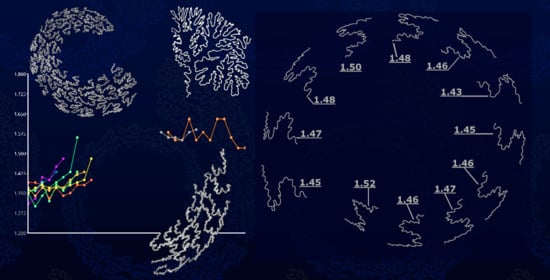
3.1. Lytoceratids
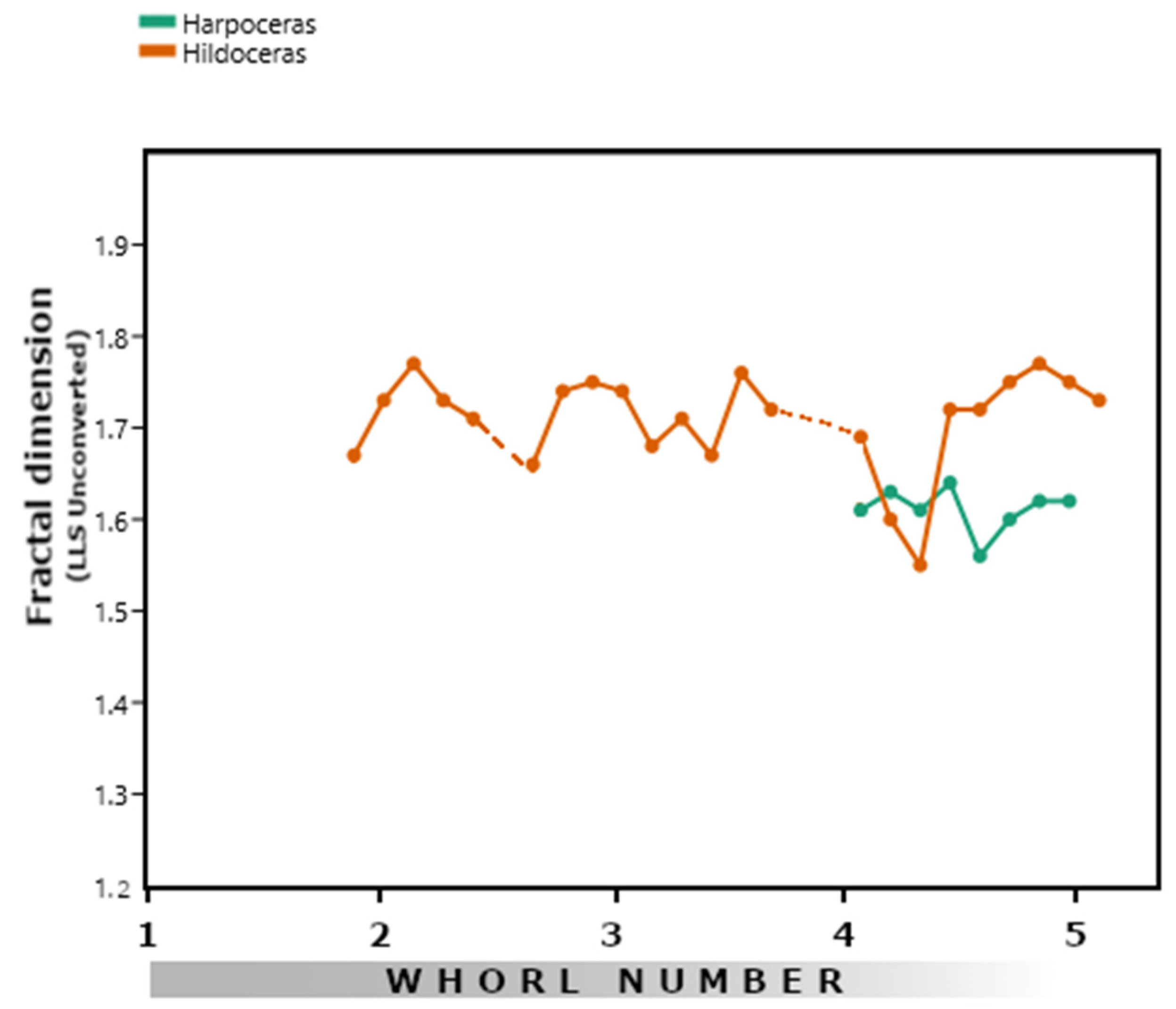
3.2. Hildoceratids
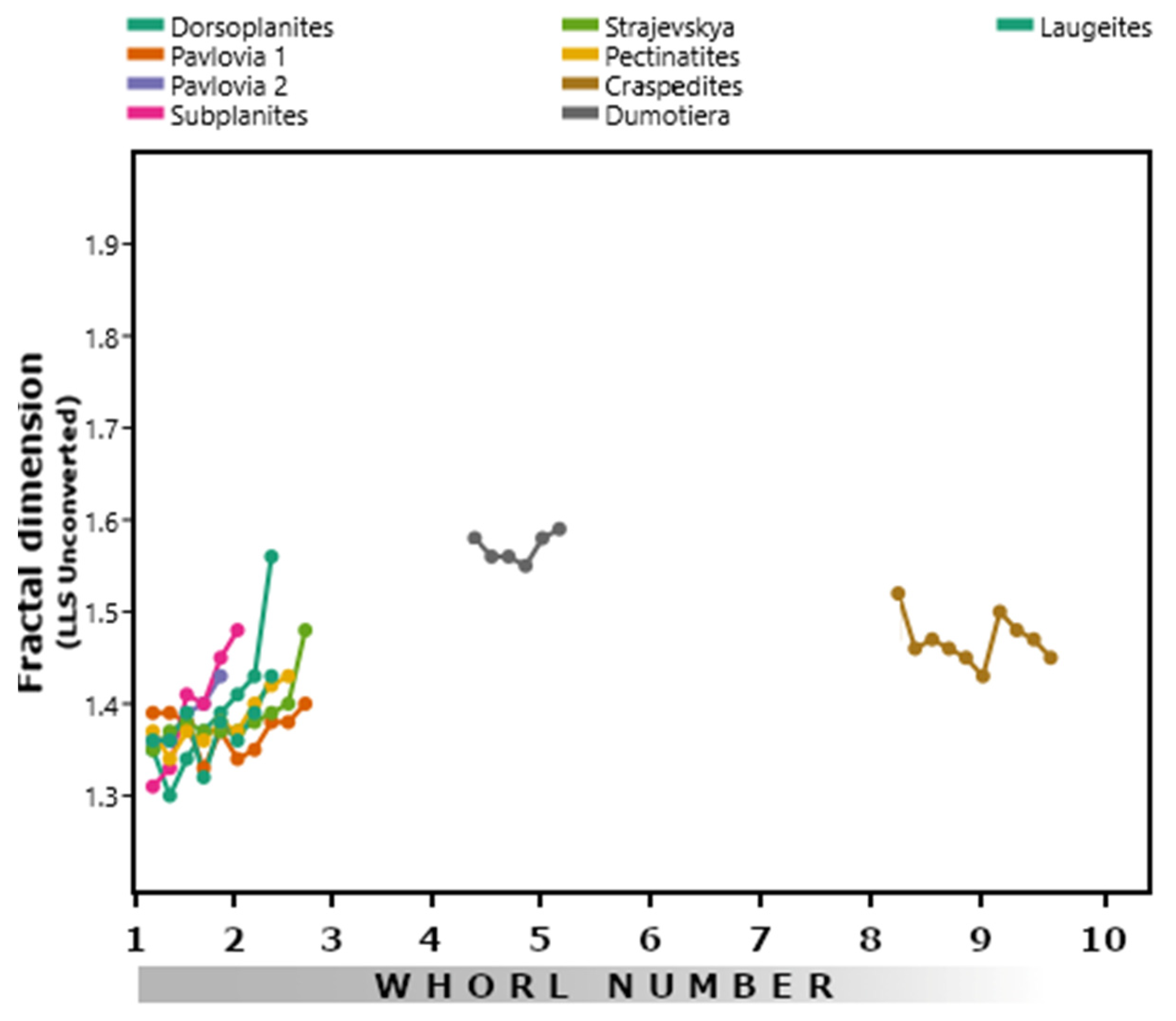
3.3. Perisphinctids
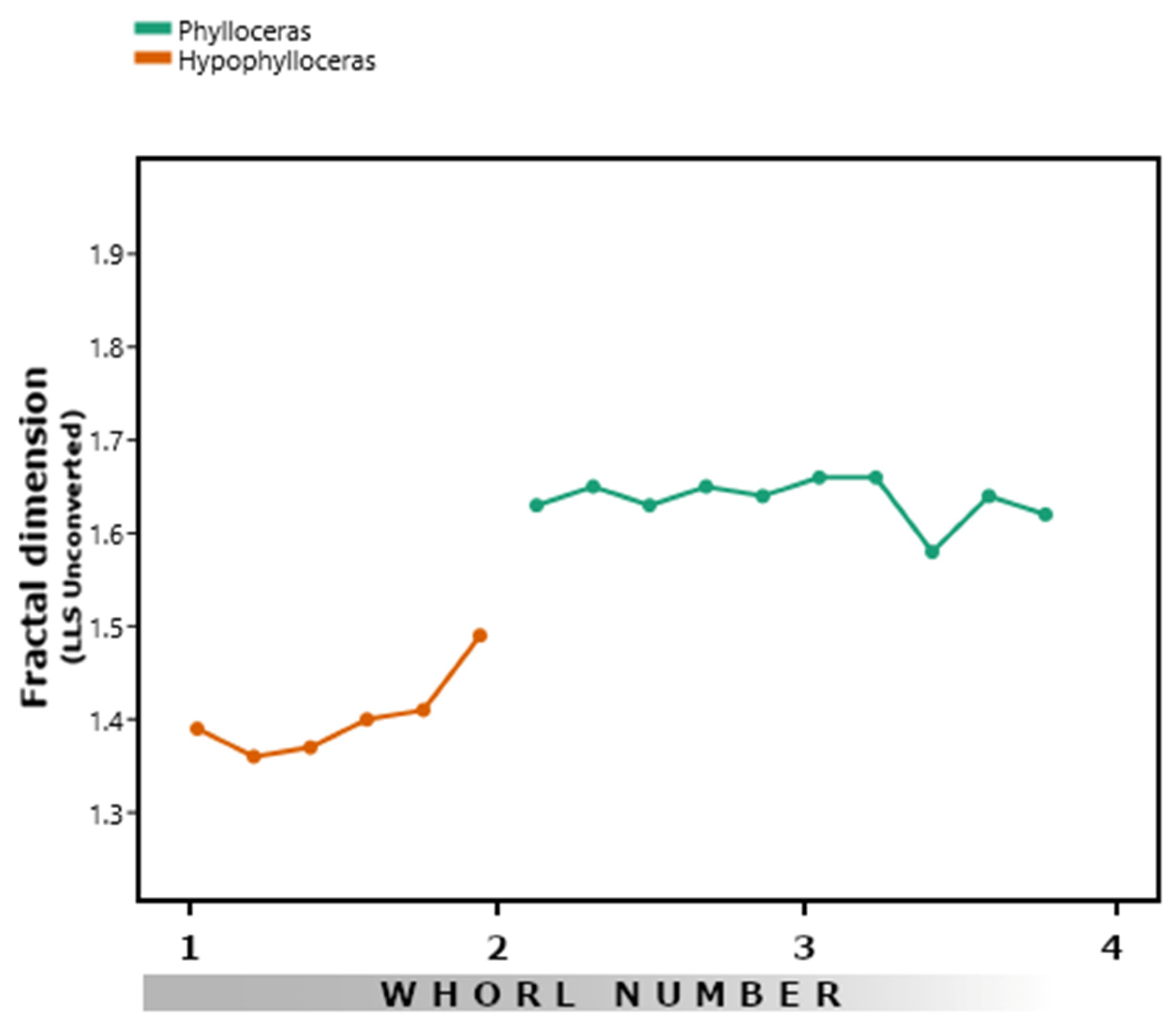
3.4. Phylloceratids
4. Conclusions
4.1. Discussion
4.2. Implication for the Formation Mechanism of Sutures
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schindewolf, O. On development, evolution, and terminology of ammonoid suture line. Bull. Mus. Comp. Zool. Harv. Coll. 1953, 112, 217–237. [Google Scholar]
- Schindewolf, O. Studien zur Stammesgeschichte der Ammoniten. Lief 1. Ash. Akad. Wiss. Lit. Mainz Math.-Nat. Kl 1960, 10, 639–743. [Google Scholar]
- Schindewolf, O. Studien zur Stammesgeschichte der Ammoniten. Lief 3. Ash. Akad. Wiss. Lit. Mainz Math.-Nat. Kl 1965, 13, 139–238. [Google Scholar]
- Schlegelmilch, R. Die Ammoniten des Suddeutschen Lias; Gustav Fischer Verlag: Jena, Germany, 1976. [Google Scholar]
- Schlegelmilch, R. Die Ammoniten des Suddeutschen Doggers; Gustav Fischer Verlag: Jena, Germany, 1985. [Google Scholar]
- Schlegelmilch, R. Die Ammoniten des Suddeutschen Malms; Gustav Fischer Verlag: Jena, Germany, 1994. [Google Scholar]
- Mandelbrot, B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- García-Ruiz, J.; Checa, A.; Rivas, P. On the origin of ammonite sutures. Paleobiology 1990, 16, 349–354. [Google Scholar] [CrossRef]
- Lutz, T.; Boyajian, G. Fractal Geometry of Ammonoid Sutures. Paleobiology 1995, 21, 329–342. [Google Scholar] [CrossRef]
- Hoffmann, R.; Maisch, M. Systematics and phylogenetic position of the lytoceratid ammonite genus Holcolytoceras Spath, 1924 (Cephalopoda, Ammonoidea) from the Lower Pliensbachian of Europe. Neues Jahrb. Geol. Paläontol. 2018, 288, 173–182. [Google Scholar] [CrossRef]
- Marriott, K.; Chamberlain, J.A., Jr. Uses for Incomplete Ammonite Sutures: Lateral Lobe and Second Saddle as Markers of Sutural Complexity. Geosciences 2021, 11, 476. [Google Scholar] [CrossRef]
- Yacobucci, M.M.; Manship, L.L. Ammonoid Septal Formation and Suture Asymmetry Explored with a Geographic Information Systems Approach. Palaeontologia Electronica. 2011. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.452.6924&rep=rep1&type=pdf (accessed on 4 January 2022).
- Pérez-Claros, J.; Palmqvist, P.; Oloriz, F. First and second orders of suture complexity in ammonites: A new methodological approach using fractal analysis. Math. Geol. 2002, 34, 323–332. [Google Scholar] [CrossRef]
- Oloriz, F.; Palmqvist, P.; Perez-Claros, J.A. Shell features, main colonized environments, and fractal analysis of 374 sutures in Late Jurassic ammonites. Lethaia 2007, 30, 191–204. [Google Scholar] [CrossRef]
- Pérez-Claros, J.; Olóriz, F.; Palmqvist, P. Sutural complexity in Late Jurassic ammonites and its relationship with phragmocone size and shape: A multidimensional approach using fractal analysis. Lethaia 2007, 40, 253–272. [Google Scholar] [CrossRef]
- Saunders, W.B. The ammonoid suture problem: Relationships between shell and septum thickness and suture complexity in Paleozoic ammonoids. Paleobiology 1995, 21, 343–355. [Google Scholar] [CrossRef]
- Saunders, W.B.; Work, D.M. Shell morphology and suture complexity in Upper Carboniferous ammonoids. Paleobiology 1996, 22, 189–218. [Google Scholar] [CrossRef]
- Fractal Dimension Estimator. The Fractal Lab-Fractal Geometry in Medicine and Biology-Virtual Laboratory. (n.d.). Available online: http://fractal-lab.org/Downloads/FDEstimator.html (accessed on 20 December 2021.).
- Hammer, Ø.; Harper, D.A.T.; Ryan, P.D. PAST: Paleontological Statistics Software Package for Education and Data Analysis. Palaeontol. Electron. 2001, 4, 9. [Google Scholar]
- Peterman, D.J.; Barton, C.C. Power scaling of ammonitic suture patterns from Cretaceous Ancyloceratina: Constraints on septal/sutural complexity. Lethaia 2019, 52, 77–90. [Google Scholar] [CrossRef] [Green Version]
- García-Ruiz, J.M.; Checa, A. A model for the morphogenesis of ammonoid septal sutures. Geobios 1993, 26, 157–162. [Google Scholar] [CrossRef]
- Hoffmann, R. New insights on the phylogeny of the Lytoceratoidea (ammonitina) from the septal lobe and its functional interpretation. Revue Paleobiol. 2010, 29, 1–156. [Google Scholar]
- Shevyrev, A.A. The development of the suture line in Mesozoic ammonoids and the terminology of its elements. Int. Geol. Rev. 1963, 5, 1659–1669. [Google Scholar] [CrossRef]
- Khiami, N.M.; Murphy, M.A. Ontogenetic Study of Phylloceras (Hypophylloceras) onoense, Holcophylloceras aldersoni, and Phyllopachyceras theresae, Lower Cretaceous Phylloceratina (Ammonoidea) of California. J. Paleontol. 1988, 62, 587–598. [Google Scholar]
- Mikhailov, N.P.; Gustomenov, V.A. Boreal Late Jurassic Cephalopods; Academy of Sciences of the USSR, Geological Institute, Transactions: Moscow, Russia, 1964. [Google Scholar]
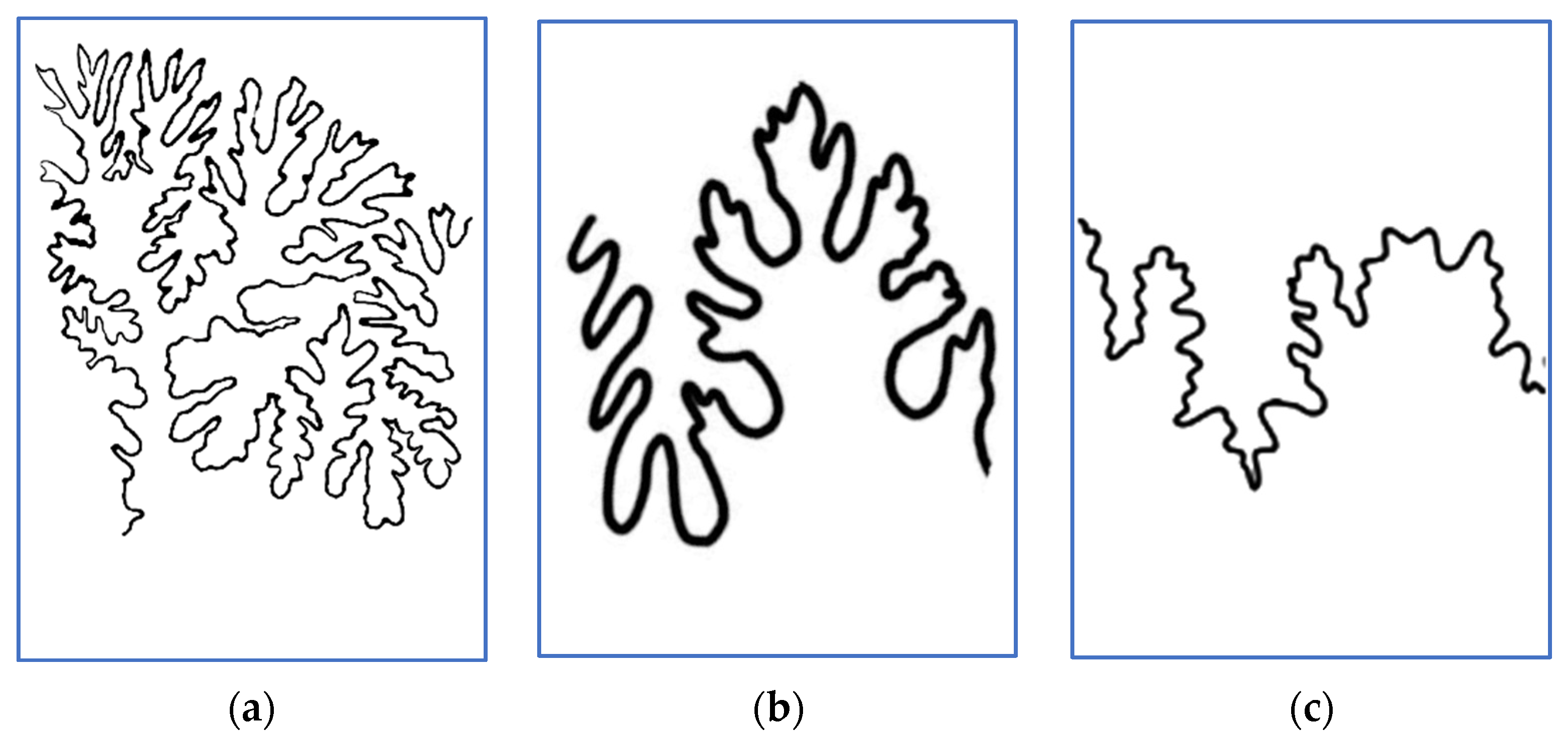

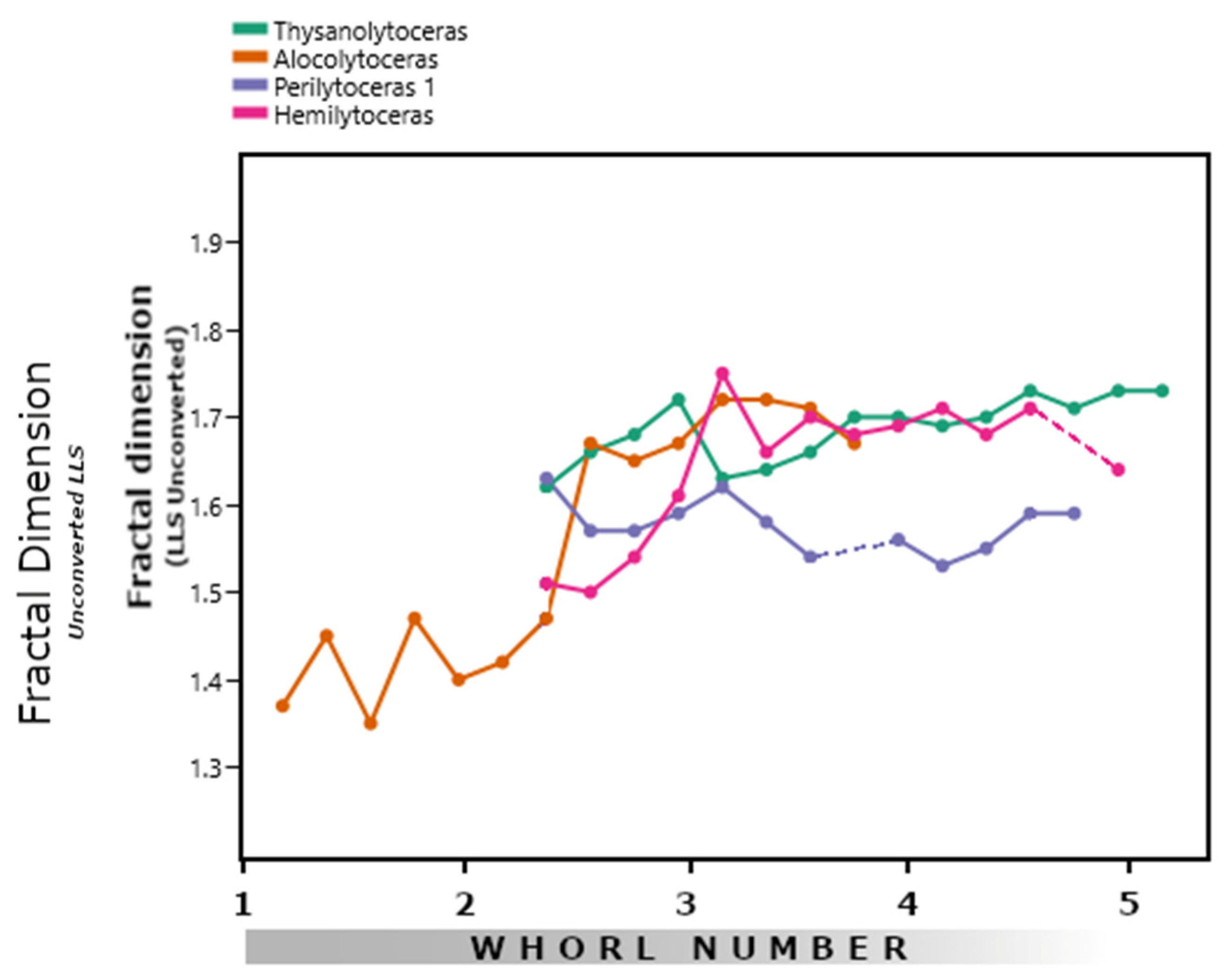
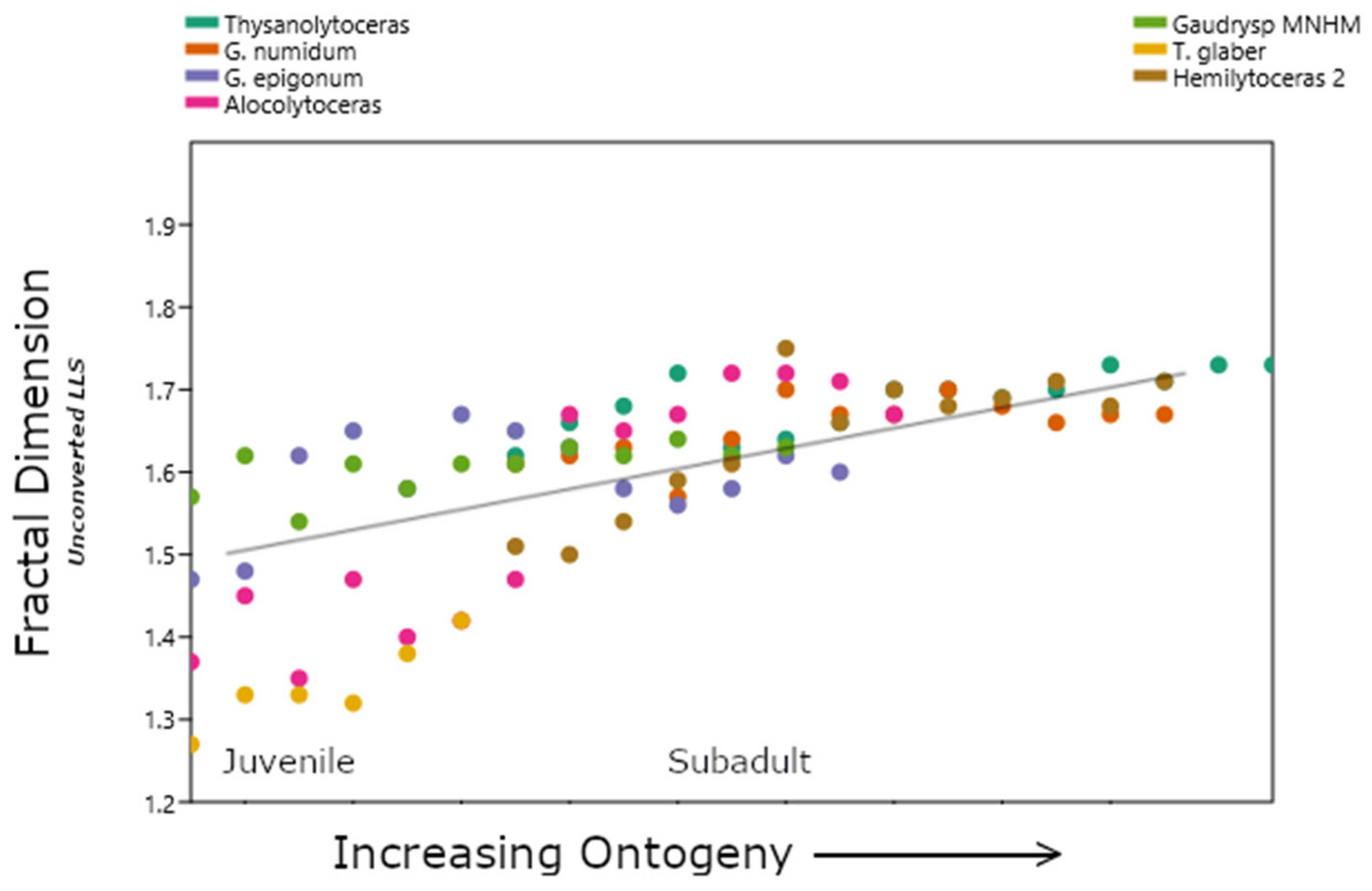
| Genus | Average Df | LLS V | S2U3 V | V′ to V |
|---|---|---|---|---|
| Hildoceras | 1.227 | 1.4 | 1 | ×1.1 |
| Harpoceras | 1.299 | 1.144 | 1 | N/A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marriott, K.; Olson, S.; Balassa, D.; Cleaveland, C.; Watmore, K.I.; LaVine, R.J.; Olson, R.; Prothero, D.R. Ontogenetic Trends of Sutural Complexity in Jurassic Ammonites. Geosciences 2022, 12, 66. https://doi.org/10.3390/geosciences12020066
Marriott K, Olson S, Balassa D, Cleaveland C, Watmore KI, LaVine RJ, Olson R, Prothero DR. Ontogenetic Trends of Sutural Complexity in Jurassic Ammonites. Geosciences. 2022; 12(2):66. https://doi.org/10.3390/geosciences12020066
Chicago/Turabian StyleMarriott, Katherine, Sara Olson, Daniella Balassa, Casey Cleaveland, Kristin I. Watmore, Rhiannon J. LaVine, Robert Olson, and Donald R. Prothero. 2022. "Ontogenetic Trends of Sutural Complexity in Jurassic Ammonites" Geosciences 12, no. 2: 66. https://doi.org/10.3390/geosciences12020066
APA StyleMarriott, K., Olson, S., Balassa, D., Cleaveland, C., Watmore, K. I., LaVine, R. J., Olson, R., & Prothero, D. R. (2022). Ontogenetic Trends of Sutural Complexity in Jurassic Ammonites. Geosciences, 12(2), 66. https://doi.org/10.3390/geosciences12020066