Behavior of Shallow Circular Tunnels—Impact of the Soil Spatial Variability
Abstract
1. Introduction
2. Random Fields and Discretization
- -
- -
3. Numerical Modeling
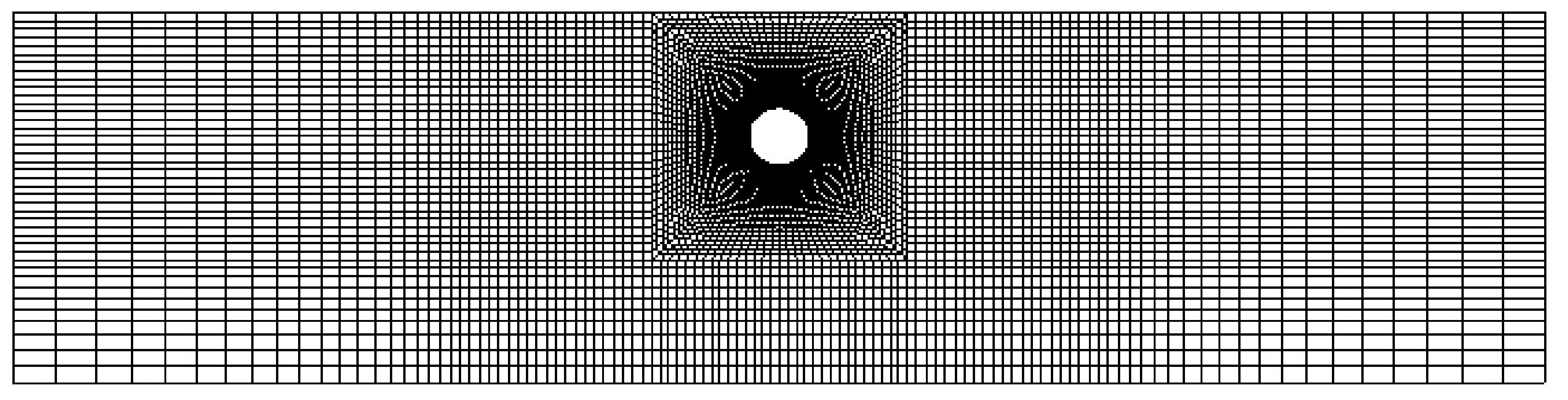
3.1. Geometry and Parameters
- Rf: the failure rate which is constant and lower than 1,
- φf: the ultimate friction angle,
- β: a calibration factor,
- m: a constant (m < 1).
- Phase 0: Initial state of stress (σ0). Considering the gravity effect and the coefficient at rest, the initial state of stresses is calculated.
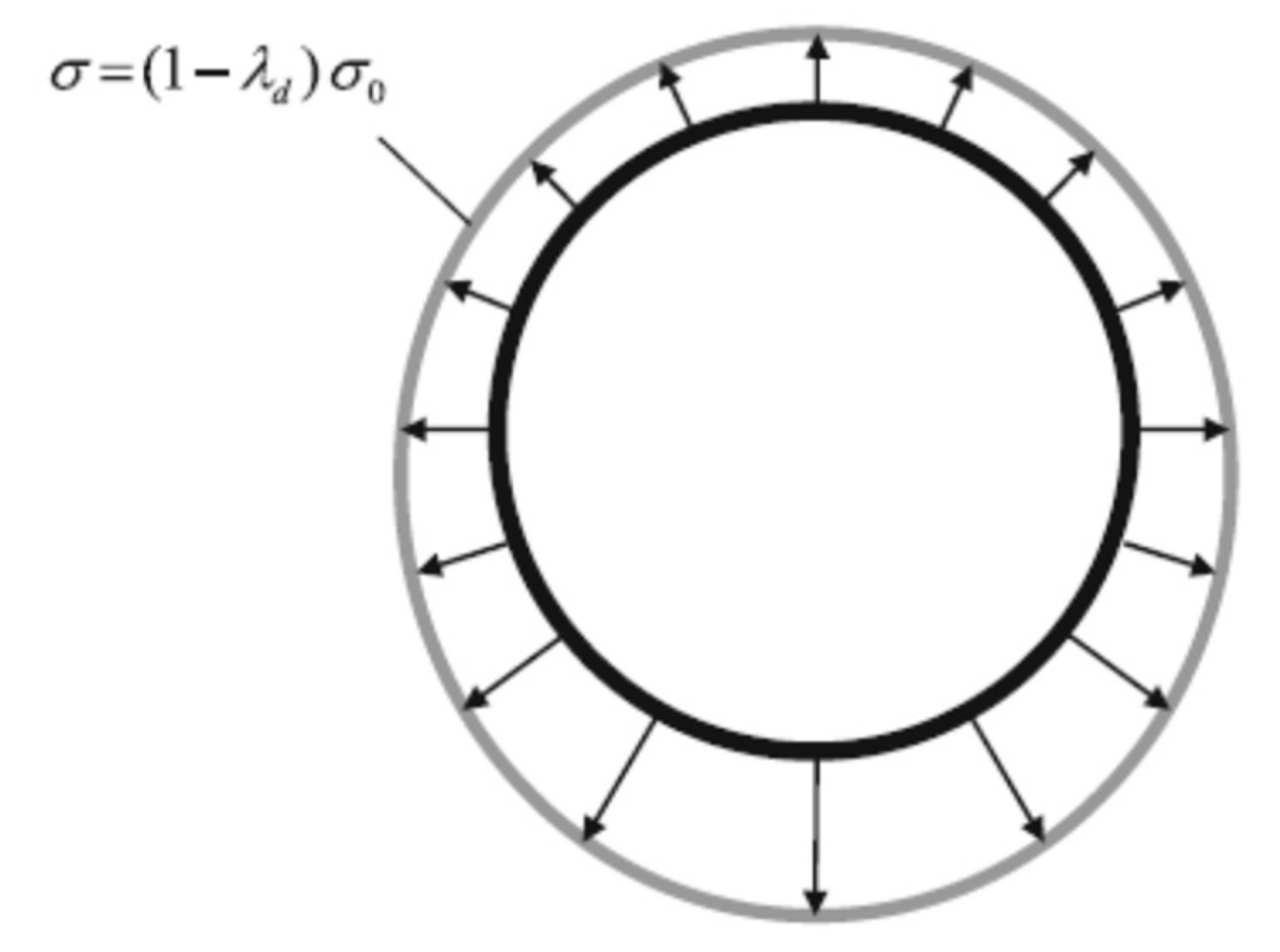
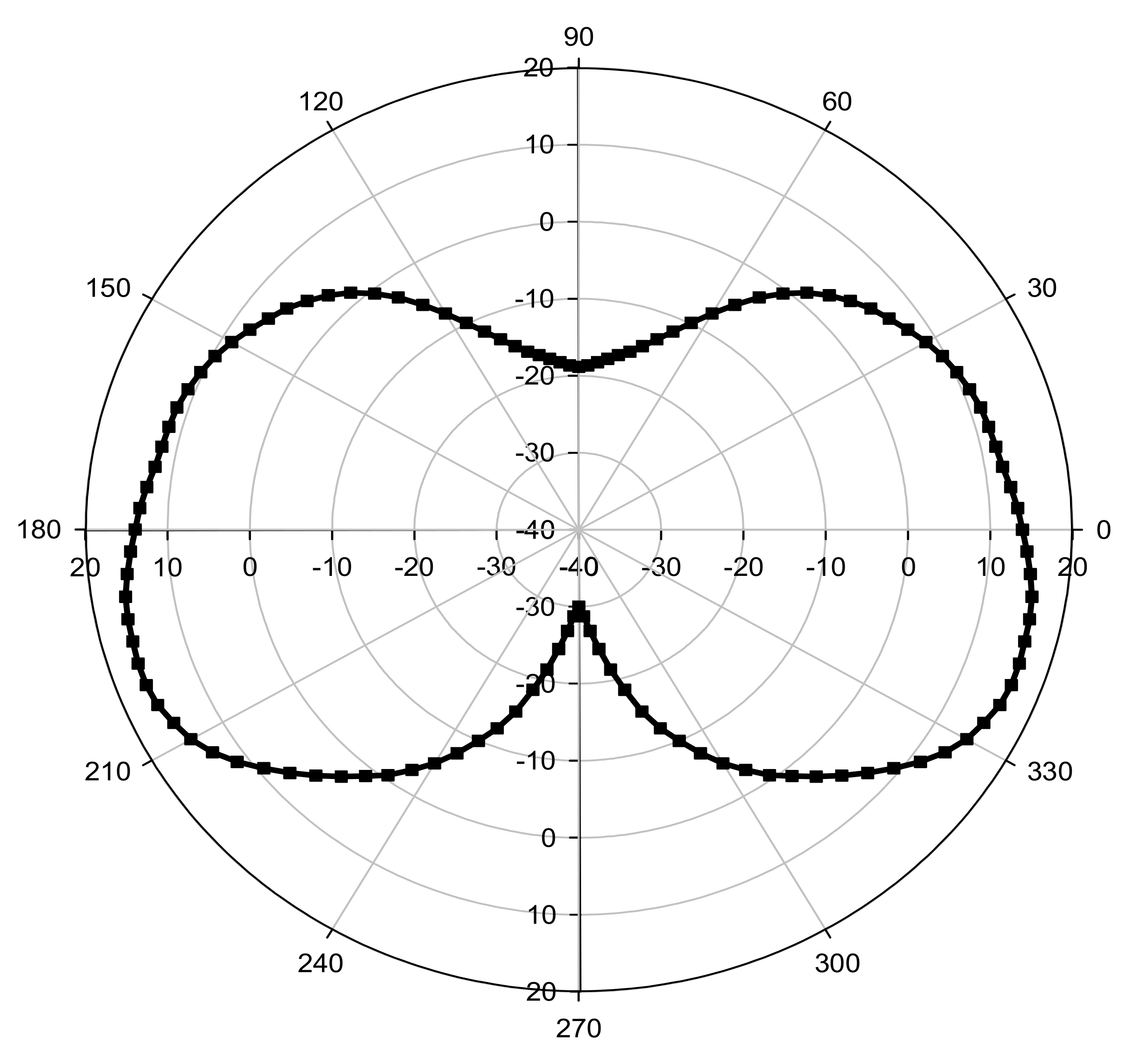
- Phase 1: Stress release phase. The excavated soil inside the tunnel is deactivated and a radial pressure to the tunnel wall is applied. The value of this pressure is done by using Equation (10). This pressure is not constant over the circumference of the tunnel and depends on the initial stresses state (Figure 3).where λd: the stress relaxation ratio; σ0: the initial soil stresses (kN/m2); σ: the applied radial pressure (kN/m2). A gradual reduction of this radial pressure is applied to the excavation circumference until its value reaches the specified stress relaxation λd. In this study, the coefficient λd is taken equal to 0.65. This value was obtained by a previous analysis in 3D calculations by [43].σ = (1 − λd) σ0
- Phase 2: Installation of the tunnel lining. The lining is activated around the tunnel wall considering its total relaxation (λd = 1).
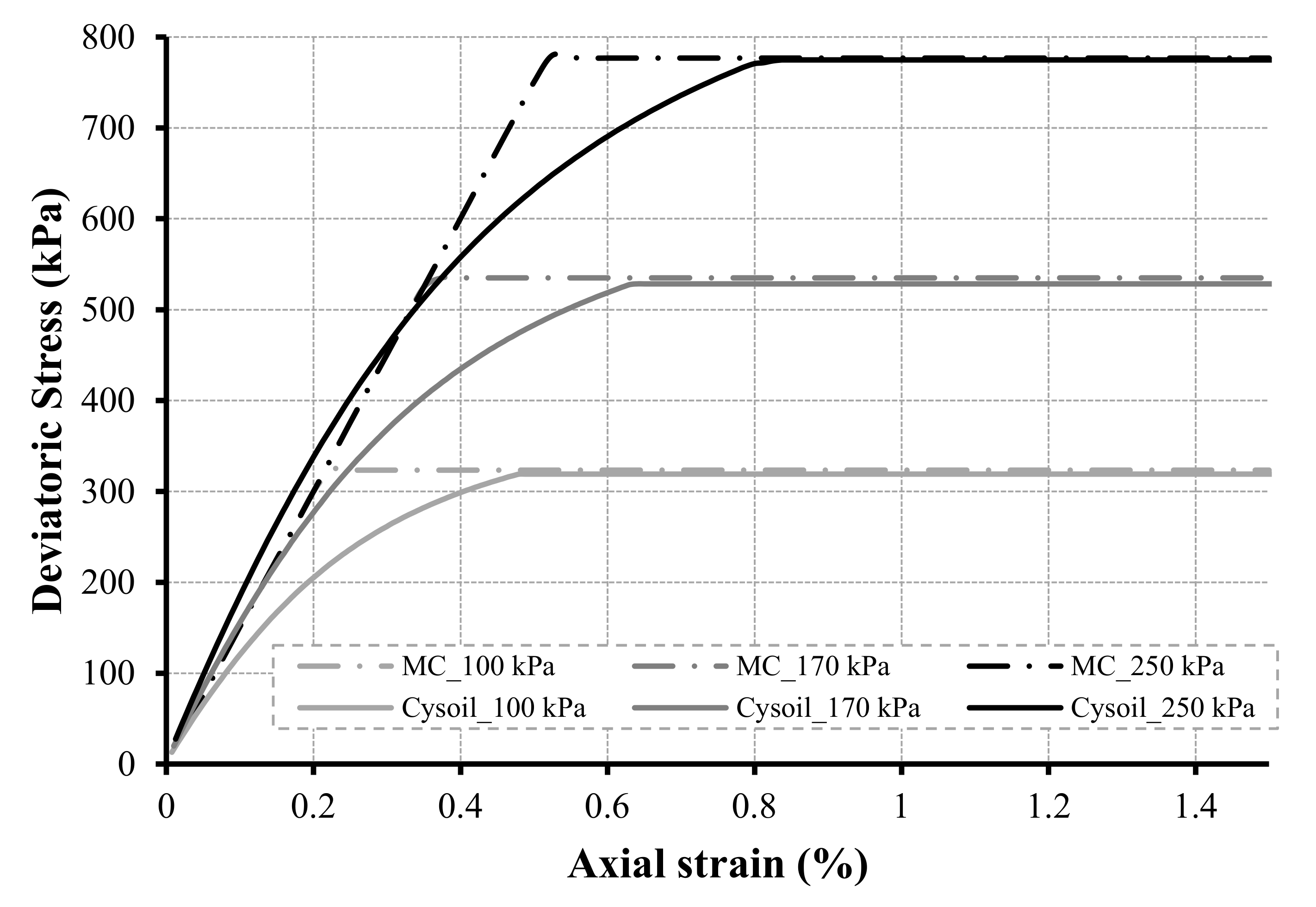
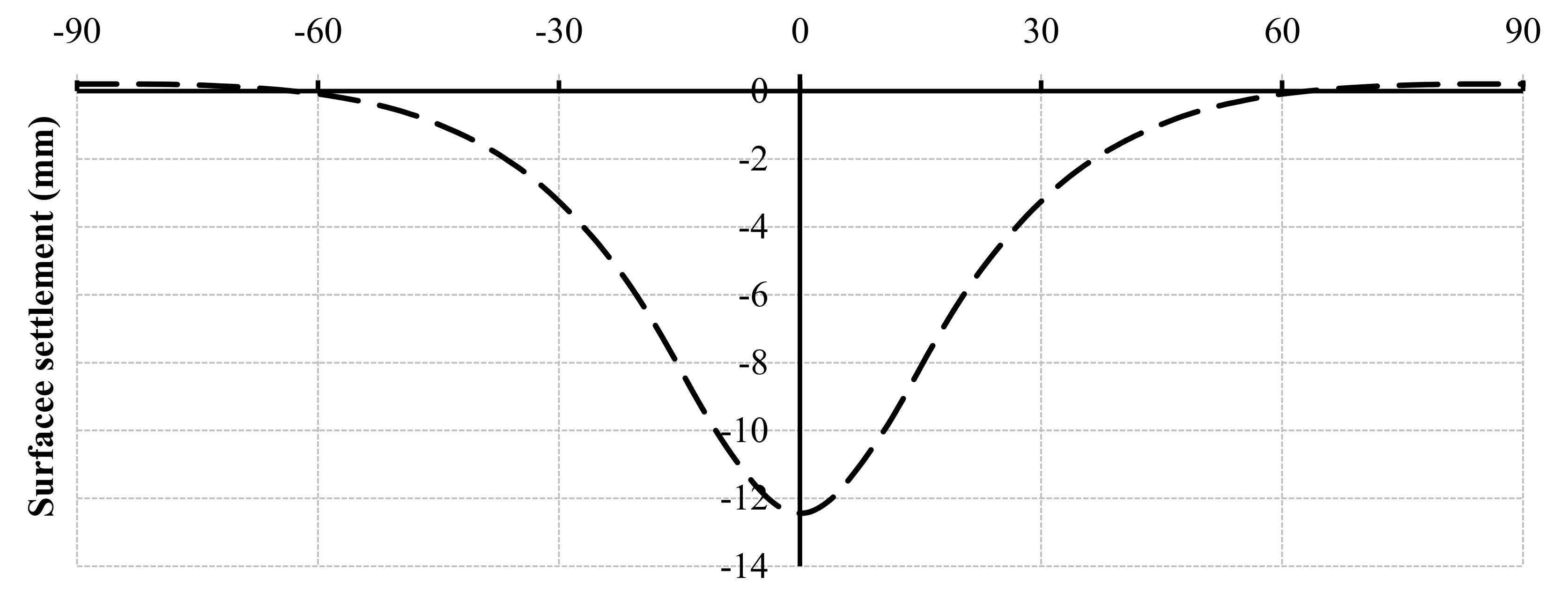
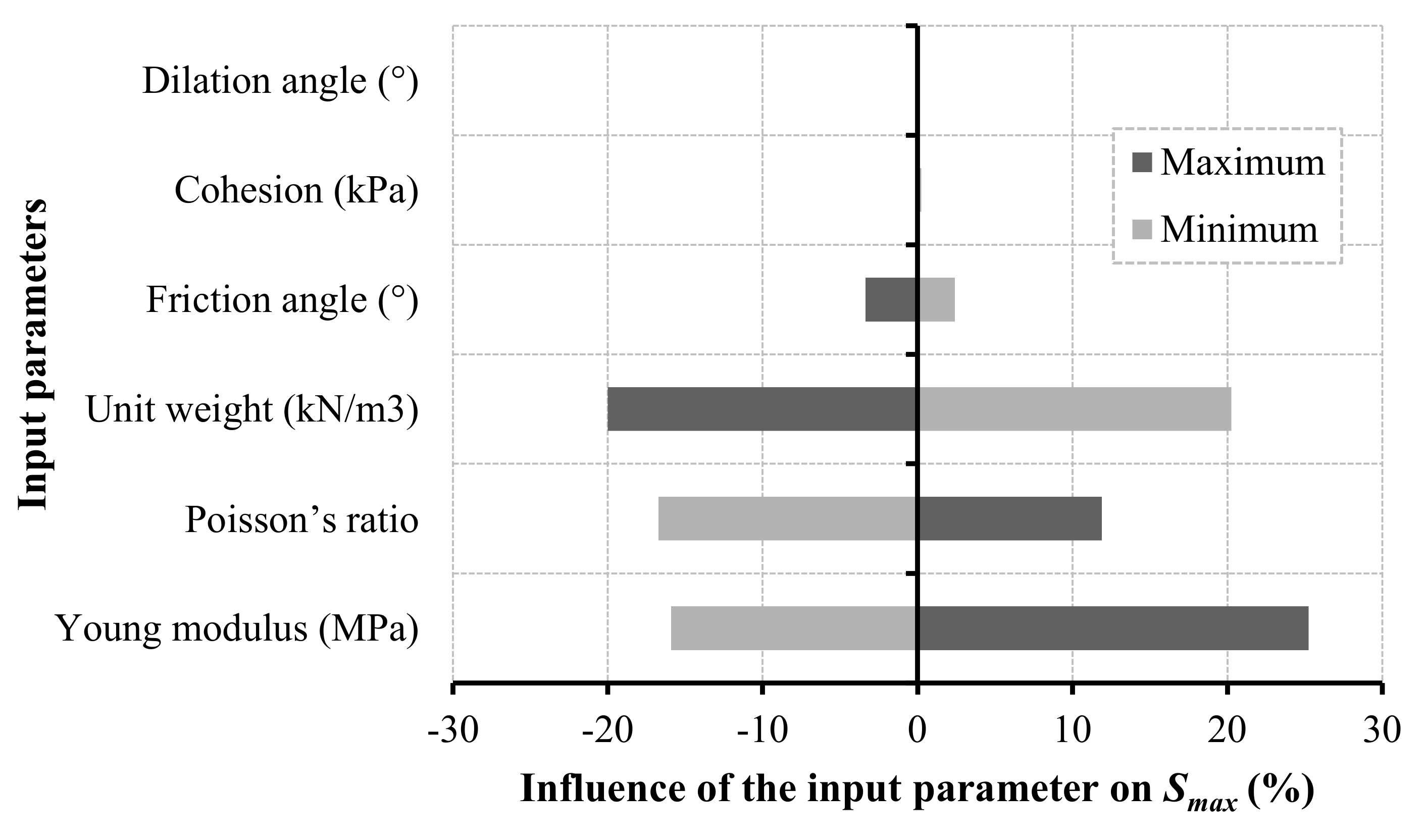
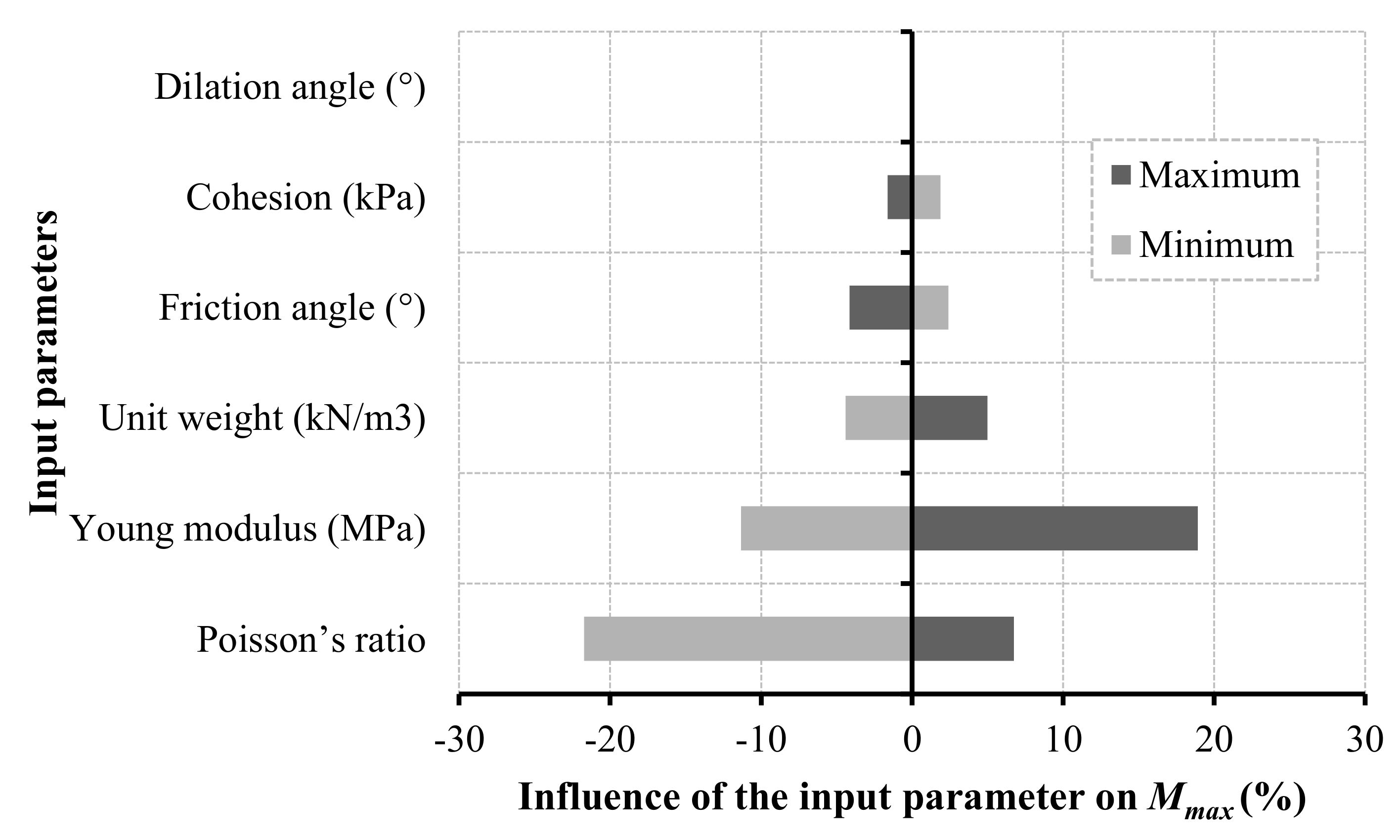
3.2. Deterministic and Sensitivity Analysis Results
4. Probabilistic Analysis Using the Monte Carlo Simulations
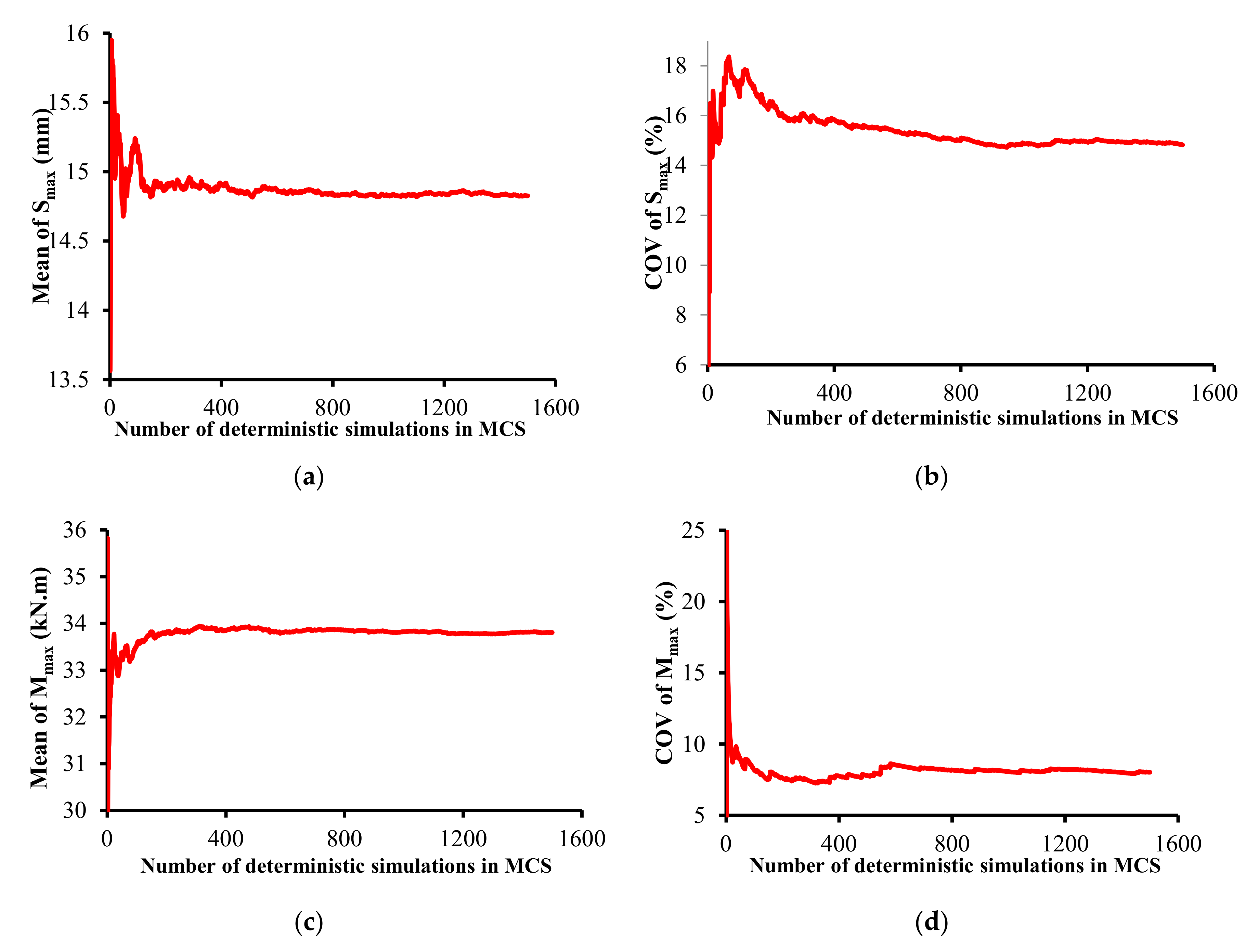
4.1. Selection of the Optimal Number of Monte Carlo Simulations
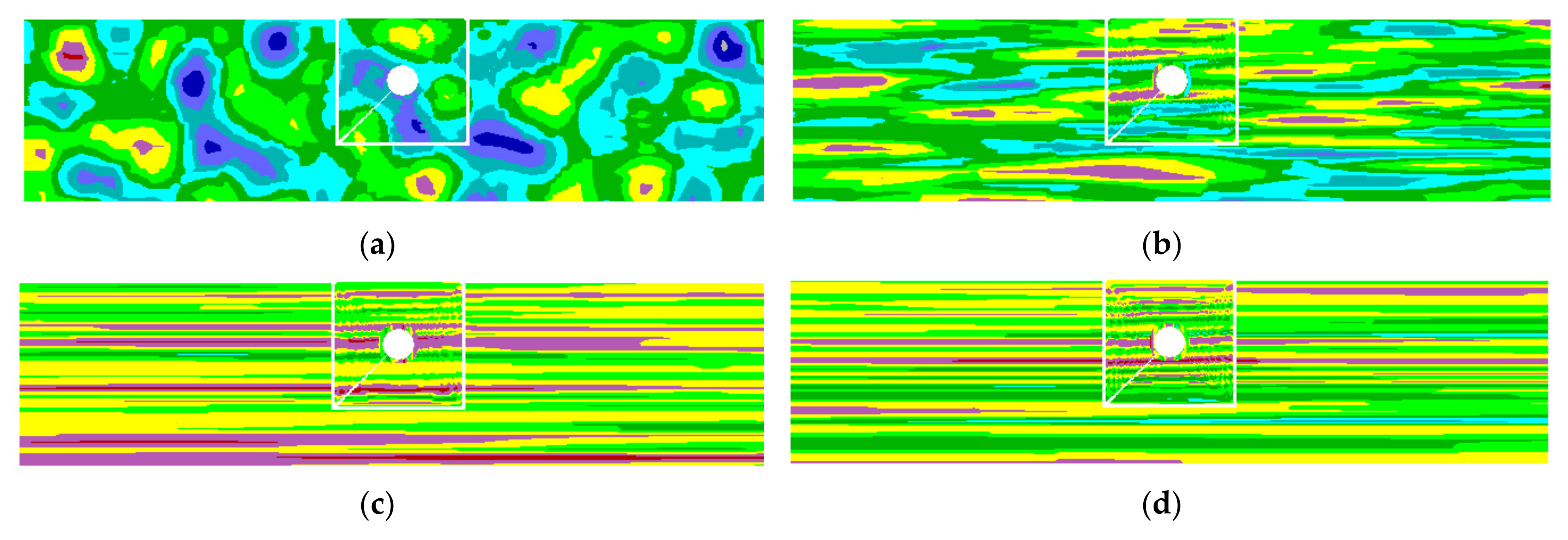
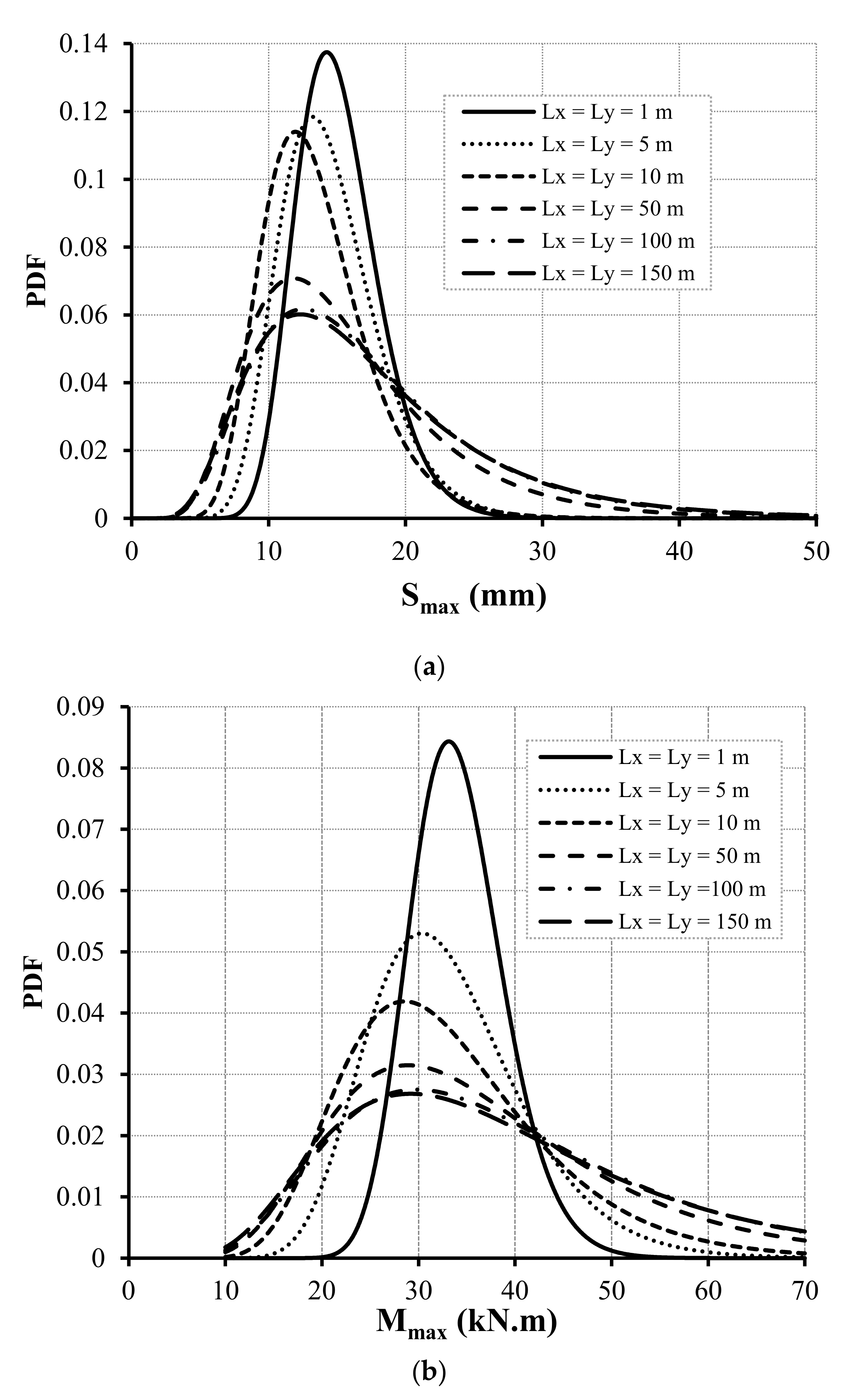
4.2. Influence of Isotropic and Anisotropic Random Fields on Smax and Mmax
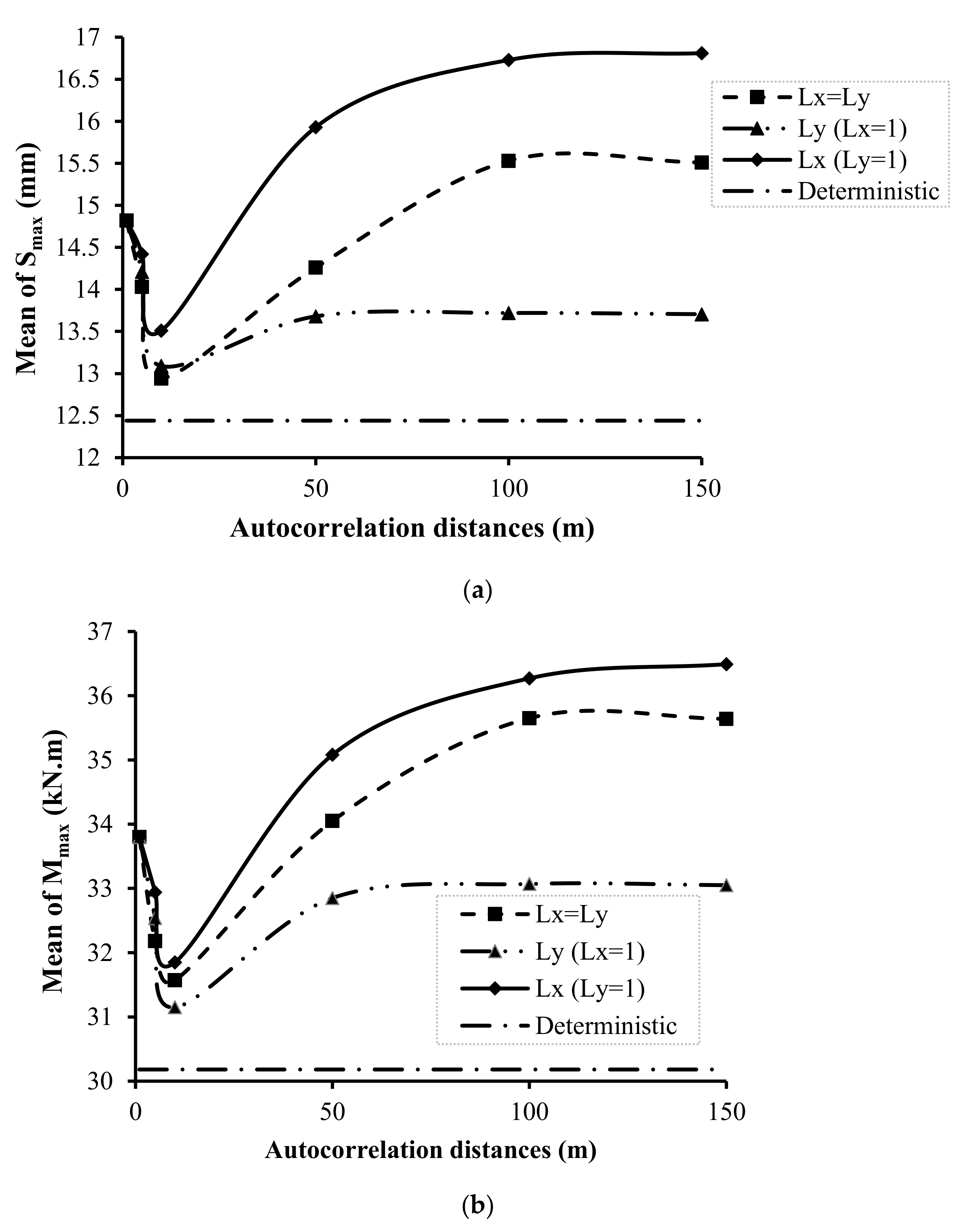
4.3. Soil Spatial Variability Effect on the Average of Smax and Mmax
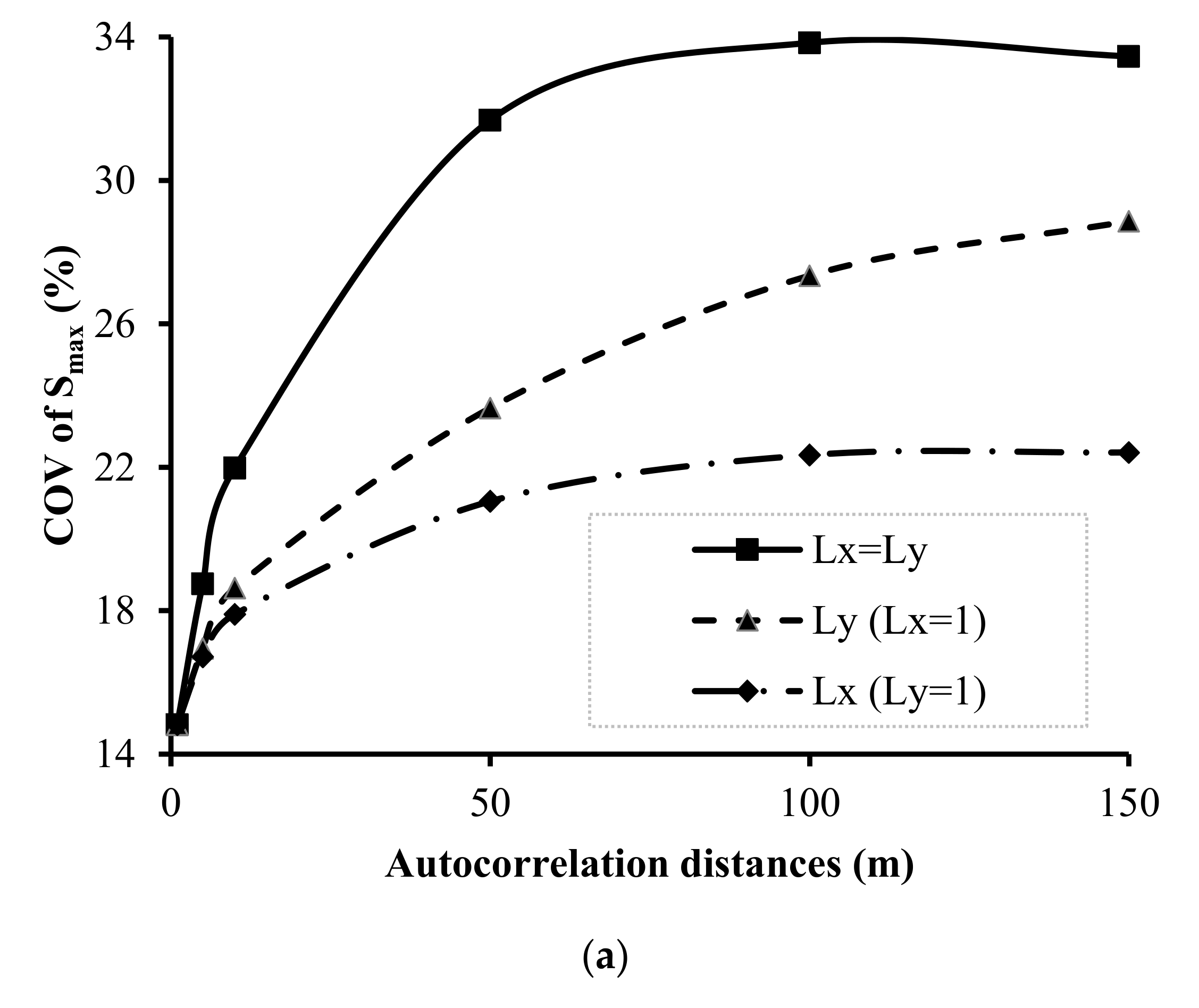
4.4. Effect of the Soil Spatial Variability on the Variance of Smax and Mmax
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Griffiths DV Fenton, G.A. Bearing capacity of spatially random soil: The undrained clay Prandtl problem revisited. Geotechnique 2001, 51, 351–359. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A.; Manoharan, N. Bearing capacity of rough rigid strip footing on cohesive soil: Probabilistic study. J. Geotech. Geoenviron. Eng. 2002, 128, 743–755. [Google Scholar] [CrossRef]
- Fenton, G.A.; Griffiths, D.V. Bearing capacity prediction of spatially random c-φ soils. Can. Geotech. J. 2003, 40, 54–65. [Google Scholar] [CrossRef]
- Popescu, R.; Deodatis, G.; Nobahar, A. Effects of random heterogeneity of soil properties on bearing capacity. Probabilistic Eng. Mech. 2005, 20, 324–341. [Google Scholar] [CrossRef]
- Ahmed ASoubra, A.H. Extension of subset simulation approach for uncertainty propagation and global sensitivity analysis. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2012, 6, 162–176. [Google Scholar] [CrossRef][Green Version]
- Al-Bittar, T.; Soubra, A.H. Bearing capacity of strip footing on spatially random soils using sparse polynomial chaos expansion. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2039–2060. [Google Scholar] [CrossRef]
- Gheris, A.; Hamrouni, A. Treatment of an expansive soil using vegetable (DISS) fibre. Innov. Infrastruct. Solut. 2020, 5, 34. [Google Scholar] [CrossRef]
- Hamrouni, A.; Dias, D.; Sbartai, B. Probabilistic analysis of a piled earth platform under a concrete floor slab. Soils Found. 2017, 57, 828–839. [Google Scholar] [CrossRef]
- Hamrouni, A.; Dias, D.; Sbartai, B. Reliability analysis of a mechanically stabilized earth wall using the surface response methodology optimized by a genetic algorithm. Geomech. Eng. 2018, 15, 937–945. [Google Scholar]
- Pan QDias, D. Sliced inverse regression-based sparse polynomial chaos expansion for reliability analysis in high dimensions. Reliab. Eng. Syst. Saf. 2017, 167, 484–493. [Google Scholar]
- Guo, X.; Dias, D.; Carvajal, C.; Peyras, L.; Breul, P.A. Comparative study of different reliability methods for high dimensional stochastic problems related to earth dam stability analyses. Eng. Struct. 2019, 188, 591–602. [Google Scholar] [CrossRef]
- Guo, X.; Du, D.; Dias, D. Reliability analysis of tunnel lining considering soil spatial variability. Eng. Struct. 2019, 196, 109332. [Google Scholar] [CrossRef]
- Hamrouni, A.; Dias, D.; Sbartai, B. Soil spatial variability impact on the behaviour of a reinforced earth wall. Front. Struct. Civ. Eng. 2020, 15, 518–531. [Google Scholar] [CrossRef]
- Hamrouni, A.; Sbartai, B.; Dias, D. Ultimate dynamic bearing capacity of shallow strip foundations—Reliability analysis using the response surface methodology. Soil Dyn. Earthq. Eng. 2021, 144, 106690. [Google Scholar] [CrossRef]
- Guo, X.; Sun, Q.; Dias, D.; Antoinet, E. Probabilistic assessment of an earth dam stability design using the adaptive polynomial chaos expansion. Bull. Eng. Geol. Environ. 2020, 79, 4639–4655. [Google Scholar] [CrossRef]
- Guo, X.; Dias, D. Kriging based reliability and sensitivity analysis—Application to the stability of an earth dam. Comput. Geotech. 2020, 120, 103411. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.-H. Probabilistic Analysis of Pressurized Tunnels against Face Stability Using Collocation-Based Stochastic Response Surface Method. J. Geotech. Geoenviron. Eng. 2011, 137, 385–397. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.-H. Probabilistic Analysis and Design of Circular Tunnels against Face Stability. Int. J. Geéomeéch. 2009, 9, 237–249. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A.-H. Probabilistic Analysis of Circular Tunnels in Homogeneous Soil Using Response Surface Methodology. J. Geotech. Geoenviron. Eng. 2009, 135, 1314–1325. [Google Scholar] [CrossRef]
- Hamrouni, A.; Dias, D.; Sbartai, B. Reliability analysis of shallow tunnels using the response surface methodology. Undergr. Space 2017, 2, 246–258. [Google Scholar] [CrossRef]
- Hamrouni, A.; Dias, D.; Sbartai, B. Probability analysis of shallow circular tunnels in homogeneous soil using the surface response methodology optimized by a genetic algorithm. Tunn. Undergr. Space Technol. 2019, 86, 22–33. [Google Scholar] [CrossRef]
- Mollon, M.G.; Phoon, K.-K.; Dias, D.; Soubra, A.-H. Influence of the Scale of Fluctuation of the Friction Angle on the Face Stability of a Pressurized Tunnel in Sands. In Proceedings of the GeoRisk 2011, Atlanta, GA, USA, 26–28 June 2011; pp. 225–232. [Google Scholar]
- Mollon, G.; Phoon, K.-K.; Dias, D.; Soubra, A.-H. Validation of a New 2D Failure Mechanism for the Stability Analysis of a Pressurized Tunnel Face in a Spatially Varying Sand. J. Eng. Mech. 2011, 137, 8–21. [Google Scholar] [CrossRef]
- Huang, H.W.; Xiao, L.; Zhang, D.M.; Zhang, J. Influence of spatial variability of soil Young’s modulus on tunnel convergence in soft soils. Eng. Geol. 2017, 228, 357–370. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, J.; Li, J. Probabilistic Analysis of Ground Movements Caused by Tunneling in a Spatially Variable Soil. Int. J. Geéomeéch. 2019, 19, 04019125. [Google Scholar] [CrossRef]
- Kroetz, H.M.; Do, N.A.; Dias, D.; Beck, A.T. Reliability of tunnel lining design using the hyperstatic reaction method. Tunn. Undergr. Space Technol. 2018, 77, 59–67. [Google Scholar] [CrossRef]
- Hejazi, Y.; Dias, D.; Kastner, R. Impact of constitutive models on the numerical analysis of underground constructions. Acta Geotech. 2008, 3, 251–258. [Google Scholar] [CrossRef]
- Spanos, P.D.; Ghanem, R. Stochastic Finite Element Expansion for Random Media. J. Eng. Mech. 1989, 115, 1035–1053. [Google Scholar] [CrossRef]
- Sahraoui, Y.; Chateauneuf, A. The effects of spatial variability of the aggressiveness of soil on system reliability of corroding underground pipelines. Int. J. Press. Vessel. Pip. 2016, 146, 188–197. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Rafiee, R.; Zhuang, X.; Lahmer, T.; Rabczuk, T. Uncertainty quantification for multiscale modeling of polymer nanocomposites with correlated parameters. Compos. Part B Eng. 2015, 68, 446–464. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Zhuang, X.; Nguyen-Thoi, T.; Rabczuk, T. A software framework for probabilistic sensitivity analysis for computationally expensive models. Adv. Eng. Softw. 2016, 100, 19–31. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: New York, NY, USA, 1991. [Google Scholar]
- Cho, S.E. Effects of spatial variability of soil properties on slope stability. Eng. Geol. 2007, 92, 97–109. [Google Scholar] [CrossRef]
- Cho, S.E.; Park, H.C. Effect of spatial variability of cross-correlated soil properties on bearing capacity of strip footing. Int. J. Numer. Anal. Methods Geéomeéch. 2010, 34, 1–26. [Google Scholar] [CrossRef]
- Sudret, B.; Berveiller, M. Stochastic finite element methods in geotechnical engineering. In Reliability-Based Design in Geotechnical Engineering: Computations and Applications; Phoon, K.K., Ed.; Taylor & Francis: Oxford, UK, 2008; p. 260296. [Google Scholar]
- Der Kiureghian, A.; Ke, J.B. The stochastic finite element method in structural reliability. Probabilistic Eng. Mech. 1988, 3, 83–91. [Google Scholar] [CrossRef]
- Shinozuka, M.; Dasgupta, G. Stochastic fields and their digital simulation. In Stochastic Methods in Structural Dynamics; Schueller, G.I., Shinozuka, M., Eds.; Martinus Nijhoff Publishers: Boston, MA, USA, 1987; pp. 93–133. [Google Scholar]
- Deodatis, G. Stochastic FEM sensitivity analysis of nonlinear dynamic problems. Probabilistic Eng. Mech. 1989, 4, 135–141. [Google Scholar] [CrossRef]
- Vanmarcke, E. Probabilistic modeling of soil profiles. J. Geotech. Eng. ASCE 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Vanmarcke, E. Random Fields: Analysis and Synthesis; MIT Press: Cambridge, UK, 1983; 382p. [Google Scholar]
- Popescu, R. Stochastic Variability of soil Properties: Data Analysis, Digital Simulation, Effects on System Behavior. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 1995. [Google Scholar]
- Croce, A. Analisi Dati di Monitoraggio del Rivestimento della Galleria del Passante Ferroviario di Bologna. Degree Dissertation, Polytechnics of Torino, Torino, Italy, 2011. [Google Scholar]
- Do, N.A.; Dias, D.; Oreste, P.P.; Djeran-Maigre, I. 2D tunnel numerical investigation - the influence of the simplified excavation method on tunnel behaviour. Geotech. Geol. Eng. 2014, 32, 43–58. [Google Scholar] [CrossRef]
- Itasca Consulting Group. FLAC fast Lagrangian Analysis of Continua, Version 7. User’s Manual. FLAC fast Lagrangian Analysis of Continua, Version 7. User’s Manual.; Itasca Consulting Group: Minneapolis, MN, USA, 2011. [Google Scholar]
- Deghoul, L.; Gabi, S.; Hamrouni, A. The influence of the soil constitutive models on the seismic analysis of pile-supported wharf structures with batter piles in cut-slope rock dike. Stud. Geotech. Et Mech. 2020, 42, 191–209. [Google Scholar] [CrossRef]
- Massih, D.S.Y.A.; Soubra, A.-H. Reliability-Based Analysis of Strip Footings Using Response Surface Methodology. Int. J. Geomech. 2008, 8, 134–143. [Google Scholar] [CrossRef]
- Low, B.K.; Tang, W.H. Efficient Reliability Evaluation Using Spreadsheet. J. Eng. Mech. 1997, 123, 749–752. [Google Scholar] [CrossRef]
- Low, B.K.; Tang, W.H. Reliability analysis of reinforced embankments on soft ground. Can. Geotech. J. 1997, 34, 672–685. [Google Scholar] [CrossRef]


| MC Model | Value | CYsoil Model | Value |
|---|---|---|---|
| E (Young’s modulus) (MPa) | 150 | Reference elastic tangent shear modulus (MPa) | 58 |
| ν (Poisson ratio) | 0.3 | Reference Elastic tangent bulk modulus (MPa) | 125 |
| φ (friction angle) (degrees) | 37 | Elastic tangent shear modulus | 98 |
| Ψ (dilation angle) (degrees) | 0 | Elastic tangent bulk modulus | 213 |
| C (cohesion) (kPa) | 5 | Reference effective pressure pref (kPa) | 100 |
| k0 (lateral earth pressure factor) | 0.5 | Failure ratio Rf | 0.90 |
| Density (kg/m3) | 1700 | Ultimate friction angle φf (degrees) | 37 |
| Calibration factor β | 2.35 | ||
| Cohesion (kPa) | 5 | ||
| M | Constant (m < 1) | 0.5 |
| Parameter | E (Young’s Modulus) (MPa) | ν (Poisson’s Ratio) | γ (Unit Weight) (kN/m3) |
|---|---|---|---|
| Tunnel Lining | 35000 | 0.2 | 25 |
| Parameters | Reference Value | Variation | |
|---|---|---|---|
| Min | Max | ||
| Young modulus (MPa) | 150 | 120 | 180 |
| Poisson’s ratio | 0.3 | 0.24 | 0.36 |
| Friction angle (°) | 37 | 29.6 | 44.4 |
| Cohesion (kPa) | 5 | 4 | 6 |
| Dilation angle (°) | 0 | 0 | 5 |
| Unit weight (kN/m3) | 17 | 13.6 | 20.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamrouni, A.; Dias, D.; Guo, X. Behavior of Shallow Circular Tunnels—Impact of the Soil Spatial Variability. Geosciences 2022, 12, 97. https://doi.org/10.3390/geosciences12020097
Hamrouni A, Dias D, Guo X. Behavior of Shallow Circular Tunnels—Impact of the Soil Spatial Variability. Geosciences. 2022; 12(2):97. https://doi.org/10.3390/geosciences12020097
Chicago/Turabian StyleHamrouni, Adam, Daniel Dias, and Xiangfeng Guo. 2022. "Behavior of Shallow Circular Tunnels—Impact of the Soil Spatial Variability" Geosciences 12, no. 2: 97. https://doi.org/10.3390/geosciences12020097
APA StyleHamrouni, A., Dias, D., & Guo, X. (2022). Behavior of Shallow Circular Tunnels—Impact of the Soil Spatial Variability. Geosciences, 12(2), 97. https://doi.org/10.3390/geosciences12020097








