Impacts on Protective Structures against Gravitational Mass Movements—Scaling from Model Tests to Real Events
Abstract
:1. Introduction
2. Model Tests for the Investigation of Dry Gravitational Mass Movements
2.1. Overview of Existing Model Tests
2.2. Model Test for This Work
2.3. Buckingham’s π Theorems and the Determination of Dimensionless Parameters
| Statistical Parameters | Value | Description |
|---|---|---|
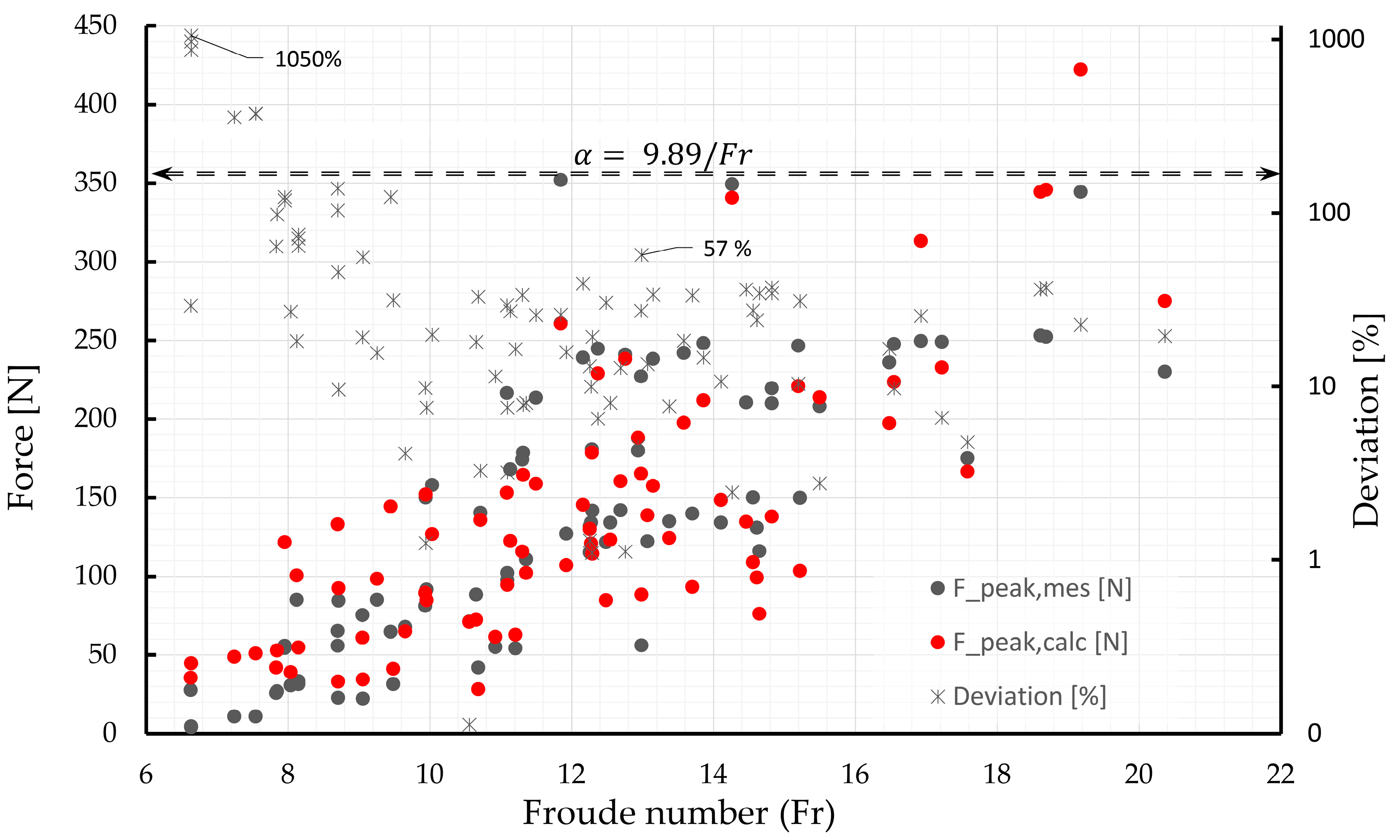
| Analyzed values | 86 | Number of model tests for the analysis of Fpeak,mes |
| Coefficient of determination | 0.93 | - |
| Intersection/Constraint point | 0/0 | [N] results in a Froude number Fr = 0 [–] |
| Coefficient X | 9.89 | |
| 2.5% Quantile of X | 9.31 | |
| 97.5% Quantile of X | 10.46 |
3. Dimensional Analysis
3.1. Base Quantities
- Length–Mass–Time [L-M-T].
3.2. Similarity Laws
3.2.1. Geometric Similarity
3.2.2. Dynamic Similarity
3.2.3. Kinematic Similarity
3.3. Model Laws 1 G
3.4. Froude’s Model Law
3.5. Scale Factor of the Mass and the Force
4. Scaling of the Model Test for This Work
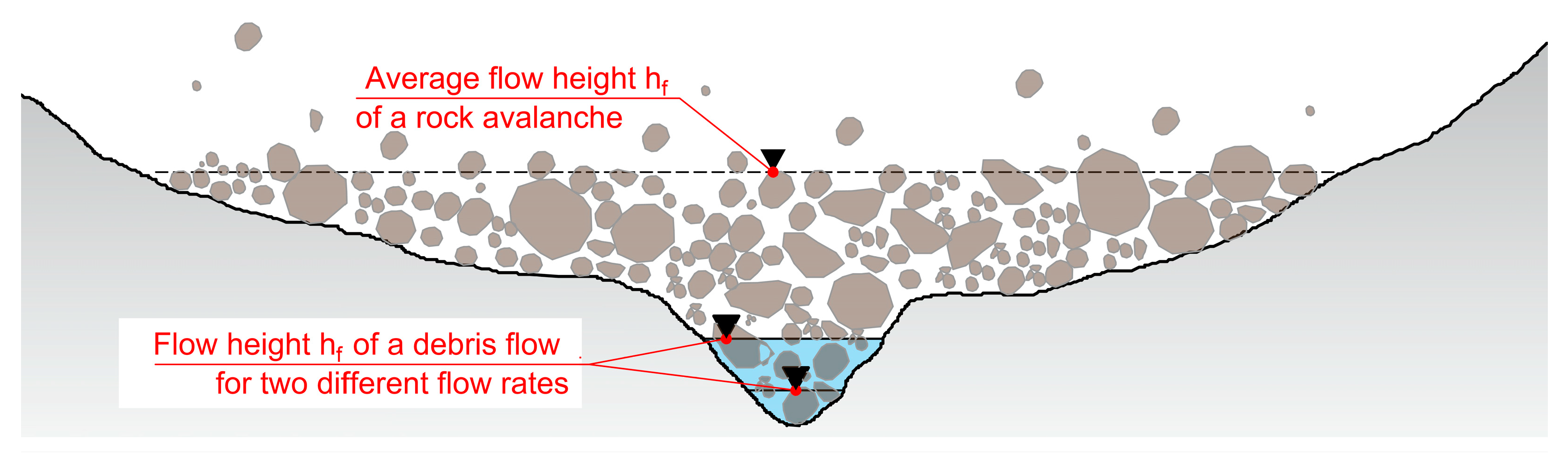
- Protective dams are usually built on a slope inclination of up to 35° for design purposes. This rather “flat” slope has a greater resistance compared to steep rock faces. It follows that the velocity at the time of impact is smaller than the maximum observed velocities in Table 6.
- Protective structures against rock avalanches in narrow valley cross sections are unsuitable because large mass movements quickly backfill a protective structure, and the shooting mass immediately fills the uphill terrain.
- Protective dams are usually designed as linear structures. The length of the dams allows a strong lateral deflection of the mass. This results in considerably lower flow heights (hf).
- Typical construction heights of protective dams reach approximately 25–30 m and are built where the rock avalanche does not reach the flow depth (hf), which can “run up” the dam crest.
- The block sizes occurring in rock avalanches usually reach several meters, so the flow height should be assumed to be hf > 1–2 m based on the block size alone.
5. DEM Simulation of the Model Test for This Work
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gariano, S.L.; Guzzetti, F. Landslides in a changing climate. Earth Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef] [Green Version]
- Gobiet, A.; Kotlarski, S.; Beniston, M.; Heinrich, G.; Rajczak, J.; Stoffel, M. 21st century climate change in the European Alps—A review. Sci. Total Environ. 2014, 493, 1138–1151. [Google Scholar] [CrossRef] [PubMed]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Abele, G. Bergstürze in den Alpen—Ihre Verbreitung, Morphologie und Folgeerscheinungen; Wissenschafltiche Alpenvereinshefte: Munich, Germany, 1974; Volume 25, pp. 1–165. [Google Scholar]
- ONR 24800; Schutzbauwerke der Wildbachverbauung—Begriff und Ihre Definitionen Sowie Klassifizierung. ASI Austrian Standards Institute: Vienna, Austria, 2009.
- ONR, 24801; Schutzbauwerke der Wildbachverbauung—Statische und Dynamische Einwirkungen. ASI Austrian Standards Institute: Vienna, Austria, 2013.
- ONR 24802; Schutzbauwerke der Wildbachverbauung—Projektierung, Bemessung und Konstruktive Durchbildung. ASI Austrian Standards Institute: Vienna, Austria, 2011.
- Hofmann, R.; Vollmert, L. Rockfall embankments: Construction and Design. Geomech. Tunn. 2020, 13, 21–31. [Google Scholar] [CrossRef]
- Hofmann, R.; Kolymbas, D. Wasserdruck auf Konsolidierungssperren/Design of torrential barriers. Bauingenieur 2020, 95, 201–209. [Google Scholar] [CrossRef]
- Hofmann, R.; Berger, S.; Kolymbas, D. Wasserdruck auf Konsolidierungssperren—Messungen In Situ; Bauingenieur BD. 6; Universität Innsbruck: Innsbruck, Austria, 2022. [Google Scholar]
- Mizuyama, T. Evaluation of Impact of Debris Flow on Check Dams. J. Jpn. Soc. Eros. Control. Eng. 1979, 32, 40–49. [Google Scholar]
- Yamaguchi, I. Erosion Control Engineering; Earth Press: Brisbane City, QLD, Australia, 1985; ISBN 4-8049-5064-8. [Google Scholar]
- Nakano, K.; Ukon, S. Experiments of Impact of Sand Avalanches. J. Jpn. Soc. Eros. Control. Eng. 1986, 39, 17–23. [Google Scholar]
- Yu, F.C. A study on the Impact Forces of Debris Flow. Proc. NSC Part A Phys. Sci. Eng. 1992, 16, 32–39. [Google Scholar]
- Armanini, A.; Scotton, P. On the dynamic impact of a debris flow on structures. In Proceedings of the XXV IAHR Congress (Tech. Sess. B, III), Tokyo, Japan, 30 August–3 September 1993; pp. 203–210. [Google Scholar]
- Daido, A. Impact force of mud-debris flows on structures. In Proceedings of the Congress-International Association for Hydraulic Research, Local Organizing Committee of the XXV Congress, Tokyo, Japan, 30 August–3 September 1993; Volume 3, p. 211. [Google Scholar]
- Song, Y.D. A Study of Impact of the Debris Flow. Master’s Thesis, National Chung Hsing University, Taichung, Taiwan, 1994. [Google Scholar]
- Lin, H.C. The Study of Impact Force of Debris Flow upon Model Dams of Different Types. Master’s Thesis, National Chung Hsing University, Taichung, Taiwan, 1994. [Google Scholar]
- Scotton, P.; Deganutti, A.M. Phreatic line and dynamic impact in laboratory debris flow experiments. In Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment; ASCE: Reston, VA, USA, 1997; pp. 777–786. [Google Scholar]
- Lien, H.P. Study on Treatments of Debris Flow (Ⅱ); Soil and Water Conservation Bureau, Council of Agriculture (COA): Nantou City, Taiwan, 2002.
- Zanuttigh, B.; Lamberti, A. Experimental analysis of the impact of dry avalanches on structures and implication for debris flows. J. Hydraul. Res. 2006, 44, 522–534. [Google Scholar] [CrossRef]
- Bugnion, L.; McArdell, B.W.; Bartelt, P.; Wendeler, C. Measurements of hillslope debris flow impact pressure on obstacles. Landslides 2012, 9, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Ashwood, W.; Hungr, O. Estimating total resisting force in flexible barrier impacted by a granular avalanche using physical and numerical modeling. Can. Geotech. J. 2016, 53, 1700–1717. [Google Scholar] [CrossRef]
- Iverson, R.M. Scaling and design of landslide and debris-flow experiments. Geomorphology 2015, 244, 9–20. [Google Scholar] [CrossRef]
- Valentino, R.; Barla, G.; Montrasio, L. Experimental Analysis and Micromechanical Modelling of Dry Granular Flow and Impacts in Laboratory Flume Tests. Rock Mech. Rock Eng. 2008, 41, 153–177. [Google Scholar] [CrossRef]
- Berger, S.; Hofmann, R.; Wimmer, L. Einwirkungen auf starre Barrieren durch fließähnliche gravitative Massenbewegungen. Geotechnik 2021, 44, 77–91. [Google Scholar] [CrossRef]
- Moriguchi, S.; Borja, R.I.; Yashima, A.; Sawada, K. Estimating the impact force generated by granular flow on a rigid obstruction. Acta Geotech. 2009, 4, 57–71. [Google Scholar] [CrossRef]
- Jiang, Y.-J.; Towhata, I. Experimental Study of Dry Granular Flow and Impact Behavior Against a Rigid Retaining Wall. Rock Mech. Rock Eng. 2013, 46, 713–729. [Google Scholar] [CrossRef]
- Choi, C.E.; Ng, C.W.W.; Au-Yeung, S.C.H.; Goodwin, G.R. Froude characteristics of both dense granular and water flows in flume modelling. Landslides 2015, 12, 1197–1206. [Google Scholar] [CrossRef]
- Buckingham, E. On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Sonin, A.A. A generalization of the Π-theorem and dimensional analysis. Proc. Natl. Acad. Sci. USA 2004, 101, 8525–8526. [Google Scholar] [CrossRef] [Green Version]
- Misic, T.; Najdanovic-Lukic, M.; Nesic, L. Dimensional analysis in physics and the Buckingham theorem. Eur. J. Phys. 2010, 31, 893–906. [Google Scholar] [CrossRef]
- Karam, M.; Saad, T. BuckinghamPy: A Python software for dimensional analysis. SoftwareX 2021, 16, 100851. [Google Scholar] [CrossRef]
- Worthoff, R.; Siemes, W. Grundbegriffe der Verfahrenstechnik: Mit Aufgaben und Lösungen; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 1–15. [Google Scholar]
- Snay, H.G. Model Tests and Scaling; Naval Ordnance Lab: White Oak, MD, USA, 1964. [Google Scholar]
- Strobl, T.; Zunic, F. Wasserbau—Aktuelle Grundlagen—Neue Entwicklungen; Springer: New York, NY, USA, 2006. [Google Scholar]
- Walz, B. Bodenmechanische Modelltechnik als Mittel zur Bemessung von Grundbauwerken; Fachbereich Bautechnik, Bericht 1; Universität-GH Wuppertal: Wuppertal, Germany, 1982. [Google Scholar]
- Zhang, B.; Huang, Y. Impact behavior of superspeed granular flow: Insights from centrifuge modeling and DEM simulation. Eng. Geol. 2022, 299, 106569. [Google Scholar] [CrossRef]
- Baek, S.-H.; Kim, J. Applicability of the 1g similitude law to the physical modeling of soil-track interaction. J. Terramechanics 2019, 85, 27–37. [Google Scholar] [CrossRef]
- Thouret, J.-C.; Antoine, S.; Magill, C.; Ollier, C. Lahars and debris flows: Characteristics and impacts. Earth-Sci. Rev. 2020, 201, 103003. [Google Scholar] [CrossRef]
- Proske, D.; Suda, J.; Hübl, J. Debris flow impact estimation for breakers. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2011, 5, 143–155. [Google Scholar] [CrossRef]
- Sosio, R.; Crosta, G.B.; Hungr, O. Complete dynamic modeling calibration for the Thurwieser rock avalanche (Italian Central Alps). Eng. Geol. 2008, 100, 11–26. [Google Scholar] [CrossRef]
- Preh, A.; Sausgruber, J.T. The extraordinary rock-snow avalanche of Alpl, Tyrol, Austria. Is it possible to predict the runout by means of single-phase Voellmy-or Coulomb-type models? Eng. Geol. Soc. Territ. 2015, 2, 1907–1911. [Google Scholar]
- Waldron, H.H. Debris flow and erosion control problems caused by the ash eruptions of Irazu Volcano, Costa Rica. US Geol. Surv. Bull. 1967, 1241, 1–37. [Google Scholar]
- Jia, L.; Defu, L. The formation and characteristics of mudflow and flood in the mountain area of the Dachao River and its prevention. Z. Geomorphol. 1981, 25, 470–484. [Google Scholar]
- Pierson, T.C. Debris Flows: An important process in high country gully erosion. Rev. Tussock Grassl. Mt. Lands Inst. N. Z. 1980, 39, 3–14. [Google Scholar]
- Rickenmann, D. Empirical Relationships for Debris Flows. Nat. Hazards 1999, 19, 47–77. [Google Scholar] [CrossRef]
- Lavigne, F.; Suwa, H. Contrasts between debris flows, hyperconcentrated flows and stream flows at a channel of Mount Semeru, East Java, Indonesia. Geomorphology 2004, 61, 41–58. [Google Scholar] [CrossRef]
- Porter, S.; Orombelli, G. Catastrophic rock fall of September 12, 1717 on the Italian flank of the Mt. Blanc Massif. Z. Geomorphol. N. F. 1980, 24, 200–218. [Google Scholar] [CrossRef]
- Heim, A. Bergsturz und Menschenleben; Fretz und Wasmuth Verlag: Zürich, Switzerland, 1932. [Google Scholar]
- Huggel, C.; Zgraggen-Oswald, S.; Haeberli, W.; Kaab, A.; Polkvoj, A.; Galushkin, I.; Evans, S. The 2002 rock/ice avalanche at Kolka/Karmadon, Russian Caucasus: Assessment of extraordinary avalanche formation and mobility, and application of QuickBird satellite imagery. Nat. Hazards Earth Syst. Sci. 2005, 5, 173–187. [Google Scholar] [CrossRef] [Green Version]
- McConnell, R.G.; Brock, R.W. Report on the Great Landslide at Frank, Alta; Annual Report for 1903; Department of the Interior: Ottawa, ON, Canada, 1904; p. 17. [CrossRef]
- Alden, W. Landslide and flood at Gros Ventre, Wyo. Trans. Am. Inst. Min. Metall. Eng. 1928, 76, 347–361. [Google Scholar]
- Evans, S.G.; Clague, J.J.; Woodsworth, G.J.; Hungr, O. The Pandemonium Creek rock avalanche, British Columbia. Can. Geotech. J. 1989, 26, 427–446. [Google Scholar] [CrossRef]
- Hadley, J. Landslides and related phenomena accompanying the Hebgen Lake earthquake of August 17, 1959. U.S. Geol. Surv. Prof. Pap. 1964, 435, 107–138. [Google Scholar]
- Fahnestock, R. Little Tahoma Peak Rockfalls and Avalanches; Voight, B., Ed.; Mount Raiunier: Washington, DC, USA; Elsevier: Amsterdam, The Netherlands, 1978; pp. 181–196. [Google Scholar]
- Sheridan, M.; Stinton, A.; Patra, A.; Pitman, E.; Bauer, A.; Nichita, C. Evaluating Titan2D mass-flow model using the 1963 Little Tahoma Peak avalanches, Mount Rainier, Washington. J. Volcanol. Geotherm. Res. 2005, 139, 89–102. [Google Scholar] [CrossRef]
- Plafker, G.; Ericksen, G. Nevados Huascaran Avalanches, Peru; Voight, B., Ed.; Rockslides and Avalanches; Elsevier: Amsterdam, The Netherlands, 1978; Volume 1, pp. 277–314. [Google Scholar]
- Voight, B.; Janda, J.R.; Glicken, H.X.; Douglass, P.M. Nature and mechanics of the St Helens rockslide-avalanche of 18 May 1980. Geotéchnique 1983, 33, 243–273. [Google Scholar] [CrossRef]
- Moore, J.; Rice, C. Chronology and Character of the May 18, 1980, Explosive Eruption of Mount St. Helens. In Explosive Volcanism: Inception, Evolution, Hazards; America Special Paper 229; National Academy Press: Washington, DC, USA, 1984; pp. 23–36, 133–142. [Google Scholar]
- Crosta, G.; Chen, H.; Lee, C. Replay of the 1987 Val Pola Landslide, Italian Alps. Geomorphology 2004, 60, 127–146. [Google Scholar] [CrossRef]
- Margreth, S.; Bartelt, P.; Bühler, Y.; Christen, M.; Graf, C.; Schweizer, J. Expert Report G2017.20 Modelling of the Cengalo Landslide with Different Framework Conditions, Bondo, GR; WSL Institute for Snow and Avalanche Research SLF: Davos, Switzerland, 2017. [Google Scholar]
- Thibert, E.; Baroudi, D.; Limam, A.; Berthet-Rambaud, P. Avalanche impact pressure on an instrumented structure. Cold Reg. Sci. Technol. 2008, 54, 206–215. [Google Scholar] [CrossRef]
- Matuttis, H.; Chen, J. Understanding the Discrete Element Method: Simulation of Non-Spherical Particles for Granular and Multi-Body Systems; John Wiley & Sons: New York, NY, USA, 2014. [Google Scholar]
- Wyllie, D.C. Rock Fall Engineering: Development and Calibration of an Improved Model for Analysis of Rock Fall Hazards on Highways and Railways. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2014. [Google Scholar] [CrossRef]
- Aaron, J.; McDougall, S. Rock avalanche mobility: The role of path material. Eng. Geol. 2019, 257, 105126. [Google Scholar] [CrossRef]

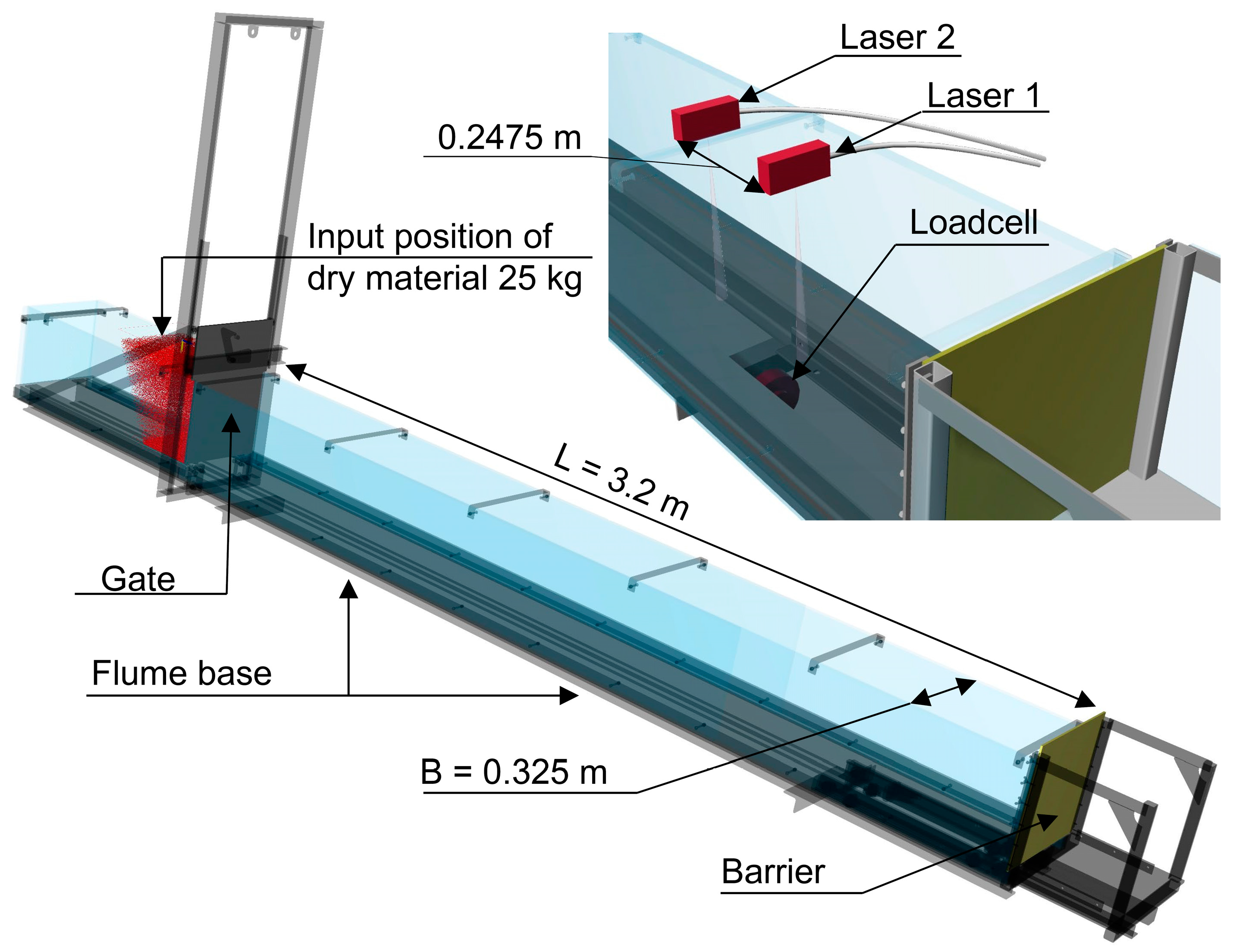


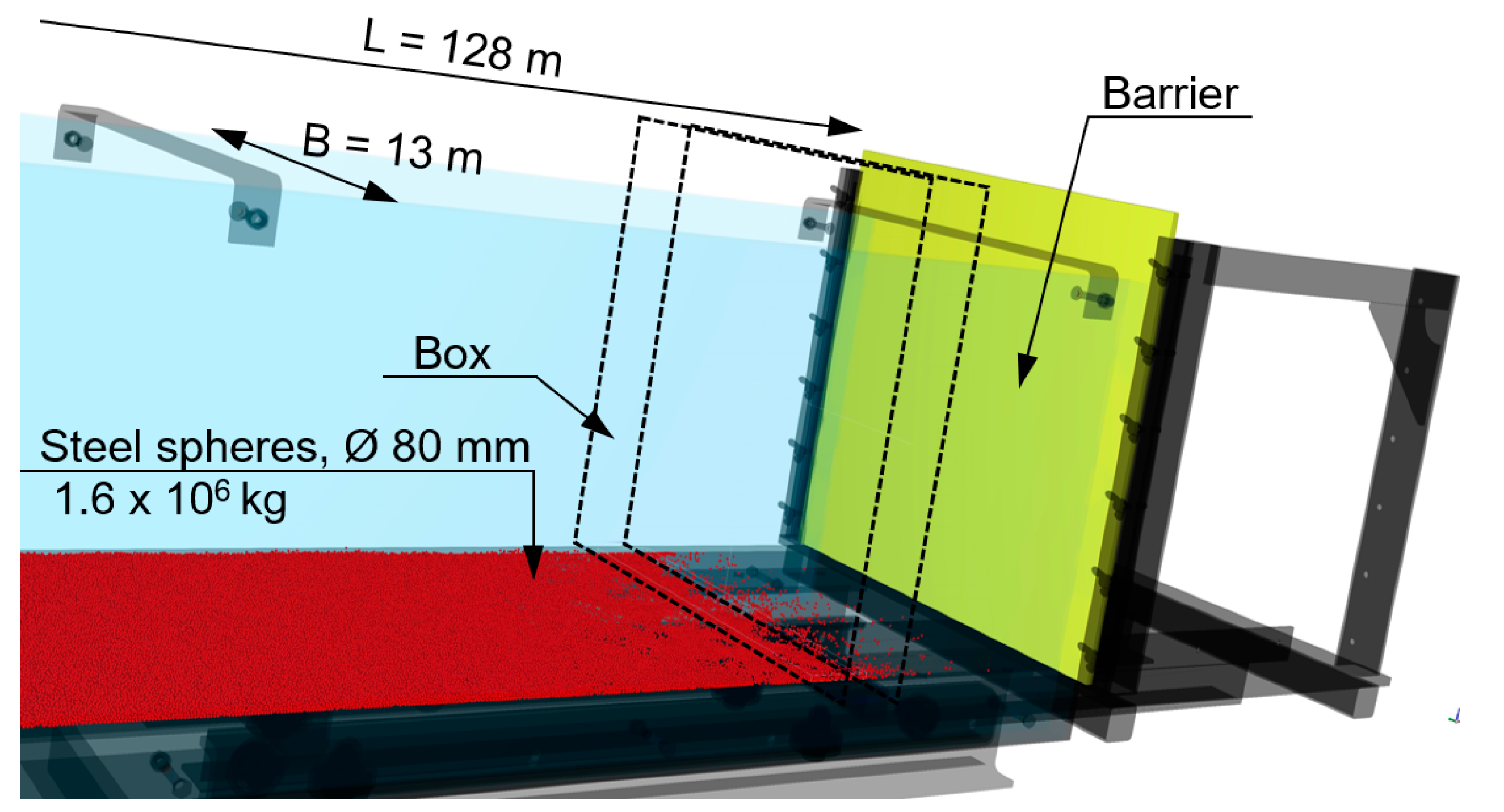
| Literature | Dimension | Material |
|---|---|---|
| [26] | Model length = 3.20 m Model width = 0.325 m Inclination = 20–39° | 25 kg material (DG) Natural grain shapes and glass and steel spheres Internal friction angle of the material φ = 0–35° |
| [27] | Model length = 1.80 m Model width = 0.30 m Inclination 45–65° | 50 kg material (DG) Natural grain shapes Internal friction angle of the material φ = 40° |
| [25] | Model length = 4.00 m Model width = 0.50 m Inclination up to 37° | DG Natural grain shapes Internal friction angle of the material φ = 32° |
| [28] | Model length = 2.2 m Model width = 0.30 m Inclination 30–45° | DG Natural grain shapes Internal friction angle of the material φ = 53° |
| [29] | Model length = 5.0 m Model width = 0.20 m Inclination 0–50° | 80 kg material (DG) Natural grain shapes Internal friction angle of the material φ = 35° |
| [23] | Model length = 3.20 m Model width = 0.325 m Inclination = 22–34° | 25 kg material (DG) Natural grain shapes Friction angle of the material φ = 31–35° |
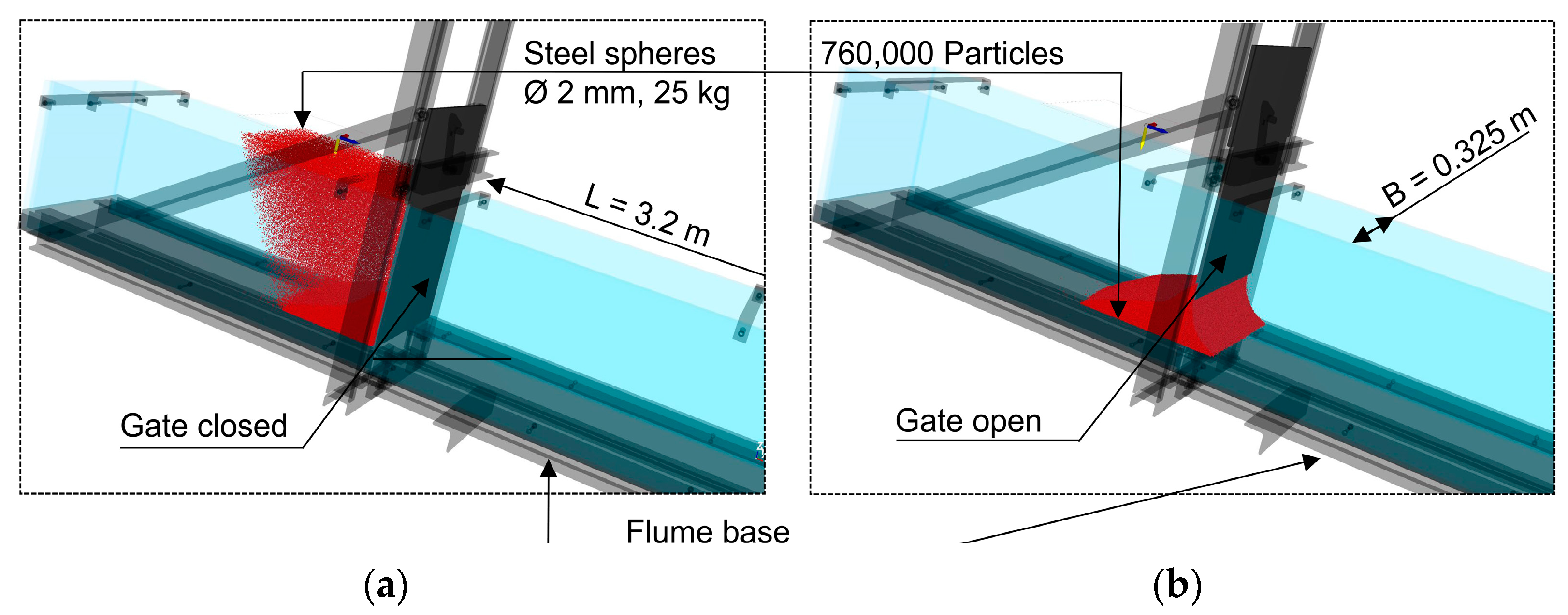
| Physical Parameters | Value | Unit |
|---|---|---|
| Inclination of the flume base (θ) | 30.2 | [°] |
| Material | Stainless steel | [–] |
| Material bulk density () | 4850 | [kg/m3] |
| Grain shape | Sphere | [–] |
| Grain diameter | 2 mm | [mm] |
| Total mass | 25 kg | [kg] |
| Number of particles | 760,000 | [–] |
| Physical Parameters | Description | Base Value | Unit |
|---|---|---|---|
| Inclination | tan(θ) | 1 | - |
| Friction angle | tan(φ) | 1 | - |
| Particle size | d | L | m |
| Density | ρ | M · L−3 | kg m−3 |
| Velocity | v | L · T−1 | m s−1 |
| Gravity | g | L · T−2 | m s−2 |
| Force | F | M · L · T−2 | kg m s−2 |
| Pressure | p | M · L−1 · T−2 | kg m−1 s−2 |
| Physical Parameter | Symbol | Dimension | Scaling Factor | |
|---|---|---|---|---|
| 1-g Model Law | Froud’s Model Law | |||
| Geometric dimensions | l | L | ||
| Duration | t | T | ||
| Mass | m | M | ||
| Inclination/Friction | tan(β)/tan(φi) | - | ||
| Velocity | v | L ∗ T | ||
| Flow height | hf | L | ||
| Acceleration/gravity | g | L/T2 | ||
| Grain diameter | d | L | ||
| Density | ρ | M/L3 | ||
| Froude number | Fr | - | ||
| Force | F | M L/T2 | ||
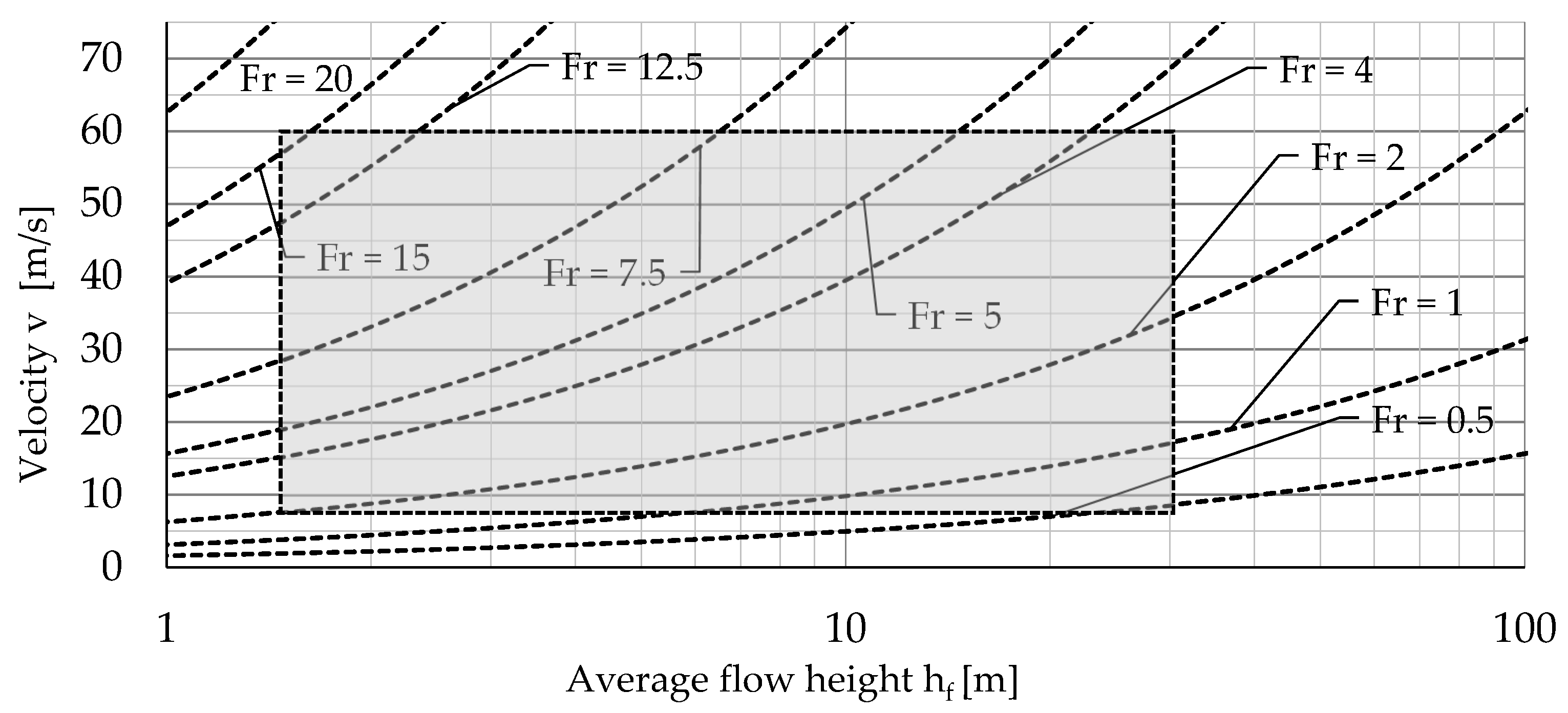
| Type | Location | Flow Parameter | Ref. | ||
|---|---|---|---|---|---|
| Velocity v (m/s) | Flow Thickness hf (m) | Froude Number Fr (−) | |||
| Debris-Flow | Rio Reventado, Costa Rica | 2.9–10 | 1.2–5.5 | 1.08 | [40,41,44] |
| Hunshui Gully, China | 10–12 | 3–5 | 1.90 | [40,41,45] | |
| Bullock Creek, New Zealand | 2.5–5.0 | 3–5 | 1.26 | [40,41,46] | |
| Pine Creek, USA | 10–31.1 | 0.1–1.5 | 7.56 | [40,41,46,47] | |
| Wrightwood Canyon | 1.0–1.2 | 0.6–4.4 | 0.87–0.95 | [41,47] | |
| Nojiri River, Japan | 4.8–13 | 2.4–3.2 | 2.71 | [41,47] | |
| Malaya Almatinka River, Kazakhstan | 4.3–9.4 | 2.0–8.5 | 6.12 | [47] | |
| Semeru, Indonesia | 1.0–5.0 | 0.6–3.5 | 1–1.7 | [48] | |
| Rock Avalanche | Triolet Glacier, Italy | 35–44 | - | - | [42,49] |
| Goldeau, Switzerland | 70 | - | - | [42,50] | |
| Elm, Switzerland | 70 | - | - | [42,50] | |
| Kolka, Russia | 50–80 | - | - | [42,51] | |
| Frank, Canada | 40 | - | - | [42,52] | |
| Gros Ventre, USA | 45 | - | - | [42,53] | |
| Pandemonium, Canada | 81–100 (30) | - | - | [42,54] | |
| Madison Canyon, USA | 50 | - | - | [42,55] | |
| Little Tahoma Peak, USA | 29–42 | - | - | [42,56] | |
| Little Tahoma Peak, USA | 60 | - | - | [42,57] | |
| Huascaran, Peru | 278 (76) | - | - | [42,58] | |
| Mount St. Helens, USA | 70 (39) | - | - | [42,59,60] | |
| Val Pola, Italy | 76–108 | - | - | [42,61] | |
| Thurwieser, Italy | 60–65 (38) | - | - | [42] | |
| Alpl, Austria * | 6–7 | 1 | 4.5 | [43] | |
| Piz Cengalo, Switzerland * | 30–65 | 2–14 | 2.6–14.7 | [62] | |
| Physical Parameter | Value | Unit | Description of How the Value Was Determined |
|---|---|---|---|
| Static Friction | Determination of the static friction angle was carried out by tilting tests using a cylinder. By eliminating the rolling of the spheres in the cylinder, the value of the sliding friction can be determined. Based on the tilt test, approximately 13—16°. | ||
| Particle–Particle | 0.26 | [–] | |
| Particle–Model | 0.26 | [–] | |
| Dynamic Friction | Determined according to the static friction [64]. | ||
| Particle–Particle | 0.26 | [–] | |
| Particle–Model | 0.26 | [–] | |
| Tangential Stiffness Ratio | 1 | [–] | Assumed to be 1, since no different effect is expected between normal and tangential. |
| Restitution Coefficient | [–] | Determined with the help of the height in the drop test. H before impact = 50 cm H after impact = 14.7 cm Restitution coefficient from energy balance is approximately 0.54 | |
| Particle–Particle | 0.54 | [–] | |
| Particle–Model | 0.54 | [–] | |
| Rolling Resistance | 0 | [–] | No resistance to rolling friction is assumed for the nearly perfect steel spheres. |
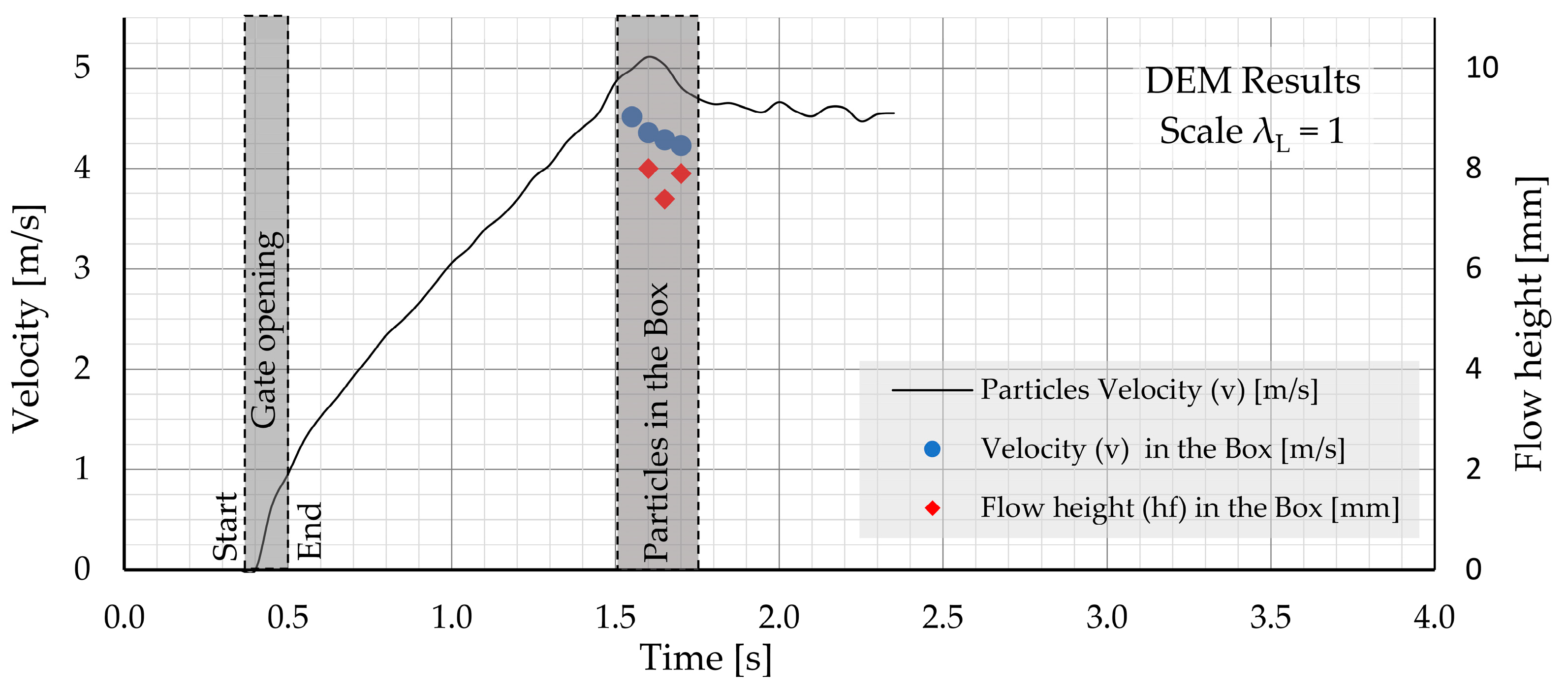
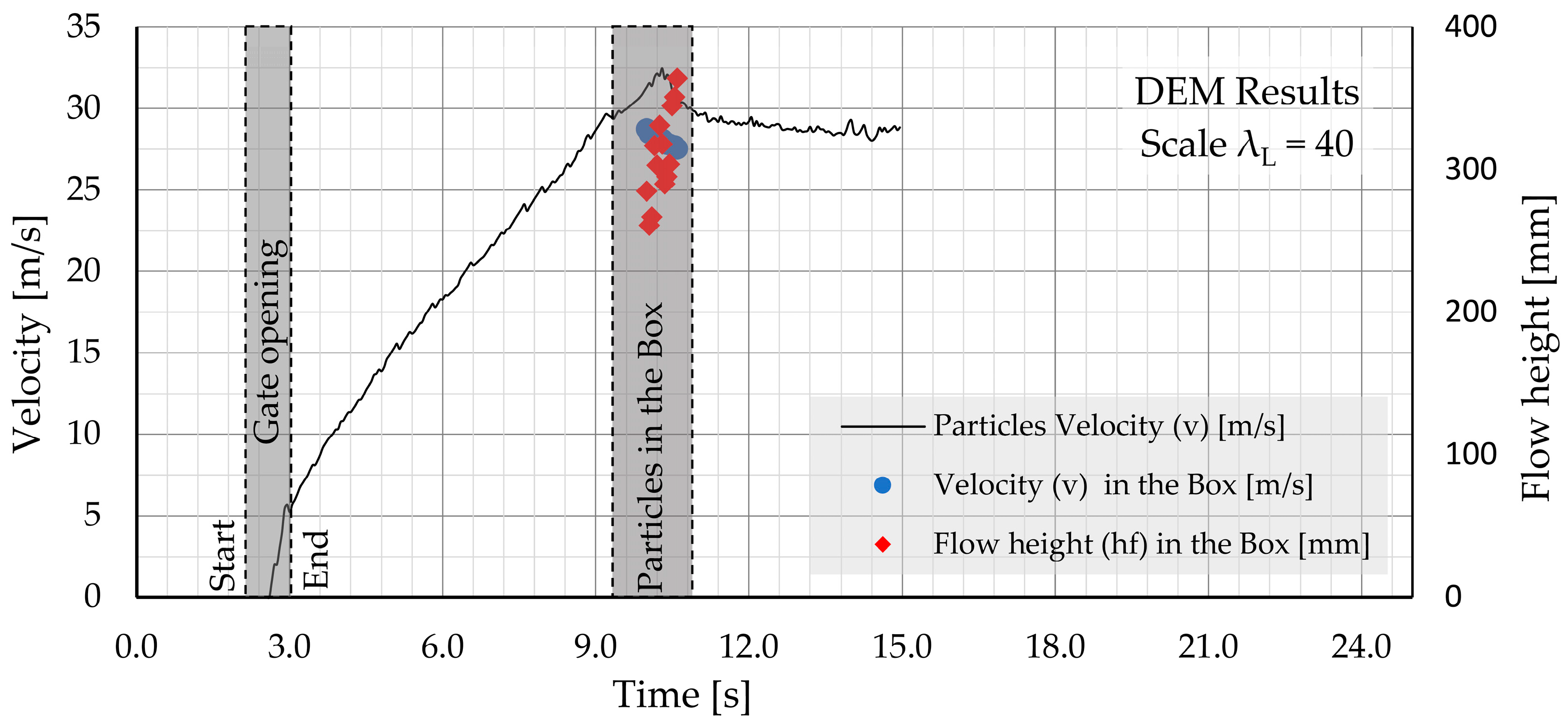
| Physical Parameter | Unit | Value Measured “Model Test” | Value DEM Calculation | Deviation | ||||
|---|---|---|---|---|---|---|---|---|
| Force | Min | Max | Mean | Min | Max | Mean | ||
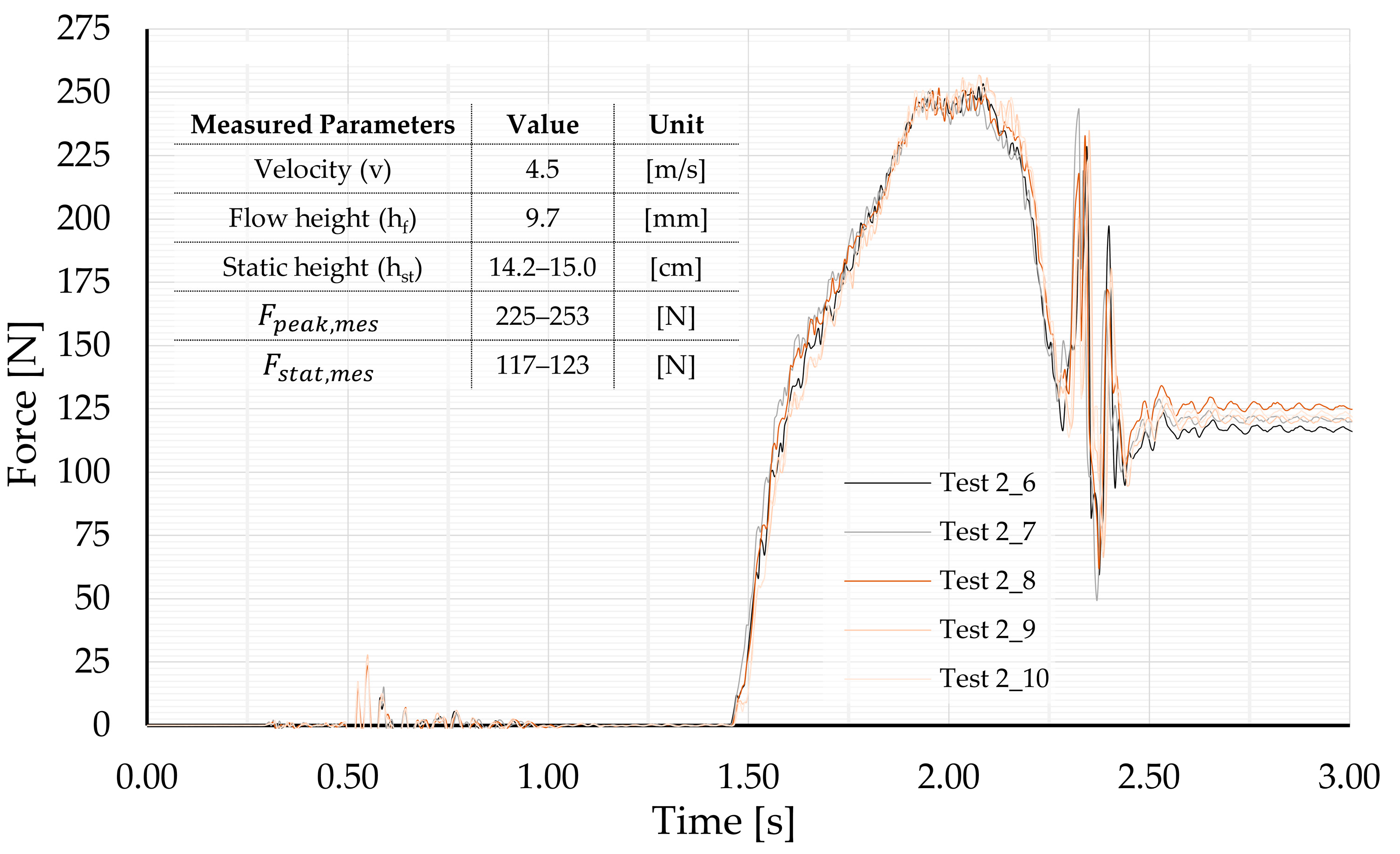
| Fpeak | [N] | 242.97 | 256.65 | 249.81 | - | 252.46 | 252.46 | ~1.1% |
| Fstat | [N] | 117.9 | 122.52 | 120.21 | 117.9 | - | 117.9 | ~1.9% |
| Velocity | ||||||||
| v | [m/s] | - | - | 4.5 | 4.25 | 4.6 | 4.4 | ~1.5% |
| Flow height | ||||||||
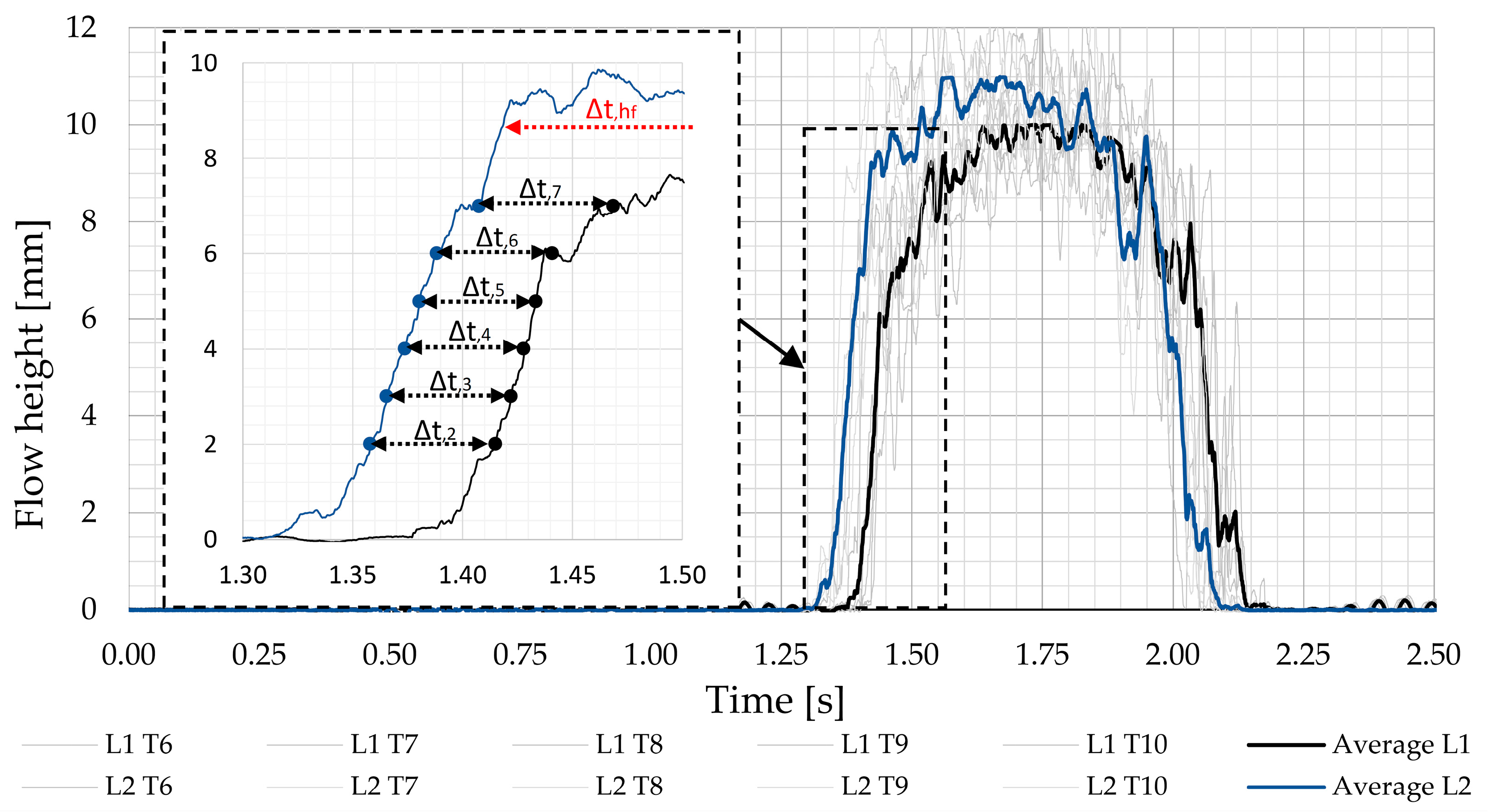
| hf | [mm] | - | - | 9.7 (Laser_1) | - | 8 | 8 | 17.0% |
| Static height | ||||||||
| hst | [mm] | 14.2 | 15.0 | 14.6 | - | 15.6 | 15.6 | 6.8% |
| Physical Parameter | Unit | Measured Values of the Model Test λL = 1 | Scale Factor | Scaled Measured Values of the Model Test λL = 40 |
|---|---|---|---|---|
| Geometric size | ||||
| Grain size | [mm] | 2 | 80 ** | |
| Model length | [m] | 3.2 | 128 ** | |
| Model width | [m] | 0.325 | 13 ** | |
| Density | [kg/m3] | 7850 | 7850 ** | |
| Mass | [kg] | 25 | 1.6 × 106 ** | |
| Velocity | [m/s] | 4.5 | 28.5 * | |
| Force | ||||
| Fpeak | [kN] | 0.24981 | 16.0 × 103 * | |
| Fstat | [kN] | 0.12021 | 7.7 103 * |
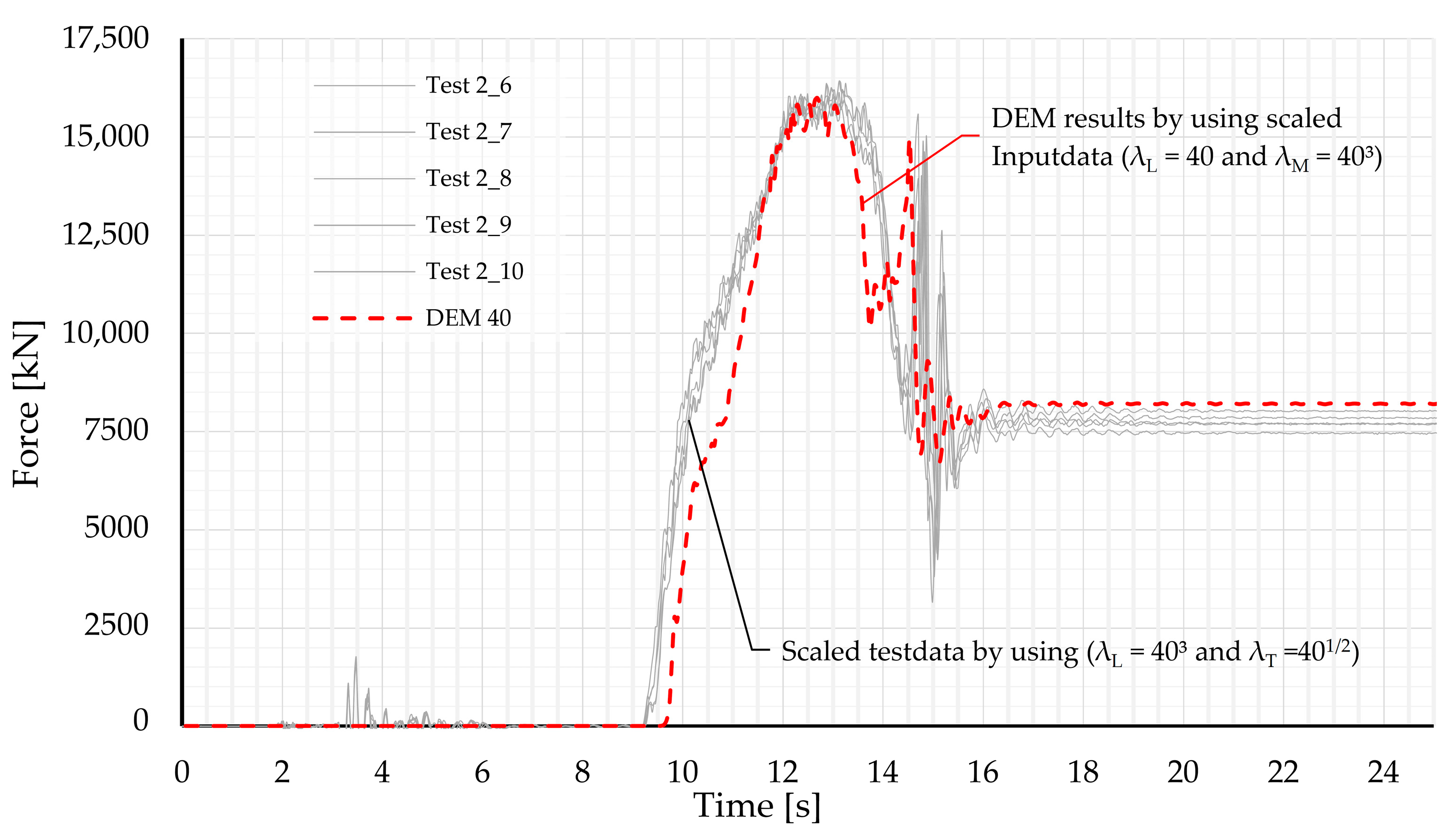
| Physical Parameter | Unit | Scaled Value Measured “Model Test” | Value DEM Calculation | Deviation |
|---|---|---|---|---|
| Force | ||||
| Fpeak | [kN] | 16.0 × 103 | 15.8 × 103 | 1.1% |
| Fstat | [kN] | 7.7 × 103 | 8.2 × 103 | 6.5% |
| Velocity | ||||
| v | [m/s] | 28.5 | 28.2 | 1.1% |
| Flow height | ||||
| hf | [mm] | 388 | 345 | 11.1% |
| Static height | ||||
| hst | [mm] | = 5860 mm | 6403 | 9.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berger, S.; Hofmann, R. Impacts on Protective Structures against Gravitational Mass Movements—Scaling from Model Tests to Real Events. Geosciences 2022, 12, 278. https://doi.org/10.3390/geosciences12070278
Berger S, Hofmann R. Impacts on Protective Structures against Gravitational Mass Movements—Scaling from Model Tests to Real Events. Geosciences. 2022; 12(7):278. https://doi.org/10.3390/geosciences12070278
Chicago/Turabian StyleBerger, Simon, and Robert Hofmann. 2022. "Impacts on Protective Structures against Gravitational Mass Movements—Scaling from Model Tests to Real Events" Geosciences 12, no. 7: 278. https://doi.org/10.3390/geosciences12070278
APA StyleBerger, S., & Hofmann, R. (2022). Impacts on Protective Structures against Gravitational Mass Movements—Scaling from Model Tests to Real Events. Geosciences, 12(7), 278. https://doi.org/10.3390/geosciences12070278





