A Field-Based Evaluation of the Reliability of Empirical Formulae for Quantifying the Longitudinal Dispersion Coefficient in Small Channels
Abstract
:1. Introduction
2. Basic Theory of Advection-Dispersion
3. Formulae for Predicting the Longitudinal Dispersion Coefficient—Parameterization and Uncertainty
4. Methods
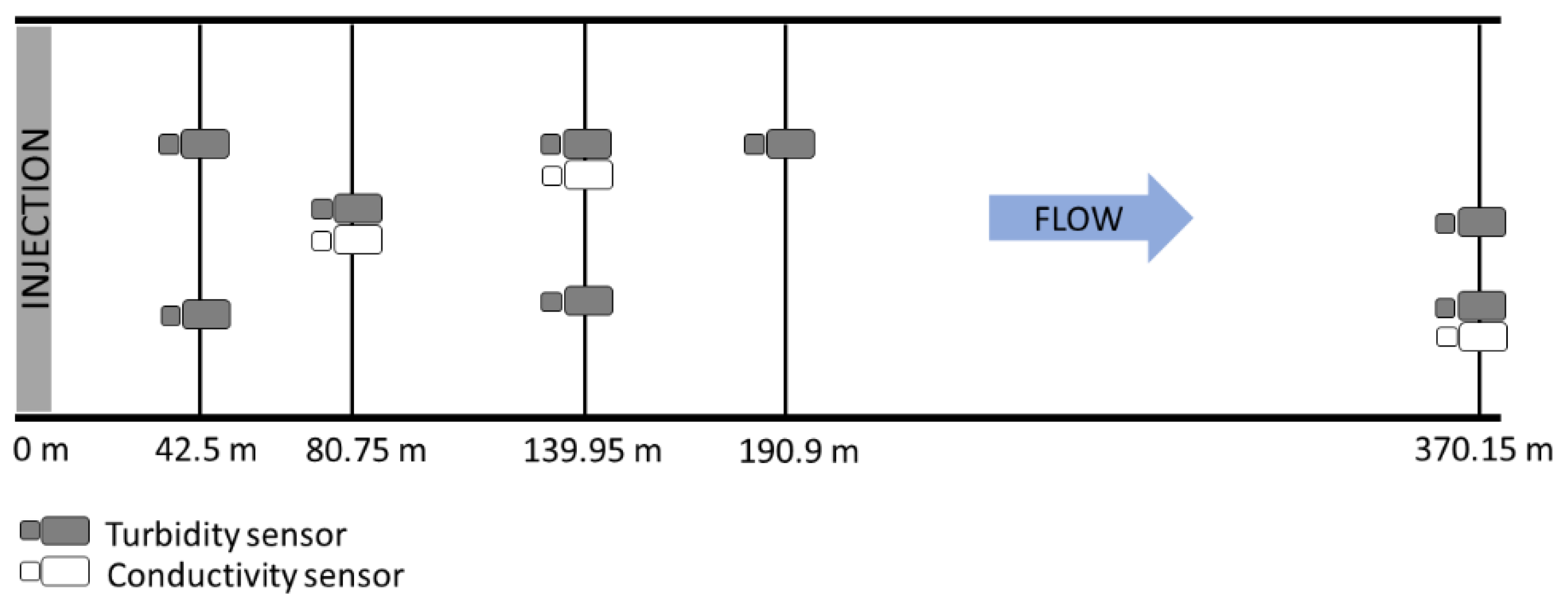
4.1. Field Experiments
4.2. Analytical Procedures
5. Results
5.1. General Hydraulic Conditions
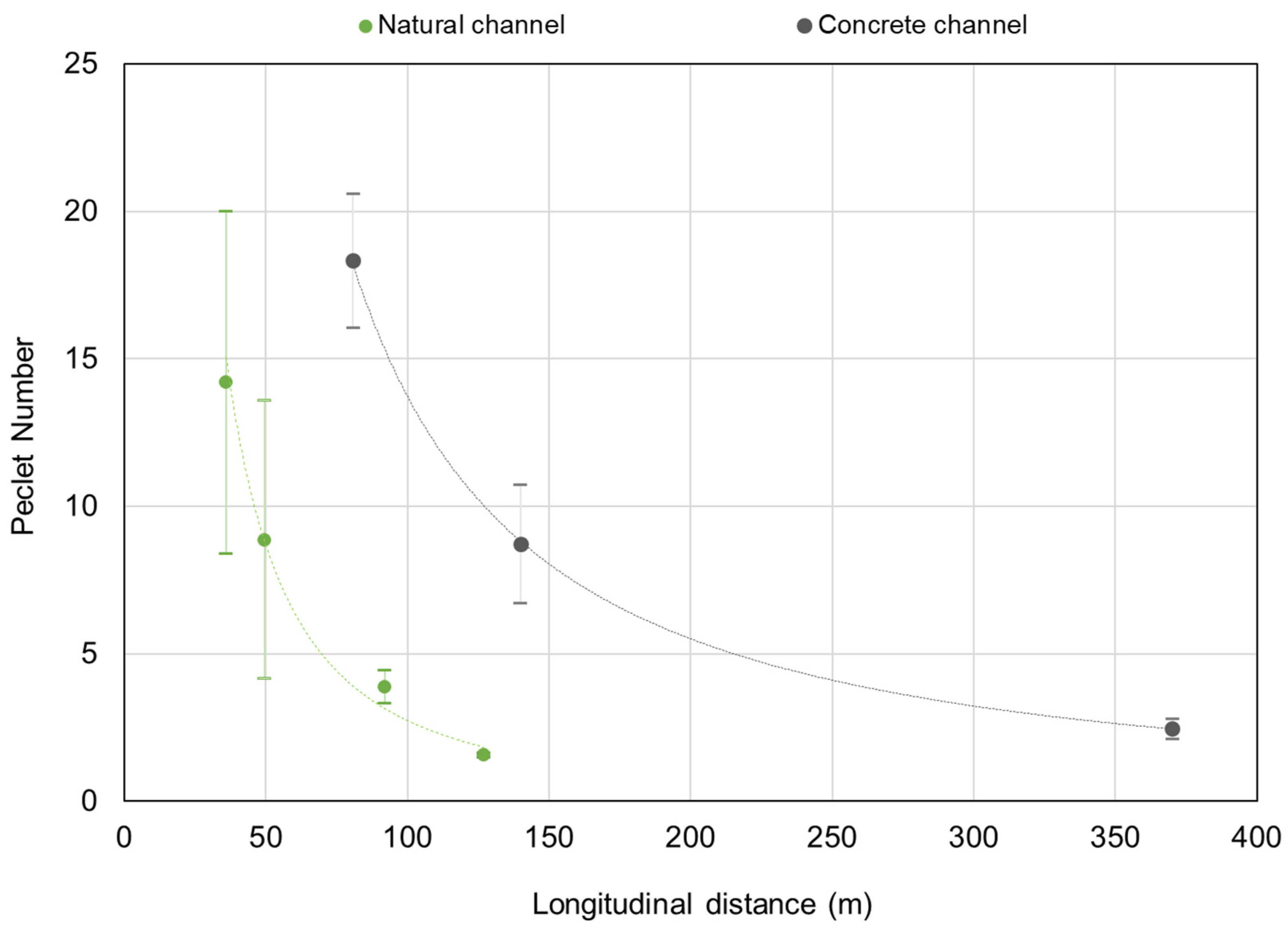
5.2. Quantification of Kx Values Based on Field Measurements
5.3. Comparison of Kx Values from Formulae and from Field Measurements
5.3.1. Concrete Channel Results
5.3.2. Natural Channel Results
5.3.3. Comparison of Measured and Modeled Plumes
6. Discussion
6.1. General Performance of Kx Formulae
6.2. Comparative Performance of Kx Formulae
6.3. Contextual Considerations and Caveats
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Advective Zone Length Calculations and Their Inherent Uncertainties
“…there is no convincing evidence in the empirical data that the mixing length of Equation (20) [i.e., Equation (A1) in this paper with = 1.8 as recommended by Fisher [45]] or the time scale of Equation (36) is a sufficient criterion to classify the dispersion process…Actually, the mixing length criterion is somewhat arbitrary, and there are possibilities for wide deviations from Equation (20).”
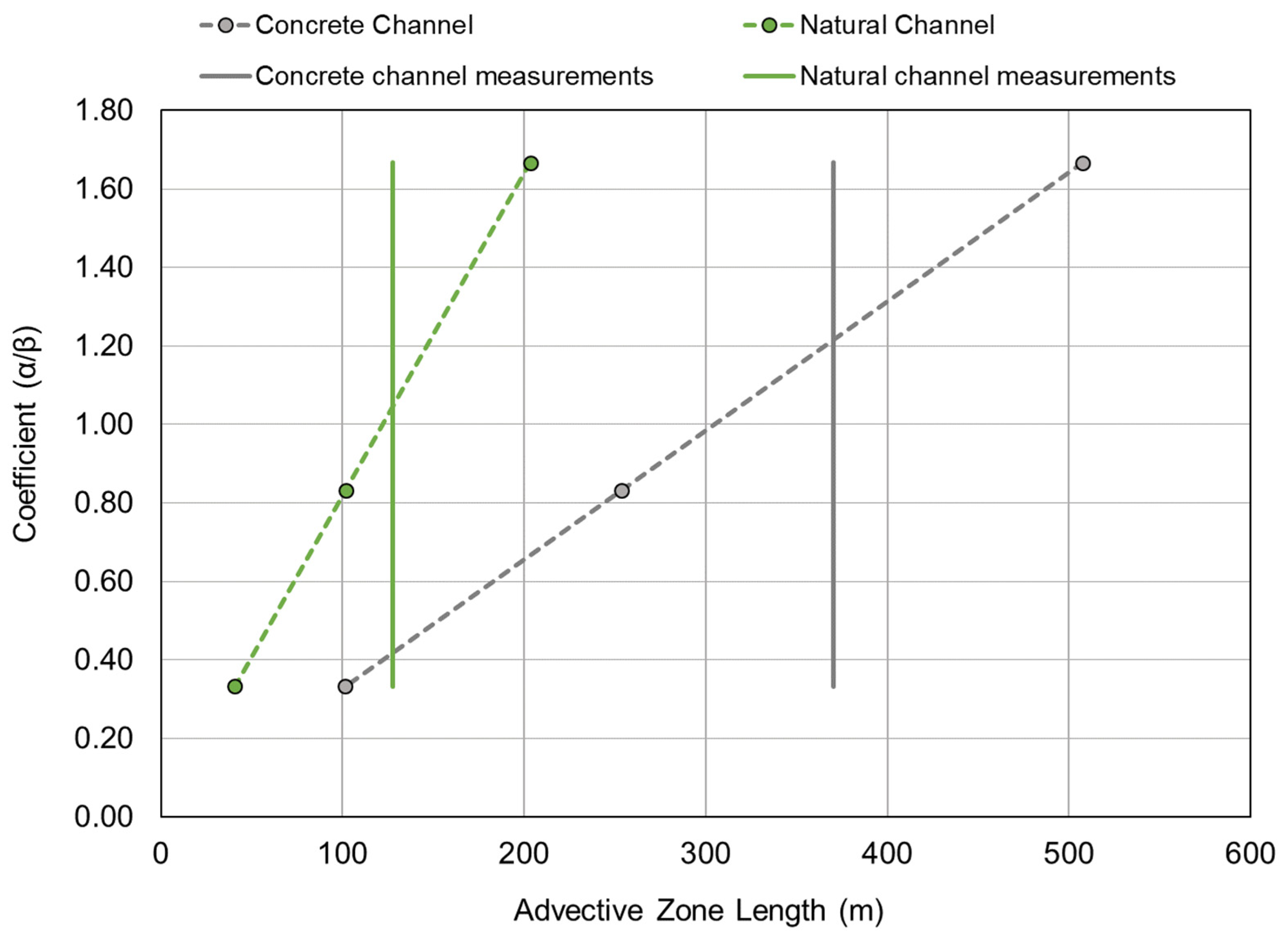
“from a practical point of view, if the convective influence extends downstream much farther than the length given by Equation (20) (Equation (A1) in this paper with = 1.8), the one-dimensional model is not likely to be of much value because the dispersant would be completely out of the reach of interest before the theory applies.”
References
- Camacho Suarez, V.V.; Schellart, A.N.A.; Brevis, W.; Shucksmith, J.D. Quantifying the impact of uncertainty within the longitudinal dispersion coefficient on concentration dynamics and regulatory compliance in rivers. Water Resour. Res. 2019, 55, 4393–4409. [Google Scholar] [CrossRef]
- Launay, M.; Le Coz, J.; Camenen, B.; Walter, C.; Angot, H.; Dramais, G.; Faure, J.B.; Coquery, M. Calibrating pollutant dispersion in 1-D hydraulic models of river networks. J. Hydro-Environ. Res. 2015, 9, 120–132. [Google Scholar] [CrossRef] [Green Version]
- Holley, E.R.; Siemons, J.; Abraham, G. Some aspects of analyzing transverse diffusion in rivers. J. Hydraul. Res. 1972, 10, 27–57. [Google Scholar] [CrossRef]
- Julien, P.Y. Erosion and Sedimentation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010; pp. 1–371. [Google Scholar] [CrossRef]
- Rutherford, V.J.C. River Mixing; John Wiley & Sons, Ltd.: New York, NY, USA, 1994; pp. 1–347. [Google Scholar] [CrossRef]
- Fick, A. On liquid diffusion. J. Membr. Sci. 1995, 100, 33–38. [Google Scholar] [CrossRef]
- Nordin, C.F.; Sabol, G.V. Empirical data on longitudinal dispersion in rivers. In US Geological Survey Water-Resources Investigations Report; U.S. Geological Survey: New York, NY, USA, 1974; Volume 74-20, 332p. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Leij, F.J.; Skaggs, T.H.; Toride, N.; Bradford, S.A.; Pontedeiro, E.M. Exact analytical solutions for contaminant transport in rivers 1. The equilibrium advection-dispersion equation. J. Hydrol. Hydromech. 2013, 61, 146–160. [Google Scholar] [CrossRef]
- McQuivey, R.S.; Keefer, T.N. Simple method for predicting dispersion in streams. J. Environ. Eng. Div. 1974, 100, 977–1011. [Google Scholar] [CrossRef]
- Parker, F.L. Eddy diffusion in reservoirs and pipelines. J. Hydraul. Div. 1961, 87, 151–171. [Google Scholar] [CrossRef]
- Devens, J.A. Quantification of Longitudinal Dispersion Coefficient in Streams with the Use of Neutral Tracer. Master’s Thesis, Federal University of Ouro Preto, Ouro Preto, Brazil, 2006. Available online: http://www.repositorio.ufop.br/jspui/handle/123456789/2226 (accessed on 18 July 2022).
- Disley, T.; Gharabaghi, B.; Mahboubi, A.A.; Mcbean, E.A. Predictive equation for longitudinal dispersion coefficient. Hydrol. Process 2015, 29, 161–172. [Google Scholar] [CrossRef]
- Sattar, A.M.A.; Gharabaghi, B. Gene expression models for prediction of longitudinal dispersion coefficient in streams. J. Hydrol. 2015, 524, 587–596. [Google Scholar] [CrossRef]
- Sahay, R.R.; Dutta, S. Prediction of longitudinal dispersion coefficients in natural rivers using genetic algorithm. Hydrol. Res. 2009, 40, 544–552. [Google Scholar] [CrossRef]
- Etemad-Shahidi, A.; Taghipour, M. Predicting longitudinal dispersion coefficient in natural streams using M5′ model tree. J. Hydraul. Eng. 2012, 138, 542–554. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Ahmadyar, D.; Afghantoloee, A. Improvement on the existing equations for predicting longitudinal dispersion coefficient. Water Resour. Manag. 2017, 31, 1777–1794. [Google Scholar] [CrossRef]
- Wang, Y.F.; Huai, W.X.; Wang, W.J. Physically sound formula for longitudinal dispersion coefficients of natural rivers. J. Hydrol. 2017, 544, 511–523. [Google Scholar] [CrossRef]
- Deng, Z.-Q.; Singh, V.P.; Bengtsson, L. Longitudinal dispersion coefficients in straight rivers. J. Hydraul. Eng. 2001, 127, 919–927. [Google Scholar] [CrossRef]
- Wang, Y.; Huai, W. Estimating the longitudinal dispersion coefficient in straight natural rivers. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Zeng, Y.H.; Huai, W.X. Estimation of longitudinal dispersion coefficient in rivers. J. Hydro-Environ. Res. 2014, 8, 2–8. [Google Scholar] [CrossRef]
- Oliveira, V.V.; Mateus, M.V.; Gonçalves, J.C.D.S.I.; Utsumi, A.G.; Giorgetti, M.F. Prediction of the longitudinal dispersion coefficient for small watercourses. Acta Sci. Technol. 2017, 39, 291–299. [Google Scholar] [CrossRef] [Green Version]
- El Kadi Abderrezzak, K.; Ata, R.; Zaoui, F. One-dimensional numerical modelling of solute transport in streams: The role of longitudinal dispersion coefficient. J. Hydrol. 2015, 527, 978–989. [Google Scholar] [CrossRef]
- Iwasa, Y.; Aya, S. Predicting Longitudinal Dispersion Coefficient in Open-Channel Flows. In Proceedings of the International Symposium on Environmental Hydraulics, Hong Kong, China, 16–18 December 1991; pp. 505–510. [Google Scholar]
- Hayami, H. On the of Propagation of Flood Waves, Disaster Prevention Research Institute, Bulletin No. 1; Kyoto University: Kyoto, Japan, 1951; Available online: http://hdl.handle.net/2433/123641 (accessed on 18 July 2022).
- Shucksmith, J.; Boxall, J.; Guymer, I. Importance of advective zone in longitudinal mixing experiments. Acta Geophys. 2007, 55, 95–103. [Google Scholar] [CrossRef]
- Taylor, G. The dispersion of matter in turbulent flow through a pipe. Proc. R. Soc. A Math. Phys. Eng. Sci. 1954, 223, 446–468. [Google Scholar] [CrossRef]
- Elder, J.W. The dispersion of marked fluid in turbulent shear flow. J. Fluid Mech. 1959, 5, 544–560. [Google Scholar] [CrossRef]
- Fischer, H.B. Discussion of “Simple method for predicting dispersion in streams”. J. Environ. Eng. Div. 1975, 101, 453–455. [Google Scholar] [CrossRef]
- Liu, H. Predicting dispersion coefficients of streams. J. Environ. Eng. Div. 1977, 103, 56–69. [Google Scholar] [CrossRef]
- Koussis, A.D.; Rodríguez-Mirasol, J. Hydraulic estimation of dispersion coefficient for streams. J. Hydraul. Eng. 1998, 124, 317–320. [Google Scholar] [CrossRef]
- Seo, W.; Cheong, T.S. Predicting longitudinal dispersion coefficient in natural streams. J. Hydraul. Eng. 1998, 124, 25–32. [Google Scholar] [CrossRef]
- Kashefipour, S.M.; Falconer, R.A. Longitudinal dispersion coefficients in natural streams. Water Res. 2002, 36, 1596–1608. [Google Scholar] [CrossRef]
- Ribeiro, C.B.M.; da Silva, D.D.; Soares, J.H.P.; Guedes, H.A.S. Development and validation of an equation to estimate longitudinal dispersion coefficient in medium-sized rivers. Eng. Sanit. E Ambient. 2010, 15, 393–400. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Liu, H.; Yin, M. Differential evolution for prediction of longitudinal dispersion coefficients in natural streams. Water Resour. Manag. 2013, 27, 5245–5260. [Google Scholar] [CrossRef]
- Sahay, R.R. Predicting longitudinal dispersion coefficients in sinuous rivers by genetic algorithm. J. Hydrol. Hydromech. 2013, 61, 214–221. [Google Scholar] [CrossRef] [Green Version]
- Carr, M.L. An Efficient Method for Measuring the Dispersion Coefficient in Rivers. Ph.D. Thesis, University of Illinois, Urbana, IL, USA, 2007. [Google Scholar]
- Ahsan, N. Estimating the coefficient of dispersion for a natural stream. World Acad. Sci. Eng. Technol. 2008, 44, 131–135. [Google Scholar]
- Fischer, H.B.; List, E.J.; Koh, R.C.Y.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press, INC.: New York, NY, USA, 1979; p. 4. [Google Scholar]
- Fischer, H.B. The mechanics of dispersion in natural streams. J. Hydraul. Div. 1967, 93, 187–216. [Google Scholar] [CrossRef]
- Sharma, H.; Ahmad, Z. Transverse mixing of pollutants in streams: A review. Can. J. Civ. Eng. 2014, 41, 472–482. [Google Scholar] [CrossRef]
- Fischer, H.B. Longitudinal dispersion and turbulent mixing in open channel flow. Ann. Rev. Fluid Mech. 1973, 5, 59–78. [Google Scholar] [CrossRef]
- Sayre, W.W. Dispersion of Mass in Open Channel Flow. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 1968. [Google Scholar]
- Chatwin, P.C. The cumulants of the distribution of concentration of a solute in a solvent flowing along a straight tube. J. Fluid Mech. 1972, 51, 63–67. [Google Scholar] [CrossRef]
- Pannone, M. An analytical model of Fickian and non-Fickian dispersion in evolving-scale log-conductivity distributions. Water 2017, 9, 751. [Google Scholar] [CrossRef] [Green Version]
- Fischer, H.B. Dispersion predictions in natural streams. J. Sanit. Eng. Div. 1968, 94, 927–944. [Google Scholar] [CrossRef]
- Pannone, M.; Mirauda, D.; De Vincenzo, A.; Molino, B. Longitudinal Dispersion in Straight Open Channels: Anomalous Breakthrough Curves and First-Order Analytical Solution for the Depth-Averaged Concentration. Water 2018, 10, 478. [Google Scholar] [CrossRef] [Green Version]
- Aquino, T.; Aubeneau, A.; Bolster, D. Peak and tail scaling of breakthrough curves in hydrologic tracer tests. Adv. Water Resour. 2015, 78, 1–8. [Google Scholar] [CrossRef]
- Koussis, A.D.; Saenz, M.A.; Tollis, I.G. Pollution routing in streams. J. Hydraul. Eng. 1983, 109, 1636–1651. [Google Scholar] [CrossRef]


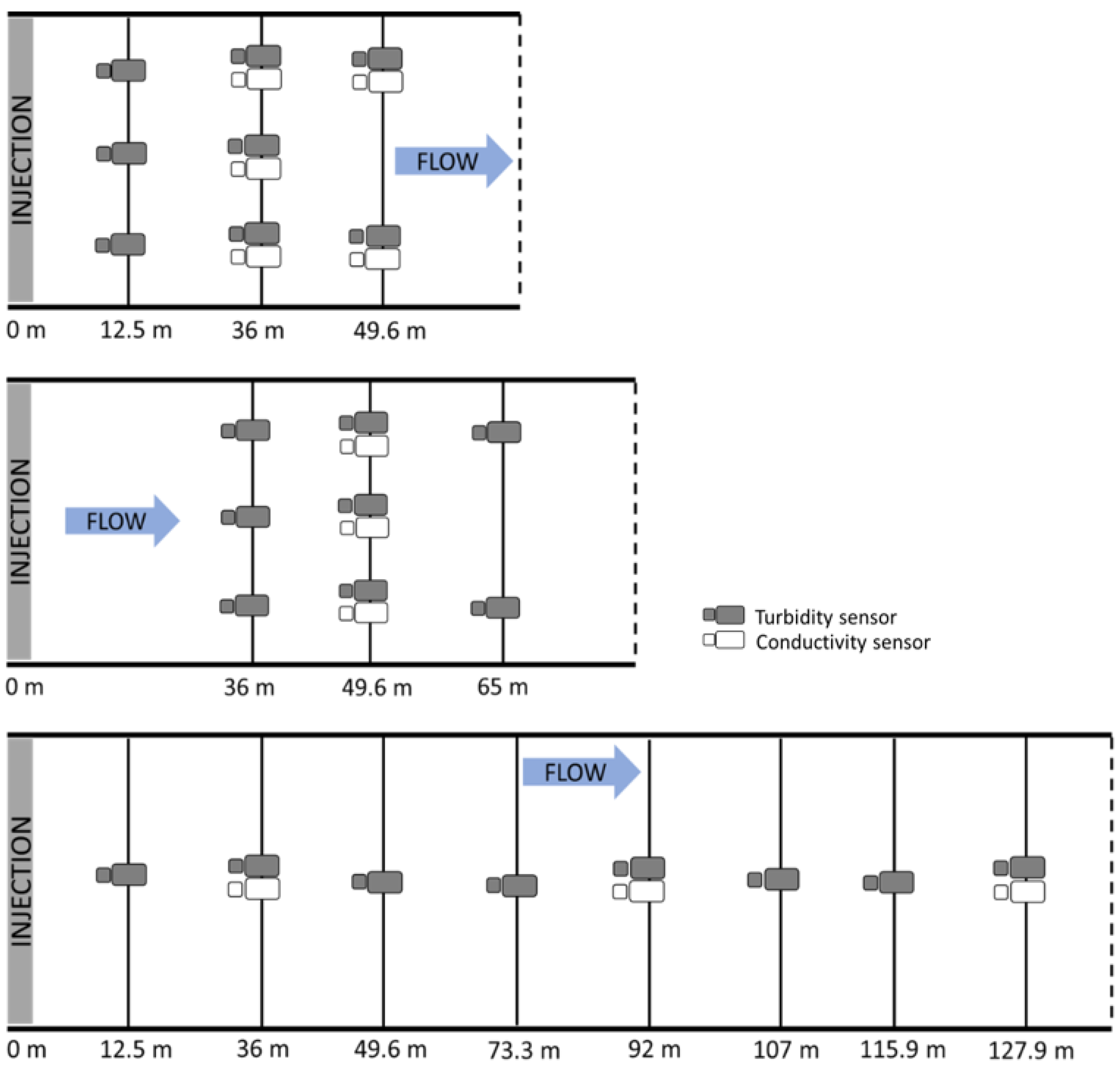


| Channel | Velocity (m s−1) | Flow Depth (m) | Top Width (m) | Shear Velocity (m s−1) | Froude Number |
|---|---|---|---|---|---|
| Concrete | 1.29 | 0.05 | 2.24 | 0.11 | 1.86 |
| Natural (runs NC 1.1–1.3) | 0.18 | 0.11 | 4.90 | 0.09 | 0.17 |
| Natural (runs NC 2.1–2.6) | 0.15 | 0.08 | 3.71 | 0.08 | 0.17 |
| Concrete Channel (Measurement Mocation 370.15 m) | |||
| Run | Kx (m2 s−1) | Peclet Number | R2 |
| CC-1 | 1.00 | 2.95 | 0.89 |
| CC-2 | - | - | - |
| CC-3 | 1.12 | 2.63 | 0.79 |
| CC-4 | 1.10 | 2.61 | 0.71 |
| CC-5 | 1.30 | 2.22 | 0.84 |
| CC-6 | 1.15 | 2.59 | 0.87 |
| CC-7 | 1.65 | 1.77 | 0.95 |
| CC-8 | 1.20 | 2.46 | 0.92 |
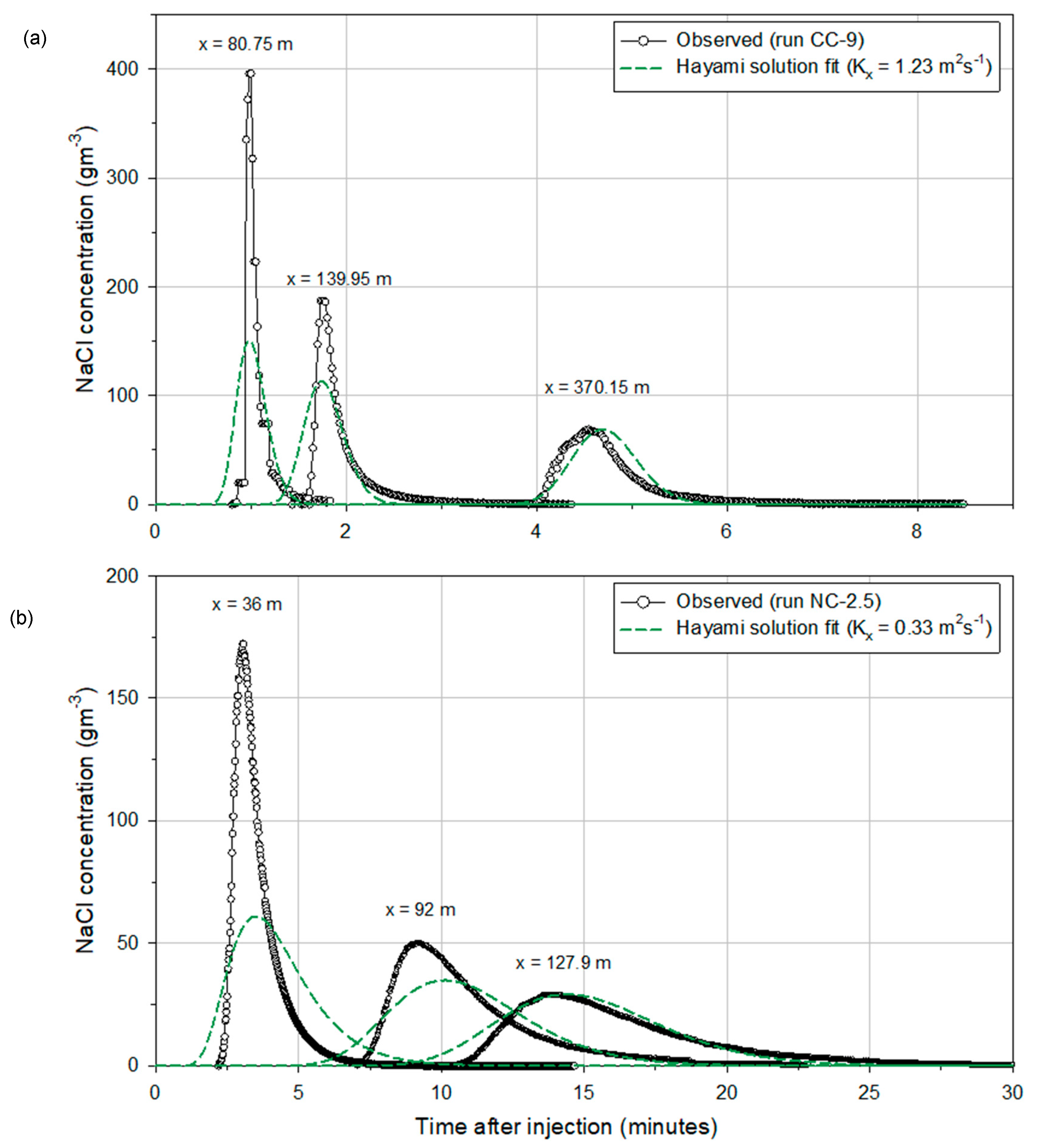
| CC-9 | 1.23 | 2.40 | 0.91 |
| AVG | 1.23 | 2.45 | |
| SD | 0.20 | 0.35 | |
| CV | 16% | 14 | |
| Natural Channel (Measurement Location 127.9 m) | |||
| Run | Kx (m2 s−1) | Peclet Number | R2 |
| NC-5 | 0.33 | 1.50 | 0.96 |
| NC-6 | 0.31 | 1.60 | 0.86 |
| Variable | Concrete Channel | Natural Channel |
|---|---|---|
| Location (m) | 370.15 | 127.9 |
| W (m) | 2.27 | 3.58 |
| H (m) | 0.05 | 0.09 |
| (m s−1) | 1.30 | 0.14 |
| A (m2) | 0.11 | 0.31 |
| Q (m3 s−1) | 0.143 | 0.042 |
| (m s−1) | 0.11 | 0.08 |
| W/H | 45 | 39.78 |
| 12 | 1.75 | |
| S | 0.025 | 0.012 |
| Fr | 1.87 | 0.16 |
| Si | 1.00 | 1.54 |
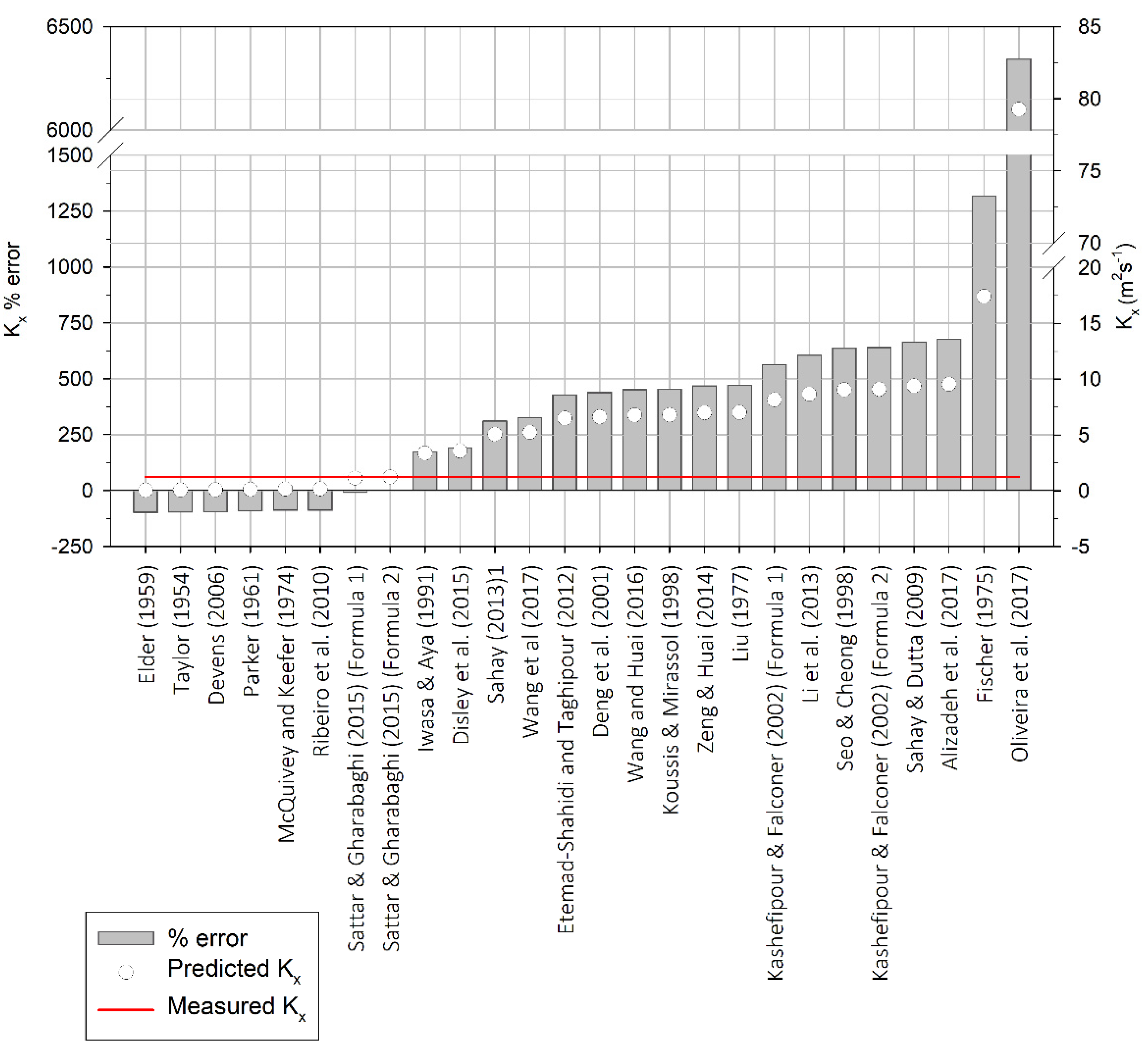
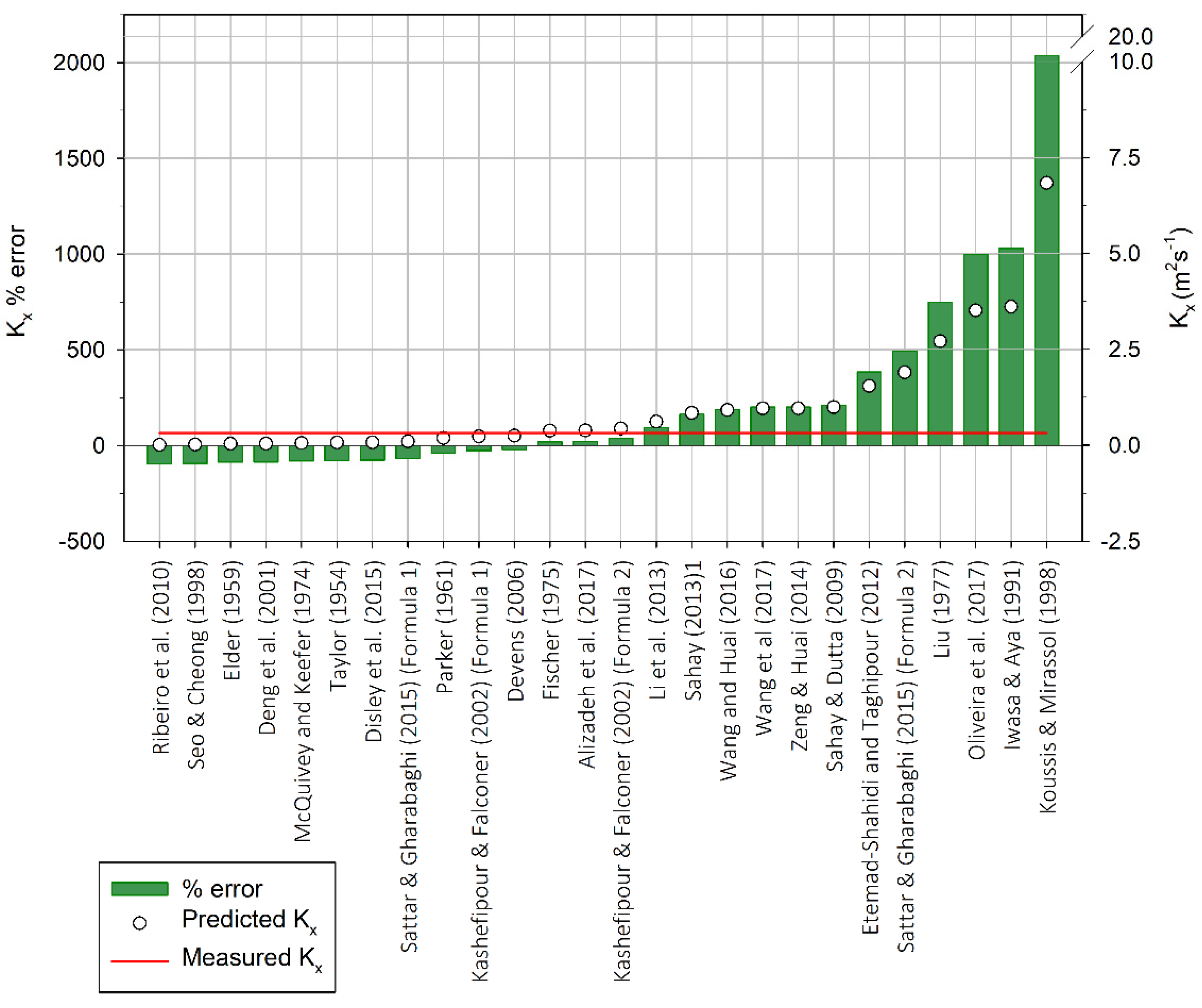
| Reference | Concrete Channel | Natural Stream |
|---|---|---|
| Kx (m2 s−1) | Kx (m2 s−1) | |
| Observed value (Hayami solution best-fit) | 1.23 | 0.32 |
| Taylor (1954) [26] | 0.06 | 0.07 |
| Elder (1959) [27] | 0.03 | 0.04 |
| Parker (1961) [10] | 0.11 | 0.19 |
| McQuivey and Keefer (1974) [9] | 0.15 | 0.06 |
| Fischer (1975) [28] | 17.42 | 0.38 |
| Liu (1977) [29] | 7.01 | 2.71 |
| Iwasa and Aya (1991) [23] | 3.36 | 3.61 |
| Koussis and Mirassol (1998) [30] | 6.80 | 6.84 |
| Seo and Cheong (1998) [31] | 9.05 | 0.02 |
| Deng et al. (2001) [18] | 6.62 | 0.04 |
| Kashefipour and Falconer (2002) [32] (Formula (1)) | 8.15 | 0.23 |
| Kashefipour and Falconer (2002) [32] (Formula (2)) | 9.10 | 0.44 |
| Devens (2006) [11] | 0.08 | 0.25 |
| Sahay and Dutta (2009) [14] | 9.39 | 0.99 |
| Ribeiro et al. (2010) [33] | 0.15 | 0.01 |
| Etemad-Shahidi and Taghipour (2012) [15] | 6.50 | 1.55 |
| Li et al. (2013) [34] | 8.67 | 0.62 |
| Sahay (2013) [35] | 5.06 | 0.84 |
| Zeng and Huai (2014) [20] | 6.99 | 0.96 |
| Disley et al. (2015) [12] | 3.56 | 0.07 |
| Sattar and Gharabaghi (2015) [13] (Formula (1)) | 1.13 | 0.10 |
| Sattar and Gharabaghi (2015) [13] (Formula (2)) | 1.23 | 1.90 |
| Wang and Huai (2016) [19] | 6.77 | 0.92 |
| Alizadeh et al. (2017) [16] | 9.55 | 0.39 |
| Oliveira et al. (2017) [21] | 79.26 | 3.51 |
| Wang et al. (2017) [17] | 5.23 | 0.96 |
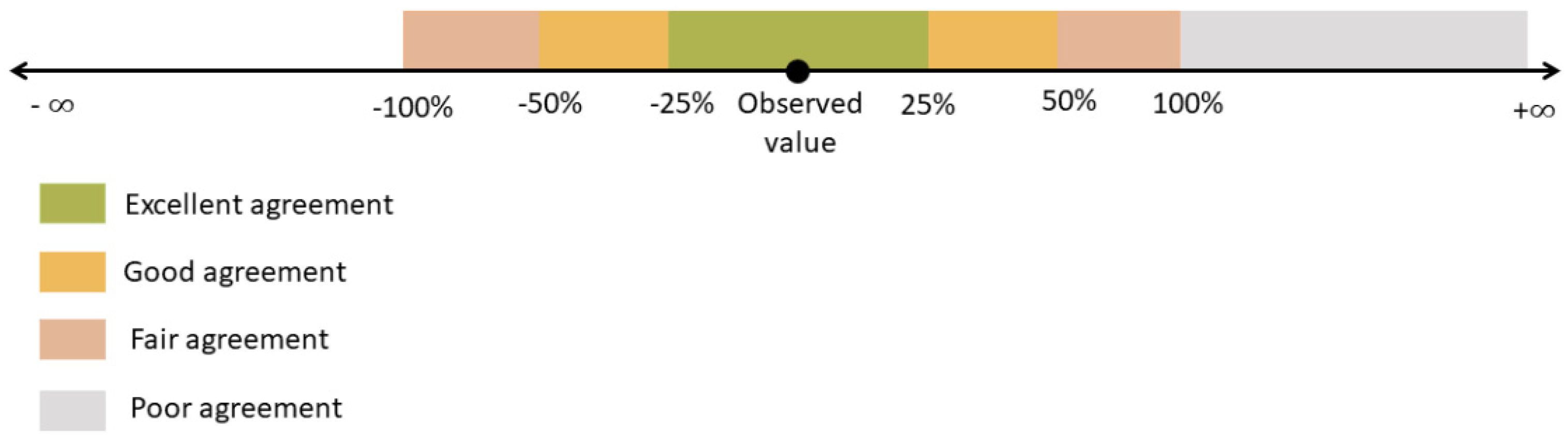
| Reference | Kx | Relative % Error | Level of Agreement | |||
|---|---|---|---|---|---|---|
| Cpeak | tpeak | tstart | Duration | |||
| Elder (1959) [27] | 0.03 | 506 | 4 | 15 | −83 | P |
| Taylor (1954) [26] | 0.06 | 365 | 4 | 13 | −77 | P |
| Devens (2006) [11] | 0.08 | 299 | 4 | 12 | −74 | P |
| Parker (1961) [10] | 0.11 | 228 | 4 | 11 | −68 | P |
| McQuivey and Keefer (1974) [9] | 0.15 | 183 | 4 | 9 | −64 | P |
| Ribeiro et al. (2010) [33] | 0.15 | 180 | 4 | 9 | −63 | P |
| Sattar and Gharabaghi (2015) [13] (Formula (1)) | 1.13 | 4 | 3 | −7 | −5 | E |
| Sattar and Gharabaghi (2015) [13] (Formula (2)) | 1.23 | 0 | 3 | −7 | −2 | E |
| Iwasa and Aya (1991) [23] | 3.36 | −39 | 2 | −21 | 56 | F |
| Disley et al. (2015) [12] | 3.56 | −41 | 1 | −22 | 60 | F |
| Sahay (2013) [35] | 5.06 | −50 | 1 | −28 | 88 | F |
| Wang et al. (2017) [17] | 5.23 | −51 | 1 | −29 | 92 | F |
| Etemad-Shahidi and Taghipour (2012) [15] | 6.50 | −56 | 0 | −33 | 111 | P |
| Deng et al. (2001) [18] | 6.62 | −56 | 0 | −33 | 113 | P |
| Wang and Huai (2016) [19] | 6.77 | −56 | 0 | −34 | 115 | P |
| Koussis and Mirassol (1998) [30] | 6.80 | −56 | 0 | −34 | 116 | P |
| Zeng and Huai (2014) [20] | 6.99 | −57 | 0 | −34 | 118 | P |
| Liu (1977) [29] | 7.01 | −57 | 0 | −34 | 119 | P |
| Kashefipour and Falconer (2002) [32] (Formula (1)) | 8.15 | −60 | −1 | −37 | 134 | P |
| Li et al. (2013) [34] | 8.67 | −61 | −2 | −39 | 141 | P |
| Seo and Cheong (1998) [31] | 9.05 | −62 | −2 | −39 | 146 | P |
| Kashefipour and Falconer (2002) [32] (Formula (2)) | 9.10 | −62 | −2 | −39 | 146 | P |
| Sahay and Dutta (2009) [14] | 9.39 | −62 | −2 | −40 | 149 | P |
| Alizadeh et al. (2017) [16] | 9.55 | −63 | −2 | −40 | 151 | P |
| Fischer (1975) [28] | 17.42 | −71 | −7 | −53 | 229 | P |
| Oliveira et al. (2017) [21] | 79.26 | −82 | −35 | −82 | 520 | P |
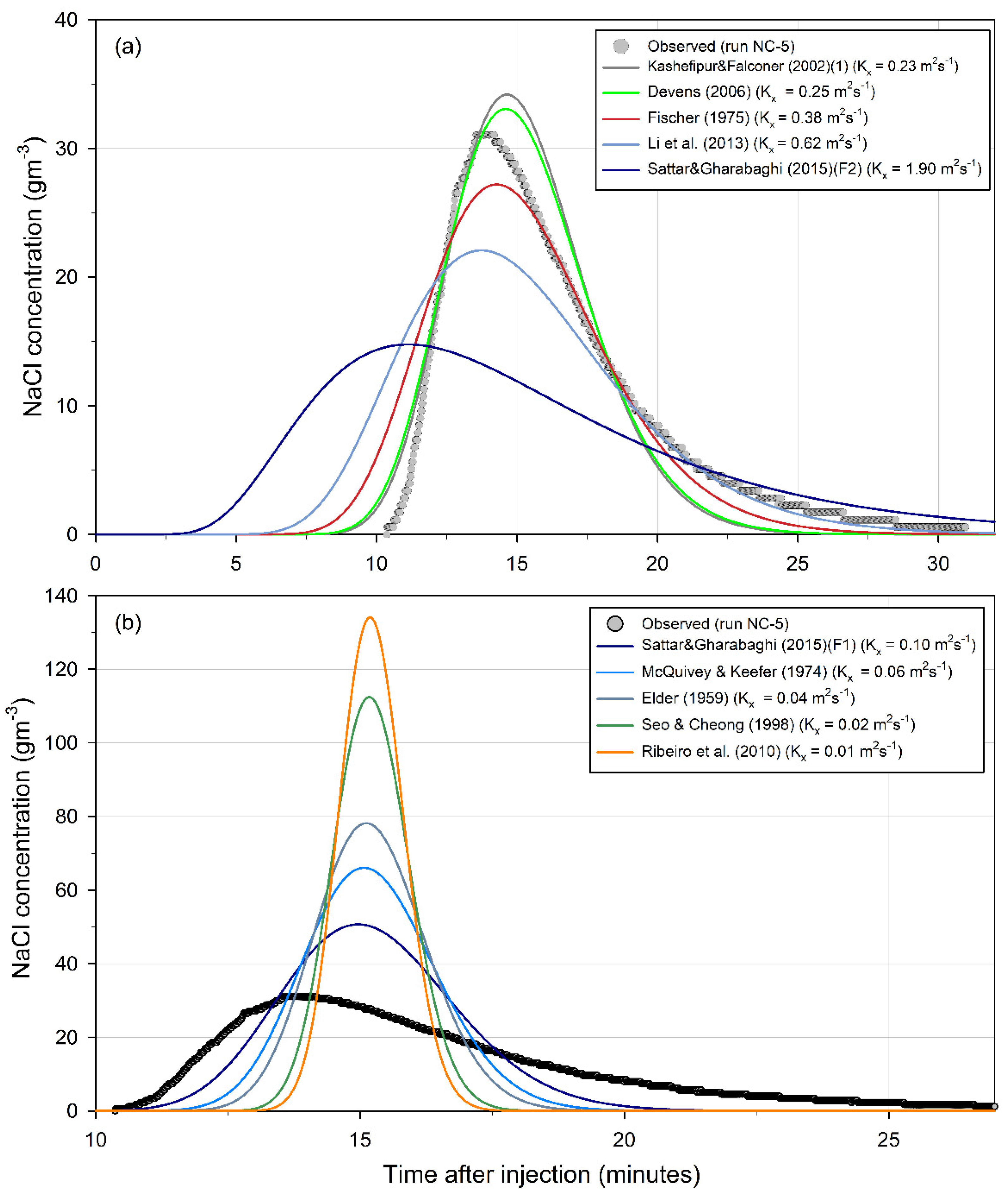
| Reference | Kx | Relative % Error | Level of Agreement | |||
|---|---|---|---|---|---|---|
| Cpeak | tpeak | tstart | Duration | |||
| Ribeiro et al. (2010) [33] | 0.01 | 338 | 18 | 33 | −78 | P |
| Seo and Cheong (1998) [31] | 0.02 | 267 | 18 | 30 | −75 | P |
| Elder (1959) [27] | 0.04 | 155 | 18 | 20 | −64 | P |
| Deng et al. (2001) [18] | 0.04 | 154 | 18 | 20 | −64 | P |
| McQuivey and Keefer (1974) [9] | 0.06 | 116 | 17 | 15 | −58 | P |
| Taylor (1954) [26] | 0.07 | 96 | 17 | 12 | −54 | F |
| Disley et al. (2015) [12] | 0.07 | 94 | 17 | 11 | −53 | F |
| Sattar and Gharabaghi (2015) [13] (Formula (1)) | 0.10 | 66 | 17 | 5 | −46 | F |
| Parker (1961) [10] | 0.19 | 24 | 15 | −8 | −29 | G |
| Kashefipour and Falconer (2002) [32] (Formula (1)) | 0.23 | 12 | 14 | −13 | −21 | E |
| Devens (2006) [11] | 0.25 | 8 | 14 | −15 | −19 | E |
| Fischer (1975) [28] | 0.38 | −11 | 11 | −26 | −2 | G |
| Alizadeh et al. (2017) [16] | 0.39 | −12 | 11 | −26 | −1 | G |
| Kashefipour and Falconer (2002) [32] (Formula (2)) | 0.44 | −16 | 10 | −29 | 4 | G |
| Li et al. (2013) [34] | 0.62 | −28 | 7 | −38 | 22 | G |
| Sahay (2013) [35] | 0.84 | −37 | 3 | −47 | 40 | G |
| Wang and Huai (2016) [19] | 0.92 | −39 | 2 | −49 | 45 | G |
| Wang et al. (2017) [17] | 0.96 | −40 | 1 | −50 | 48 | G |
| Zeng and Huai (2014) [20] | 0.96 | −40 | 1 | −51 | 48 | F |
| Sahay and Dutta (2009) [14] | 0.99 | −40 | 0 | −51 | 50 | F |
| Etemad-Shahidi and Taghipour (2012) [15] | 1.55 | −49 | −8 | −63 | 81 | F |
| Sattar and Gharabaghi (2015) [13] (Formula (2)) | 1.90 | −52 | −13 | −68 | 98 | F |
| Liu (1977) [29] | 2.71 | −55 | −24 | −75 | 129 | P |
| Oliveira et al. (2017) [21] | 3.51 | −57 | −32 | −80 | 153 | P |
| Iwasa and Aya (1991) [23] | 3.61 | −57 | −33 | −80 | 156 | P |
| Koussis and Mirassol (1998) [30] | 6.84 | −56 | −55 | −89 | 221 | P |
| Reference | Consistent Overestimate | Consistent Underestimate | CC Overestimate, NC Underestimate |
|---|---|---|---|
| Taylor (1954) [26] | ● | ||
| Elder (1959) [27] | ● | ||
| Parker (1961) [10] | ● | ||
| McQuivey and Keefer (1974) [9] | ● | ||
| Fischer (1975) [28] | ● | ||
| Liu (1977) [29] | ● | ||
| Iwasa and Aya (1991) [23] | ● | ||
| Koussis and Mirassol (1998) [30] | ● | ||
| Seo and Cheong (1998) [31] | ● | ||
| Deng et al. (2001) [18] | ● | ||
| Kashefipour and Falconer (2002) [32] (Formula (1)) | ● | ||
| Kashefipour and Falconer (2002) [32] (Formula (2)) | ● | ||
| Devens (2006) [11] | ● | ||
| Sahay and Dutta (2009) [14] | ● | ||
| Ribeiro et al. (2010) [33] | ● | ||
| Etemad-Shahidi and Taghipour (2012) [15] | ● | ||
| Li et al. (2013) [34] | ● | ||
| Sahay (2013) [35] | ● | ||
| Zeng and Huai (2014) [20] | ● | ||
| Disley et al. (2015) [12] | ● | ||
| Sattar and Gharabaghi (2015) [13] (Formula (1)) | ● | ||
| Sattar and Gharabaghi (2015) [13] (Formula (2)) | ● | ||
| Wang and Huai (2016) [19] | ● | ||
| Alizadeh et al. (2017) [16] | ● | ||
| Oliveira et al. (2017) [21] | ● | ||
| Wang et al. (2017) [17] | ● |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nogare, M.A.; Bauer, B.O. A Field-Based Evaluation of the Reliability of Empirical Formulae for Quantifying the Longitudinal Dispersion Coefficient in Small Channels. Geosciences 2022, 12, 281. https://doi.org/10.3390/geosciences12070281
Nogare MA, Bauer BO. A Field-Based Evaluation of the Reliability of Empirical Formulae for Quantifying the Longitudinal Dispersion Coefficient in Small Channels. Geosciences. 2022; 12(7):281. https://doi.org/10.3390/geosciences12070281
Chicago/Turabian StyleNogare, Marianni A., and Bernard O. Bauer. 2022. "A Field-Based Evaluation of the Reliability of Empirical Formulae for Quantifying the Longitudinal Dispersion Coefficient in Small Channels" Geosciences 12, no. 7: 281. https://doi.org/10.3390/geosciences12070281






