Full Waveform Inversion Based on an Asymptotic Solution of Helmholtz Equation

Abstract

This study considers the full waveform inversion (FWI) method based on the asymptotic solution of the Helmholtz equation. We provide frequency-dependent ray tracing to obtain the wave field used to compute the FWI gradient and calculate the modeled data. With a comparable quality of the inverse problem solution as applied to the standard finite difference approach, the speed of the calculations in the asymptotic method is an order of magnitude higher. A series of numerical experiments demonstrate the approach’s effectiveness in reconstructing the macro velocity structure of complex media for low frequencies.

1. Introduction

In recent years, seismic methods have been used to solve geological problems that have become more difficult. The requirements have become greater for more detailed and reliable forecasts when interpreting seismic data. The search for new deposits is carried out in difficult geological or engineering conditions. To successfully address the emergence of new deposits in practice, it is necessary to involve new methods of seismic data processing to extract as complete and reliable information about the structure as possible in the environment. One such method that has attracted the increased attention of specialists in recent years is full waveform inversion (FWI).

In the early 1980s, P. Lailly and A. Tarantola [1,2] reformulated the principle construction of migration images [3] as a local minimization problem based on the least-squares method in relation to the reduction in the difference between the observed and synthetic data. They showed that the penalty function gradient, along which they sought the model perturbation, can be constructed by cross-correlation of the incident wave emitted by the source, and the difference between the observed and simulated wave fields continues in reverse time. When the model is adjusted after the first iteration it appears to be applying the migration in reverse time (RTM is an abbreviation for reverse time migration). The received updated model is used as a starting point for the next iteration of the FWI method. Thus, the gradient calculation provides a very impressive increase in the amount of information and the possibility of moving on to determining the physical parameters of the studied geological object. The process of constructing images by comparing the recorded and calculated wave fields requires very significant computing resources, even for two-dimensional settings [4].

Nevertheless, this approach has been successfully applied in several studies using various methods for modeling wave fields, such as finite difference methods [5,6] and finite element methods [7]. An approach that does not require such significant computational costs was proposed in the works of [8,9]. This modification uses the theoretical relationship between the generalized Radon transform [10] and the least-squares minimization proposed in [11]. Usage of a particular norm in the data space allows interpreting the asymptotic representation of the Radon transform as iterative least-squares minimization. Since Green’s functions calculation uses the ray method in a smoothed model, the direct problem utilizes linearized Born approximation. The family of these methods is called “migration/inversion” or pre-stack true amplitude migration. The major difference between this approach and FWI is that the smooth macro velocity model does not change from iteration to iteration during the minimization process. The changes undergo only local perturbations of the smooth macro velocity model to generate scattered wave fields. Conversely, FWI simulates the full wave field at each iteration. Thus, all types of waves are included in the consideration: refracted waves, supercritical reflections, multiple reflections, etc.

Methods for numerical modeling of wave fields are highly diverse. They include the finite element method [12], the finite difference method [13], the finite volume method [14], pseudospectral methods representations [15], the generalized screen method, the discrete wave number method, the generalized ray method WKBJ, Maslov’s method [16], and the Born series method [17].

Modern implementations of FWI attempt to recover a sufficiently broad spatial spectrum of the model, combining the construction of a macro velocity model and a migration image in one procedure. Examples of wide azimuth data illustrate the possibility of recovering all spatial spectrums of the medium [18]. We emphasize that sustainability data inversion at large offsets is not yet a fully explored problem due to the increasing nonlinearity of the problem introduced by wave fields propagating over tens of lengths waves and the need to take different propagation angles into account [19]. However, the source-extended formulation of FWI solved this issue by adding wave fields as an extra variable into the inversion [20,21,22]. Some of the recent researches have investigated multiparameter FWI [23], and FWI solutions in complex models, for example, containing high contrast salt bodies [24]. Another important direction for providing new solutions is based on the application of accurate forward modeling techniques [25].

The standard acquisition system used in 3D seismic surveys includes tens of thousands to hundreds of thousands of sources corresponding to different right-hand sides in the seismic modeling problem. When calculating a complete set of seismic data, it is necessary to solve a series of hundreds of thousands of tasks. At the same time, the spatial discretization of each such problem requires more than 10¹¹ degrees of freedom and, as a result, several TB of RAM. Each separate task, the calculation of one source’s field, requires a supercomputer. As a result, the necessary computational resources for modeling seismic data for a typical acquisition system can be estimated at 10⁸ core hours (per CPU). These estimates are correct for an isotropic elastic medium. There will be multiple increases in the need for computing resources with the complication model. As a result, such full-scale calculations are practically tricky to solve (one calculation takes several months). Therefore, developing new methods for numerical modeling of wave seismic fields and the acceleration of algorithms for such modeling is an extremely urgent task.

Asymptotic methods are much faster than finite difference or finite element methods, which are used in most of the developed inversion algorithms. Asymptotic solutions exist both in acoustic and isotropic, anisotropic, and viscoelastic media [26,27,28], making it possible to consider these complex features of the geological environment. At the same time, the computational cost does not increase in contrast to the use of “heavy” standard inversion. Of course, it is worth noting here that the frequency-dependent asymptotic solutions have advantages compared with the classical ray-based approaches to solving the wave equation. Therefore, in this work, we use frequency-dependent rays (Lomax, 1984), and we pose the task of checking the possibility of the practical application of the frequency-dependent asymptotic solution of the Helmholtz equation in the FWI method in a two-dimensional setting in the time–frequency domain.

2. FWI: From Standard to Asymptotic

Let the function $u(x,z;\omega )$ (full waveform in the frequency domain (time frequency)) satisfy the Helmholtz equation:

$$\left(∆+{\omega }^{2}m\right)u=-f\left(\omega \right)\delta (x-x_s)\delta (z-z_s),$$

(1)

where $f\left(\omega \right)$ is the spectral characteristic of the source signature, $\omega$ is the angular frequency, ${(x}_s,z_s)$ is the source coordinates, $m=c^{-2}(x,z)$ is the squared slowness, and $c(x,z)$ is the wave propagation speed. The Helmholtz equation applies to the pressure in an acoustic medium with constant density rather than in a general acoustic medium.

Let us introduce an operator that calculates the data of the full waveform from one point source for a fixed time–frequency at the points corresponding to the location of the receivers, so we obtain the following forward modeling operator:

$$F:M\to D,$$

(2)

where $D$ is the data space, and $M$ is the model space. In this notation, the inverse dynamical problem of constructing a velocity model from seismic data is reduced to solving a nonlinear operator equation:

$$d^{obs}=F\left(m_{true}\right),$$

(3)

where $d^{obs}$ is the observed data and $m_{true}$ is the “true” velocity model. The full waveform inversion (FWI) applies a nonlinear least-squares method to Equation (3). The FWI formulation is to find the minimum point of the misfit functional characterizing the mean square deviation of the recorded data from those calculated for the current velocity model [2,11]:

$$m_{\ast }=arg \underset{m\in M}{min}{\Vert F\left(m\right)-d^{obs}\Vert }_D^2.$$

(4)

Typically, local optimization techniques such as the nonlinear conjugate gradient method are applied to minimize the objective function (its application in the context of FWI can be found in the paper by [29]):

$$m_{k+1}=m_k+{\mu }_k{S}_k, S_0={\nabla }_0,$$

(5)

$$S_k=-{\nabla }_k-\frac{〈{\nabla }_k,{\nabla }_k-{\nabla }_{k-1}〉}{〈{\nabla }_{k-1},{\nabla }_{k-1}〉}{S}_{k-1},$$

(6)

where $m_k$ is the model at the k-th iteration, and ${\mu }_k$ is the parameter that controls the length of the step along the gradient at the k-th iteration. The gradient ${\nabla }_k$ is calculated as follows:

$${\nabla }_k=Re\{{\omega }^2{\sum }_{s,r,\omega }G\left({x,z;x}_s,z_s;\omega ;m_k\right)·G({x,z;x}_r,z_r;\omega ;m_k)\overline{\delta d_{s,r}}\},$$

(7)

where $Re$ is the real part, $G\left({x,z;x}_s,z_s;\omega ;m_k\right)$ is the Green’s function calculated in the model $m_k$ for the source located in the point $\left(x_s,z_s\right)$, $G({x,z;x}_r,z_r;\omega ;m_k)$ is the Green’s function calculated in the model $m_k$ for the receiver point ($x,z)$ and the source point ${(x}_r,z_r)$, $\delta d_{s,r}={F\left(m_k\right)}_{s,r}-d_{s,r}$ is the data misfit registered in the receiver point ${(x}_r,z_r)$ and generated in the source point $\left(x_s,z_s\right),$ $\overline{\delta d_{s,r}}$ is the adjoint of $\delta d_{s,r}$. Thus, the gradient calculation is reduced to the calculation of Green’s functions for all positions of sources and receivers, which means that the acceleration of the calculations of this particular part is of big interest. In this approach, Green’s functions are calculated using the asymptotic method based on frequency-dependent ray tracing [30].

3. Asymptotic Solution of Helmholtz Equation

This section briefly describes the algorithm for constructing frequency-dependent Lomax rays [30] and emphasizes their difference from standard rays.

The key point in the Lomax method is the smoothing of velocities along with the current position on the front. A smooth Gaussian function within the Fresnel volume averages the velocity for a given frequency. The points for averaging are located symmetrically with respect to the central point. The maximum distance from the central point (or averaging aperture) is determined by the frequency specified in wavelengths. Then edge points (at the aperture edge) are selected symmetrically. The smoothed velocities are calculated at each of the three points (central and two edge points). For them, the same direction of smoothing along the normal is used. Assuming that the front remains locally flat, from simple geometric considerations, one can obtain an expression for the correction to the tangent vector to the ray and find the direction vector at the next point on the ray. Thus, there is a movement along the ray. The tracing is carried out in a particular volume of the medium since the movement of edge points affects the front position. This algorithm becomes equivalent to the standard ray tracing when the local velocity replaces the average velocity at a point on the ray.

Next, we present the formulas needed to calculate Green’s functions in the full wave inversion problem in the frequency domain using the described frequency-dependent rays. For that, it is necessary to calculate the Green’s function at a given frequency $\omega$ on a regular grid for a fixed position of the source $S={(x}_s,z_s)$. In the two-dimensional case, the expression for the Green’s function calculated in the model $m_k$ at the point ${R=(x}_r,z_r)$ with a source located at a point $S$, is defined as [31]:

$$G\left(S,R;\omega ;m_k\right)=S\left(\omega \right)A(S,R;\omega )exp \left(i\omega \tau \right(S,R;\omega \left)\right).$$

(8)

Here $\mathrm{\tau }(S,R;\omega )$ is the frequency-dependent travel time, multiplier $S\left(\omega \right)=\sqrt{-1/i\omega }$, $A(S,R)$ is the frequency-dependent amplitude determined by the ray method and is given by the expression:

$$A\left(S,R;\omega \right)=\sqrt{c_k\left(R\right)/(8\pi {·c}_k\left(S\right)·J\left(S,R;\omega \right))}.$$

(9)

Here $c_k\left(R\right),c_k\left(S\right)$ are the velocity values in the corresponding points, $J\left(S,R;\omega \right)$ is the frequency-dependent geometrical spreading:

$$J\left(S,R;\omega \right) ~ \delta L(S,R;\omega )/\delta {\theta }_s.$$

(10)

Here $\delta L(S,R;\omega )$ is the frequency-dependent width of the ray tube in the point $R$, $\delta {\theta }_s$ is a variation of the takeoff ray angle providing the ray tube. Travel times, geometrical spreading, and the ray tube are frequency-dependent because the rays are frequency-dependent. Thus, having a calculated field of rays at a given position of the source, Equations (8)–(10) can be used to calculate the corresponding Green’s function.

4. Numerical Experiments

The purpose of our numerical experiments is to determine the limits of applicability of the asymptotic full waveform inversion method. For that, we provide a comparison of the asymptotic and the finite difference solutions of the Helmholtz equation, FWI gradients, and, finally, full waveform inversion. We consider the finite difference solution as the best achievable reference solution in all experiments.

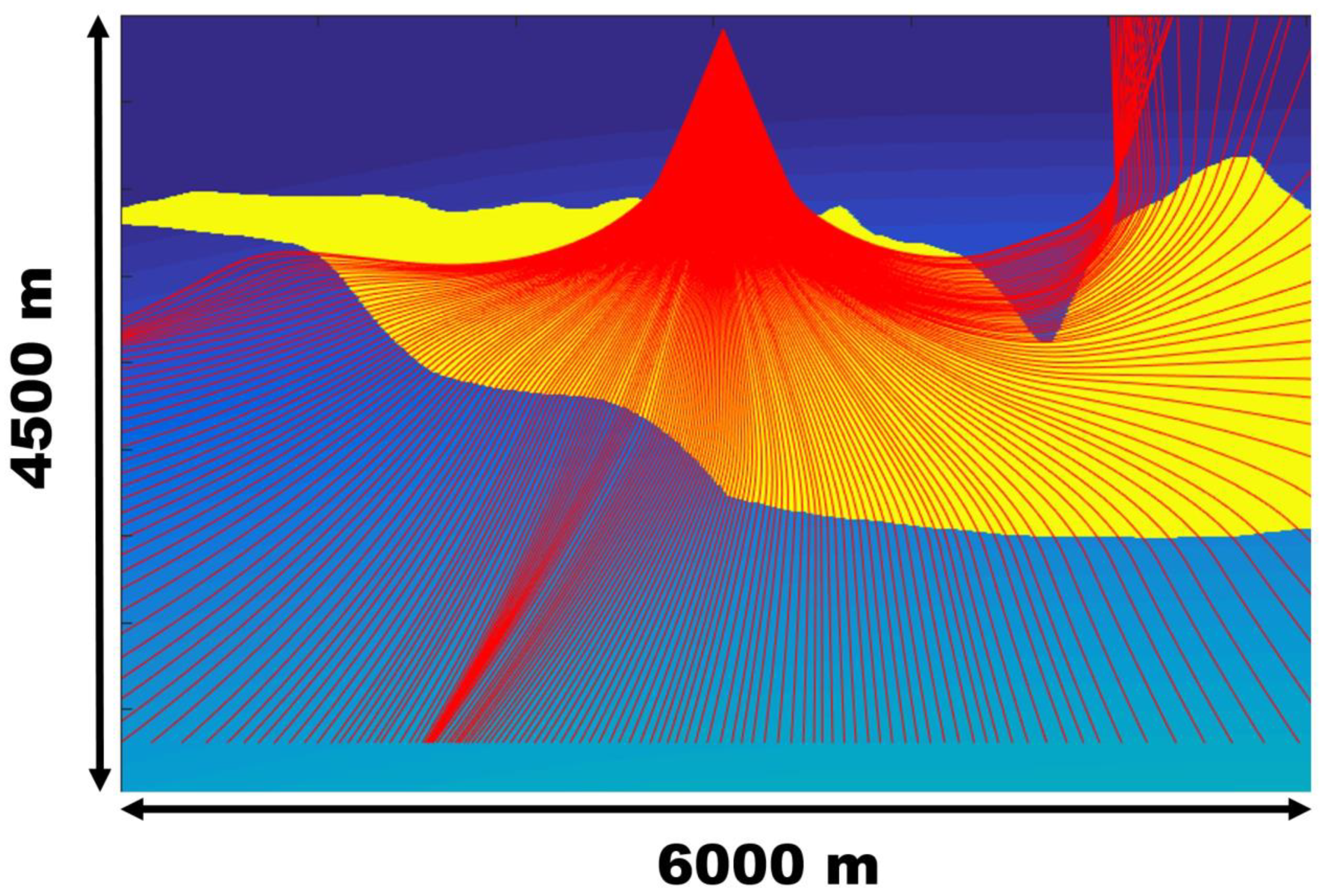
One of the significant problems that arises when using the ray method is tracing through contrast interfaces, for example, the boundaries of salt bodies. Salt bodies can have a very complex shape, and seismic wave velocities in salt are higher than in sedimentary rocks surrounding the salt intrusion. For these reasons, it is very problematic to construct rays passing through the salt body. Figure 1 shows a fragment of the famous Sigsbee model with a salt body of complex shape (shown in yellow), where the speed is 4500 m/s. There are also Lomax rays constructed for 5 Hz (shown in red). As one can see, rays pass through the salt body, do not form shadow zones, and generally correspond to the “physics” of the wave field propagation process.

Next, we give an example of calculating the wavefield using Lomax rays and comparing it with the finite difference method results. Figure 2a,b show the wave fields in the frequency domain at a frequency of 10 Hz (real part), constructed by finite difference and ray methods. One can see that the wave field formed using the Lomax rays corresponds to the wave field calculated by the finite difference method. Moreover, Figure 2 shows the vertical and horizontal sections of the wave field computed by the finite difference solution and the frequency-dependent Lomax ray solution, where one can observe a good match between the solutions. The relative difference in the target area does not exceed 3%. Thus, we have shown numerically that Lomax rays effectively calculate wave fields in fairly complex media.

Table 1. Calculation times of wave field for one source on one processor core in the Sigsbee model and the error of the ray method relative to the result of finite difference modeling.

	Calculation Time	Relative Error
Finite difference	~80 s	-
Standard rays	~2 s	7.5%
Lomax rays	~5 s	3.6%

summarizes the characteristics of the described numerical experiments. We compare the computation time for the finite difference and ray methods and the error of the ray method relative to finite difference modeling. One can see that the calculation time of the ray method, both using standard rays and Lomax rays, is several tens of times less than the calculation time of the finite difference method. At the same time, the solution error when using Lomax rays does not exceed 4%, even for such a complex model as Sigsbee.

To test the proposed approach of the asymptotic full waveform inversion, we took the Marmousi model, which is the benchmark for testing inversion algorithms (Figure 3a). Target dimensions of the investigated area are 9200 m laterally and 3000 m in depth (the first 500 m of the velocity model is a water layer, which is considered as being known). The computational grid consists of 921 horizontal points and 351 points vertically (space step 10 m). The acquisition system consists of 91 sources and 459 geophones located on the water’s surface, with steps of 100 m and 20 m, respectively. We use a Gaussian smoothed true velocity distribution as an initial approximation (Figure 3b).

Before providing FWI numerical experiments, we compare the gradients. We calculate the gradients in the starting model (Figure 3b) for the classical formulation and the asymptotic FWI. We show the calculated gradients for a frequency of 3 Hz in Figure 4. As one can see, the gradients visually coincide, which is explained by the fact that the starting model is smooth, the wave pattern in it is pretty simple, and, consequently, the asymptotic solution based on the ray approximation works well.

For quantitative estimates of the comparison of the gradients, we introduce the value MAPE (Mean Absolute Percentage Error)—the average relative error in a percent:

$$MAPE\left(a,b\right)=\sum _{i=1}^{nx}\sum _{j=1}^{ny}\left|\frac{a_{i,j}-b_{i,j}}{nx·ny·a_{i,j}}\right|\times 100\%$$

(11)

where a is the reference grid function (standard), b is the grid function for which the comparison is made, nx and nz are the numbers of points in the computational grid horizontally and in depth, respectively. The MAPE value between the classical and asymptotic gradient is 2.7%.

With this numerical experiment, we demonstrate the possibility of applying the asymptotic approach to the inversion full wave field to refine the macro velocity model at a frequency of 3 Hz. Figure 5 presents the inversion results. As one can observe, the model reconstructed using the asymptotic solution of the Helmholtz equation is generally similar to the result of the classical inversion (MAPE is 1.5%, see

Table 2. The MAPE value between the velocity models obtained via different inversion scenarios: v_true is the true velocity model; v_fd is the result of the classical full waveform inversion method; v_asym is the result of the asymptotic inversion.

Inversion\MAPE	(vasym, vfd)	(vtrue, vfd)	(vtrue, vasym)
3 Hz	1.5%	7.5%	7.7%
{5,7,10} Hz	4.0%	5.7%	7.1%

). For a more detailed analysis of the results, we compare vertical profiles for three different lateral coordinates (Figure 6). Based on this comparison, one can conclude that even for such a complex model as Marmousi, usage of the asymptotic approximation provides the refinement of the macro velocity model at low frequencies. Indirectly, we confirm this observation by comparing the observed and calculated wave fields in the model after inversion (Figure 7). One can see that for low temporal frequencies, the reconstructed velocity models for both scenarios can explain most of the observed data.

At the final stage, we performed a simultaneous inversion experiment for a set of three temporal frequencies: {5, 7, 10} Hz. Here, as the initial velocity model for minimization by the conjugate gradient method, we use the models obtained after inversion for a frequency of 3 Hz (Figure 5), respectively, for each inversion scenario. We show the corresponding inversion results in Figure 8. The MAPE value between classical inversion and asymptotic is 4%.

More detailed MAPE analysis for various treatment scenarios is presented in Table 2. By reducing the error of the result of the conversion relative to the true model, one can see that in both cases, the model improves. However, the result of classical inversion is better because the error with respect to the true model is smaller. Visual quality control leads us to conclude that the refined velocity model for the classical reversal scenario looks better, especially in the area from X = 4000 m to X = 7000 m. We explain this observation by the presence of complex geological structures in this part of the model and, as a result, with a complex wave pattern. The asymptotic solution starts to deviate more from the true velocity model than in the previous experiment for a frequency of 3 Hz, and, therefore, the inversion result becomes worse.

Figure 9 provides a more detailed comparison of the vertical velocity profiles. One can see that for the vertical profiles corresponding to the coordinates X = 2000 m and X = 8000 m, the inversion results are comparable. At that time, for the vertical profile X = 5000 m, the result of the asymptotic treatment is significantly inferior to the classical approach.

5. Conclusions and Discussions

This paper considers the numerical implementation of the full waveform inversion method for two-dimensional acoustic media in two settings: classical and asymptotic. The classic solution consists of implementing the nonlinear least-squares method as applied to the inverse dynamic seismic problem and is based on a computationally expensive procedure for the finite difference solution of the Helmholtz equation using an explicit fourth-order scheme. The asymptotic approach applies the frequency-dependent ray method to solve the wave equation and allows an order of magnitude to speed up the procedure for constructing the gradient—the most challenging part of solving the inverse problem. Solutions to the inverse problem at low frequencies show that the asymptotic result is comparable to the result of the classical inversion algorithm. However, at higher time frequencies, the quality of the asymptotic solution is not as good as finite difference in areas with complex geological structures. These conclusions mean that the proposed asymptotic FWI provides the possibility of recovering the macro velocity component of the model within a reasonable computational time without losing the accuracy of reconstruction. A series of numerical experiments on test material demonstrates the possibility of applying the proposed modification of the full waveform inversion method even for complex environment models.

The basis of the asymptotic FWI method and of the standard FWI is the same. The difference is Green’s function computations only. Therefore, results of the standard FWI are the best achievable results of the asymptotic FWI. Thus, we can expect a difference in the FWI results when Green’s function has a difference, and vice versa if the asymptotic Green’s function provides a solution that is close to the finite difference solution, and then the FWI results are similar. In this sense, on one hand, we can expect good asymptotic FWI results when we have a 1D initial model or any smooth initial model where the frequency-dependent ray method works. On the other hand, the asymptotic FWI inherits most of the problems of the standard FWI; for example, the local minimum problem. Moreover, we note that in this paper we consider acoustic media without a free surface. From our point of view, one can directly generalize asymptotic FWI for other important practical cases (with free surface, elastic isotropic, anisotropic, viscoelastic), and those solutions can provide some additional benefits. The major benefit is that one can use FWI for different waves (diving, reflected, multiples, etc.) separately, and therefore we can provide control of the influence of the wave type on the FWI process. However, of course, these suggestions must be investigated, and therefore these are topics for future research.