Agent-Based Modeling of Tsunami Evacuation at Figueirinha Beach, Setubal, Portugal
Abstract
:1. Introduction
2. Materials and Methods
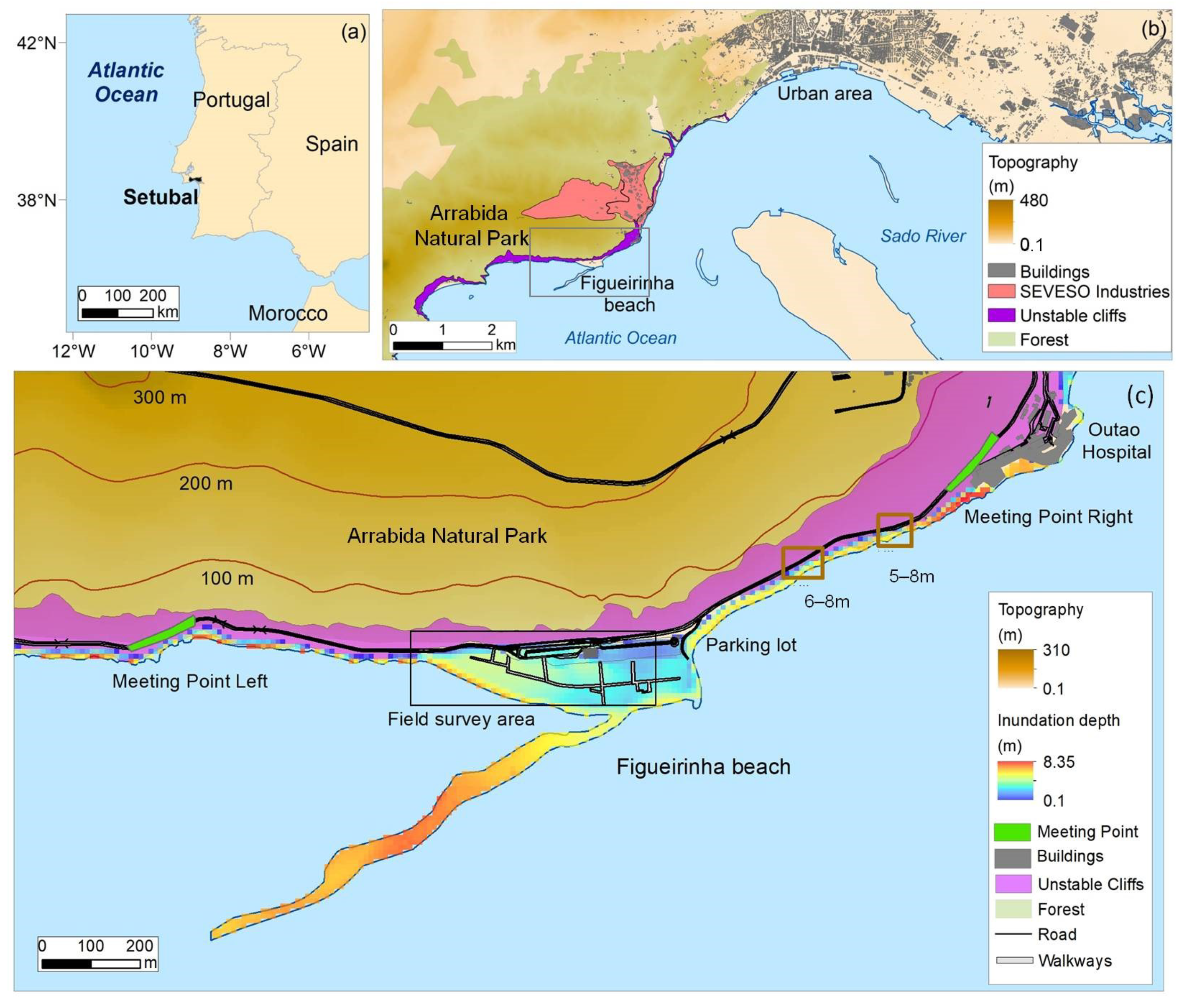
2.1. Study Area
2.2. Field Survey
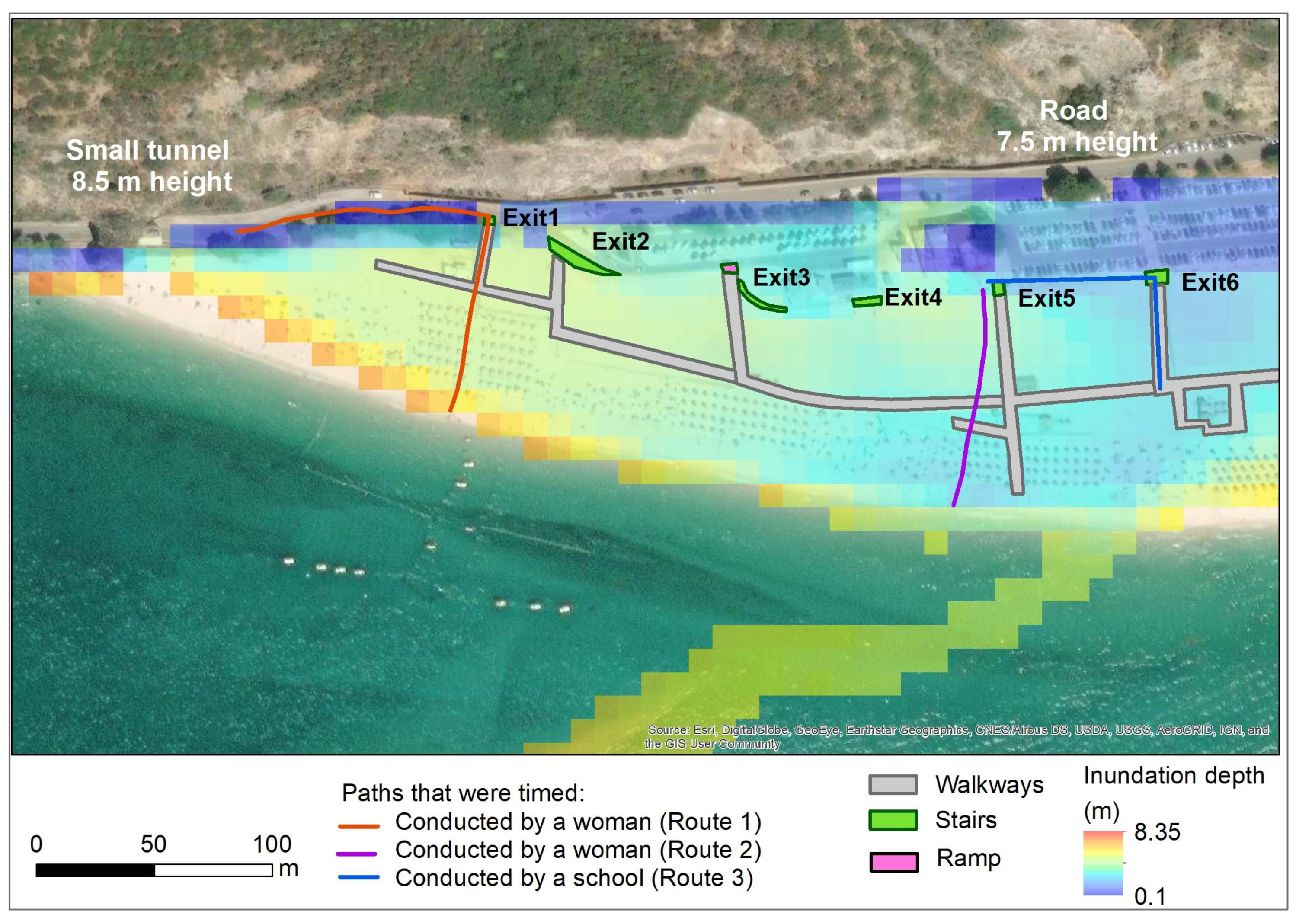
2.3. Data
2.4. The Model
2.4.1. Agents
2.4.2. Landmark-Based Routes
2.4.3. Agent Navigation, Walking Speed, and Collision Management
2.4.4. Group Management
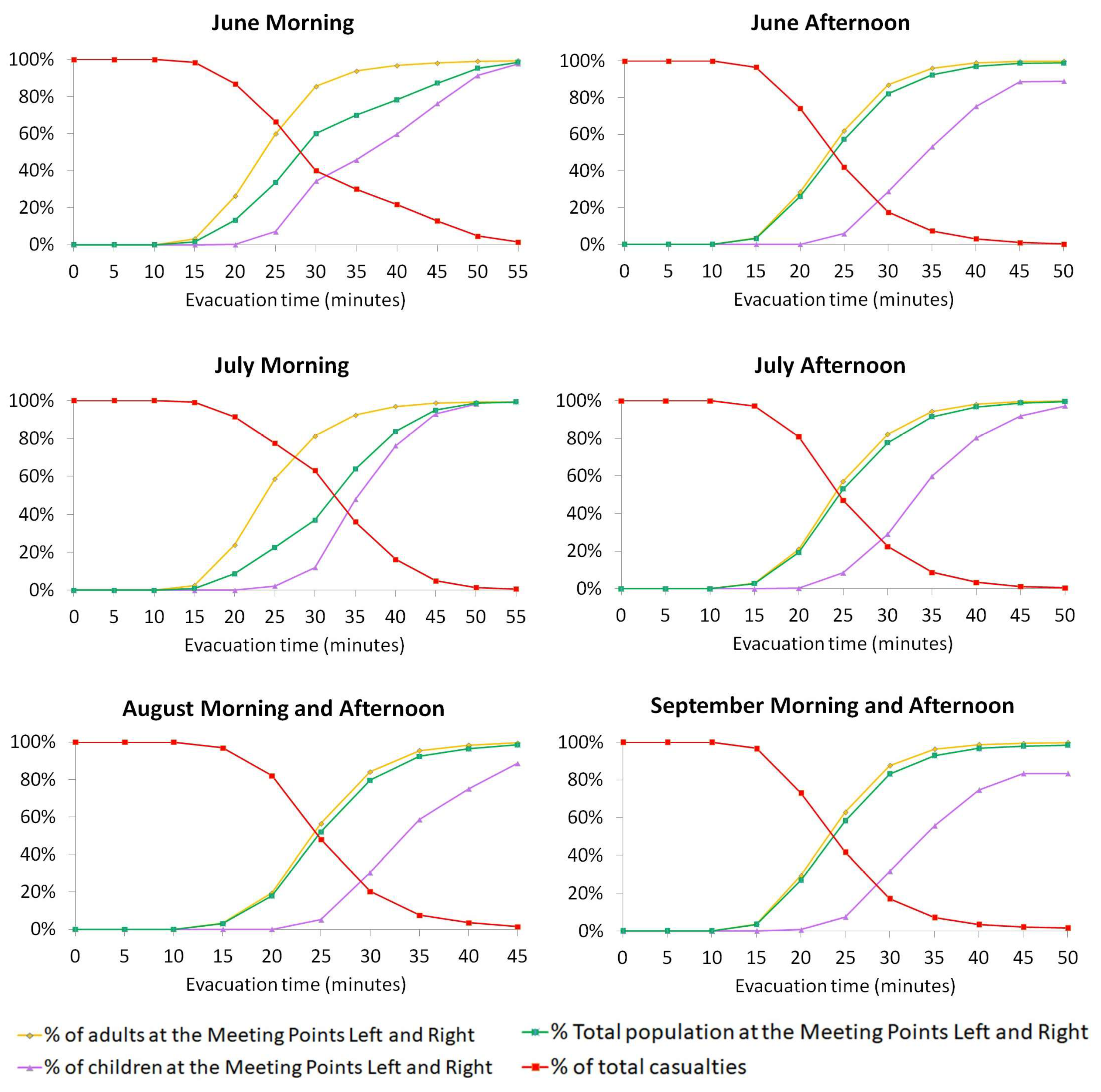
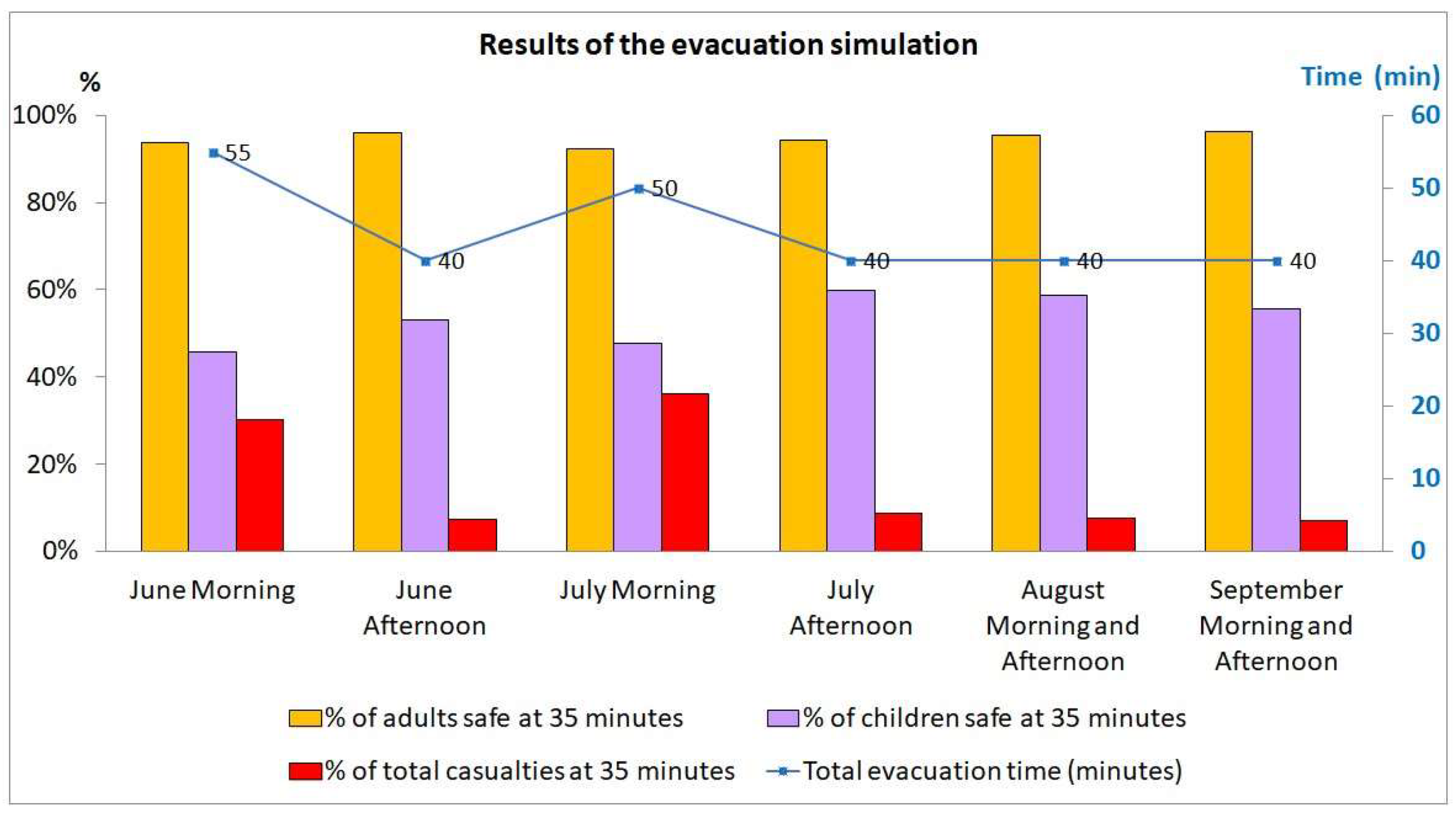
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| % of Adults | % of Children | % of Total Population | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | |||||||
| Time (Minutes) | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. |
| 0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| 5 | 6.3 | 1.1 | 0.0 | 0.0 | 36.8 | 4.0 | 0.0 | 0.0 | 22.2 | 1.2 | 0.0 | 0.0 |
| 10 | 2.3 | 0.8 | 0.0 | 0.0 | 6.6 | 3.2 | 0.0 | 0.0 | 3.7 | 2.1 | 0.0 | 0.0 |
| 15 | 0.1 | 0.2 | 3.1 | 0.3 | 2.1 | 2.1 | 0.0 | 0.0 | 0.6 | 0.6 | 1.6 | 0.2 |
| 20 | 0.0 | 0.0 | 26.3 | 1.3 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 13.2 | 0.6 |
| 25 | 0.0 | 0.0 | 59.9 | 2.0 | 0.0 | 0.0 | 7.1 | 3.1 | 0.0 | 0.0 | 33.6 | 2.2 |
| 30 | 0.0 | 0.0 | 85.5 | 1.3 | 0.0 | 0.0 | 34.3 | 4.6 | 0.0 | 0.0 | 60.0 | 2.7 |
| 35 | 0.0 | 0.0 | 93.8 | 1.4 | 0.0 | 0.0 | 45.8 | 7.5 | 0.0 | 0.0 | 69.9 | 4.0 |
| 40 | 0.0 | 0.0 | 96.8 | 0.6 | 0.0 | 0.0 | 59.7 | 5.5 | 0.0 | 0.0 | 78.3 | 2.8 |
| 45 | 0.0 | 0.0 | 98.1 | 0.7 | 0.0 | 0.0 | 76.2 | 3.8 | 0.0 | 0.0 | 87.2 | 2.0 |
| 50 | 0.0 | 0.0 | 99.1 | 0.6 | 0.0 | 0.0 | 91.5 | 3.6 | 0.0 | 0.0 | 95.3 | 2.1 |
| 55 | 0.0 | 0.0 | 99.4 | 0.5 | 0.0 | 0.0 | 97.7 | 2.3 | 0.0 | 0.0 | 98.6 | 1.2 |
| % of Adults | % of Children | % of Total Population | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | |||||||
| Time (Minutes) | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. |
| 0 | 100.0 | 0.1 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| 5 | 5.1 | 2.1 | 0.0 | 0.0 | 91.7 | 7.0 | 0.0 | 0.0 | 12.4 | 2.5 | 0.0 | 0.0 |
| 10 | 2.0 | 0.9 | 0.0 | 0.0 | 31.2 | 10.0 | 0.0 | 0.0 | 4.5 | 1.6 | 0.0 | 0.0 |
| 15 | 0.2 | 0.3 | 3.5 | 0.8 | 6.8 | 6.1 | 0.0 | 0.0 | 0.8 | 0.8 | 3.2 | 0.7 |
| 20 | 0.0 | 0.0 | 28.7 | 4.5 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 26.3 | 4.2 |
| 25 | 0.0 | 0.0 | 62.0 | 3.8 | 0.0 | 0.0 | 5.9 | 5.6 | 0.0 | 0.0 | 57.2 | 3.9 |
| 30 | 0.0 | 0.0 | 87.0 | 3.1 | 0.0 | 0.0 | 28.8 | 13.7 | 0.0 | 0.0 | 82.1 | 3.9 |
| 35 | 0.0 | 0.0 | 96.0 | 1.3 | 0.0 | 0.0 | 53.2 | 19.5 | 0.0 | 0.0 | 92.4 | 2.5 |
| 40 | 0.0 | 0.0 | 99.0 | 0.5 | 0.0 | 0.0 | 75.1 | 12.6 | 0.0 | 0.0 | 96.9 | 1.5 |
| 45 | 0.0 | 0.0 | 99.7 | 0.2 | 0.0 | 0.0 | 88.8 | 8.9 | 0.0 | 0.0 | 98.8 | 0.9 |
| 50 | 0.0 | 0.0 | 99.8 | 0.3 | 0.0 | 0.0 | 89.0 | 12.1 | 0.0 | 0.0 | 98.9 | 1.3 |
| % of Adults | % of Children | % of Total Population | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | |||||||
| Time (Minutes) | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. |
| 0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| 5 | 10.9 | 2.3 | 0.0 | 0.0 | 42.7 | 6.3 | 0.0 | 0.0 | 31.2 | 4.9 | 0.0 | 0.0 |
| 10 | 4.1 | 1.5 | 0.0 | 0.0 | 9.4 | 2.5 | 0.0 | 0.0 | 7.5 | 2.0 | 0.0 | 0.0 |
| 15 | 0.7 | 0.5 | 2.5 | 0.5 | 2.6 | 1.1 | 0.0 | 0.0 | 1.9 | 0.8 | 0.9 | 0.2 |
| 20 | 0.0 | 0.0 | 23.8 | 2.0 | 0.1 | 0.1 | 0.0 | 0.1 | 0.0 | 0.1 | 8.6 | 0.7 |
| 25 | 0.0 | 0.0 | 58.7 | 1.7 | 0.1 | 0.1 | 2.2 | 1.3 | 0.0 | 0.1 | 22.6 | 1.1 |
| 30 | 0.0 | 0.0 | 81.3 | 1.5 | 0.0 | 0.0 | 11.9 | 2.7 | 0.0 | 0.0 | 36.9 | 2.0 |
| 35 | 0.0 | 0.0 | 92.3 | 1.7 | 0.0 | 0.0 | 47.8 | 8.1 | 0.0 | 0.0 | 63.9 | 5.7 |
| 40 | 0.0 | 0.0 | 96.9 | 0.8 | 0.0 | 0.0 | 76.2 | 6.0 | 0.0 | 0.0 | 83.7 | 4.1 |
| 45 | 0.0 | 0.0 | 98.7 | 0.2 | 0.0 | 0.0 | 92.9 | 2.6 | 0.0 | 0.0 | 95.0 | 1.7 |
| 50 | 0.0 | 0.0 | 99.2 | 0.1 | 0.0 | 0.0 | 98.3 | 0.4 | 0.0 | 0.0 | 98.6 | 0.3 |
| 55 | 0.0 | 0.0 | 99.3 | 0.0 | 0.0 | 0.0 | 99.3 | 0.7 | 0.0 | 0.0 | 99.3 | 0.5 |
| % of Adults | % of Children | % of Total Population | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | |||||||
| Time (Minutes) | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. |
| 0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| 5 | 13.6 | 3.0 | 0.0 | 0.0 | 93.3 | 3.6 | 0.0 | 0.0 | 20.4 | 2.9 | 0.0 | 0.0 |
| 10 | 2.5 | 0.5 | 0.0 | 0.0 | 38.9 | 10.5 | 0.0 | 0.0 | 5.6 | 1.2 | 0.0 | 0.0 |
| 15 | 0.3 | 0.3 | 3.0 | 0.6 | 6.7 | 2.8 | 0.0 | 0.0 | 0.9 | 0.4 | 2.7 | 0.6 |
| 20 | 0.0 | 0.0 | 21.1 | 1.0 | 1.5 | 2.3 | 0.2 | 0.5 | 0.1 | 0.2 | 19.3 | 0.9 |
| 25 | 0.0 | 0.0 | 57.2 | 1.6 | 0.0 | 0.0 | 8.5 | 5.5 | 0.0 | 0.0 | 53.0 | 1.7 |
| 30 | 0.0 | 0.0 | 82.2 | 1.9 | 0.0 | 0.0 | 28.9 | 4.9 | 0.0 | 0.0 | 77.6 | 2.1 |
| 35 | 0.0 | 0.0 | 94.3 | 0.7 | 0.0 | 0.0 | 59.8 | 9.6 | 0.0 | 0.0 | 91.3 | 0.5 |
| 40 | 0.0 | 0.0 | 98.2 | 0.4 | 0.0 | 0.0 | 80.2 | 3.3 | 0.0 | 0.0 | 96.6 | 0.6 |
| 45 | 0.0 | 0.0 | 99.4 | 0.4 | 0.0 | 0.0 | 91.7 | 2.6 | 0.0 | 0.0 | 98.8 | 0.6 |
| 50 | 0.0 | 0.0 | 99.8 | 0.3 | 0.0 | 0.0 | 97.2 | 2.7 | 0.0 | 0.0 | 99.5 | 0.4 |
| % of Adults | % of Children | % of Total Population | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | |||||||
| Time (Minutes) | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. |
| 0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| 5 | 12.0 | 2.8 | 0.0 | 0.0 | 87.7 | 3.7 | 0.0 | 0.0 | 18.5 | 2.9 | 0.0 | 0.0 |
| 10 | 2.8 | 1.9 | 0.0 | 0.0 | 36.5 | 9.0 | 0.0 | 0.0 | 5.7 | 2.4 | 0.0 | 0.0 |
| 15 | 0.6 | 0.4 | 3.2 | 0.4 | 7.9 | 5.7 | 0.0 | 0.0 | 1.2 | 0.9 | 3.0 | 0.4 |
| 20 | 0.1 | 0.1 | 19.6 | 1.1 | 1.3 | 1.9 | 0.0 | 0.0 | 0.2 | 0.2 | 17.9 | 1.0 |
| 25 | 0.0 | 0.0 | 56.5 | 1.7 | 0.2 | 0.4 | 5.2 | 4.3 | 0.0 | 0.0 | 52.1 | 1.6 |
| 30 | 0.0 | 0.0 | 84.2 | 0.9 | 0.0 | 0.0 | 30.4 | 5.4 | 0.0 | 0.0 | 79.6 | 1.2 |
| 35 | 0.0 | 0.0 | 95.5 | 0.5 | 0.0 | 0.0 | 58.7 | 3.0 | 0.0 | 0.0 | 92.3 | 0.7 |
| 40 | 0.0 | 0.0 | 98.4 | 0.2 | 0.0 | 0.0 | 75.0 | 8.2 | 0.0 | 0.0 | 96.4 | 0.8 |
| 45 | 0.0 | 0.0 | 99.5 | 0.1 | 0.0 | 0.0 | 88.8 | 0.6 | 0.0 | 0.0 | 98.6 | 0.1 |
| % of Adults | % of Children | % of Total Population | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | At the Beach | At the Meeting Point | |||||||
| Time (Minutes) | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. | Mean | Stand. Dev. |
| 0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| 5 | 4.7 | 0.9 | 0.0 | 0.0 | 87.3 | 7.8 | 0.0 | 0.0 | 11.5 | 1.3 | 0.0 | 1.3 |
| 10 | 1.2 | 0.6 | 0.0 | 0.0 | 27.9 | 9.9 | 0.0 | 0.0 | 3.4 | 1.3 | 0.0 | 1.3 |
| 15 | 0.4 | 0.3 | 3.6 | 0.7 | 10.3 | 4.1 | 0.0 | 0.0 | 1.2 | 0.6 | 3.3 | 0.6 |
| 20 | 0.1 | 0.1 | 29.4 | 2.0 | 2.4 | 5.4 | 0.6 | 1.4 | 0.3 | 0.6 | 27.0 | 0.6 |
| 25 | 0.0 | 0.0 | 62.9 | 2.2 | 0.0 | 0.0 | 7.3 | 7.6 | 0.0 | 0.0 | 58.3 | 0.0 |
| 30 | 0.0 | 0.0 | 87.6 | 2.0 | 0.0 | 0.0 | 31.5 | 14.8 | 0.0 | 0.0 | 83.0 | 0.0 |
| 35 | 0.0 | 0.0 | 96.3 | 1.0 | 0.0 | 0.0 | 55.8 | 13.0 | 0.0 | 0.0 | 92.9 | 0.0 |
| 40 | 0.0 | 0.0 | 98.7 | 0.4 | 0.0 | 0.0 | 74.5 | 9.7 | 0.0 | 0.0 | 96.7 | 0.0 |
| 45 | 0.0 | 0.0 | 99.3 | 0.6 | 0.0 | 0.0 | 83.3 | 12.5 | 0.0 | 0.0 | 98.0 | 0.0 |
| 50 | 0.0 | 0.0 | 99.7 | 0.4 | 0.0 | 0.0 | 83.3 | 10.7 | 0.0 | 0.0 | 98.4 | 0.0 |
References
- Santos, A.; Sousa, N.; Kremers, H.; Bucho, J.L. Building resilient urban communities: The case study of Setubal Municipality. Portugal. Geosciences 2020, 10, 243. [Google Scholar] [CrossRef]
- United Nations Office for Disaster Reduction UNDRR. Sendai Framework for Disaster Risk Reduction 2015–2030; UNISDR: Geneva, Switzerland, 2015; p. 32. Available online: https://www.undrr.org/publication/sendai-framework-disaster-risk-reduction-2015-2030 (accessed on 15 July 2023).
- National Authority of Emergency and Civil Protection. General Law. 2023. Available online: https://prociv.gov.pt/pt/legislacao/ (accessed on 15 July 2023). (In Portuguese)
- National Platform for Disaster Risk Reduction. 2023. Available online: https://www.pnrrc.pt/ (accessed on 15 July 2023). (In Portuguese).
- Aleluia, A. Digital Cartography of the Setubal Municipality at Scale 1:10,000; Department of Urbanism, Cabinet of Geographical Information System; Setubal City Hall: Setubal, Portugal, 2011. (In Portuguese) [Google Scholar]
- Sousa, N. The Civil Planning of Emergency in the New Paradigm of Safety. Master’s Thesis, University of Lisbon, Lisbon, Portugal, 2016. Available online: https://www.repository.utl.pt/handle/10400.5/11567 (accessed on 15 July 2023). (In Portuguese).
- European Commission. Seveso Directive. 2019. Available online: https://ec.europa.eu/environment/seveso/legislation.htm (accessed on 15 July 2023).
- Santos, A.; Fonseca, N.; Queirós, M.; Zêzere, J.L.; Bucho, J.L. Implementation of Tsunami Evacuation Maps at Setubal Municipality. Portugal. Geosciences 2017, 7, 116. [Google Scholar] [CrossRef]
- Kobes, M.; Helsloot, I.; de Vries, B.; Post, J.G.; Oberijé, N.; Groenewegen, K. Way finding during fire evacuation; an analysis of unannounced fire drills in a hotel at night. Build. Environ. 2010, 45, 537–548. [Google Scholar] [CrossRef]
- Bird, D.K.; Chagué-Goff, C.; Gero, A. Human Response to Extreme Events: A review of three post-tsunami disaster case studies. Aust. Geogr. 2011, 42, 225–239. [Google Scholar] [CrossRef]
- Dengler, L.; Goltz, J.; Fenton, J.; Miller, K.; Wilson, R. Building tsunami-resilient communities in the United States: An example from California. TsuInfo Alert 2011, 13, 2. [Google Scholar]
- SMPCB. MITREX Exercise; Setubal City Hall: Setubal, Portugal, 2012; p. 487. (In Portuguese) [Google Scholar]
- Setubal City Hall. Bocage 2013. 2013. Available online: https://www.youtube.com/watch?v=Z5tRO0ldcrY (accessed on 15 July 2023). (In Portuguese).
- Gu, Z.; Liu, Z.; Shiwakoti, N.; Yang, M. Video-based analysis of school students’ emergency evacuation behavior in earthquakes. Int. J. Disaster Risk Reduct. 2016, 18, 1–11. [Google Scholar] [CrossRef]
- David, N.; Fachada, N.; Rosa, A.C. Verifying and Validating Simulations. In Simulating Social Complexity. Understanding Complex Systems, 1st ed.; Edmonds, B., Meyer, R., Eds.; Springer Nature: Cham, Switzerland, 2017; pp. 173–204. [Google Scholar] [CrossRef]
- Edmonds, B.; Meyer, R. Simulating Social Complexity; Springer Nature: Cham, Switzerland, 2017; p. 409. [Google Scholar] [CrossRef]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1984; ISBN 978-0-465-02121-5. Available online: http://bert.stuy.edu/pbrooks/spring2015/materials/HumanReasoning-2/Axelrod_Robert_The_Evolution_of_Cooperation.pdf (accessed on 15 July 2023).
- Antelmi, A.; Cordasco, G.; D’Ambrosio, G.; De Vinco, D.; Spagnuolo, C. Experimenting with Agent-Based Model Simulation Tools. Appl. Sci. 2022, 13, 13. [Google Scholar] [CrossRef]
- Filomena, G.; Verstegen, J.A. Modelling the effect of landmarks on pedestrian dynamics in urban environments. Comput. Environ. Urban Syst. 2021, 86, 101573. [Google Scholar] [CrossRef]
- Jumadi; Heppenstall, A.; Malleson, N.; Carver, S.; Quincey, D.; Manville, V. Modelling Individual Evacuation Decisions during Natural Disasters: A Case Study of Volcanic Crisis in Merapi. Indonesia. Geosciences. 2018, 8, 196. [Google Scholar] [CrossRef]
- Goto, Y.; Affan, M.; Agussabti; Nurdin, Y.; Yuliana, D.K.; Ardiansyah. Tsunami evacuation simulation for disaster education and city planning. J. Disaster Res. 2012, 7, 92–101. [Google Scholar] [CrossRef]
- Mls, K.; Kořínek, M.; Štekerová, K.; Tučník, P.; Bureš, V.; Čech, P.; Husáková, M.; Mikulecký, P.; Nacházel, P.; Ponce, D.; et al. Agent-based models of human response to natural hazards: Systematic review of tsunami evacuation. Nat. Hazards 2023, 115, 1887–1908. [Google Scholar] [CrossRef] [PubMed]
- Mas, E.; Koshimura, S.; Imamura, F.; Suppasri, A.; Muhari, A.; Adriano, B. Recent Advances in Agent-Based Tsunami Evacuation Simulations: Case Studies in Indonesia, Thailand. Japan and Peru. Pure Appl. Geophys. 2015, 172, 3409–3424. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, G. Simulation-Based and Risk-Informed Assessment of the Effectiveness of Tsunami Evacuation Routes Using Agent-Based Modeling: A Case Study of Seaside. Oregon. Int. J. Disaster Risk Sci. 2022, 13, 66–86. [Google Scholar] [CrossRef]
- ANPC. Estudo do Risco Sísmico e de Tsunami do Algarve. 2010; 85p. Available online: https://prociv.gov.pt/pt/home/ (accessed on 15 July 2023). (In Portuguese)
- INE. Preliminary Census Data of the Resident Population in Setubal in 2020 and 2021. 2022. Available online: https://www.ine.pt (accessed on 15 July 2023). (In Portuguese).
- Cândido, E. Modelação Baseada em Agentes da Evacuação da Praia da Figueirinha. Master’s Thesis, Iscte—Instituto Universitário de Lisboa, Lisboa, Portugal, 2022. Available online: http://hdl.handle.net/10071/27712 (accessed on 15 July 2023).
- Kazil, J.; Masad, D.; Crooks, A. Utilizing Python for Agent-Based Modeling: The Mesa Framework. In Social, Cultural, and Behavioral Modeling, Proceedings of the 13th International Conference, SBP-BRiMS 2020, Washington, DC, USA, 18–21 October 2020; Thomson, R., Bisgin, H., Dancy, C., Hyder, A., Hussain, M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2020; Volume 12268. [Google Scholar] [CrossRef]
- Wang, B.; Hess, V.; Crooks, A. Mesa-Geo: A GIS Extension for the Mesa Agent Based Modeling Framework in Python. In Proceedings of the 5th ACM SIGSPATIAL International Workshop on GeoSpatial Simulation, Seattle, WA, USA, 1 November 2022. [Google Scholar] [CrossRef]
- Stern, R. Multi-Agent Path Finding—An Overview. In Artificial Intelligence; Osipov, G., Panov, A., Yakovlev, K., Eds.; Springer Nature: Cham, Switzerland, 2019; Volume 11866, pp. 96–115. [Google Scholar] [CrossRef]
- Sohn, S.S.; DeStefani, S.; Kapadia, M. Dynamic cognitive maps for agent landmark navigation in unseen environments. In Proceedings of the 11th ACM SIGGRAPH Conference on Motion Interaction and Games, Limassol, Cyprus, 8–10 November 2018. [Google Scholar] [CrossRef]
- Yesiltepe, D.; Conroy Dalton, R.; Ozbil Torun, A. Landmarks in wayfinding: A review of the existing literature. Cogn. Process. 2021, 22, 369–410. [Google Scholar] [CrossRef]
- Röser, F.A. Cognitive Observer-Based Landmark-Preference Model. KI-Künstliche Intell. 2017, 31, 169–171. [Google Scholar] [CrossRef]
- Schimpl, M.; Moore, C.; Lederer, C.; Neuhaus, A.; Sambrook, J.; Danesh, J.; Ouwehand, W.; Daumer, M. Association between walking speed and age in healthy. free-living individuals using mobile accelerometry—A cross-sectional study. PLoS ONE 2011, 6, e23299. [Google Scholar] [CrossRef]
- Silva, A.M.; da Silva, J.P.; da Cunha, J.R. Estimation of pedestrian walking speeds on footways. In Proceedings of the Institution of Civil Engineers-Municipal Engineer; Thomas Telford Ltd.: London, UK, 2014; Volume 167, pp. 32–43. [Google Scholar] [CrossRef]
- Nazir, M.; Razi, K.; Hossain, Q.; Adhikary, S. Pedestrian Flow Characteristics at Walkways in Rajshahi Metropolitan City of Bangladesh. In Proceedings of the 2nd International Conference on Civil Engineering for Sustainable Development (ICCESD-2014), KUET, Khulna, Bangladesh, 14–16 February 2014; ISBN 978-984-33-6373-2 (CD-ROM). Available online: https://www.researchgate.net/publication/321759346_Pedestrian_Flow_Characteristics_at_Walkways_in_Rajshahi_Metropolitan_City_of_Bangladesh (accessed on 15 July 2023).
- Leicht, A.; Crowther, R. Pedometer Accuracy during Walking over Different Surfaces. Med. Sci. Sports Exerc. 2007, 39, 1847–1850. [Google Scholar] [CrossRef]
- Aghabayk, K.; Parishad, N.; Shiwakoti, N. Investigation on the impact of walkways slope and pedestrians physical characteristics on pedestrians normal walking and jogging speeds. Saf. Sci. 2021, 133, 105012. [Google Scholar] [CrossRef]
- Yu, J.; Petnga, L. Space-based Collision Avoidance Framework for Autonomous Vehicles. Procedia Comput. Sci. 2018, 140, 37–45. [Google Scholar] [CrossRef]
- Foudil, C.; Djedi, N.; Sanza, C.; Duthen, Y. Path Finding and Collision Avoidance in Crowd Simulation. J. Comput. Inf. Technol. 2009, 3, 217–228. [Google Scholar] [CrossRef]
- Fraser, S.A.; Wood, N.J.; Johnston, D.M.; Leonard, G.S.; Greening, P.D.; Rossetto, T. Variable population exposure and distributed travel speeds in least-cost tsunami evacuation modelling. Nat. Hazards Earth Syst. Sci. 2014, 14, 2975–2991. [Google Scholar] [CrossRef]
- Kohns, J.; Stempniewski, L.; Stark, A. Fragility Functions for Reinforced Concrete Structures Based on Multiscale Approach for Earthquake Damage Criteria. Buildings 2022, 12, 1253. [Google Scholar] [CrossRef]
- Koshimura, S.; Oie, T.; Yanagisawa, H.; Imamura, F. Developing Fragility Functions for Tsunami Damage Estimation Using Numerical Model and Post-tsunami Data from Banda Aceh Indonesia. Coast. Eng, J. 2009, 51, 243–273. [Google Scholar] [CrossRef]
- Mizutani, A.; Yomogida, K.; Tanioka, Y. Early tsunami detection with near-fault ocean-bottom pressure gauge records based on the comparison with seismic data. J. Geophys. Res Ocean. 2020, 125, e2020JC016275. [Google Scholar] [CrossRef]
- Wang, Y.; Tsushima, H.; Satake, K.; Navarrete, P. Review on recent progress in near-field tsunami forecasting using offshore tsunami measurements: Source inversion and data assimilation. Pure Appl. Geophys. 2021, 178, 5109–5128. [Google Scholar] [CrossRef]

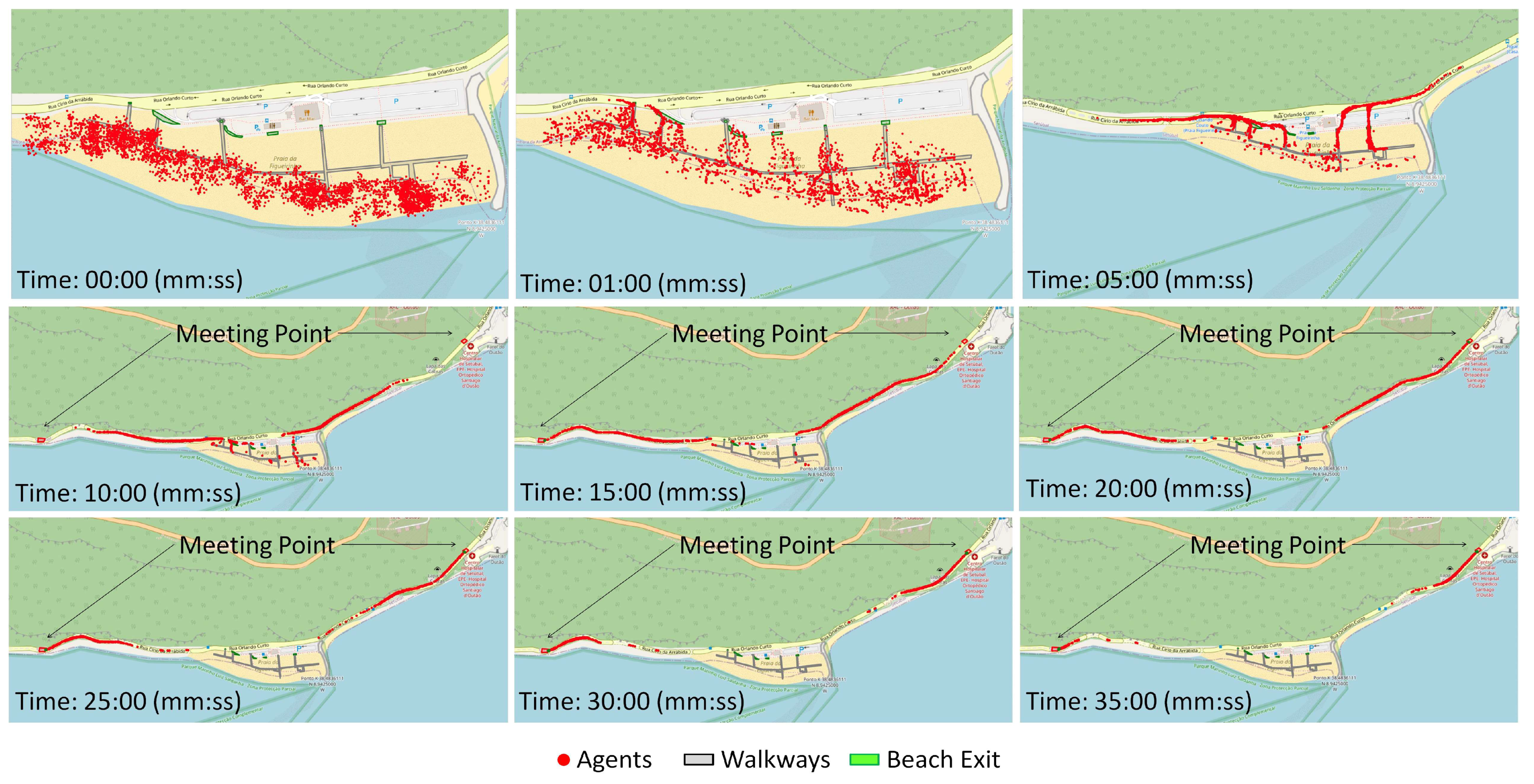
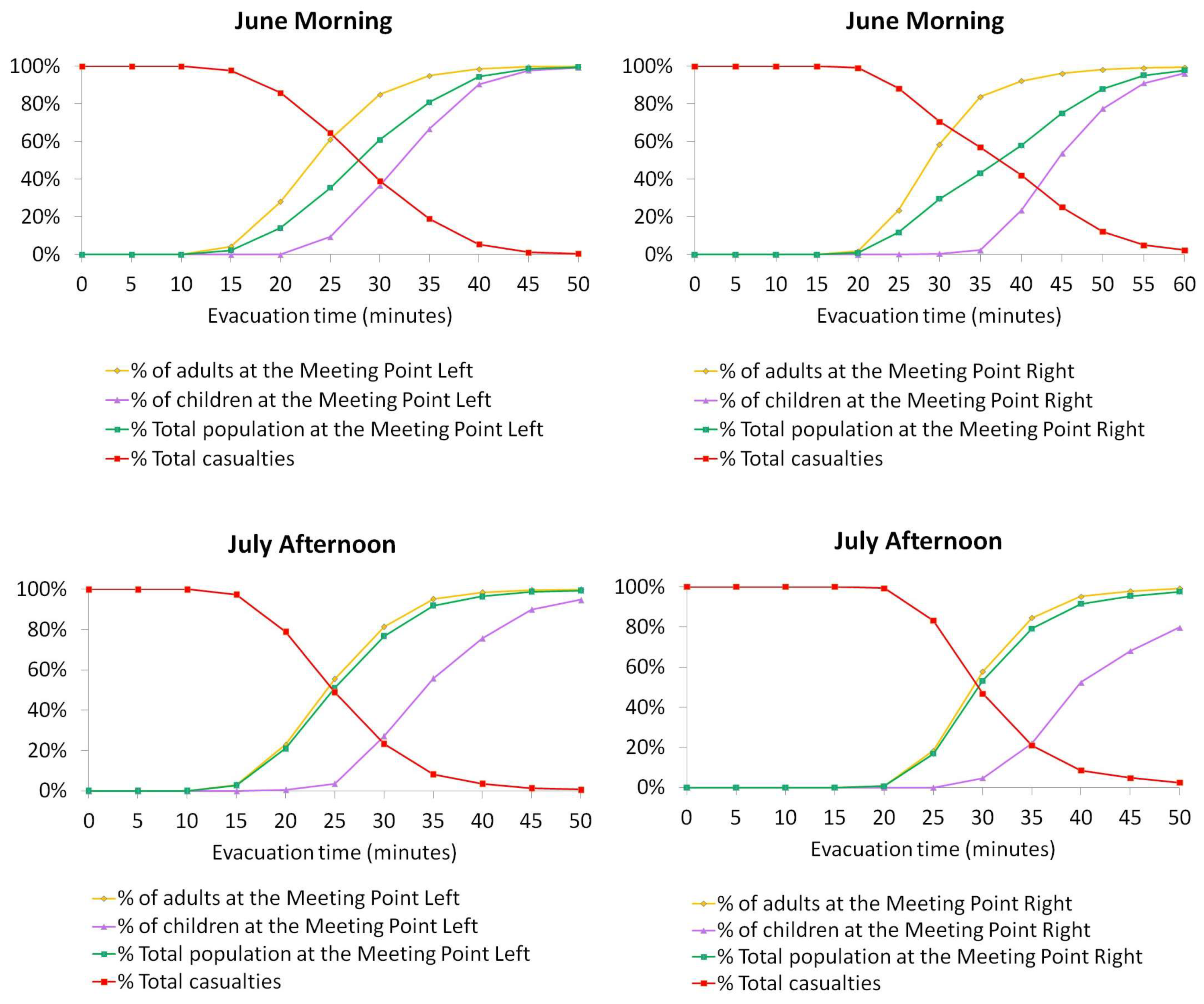
| Meeting Point | Exit 1 | Exit 2 | Exit 3 | Exit 4 | Exit 5 | Exit 6 |
|---|---|---|---|---|---|---|
| Left | 757 | 794 | 869 | 944 | 988 | 1068 |
| Right | 1084 | 1050 | 992 | 967 | 902 | 853 |
| Month | Period | Public Buses C/A/T | Cars C/A/T | School Buses C/A/T | Total C/A/T |
|---|---|---|---|---|---|
| June | Morning | 11/122/133 | 30/321/351 | 424/21/445 | 465/464/929 |
| Afternoon | 11/122/133 | 30/321/351 | 0/0/0 | 41/443/484 | |
| July | Morning | 60/634/694 | 32/344/376 | 1811/91/1902 | 1903/1069/2972 |
| Afternoon | 60/634/694 | 32/344/376 | 0/0/0 | 92/978/1070 | |
| August | Morning and afternoon | 66/699/765 | 39/413/452 | 0/0/0 | 105/1112/1217 |
| September | Morning and afternoon | 11/120/131 | 23/244/267 | 0/0/0 | 34/364/398 |
| Scenario | Meeting Point | % of Children | % of Adults | % of Total Population |
|---|---|---|---|---|
| June morning (929 agents, with school groups) | Left | 33.2 | 5.0 | 19.0 |
| Both | 54.2 | 6.2 | 30.1 | |
| Right | 97.7 | 16.3 | 56.9 | |
| July afternoon (1070 agents, without school groups) | Left | 44.2 | 4.8 | 8.2 |
| Both | 40.2 | 5.7 | 8.7 | |
| Right | 77.9 | 15.5 | 20.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, A.; David, N.; Perdigão, N.; Cândido, E. Agent-Based Modeling of Tsunami Evacuation at Figueirinha Beach, Setubal, Portugal. Geosciences 2023, 13, 327. https://doi.org/10.3390/geosciences13110327
Santos A, David N, Perdigão N, Cândido E. Agent-Based Modeling of Tsunami Evacuation at Figueirinha Beach, Setubal, Portugal. Geosciences. 2023; 13(11):327. https://doi.org/10.3390/geosciences13110327
Chicago/Turabian StyleSantos, Angela, Nuno David, Nelson Perdigão, and Eduardo Cândido. 2023. "Agent-Based Modeling of Tsunami Evacuation at Figueirinha Beach, Setubal, Portugal" Geosciences 13, no. 11: 327. https://doi.org/10.3390/geosciences13110327
APA StyleSantos, A., David, N., Perdigão, N., & Cândido, E. (2023). Agent-Based Modeling of Tsunami Evacuation at Figueirinha Beach, Setubal, Portugal. Geosciences, 13(11), 327. https://doi.org/10.3390/geosciences13110327








