Escape Mechanism with Shallow Ramp and Décollements in Southwest Taiwan
Abstract
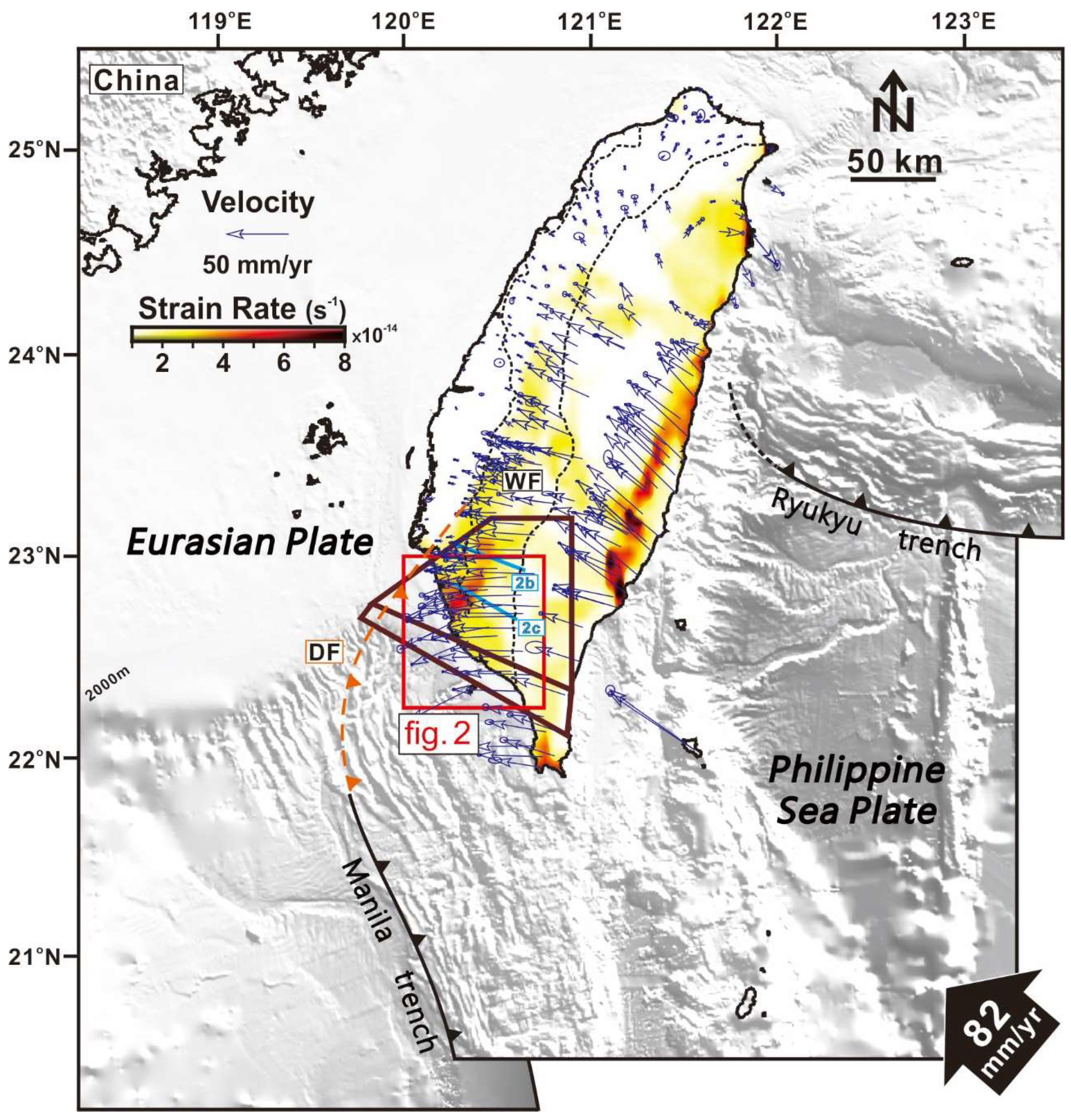
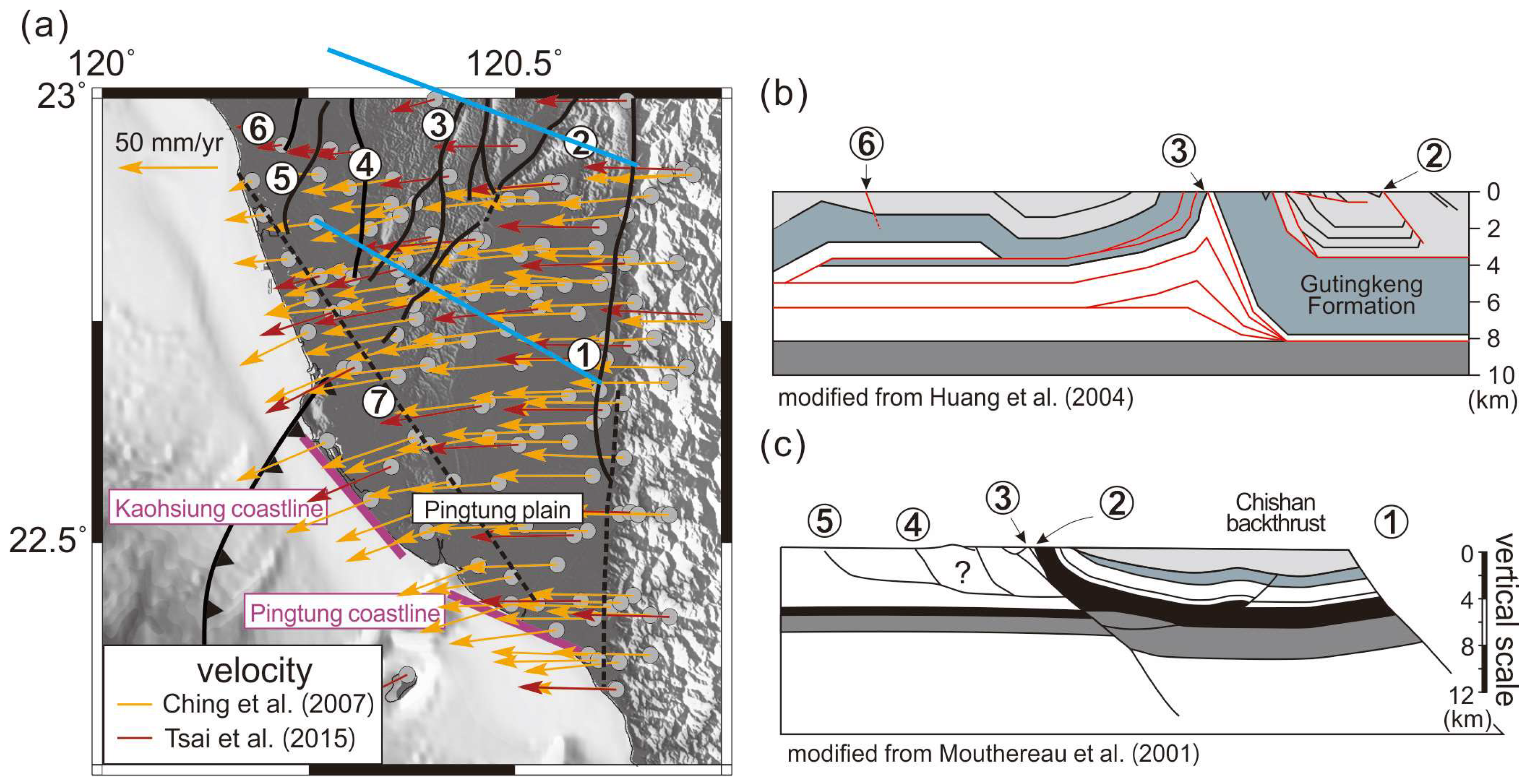
:1. Introduction
2. Methods and Materials—Numerical Solver and Models
2.1. Numerical Solver
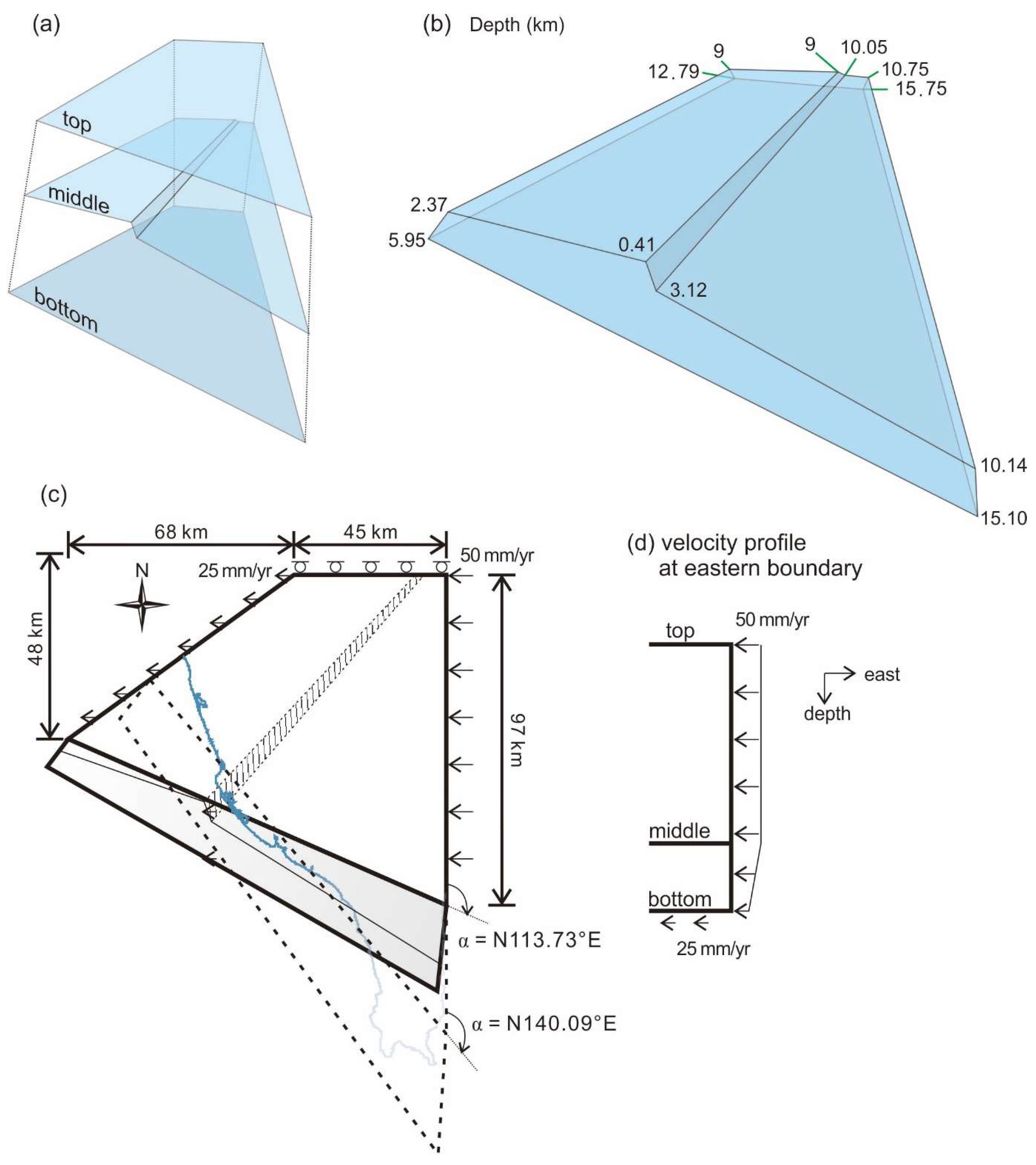
2.2. Model Settings
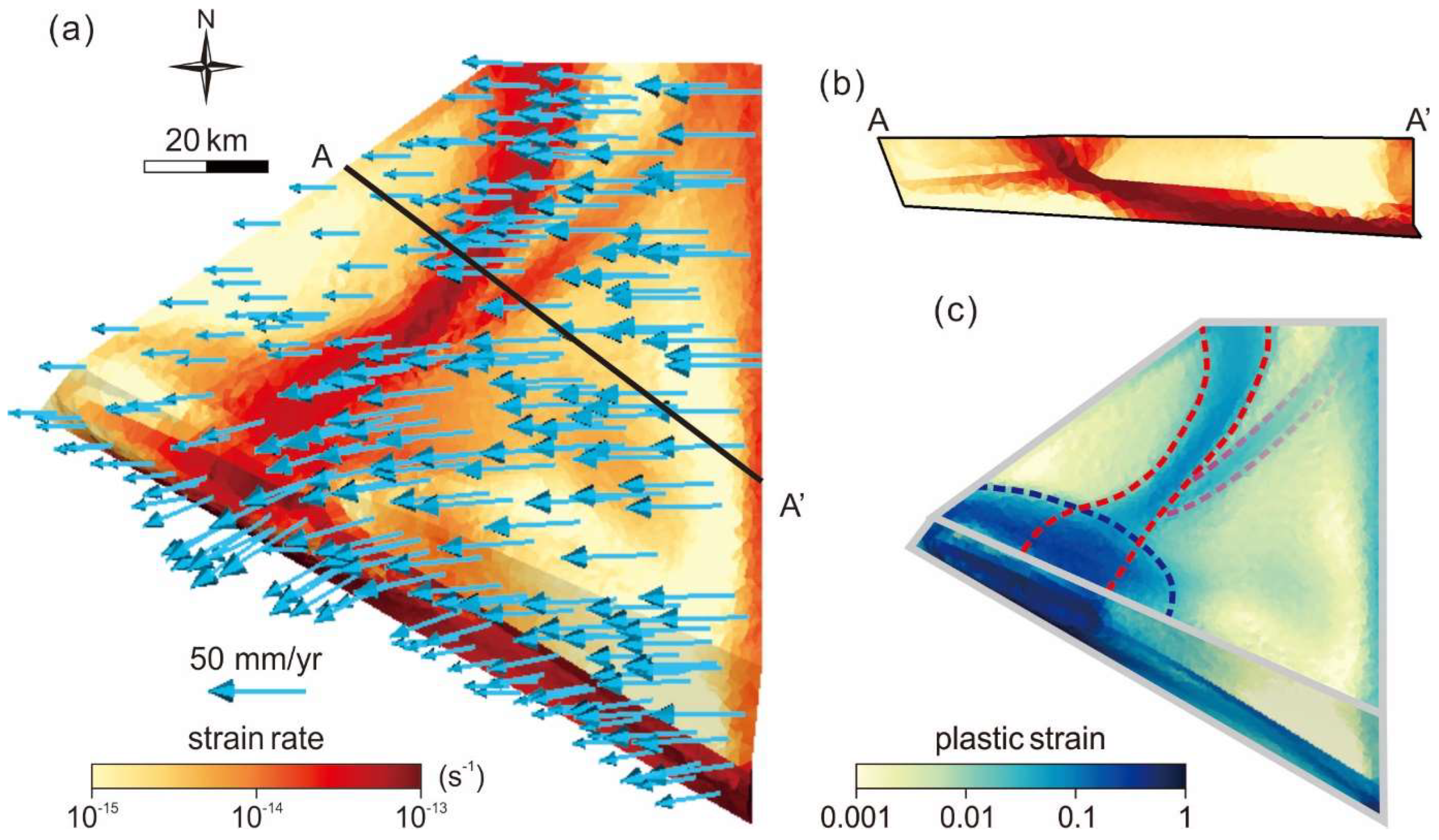
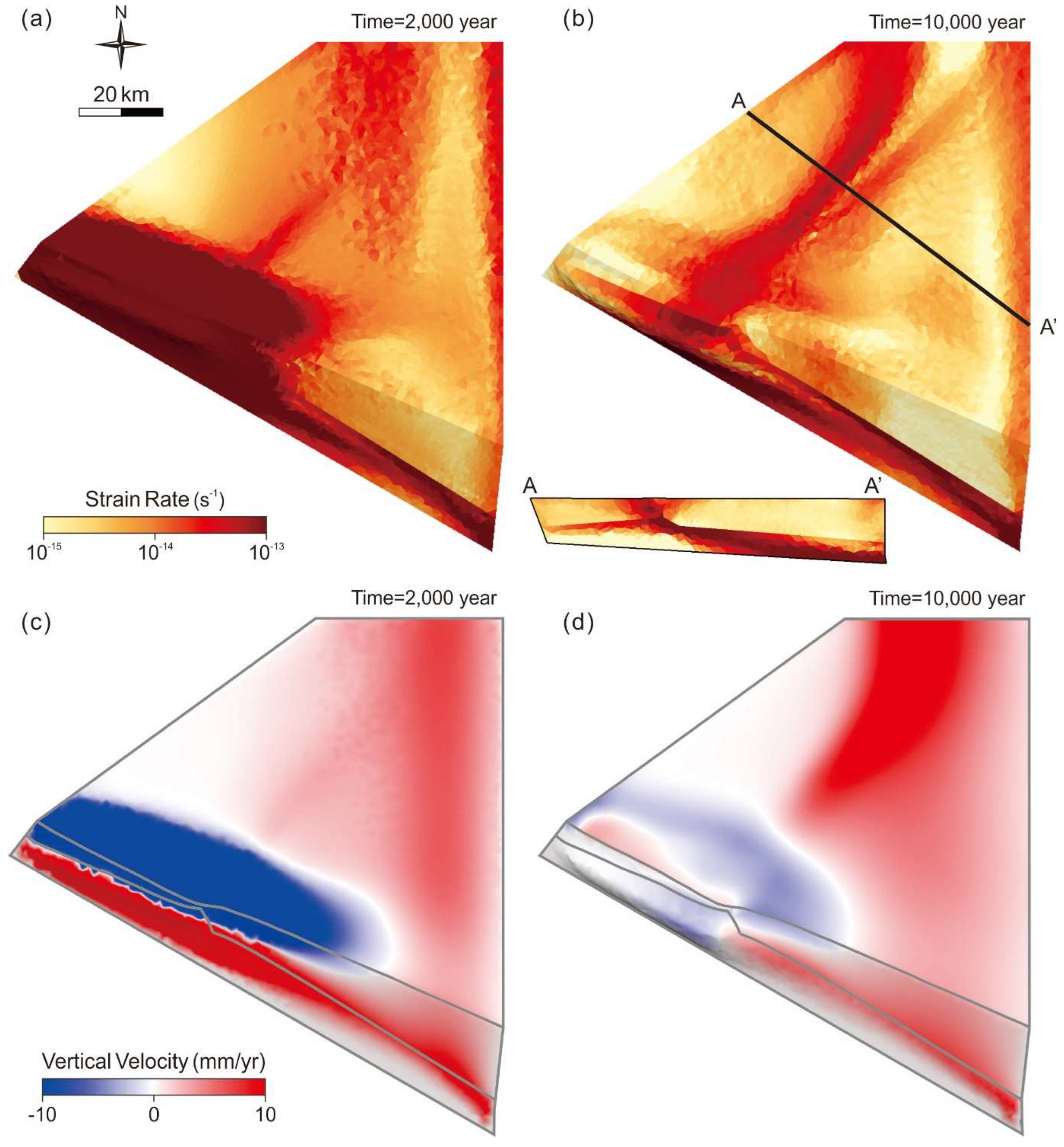
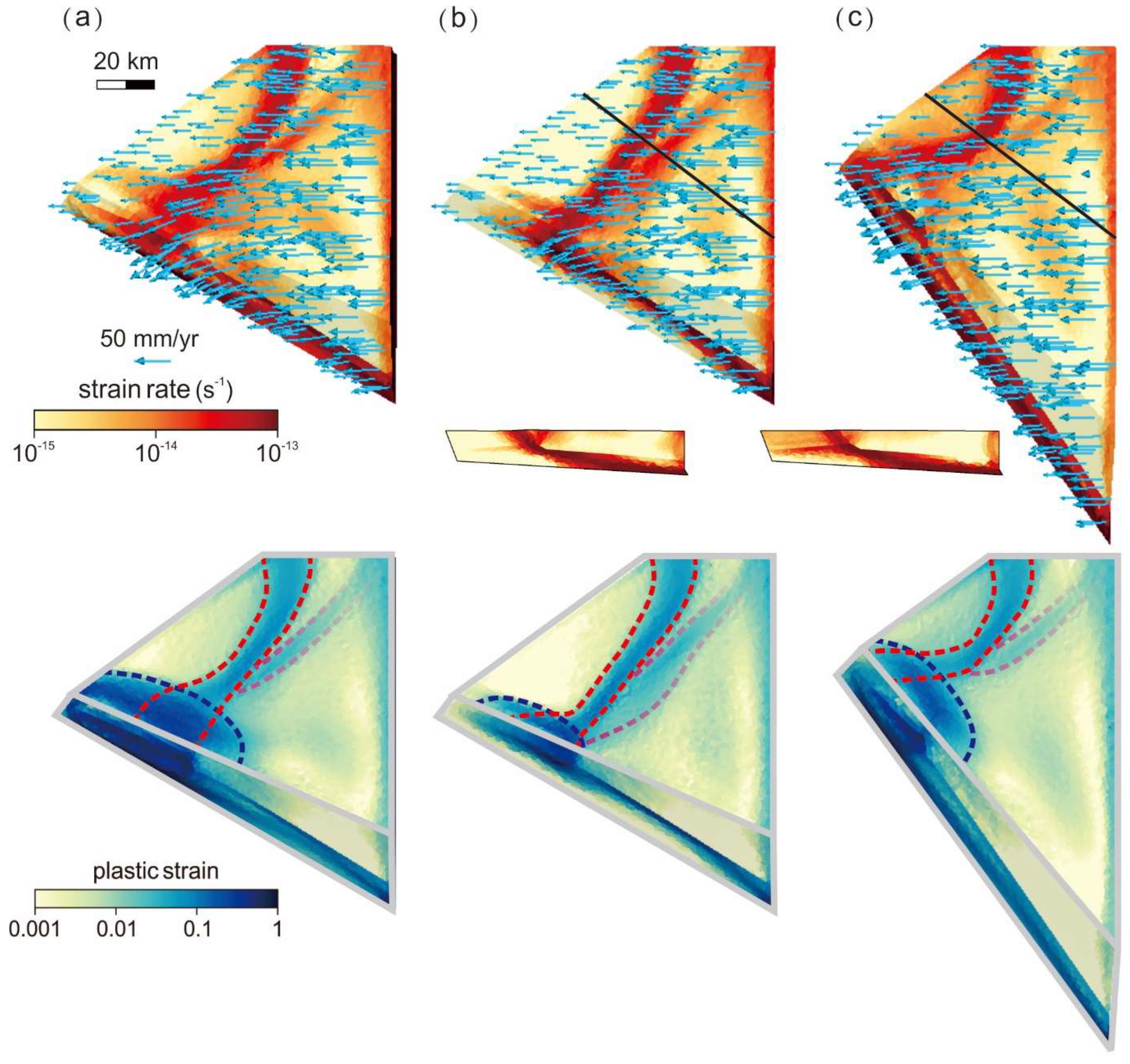
3. Results
4. Discussion
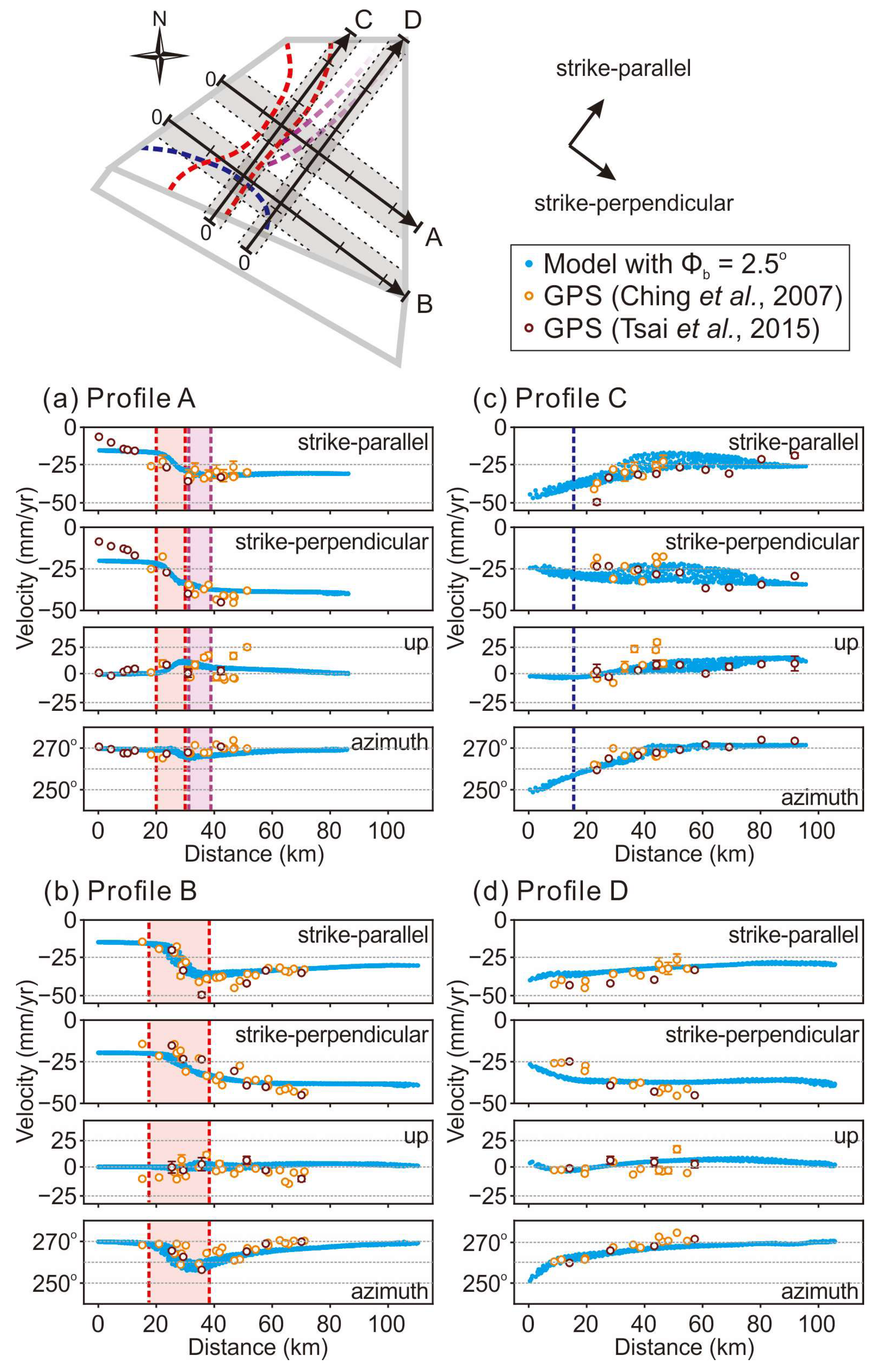
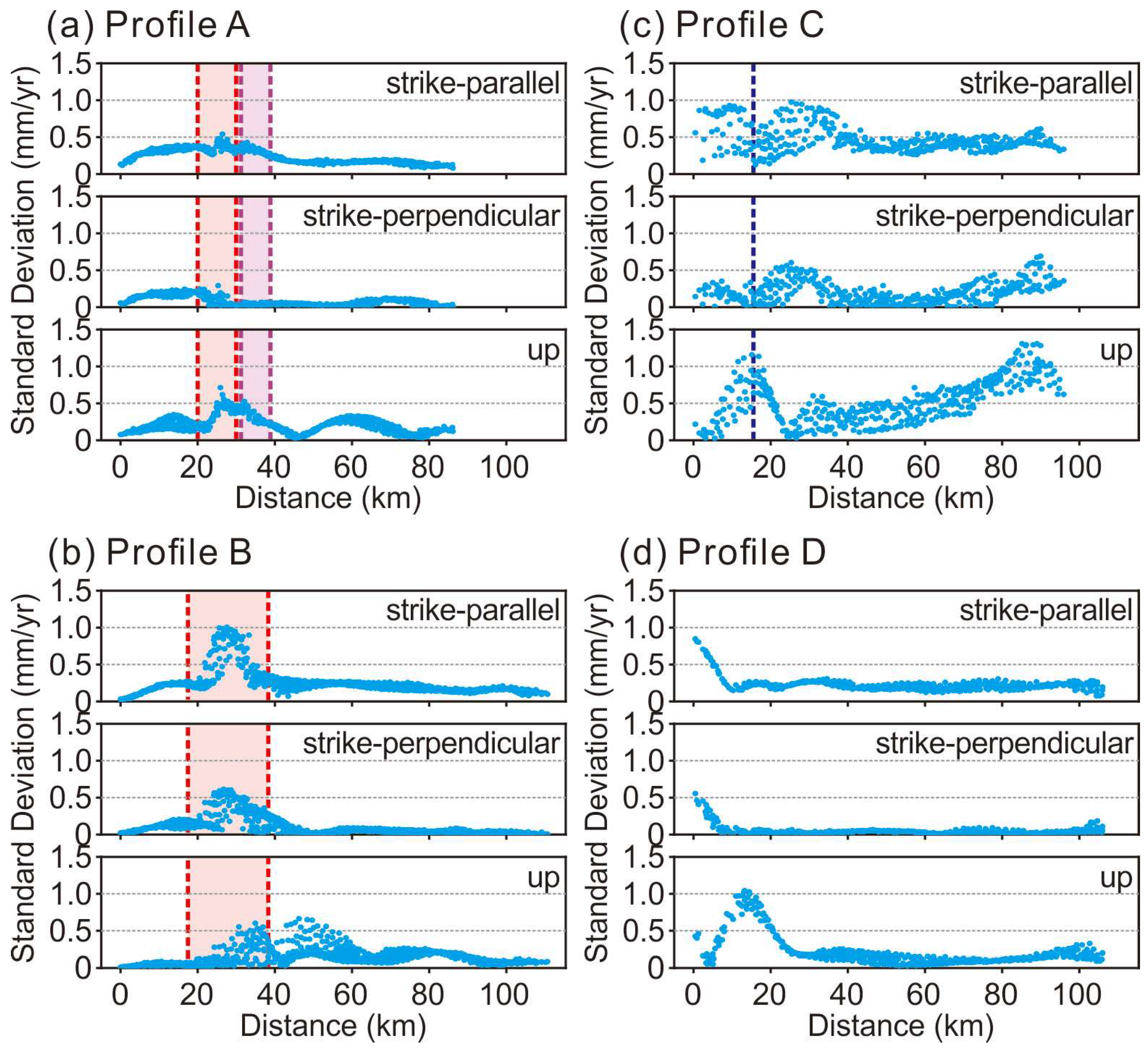
4.1. Comparison with GPS Ground Motion
4.2. Extremely low Basal Friction
4.3. Orientation and Geometry of the Open Boundary
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Byrne, T.; Chan, Y.-C.; Rau, R.-J.; Lu, C.-Y.; Lee, Y.-H.; Wang, Y.-J. The Arc–Continent Collision in Taiwan. In Arc-Continent Collision; Brown, D., Ryan, P.D., Eds.; Frontiers in Earth Sciences; Springer: Berlin, Heidelberg, 2011; pp. 213–245. ISBN 978-3-540-88558-0. [Google Scholar]
- Ho, C.S. Introduction to the Geology of Taiwan: Explanatory Text of the Geologic Map of Taiwan; Central Geologic Survey; MOEA: Taipei, Taiwan, 1986; ISBN 978-986-533-178-8. [Google Scholar]
- Tsai, M.-C.; Yu, S.-B.; Shin, T.-C.; Kuo, K.-W.; Leu, P.-L.; Chang, C.-H.; Ho, M.-Y. Velocity Field Derived from Taiwan Continuous GPS Array (2007–2013). Terr. Atmos. Ocean. Sci. 2015, 26, 527–556. [Google Scholar] [CrossRef] [Green Version]
- Ching, K.-E.; Rau, R.-J.; Lee, J.-C.; Hu, J.-C. Contemporary Deformation of Tectonic Escape in SW Taiwan from GPS Observations, 1995–2005. Earth Planet. Sci. Lett. 2007, 262, 601–619. [Google Scholar] [CrossRef]
- Hu, J.-C.; Hou, C.-S.; Shen, L.-C.; Chan, Y.-C.; Chen, R.-F.; Huang, C.; Rau, R.-J.; Chen, K.H.-H.; Lin, C.-W.; Huang, M.-H.; et al. Fault Activity and Lateral Extrusion Inferred from Velocity Field Revealed by GPS Measurements in the Pingtung Area of Southwestern Taiwan. J. Asian Earth Sci. 2007, 31, 287–302. [Google Scholar] [CrossRef]
- Angelier, J.; Chang, T.-Y.; Hu, J.-C.; Chang, C.-P.; Siame, L.; Lee, J.-C.; Deffontaines, B.; Chu, H.-T.; Lu, C.-Y. Does Extrusion Occur at Both Tips of the Taiwan Collision Belt? Insights from Active Deformation Studies in the Ilan Plain and Pingtung Plain Regions. Tectonophysics 2009, 466, 356–376. [Google Scholar] [CrossRef]
- Lacombe, O.; Mouthereau, F.; Angelier, J.; Deffontaines, B. Structural, Geodetic and Seismological Evidence for Tectonic Escape in SW Taiwan. Tectonophysics 2001, 333, 323–345. [Google Scholar] [CrossRef]
- Lu, C.-Y.; Malavieille, J. Oblique Convergence, Indentation and Rotation Tectonics in the Taiwan Mountain Belt: Insights from Experimental Modelling. Earth Planet. Sci. Lett. 1994, 121, 477–494. [Google Scholar] [CrossRef]
- Shyu, J.B.H.; Sieh, K.; Chen, Y.-G.; Liu, C.-S. Neotectonic Architecture of Taiwan and Its Implications for Future Large Earthquakes. J. Geophys. Res. Solid Earth 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Deffontaines, B.; Lacombe, O.; Angelier, J.; Chu, H.T.; Mouthereau, F.; Lee, C.T.; Deramond, J.; Lee, J.F.; Yu, M.S.; Liew, P.M. Quaternary Transfer Faulting in the Taiwan Foothills: Evidence from a Multisource Approach. Tectonophysics 1997, 274, 61–82. [Google Scholar] [CrossRef]
- Lacombe, O.; Mouthereau, F.; Deffontaines, B.; Angelier, J.; Chu, H.T.; Lee, C.T. Geometry and Quaternary Kinematics of Fold-and-Thrust Units of Southwestern Taiwan. Tectonics 1999, 18, 1198–1223. [Google Scholar] [CrossRef] [Green Version]
- Mouthereau, F.; Lacombe, O.; Deffontaines, B.; Angelier, J.; Brusset, S. Deformation History of the Southwestern Taiwan Foreland Thrust Belt: Insights from Tectono-Sedimentary Analyses and Balanced Cross-Sections. Tectonophysics 2001, 333, 293–322. [Google Scholar] [CrossRef]
- Huang, S.-T.; Yang, K.-M.; Hung, J.-H.; Wu, J.-C.; Ting, H.-H.; Mei, W.-W.; Hsu, S.-H.; Lee, M. Deformation Front Development at the Northeast Margin of the Tainan Basin, Tainan–Kaohsiung Area, Taiwan. Mar. Geophys. Res. 2004, 25, 139–156. [Google Scholar] [CrossRef]
- Wu, Y.-M.; Chang, C.-H.; Zhao, L.; Teng, T.-L.; Nakamura, M. A Comprehensive Relocation of Earthquakes in Taiwan from 1991 to 2005. Bull. Seismol. Soc. Am. 2008, 98, 1471–1481. [Google Scholar] [CrossRef] [Green Version]
- Cobbold, P.R.; Davy, P. Indentation Tectonics in Nature and Experiment. II: Central Asia. Indentation Tecton. Nat. Exp. II Cent. Asia 1988, 14, 143–162. [Google Scholar]
- Lu, C.-Y.; Angelier, J.; Chu, H.-T.; Lee, J.-C. Contractional, Transcurrent, Rotational and Extensional Tectonics: Examples from Northern Taiwan. Tectonophysics 1995, 246, 129–146. [Google Scholar] [CrossRef]
- Molnar, P.; Tapponnier, P. Cenozoic Tectonics of Asia: Effects of a Continental Collision. Science 1975, 189, 419–426. [Google Scholar] [CrossRef] [PubMed]
- Tapponnier, P.; Peltzer, G.; Le Dain, A.Y.; Armijo, R.; Cobbold, P. Propagating Extrusion Tectonics in Asia: New Insights from Simple Experiments with Plasticine. Geology 1982, 10, 611–616. [Google Scholar] [CrossRef]
- Dewey, J.F.; Şengör, A.M.C. Aegean and Surrounding Regions: Complex Multiplate and Continuum Tectonics in a Convergent Zone. GSA Bull. 1979, 90, 84–92. [Google Scholar] [CrossRef]
- McKenzie, D. Active Tectonics of the Mediterranean Region. Geophys. J. Int. 1972, 30, 109–185. [Google Scholar] [CrossRef] [Green Version]
- Capitanio, F.A. The Dynamics of Extrusion Tectonics: Insights from Numerical Modeling. Tectonics 2014, 33, 2361–2381. [Google Scholar] [CrossRef]
- Tapponnier, P.; Zhiqin, X.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Jingsui, Y. Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef]
- Nyst, M.; Thatcher, W. New Constraints on the Active Tectonic Deformation of the Aegean. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Lazos, I.; Sboras, S.; Chousianitis, K.; Kondopoulou, D.; Pikridas, C.; Bitharis, S.; Pavlides, S. Temporal Evolution of Crustal Rotation in the Aegean Region Based on Primary Geodetically-Derived Results and Palaeomagnetism. Acta Geod. Geophys. 2022, 57, 317–334. [Google Scholar] [CrossRef]
- Sun, C.-H.; Chang, S.-C.; Kuo, C.-L.; Wu, J.-C.; Shao, P.-H.; Oung, J.-N. Origins of Taiwan’s Mud Volcanoes: Evidence from Geochemistry. J. Asian Earth Sci. 2010, 37, 105–116. [Google Scholar] [CrossRef]
- Mouthereau, F.; Deffontaines, B.; Lacombe, O.; Angelier, J. Variations along the Strike of the Taiwan Thrust Belt: Basement Control on Structural Style, Wedge Geometry, and Kinematics. Geol. Soc. Am. 2002, 358. [Google Scholar] [CrossRef]
- Suppe, J. Mechanics of Mountain Building and Metamorphism in Taiwan. Mem. Geol. Soc. China Taiwan 1981, 4, 67–89. [Google Scholar]
- Lin, A.T.; Watts, A.B.; Hesselbo, S.P. Cenozoic Stratigraphy and Subsidence History of the South China Sea Margin in the Taiwan Region. Basin Res. 2003, 15, 453–478. [Google Scholar] [CrossRef]
- Fuller, C.W.; Willett, S.D.; Fisher, D.; Lu, C.Y. A Thermomechanical Wedge Model of Taiwan Constrained by Fission-Track Thermochronometry. Tectonophysics 2006, 425, 1–24. [Google Scholar] [CrossRef]
- Yamato, P.; Mouthereau, F.; Burov, E. Taiwan Mountain Building: Insights from 2-D Thermomechanical Modelling of a Rheologically Stratified Lithosphere. Geophys. J. Int. 2009, 176, 307–326. [Google Scholar] [CrossRef] [Green Version]
- Huchon, P.; Barrier, E.; de Bremaecker, J.-C.; Angelier, J. Collision and Stress Trajectories in Taiwan: A Finite Element Model. Tectonophysics 1986, 125, 179–191. [Google Scholar] [CrossRef]
- Hu, J.-C.; Angelier, J.; Lee, J.-C.; Chu, H.-T.; Byrne, D. Kinematics of Convergence, Deformation and Stress Distribution in the Taiwan Collision Area: 2-D Finite-Element Numerical Modelling. Tectonophysics 1996, 255, 243–268. [Google Scholar] [CrossRef]
- Hu, J.-C.; Yu, S.-B.; Angelier, J.; Chu, H.-T. Active Deformation of Taiwan from GPS Measurements and Numerical Simulations. J. Geophys. Res. Solid Earth 2001, 106, 2265–2280. [Google Scholar] [CrossRef]
- Lin, S.-C.; Kuo, B.-Y. Dynamics of the Opposite-Verging Subduction Zones in the Taiwan Region: Insights from Numerical Models. J. Geophys. Res. Solid Earth 2016, 121, 2174–2192. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Kaus, B.J.P.; Yang, J.; Wang, K.; Li, Y.; Chen, L.; Zhao, L. 3D Geodynamic Models for HP-UHP Rock Exhumation in Opposite-Dip Double Subduction-Collision Systems. J. Geophys. Res. Solid Earth 2021, 126, e2021JB022326. [Google Scholar] [CrossRef]
- Choi, E.; Tan, E.; Lavier, L.L.; Calo, V.M. DynEarthSol2D: An Efficient Unstructured Finite Element Method to Study Long-term Tectonic Deformation. J. Geophys. Res. Solid Earth 2013, 118, 2429–2444. [Google Scholar] [CrossRef] [Green Version]
- Ta, T.; Choo, K.; Tan, E.; Jang, B.; Choi, E. Accelerating DynEarthSol3D on Tightly Coupled CPU–GPU Heterogeneous Processors. Comput. Geosci. 2015, 79, 27–37. [Google Scholar] [CrossRef]
- Cundall, P.A. Numerical Experiments on Localization in Frictional Materials. Ing. Arch. 1989, 59, 148–159. [Google Scholar] [CrossRef]
- Culling, W.E.H. Analytical Theory of Erosion. J. Geol. 1960, 68, 336–344. [Google Scholar] [CrossRef]
- Yang, K.-M.; Rau, R.-J.; Chang, H.-Y.; Hsieh, C.-Y.; Ting, H.-H.; Huang, S.-T.; Wu, J.-C.; Tang, Y.-J. The Role of Basement-Involved Normal Faults in the Recent Tectonics of Western Taiwan. Geol. Mag. 2016, 153, 1166–1191. [Google Scholar] [CrossRef] [Green Version]
- Le Béon, M.; Huang, M.-H.; Suppe, J.; Huang, S.-T.; Pathier, E.; Huang, W.-J.; Chen, C.-L.; Fruneau, B.; Baize, S.; Ching, K.-E.; et al. Shallow Geological Structures Triggered during the Mw 6.4 Meinong Earthquake, Southwestern Taiwan. Terr. Atmos. Ocean. Sci. 2017, 28, 663–681. [Google Scholar] [CrossRef] [Green Version]
- Doo, W.-B.; Lo, C.-L.; Hsu, S.-K.; Tsai, C.-H.; Huang, Y.-S.; Wang, H.-F.; Chiu, S.-D.; Ma, Y.-F.; Liang, C.-W. New Gravity Anomaly Map of Taiwan and Its Surrounding Regions with Some Tectonic Interpretations. J. Asian Earth Sci. 2018, 154, 93–100. [Google Scholar] [CrossRef]
- Doo, W.-B.; Hsu, S.-K.; Lo, C.-L.; Chen, S.-C.; Tsai, C.-H.; Lin, J.-Y.; Huang, Y.-P.; Huang, Y.-S.; Chiu, S.-D.; Ma, Y.-F. Gravity Anomalies of the Active Mud Diapirs off Southwest Taiwan. Geophys. J. Int. 2015, 203, 2089–2098. [Google Scholar] [CrossRef]
- Hwang, C.; Hsu, H.-J.; Chang, E.T.Y.; Featherstone, W.E.; Tenzer, R.; Lien, T.; Hsiao, Y.-S.; Shih, H.-C.; Jai, P.-H. New Free-Air and Bouguer Gravity Fields of Taiwan from Multiple Platforms and Sensors. Tectonophysics 2014, 611, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Suppe, J. Imbricated Structure of Western Foothills Belt, Southcentral Taiwan. Pet. Geol. Taiwan 1980, 17, 1–16. [Google Scholar]
- Dahlen, F.A. Noncohesive Critical Coulomb Wedges: An Exact Solution. J. Geophys. Res. Solid Earth 1984, 89, 10125–10133. [Google Scholar] [CrossRef]
- Dahlen, F.A.; Barr, T.D. Brittle Frictional Mountain Building: 1. Deformation and Mechanical Energy Budget. J. Geophys. Res. Solid Earth 1989, 94, 3906–3922. [Google Scholar] [CrossRef]
- Davis, D.; Suppe, J.; Dahlen, F.A. Mechanics of Fold-and-Thrust Belts and Accretionary Wedges. J. Geophys. Res. Solid Earth 1983, 88, 1153–1172. [Google Scholar] [CrossRef]
- Costa, E.; Vendeville, B.C. Experimental Insights on the Geometry and Kinematics of Fold-and-Thrust Belts above Weak, Viscous Evaporitic Décollement. J. Struct. Geol. 2002, 24, 1729–1739. [Google Scholar] [CrossRef]
- Malavieille, J. Impact of Erosion, Sedimentation, and Structural Heritage on the Structure and Kinematics of Orogenic Wedges: Analog Models and Case Studies. GSA Today 2010, 20, 4–10. [Google Scholar] [CrossRef]
- Ruh, J.B.; Kaus, B.J.P.; Burg, J.-P. Numerical Investigation of Deformation Mechanics in Fold-and-Thrust Belts: Influence of Rheology of Single and Multiple Décollements: Deformation of fold-and-thrust belts. Tectonics 2012, 31. [Google Scholar] [CrossRef]
- Stockmal, G.S.; Beaumont, C.; Nguyen, M.; Lee, B. Mechanics of Thin-Skinned Fold-and-Thrust Belts: Insights from Numerical Models. In Special Paper 433: Whence the Mountains? Inquiries into the Evolution of Orogenic Systems: A Volume in Honor of Raymond A. Price; Geological Society of America: Boulder, CO, USA, 2007; Volume 433, pp. 63–98. ISBN 978-0-8137-2433-1. [Google Scholar]

| Parameter | Upper Zone | Basal Weak Zone |
|---|---|---|
| Density (ρ) | 2800 kg/m3 | |
| Shear Modulus (G) | 30 GPa | |
| Lame’s First Parameter (λ) | 30 GPa | |
| Surface Diffusivity (Κero) | 31.5 m2/year | |
| Critical Plastic Strain | 0.1 | |
| Initial Cohesion | 4 MPa | 0.4 MPa |
| Weakened Cohesion | 2 MPa | 0.4 MPa |
| Friction Angle | 30° | 2.5°/5° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, F.-Y.; Tan, E.; Chang, E.T.-Y. Escape Mechanism with Shallow Ramp and Décollements in Southwest Taiwan. Geosciences 2023, 13, 41. https://doi.org/10.3390/geosciences13020041
Lee F-Y, Tan E, Chang ET-Y. Escape Mechanism with Shallow Ramp and Décollements in Southwest Taiwan. Geosciences. 2023; 13(2):41. https://doi.org/10.3390/geosciences13020041
Chicago/Turabian StyleLee, Fang-Yi, Eh Tan, and Emmy T.-Y. Chang. 2023. "Escape Mechanism with Shallow Ramp and Décollements in Southwest Taiwan" Geosciences 13, no. 2: 41. https://doi.org/10.3390/geosciences13020041
APA StyleLee, F.-Y., Tan, E., & Chang, E. T.-Y. (2023). Escape Mechanism with Shallow Ramp and Décollements in Southwest Taiwan. Geosciences, 13(2), 41. https://doi.org/10.3390/geosciences13020041








