Earthquake Damage Susceptibility Analysis in Barapani Shear Zone Using InSAR, Geological, and Geophysical Data
Abstract
1. Introduction
2. Geology and Tectonics of Barapani Shear Zone (BSZ)
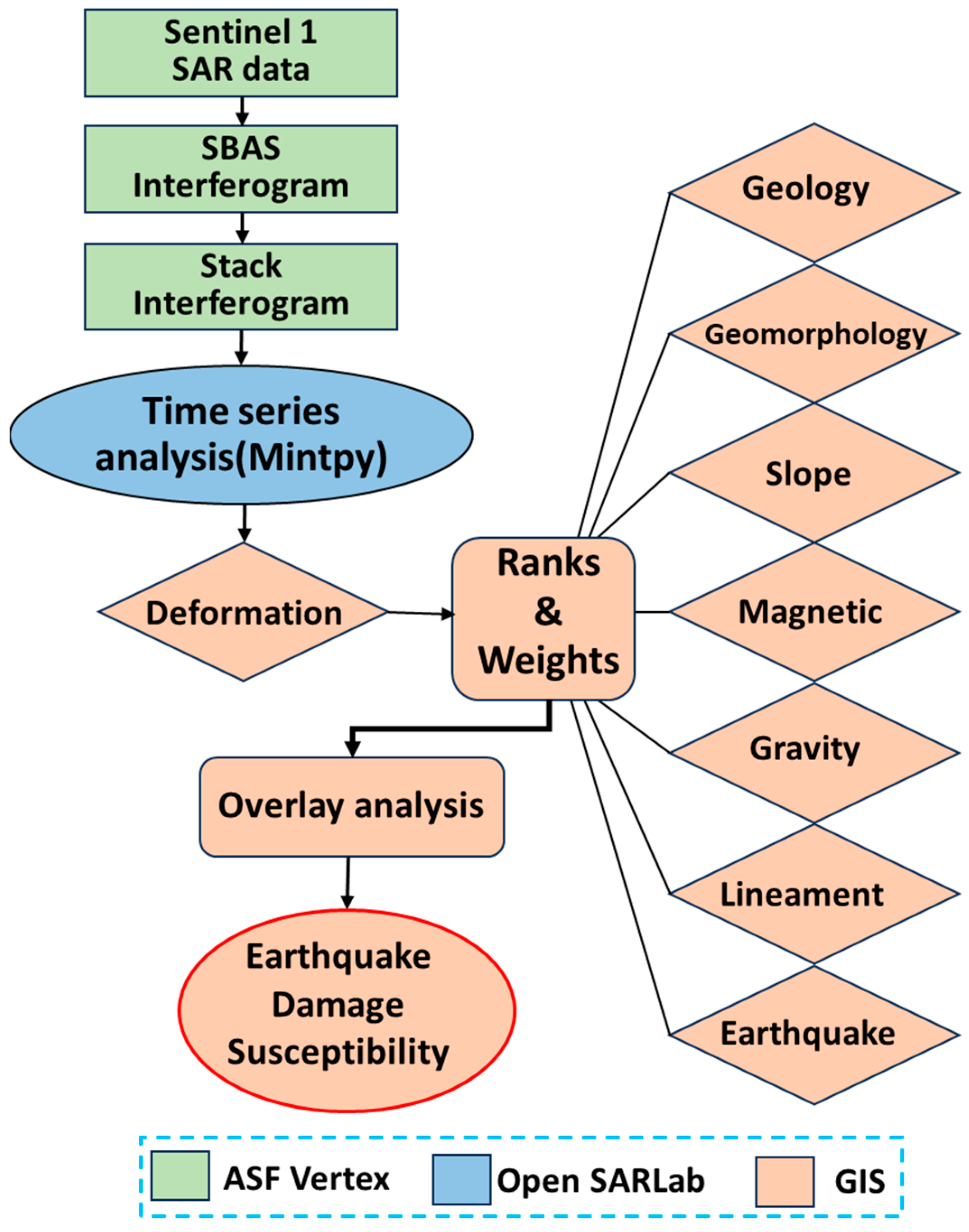
3. Data and Methodology
3.1. Data Utilized
3.2. InSAR Time Series Analysis
3.3. Weighted Overlay Analysis
4. Results and Discussion
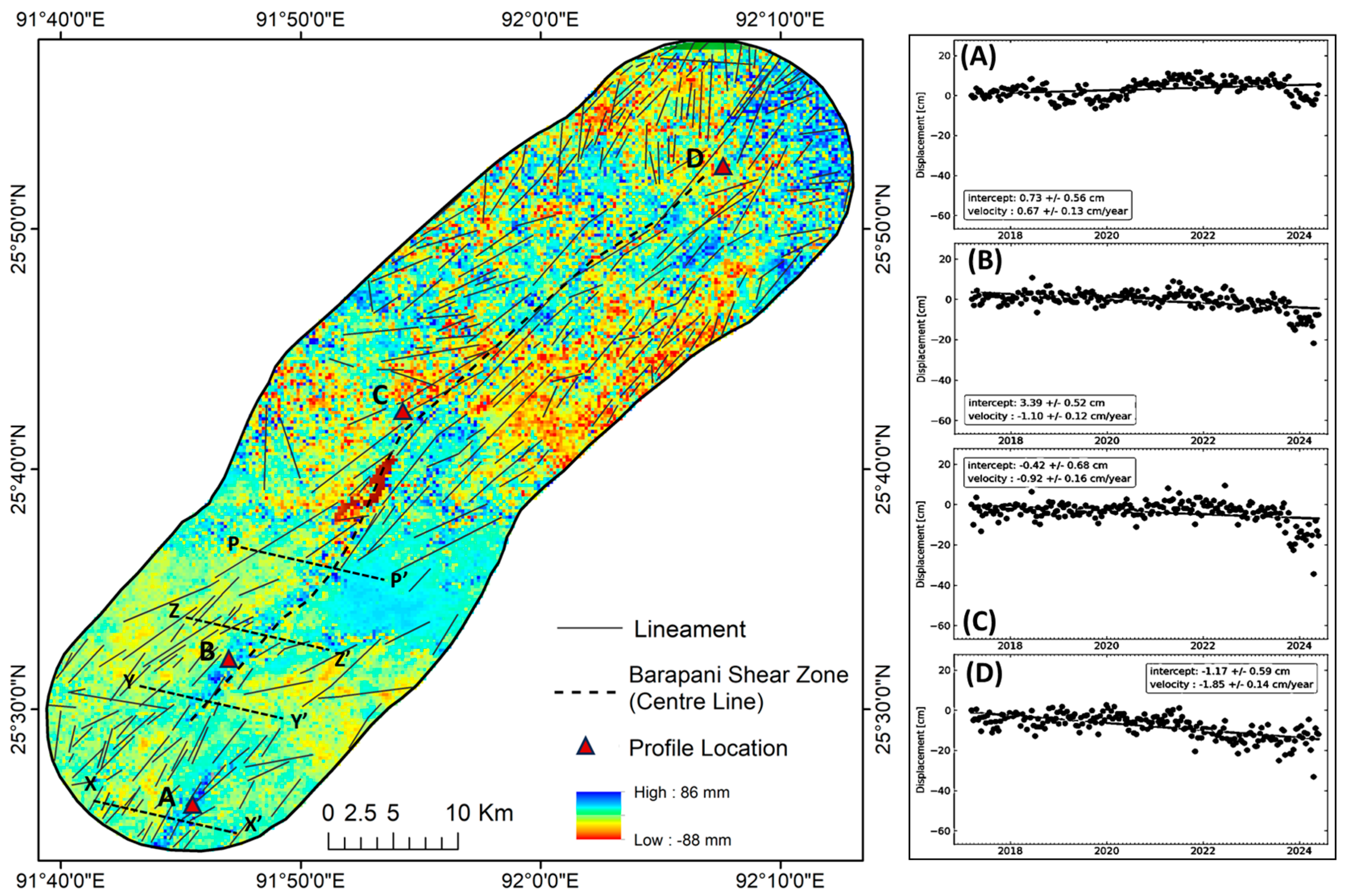
4.1. InSAR-Based Time Series Analysis
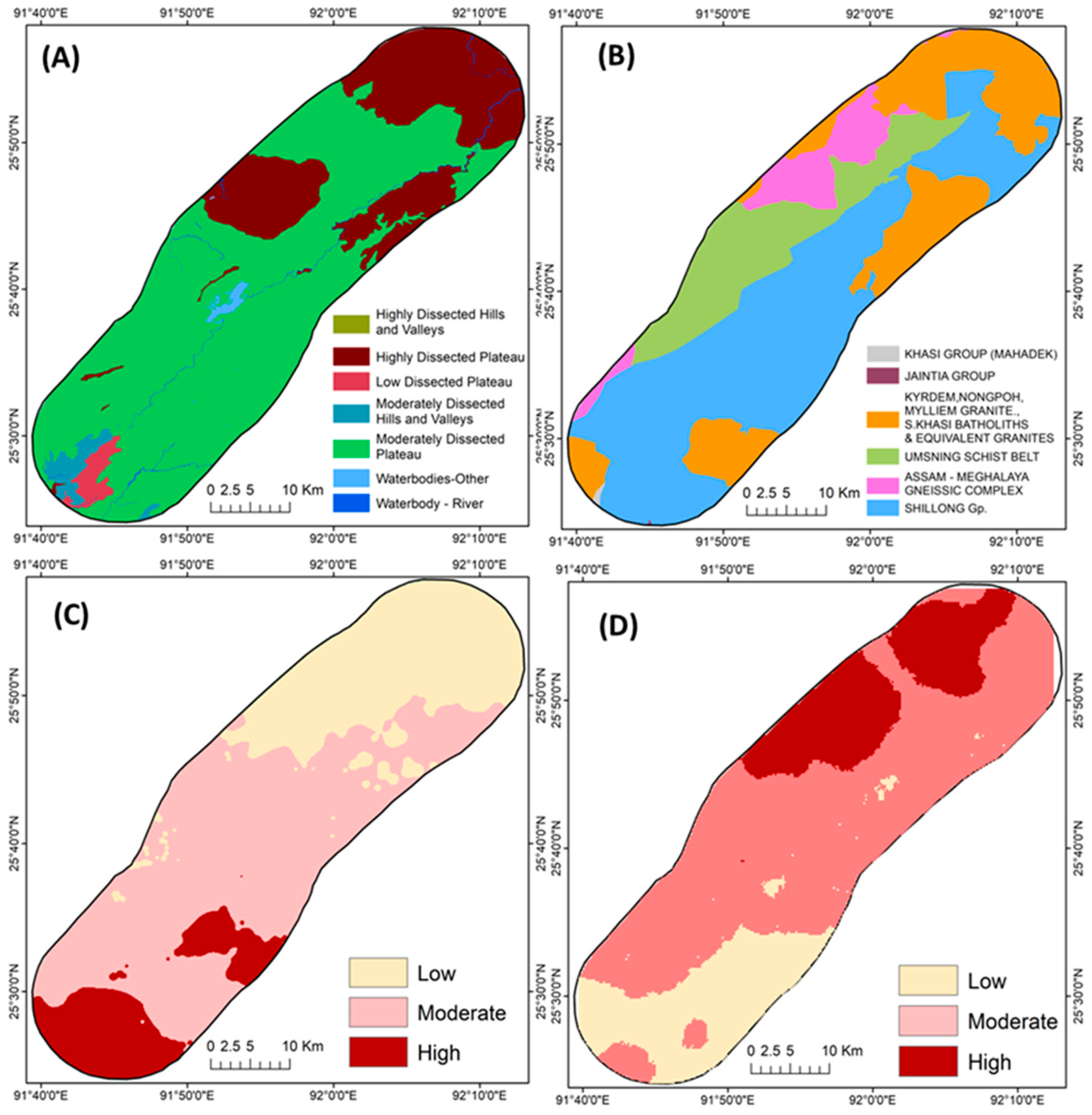
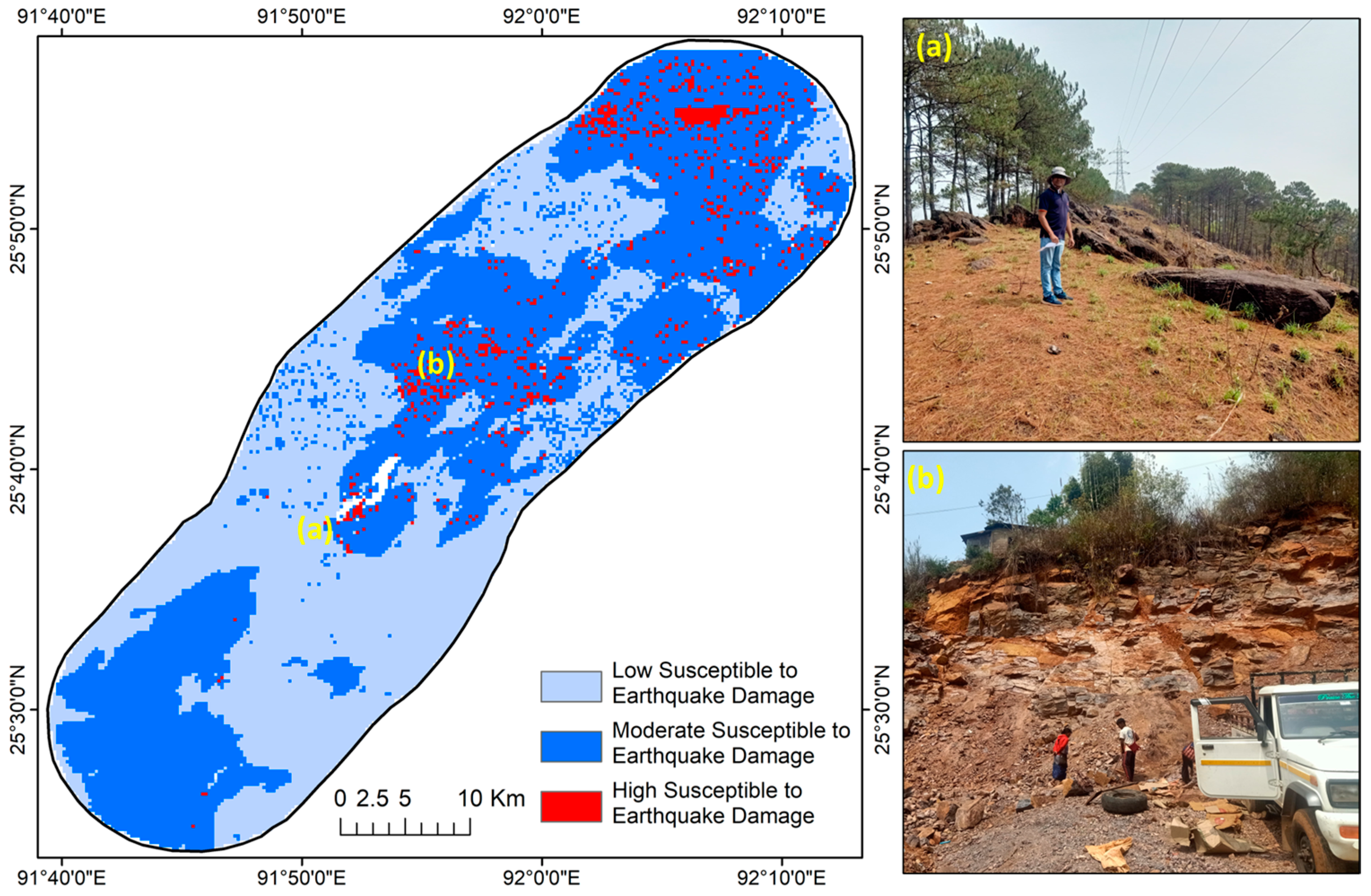
4.2. Data Integration and Earthquake Damage Susceptibility Mapping
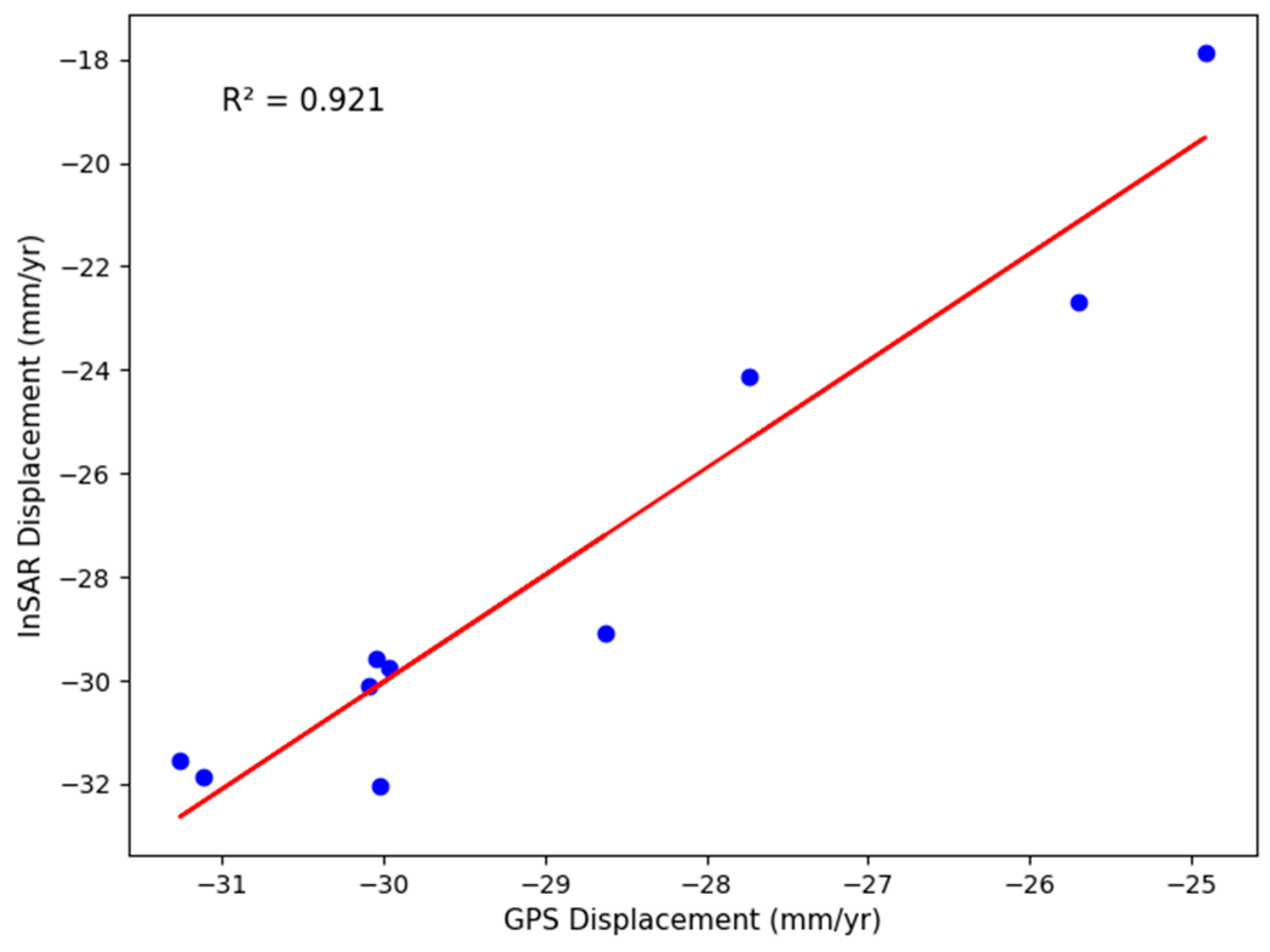
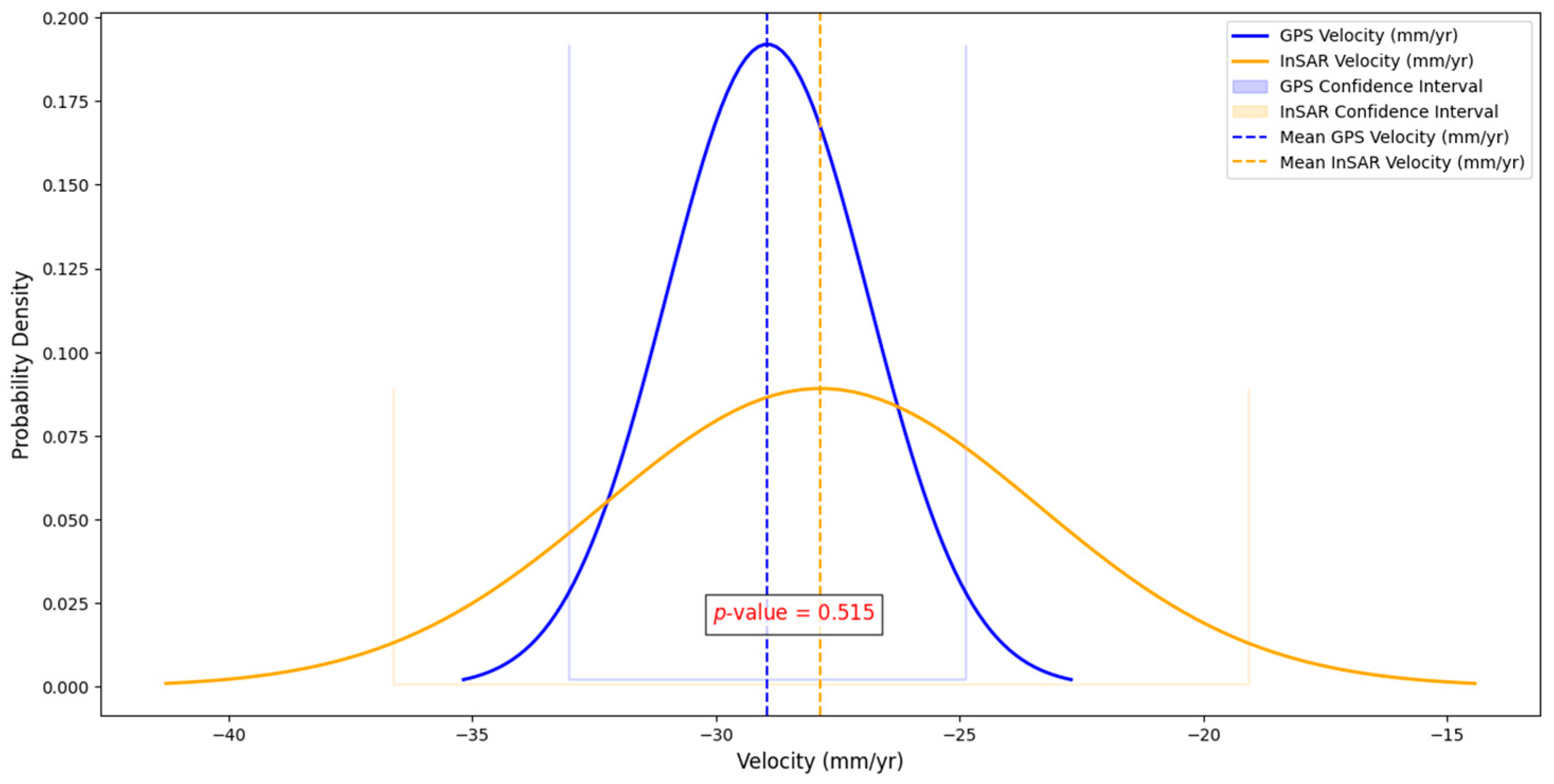
5. Validation of InSAR Velocity Rates
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Passchier, C.W.; Trouw RA, J. Microtectonics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 200–230. [Google Scholar] [CrossRef]
- Ramsay, J.G.; Huber, M.I. Modern structural geology. Folds Fract. 1987, 2, 309–700. [Google Scholar]
- Sibson, R.H. Fault rocks and fault mechanisms. J. Geol. Soc. 1977, 133, 191–213. [Google Scholar] [CrossRef]
- Lister, G.S.; Snoke, A.W. S-C mylonites. J. Struct. Geol. 1984, 6, 617–638. [Google Scholar] [CrossRef]
- Hirth, G.; Tullis, J. Dislocation creep regimes in quartz aggregates. J. Struct. Geol. 1992, 14, 145–159. [Google Scholar] [CrossRef]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Discrimination of geophysical phenomena in satellite radar interferograms. Geophys. Res. Lett. 1995, 22, 1537–1540. [Google Scholar] [CrossRef]
- Peltzer, G.; Rosen, P. Surface displacement of the 17 May 1993 Eureka Valley, California, earthquake observed by SAR interferometry. Science 1995, 268, 1333–1336. [Google Scholar] [CrossRef] [PubMed]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent scatterer interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Casagli, N.; Catani, F.; Del Ventisette, C.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Manzo, M.; Ricciardi, G.P.; Casu, F.; Ventura, G.; Zeni, G.; Borgström, S.; Lanari, R. Surface deformation analysis in the Ischia Island (Italy) based on spaceborne radar interferometry. J. Volcanol. Geotherm. Res. 2006, 151, 399–416. [Google Scholar] [CrossRef]
- Cabral-Cano, E.; Dixon, T.H.; Miralles-Wilhelm, F.; Díaz-Molina, O.; Sánchez-Zamora, O.; Carande, R.E. Space geodetic imaging of rapid ground subsidence in Mexico City. Geol. Soc. Am. Bull. 2008, 120, 1556–1566. [Google Scholar] [CrossRef]
- Castellazzi, P.; Arroyo-Domínguez, N.; Martel, R.; Calderhead, A.I.; Normand, J.C.; Gárfias, J.; Rivera, A. Land subsidence in major cities of Central Mexico: Interpreting InSAR-derived land subsidence mapping with hydrogeological data. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 102–111. [Google Scholar] [CrossRef]
- Rott, H. Advances in interferometric synthetic aperture radar (InSAR) in earth system science. Prog. Phys. Geogr. Earth Environ. 2009, 33, 769–791. [Google Scholar] [CrossRef]
- Nayak, K.; López-Urías, C.; Romero-Andrade, R.; Sharma, G.; Guzmán-Acevedo, G.M.; Trejo-Soto, M.E. Ionospheric Total Electron Content (TEC) Anomalies as Earthquake Precursors: Unveiling the Geophysical Connection Leading to the 2023 Moroccan 6.8 Mw Earthquake. Geosciences 2023, 13, 319. [Google Scholar] [CrossRef]
- Reinisch, E.C.; Abolt, C.J.; Swanson, E.M.; Rouet-Leduc, B.; Snyder, E.E.; Sivaraj, K.; Solander, K.C. Advancing the Limits of InSAR to Detect Crustal Displacement from Low-Magnitude Earthquakes through Deep Learning. Remote Sens. 2024, 16, 2019. [Google Scholar] [CrossRef]
- Alatza, S.; Papoutsis, I.; Paradissis, D.; Kontoes, C.; Papadopoulos, G.A. Multi-Temporal InSAR Analysis for Monitoring Ground Deformation in Amorgos Island, Greece. Sensors 2020, 20, 338. [Google Scholar] [CrossRef] [PubMed]
- Medhat, N.I.; Yamamoto, M.Y.; Tolomei, C.; Harbi, A.; Maouche, S. Multi-temporal InSAR analysis to monitor landslides using the small baseline subset (SBAS) approach in the Mila Basin, Algeria. Terra Nova 2022, 34, 407–423. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Khodaei, B.; Hashemi, H. An integrated InSAR-machine learning approach for ground deformation rate modeling in arid areas. J. Hydrol. 2022, 608, 127627. [Google Scholar] [CrossRef]
- Brengman, C.M.; Barnhart, W.D. Identification of surface deformation in InSAR using machine learning. Geochem. Geophys. Geosystems 2021, 22, e2020GC009204. [Google Scholar] [CrossRef]
- Zeng, T.; Wu, L.; Hayakawa, Y.S.; Yin, K.; Gui, L.; Jin, B.; Peduto, D. Advanced integration of ensemble learning and MT-InSAR for enhanced slow-moving landslide susceptibility zoning. Eng. Geol. 2024, 331, 107436. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Y.; Wei, J.; Duan, M.; Wu, L.; Hou, J.; Zhu, J. Time-series InSAR ground deformation monitoring: Atmospheric delay modeling and estimating. Earth Sci. Rev. 2019, 192, 258–284. [Google Scholar] [CrossRef]
- Raspini, F.; Caleca, F.; Del Soldato, M.; Festa, D.; Confuorto, P.; Bianchini, S. Review of satellite radar interferometry for subsidence analysis. Earth Sci. Rev. 2022, 235, 104239. [Google Scholar] [CrossRef]
- Baruah, S.; Baruah, S.; Das, R. Tectonics and Seismogenesis in Northeast India and Adjoining Regions: Seismological and Geological Appraisal. J. Geol. Soc. India 2013, 82, 369–376. [Google Scholar] [CrossRef]
- Ghosh, P.; Bhattacharya, A.; Majumdar, R. Geological and Structural Setting of the Shillong Plateau and Adjacent Regions. Mem. Geol. Surv. India 2005, 123, 1–48. [Google Scholar]
- Yin, A.; Dubey, C.S.; Bhattacharya, A. Structural Evolution of the Shillong Plateau and its Implications for Understanding the India-Asia Collision. J. Asian Earth Sci. 2010, 39, 691–703. [Google Scholar]
- Baruah, S.; Baruah, S.; Saikia, S.; Shrivastava, M.N.; Sharma, A.; Reddy, C.D.; Kayal, J.R. State of tectonic stress in Shillong Plateau of northeast India. Phys. Chem. Earth 2016, 95, 36–49. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef]
- Hogenson, K.; Meyer, F.; Logan, T.; Lewandowski, A.; Stern, T.; Lundell, E.; Miller, R. The ASF OpenSARLab A Cloud-Based (SAR) Remote Sensing Data Analysis Platform. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2021; Volume 2021, p. G35C-0312. [Google Scholar]
- Liu, M.; Tang, X.; Zhu, K.; Chen, H.; Sun, N.; Pan, D.Z. OpenSAR: An Open Source Automated End-to-End SAR ADC Compiler. In Proceedings of the 2021 IEEE/ACM International Conference on Computer Aided Design (ICCAD), IEEE, Munich, Germany, 1–4 November 2021; pp. 1–9. [Google Scholar]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorquí, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Lundgren, P.; Casu, F.; Manzo, M.; Pepe, A.; Berardino, P.; Sansosti, E.; Lanari, R. Gravity and magma-induced spreading of Mount Etna volcano revealed by satellite radar interferometry. Geophys. Res. Lett. 2004, 31, L04602. [Google Scholar] [CrossRef]
- Manzo, M.; Fialko, Y.; Casu, F.; Pepe, A.; Lanari, R. A quantitative assessment of DInSAR measurements of interseismic deformation: The southern San Andreas Fault case study. Pure Appl. Geophys. 2012, 169, 1463–1482. [Google Scholar] [CrossRef]
- Cascini, L.; Peduto, D.; Fornaro, G.; Lanari, R.; Zeni, G.; Guzzetti, F. Spaceborne Radar Interferometry for Landslide Monitoring. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July–4 August 2006. [Google Scholar]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic: Dordrecht, The Netherlands; Boston, MA, USA, 2001. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward mapping surface deformation in three dimensions using InSAR. Geophys. Res. Lett. 2004, 31, L01607. [Google Scholar] [CrossRef]
- United State Geological Survey (USGS). Available online: https://earthexplorer.usgs.gov/ (accessed on 12 October 2024).
- National Center for Seismology. Ministry of Earth Sciences, Government of India. Available online: https://seismo.gov.in/ (accessed on 12 October 2024).
- Geological Survey of India (GSI). Available online: https://www.data.gov.in/catalog/bhukosh (accessed on 12 October 2024).
- Weiss, J.R.; Walters, R.J.; Morishita, Y.; Wright, T.J.; Lazecky, M.; Wang, H.; Parsons, B. High-resolution surface velocities and strain for Anatolia from Sentinel-1 InSAR and GNSS data. Geophys. Res. Lett. 2020, 47, e2020GL087376. [Google Scholar] [CrossRef]
- Su, X.; Bao, Q.; Gao, Z.; Huang, J. Three-dimensional interseismic crustal deformation in the northeastern margin of the Tibetan Plateau using GNSS and InSAR. J. Asian Earth Sci. 2024, 276, 106328. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Yi, Y.; Zhang, Z.; Zhang, W.; Xu, Q.; Deng, C.; Li, Q. GIS-based earthquake-triggered-landslide susceptibility mapping with an integrated weighted index model in Jiuzhaigou region of Sichuan Province, China. Nat. Hazards Earth Syst. Sci. 2019, 19, 1973–1988. [Google Scholar] [CrossRef]
- Shano, L.; Raghuvanshi, T.K.; Meten, M. Landslide susceptibility evaluation and hazard zonation techniques–a review. Geoenviron. Dis. 2020, 7, 1–19. [Google Scholar] [CrossRef]
- Mukul, M.; Jade, S.; Bhattacharyya, A.K.; Bhusan, K. Crustal shortening in convergent orogens: Insights from global positioning system (GPS) measurements in northeast India. J. Geol. Soc. India 2010, 75, 302–312. [Google Scholar] [CrossRef]
- Barman, P.; Jade, S.; Shrungeshwara, T.S.; Kumar, A.; Bhattacharyya, S.; Ray, J.D.; Jagannathan, S.; Jamir, W.M. Crustal deformation rates in Assam Valley, Shillong Plateau, Eastern Himalaya, and Indo-Burmese region from 11 years (2002–2013) of GPS measurements. Int. J. Earth Sci. 2017, 106, 2025–2038. [Google Scholar] [CrossRef]
- Jade, S.; Mukul, M.; Bhattacharyya, A.K.; Vijayan, M.S.M.; Jaganathan, S.; Kumar, A.; Gaur, V.K. Estimates of interseismic deformation in Northeast India from GPS measurements. Earth Planet. Sci. Lett. 2007, 263, 221–234. [Google Scholar] [CrossRef]



| Parameter Derived in Present Study | Weight | Rank | Parameter Obtained from GSI Data Products | Weight | Rank |
|---|---|---|---|---|---|
| InSAR Velocity (mm/yr) Low (>−30) Medium (−30 to 30) High (>30 mm/yr) | 30 | 9 5 9 | Geology Assam–Meghalaya Gneissic Complex Jaintia Gp. Khasi Gp. (Mahadek Fm.) Kyrdem, Nongpoh, Mylliem Granite., S.Khasi Batholiths and Equivalent Granites Shillong Gp. Umsning Schist Belt Gr. | 10 | 2 5 8 3 9 7 |
| Lineation Density Low (60) Medium (120) High (180) | 20 | 4 7 9 | Geomorphology Highly Dissected Hills and Valleys Highly Dissected Plateau Low Dissected Plateau Moderately Dissected Hills and Valleys Moderately Dissected Plateau Waterbodies—Other Waterbody—River | 10 | 8 7 5 6 5 3 3 - |
| Slope (Degree) Low (0–30) Medium (30–45) High (45–90) | 10 | 3 5 9 | Gravity (mGal) Low (−52–40) Medium (−40–−25) High (−25–−10) | 5 | 9 5 2 |
| Earthquakes (Mw) Low (2.2–2.8) Medium (2.8–3.4) High (3.4–4) | 10 | 3 6 9 | Magnetic (nT) Low (−479–−133) Medium (−133–214) High (>214) | 5 | 5 3 2 |
| S. No. | Station Name | Location | ITRF08 (mm/Year) | GPSLOS (mm/Year) | InSAR (mm/Year) | |
|---|---|---|---|---|---|---|
| VE | VN | |||||
| 1 | NONG | Nongpoh, Meghalaya | 39.33 ± 0.28 | 29.86 ± 0.28 | −27.75 | −24.11 |
| 2 | SHIL | Shillong, Meghalaya | 35.80 ± 0.80 | 30.50 ± 0.50 | −25.70 | −22.68 |
| 3 | MOPE | Mopen, Meghalaya | 37.20 ± 0.80 | 30.70 ± 0.60 | −24.91 | −17.87 |
| 4 | SOKR | Sokra Pam, Assam | 38.94 ± 0.91 | 27.51 ± 0.9 | −30.05 | −29.56 |
| 5 | PANI | Panimura, Assam | 38.07 ± 0.46 | 29.19 ± 0.46 | −29.98 | −29.74 |
| 6 | NIM | Nim, West Bengal | 36.83 ± 0.80 | 31.41 ± 0.60 | −30.09 | −30.10 |
| 7 | MUNGPU | Mungpoo, West Bengal | 36.25 ± 0.50 | 32.03 ± 0.40 | −28.63 | −29.10 |
| 8 | GBSK | Panthang, Sikkim | 39.49 ± 0.31 | 28.65 ± 0.32 | −31.27 | −31.53 |
| 9 | BOMP | Bomdila, Arunachal Pradesh | 41.88 ± 0.16 | 19.87 ± 0.55 | −31.13 | −31.86 |
| 10 | RAIM | Raimana, Assam | 39.95 ± 0.30 | 33.67 ± 0.29 | −30.03 | −32.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, G.; Singh, M.S.; Nayak, K.; Dutta, P.P.; Sarma, K.K.; Aggarwal, S.P. Earthquake Damage Susceptibility Analysis in Barapani Shear Zone Using InSAR, Geological, and Geophysical Data. Geosciences 2025, 15, 45. https://doi.org/10.3390/geosciences15020045
Sharma G, Singh MS, Nayak K, Dutta PP, Sarma KK, Aggarwal SP. Earthquake Damage Susceptibility Analysis in Barapani Shear Zone Using InSAR, Geological, and Geophysical Data. Geosciences. 2025; 15(2):45. https://doi.org/10.3390/geosciences15020045
Chicago/Turabian StyleSharma, Gopal, M. Somorjit Singh, Karan Nayak, Pritom Pran Dutta, K. K. Sarma, and S. P. Aggarwal. 2025. "Earthquake Damage Susceptibility Analysis in Barapani Shear Zone Using InSAR, Geological, and Geophysical Data" Geosciences 15, no. 2: 45. https://doi.org/10.3390/geosciences15020045
APA StyleSharma, G., Singh, M. S., Nayak, K., Dutta, P. P., Sarma, K. K., & Aggarwal, S. P. (2025). Earthquake Damage Susceptibility Analysis in Barapani Shear Zone Using InSAR, Geological, and Geophysical Data. Geosciences, 15(2), 45. https://doi.org/10.3390/geosciences15020045






