Hybrid Fixed-Point Fixed-Stress Splitting Method for Linear Poroelasticity
Abstract
:1. Introduction
2. Fixed Stress Splitting
3. Hybrid Method
4. Convergence
5. Numerical Experiments
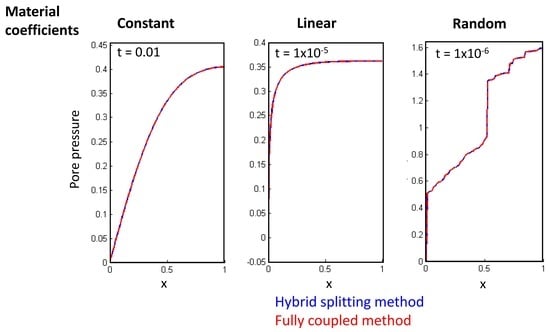
6. Results
6.1. Case I
6.2. Case II
6.3. Case III
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| Dilation (N/m) | |
| Shear moduli of elasticity (N/m) | |
| Combined porosity of the medium & compressibility of the fluid (m/N) | |
| k | Hydraulic conductivity (m/N s) |
| f | Body force per unit volume (N/m) |
| Stress vector (N/m) | |
| p | Pore pressure (N/m) |
| Bulk modulus (N/m) | |
| Time step (s) | |
| (m/N) | |
| u | Displacement (m) |
| Strain tensor | |
| Biot’s coefficient | |
| Variation | |
| x | Spatial co-ordinate |
| Amplication factor | |
| Domain | |
| N | Number of intervals |
| Subscript | |
| v | Volumetric |
| j | jth cell |
| L | Left |
| R | Right |
| Superscript | |
| t | A quantities at time t |
| n | A quantities at nth iteration |
| . | Rate of a quantity |
| Non dimensional value of a quantity | |
| Predicted value |
References
- Hudson, J.; Stephansson, O.; Andersson, J.; Tsang, C.F.; Jing, L. Coupled T-H-M issues relating to radioactive waste repository design and performance. Int. J. Rock Mech. Min. Sci. 2001, 38, 143–161. [Google Scholar] [CrossRef]
- Descamps, F.; Descamps, F. Engineering Challenges in the Geological Disposal of Radioactive Waste and Carbon Dioxide. In Geological Disposal of Carbon Dioxide and Radioactive Waste: A Comparative Assessment; Springer: Berlin, Germany, 2011; pp. 185–213. [Google Scholar]
- Shukla, R.; Ranjith, P.; Choi, S.; Haque, A. Study of caprock integrity in geosequestration of carbon dioxide. Int. J. Geomech. 2010, 11, 294–301. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Rinaldi, A.P.; Borgia, A.; Rutqvist, J. Induced seismicity within geological carbon sequestration projects: Maximum earthquake magnitude and leakage potential from undetected faults. Int. J. Greenh. Gas Control 2012, 10, 434–442. [Google Scholar] [CrossRef]
- Harris, R.A. Introduction to Special Section: Stress Triggers, Stress Shadows, and Implications for Seismic Hazard. J. Geophys. Res. Solid Earth 1998, 103, 24347–24358. [Google Scholar] [CrossRef] [Green Version]
- Jing, L. A review of techniques, advances and outstanding issues in numerical modeling for rock mechanics and rock engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Baig, A.; Urbancic, T.; Viegas, G.; Karimi, S. Can small events (M < 0) observed during hydraulic fracture stimulations initiate large events (M > 0)? Lead. Edge 2012, 31, 1470–1474. [Google Scholar]
- Davies, R.; Foulger, G.; Bindley, A.; Styles, P. Induced Seismicity and Hydraulic Fracturing for the Recovery of Hydrocarbons. Mar. Pet. Geol. 2013, 171–185. [Google Scholar] [CrossRef]
- Detournay, E.; Cheng, A.D. Poroelastic response of a borehole in a non-hydrostatic stress field. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1988, 25, 171–182. [Google Scholar] [CrossRef]
- Rajapakse, R.K.N.D. Stress Analysis of Borehole in Poroelastic Medium. J. Eng. Mech. 1993, 119, 1205–1227. [Google Scholar] [CrossRef]
- Roose, T.; Netti, P.A.; Munn, L.L.; Boucher, Y.; Jain, R.K. Solid stress generated by spheroid growth estimated using a linear poroelasticity model. Microvasc. Res. 2003, 66, 204–212. [Google Scholar] [CrossRef]
- Byrne, H.; Preziosi, L. Modelling solid tumor growth using the theory of mixtures. Math. Med. Biol. J. IMA 2003, 20, 341–366. [Google Scholar] [CrossRef]
- Zoback, M.D.; Gorelick, S.M. Earthquake triggering and large-scale geologic storage of carbon dioxide. Proc. Natl. Acad. Sci. USA 2012, 109, 10164–10168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rutqvist, J.; Liu, H.H.; Vasco, D.W.; Pan, L.; Kappler, K.; Majer, E. Coupled non-isothermal, multiphase fluid flow, and geomechanical modeling of ground surface deformations and potential for induced micro-seismicity at the In Salah CO2 storage operation. Energy Procedia 2011, 4, 3542–3549. [Google Scholar] [CrossRef]
- Oldenburg, C.M. The risk of induced seismicity: Is cap-rock integrity on shaky ground? Greenh. Gases Sci. Technol. 2012, 2, 217–218. [Google Scholar] [CrossRef]
- Moos, D.; Peska, P.; Finkbeiner, T.; Zoback, M. Comprehensive wellbore stability analysis utilizing quantitative risk assessment. J. Pet. Sci. Eng. 2003, 38, 97–109. [Google Scholar] [CrossRef]
- Le Maitre, O.O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification: With Applications to Computational Fluid Dynamics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Govindarajan, S. Geomechanical Characterization of Reservoir & Cap Rocks for CO2 Sequestration. Master’s Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2012. [Google Scholar]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Foo, J.; Karniadakis, G.E. Multi-element probabilistic collocation method in high dimensions. J. Comput. Phys. 2010, 229, 1536–1557. [Google Scholar] [CrossRef]
- Wang, S.J.; Hsu, K.C. The application of the first-order second-moment method to analyze poroelastic problems in heterogeneous porous media. J. Hydrol. 2009, 369, 209–221. [Google Scholar] [CrossRef]
- Mendes, M.A.; Murad, M.A.; Pereira, F. A new computational strategy for solving two-phase flow in strongly heterogeneous poroelastic media of evolving scales. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 1683–1716. [Google Scholar] [CrossRef]
- Farnoosh, R.; Ebrahimi, M. Monte Carlo method for solving Fredholm integral equations of the second kind. Appl. Math. Comput. 2008, 195, 309–315. [Google Scholar] [CrossRef]
- Venkovic, N.; Sorelli, L.; Sudret, B.; Yalamas, T.; Gagné, R. Uncertainty propagation of a multiscale poromechanics-hydration model for poroelastic properties of cement paste at early-age. Probab. Eng. Mech. 2013, 32, 5–20. [Google Scholar] [CrossRef] [Green Version]
- Azevedo, J.S.; Murad, M.A.; Borges, M.R.; Oliveira, S.P. A space-time multiscale method for computing statistical moments in strongly heterogeneous poroelastic media of evolving scales. Int. J. Numer. Methods Eng. 2012, 90, 671–706. [Google Scholar] [CrossRef]
- Frias, D.G.; Murad, M.A.; Pereira, F. Stochastic computational modeling of highly heterogeneous poroelastic media with long-range correlations. Int. J. Numer. Anal. Methods Geomech. 2004, 28, 1–32. [Google Scholar] [CrossRef]
- Menéndez, C.; Nieto, P.; Ortega, F.; Bello, A. Non-linear analysis of the consolidation of an elastic saturated soil with incompressible fluid and variable permeability by {FEM}. Appl. Math. Comput. 2010, 216, 458–476. [Google Scholar] [CrossRef]
- El-Maghraby, N.M.; Yossef, H.M. State space approach to generalized thermoelastic problem with thermomechanical shock. Appl. Math. Comput. 2004, 156, 577–586. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X. Analytic solution of poromechanical problems in a hollow axisymmetric domain. Appl. Math. Comput. 1998, 97, 209–221. [Google Scholar]
- Bäck, J.; Nobile, F.; Tamellini, L.; Tempone, R. Stochastic spectral Galerkin and collocation methods for PDEs with random coefficients: A numerical comparison. In Spectral and High Order Methods for Partial Differential Equations; Springer: Berlin, Germany, 2011; pp. 43–62. [Google Scholar]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Najm, H.N. Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics. Ann. Rev. Fluid Mech. 2009, 41, 35–52. [Google Scholar] [CrossRef]
- Xiu, D.; Lucor, D.; Su, C.; Karniadakis, G.E. Stochastic modeling of flow-structure interactions using generalized polynomial chaos. J. Fluid Eng. 2002, 124, 51–59. [Google Scholar] [CrossRef]
- Chen, X.; Ng, B.; Sun, Y.; Tong, C. A flexible uncertainty quantification method for linearly coupled multi-physics systems. J. Comput. Phys. 2013, 248, 383–401. [Google Scholar] [CrossRef]
- Chen, Y.; Luo, Y.; Feng, M. Analysis of a discontinuous Galerkin method for the Biot’s consolidation problem. Appl. Math. Comput. 2013, 219, 9043–9056. [Google Scholar] [CrossRef]
- Zienkiewicz, O. Coupled Problems and Their Numerical Solution. In Numerical Methods in Coupled Systems; Lewis, R.W., Bettess, P., Hinton, E., Eds.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1984. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Butterworth-Heinemann: Oxford, UK, 2005; Volume 1. [Google Scholar]
- Kumar, V. Advanced Computational Techniques For Incompressible/Compressible Fluid-Structure Interactions. Ph.D. Thesis, Rice University, Houston, TX, USA, 2005. [Google Scholar]
- Carcione, J.M.; Morency, C.; Santos, J.E. Computational poroelasticity—A review. Geophysics 2010, 75, 75A229–75A243. [Google Scholar] [CrossRef]
- Chinesta, F.; Ladeveze, P.; Cueto, E. A Short Review on Model Order Reduction Based on Proper Generalized Decomposition. Arch. Comput. Methods Eng. 2011, 18, 395. [Google Scholar] [CrossRef]
- Powell, C.E.; Ullmann, E. Preconditioning stochastic Galerkin saddle point systems. SIAM J. Matrix Anal. Appl. 2010, 31, 2813–2840. [Google Scholar] [CrossRef]
- Sousedík, B.; Ghanem, R.G.; Phipps, E.T. Hierarchical Schur complement preconditioner for the stochastic Galerkin finite element methods. Numer. Linear Algebra Appl. 2013, arXiv:1205.1864. [Google Scholar] [CrossRef]
- Kim, J. Sequential Methods for Coupled Geomechanics and Multiphase Flow. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2010. [Google Scholar]
- Kim, J.; Tchelepi, H.; Juanes, R. Stability and convergence of sequential methods for coupled flow and geomechanics: Fixed-stress and fixed-strain splits. Comput. Methods Appl. Mech. Eng. 2011, 200, 1591–1606. [Google Scholar] [CrossRef]
- Kim, J.; Tchelepi, H.; Juanes, R. Stability and convergence of sequential methods for coupled flow and geomechanics: Drained and undrained splits. Comput. Methods Appl. Mech. Eng. 2011, 200, 2094–2116. [Google Scholar] [CrossRef]
- Mikelić, A.; Wheeler, M.F. Convergence of iterative coupling for coupled flow and geomechanics. Comput. Geosci. 2013, 17, 455–461. [Google Scholar] [CrossRef]
- Delgado, P.M. A Block Operator Splitting Method for Heterogeneous Multiscale Poroelasticity. Ph.D. Thesis, The University of Texas at El Paso, El Paso, TX, USA, 2013. [Google Scholar]
- Delgado, P.; Kumar, V. A stochastic Galerkin approach to uncertainty quantification in poroelastic media. Appl. Math. Comput. 2015, 266, 328–338. [Google Scholar] [CrossRef]
- Jin, L.; Zoback, M.D. Fully Coupled Nonlinear Fluid Flow and Poroelasticity in Arbitrarily Fractured Porous Media: A Hybrid-Dimensional Computational Model. J. Geophys. Res. Solid Earth 2017, 122, 7626–7658. [Google Scholar] [CrossRef] [Green Version]
- Jia, B.; Tsau, J.S.; Barati, R. A workflow to estimate shale gas permeability variations during the production process. Fuel 2018, 220, 879–889. [Google Scholar] [CrossRef]
- Chu, C.C. Multiscale Methods for Elliptic Partial Differential Equations And Related Applications. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2010. [Google Scholar]
- Chu, J.; Engquist, B.; Prodanović, M.; Tsai, R. A Multiscale Method Coupling Network and Continuum Models in Porous Media II-Single-and Two-Phase Flows. In Advances in Applied Mathematics, Modeling, and Computational Science; Springer: Berlin, Germany; pp. 161–185.
- Showalter, R. Diffusion in Poro-Elastic Media. J. Math. Anal. Appl. 2000, 251, 310–340. [Google Scholar] [CrossRef] [Green Version]
- Gaspar, F.J.; Lisbona, F.J.; Vabishchevich, P.N. Finite difference schemes for poro-elastic problems. Comput. Methods Appl. Math. 2002, 2, 132–142. [Google Scholar] [CrossRef]
- Mitchison, T.; Charras, G.; Mahadevan, L. Implications of a poroelastic cytoplasm for the dynamics of animal cell shape. In Seminars in Cell & Developmental Biology; Elsevier: New York, NY, USA, 2008; Volume 19, pp. 215–223. [Google Scholar]









© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Delgado, P.M.; Kotteda, V.M.K.; Kumar, V. Hybrid Fixed-Point Fixed-Stress Splitting Method for Linear Poroelasticity. Geosciences 2019, 9, 29. https://doi.org/10.3390/geosciences9010029
Delgado PM, Kotteda VMK, Kumar V. Hybrid Fixed-Point Fixed-Stress Splitting Method for Linear Poroelasticity. Geosciences. 2019; 9(1):29. https://doi.org/10.3390/geosciences9010029
Chicago/Turabian StyleDelgado, Paul M., V. M. Krushnarao Kotteda, and Vinod Kumar. 2019. "Hybrid Fixed-Point Fixed-Stress Splitting Method for Linear Poroelasticity" Geosciences 9, no. 1: 29. https://doi.org/10.3390/geosciences9010029
APA StyleDelgado, P. M., Kotteda, V. M. K., & Kumar, V. (2019). Hybrid Fixed-Point Fixed-Stress Splitting Method for Linear Poroelasticity. Geosciences, 9(1), 29. https://doi.org/10.3390/geosciences9010029