Geothermal Model of the Shallow Crustal Structure across the “Mountain Front Fault” in Western Lurestan, Zagros Thrust Belt, Iran
Abstract
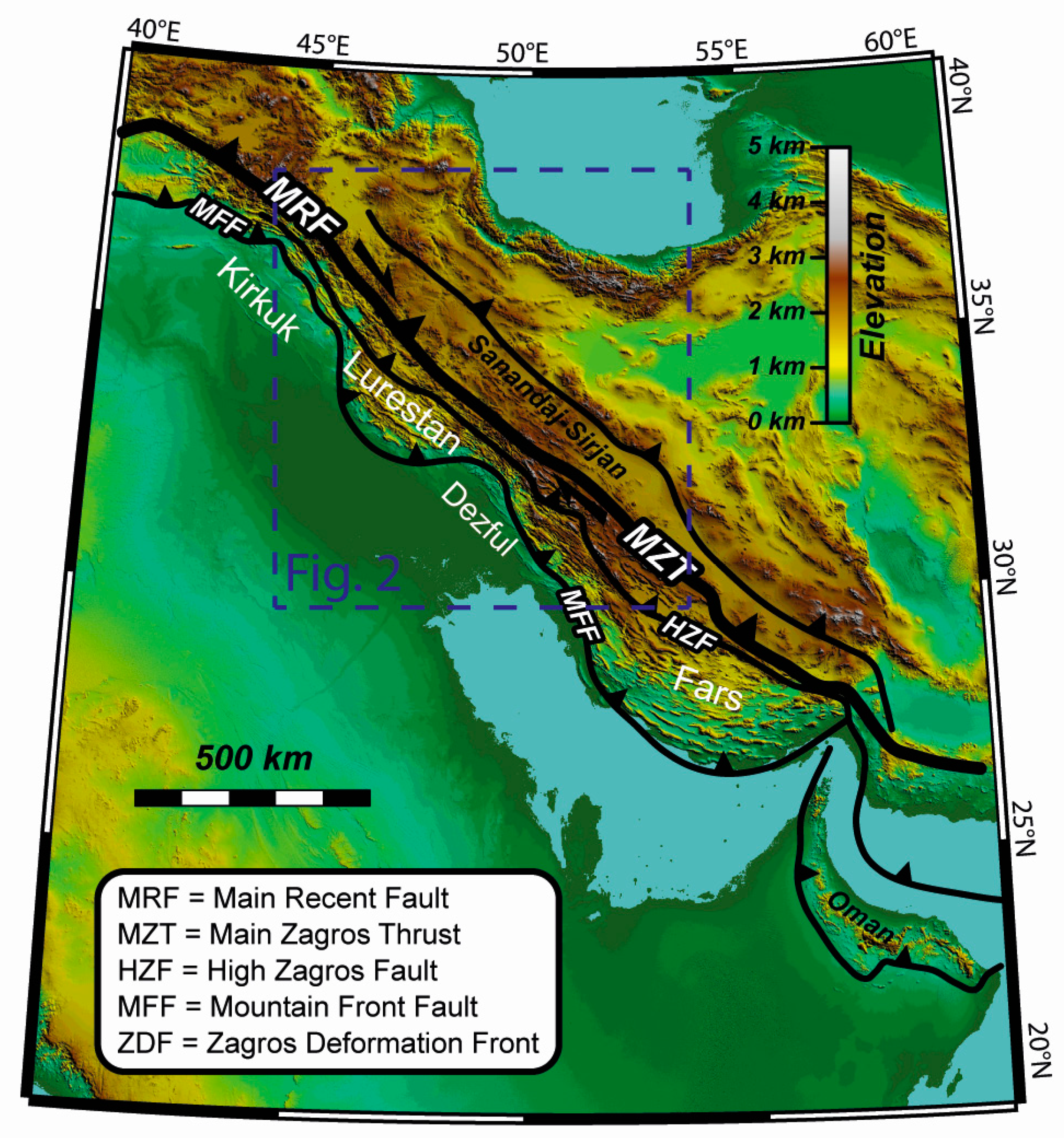
:1. Introduction
2. Geological Background
3. Methods
3.1. Geometric Model
3.2. Conceptual Model
3.3. Analytical Procedure
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vernant, P.; Nilforoushan, F.; Hatzfeld, D.; Abassi, M.; Vigny, C.; Masson, F.; Nankali, H.; Martinod, J.; Ashtiani, A.; Bayer, R.; et al. Contemporary Crustal Deformation and Plate Kinematics in Middle East constrained by GPS Measurements in Iran and North Oman. Geophys. J. Int. 2004, 157, 381–398. [Google Scholar] [CrossRef]
- Jackson, J.; McKenzie, D. Active tectonics of the Alpine-Himalayan belt between Turkey and Pakistan. Geophys. J. Int. 1984, 77, 185–264. [Google Scholar] [CrossRef]
- USGS.gov|Science for a Changing World. Available online: https://www.usgs.gov/ (accessed on 26 November 2018).
- Tavani, S.; Parente, M.; Puzone, F.; Corradetti, A.; Gharabeigli, G.; Valinejad, M.; Morsalnejad, D.; Mazzoli, S. The seismogenic fault system of the 2017 Mw 7.3 Iran-Iraq earthquake: Constraints from surface and subsurface data, cross-section balancing, and restoration. Solid Earth 2018, 9, 821–831. [Google Scholar] [CrossRef]
- Vergés, J.; Saura, E.; Casciello, E.; Fernàndez, M.; Villaseñor, A.; Jiménez-Munt, I.; García-Castellanos, D. Crustal-scale cross-sections across the NW Zagros belt: Implications for the Arabian margin reconstruction. Geol. Mag. 2011, 148, 739–761. [Google Scholar] [CrossRef]
- Paul, A.; Hatzfeld, D.; Kaviani, A.; Tatar, M.; Péquegnat, C. Seismic imaging of the lithospheric structure of the Zagros mountain belt (Iran). Geol. Soc. Lond. Spec. Publ. 2010, 330, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Vernant, P.; Chéry, J. Mechanical modelling of oblique convergence in the Zagros, Iran. Geophys. J. Int. 2006, 165, 991–1002. [Google Scholar] [CrossRef] [Green Version]
- Tunini, L.; Jiménez-Munt, I.; Fernàndez, M.; Vergés, J.; Villaseñor, A. Lithospheric mantle heterogeneities beneath the Zagros Mountains and the Iranian Plateau: A petrological-geophysical study. Geophys. J. Int. 2015, 200, 596–614. [Google Scholar] [CrossRef]
- Stocklin, J. Structural History and Tectonic of Iran: A Review. Am. Assoc. Pet. Geol. Bull. 1968, 52, 1229–1258. [Google Scholar] [CrossRef]
- Ricou, L.E.; Braud, J.; Brunn, J.H. Le Zagros. In Livre à la Mémoire de Albert, F. de Lapparent; Mémoire hors-série; Societe Geologique de France: Paris, France, 1977; No. 8; pp. 33–52. (In French) [Google Scholar]
- Berberian, M.; King, G.C.P. Towards a paleogeography and tectonic evolution of Iran. Can. J. Earth Sci. 1981, 18, 2010–2065. [Google Scholar] [CrossRef]
- Dercourt, J.; Zonenshain, L.P.; Ricou, L.E.; Kazmin, V.G.; Le Pichon, X.; Knipper, A.L.; Grandjacquet, C.; Sbortshikov, I.M.; Geyssant, J.; Lepvrier, C.; et al. Geological evolution of the Tethys belt from the Atlantic to the Pamirs since the LIAS. Tectonophysics 1986, 123, 241–315. [Google Scholar] [CrossRef]
- Braud, J. La suture du Zagros au niveau de Kermanshah (Kurdistan Iranien): Reconstitution Paléogéographique, Evolution Géodynamique, Magmatique et Structurale. Ph.D. Thesis, University of Paris-Sud, Paris, France, 1987. Unpublished Thesis (In French). [Google Scholar]
- Alavi, M. Tectonics of the Zagros orogenic belt of Iran: New data and interpretations. Tectonophysics 1994, 229, 211–238. [Google Scholar] [CrossRef]
- Stampfli, G.M.; Borel, G.D. A plate tectonic model for the Paleozoic and Mesozoic constrained by dynamic plate boundaries and restored synthetic oceanic isochrons. Earth Planet. Sci. Lett. 2002, 196, 17–33. [Google Scholar] [CrossRef]
- Agard, P.; Omrani, J.; Jolivet, L.; Mouthereau, F. Convergence history across Zagros (Iran): Constraints from collisional and earlier deformation. Int. J. Earth Sci. 2005, 94, 401–419. [Google Scholar] [CrossRef]
- Koshnaw, R.I.; Horton, B.K.; Stockli, D.F.; Barber, D.; Tamar-Agha, M.; Kendall, J.J. Neogene shortening and exhumation of the Zagros fold-thrust belt and foreland basin in the Kurdistan region of northern Iraq. Tectonophysics 2017, 694, 332–355. [Google Scholar] [CrossRef]
- Berberian, F.; Berberian, M. Tectono-Plutonic Episodes in Iran. In Zagros-Hindu Kush-Himalaya Geodynamic Evolution; American Geophysical Union: Washington, DC, USA, 1981; Volume 3, pp. 5–32. [Google Scholar]
- McQuarrie, N.; van Hinsbergen, D.J.J. Retrodeforming the Arabia-Eurasia Collision zone: Age of collision versus magnitude of continental subduction. Geology 2013, 41, 315–318. [Google Scholar] [CrossRef]
- Tavani, S.; Parente, M.; Vitale, S.; Iannace, A.; Corradetti, A.; Bottini, C.; Morsalnejad, D.; Mazzoli, S. Early Jurassic Rifting of the Arabian Passive Continental Margin of the Neo-Tethys. Field Evidence from the Lurestan Region of the Zagros Fold-and-Thrust Belt, Iran. Tectonics 2018, 37, 2586–2607. [Google Scholar] [CrossRef]
- Talebian, M.; Jackson, J. Offset on the Main Recent Fault of NW Iran and implications for the late Cenozoic tectonics of the Arabia–Eurasia collision zone. Geophys. J. Int. 2002, 157, 381–398. [Google Scholar] [CrossRef]
- Allen, M.; Jackson, J.; Walker, R. Late Cenozoic reorganization of the Arabia-Eurasia collision and the comparison of short-term deformation rates. Tectonics 2004, 23, TC2008. [Google Scholar] [CrossRef]
- Authemayou, C.; Chardon, D.; Bellier, O.; Malekzadeh, Z.; Shabanian, E.; Abbassi, M.R. Late Cenozoic partitioning of oblique plate convergence in the Zagros fold-and-thrust belt (Iran). Tectonics 2006, 25, TC3002. [Google Scholar] [CrossRef]
- Sadeghi, S.; Yassaghi, A. Spatial evolution of Zagros collision zone in Kurdistan, NW Iran: Constraints on Arabia–Eurasia oblique convergence. Solid Earth 2016, 7, 659–672. [Google Scholar] [CrossRef]
- Colman-Saad, S.P. Fold development in Zagros simply folded belt, southwest Iran. Am. Assoc. Pet. Geol. Bull. 1978, 62, 984–1003. [Google Scholar]
- Sepeher, M.; Cosgrove, J.W. Structural framework of the Zagros Fold–Thrust Belt, Iran. Mar. Pet. Geol. 2004, 21, 829–843. [Google Scholar] [CrossRef]
- Rudkiewicz, J.L.; Sherkati, S.; Letouzey, J. Evolution of Maturity in Northern Fars and in the Izeh Zone (Iranian Zagros) and Link with Hydrocarbon Prospectivity. In Thrust Belts and Foreland Basins; Lacombe, O., Roure, F., Lavé, J., Vergés, J., Eds.; Frontiers in Earth Sciences book series; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Casciello, E.; Vergés, J.; Saura, E.; Casini, G.; Fernàndez, N.; Blanc, E.J.P.; Homke, S.; Hunt, D. Fold patterns and multilayer rheology of the Lurestan Province, Zagros Simply Folded Belt (Iran). J. Geol. Soc. Lond. 2009, 166, 947–959. [Google Scholar] [CrossRef] [Green Version]
- Gavillot, Y.G.; Axen, G.J.; Stockli, D.F.; Horton, B.K.; Fakhari, M. Timing of thrust activity in the High Zagros fold-thrust belt, Iran, from (U-Th)/He thermochronometry. Tectonics 2010, 29, TC4025. [Google Scholar] [CrossRef]
- Leterrier, J. Mineralogical, Geochemical and isotopic evolution of two Miocene mafic intrusions from the Zagros (Iran). Lithos 1985, 18, 311–329. [Google Scholar] [CrossRef]
- Baharifar, A.; Moinevaziri, H.; Bellon, H.; Pique, A. The crystalline complexes of Hamadan (Sanandaj-Sirjan zone, western Iran): Metasedimentary Mesozoic sequences affected by Late Cretaceous tectono-metamorphic and plutonic events. C. R. Geosci. 2004, 336, 257–282. [Google Scholar] [CrossRef]
- Le Garzic, E.; Vergés, J.; Sapin, F.; Saura, E.; Meresse, F.; Ringenbach, J.C. Evolution of the NW Zagros Fold-and-Thrust Belt in Kurdistan Region of Iraq from balanced and restored crustal-scale sections and forward modeling. J. Struct. Geol. 2019, 124, 51–69. [Google Scholar] [CrossRef]
- Francois, T.; Burov, E.; Agard, P.; Meyer, B. Buildup of a dynamically supported orogenic plateau: Numerical modeling of the Zagros/Central Iran case study. Geochem. Geophys. Geosyst. 2014, 15, 2632–2654. [Google Scholar] [CrossRef] [Green Version]
- Förster, H.J.; Förster, A.; Oberhänsli, R.; Stromeyer, D. Lithospheric composition and thermal structure of the Arabian Shield in Jordan. Tectonophysics 2010, 481, 29–37. [Google Scholar] [CrossRef]
- Schütz, F.; Förster, H.J.; Förster, A. Thermal conditions of the central Sinai Microplate inferred from new surface heat-flow values and continuous borehole temperature logging in central and southern Israel. J. Geodyn. 2014, 76, 8–24. [Google Scholar] [CrossRef]
- Sibson, R.H. Frictional constraints on thrust, wrench and normal faults. Nature 1974, 249, 542–544. [Google Scholar] [CrossRef]
- Molnar, P.; Chen, W.P.; Padovani, E. Calculated temperatures in overthrust terrains and possible combinations of heat sources responsible for the tertiary granites in the greater Himalaya. J. Geophys. Res. 1983, 88, 6415–6429. [Google Scholar] [CrossRef]
- Candela, S.; Mazzoli, S.; Megna, A.; Santini, S. Finite element modelling of stress field perturbations and interseismic crustal deformation in the Val d’Agri region, southern Apennines, Italy. Tectonophysics 2015, 657, 245–259. [Google Scholar] [CrossRef]
- Megna, A.; Candela, S.; Mazzoli, S.; Santini, S. An analytical model for the geotherm in the Basilicata oil fields area (southern Italy). Ital. J. Geosci. 2014, 133, 204–213. [Google Scholar] [CrossRef]
- Kargaran, F.; Neubauer, F. Lithospheric thinning associated with formation of a metamorphic core complex and subsequent formation of the Iranian plateau. GSA Today 2015, 25, 4–8. [Google Scholar] [CrossRef]
- Shekarifard, A.; Baudin, F.; Seyed-Emami, K.; Schnyder, J.; Laggoun-Défarge, F.; Riboulleau, A.; Brunet, M.F.; Shahidi, A. Thermal maturity of the Upper Triassic-Middle Jurassic Shemshak Group (Alborz Range, Northern Iran) based on organic petrography, geochemistry and basin modelling: Implications for source rock evaluation and petroleum exploration. Geol. Mag. 2012, 149, 19–38. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basilici, M.; Mazzoli, S.; Megna, A.; Santini, S.; Tavani, S. Geothermal Model of the Shallow Crustal Structure across the “Mountain Front Fault” in Western Lurestan, Zagros Thrust Belt, Iran. Geosciences 2019, 9, 301. https://doi.org/10.3390/geosciences9070301
Basilici M, Mazzoli S, Megna A, Santini S, Tavani S. Geothermal Model of the Shallow Crustal Structure across the “Mountain Front Fault” in Western Lurestan, Zagros Thrust Belt, Iran. Geosciences. 2019; 9(7):301. https://doi.org/10.3390/geosciences9070301
Chicago/Turabian StyleBasilici, Matteo, Stefano Mazzoli, Antonella Megna, Stefano Santini, and Stefano Tavani. 2019. "Geothermal Model of the Shallow Crustal Structure across the “Mountain Front Fault” in Western Lurestan, Zagros Thrust Belt, Iran" Geosciences 9, no. 7: 301. https://doi.org/10.3390/geosciences9070301
APA StyleBasilici, M., Mazzoli, S., Megna, A., Santini, S., & Tavani, S. (2019). Geothermal Model of the Shallow Crustal Structure across the “Mountain Front Fault” in Western Lurestan, Zagros Thrust Belt, Iran. Geosciences, 9(7), 301. https://doi.org/10.3390/geosciences9070301






