Neuromodulatory Control and Language Recovery in Bilingual Aphasia: An Active Inference Approach
Abstract
:1. Introduction
1.1. Recovery Patterns and Control
1.2. Active Inference, Generative Models and Bayes-Optimality
2. Methods
2.1. Active Inference
2.2. Generative Model of Picture Naming, Word Repetition and Translation
2.3. In-Silico Lesions
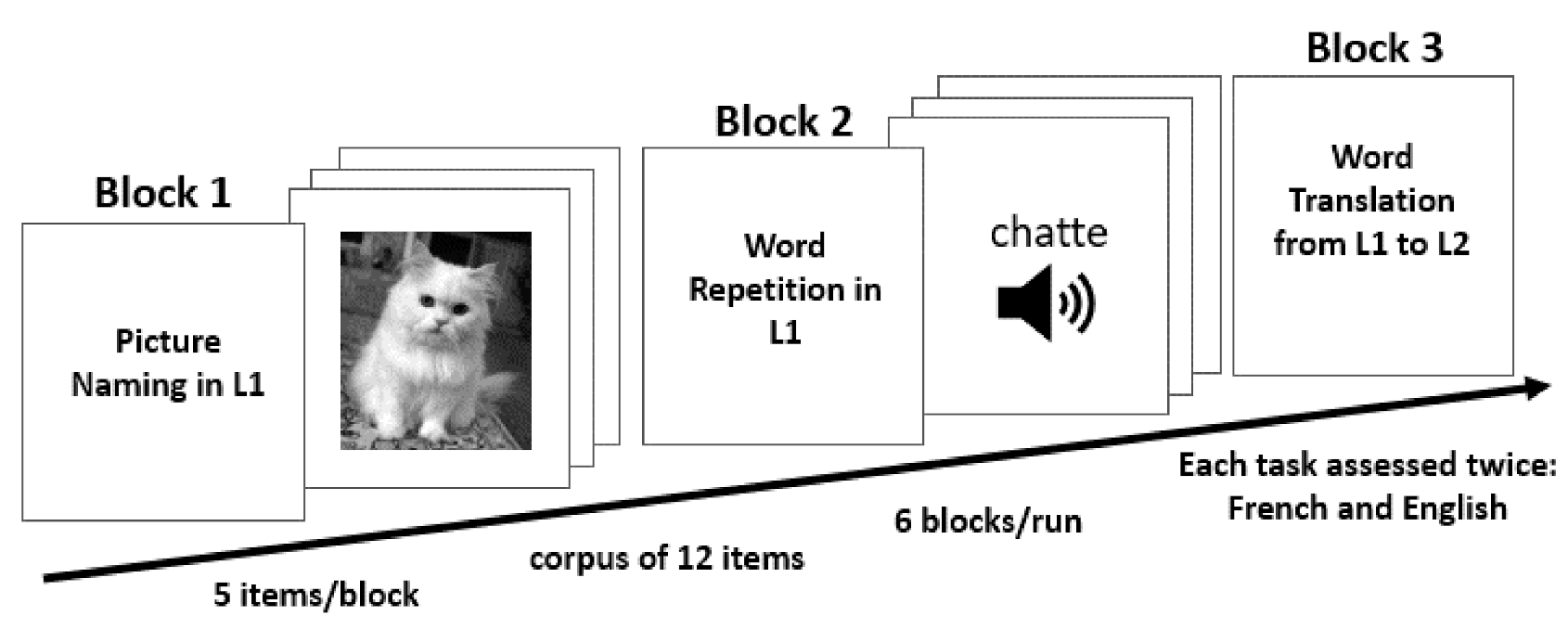
2.4. Paradigm Procedure
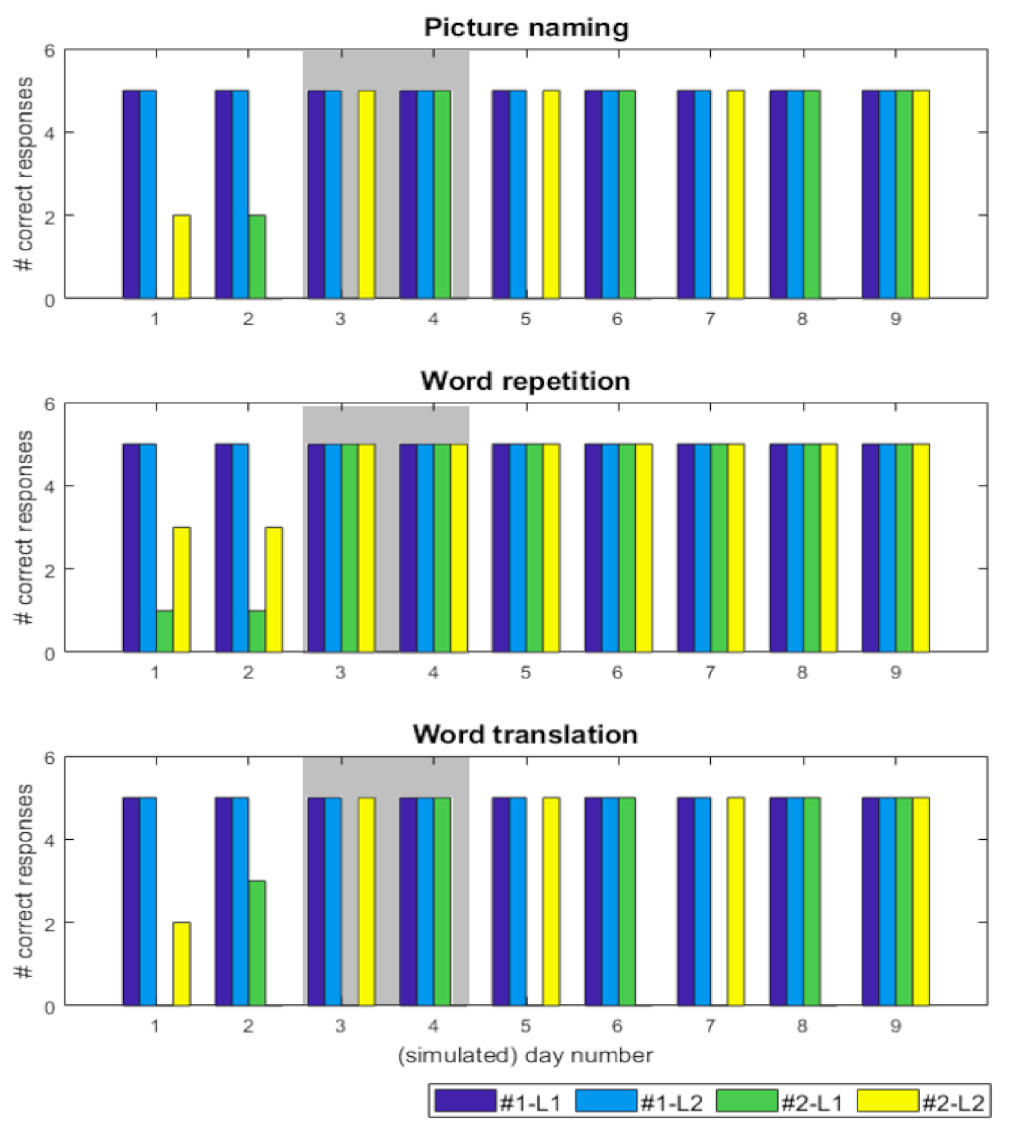
3. Results
4. Discussion
4.1. Neuromodulation and Precision
4.2. Generalisation and Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Paradis, M. Bilingual and polyglot aphasia. In Handbook of Neuropsychology; Boller, F., Grafman, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; pp. 117–140. [Google Scholar]
- Albert, M.L.; Obler, L.K. The Bilingual Brain: Neuropsychological and Neurolinguistics Aspects of Bilingualism; Academic Press: New York, NY, USA; London, UK, 1978. [Google Scholar]
- Kiran, S.; Grasemann, U.; Sandberg, C.; Miikkulainen, R. A computational account of bilingual aphasia rehabilitation. Bilingualism (Camb. Engl.) 2013, 16, 325. [Google Scholar] [CrossRef] [Green Version]
- Parr, T.; Rees, G.; Friston, K.J. Computational Neuropsychology and Bayesian Inference. Front. Hum. Neurosci. 2018, 12, 61. [Google Scholar] [CrossRef] [Green Version]
- Fabbro, F.; Skrap, M.; Aglioti, S. Pathological switching between languages after frontal lesions in a bilingual patient. J. Neurol. Neurosurg. Psychiatry 2000, 68, 650–652. [Google Scholar] [CrossRef]
- Green, D.W. Bilingual aphasia: Adapted language networks and their control. Annu. Rev. Appl. Linguist. 2008, 28, 25–48. [Google Scholar] [CrossRef] [Green Version]
- Abutalebi, J.; Della Rosa, P.A.; Tettamanti, M.; Green, D.W.; Cappa, S.F. Bilingual aphasia and language control: A follow-up fMRI and intrinsic connectivity study. Brain Lang. 2009, 109, 141–156. [Google Scholar] [CrossRef] [PubMed]
- Calabria, M.; Costa, A.; Green, D.W.; Abutalebi, J. Neural basis of bilingual language control. Ann. N. Y. Acad. Sci. 2018, 1426, 221–235. [Google Scholar] [CrossRef] [PubMed]
- Green, D.W.; Grogan, A.; Crinion, J.; Ali, N.; Sutton, C.; Price, C.J. Language control and parallel recovery of language in individuals with aphasia. Aphasiology 2010, 24, 188–209. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paradis, M.; Goldblum, M.-C.; Abidi, R. Alternate antagonism with paradoxical translation behavior in two bilingual aphasic patients. Brain Lang. 1982, 15, 55–69. [Google Scholar] [CrossRef]
- Shallice, T. Case study approach in neuropsychological research. J. Clin. Exp. Neuropsychol. 1979, 1, 183–211. [Google Scholar] [CrossRef]
- Green, D.W. Control, activation, and resource: A framework and a model for the control of speech in bilinguals. Brain Lang. 1986, 27, 210–223. [Google Scholar] [CrossRef]
- Green, D.W. Mental control of the bilingual lexico-semantic system. Biling. Lang. Cogn. 1998, 1, 67–81. [Google Scholar] [CrossRef]
- Friston, K.; FitzGerald, T.; Rigoli, F.; Schwartenbeck, P.; Pezzulo, G. Active Inference: A Process Theory. Neural Comput. 2017, 29, 1–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sajid, N.; Ball, P.J.; Friston, K.J. Active inference: Demystified and compared. arXiv 2019, arXiv:1909.10863. [Google Scholar]
- Friston, K. A free energy principle for a particular physics. arXiv 2019, arXiv:1906.10184. [Google Scholar]
- Grasemann, U.; Sandberg, C.; Kiran, S.; Miikkulainen, R. Impairment and rehabilitation in bilingual aphasia: A SOM-based model. In International Workshop on Self-Organizing Maps; Springer: Berlin/Heidelberg, Germany, 2011; pp. 207–217. [Google Scholar]
- Tourville, J.A.; Guenther, F.H. The DIVA model: A neural theory of speech acquisition and production. Lang. Cogn. Process. 2011, 26, 952–981. [Google Scholar] [CrossRef] [PubMed]
- Walker, G.M.; Hickok, G. Bridging computational approaches to speech production: The semantic–lexical–auditory–motor model (SLAM). Psychon. Bull. Rev. 2016, 23, 339–352. [Google Scholar] [CrossRef]
- Ueno, T.; Saito, S.; Rogers, T.T.; Lambon-Ralph, M.A. Lichtheim 2: Synthesizing aphasia and the neural basis of language in a neurocomputational model of the dual dorsal-ventral language pathways. Neuron 2011, 72, 385–396. [Google Scholar] [CrossRef]
- Miikkulainen, R.; Elman, J. Subsymbolic Natural Language Processing: An Integrated Model of Scripts, Lexicon, and Memory; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Schwartenbeck, P.; FitzGerald, T.H.; Mathys, C.; Dolan, R.; Wurst, F.; Kronbichler, M.; Friston, K. Optimal inference with suboptimal models: Addiction and active Bayesian inference. Med. Hypotheses 2015, 84, 109–117. [Google Scholar] [CrossRef] [Green Version]
- Schwartenbeck, P.; Friston, K. Computational Phenotyping in Psychiatry: A Worked Example. ENeuro 2016, 3. [Google Scholar] [CrossRef] [PubMed]
- Hohwy, J. The Self-Evidencing Brain. Noûs 2016, 50, 259–285. [Google Scholar] [CrossRef]
- Angela, J.Y.; Dayan, P. Uncertainty, neuromodulation, and attention. Neuron 2005, 46, 681–692. [Google Scholar]
- Angela, J.Y.; Dayan, P. Acetylcholine in cortical inference. Neural Netw. 2002, 15, 719–730. [Google Scholar]
- Parr, T.; Friston, K.J. Uncertainty, epistemics and active inference. J. R. Soc. Interface 2017, 14. [Google Scholar] [CrossRef]
- Friston, K.J. The free-energy principle: A rough guide to the brain? Trends Cogn. Sci. 2009, 13, 293–301. [Google Scholar] [CrossRef] [PubMed]
- Dayan, P.; Hinton, G.E.; Neal, R. The Helmholtz machine. Neural Comput. 1995, 7, 889–904. [Google Scholar] [CrossRef]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef] [Green Version]
- Parr, T.; Friston, K.J. Generalised free energy and active inference: Can the future cause the past? bioRxiv 2018. [Google Scholar] [CrossRef] [Green Version]
- Da Costa, L.; Parr, T.; Sajid, N.; Veselic, S.; Neacsu, V.; Friston, K. Active inference on discrete state-spaces: A synthesis. arXiv 2020, arXiv:2001.07203. [Google Scholar]
- Friston, K.J.; Rosch, R.; Parr, T.; Price, C.; Bowman, H. Deep temporal models and active inference. Neurosci. Biobehav. Rev. 2017, 77, 388–402. [Google Scholar] [CrossRef]
- Parr, T.; Markovic, D.; Kiebel, S.J.; Friston, K.J. Neuronal message passing using Mean-field, Bethe, and Marginal approximations. Sci. Rep. 2019, 9, 1889. [Google Scholar] [CrossRef]
- Parr, T.; Rikhye, R.V.; Halassa, M.M.; Friston, K.J. Prefrontal computation as active inference. Cereb. Cortex 2019, 30, 682–695. [Google Scholar] [CrossRef] [Green Version]
- de Vries, B.; Friston, K.J. A Factor Graph Description of Deep Temporal Active Inference. Front. Comput. Neurosci. 2017, 11, 1–16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Friston, K.J.; Parr, T.; de Vries, B. The graphical brain: Belief propagation and active inference. Netw. Neurosci. 2017, 1, 381–414. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.; Buzsaki, G. The Functional Anatomy of Time: What and When in the Brain. Trends Cogn. Sci. 2016, 20, 500–511. [Google Scholar] [CrossRef]
- Parker Jones, Ō.; Green, D.W.; Grogan, A.; Pliatsikas, C.; Filippopolitis, K.; Ali, N.; Lee, H.L.; Ramsden, S.; Gazarian, K.; Prejawa, S. Where, when and why brain activation differs for bilinguals and monolinguals during picture naming and reading aloud. Cereb. Cortex 2012, 22, 892–902. [Google Scholar] [CrossRef] [PubMed]
- Moritz-Gasser, S.; Duffau, H. The anatomo-functional connectivity of word repetition: Insights provided by awake brain tumor surgery. Front. Hum. Neurosci. 2013, 7, 405. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nozari, N.; Dell, G.S. How damaged brains repeat words: A computational approach. Brain Lang. 2013, 126, 327–337. [Google Scholar] [CrossRef] [Green Version]
- Hope, T.M.H.; Prejawa, S.; Parker Jones, Ō.; Oberhuber, M.; Seghier, M.L.; Green, D.W.; Price, C.J. Dissecting the functional anatomy of auditory word repetition. Front. Hum. Neurosci. 2014, 8, 246. [Google Scholar] [CrossRef] [Green Version]
- Price, C.J.; Green, D.W.; Von Studnitz, R. A functional imaging study of translation and language switching. Brain J. Neurol. 1999, 122, 2221–2235. [Google Scholar] [CrossRef] [Green Version]
- Sarter, M.; Bruno, J.P. Cognitive functions of cortical acetylcholine: Toward a unifying hypothesis. Brain Res. Rev. 1997, 23, 28–46. [Google Scholar] [CrossRef]
- Sarter, M.; Hasselmo, M.E.; Bruno, J.P.; Givens, B. Unraveling the attentional functions of cortical cholinergic inputs: Interactions between signal-driven and cognitive modulation of signal detection. Brain Res. Rev. 2005, 48, 98–111. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, R. Two decades of statistical language modeling: Where do we go from here? Proc. IEEE 2000, 88, 1270–1278. [Google Scholar] [CrossRef]
- Christoffels, I.K.; Ganushchak, L.; Koester, D. Language conflict in translation: An ERP study of translation production. J. Cogn. Psychol. 2013, 25, 646–664. [Google Scholar] [CrossRef]
- Ansaldo, A.I.; Saidi, L.G.; Ruiz, A. Model-driven intervention in bilingual aphasia: Evidence from a case of pathological language mixing. Aphasiology 2010, 24, 309–324. [Google Scholar] [CrossRef]
- Moran, R.J.; Campo, P.; Symmonds, M.; Stephan, K.E.; Dolan, R.J.; Friston, K.J. Free energy, precision and learning: The role of cholinergic neuromodulation. J Neurosci 2013, 33, 8227–8236. [Google Scholar] [CrossRef] [Green Version]
- Krizman, J.; Marian, V.; Shook, A.; Skoe, E.; Kraus, N. Subcortical encoding of sound is enhanced in bilinguals and relates to executive function advantages. Proc. Natl. Acad. Sci. USA 2012, 109, 7877–7881. [Google Scholar] [CrossRef] [Green Version]
- Krizman, J.; Skoe, E.; Marian, V.; Kraus, N. Bilingualism increases neural response consistency and attentional control: Evidence for sensory and cognitive coupling. Brain Lang. 2014, 128, 34–40. [Google Scholar] [CrossRef] [Green Version]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Wiley: Hoboken, NJ, USA; Chapman & Hall: London, UK, 1949. [Google Scholar]
- Watamori, T.S.; Sasanuma, S. The recovery processes of two English-Japanese bilingual aphasics. Brain Lang. 1978, 6, 127–140. [Google Scholar] [CrossRef]
- Gil, M.; Goral, M. Nonparallel recovery in bilingual aphasia: Effects of language choice, language proficiency, and treatment. Int. J. Biling. 2004, 8, 191–219. [Google Scholar] [CrossRef]
- Friston, K.J.; Sajid, N.; Quiroga-Martinez, D.R.; Parr, T.; Price, C.J.; Holmes, E. Active listening. Hear. Res. 2020, 107998. [Google Scholar] [CrossRef]
- Brownsett, S.L.; Warren, J.E.; Geranmayeh, F.; Woodhead, Z.; Leech, R.; Wise, R.J. Cognitive control and its impact on recovery from aphasic stroke. Brain J. Neurol. 2014, 137, 242–254. [Google Scholar] [CrossRef] [PubMed] [Green Version]



| Term | Description |
|---|---|
| Probability distribution, | The probability of a random variable taking a particular value. |
| Variational distribution, | An approximate posterior distribution (i.e., Bayesian belief) over the causes of outcomes, given those outcomes. |
| Hidden states, | Latent or hidden states of the world generating outcomes. |
| Outcomes, | Outcomes or (sensory) observations. |
| Action, | A (control) state that can influence states of the world. |
| Policy, | Sequence of actions. |
| Generative model, | A joint probability distribution over hidden states and outcomes. |
| Free energy, | An information theory measure that bounds the surprise when sampling and outcome, given a generative model. |
| Complexity, | A measure of how much the posterior beliefs have to move away from prior beliefs to provide an accurate account of sensory data. |
| Accuracy, | The expected log likelihood of the sensory outcomes, given some posterior beliefs about the causes of those data. |
| Expected free energy, | Free energy expected under future outcomes—an uncertainty measure, associated with a particular policy. |
| KL-Divergence, | A measure of how one probability distribution differs from a second, reference probability distribution. |
| Temporal horizon, | Number of timesteps in a sequence of actions, i.e., policy depth. |
| Posterior | Beliefs about their causes of outcomes after they are observed. The products of belief updating. |
| Prior | Beliefs about the causes of outcomes before they are observed. A likelihood and prior beliefs constitute the generative model. |
| Likelihood, | Probabilistic mapping between states and outcomes. |
| Transitions, | Probabilistic transitions from one state to another over time. |
| Expectation, | The average of a random variable. |
| Precision, | Confidence or inverse uncertainty. |
| Sufficient statistics | Quantities which are sufficient to parameterise a probability distribution. |
| Gradient Descent | An optimisation scheme used to minimise a particular function by iteratively moving in the direction of steepest descent. |
| Softmax function, | A function that converts a set of real values into probabilities that sum to 1. |
| Language (Naming, etc.) | Translation | |
|---|---|---|
| First Patient (A.D.) | ||
| 1st Period | Total aphasia | |
| 2nd Period | L1 > L2 | |
| +1 Day | L2 > L1 | |
| +2 Day | L1 > L2 | L2 → L1 Bad; L1 → L2 Good |
| +3 Day | L2 > L1 | L2 → L1 Excellent; L1 → L2 Poor |
| +4 Day | L1 = good | |
| +11 Day | L2 > L1 | L2 → L1 Very poor; L1 → L2 Very poor |
| +24 Day | L2 ≥ L1 | L2 → L1 Poor; L1 → L2 Poor |
| +25 Day | L2 ≥ L1 | L2 → L1 Poor; L1 → L2 Good |
| Second Patient | ||
| 1st Week | L1 > L2 | |
| 2nd Week | L2 > L1 | |
| 3rd Week | L2 ≥ L1 | L2 → L1 Excellent; L1 → L2 Very poor |
| 4th Week | L2 = L1 | L2 → L1 Excellent; L1 → L2 Excellent |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sajid, N.; Friston, K.J.; Ekert, J.O.; Price, C.J.; Green, D.W. Neuromodulatory Control and Language Recovery in Bilingual Aphasia: An Active Inference Approach. Behav. Sci. 2020, 10, 161. https://doi.org/10.3390/bs10100161
Sajid N, Friston KJ, Ekert JO, Price CJ, Green DW. Neuromodulatory Control and Language Recovery in Bilingual Aphasia: An Active Inference Approach. Behavioral Sciences. 2020; 10(10):161. https://doi.org/10.3390/bs10100161
Chicago/Turabian StyleSajid, Noor, Karl J. Friston, Justyna O. Ekert, Cathy J. Price, and David W. Green. 2020. "Neuromodulatory Control and Language Recovery in Bilingual Aphasia: An Active Inference Approach" Behavioral Sciences 10, no. 10: 161. https://doi.org/10.3390/bs10100161
APA StyleSajid, N., Friston, K. J., Ekert, J. O., Price, C. J., & Green, D. W. (2020). Neuromodulatory Control and Language Recovery in Bilingual Aphasia: An Active Inference Approach. Behavioral Sciences, 10(10), 161. https://doi.org/10.3390/bs10100161






