Species Sensitivity to Hydrologic Whiplash in The Tree-Ring Record of the High Sierra Nevada
Abstract
:1. Introduction
2. Materials and Methods
2.1. Climate Data
2.2. Tree-Ring Data
2.3. Climate Reconstruction
2.4. Analysis of Whiplash Events
3. Results
3.1. Species-Specific and Full-Network Reconstructions
3.2. Single-Site Reconstructions
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wahl, E.R.; Zorita, E.; Trouet, V.; Taylor, A.H. Jet stream dynamics, hydroclimate, and fire in California from 1600 CE to present. Proc. Natl. Acad. Sci. USA 2019, 116, 5393–5398. [Google Scholar] [CrossRef] [Green Version]
- Wahl, E.R.; Hoell, A.; Zorita, E.; Gille, E.; Diaz, H.F. A 450-Year Perspective on California Precipitation “Flips”. J. Clim. 2020, 33, 10221–10237. [Google Scholar] [CrossRef]
- Zamora-Reyes, D.; Black, B.; Trouet, V. Enhanced winter, spring, and summer hydroclimate variability across California from 1940 to 2019. Int. J. Clim. 2022, 42, 4940–4952. [Google Scholar] [CrossRef]
- Pandey, G.R.; Cayan, D.R.; Georgakakos, K.P. Precipitation structure in the Sierra Nevada of California during winter. J. Geophys. Res. Atmos. 1999, 104, 12019–12030. [Google Scholar] [CrossRef] [Green Version]
- Mason, S.J.; Goddard, L. Probabilistic Precipitation Anomalies Associated with ENSO. Bull. Am. Meteorol. Soc. 2001, 82, 619–638. [Google Scholar] [CrossRef]
- Biondi, F.; Meko, D.M. Long-Term Hydroclimatic Patterns in the Truckee-Carson Basin of the Eastern Sierra Nevada, USA. Water Resour. Res. 2019, 55, 5559–5574. [Google Scholar] [CrossRef] [Green Version]
- Sterle, K.; Singletary, L. Adapting to Variable Water Supply in the Truckee-Carson River System, Western USA. Water 2017, 9, 768. [Google Scholar] [CrossRef] [Green Version]
- Hayhoe, K.; Cayan, D.; Field, C.B.; Frumhoff, P.C.; Maurer, E.P.; Miller, N.L.; Moser, S.C.; Schneider, S.H.; Cahill, K.N.; Cleland, E.E.; et al. Emissions pathways, climate change, and impacts on California. Proc. Natl. Acad. Sci. USA 2004, 101, 12422–12427. [Google Scholar] [CrossRef] [Green Version]
- Cayan, D.R.; Maurer, E.; Dettinger, M.D.; Tyree, M.; Hayhoe, K. Climate change scenarios for the California region. Clim. Chang. 2008, 87, 21–42. [Google Scholar] [CrossRef]
- Dettinger, M.D.; Alpert, H.; Battles, J.J.; Kusel, J.; Safford, H.; Fougeres, D.; Knight, C.; Miller, L.; Sawyer, S. Sierra Nevada Summary Report. California’s Fourth Climate Change Assessment; Publication No. SUMCCCA4-2018-004; California Energy Commission: Sacramento, CA, USA; Natural Resoources Agency: Sacramento, CA, USA, 2018; 94p. [Google Scholar]
- Dettinger, M. Climate Change, Atmospheric Rivers, and Floods in California—A Multimodel Analysis of Storm Frequency and Magnitude Changes1. JAWRA J. Am. Water Resour. Assoc. 2011, 47, 514–523. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 California drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef] [Green Version]
- Casson, N.J.; Contosta, A.R.; Burakowski, E.A.; Campbell, J.L.; Crandall, M.S.; Creed, I.F.; Eimers, M.C.; Garlick, S.; Lutz, D.A.; Morison, M.Q.; et al. Winter Weather Whiplash: Impacts of Meteorological Events Misaligned With Natural and Human Systems in Seasonally Snow-Covered Regions. Earth’s Futur. 2019, 7, 1434–1450. [Google Scholar] [CrossRef] [Green Version]
- McCabe, G.J.; Wolock, D.M. Recent Declines in Western U.S. Snowpack in the Context of Twentieth-Century Climate Variability. Earth Interact. 2009, 13, 1–15. [Google Scholar] [CrossRef]
- Null, S.E.; Viers, J.H.; Mount, J.F. Hydrologic Response and Watershed Sensitivity to Climate Warming in California’s Sierra Nevada. PLoS ONE 2010, 5, e9932. [Google Scholar] [CrossRef] [Green Version]
- Yoon, J.-H.; Wang, S.-Y.S.; Gillies, R.R.; Kravitz, B.; Hipps, L.; Rasch, P.J. Increasing water cycle extremes in California and in relation to ENSO cycle under global warming. Nat. Commun. 2015, 6, 8657. [Google Scholar] [CrossRef] [Green Version]
- Berg, N.; Hall, A. Increased Interannual Precipitation Extremes over California under Climate Change. J. Clim. 2015, 28, 6324–6334. [Google Scholar] [CrossRef]
- Swain, D.L.; Langenbrunner, B.; Neelin, J.D.; Hall, A. Increasing precipitation volatility in twenty-first-century California. Nat. Clim. Chang. 2018, 8, 427–433. [Google Scholar] [CrossRef]
- Meko, D.M.; Woodhouse, C.A. Application of Streamflow Reconstruction to Water Resources Management. In Dendroclimatology; Hughes, M., Swetnam, T., Diaz, H., Eds.; Developments in Paleoenvironmental Research; Springer: Dordrecht, The Netherlands, 2011; Volume 11, pp. 231–261. [Google Scholar] [CrossRef]
- Belmecheri, S.; Babst, F.; Wahl, E.R.; Stahle, D.W.; Trouet, V. Multi-century evaluation of Sierra Nevada snowpack. Nat. Clim. Chang. 2015, 6, 2–3. [Google Scholar] [CrossRef]
- Lepley, K.; Touchan, R.; Meko, D.; Shamir, E.; Graham, R.; Falk, D. A multi-century Sierra Nevada snowpack reconstruction modeled using upper-elevation coniferous tree rings (California, USA). Holocene 2020, 30, 1266–1278. [Google Scholar] [CrossRef]
- Meko, D.M.; Therrell, M.D.; Baisan, C.H.; Hughes, M.K. Sacramento river flow reconstructed to A.D. 869 from tree rings1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 1029–1039. [Google Scholar] [CrossRef]
- Graumlich, L.J. A 1000-Year Record of Temperature and Precipitation in the Sierra Nevada. Quat. Res. 1993, 39, 249–255. [Google Scholar] [CrossRef]
- Williams, A.P.; Anchukaitis, K.J.; Woodhouse, C.A.; Meko, D.M.; Cook, B.I.; Bolles, K.; Cook, E.R. Tree Rings and Observations Suggest No Stable Cycles in Sierra Nevada Cool-Season Precipitation. Water Resour. Res. 2021, 57, e2020WR028599. [Google Scholar] [CrossRef]
- Borkotoky, S.S.; Williams, A.P.; Cook, E.R.; Steinschneider, S. Reconstructing Extreme Precipitation in the Sacramento River Watershed Using Tree-Ring Based Proxies of Cold-Season Precipitation. Water Resour. Res. 2021, 57, e2020WR028824. [Google Scholar] [CrossRef]
- Fritts, H.C. Tree Rings and Climate; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar] [CrossRef]
- Anderegg, W.R.L.; Schwalm, C.R.; Biondi, F.; Camarero, J.J.; Koch, G.W.; Litvak, M.; Ogle, K.; Shaw, J.D.; Shevliakova, E.; Williams, A.P.; et al. Pervasive drought legacies in forest ecosystems and their implications for carbon cycle models. Science 2015, 349, 528–532. [Google Scholar] [CrossRef] [Green Version]
- Gazol, A.; Camarero, J.J.; Sánchez-Salguero, R.; Vicente-Serrano, S.M.; Serra-Maluquer, X.; Gutiérrez, E.; De Luis, M.; Sangüesa-Barreda, G.; Novak, K.; Rozas, V.; et al. Drought legacies are short, prevail in dry conifer forests and depend on growth variability. J. Ecol. 2020, 108, 2473–2484. [Google Scholar] [CrossRef]
- Peltier, D.M.P.; Ogle, K. Legacies of more frequent drought in ponderosa pine across the western United States. Glob. Chang. Biol. 2019, 25, 3803–3816. [Google Scholar] [CrossRef] [PubMed]
- Kannenberg, S.A.; Maxwell, J.; Pederson, N.; D’Orangeville, L.; Ficklin, D.L.; Phillips, R.P. Drought legacies are dependent on water table depth, wood anatomy and drought timing across the eastern US. Ecol. Lett. 2018, 22, 119–127. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Wang, X.; Keenan, T.F.; Piao, S. Drought timing influences the legacy of tree growth recovery. Glob. Chang. Biol. 2018, 24, 3546–3559. [Google Scholar] [CrossRef]
- Bose, A.K.; Wagner, R.G.; Weiskittel, A.R.; D’Amato, A.W. Effect magnitudes of operational-scale partial harvesting on residual tree growth and mortality of ten major tree species in Maine USA. For. Ecol. Manag. 2021, 484, 118953. [Google Scholar] [CrossRef]
- Gazol, A.; Camarero, J.J.; Anderegg, W.R.L.; Vicente-Serrano, S.M. Impacts of droughts on the growth resilience of Northern Hemisphere forests. Glob. Ecol. Biogeogr. 2016, 26, 166–176. [Google Scholar] [CrossRef]
- Bose, A.K.; Scherrer, D.; Camarero, J.J.; Ziche, D.; Babst, F.; Bigler, C.; Bolte, A.; Dorado-Liñán, I.; Etzold, S.; Fonti, P.; et al. Climate sensitivity and drought seasonality determine post-drought growth recovery of Quercus petraea and Quercus robur in Europe. Sci. Total. Environ. 2021, 784, 147222. [Google Scholar] [CrossRef]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Clim. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Buban, M.S.; Lee, T.R.; Baker, C.B. A Comparison of the U.S. Climate Reference Network Precipitation Data to the Parameter-Elevation Regressions on Independent Slopes Model (PRISM). J. Hydrometeorol. 2020, 21, 2391–2400. [Google Scholar] [CrossRef]
- Serreze, M.C.; Clark, M.P.; Armstrong, R.L.; McGinnis, D.A.; Pulwarty, R.S. Characteristics of the western United States snowpack from snowpack telemetry (SNOTEL) data. Water Resour. Res. 1999, 35, 2145–2160. [Google Scholar] [CrossRef] [Green Version]
- Cook, E.R.; Seager, R.; Heim, R.R., Jr.; Vose, R.S.; Herweijer, C.; Woodhouse, C. Megadroughts in North America: Placing IPCC projections of hydroclimatic change in a long-term paleoclimate context. J. Quat. Sci. 2010, 25, 48–61. [Google Scholar] [CrossRef] [Green Version]
- Cook, E.R.; Kairiukstis, L.A. (Eds.) Methods of Dendrochronology: Applications in The environmental Sciences; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef]
- Meko, D.; Graybill, D.A. Tree-ring reconstruction of upper gila rwer discharge. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 605–616. [Google Scholar] [CrossRef]
- Meko, D.M.; Stahle, D.W.; Griffin, D.; Knight, T.A. Inferring precipitation-anomaly gradients from tree rings. Quat. Int. 2011, 235, 89–100. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier Academic Press: New York, NY, USA, 2019; 395p. [Google Scholar]
- Fritts, H.C.; Guiot, J.; Gordon, G.A. Verification. In Methods of Dendro-Chronology: Applications in the Environmental Sciences; Cook, E.R., Kairiukstis, L.A., Eds.; Kluwer Academic Publishers: Amsterdam, The Netherlands, 1990; pp. 178–185. [Google Scholar]
- Meko, D. Dendroclimatic Reconstruction with Time Varying Predictor Subsets of Tree Indices. J. Clim. 1997, 10, 687–696. [Google Scholar] [CrossRef]
- Dracup, J.A.; Kahya, E. The relationships between U.S. streamflow and La Niña Events. Water Resour. Res. 1994, 30, 2133–2141. [Google Scholar] [CrossRef]
- Kozlowski, T.T.; Kramer, P.J.; Pallardy, S.G. The Physiological Ecology of Woody Plants; Academic Press: San Diego, CA, USA, 1991. [Google Scholar]
- Declerck, F.A.J.; Barbour, M.G.; Sawyer, J.O. Species richness and stand stability in conifer forests of the Sierra Nevada. Ecology 2006, 87, 2787–2799. [Google Scholar] [CrossRef]
- Dolanc, C.R.; Westfall, R.D.; Safford, H.D.; Thorne, J.H.; Schwartz, M.W. Growth–climate relationships for six subalpine tree species in a Mediterranean climate. Can. J. For. Res. 2013, 43, 1114–1126. [Google Scholar] [CrossRef]
- Hurteau, M.; Zald, H.; North, M. Species-specific response to climate reconstruction in upper-elevation mixed-conifer forests of the western Sierra Nevada, California. Can. J. For. Res. 2007, 37, 1681–1691. [Google Scholar] [CrossRef] [Green Version]
- Shamir, E.; Meko, D.; Touchan, R.; Lepley, K.S.; Campbell, R.; Kaliff, R.N.; Georgakakos, K.P. Snowpack- and soil water content-related hydrologic indices and their association with radial growth of conifers in the Sierra Nevada, California. J. Geophys. Res. Biogeosci. 2019, 125, e2019JG005331. [Google Scholar] [CrossRef]
- Graumlich, L.J. Subalpine Tree Growth, Climate, and Increasing CO_2: An Assessment of Recent Growth Trends. Ecology 1991, 72, 1–11. [Google Scholar] [CrossRef]
- Peterson, D.W.; Peterson, D.L. Mountain Hemlock Growth Responds to Climatic Variability at Annual and Decadal Time Scales. Ecology 2001, 82, 3330–3345. [Google Scholar] [CrossRef]
- Bartholomeus, R.P.; Witte, J.-P.M.; Runhaar, J. Drought stress and vegetation characteristics on sites with different slopes and orientations. Ecohydrology 2011, 5, 808–818. [Google Scholar] [CrossRef]
- Bales, R.C.; Hopmans, J.W.; O’Geen, A.T.; Meadows, M.; Hartsough, P.C.; Kirchner, P.; Hunsaker, C.T.; Beaudette, D. Soil Moisture Response to Snowmelt and Rainfall in a Sierra Nevada Mixed-Conifer Forest. Vadose Zone J. 2011, 10, 786–799. [Google Scholar] [CrossRef]
- Goldstein, A.; Hultman, N.; Fracheboud, J.; Bauer, M.; Panek, J.; Xu, M.; Qi, Y.; Guenther, A.; Baugh, W. Effects of climate variability on the carbon dioxide, water, and sensible heat fluxes above a ponderosa pine plantation in the Sierra Nevada (CA). Agric. For. Meteorol. 2000, 101, 113–129. [Google Scholar] [CrossRef] [Green Version]
- Kapnick, S.; Hall, A. Observed Climate–Snowpack Relationships in California and their Implications for the Future. J. Clim. 2010, 23, 3446–3456. [Google Scholar] [CrossRef] [Green Version]
- Cooper, A.E.; Kirchner, J.W.; Wolf, S.; Lombardozzi, D.L.; Sullivan, B.W.; Tyler, S.W.; Harpold, A.A. Snowmelt causes different limitations on transpiration in a Sierra Nevada conifer forest. Agric. For. Meteorol. 2020, 291, 108089. [Google Scholar] [CrossRef]
- Meko, D.; Stockton, C.W.; Boggess, W.R. The tree-ring record of severe sustained drought. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 789–801. [Google Scholar] [CrossRef]
- Peltier, D.M.P.; Fell, M.; Ogle, K. Legacy effects of drought in the southwestern United States: A multi-species synthesis. Ecol. Monogr. 2016, 86, 312–326. [Google Scholar] [CrossRef]
- Meko, D.; Touchan, R.; Anchukaitis, K. Seascorr: A MATLAB program for identifying the seasonal climate signal in an annual tree-ring time series. Comput. Geosci. 2011, 37, 1234–1241. [Google Scholar] [CrossRef]
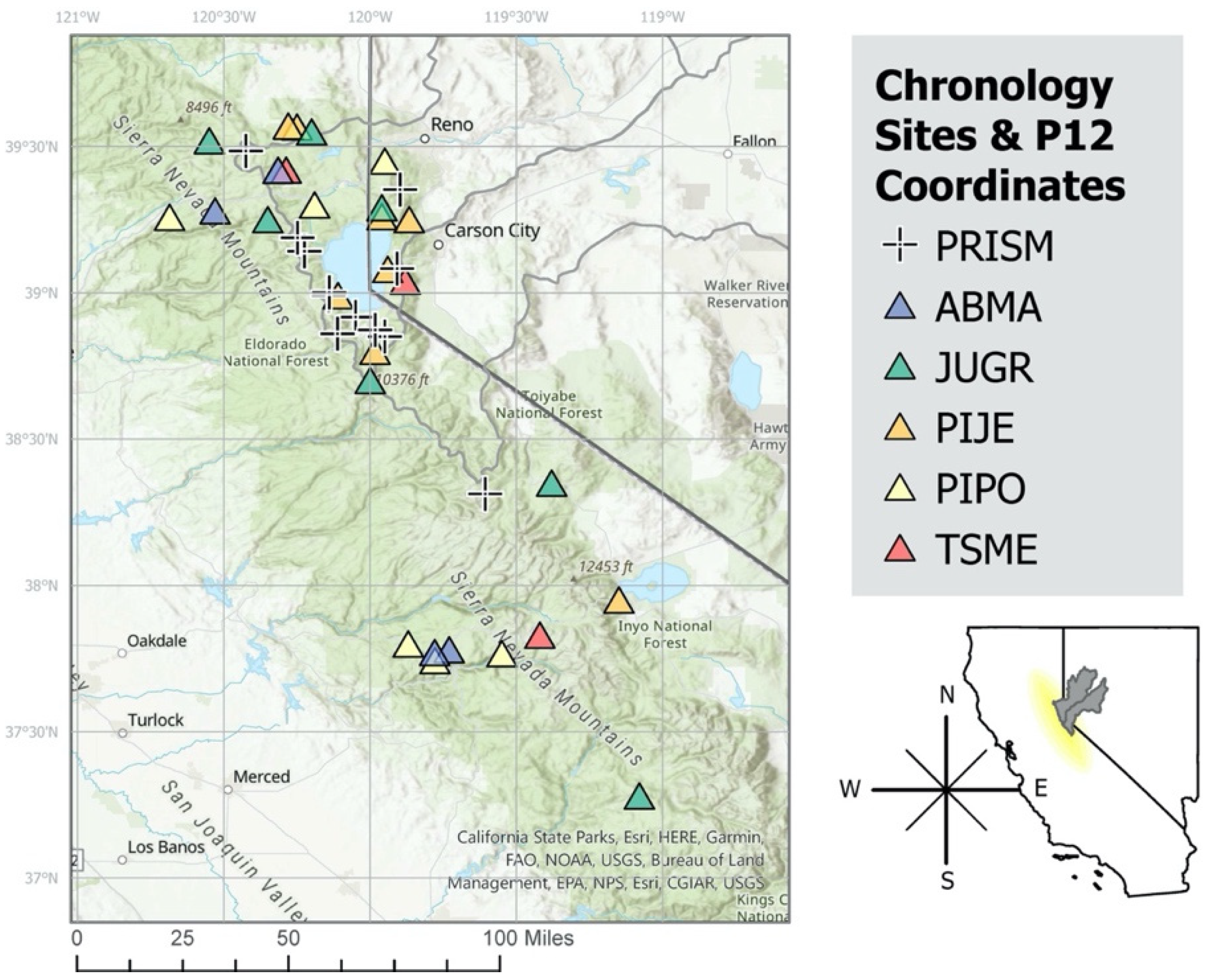




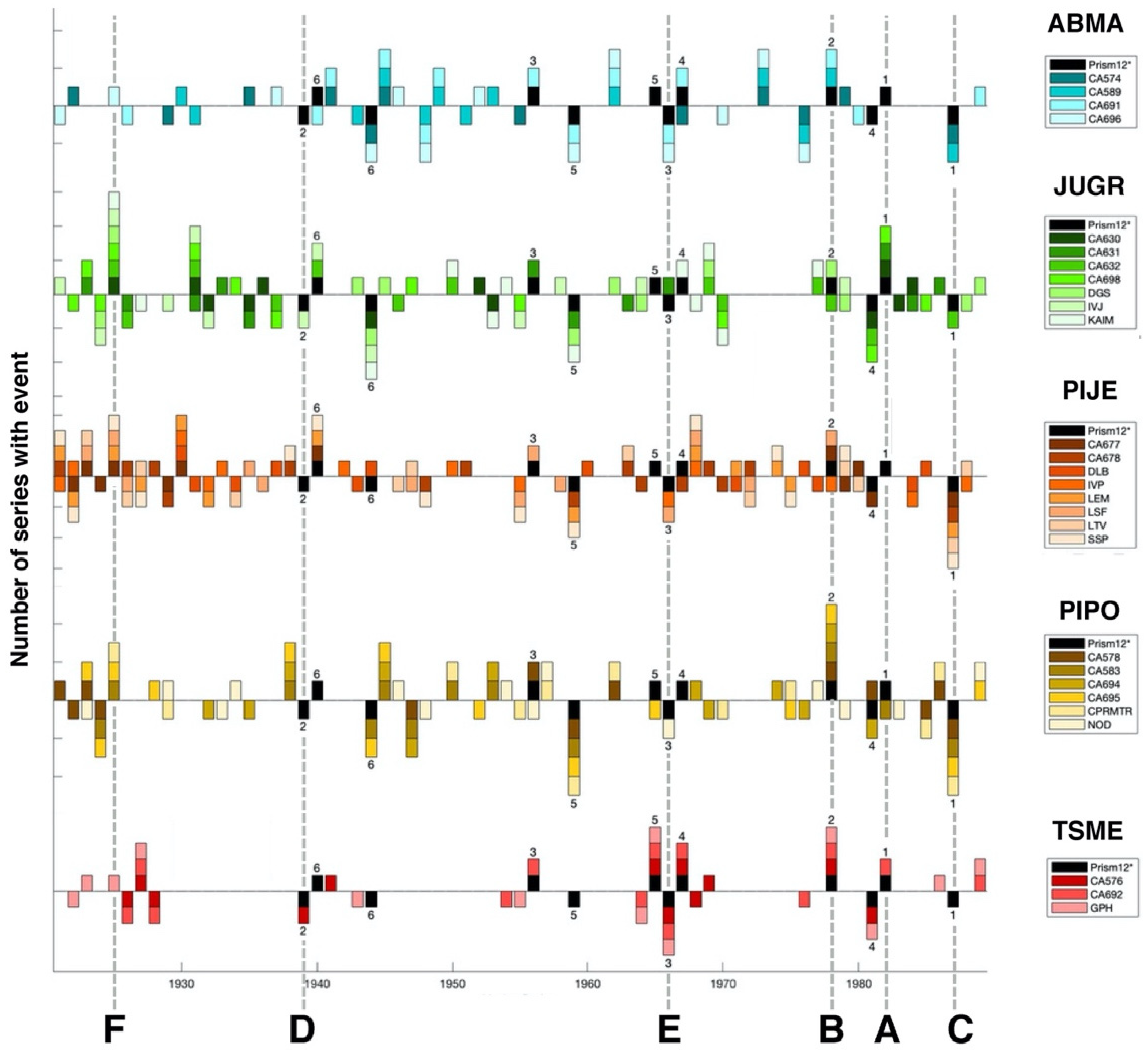

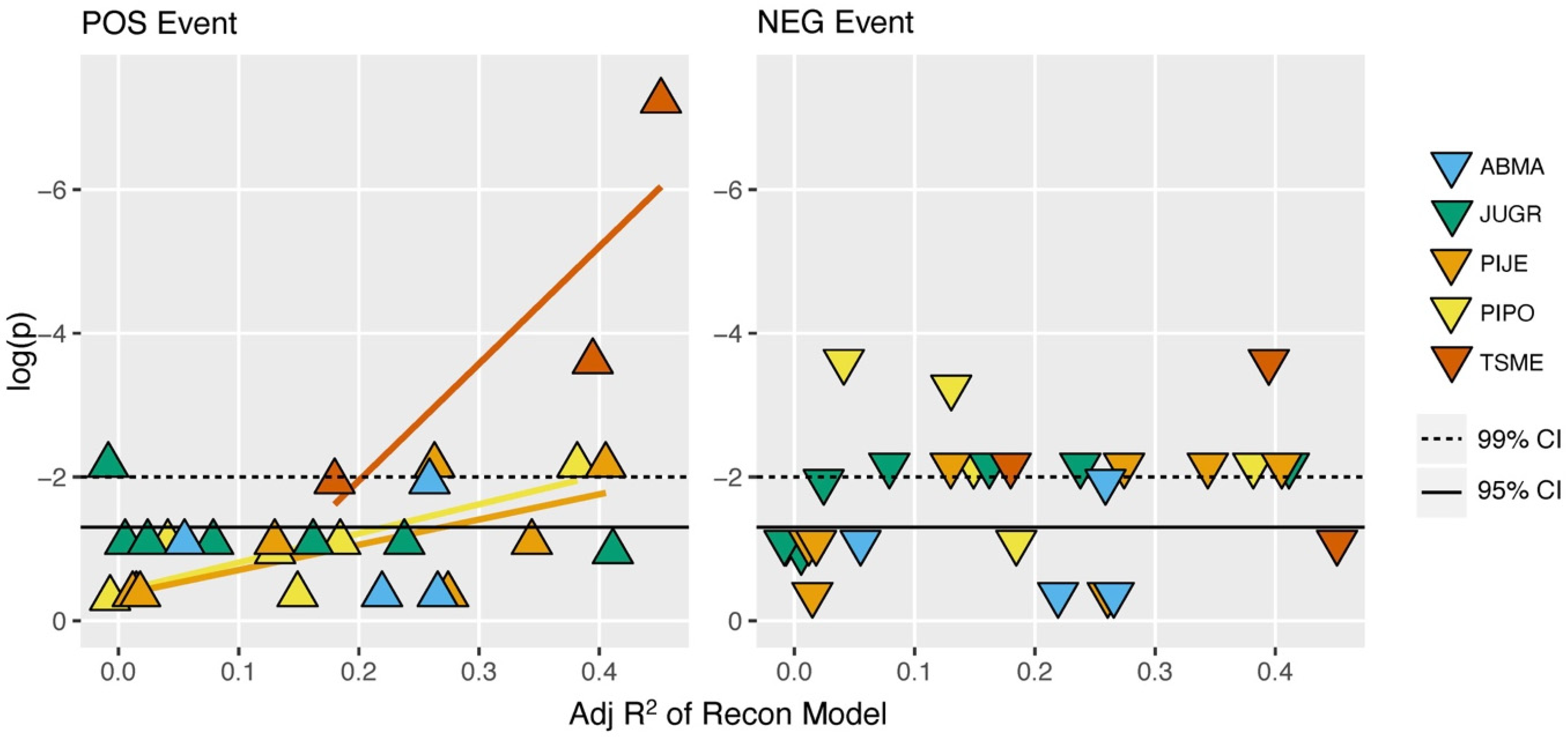
| Site Code | Species Code | Lat. | Lon. | Elev. (m) | Source | Start Year | End Year |
|---|---|---|---|---|---|---|---|
| CA574 | ABMA | 37.77 | −119.77 | 2180 | ITRDB | 1880 | 1991 |
| CA589 | ABMA | 37.78 | −119.73 | 2075 | ITRDB | 1880 | 1991 |
| CA691 | ABMA | 39.42 | −120.31 | 2478 | ITRDB | 1540 | 2015 |
| CA696 | ABMA | 39.28 | −120.53 | 2008 | ITRDB | 1799 | 2014 |
| CA630 | JUGR | 38.42 | −120 | 2591 | ITRDB | −420 | 1999 |
| CA631 | JUGR | 39.52 | −120.55 | 1921 | ITRDB | 930 | 1999 |
| CA632 | JUGR | 39.33 | −120.12 | 2268 | ITRDB | 1010 | 1999 |
| CA698 | JUGR | 39.15 | −120.21 | 1809 | ITRDB | 1600 | 2014 |
| DGS | JUGR | 38.35 | −119.38 | 2370 | Biondi | −300 | 2000 |
| IVJ | JUGR | 39.28 | −119.96 | 2563 | Taylor | 1142 | 2000 |
| KAIM | JUGR | 37.28 | −119.08 | 2730 | Meko | 1140 | 2011 |
| CA677 | PIJE | 39.34 | −120.17 | 1688 | ITRDB | 1415 | 2010 |
| CA678 | PIJE | 37.57 | −119.09 | 2499 | ITRDB | 1304 | 2010 |
| DLB | PIJE | 38.99 | −120.11 | 2004 | Taylor | 1306 | 2000 |
| IVP | PIJE | 39.27 | −119.96 | 2332 | Taylor | 1305 | 2000 |
| LEM | PIJE | 39.34 | −120.015 | 2008 | Biondi | 1542 | 2020 |
| LSF | PIJE | 38.48 | −119.59 | 2416 | Biondi | 1474 | 2020 |
| LTV | PIJE | 39.15 | −119.52 | 2006 | Biondi | 1418 | 2020 |
| SSP | PIJE | 39.08 | −119.94 | 2132 | Taylor | 1190 | 1999 |
| CA578 | PIPO | 37.8 | −119.87 | 1722 | ITRDB | 1880 | 1990 |
| CA583 | PIPO | 37.75 | −119.77 | 1803 | ITRDB | 1880 | 1990 |
| CA694 | PIPO | 39.2988 | −120.1915 | 1975 | ITRDB | 1829 | 2014 |
| CA695 | PIPO | 39.258 | −120.6857 | 1537 | ITRDB | 1838 | 2014 |
| CPRMTR | PIPO | 39.27 | −119.57 | 2507 | Biondi | 1474 | 2020 |
| NOD | PIPO | 37.46 | −119.33 | 1539 | Biondi | 1539 | 2002 |
| CA567 | TSME | 37.83 | −119.42 | 2960 | ITRDB | 1880 | 1990 |
| CA692 | TSME | 39.42 | −120.31 | 2478 | ITRDB | 1615 | 2015 |
| GPH | TSME | 39.04 | −119.88 | 2728 | Taylor | 1349 | 2000 |
| Recon | Chronologies | R2 | R2adj | F | REcv | RSME |
|---|---|---|---|---|---|---|
| ALL | DGS CA574 CA567P1 | 0.613 | 0.595 | 34.327 | 0.583 | 227.276 |
| ABMA | CA696P1 CA691P1 CA574P1 CA574 CA589P1 CA696 | 0.430 | 0.375 | 7.800 | 0.384 | 276.220 |
| JUGR | DGS KAIM IVJN2 CA630 | 0.540 | 0.515 | 21.421 | 0.498 | 253.836 |
| PIJE | CA677 CA678 LSFP1 LEM LSF | 0.486 | 0.450 | 13.622 | 0.426 | 271.409 |
| PIPO | CA578 CA694P1 | 0.321 | 0.301 | 15.634 | 0.247 | 305.411 |
| TSME | CA692P1 CA567P1 GPH GPHP2 CA692N2 | 0.463 | 0.420 | 10.855 | 0.409 | 270.588 |
| Name | m (POS) | m (NEG) | k (POS) | k (NEG) | p-Val (POS) | p-Val (NEG) |
|---|---|---|---|---|---|---|
| ALL | 3 | 3 | 7 | 6 | <0.001 | <0.001 |
| ABMA | 1 | 2 | 6 | 7 | 0.0814 | 0.0116 |
| JUGR | 3 | 4 | 7 | 6 | <0.001 | <0.001 |
| PIJE | 3 | 1 | 7 | 6 | <0.001 | 0.0814 |
| PIPO | 3 | 3 | 7 | 6 | <0.001 | <0.001 |
| TSME | 3 | 3 | 6 | 6 | <0.001 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Winitsky, A.G.; Meko, D.M.; Taylor, A.H.; Biondi, F. Species Sensitivity to Hydrologic Whiplash in The Tree-Ring Record of the High Sierra Nevada. Environments 2023, 10, 12. https://doi.org/10.3390/environments10010012
Winitsky AG, Meko DM, Taylor AH, Biondi F. Species Sensitivity to Hydrologic Whiplash in The Tree-Ring Record of the High Sierra Nevada. Environments. 2023; 10(1):12. https://doi.org/10.3390/environments10010012
Chicago/Turabian StyleWinitsky, Anabel G., David M. Meko, Alan H. Taylor, and Franco Biondi. 2023. "Species Sensitivity to Hydrologic Whiplash in The Tree-Ring Record of the High Sierra Nevada" Environments 10, no. 1: 12. https://doi.org/10.3390/environments10010012
APA StyleWinitsky, A. G., Meko, D. M., Taylor, A. H., & Biondi, F. (2023). Species Sensitivity to Hydrologic Whiplash in The Tree-Ring Record of the High Sierra Nevada. Environments, 10(1), 12. https://doi.org/10.3390/environments10010012







