Modeling and Optimization of Hexavalent Chromium Adsorption by Activated Eucalyptus Biochar Using Response Surface Methodology and Adaptive Neuro-Fuzzy Inference System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation and Characterization of Biochar-Based Adsorbent
2.3. Adsorption Studies
2.4. Model Development
2.4.1. RSM Model Development
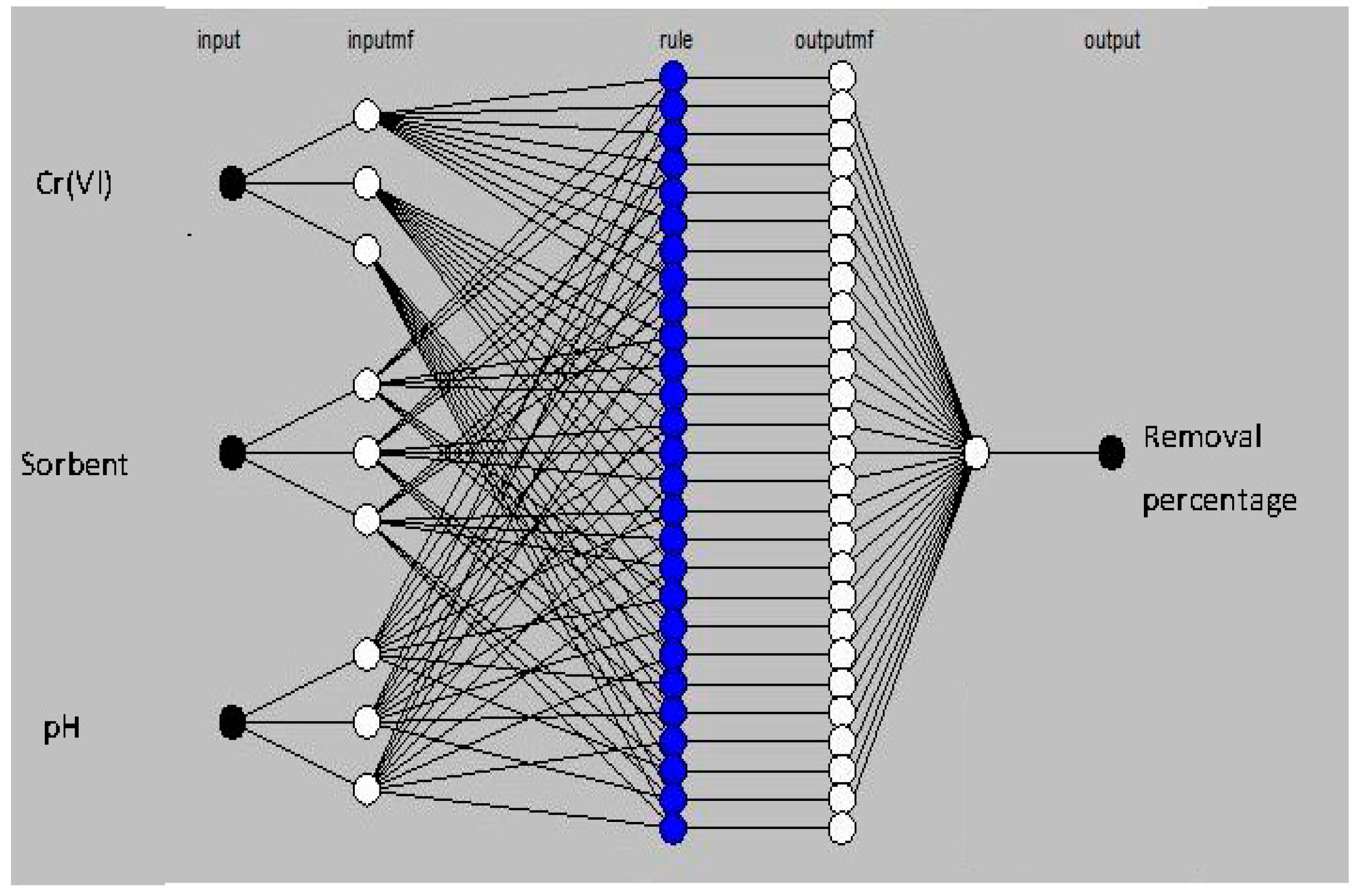
2.4.2. ANFIS Model Development
2.5. Optimization of Process Parameters
2.6. Appraisal of the Developed RSM and ANFIS Models
2.7. Sensitivity Analysis of the Operating Parameters on Model Response
3. Results and Discussion
3.1. AEB Analysis
3.2. RSM Model Analysis for the Adsorption Process
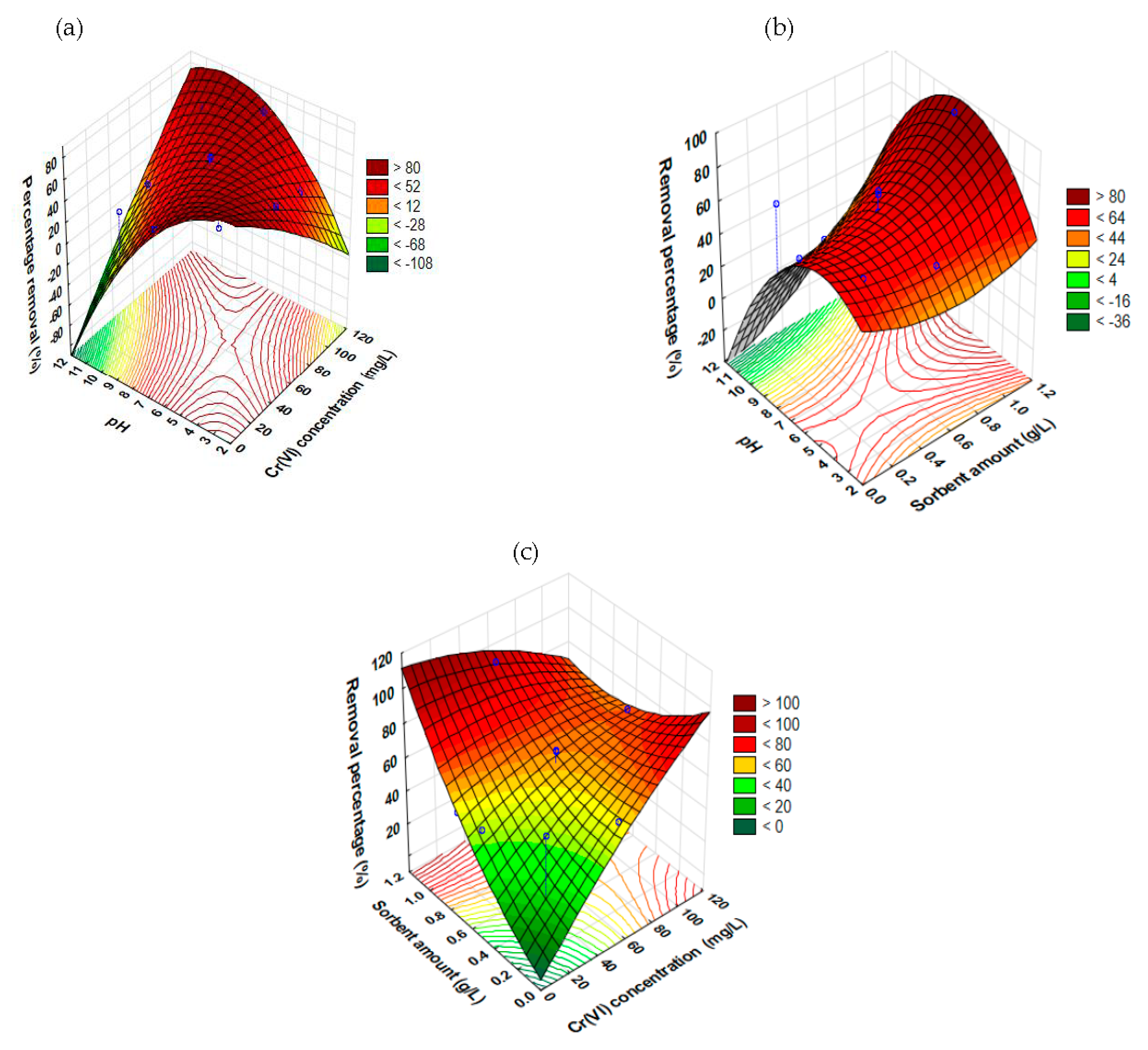
Synergistic Impacts of Factors on the Removal of Cr6+ Using the RSM Model
- Influence of pH and Cr6+ concentration
- Influence of pH and sorbent amount
- Influence of Cr6+ concentration and sorbent amount
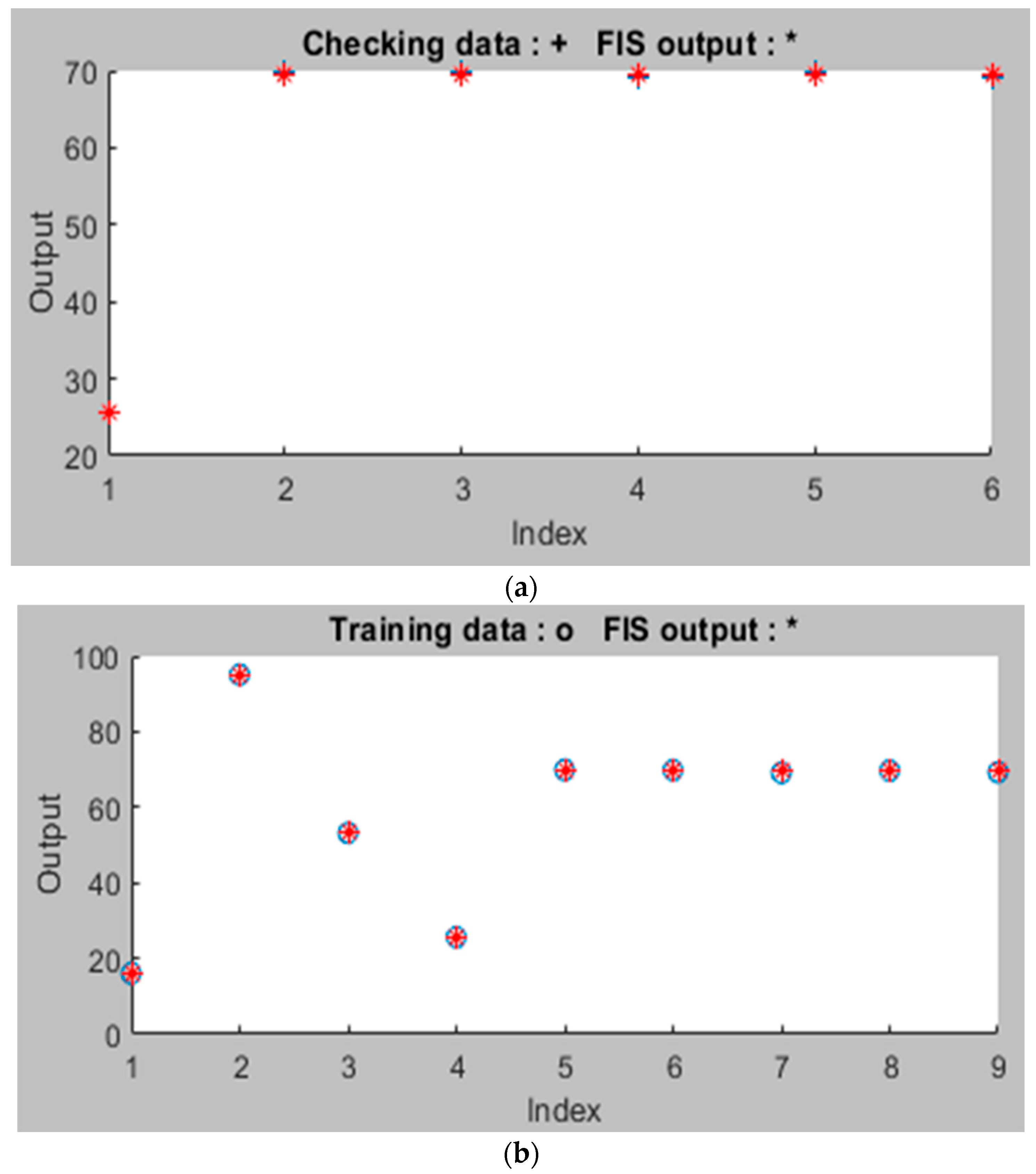
3.3. ANFIS Model Analysis for the Adsorption Process
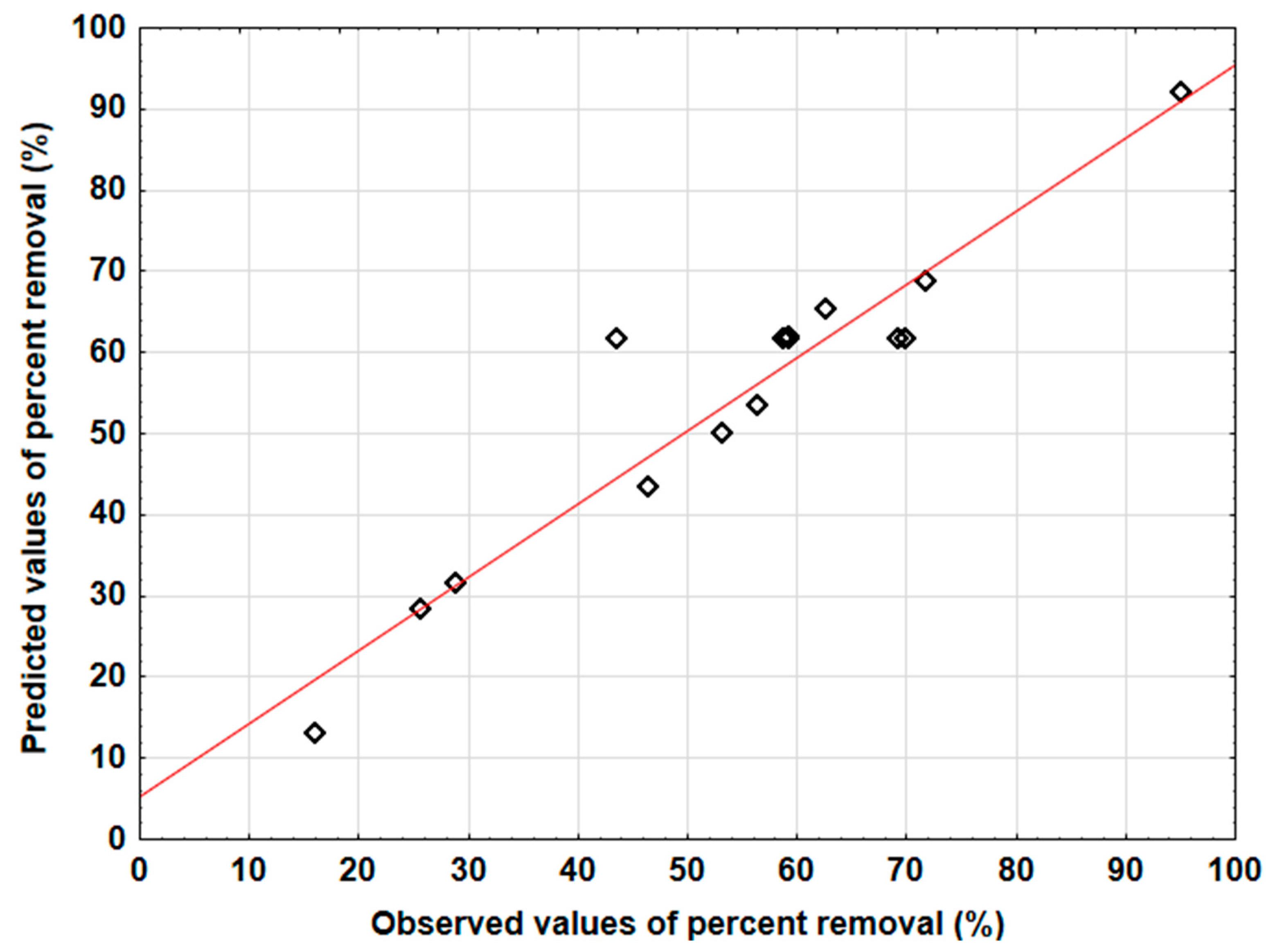
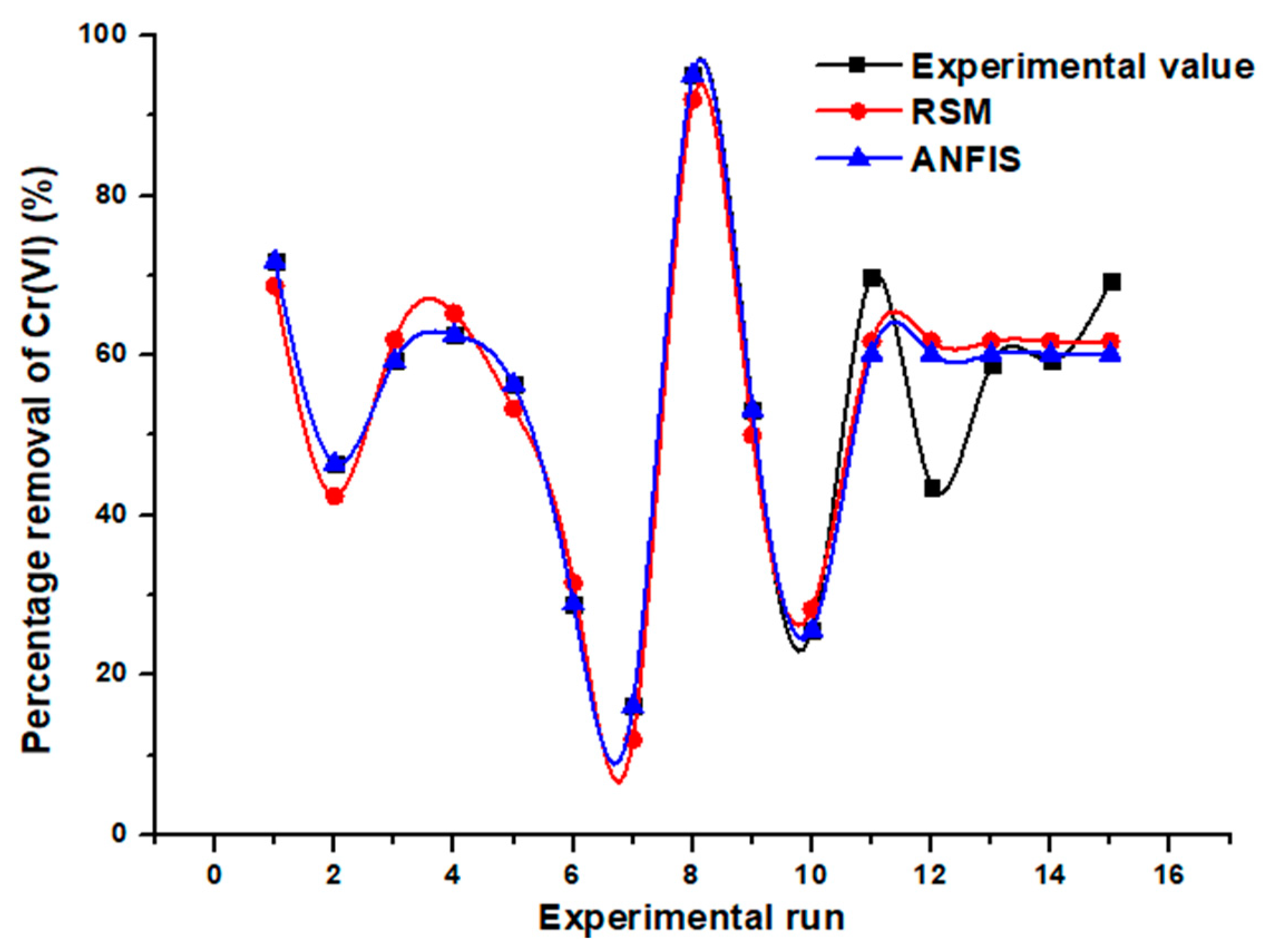
3.4. Evaluation of the Two Models’ Predictive Effectiveness
3.5. Results of Operating Parameter Optimization
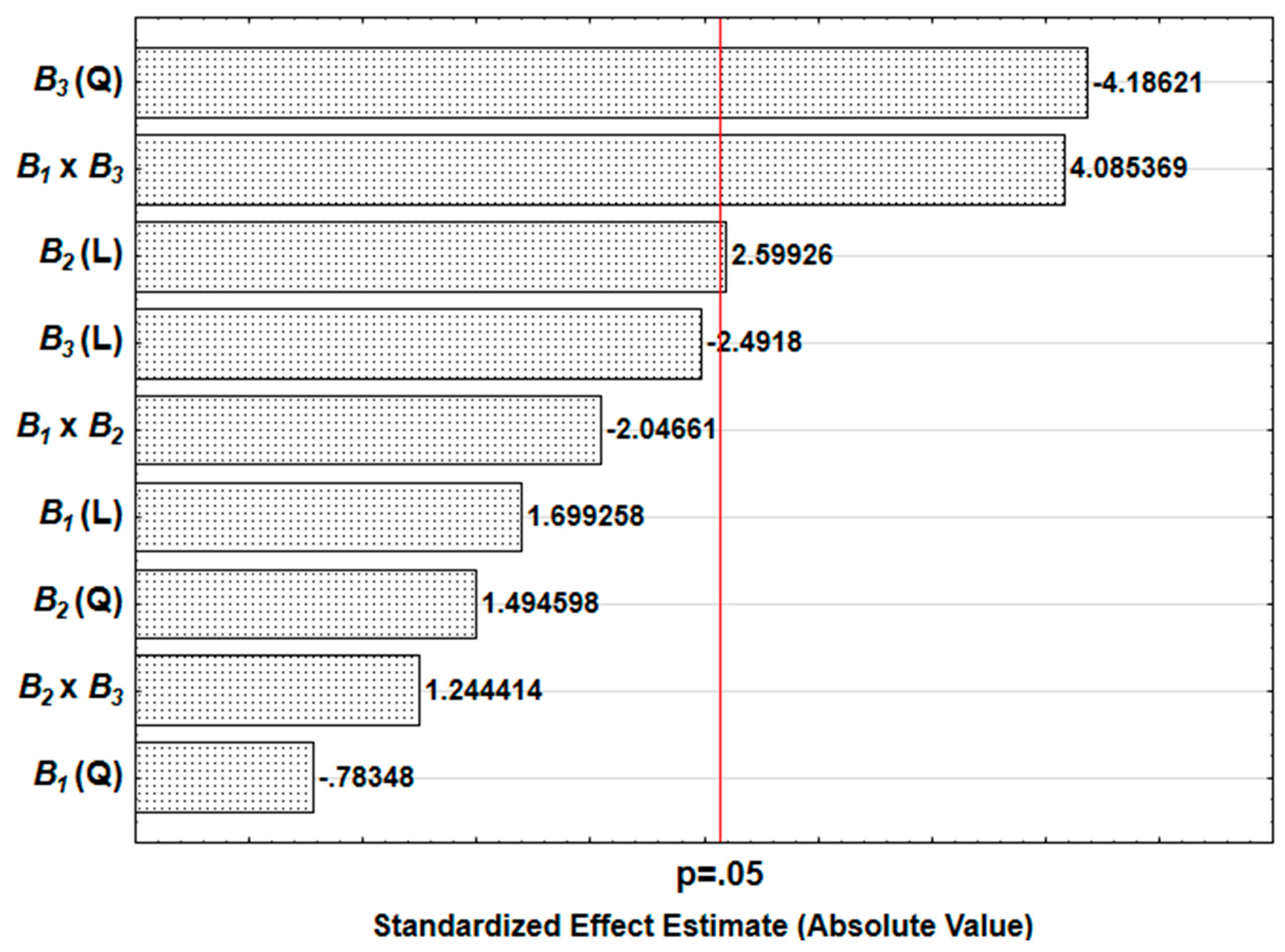
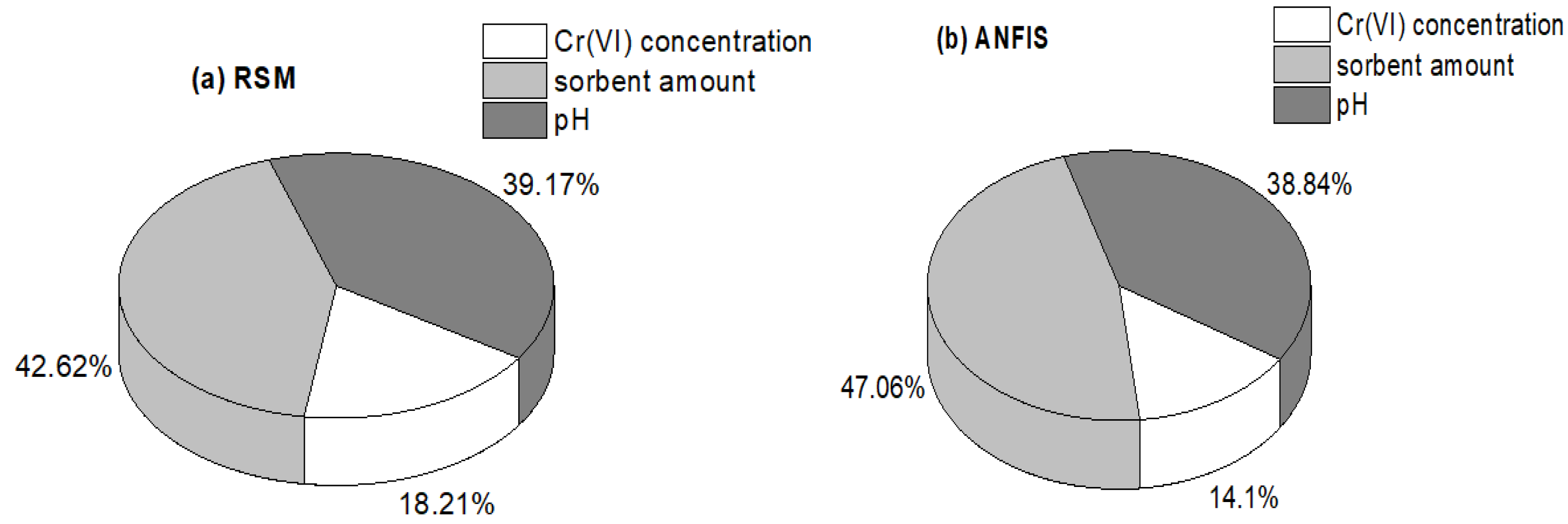
3.6. Result of the Sensitivity Study
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gorzin, F.; Bahri Rasht Abadi, M. Adsorption of Cr (VI) from aqueous solution by adsorbent prepared from paper mill sludge: Kinetics and thermodynamics studies. Adsorpt. Sci. Technol. 2018, 36, 149–169. [Google Scholar] [CrossRef] [Green Version]
- Awual, M.R. Assessing of lead (III) capturing from contaminated wastewater using ligand doped conjugate adsorbent. Chem. Eng. J. 2016, 289, 65–73. [Google Scholar] [CrossRef]
- Awual, M.R.; Yaita, T.; Kobayashi, T.; Shiwaku, H.; Suzuki, S. Improving cesium removal to clean-up the contaminated water using modified conjugate material. J. Environ. Chem. Eng. 2020, 8, 103684. [Google Scholar] [CrossRef]
- Bayazit, Ş.S.; Kerkez, Ö. Hexavalent chromium adsorption on superparamagnetic multi-wall carbon nanotubes and activated carbon composites. Chem. Eng. Res. Des. 2014, 92, 2725–2733. [Google Scholar] [CrossRef]
- Yusuff, A.S.; Popoola, L.T.; Igbafe, A.I. Response surface modeling and optimization of hexavalent chromium adsorption onto eucalyptus tree bark-derived pristine and chemically-modified biochar. Chem. Eng. Res. Des. 2022, 182, 592–603. [Google Scholar] [CrossRef]
- Mitra, S.; Chakraborty, A.J.; Tareq, A.M.; Emran, T.B.; Nainu, F.; Khusro, A.; Idris, A.M.; Khandaker, M.U.; Osman, H.; Alhumaydhi, F.A.; et al. Impact of heavy metals on the environment and human health: Novel therapeutic insights to counter the toxicity. J. King Saud Univ. Sci. 2022, 34, 101865. [Google Scholar] [CrossRef]
- Cavaco, S.A.; Fernandes, S.; Quina, M.M.; Ferreira, L.M. Removal of chromium from electroplating industry effluents by ion exchange resins. J. Hazard. Mater. 2007, 144, 634–638. [Google Scholar] [CrossRef] [PubMed]
- Kostas, V.; Baikousi, M.; Dimos, K.; Vasilopoulos, K.C.; Koutselas, I.; Karakassides, M.A. Efficient and rapid photocatalytic reduction of hexavalent chromium achieved by a phloroglucinol-derived microporous polymeric organic framework solid. J. Phys. Chem. C 2017, 121, 7303–7311. [Google Scholar] [CrossRef]
- Yusuff, A.S.; Ajayi, O.A.; Popoola, L.T. Application of Taguchi design approach to parametric optimization of adsorption of crystal violet dye by activated carbon from poultry litter. Sci. Afr. 2021, 13, e00850. [Google Scholar] [CrossRef]
- Fito, J.; Tibebu, S.; Nkambule, T.T. Optimization of Cr (VI) removal from aqueous solution with activated carbon derived from Eichhornia crassipes under response surface methodology. BMC Chem. 2023, 17, 4. [Google Scholar] [CrossRef]
- Yang, T.; Han, C.; Tang, J.; Luo, Y. Removal performance and mechanisms of Cr (VI) by an in-situ self-improvement of mesoporous biochar derived from chicken bone. Environ. Sci. Pollut. Res. 2020, 27, 5018–5029. [Google Scholar] [CrossRef]
- Kumar, A.; Jena, H.M. Adsorption of Cr (VI) from aqueous solution by prepared high surface area activated carbon from Fox nutshell by chemical activation with H3PO4. J. Environ. Chem. Eng. 2017, 5, 2032–2041. [Google Scholar] [CrossRef]
- Yusuff, A.S. Adsorption of hexavalent chromium from aqueous solution by Leucaena leucocephala seed pod activated carbon: Equilibrium, kinetic and thermodynamic studies. Arab. J. Basic Appl. Sci. 2019, 26, 89–102. [Google Scholar] [CrossRef] [Green Version]
- Kabir, M.M.; Akter, M.M.; Khandaker, S.; Gilroyed, B.H.; Didar-ul-Alam, M.; Hakim, M.; Awual, M.R. Highly effective agro-waste based functional green adsorbents for toxic chromium (VI) ion removal from wastewater. J. Mol. Liq. 2022, 347, 118327. [Google Scholar] [CrossRef]
- Meshram, P.; Ghosh, A.; Ramamurthy, Y.; Pandey, B.D.; Torem, M.L. Removal of hexavalent chromium from mine effluents by ion exchange resins-comparative study of Amberlite IRA 400 and IRA 900. Russ. J. Non Ferr. Met. 2018, 59, 533–542. [Google Scholar] [CrossRef]
- Salahshoori, I.; Seyfaee, A.; Babapoor, A.; Cacciotti, I. Recovery of Manganese Ions from Aqueous Solutions with Cyanex 272 Using Emulsion Liquid Membrane Technique: A Design of Experiment Study. J. Sustain. Metall. 2021, 7, 1074–1090. [Google Scholar] [CrossRef]
- Yusuff, A.S.; Bhonsle, A.K.; Bangwal, D.P.; Atray, N. Development of a barium-modified zeolite catalyst for biodiesel production from waste frying oil: Process optimization by design of experiment. Renew. Energy 2021, 177, 1253–1264. [Google Scholar] [CrossRef]
- Salahshoori, I.; Ramezani, Z.; Cacciotti, I.; Yazdanbakhsh, A.; Hossain, M.K.; Hassanzadeganroudsari, M. Cisplatin uptake and release assessment from hydrogel synthesized in acidic and neutral medium: An experimental and molecular dynamics simulation study. J. Mol. Liq. 2021, 344, 117890. [Google Scholar] [CrossRef]
- Zaroual, Z.; Chaair, H.; Essadki, A.; El Ass, K.; Azzi, M. Optimizing the removal of trivalent chromium by electrocoagulation using experimental design. Chem. Eng. J. 2009, 148, 488–495. [Google Scholar] [CrossRef]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Malik, Z.; Rashid, K. Comparison of optimization by response surface methodology with neurofuzzy methods. IEEE Trans. Magn. 2000, 36, 241–257. [Google Scholar] [CrossRef]
- Garg, U.K.; Kaur, M.; Sud, D.; Garg, V. Removal of hexavalent chromium from aqueous solution by adsorption on treated sugarcane bagasse using response surface methodological approach. Desalination 2009, 249, 475–479. [Google Scholar] [CrossRef]
- Jain, M.; Garg, V.; Kadirvelu, K. Investigation of Cr (VI) adsorption onto chemically treated Helianthus annuus: Optimization using response surface methodology. Bioresour. Technol. 2011, 102, 600–605. [Google Scholar] [CrossRef] [PubMed]
- Kiran, B.; Kaushik, A.; Kaushik, C. Response surface methodological approach for optimizing removal of Cr (VI) from aqueous solution using immobilized cyanobacterium. Chem. Eng. J. 2007, 126, 147–153. [Google Scholar] [CrossRef]
- Tarangini, K.; Kumar, A.; Satpathy, G.; Sangal, V.K. Statistical optimization of process parameters for Cr (VI) biosorption onto mixed cultures of Pseudomonas aeruginosa and Bacillus subtilis. Clean Soil Air Water 2009, 37, 319–327. [Google Scholar] [CrossRef]
- Halder, G.; Dhawane, S.; Barai, P.K.; Das, A. Optimizing chromium (VI) adsorption onto superheated steam activated granular carbon through response surface methodology and artificial neural network. Environ. Prog. Sustain. Energy 2015, 34, 638–647. [Google Scholar] [CrossRef]
- Khan, H.; Hussain, S.; Hussain, S.F.; Gul, S.; Ahmad, A.; Ullah, S. Multivariate modeling and optimization of Cr (VI) adsorption onto carbonaceous material via response surface models assisted with multiple regression analysis and particle swarm embedded neural network. Environ. Technol. Innov. 2021, 24, 101952. [Google Scholar] [CrossRef]
- Krishna, D.; Sree, R.P. Artificial neural network and response surface methodology approach for modeling and optimization of chromium (VI) adsorption from waste water using Ragi husk powder. Indian Chem. Eng. 2013, 55, 200–222. [Google Scholar] [CrossRef]
- Oskui, F.N.; Aghdasinia, H.; Sorkhabi, M.G. Modeling and optimization of chromium adsorption onto clay using response surface methodology, artificial neural network, and equilibrium isotherm models. Environ. Prog. Sustain. Energy 2019, 38, e13260. [Google Scholar] [CrossRef]
- Sen, S.; Nandi, S.; Dutta, S. Application of RSM and ANN for optimization and modeling of biosorption of chromium (VI) using cyanobacterial biomass. Appl. Water Sci. 2018, 8, 148. [Google Scholar] [CrossRef] [Green Version]
- Mandal, S.; Mahapatra, S.; Patel, R. Neuro fuzzy approach for arsenic (III) and chromium (VI) removal from water. J. Water Process Eng. 2015, 5, 58–75. [Google Scholar] [CrossRef]
- Rajabi Kuyakhi, H.; Tahmasebi Boldaji, R. Developing an adaptive neuro-fuzzy inference system based on particle swarm optimization model for forecasting Cr (VI) removal by NiO nanoparticles. Environ. Prog. Sustain. Energy 2021, 40, e13597. [Google Scholar] [CrossRef]
- Zafar, M.; Aggarwal, A.; Rene, E.R.; Barbusiński, K.; Mahanty, B.; Behera, S.K. Data-Driven Machine Learning Intelligent Tools for Predicting Chromium Removal in an Adsorption System. Processes 2022, 10, 447. [Google Scholar] [CrossRef]
- Betiku, E.; Odude, V.O.; Ishola, N.B.; Bamimore, A.; Osunleke, A.S.; Okeleye, A.A. Predictive capability evaluation of RSM, ANFIS and ANN: A case of reduction of high free fatty acid of palm kernel oil via esterification process. Energy Convers. Manag. 2016, 124, 219–230. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Christine, M. Anderson Cook, CM: Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Chen, M.-J.; Chen, K.-N.; Lin, C.-W. Optimization on response surface models for the optimal manufacturing conditions of dairy tofu. J. Food Eng. 2005, 68, 471–480. [Google Scholar] [CrossRef]
- Alhothali, A.; Khurshid, H.; Mustafa, M.R.U.; Moria, K.M.; Rashid, U.; Bamasag, O.O. Evaluation of Contemporary Computational Techniques to Optimize Adsorption Process for Simultaneous Removal of COD and TOC in Wastewater. Adsorpt. Sci. Technol. 2022, 2022, 7874826. [Google Scholar] [CrossRef]
- Onu, C.E.; Ohale, P.E.; Ekwueme, B.N.; Obiora-Okafo, I.A.; Okey-Onyesolu, C.F.; Onu, C.P.; Ezema, C.A.; Onu, O.O. Modeling, optimization, and adsorptive studies of bromocresol green dye removal using acid functionalized corn cob. Clean. Chem. Eng. 2022, 4, 100067. [Google Scholar] [CrossRef]
- Ramachandran, A.; Rustum, R.; Adeloye, A.J. Review of anaerobic digestion modeling and optimization using nature-inspired techniques. Processes 2019, 7, 953. [Google Scholar] [CrossRef] [Green Version]
- Blum, C. Ant colony optimization: Introduction and recent trends. Phys. Life Rev. 2005, 2, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Tan, I.; Ahmad, A.; Hameed, B. Preparation of activated carbon from coconut husk: Optimization study on removal of 2, 4, 6-trichlorophenol using response surface methodology. J. Hazard. Mater. 2008, 153, 709–717. [Google Scholar] [CrossRef]
- Ishola, N.B.; Okeleye, A.A.; Osunleke, A.S.; Betiku, E. Process modeling and optimization of sorrel biodiesel synthesis using barium hydroxide as a base heterogeneous catalyst: Appraisal of response surface methodology, neural network and neuro-fuzzy system. Neural Comput. Appl. 2019, 31, 4929–4943. [Google Scholar] [CrossRef]
- Souza, P.; Dotto, G.; Salau, N. Artificial neural network (ANN) and adaptive neuro-fuzzy interference system (ANFIS) modelling for nickel adsorption onto agro-wastes and commercial activated carbon. J. Environ. Chem. Eng. 2018, 6, 7152–7160. [Google Scholar] [CrossRef]
- Franco, D.S.; Duarte, F.A.; Salau, N.P.G.; Dotto, G.L. Adaptive neuro-fuzzy inference system (ANIFS) and artificial neural network (ANN) applied for indium (III) adsorption on carbonaceous materials. Chem. Eng. Commun. 2019, 206, 1452–1462. [Google Scholar] [CrossRef]
- Yusuff, A.S.; Ishola, N.B.; Gbadamosi, A.O.; Thompson-Yusuff, K.A. Pumice-supported ZnO-photocatalyzed degradation of organic pollutant in textile effluent: Optimization by response surface methodology, artificial neural network, and adaptive neural-fuzzy inference system. Environ. Sci. Pollut. Res. 2022, 29, 25138–25156. [Google Scholar] [CrossRef] [PubMed]
- Mashaly, A.F.; Alazba, A. ANFIS modeling and sensitivity analysis for estimating solar still productivity using measured operational and meteorological parameters. Water Sci. Technol. Water Supply 2018, 18, 1437–1448. [Google Scholar] [CrossRef]
- Liu, L.; Li, Y.; Fan, S. Preparation of KOH and H3PO4 modified biochar and its application in methylene blue removal from aqueous solution. Processes 2019, 7, 891. [Google Scholar] [CrossRef] [Green Version]
- Ngaosuwan, K.; Goodwin, J.G., Jr.; Prasertdham, P. A green sulfonated carbon-based catalyst derived from coffee residue for esterification. Renew. Energy 2016, 86, 262–269. [Google Scholar] [CrossRef]
- Gorzin, F.; Ghoreyshi, A.A. Synthesis of a new low-cost activated carbon from activated sludge for the removal of Cr (VI) from aqueous solution: Equilibrium, kinetics, thermodynamics and desorption studies. Korean J. Chem. Eng. 2013, 30, 1594–1602. [Google Scholar] [CrossRef]
- Pal, D.B.; Singh, A.; Jha, J.M.; Srivastava, N.; Hashem, A.; Alakeel, M.A.; Abd_Allah, E.F.; Gupta, V.K. Low-cost biochar adsorbents prepared from date and delonix regia seeds for heavy metal sorption. Bioresour. Technol. 2021, 339, 125606. [Google Scholar] [CrossRef]
- Hameed, B.; Krishni, R.; Sata, S. A novel agricultural waste adsorbent for the removal of cationic dye from aqueous solutions. J. Hazard. Mater. 2009, 162, 305–311. [Google Scholar] [CrossRef]
- Yusuff, A.S.; Owolabi, J.O.; Igbomezie, C.O. Optimization of process parameters for adsorption of heavy metals from aqueous solutions by alumina-onion skin composite. Chem. Eng. Commun. 2021, 208, 14–28. [Google Scholar] [CrossRef]
- Betiku, E.; Akintunde, A.M.; Ojumu, T.V. Banana peels as a biobase catalyst for fatty acid methyl esters production using Napoleon’s plume (Bauhinia monandra) seed oil: A process parameters optimization study. Energy 2016, 103, 797–806. [Google Scholar] [CrossRef]
- Mahanty, S.; Chatterjee, S.; Ghosh, S.; Tudu, P.; Gaine, T.; Bakshi, M.; Das, S.; Das, P.; Bhattacharyya, S.; Bandyopadhyay, S.; et al. Synergistic approach towards the sustainable management of heavy metals in wastewater using mycosynthesized iron oxide nanoparticles: Biofabrication, adsorptive dynamics and chemometric modeling study. J. Water Process. Eng. 2020, 37, 101426. [Google Scholar] [CrossRef]
- Malkoc, E.; Nuhoglu, Y.; Dundar, M. Adsorption of chromium (VI) on pomace—An olive oil industry waste: Batch and column studies. J. Hazard. Mater. 2006, 138, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Bashir, S.; Zhu, J.; Fu, Q.; Hu, H. Comparing the adsorption mechanism of Cd by rice straw pristine and KOH-modified biochar. Environ. Sci. Pollut. Res. 2018, 25, 11875–11883. [Google Scholar] [CrossRef]
- Dehghani, M.H.; Gholami, S.; Karri, R.R.; Lima, E.C.; Mahvi, A.H.; Nazmara, S.; Fazlzadeh, M. Process modeling, characterization, optimization, and mechanisms of fluoride adsorption using magnetic agro-based adsorbent. J. Environ. Manag. 2021, 286, 112173. [Google Scholar] [CrossRef]
- Ishola, N.B.; Adeyemi, O.O.; Adesina, A.J.; Odude, V.O.; Oyetunde, O.O.; Okeleye, A.A.; Soji-Adekunle, A.R.; Betiku, E. Adaptive neuro-fuzzy inference system-genetic algorithm vs. response surface methodology: A case of optimization of ferric sulfate-catalyzed esterification of palm kernel oil. Process Saf. Environ. Prot. 2017, 111, 211–220. [Google Scholar] [CrossRef]
- Jisieike, C.F.; Ishola, N.B.; Latinwo, L.M.; Betiku, E. Crude rubber seed oil esterification using a solid catalyst: Optimization by hybrid adaptive neuro-fuzzy inference system and response surface methodology. Energy 2022, 263, 125734. [Google Scholar] [CrossRef]
- Sekulic, M.; Pejic, V.; Brezocnik, M.; Gostimirović, M.; Hadzistevic, M. Prediction of surface roughness in the ball-end milling process using response surface methodology, genetic algorithms, and grey wolf optimizer algorithm. Adv. Prod. Eng. Manag. 2018, 13, 18–30. [Google Scholar] [CrossRef]



| Factor | Description | Level | ||||
|---|---|---|---|---|---|---|
| −α | −1 | 0 | +1 | +α | ||
| Cr(VI) concentration (mg/L) | 7.4 | 20 | 60 | 100 | 112.6 | |
| Sorbent amount (g/L) | 0.07 | 0.2 | 0.6 | 1.0 | 1.13 | |
| pH | 3.1 | 4 | 7 | 10 | 10.9 | |
| ANFIS | Property | ||
|---|---|---|---|
| Type of fuzzy | Sugeno | ||
| Input/output | 3 a/1 b | ||
| Membership function | gbellmf | ||
| And type | Product | ||
| Or type | Probabilistic | ||
| Implication type | Product | ||
| Aggregation type | Sum | ||
| Optimization type | Hybrid | ||
| Epochs | 15 | ||
| Number of rules | 27 | ||
| Linear/nonlinear parameter number | 27/27 | ||
| Total number of parameters | 54 | ||
| Genetic algorithm | Value/comment | Ant colony optimization | Value |
| Population size | 5–20 | Ant population size | 10–30 |
| Scaling function | Rank | pheromone persistence coefficient | 0.8 |
| Selection | Stochastic uniform | Iteration number | 10–30 |
| Crossover function | 0.8 | penalty factor | 0.5 |
| Mutation | Constraint dependent | ||
| Crossover | Constraint dependent |
| Factor | Minimum | Nominal | Maximum |
|---|---|---|---|
| Cr6+ concentration | 7.4 | 60 | 112.6 |
| Sorbent amount | 0.07 | 0.6 | 1.13 |
| pH | 3.1 | 7 | 10.1 |
| Ultimate Property | Composition (%) |
|---|---|
| C | 68.68 |
| H | 2.97 |
| N | 0.92 |
| O | 26.37 |
| Zn | 1.23 |
| Textural and proximate properties | Value |
| Specific surface area (m2/g) | 217.29 |
| Pore volume (cm3/g) | 0.21 |
| Pore diameter (Å) | 49.91 |
| Ash content (%) | 2.12 |
| Humidity (%) | 58.7 |
| Run No. | Cr(VI) Biosorption Process Parameters | Observed Removal Percentage (%) | Predicted Removal Percentages (%) | |||
|---|---|---|---|---|---|---|
| Cr(VI) Concentration, (mg/L) | Sorbent Amount, (g/L) | pH | RSM | ANFIS | ||
| 1 | 112.6 | 0.6 | 7.0 | 71.8 | 68.7 | 71.8 |
| 2 | 7.4 | 0.6 | 7.0 | 46.5 | 42.4 | 46.5 |
| 3 | 20 | 0.2 | 4.0 | 59.3 | 62.0 | 59.3 |
| 4 | 100 | 0.2 | 10 | 62.6 | 65.3 | 62.6 |
| 5 | 60 | 0.07 | 7.0 | 56.4 | 53.4 | 56.4 |
| 6 | 20 | 1.0 | 10 | 28.9 | 31.6 | 28.9 |
| 7 | 60 | 0.6 | 10.9 | 16.1 | 11.9 | 16.1 |
| 8 | 60 | 1.13 | 7.0 | 95.1 | 92.1 | 95.1 |
| 9 | 60 | 0.6 | 3.1 | 53.2 | 50.0 | 53.2 |
| 10 | 100 | 1.0 | 4.0 | 25.6 | 28.3 | 25.6 |
| 11 | 60 | 0.6 | 7.0 | 69.9 | 61.8 | 60.2 |
| 12 | 60 | 0.6 | 7.0 | 43.6 | 61.8 | 60.2 |
| 13 | 60 | 0.6 | 7.0 | 58.8 | 61.8 | 60.2 |
| 14 | 60 | 0.6 | 7.0 | 59.3 | 61.8 | 60.2 |
| 15 | 60 | 0.6 | 7.0 | 69.3 | 61.8 | 60.2 |
| Parameter | SoS | dF | MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| 320.045 | 1 | 320.045 | 2.82832 | 0.1534 | ||
| 748.845 | 1 | 748.845 | 6.61773 | 0.0499 | ||
| 688.205 | 1 | 688.205 | 6.08184 | 0.0568 | ||
| 460.21 | 1 | 460.21 | 4.06699 | 0.0998 | ||
| 1848.2 | 1 | 1848.2 | 16.333 | 0.0099 | ||
| 171.512 | 1 | 171.512 | 1.51569 | 0.2730 | ||
| 74.4126 | 1 | 74.4126 | 0.6576 | 0.4543 | ||
| 235.768 | 1 | 235.768 | 2.08354 | 0.2085 | ||
| 1937.76 | 1 | 1937.76 | 17.1244 | 0.0090 | ||
| ANOVA | ||||||
| Model | 5121.4 | 9 | 569.045 | 5.02879 | 0.0450 | significant |
| Residual | 565.787 | 5 | 113.157 | |||
| Lack of Fit | 110.559 | 1 | 110.559 | 0.97146 | 0.3801 | not significant |
| Pure Error | 455.228 | 4 | 113.807 | |||
| R2 | 0.9005 | |||||
| Adjusted R2 | 0.7214 | |||||
| R | 0.9487 | |||||
| Adequate precision | 9.096 |
| Pointer | RSM | ANFIS |
|---|---|---|
| R | 0.9488 | 0.9591 |
| R2 | 0.9002 | 0.9200 |
| Adjusted R2 | 0.8639 | 0.8908 |
| RMSE | 6.1575 | 5.5090 |
| MAE | 4.7057 | 2.5120 |
| MRPD | 10.3616 | 4.5950 |
| HYBRID | 103.0904 | 74.1853 |
| 12.3708 | 8.9022 |
| Optimization Technique | Cr(VI) Concentration (mg/L) | Sorbent Amount (g/L) | pH | Predicted Percentage Removal (%) | Observed Percentage Removal (%) |
|---|---|---|---|---|---|
| RSM | 99.10 | 1.00 | 9.30 | 94.95 | 97.14 0.32 |
| RSM–GA | 50.46 | 1.12 | 6.27 | 95.28 | 98.28 0.67 |
| RSM–ACO | 35.68 | 1.09 | 5.94 | 97.72 | 98.05 0.05 |
| ANFIS–GA | 40.31 | 1.12 | 5.85 | 97.92 | 98.63 0.82 |
| ANFIS–ACO | 38.14 | 1.33 | 4.35 | 99.80 | 99.92 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yusuff, A.S.; Ishola, N.B.; Gbadamosi, A.O.; Epelle, E.I. Modeling and Optimization of Hexavalent Chromium Adsorption by Activated Eucalyptus Biochar Using Response Surface Methodology and Adaptive Neuro-Fuzzy Inference System. Environments 2023, 10, 55. https://doi.org/10.3390/environments10030055
Yusuff AS, Ishola NB, Gbadamosi AO, Epelle EI. Modeling and Optimization of Hexavalent Chromium Adsorption by Activated Eucalyptus Biochar Using Response Surface Methodology and Adaptive Neuro-Fuzzy Inference System. Environments. 2023; 10(3):55. https://doi.org/10.3390/environments10030055
Chicago/Turabian StyleYusuff, Adeyinka Sikiru, Niyi Babatunde Ishola, Afeez Olayinka Gbadamosi, and Emmanuel I. Epelle. 2023. "Modeling and Optimization of Hexavalent Chromium Adsorption by Activated Eucalyptus Biochar Using Response Surface Methodology and Adaptive Neuro-Fuzzy Inference System" Environments 10, no. 3: 55. https://doi.org/10.3390/environments10030055
APA StyleYusuff, A. S., Ishola, N. B., Gbadamosi, A. O., & Epelle, E. I. (2023). Modeling and Optimization of Hexavalent Chromium Adsorption by Activated Eucalyptus Biochar Using Response Surface Methodology and Adaptive Neuro-Fuzzy Inference System. Environments, 10(3), 55. https://doi.org/10.3390/environments10030055







