Recent Developments in Sonic Crystals as Barriers for Road Traffic Noise Mitigation

Abstract

Noise barriers are the most widespread solution to mitigate noise produced by the continuous growth of vehicular traffic, thus reducing the large number of people exposed to it and avoiding unpleasant effects on health. However, conventional noise barriers present the well-known issues related to the diffraction at the edges which reduces the net insertion loss, to the reflection of sound energy in the opposite direction, and to the complaints of citizens due to the reduction of field of view, natural light, and air flow. In order to avoid these shortcomings and maximize noise abatement, recent research has moved toward the development of sonic crystals as noise barriers. A previous review found in the literature was focused on the theoretical aspects of the propagation of sound through crystals. The present work on the other hand reviews the latest studies concerning the practical application of sonic crystal as noise barriers, especially for road traffic noise mitigation. The paper explores and compares the latest developments reported in the scientific literature, focused on integrating Bragg’s law properties with other mitigation effects such as hollow scatterers, wooden or recycled materials, or porous coating. These solutions could increase the insertion loss and frequency band gap, while inserting the noise mitigation action in a green and circular economy. The pros and cons of sonic crystal barriers will also be discussed, with the aim of finding the best solution that is actually viable, as well as stimulating future research on the aspects requiring improvement.

1. Introduction

Despite the prescriptions of noise maps and action plans [1] in 2002, the recent European Environmental Noise Directive revision [2] reported that noise pollution continues to be a major health problem in Europe. About 100 million people in the 33 European Union (EU) member states are exposed to harmful road traffic noise levels exceeding 55 dB(A) of L_den, and 32 million are exposed to a noise level higher than 65 dB(A) of L_den. Even if not considered the most annoying, road traffic is the most diffused noise source, to the point that it is used as a reference for estimating other sources’ limits [3]. The continuous growth of vehicular traffic and the large number of people exposed to it have made sleep disturbance [4,5] and annoyance [6] caused by road traffic noise important issues observed both by citizens and control bodies. Studies have shown that exposure to road traffic noise can induce further adverse health effects, including cardiovascular effects [7,8], learning impairment [9,10], and hypertension ischemic heart disease [11].

Road traffic noise exposure can be reduced by applying mitigation strategies on the sources, such as improving vehicle engine and design, reducing tire/road emission by using special surfaces [12], or by controlling vehicle flow in restricted areas. Such actions are not always affordable or suitable, or can even be insufficient, and therefore the construction of noise barriers represents the most widespread solution to further reduce the exposure to those affected (i.e., receivers). The barriers are usually hermetic and sufficiently dense to shield noise along the propagation path from source to receiver. From a spectral point of view, traditional barriers have a good absorption behavior which is almost homogeneous over the A-weighted normalized traffic emission spectrum, generally between 100 Hz and 5 kHz and with a peak centered at 1 kHz [13].

Unfortunately, an obstacle to the effectiveness of traditional barriers is the diffraction at the edges of the barrier, which allows part of the sound energy to reach the receiver, thus reducing the net attenuation benefit. The insertion loss (IL), expressed in dB, represents the difference between the sound pressure level measured at the receiver with or without the barrier, and is generally used as an indicator for abatement efficacy.

Along with the problem of diffraction, installing an acoustic barrier has significant disadvantages that make this mitigation action not always welcome. Some complaints regarding their installation were raised due to the size of the structures, since a barrier of variable length and height has a strong impact that limits the field of view and reduces the natural light for those affected. In addition, even for innovative solutions [14], the presence of barriers prevents the normal air flow, hindering cooling processes during summer, and at the same time alters local wind profile creating turbulence. It has been shown how fluctuations of ±2 m/s in wind speed can even reduce by 5–7 dB the IL in frequency bands above 800–1000 Hz [15], thus decreasing the effectiveness of acoustic restoration intervention. Furthermore, a conventional noise barrier without any absorptive treatment can reflect sound energy back across the roadway to receivers on the opposite side [16].

In order to minimize the above-mentioned disadvantages while simultaneously maximizing noise abatement, research has moved in recent years toward sonic crystals.

An accurate evaluation of the propagation method through crystals has been already performed by Gupta [17] and Morandi et al. [18]. Sonic crystals are artificial periodic structures, where the scatterers have a high acoustic impedance with respect to the medium in which they are placed [17]. The periodic arrangement of scatterers causes a frequency-selective sound attenuation, known as band gap. The behavior of wave propagation in periodic structures is described by Bloch’s theorem, which was derived for the electronic wavefunction in perfect crystals. The electronic wavefunction $\psi \left(r\right)$ can be written in the form: $\psi \left(r\right)=e^{ikr}u\left(r\right)$, where u(r) is a function with the same periodicity as the atomic structure of the crystal. The solution of the Bloch wave for a periodic potential leads to the formation of bands of allowed and forbidden energy regions, called band gaps. The same principle can be applied to acoustic waves passing through periodic structures. The main difference between atomic structures and sonic crystals is the size of the scatterers, since it is known that the wavelength of the propagating wave and the size and spacing of scatterers must be of the same order of size, in order to produce the destructive interference which creates the band gap.

Considering a sound pressure represented by $p\left(x,t\right)=\Re \left[P\left(x\right)e^{i\omega t}\right]$, Bloch’s theorem restricts the function P(x) to the form: $P\left(x\right)=e^{ikx}\varphi \left(x\right)$, where $\omega$ is the angular frequency and k is the wave vector.

As the wavenumber k is varied, the solution of the wave equation yields a band structure for the different wave frequencies within the sonic crystal, with the formation of band gaps where no frequency is allowed.

The actual band structure depends on the geometric configuration of the scatterers. The works presented in [17,18], which this study refers to for insights on the theoretical aspects, offer more detailed mathematical calculations, whereas this study focuses on recent advances in the application of sonic crystal as noise barriers, especially for road traffic noise mitigation. The latest developments reported in the scientific literature will be shown and compared in order to find the best solution that is actually feasible; in addition, the difficulties that are limiting their current widespread use will be discussed.

2. Sonic Crystals as Acoustic Barriers

Years after the exhibition of Eusebio Sempere’s sculpture in Madrid in 1995, which is recognized as the first experimental work on noise attenuation from a periodic structure [19], the scientific community discovered how sonic crystals could actually be used to reduce noise pollution and research on the application of 2-D sonic crystals has increased considerably [20,21,22].

From a physical point of view, sonic crystals are non-homogeneous structures created by the arrangement of scatterers in a periodic configuration with a square, rectangular, or triangular pattern. Three different macro-categories can be distinguished: parallelepipeds, such as steel sheets, periodically arranged in a medium such as air or water are known as 1-D sonic crystals; periodically placed cylinders are called 2-D sonic crystals; and spheres periodically arranged in a volume, like a cube, are called 3-D sonic crystals. As shown in the available literature, only 2-D crystals have had a practical application, currently making them the most widespread, and this work will therefore deal exclusively with such crystals. The scatterers must be made of a material with high acoustic impedance with respect to the medium in which they are positioned, such as acrylic cylinders in air or steel plates in water [23,24].

This particular periodic arrangement of the scatterers allows the sonic crystals to acquire sound attenuation properties in a specific range of frequencies, known as the band gap. This attenuation is achieved by the destructive interference of the sound wave due to the scatterers in the band gap and the attenuation of the propagation wave caused by the evanescent effect [25]. Indeed, when an acoustic wave interacts with a periodic structure, its spectral characteristics change and only some of the incident wave frequencies pass through the structure without being attenuated [26]. The size of the scatterers and their spacing must be of the order of the incident wavelength so that the periodic structure can interact with the incident wave. The physical mechanism governing this phenomenon is Bragg’s law for destructive interference of a wave with incident glancing angle $\theta$, in which the central frequency of the band gap f_BG is determined by the lattice constant α, that is, the distance between two lattice scatterers and the speed of sound in the medium c: $f_{BG}=\frac{c}{2\alpha \sin \theta }$. The size of the band gap is influenced by the following parameters:

• the density ratio M, that is, the ratio between the densities of the scatterers’ material and that of the medium in which they are immersed;
• the filling factor ff, expressing the ratio between the volume occupied by the scatterers and the total volume of the crystal;
• the lattice designs.

The wavelength of a sound wave corresponding to the entire spectrum of audible frequencies (20 Hz–20 kHz) is of the order of 17 m–0.017 m; therefore, sonic crystals consisting of a few scatterers arranged periodically can already determine a significant attenuation of the sound in the band gap region. However, the setup requires a careful analysis of the parameters in order to match the band gap with the most disturbing frequencies.

Most of the initial works have studied how to optimize the spatial arrangement of the cylinders and the filling factor, obtaining an IL up to 25 dB [27,28,29]. Sanchis et al. [30], on the other hand, have studied the sound pressure field reflected by the sonic crystals, finding that the stationary wave ratio increases in the same frequency range in which stop-band phenomena occur. The reflection properties have been further investigated and connected to the sonic crystal band structures [31]. At present, most of the research is focused on studying different methods to increase the Bragg’s law frequency attenuation range, by adding to the sonic crystal particular absorbent materials [32] or using Helmholtz resonators as scatterers [33].

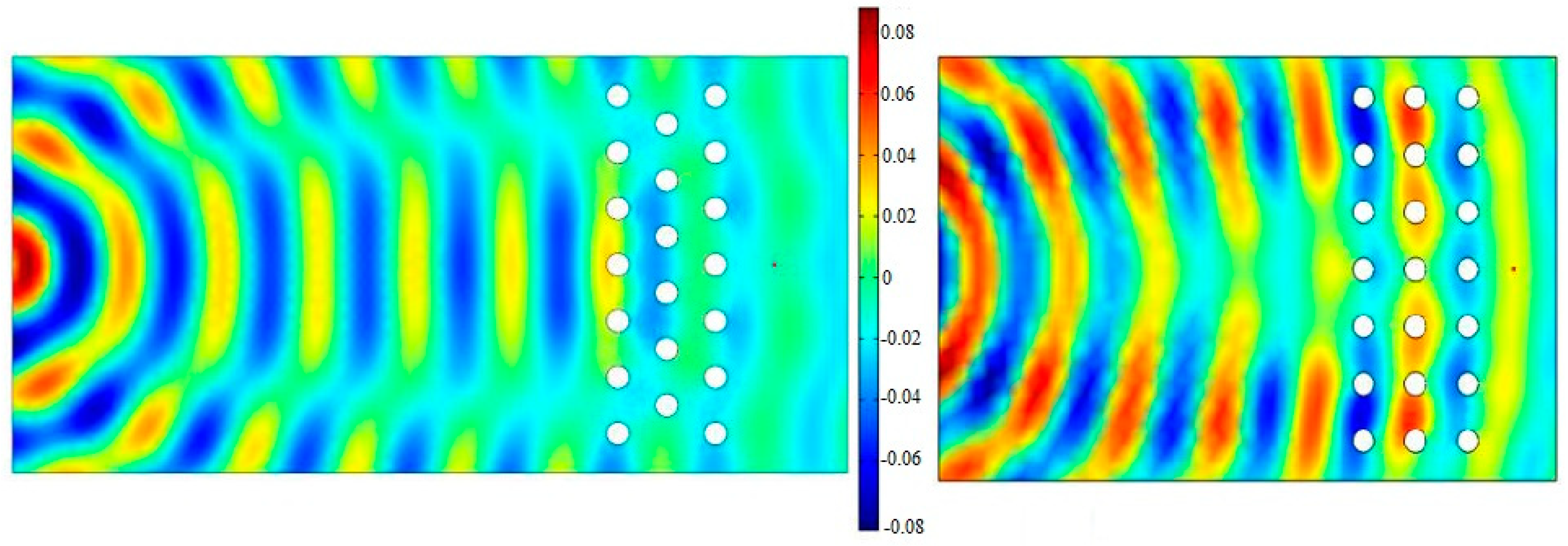
3. Parameters Influencing Insertion Loss and Band Gap

This chapter reports the choices made in some studies in order to optimize the construction of a barrier that is effective for road noise [34]. Even though several configurations of sonic crystals are currently available, their selection depends on the intended use. Numerous studies have decreed the triangular typology as the best choice for road traffic noise, compared to the square or rectangular ones, because it better responds to the change in incidence angle of a moving noise source [35,36,37,38]. However, the sound pressure level map in Figure 1 [39] also confirms this assumption for a steady point source.

The distance of receivers from the barrier is also excluded from the parameters analyzed because it is obvious that receivers further away from the barrier will typically be less protected from the incident wave field and will receive a stronger contribution of diffracted energy over the top of the barrier [40].

3.1. Shape of Scatterers

The first studies on scattering phenomena refer to rigid circular cylinders, but later studies emerged using different diffuser shapes: squares [41], squares rotated along the vertical plane, with a consequent negative refraction [42], rectangular [43], or triangular [44,45]. Different studies used different boundary conditions, making a direct comparison difficult. Chong [39] performed a Finite element Method (FEM) analysis in which he assessed the IL of different sonic crystal barriers formed by scatterers of various shapes and orientation.

The results in Figure 2 show how the triangular shape with alternately turned faces has the highest absorption peak, but that the band gap results at frequencies above 2 kHz can be suitable for the mitigation of industrial sources with a narrow noise emission spectrum. In the road traffic noise frequency band [46], the scatterers’ shape bringing the greatest IL is the elliptical one with the long side facing the source. However, the most used type is the circular one, which shows an IL of less than 5 dB in frequencies around 1 Hz with respect to the elliptical one.

3.2. Diameter of Scatterers

The size of scatterers seems to play a key role in the attenuation [47], although quantitatively it seems to depend on the other parameters such as number of rows or lattice shape. For square or triangular lattices, a smaller cylinder is best for three rows, whereas attenuation seems to worsen in the case of two rows. For square-based lattices, frequency bands with a negative IL emerge, creating a mechanism of noise amplification not occurring in a triangular lattice. When source and receiver are at the same position with respect to the barrier, a square grid could cause the sound to propagate directly, as a sort of waveguide effect. The triangular lattice can avoid this issue.

Martins et al. [35] varied the dimension of scatterers by keeping the lattice constant and fixed at 0.40 m. Due to Bragg’s principle, the changes to the dimensions of the cylinders can be limited, thus in the order of 0.05 m. Moreover, scatterers can be made of natural resources, such as logs, meaning that cylinders can have a non-uniform diameter due to manufacturing defects. Therefore, small variations in the randomly arranged diameter of the lattice were studied to produce a substantial difference in terms of sound attenuation provided by the entire structure. With a lattice constant of 0.40 m and random variations of the order of 10% and 20% of the reference diameter (0.20 m), negligible differences in attenuations were reported. In fact, even when a maximum variation of 20% occurs in some of the cylinders, the calculated insertion loss values are only slightly modified, with maximum variations of less than 0.5 dB in all frequency bands. The IL results obtained by Martins et al. [35] are shown in Figure 3.

Jean and Defrance [36] also confirm that better attenuations can be obtained by doubling the scatterer diameter D from 0.15 to 30 m, rather than doubling the filling factor ff (Figure 4).

3.3. Number of Scatterers

A sonic crystal barrier must be parallel to the source, especially if the latter is linear (like roads and railways). Rare cases of sonic crystal barriers with a radial arrangement for point sources are present in the literature, but are not applicable to linear sources [48]. The length of the barrier is site-dependent and therefore is not concerned by the present analysis, which is dedicated to the number of rows along the propagation line between source and receiver.

Using 0.2 m wooden cylindrical scatterers with 0.4 m of lattice constant, Martins et al. [35] have shown that, at road traffic frequencies, two rows of scatterers are better than three. However, it would be advisable to have a barrier of at least 40 scatterers to avoid diffraction effects at the edges (Figure 5). Morandi et al. [49] showed that increasing the number of rows leads to an increase in the sound insulation index in the frequency ranges between 600 and 1000 Hz for square-based lattices. The benefit of having multiple scatterer files, however, already saturates after the fourth row. It is reasonable to assume that four rows are the maximum number of scatterers needed for a sonic crystal barrier, as also confirmed by Godinho et al. [40].

However, for cylinders of small size (0.04 m) in a square lattice, Jiang et al. [50] suggest that there exists a relationship between the number of required rows and the size of the cylinders, just as there is a relationship between cylinder size and band-gap frequency due to the Bragg effect. Their results showed an IL that increases with the number of rows, at least up to seven rows and then flattened out by eight.

3.4. Filling Factor

Santos et al. [51] studied the effect on IL produced by different spacings between the scatterers and the repositioning of a central row or some random scatterers on scale models (Figure 6 and Figure 7). The rectangular lattice, in all cases, shows an almost constant IL, but some absorption peaks change their frequency. The triangular lattice, on the other hand, does not demonstrate the same property and results in a very effective type of lattice only if it is entirely structured. On the contrary, configurations with a smaller number of scatterers can be chosen with the rectangular lattice, thus reducing the economic load without however having a significant loss of IL, as also confirmed by Koussa et al. [52].

In addition, Martins et al. [35] studied the influence of spacing between the scatterers by varying the lattice constant between 0.5, 0.4, and 0.3 meters. For a triangular lattice, no significant changes resulted when two rows were used, whereas the choice of the lattice constant become important for three rows with respect to barrier effectiveness. In fact, a lattice constant of 0.3 m is the best solution at 630, 1250, and 1600 Hz, but it becomes almost transparent to those at 800 and 1000 Hz. Thus, for sources like road traffic a lattice constant of 0.4 or 0.5 m is suggested.

Additionally, Rubio et al. [43] observed that the attenuation peak shifts toward higher frequencies as the distance between scatterers increases, due to the destructive interference between the propagating and evanescent waves [53].

Evidently, for equal sound attenuation, a higher lattice constant is preferable due to the consequent higher visibility and air flow passage.

4. Recent Applications

Despite all the acoustic attenuation properties previously shown, the use of sonic crystals as noise barriers is still not widespread. An historical issue for their application in a real case scenario is the incidence angle of the sound waves.

Most of the studies available in the literature were performed using point sources, such as loudspeakers, which can represent real sources such as industrial sources [54], but not roads or railways, which are schematized by linear sources. A point-type source, in fact, emits acoustic waves with a spherical symmetry; conversely, linear sources possess a cylindrical symmetry. For point sources, the source–receiver relative position is very relevant and moving the source from the edge to the center of the barrier can reduce its IL by 8 dB [35] due to the waveguide effect. As previously mentioned, the effect becomes less evident for triangular lattices. Indeed, a less ordered but more irregular lattice reacts better to a change in the direction of incidence acoustic waves as compared to a lattice with a regular base [36].

To the best of the authors’ knowledge, no studies on this subject have yet been carried out on real-scale barriers, but studies on scaled barriers have shown that this effect is absent for linear sources [36]. This certifies the sonic crystal barriers as very effective for mitigating noise produced by roads or railways.

Current research on sonic crystals focuses on integrating their acoustic abatement brought about by Bragg’s law with other mitigation effects, not only in order to increase IL intensity, but also to broaden the frequency band gap. This chapter summarizes these new research studies.

4.1. Hollow Scatterers

Using thin resonant cylinders with elastic shells, hollow cylinders, or a combination of both can result in a sonic crystal whose IL benefits from both Bragg’s law and the individual scatterers’ resonance. A series of thin elastic shells exposed to atmospheric agents is a weak structure and therefore not suitable for use as an outdoor sound barrier. However, a split-ring resonator (SRR) [55,56] can be used as an alternative that increases the IL in the low frequencies if the scatterers’ resonance frequencies are correctly set so as to be below the Bragg band gap. Helmholtz resonators, a particular type of resonator, consist of a hollow container for air with a small opening that causes a coupling between the inside and outside air [57]. The size must be small compared to the wavelength. Attenuation is given by the combination of radiation loss and viscous losses due to friction.

In his studies, Chong [39] found the best setting in polyvinyl chloride (PVC) cylindrical SRRs with a 0.11 m diameter, a 3 mm thickness, and a 12 mm opening in the direction of the sound source. As presented in Figure 8, the sonic crystal’s IL has been compared with a similar configuration having solid scatterers, resulting in clear improvements in the frequency band near 1.2–2 kHz and a worse performance between 500 Hz and 800 Hz. As suggested by the same author, the best performance frequency range can be tuned by changing the size of the cylinders and using narrower holes (0.004 m) in the outer cylinders.

Cavalieri et al. [58] used a locally resonant sonic crystal made of wood that, exploiting both the multiple coupled resonances and the Bragg band gaps, obtained good absorption results even if the source studied was railway noise.

4.2. Scatterers Coated with Porous Material

An absorbing surface can dissipate the sound energy of an incident wave. Thus, the acoustic absorption coefficient of the scatterers is a factor that can influence the IL of the entire sonic crystal. The higher the acoustic absorption coefficient is, the greater the possibility that the IL will result in the frequency bands between 600 and 1600 Hz [35]. This effect can also mitigate the waveguide effect in square lattices when the source and receiver are aligned. Then, the choice of the material with which the cylinders are coated is an important parameter.

Sánchez-Dehesa et al. [59] worked on noise barriers of sonic crystals exploiting the sound absorption properties of porous materials. In their study, a rigid core was surrounded by a cylindrical shell of recycled rubber offering additional sound absorption to the multiple scattering in a periodic structure [60,61]. Three 1 m high rows of 0.08 m diameter scatterers in a triangular configuration were analyzed with 0.02, 0.03, or 0.04 m thickness of porous shell. As presented in Figure 9, the different scenarios were also compared to a conventional noise barrier with the same dimensions of 0.30 m and 1 m high.

The effectiveness of the porous shell can be seen at all frequencies if compared to a sonic crystal where the scatterers are not surrounded by the porous shell [62]. Moreover, in some frequencies, the IL exceeds even that of the conventional noise barrier. The attenuation increase carried by the 0.02 m porous layer shell over a 0.04 m metal core is three times greater than the attenuation obtained by the barrier with the metal core alone. The work of Sánchez therefore shows even better results than those obtained by a similar study performed by Umnova et al. [60], probably because of the materials and settings used, such as cylinder dimensions and lattice type. In fact, Umnova et al. used a very small-scale model with cylinders composed of an aluminum core with a 0.0635 m radius and a wool felt shell of 0.00175 m, arranged in three rows of a lattice with a square base and a lattice constant of 0.015 m.

4.3. Coupled Barriers

Koussa et al. [52] combined all the effects previously described and evaluated the IL of a sonic crystal coupled with a traditional barrier. In situations with sufficient space to insert a sonic crystal in front of a barrier, the coupled solution should increase the absorption of a normal barrier with the improvements brought by Bragg scattering, absorption of porous materials, and Helmholtz resonators. The barrier shown in Figure 10 is composed of two different sonic crystals coupled to a traditional 3 m high and 0.2 m deep barrier. The first rows of scatterers have a diameter of 0.05 m, a depth of 0.3 m, and a lattice constant of 0.085 m. The second rows are 0.5 m deep, with a lattice constant of 0.17 m and a scatterer diameter of 0.13 m. This different configuration of the two sonic crystals leads to attenuation in two different frequency bands (1000 and 2000 Hz). This barrier has been configured with three different types of scatterers and their IL has been compared to that of the single conventional barrier. The first configuration uses rigid scatterers, the second uses resonant cavities, and the third uses resonant cavities internally coated with glass wool, an absorbent material. Unlike the results reported by Sánchez-Dehesa et al. [59], the absorption of the barrier increases with the size of the opening.

The improvement of the attenuation of the composite barrier, compared to the traditional barrier, can reach 6 dB(A). Furthermore, the amplifying effects on the opposite side of the mitigation area due to reflection on the rigid wall are attenuated.

4.4. Low-Height Barriers

The recent attention of studies on acoustic barriers has been focused on reducing their visual impact by decreasing their height [63,64]. In urban environments, in fact, pedestrians and cyclists, quiet areas, and residents living in the lower floors of buildings can be protected from road, tram, or rail noise by using only 1 m high barriers if properly positioned very close to the source.

Koussa et al. [65] studied a 1 m high sonic crystal barrier made of rows of hollow cylinders of different sizes and lattice constant. The scatterers in the first row had a diameter of 0.05 m and a lattice constant of 0.085 m, while those in the second row had a diameter of 0.14 m and a lattice constant of 0.17 m. The diameter of the scatterers in the last row was 0.20 m; the scatterers were rigid and without space between them. In this configuration, the solid last row would not help to solve the problem of air flow transit and visibility for a standard height barrier, but a row of 1 m high rigid cylinders with no space between them gives the benefit that the beam transmitted is more attenuated than diffracted over the entire frequency range, without actually hindering sunlight and air flow.

The authors studied the case in which the diffusers of the two periodic bands were hollow cylinders or absorbing cavities internally coated with glass wool. With the help of numerical simulations, a significant efficiency of the sonic crystal barriers has been shown to significantly attenuate traffic noise in an urban environment, as shown in Figure 11.

For exposure to vehicular traffic noise, the IL resulted in 9.5 dB(A) with hollow scatterers and 11.9 dB(A) when the inside of the cavities was covered by an absorbing material. Both values are higher than those of the standard low-height barrier.

4.5. Green Barriers

One last practical application that has taken place in the scientific field in recent years is the use of wooden materials as scatterers in a sonic crystal. This choice would fully include the sonic crystals in the concept of green and circular economy, with recycled or directly available on-site materials.

In their studies, Godinho et al. [66], Amado-Mendes et al. [38,67], and Jean and Defrance [36] used wooden logs as scatterers in a barrier of sonic crystals. Some used on-scale prototypes, whereas others tested real dimension sonic crystal barriers made of timber logs. All studies agreed about the positive results obtained by using these materials and that further improvement seems possible by finding the right optimization of the periodic arrangements and log diameters.

Other authors have even studied how whole trees can attenuate noise if properly distributed in space. Martínez-Sala et al. [68] showed that trees organized in a periodic array produce attenuation at low frequencies. This attenuation is not due to the ground effect but to the destructive interference of the scattered waves in the crystal. A periodic array of trees can be used as a green acoustic barrier with IL dependent on the filling fraction and frequency behavior dependent on the type of lattice used. Gulia and Gupta [69] obtained a reduction for noise impact by modelling rows of Thuja trees arranged in a periodic pattern on the sides of a road. Significant sound attenuation, with a maximum of 19 dB, has been obtained in frequencies up to 500 Hz, coherently with what was reported by Martínez-Sala et al. [68], showing that properly arranged trees can be used to mitigate noise pollution while helping to reduce air pollution and vibrations to receivers [70]. Lagarrigue et al. [71], by using a fast-growing plant, applied the principle of Helmholtz resonators to the green barriers. With hollow bamboo rods drilled between each node, it is possible to gain an additional band gap in the low-frequency range, but real-scale applications are needed for a proper quantification.

5. Discussion

As previously reported, rigid scatterers made of wood, aluminum, or PVC have been used in the literature as elements of sonic crystals in order to exploit Bragg’s law and create acoustic barriers. Parameters affecting this absorption have been discussed, showing that different authors do not completely agree on all settings and research teams are following different approaches. In particular, not many studies have been conducted on real-scale barriers applicable to real road noise impact mitigations, thus research on this aspect should be encouraged, instead of on-scale studies.

Recent developments have shown how sound crystals in mixed materials improve their frequency response thanks to the use of porous materials, solving the problem of the angular dependence of acoustic attenuation and increasing the absorption frequency range with the reflection and absorption properties of the materials themselves. Additional improvements can be obtained using scatterers with Helmholtz resonant cavity shape, allowing the sound to penetrate into the periodic structure elements with consequent additional sound absorption properties that lead to a new attenuation band in a lower frequency range. The depth of the sonic crystal can be also reduced this way, while making the noise crystals relatively more efficient for some frequency bands.

Some studies reported that sonic crystal barriers can have absorption peaks even higher than conventional barriers in some frequencies, but they are generally less efficient in the other frequencies. In order to optimize the absorption, some studies developed a coupled barrier made of rows of sonic crystals, some with different sizes, and a conventional noise barrier. However, this solution appears more like an improvement of a standard barrier rather than an improvement of a sonic crystal barrier because it does not solve the issues for which they were created: reducing the visual impact on receivers and allowing air flow through it.

Table 1. Comparative analysis of insertion loss (IL) obtained in different studies. d_r is the distance of IL evaluation from the barrier, D is the scatterer diameter (or side), and α is the lattice constant.

Authors	IL (dB)				dr (m)	Scatterer’s Shape and Material	D (m)	Lattice’s Shape and Depth (m)	α (m)	Hollow	Porous	Note
	250 Hz	500 Hz	1 kHz	2 kHz
Morandi et al. [49]	-	9	15	0	0.4	Polyvinyl chloride cylinders	0.2	Square 0.8	0.2	No	No	Real dimension
Morandi et al. [80]	-	9	15	18	0.25	Polyvinyl chloride cylinders	0.08	Square 0.96	0.2	Yes	No	Different configurations
Martins et al. [35]	-	5	9	9	1	Rigid cylinders	0.2	Triangular 1.4	0.4	No	Yes outside	Numerical simulations
Santos et al. [51]	0	12	10	10	0.65	Polyvinyl chloride cylinders	0.2	1.4	0.2	No	No	In scale; various shapes
Amado-Mendes et al. [38]	7	5	15	-	0.5	Wooden cylinders	0.1 0.2	Square 1.0	0.1	No	No	Real dimension
Jiang et al. [50]	11	2	0	15	0.8	Steel cylinders	0.04	Square 0.75	0.08	No	No	Non-real scale
Chong [39]	3	0	20	-	0.05	Polyvinyl chloride cylinders	0.11	Square 0.7	0.16	Yes	Yes	Non-real scale, resonant cavities
Jean and Defrance [36]	7	10	9	9	10	Wooden cylinders	0.3 0.7	Rectangular 2.1	0.40	No	No	Cylinders of 2 different diameters
Sánchez-Dehesa et al. [59]	3	5	16	0	1	Steel cylinders covered by porous material	0.04 0.08	Square 0.58	0.11	No	Yes	Porous material outside
Koussa et al. [52]	15	20	25	30	0.4	Aluminum cylinders	0.05 0.13	Rectangular, 1st section 0.3 and 2nd section 0.5	0.08 0.17	No	No	2 noise crystals combined to a conventional noise barrier
Koussa et al. [52]	15	23	25	33	0.4	Aluminum cylinders	0.05 0.13	Rectangular, 1st section 0.3 and 2nd section 0.5	0.08 0.17	Yes	No	2 noise crystals combined to a conventional noise barrier
Koussa et al. [52]	15	26	30	33	0.4	Aluminum cylinders	0.05 0.13	Rectangular, 1st section 0.3 and 2nd section 0.5	0.08 0.17	Yes	Rock wool	2 noise crystals combined to a conventional noise barrier
Koussa et al. [65]	14	10	13	14	0.4	Aluminum cylinders	0.05 0.13	Rectangular, 1st section 0.3 and 2nd section 0.5	0.08 0.17	Yes	No	Low-height barrier of 3 different sections
Koussa et al. [65]	15	10	13	14	0.4	Aluminum cylinders	0.05 0.13	Rectangular, 1st section 0.3 and 2nd section 0.5	0.08 0.17	Yes	Rock wool inside	Low-height barrier of 3 different sections
Lee et al. [57]	1.5	8	10	3	1	Aluminum parallelepiped	0.04	Square 0.37	0.1225	Yes	No	Outdoor measurements, Helmholtz resonator
Godinho et al. [66]	4	5	15	18	0.5	Maritime pine timber logs	0.1 0.2	Square 1.0	0.1 0.2	No	No	On field measurements
Cavalieri et al. [58]	2	20	12	18	0.45	Wooden rods of square cross-section	0.05	Square 0.3	0.05	Yes	No	Helmholtz resonator

summarizes the design and IL obtained in the best settings of the studies analyzed, excluding those using a very tiny scale, such as [72,73,74,75,76,77,78,79].

6. Conclusions

The solutions most commonly used to mitigate the noise produced by infrastructures is to install conventional noise barriers, which have a valid mitigation effect but prevent air flow and limit the view of those affected. The present paper carried out an analysis of the recent literature concerning sonic crystals as noise barriers especially for road traffic noise reduction.

Starting from the first simple structures composed of rigid cylinders arranged in a regular lattice in order to exploit the Bragg diffraction principle, this work studied the influence that cylinder parameters (such as shape, number, diameter, and absorption coefficient) and crystal settings (such as lattice constant, possible presence of holes, and incidence angle of the sound waves) have on the sonic crystal’s insertion loss (IL).

Furthermore, it has been shown how current research is focused on integrating the Bragg’s law abatement properties to the absorption properties of some materials. Thus, scatterers have been externally coated with porous materials, or they have been produced with Helmholtz resonant cavities in them or with cavities filled with absorbent material. Finally, the sonic crystals have also been coupled to a standard barrier to expand the insertion loss to some specific frequencies, including a low-height variant for particular urban applications. Some authors have also shown that the reduction of some random scatterers in the lattice does not compromise the IL, but allows a saving in the construction.

The analysis showed that sonic crystals have the benefits of being effective in noise abatement, while ensuring the possibility of passing air and light through them. Some authors have even proposed the application of a special window as mitigation at source for industrial noise [81,82]. The possibility of using natural materials as scatterers, such as wood derivatives or even whole wooden logs [66], or rubber powder as an absorbent material can also push this product into the actual “green” policy and circular economy.

However, the comparative analysis carried out in order to find the best design for road traffic noise abatement purposes showed that, in some cases, the results of an author do not correspond to those of others. Moreover, an ideal sonic crystal barrier set-up has not yet emerged, but the optimization of the barrier at each site plays a key role [76].

Despite all the acoustic attenuation properties previously shown, the use of sonic crystals as noise barriers is still struggling to become widespread. Indeed, real case scenarios demand a tribute in terms of space usage, which is higher than a conventional noise barrier and not always affordable along roads. Moreover, in practical cases where the sonic crystals are installed next to a road, they can accumulate much dirt or many animal remains between the cylinders under normal use. In order to preserve hygiene and their effectiveness, a constant cleaning is necessary, representing an increased maintenance cost.

The most important limitation to the current widespread use of sonic crystals is however represented by the effective area of mitigation behind them. In fact, all the works presented were carried out close to the barrier, whereas studies showing how sonic crystals can be effective at greater distances are needed. In order to expand the mitigation area to residential distances, cylinder height could be increased, but this would make it difficult to secure the foundations. In order to overcome this issue, it could be possible to integrate sonic crystals over natural or artificial bumps, which would make their use safer, more effective and visually acceptable, thus obviously increasing the space required for their installation. Another possible solution to widening their range of action could be to integrate a mitigation aimed at some frequencies with a more broadband intervention, for example, by changing road pavements into less noisy ones, such as rubber asphalts. In this way, the mitigation would be even more oriented toward a green and circular economy, by recycling old tires for both asphalts and porous materials to be placed in scatterers, perhaps made of local wood or PVC from recycled materials.