Modern Optimization and Simulation Methods in Managerial and Business Economics: A Review

Abstract

Managerial and Business Economics (ME/BE) aims at using quantitative and computational methods to make an efficient (ideally optimal) assignment of the scarce resources owned by firms and organizations. In the current global market, characterized by a fierce competition, an optimal use of the available resources is more important than ever for guaranteeing the economical sustainability of organizations and enterprises of any size. Heuristic optimization algorithms and simulation methods have been successfully employed to analyze and enhance complex systems and processes in a myriad of ME/BE-related fields. This paper reviews recent works on the use of these methodologies in competitive markets, as well as in imperfect markets considering externalities. The paper also discusses open challenges and how state-of-the art methods combining optimization, simulation, and machine learning can contribute to properly address them.

1. Introduction

Managerial Economics (ME) is an interdisciplinary discipline that aims at efficiently assign scarce resources to achieve a managerial goal, either in an enterprise or an organization (Baye et al. 2006). ME, which is sometimes referred to as Business Economics (BE), combines concepts and methods from different knowledge areas, including: Economics (especially Microeconomics), Econometrics, Decision Sciences, Operations Management, and Management Science. ME/BE supports managers in answering complex questions such as: which price strategy allows our company to maximize revenue? how should we design our marketing campaign in order for it to be as efficient as possible? which is the right level of outsourcing in our enterprise to enhance our long-term sustainability? in which assets should the firm invest to maximize its wealthiness at the end of a time horizon? and many more (Hirschey and Bentzen 2016). ME/BE deals with different types of scenarios, ranging from competitive markets to monopolies, oligopolies, and even government decisions. Many challenges in ME/BE can be formulated as optimization problems, which are usually computationally demanding. Hence, advanced methods from Operations Research, Computer Science, Artificial Intelligence, and Behavioral Sciences are requested. The latter use to employ descriptive research—either qualitative or quantitative—and correlation research. In addition, other methods can be applied as well (Gravetter and Forzano 2018).

This paper focuses on the applications of metaheuristic algorithms and simulation methods in ME/BE. Both families of analytical methods have been successfully employed to optimize and perform what-if analyses on different ME/BE-related systems and processes. The main research questions of this work can be summarized as follows: (i) how many types of market structures have been analyzed with the use of these methodologies?; (ii) are there common characteristics in the applied methods and methodologies?; and (iii) which are the most promising research lines in the application of simulation and metaheuristics in the ME/BE-related systems and processes? To the best of our knowledge, there is not any updated review in the ME/BE literature illustrating the use and potential of the aforementioned methodologies. Hence, our paper contributes to fill this gap by: (i) classifying existing work according to the market structure (competitive and imperfect); (ii) providing a review of recent ME/BE studies that employ either one of these methods or both of them simultaneously; and (iii) discussing open challenges in research on ME/BE topics, as well as proposing the use of hybrid approaches such as simheuristics (Juan et al. 2018) and learnheuristics (Calvet et al. 2017) to deal with scenarios characterized by some degree of uncertainty or dynamism, respectively.

The rest of this paper is structured as follows. Section 2 and Section 3 provide and overview of managerial economics as well as of metaheuristics and simulation methods, respectively. These sections allow the non-experts in one of these areas to have at least a good grasp of the main concepts involved. Section 4 reviews recent applications of metaheuristic algorithms and simulation methods in the context of competitive markets. Section 5 and Section 6 perform a similar analysis, but this time focusing on imperfect markets and government decisions, respectively. Afterwards, Section 7 identifies and discusses common trends and open challenges, while Section 8 illustrates the potential use of simheuristics and learnheuristics in managerial economics. Finally, Section 9 highlights the main conclusions of this work.

2. Overview of Managerial Economics

After the publication of the book “Managerial Economics” (Dean 1951), this subject gained popularity in the USA and other countries. ME mainly refers to the firm’s decision-making process. It could be also interpreted as “Economics of Management”, since it is a bridge between both disciplines: the Management discipline focuses on the decision-making, whereas Economics relates to the optimal allocation of limited resources owned by the companies to accomplish certain objectives. Managerial Economics is sometimes referred to as “Industrial Economics” or “Business Economics”. ME/BE shows how economic analysis can be used in formulating business policies. According to Agarwal and Helfat (2009) choices of resources have to be made at every stage. The author considers three economic problems: what to produce, how to produce, and for whom to produce. The knowledge of the economics is crucial to find solutions to the aforementioned problems. Since the pioneering work of Dean (1951), other studies have aroused. Spencer and Siegelman (1959) defines managerial economics as the integration of economic theory with business practice for the purpose of facilitating decision-making and forward planning by management. Douglas (1983) adds the uncertainty factor to the definition, saying that managerial economics is the application of economic principles to the decision-making process under the conditions of uncertainty. ME/BE has been popularized as a result of the increasing variability of business environments (Ahuja and Ahuja 2017). As there is a close interrelationship between economics and management, a closer look at both concepts is necessary. Regarding management, the scope of managerial economics is applied to five types of decisions (Hirschey and Bentzen 2016): (i) the selection of products to be produced or services to be offered; (ii) the choice of production methods and resources to be allocated; (iii) the determination of the best price; (iv) promotional strategies and activities; and (v) the selection of the location from which the customer is serviced.

When viewed in this way, ME/BE can be summarized as the study of allocation of resources available to a firm. Therefore, the scope of ME/BE is based on these problems in which both decision-making and resource allocation are needed: (i) resource allocation; (ii) inventory management; (iii) pricing; and (iv) investment. ME/BE can also include assessment and evaluation of funds, selection of business area, choice of products to deal with, determination of the optimum level of output, determination of the price of each product, determination of input combinations, as well as publicity and sales promotion (Agarwal and Helfat 2009). ME/BE fills the gap between the traditional economics theory and real business practices in two different ways. Firstly, it offers tools and techniques that allow managers to be more competitive in decision-making. Secondly, it is a link between all the areas in which a company operates. In addition to macroeconomics and microeconomics, capital management, profit management, and demand analysis/forecasting are also considered under the scope of ME/BE (Werden et al. 2005). Ghosh and Chowdhury (2008) considers that ME/BE applies the most useful concepts and theories from two areas, microeconomics and industrial organization, to create a systematic way of analyzing business practices and formulating strategies in the long run. Alhabeeb and Moffitt (2012) adds the concept of mathematics and statistics as supportive quantitative methods to ME/BE. They also mentioned the concept of economic scarcity, stating that it epitomized the paradox of the finite nature of resources and the infinite nature of human needs and willings.

Contrary to what many authors say, Allen et al. (2013) conclude that ME/BE differs from microeconomics because managerial economics prescribes behavior, whereas microeconomics describes the environment. This focus on managerial behavior provides powerful tools and frameworks to guide managers to better decisions and better identify the consequences of alternative courses of action. Research made by Samuelson and Marks (2015) considers the theory of the firm. The main tenet of this theory is that management strives to maximize the firm’s profits although firm’s revenues and costs are uncertain and accrue at different times in the future. The firm’s value under this theory is defined as the present value of expected future profits. It also considers factors such as satisfactory levels of performance, maximizing total sales, and the social responsibility of business. Baye et al. (2006) considers ME/BE as the study of how to direct scarce resources in the way that most efficiently achieves a managerial goal. These authors organize the decision-making issues into categories or “forces”, as defined by Porter (2011): entry, power of suppliers, power of buyers, industry rivalry, and substitute/complements. Perfect competition serves as an ideal of benchmark for other industries and that is why the study of competition is so important when defining ME/BE (Perloff and Brander 2017). Recent investigation (Hirschey and Bentzen 2016) considers ME/BE as a tool for improving management decision-making, linking economic concepts and quantitative methods. These theories can be summarized as described in Figure 1.

Hirschey and Bentzen (2016) and McGuigan (2010) add non-profit organizations, government agencies, and other organizations such as schools, hospitals, and museums to the theory of ME/BE. Hirschey and Bentzen (2016) also used the concept of multivariate optimization. This is important in ME/BE because many demand and supply relations involve more than two variables. In demand analysis, it is typical to consider the quantity sold as a function of the price of the product itself, the price of other goods, advertising, income, and other factors. In cost analysis, cost is determined by output, input prices, the nature of technology, and so on. In addition, difficult-to-predict ties between economic and political events make macroeconomic forecasting one of the toughest challenges faced in ME/BE.

Most decision-making processes can be formulated as optimization problems. Among methods to address these problems, one can mention game theory (Sadeghi and Zandieh 2011), metaheuristics (Buer and Kopfer 2014), neural networks (Göçken et al. 2016), simulation (Ivanov 2017), fuzzy sets (Graham et al. 2019), econometrics (Longo et al. 2017), and forecasting (Al Shehhi and Karathanasopoulos 2020). Linear programming (LP) (Vanderbei et al. 2015) constitutes one of the most classical and popular approaches. LP is a method of formulating and solving decision-making problems. In particular, LP returns a solution for an optimization problem consisting of a system of linear constraints and a linear objective function. Despite its popularity in ME/BE, LP presents several important limitations, mainly because most real-life problems are non-linear and too complex (NP-hard) (Grasas et al. 2017). This is the reason why heuristics and metaheuristics are increasingly being used in ME/BE applications. Another fundamental tool is simulation. As it will be discussed later, simulation techniques allow us to create what-if scenarios and assess the sensitive to uncertain outcomes of key economic variables. An important approach is that of innovation and new technological ventures. Karbowski (2019) suggests that a market with a high sensitivity to product quality improvements and a high competition will end up with the creation of a cartel. In addition, Monahan (2018) explores management alternatives with a behavioral economic lens and presents a new paradigm using Behavioral Sciences to account for the human factor. In this sense, the author concludes that people work for more than financial gain, and that they seek to collaborate with others. This fact challenges the dominant rational economic paradigm, which has been predominant in the existing literature.

3. Overview of Heuristic Optimization and Simulation Methods

Optimization and simulation methods are often used to analyze complex systems or processes. In the case of optimization methods, they allow obtaining optimal or near-optimal solutions for complex decision-making processes. Regarding simulation methods, these are usually employed when the system is dynamic or its behavior is stochastic (a clear example is those processes that change over time). In fact, simulation has wide applicability in different fields: from the design and analysis of networks in the supply chain to the determination of investment portfolios or the redesign of business processes. Thus, given a specific set of parameters, what-if scenarios can be analyzed. There are mainly three simulation techniques that can be used for the analysis of complex stochastic systems and processes (Law 2014):

• Continuous simulation refers to the modeling of a system with random variables that change continuously over time. This methodology makes use of differential equations and frequently employs numerical approaches for their resolution (Amaran et al. 2016).
• Discrete-event simulation points out to the modeling of a system with random variables that can vary over time (i.e., dynamic systems) but just in a discrete way (when specific events happen during a time). This approach is traditionally utilized to analyze the behavior of time-dependent network systems, such as a supply chain (Fishman 2013).
• Monte Carlo simulation (MCS) employs random sampling for addressing stochastic problems that do not evolve over time (i.e., static systems). This method is extensively used for dealing with not analytically tractable stochastic optimization problems (Bianchi et al. 2009).

Apart from employing simulation, optimization methods also allow to find those parameter values for which the system works best. Optimization methods are divided into exact and approximate (for example, those based on heuristics). The former guarantees the optimality of the solution to a given problem. However, as the complexity of the system grows, the time it takes to find the optimal solution also increases, sometimes exponentially, with the size of the instance problem. In order to perform the computations in a reasonable time, metaheuristic methods do not guarantee an optimal solution, but a near-optimal one instead. As a consequence, the hybridization of exact methods with metaheuristics is gaining momentum as an improved methodology for solving more complex problems (Jourdan et al. 2009). Metaheuristic algorithms can be divided into population-based—e.g., genetic algorithms (GA), particle swarm optimization (PSO), or ant colony optimization (ACO)—and single-solution—e.g., tabu search (TS), simulated annealing (SA), or iterated local search (ILS), just to name a few. According to Dunke and Nickel (2017), there are four different combinations of simulation with optimization techniques:

• Optimization integrated with simulation: In this approach, the optimization is used to evaluate a specific problem. Then, the result comes back to the simulation, which then re-starts its activity. For instance, the ordering of jobs could be re-scheduled according to the current state of the simulation (Dias et al. 2018).
• Simulation as objective function: In this case, the optimization provides a feasible solution, evaluated through the simulation. Then, these results are used by the optimization in order to generate alternative solutions. This, for instance, can be applied for determining the staff assigned to a given project (Zhang et al. 2019).
• Simulation results as a start for optimization: Using this combination, the simulation is conducted before the optimization, and is the one that provides the initialization parameters for the optimization process. For instance, the determination of the required staff for a certain production process and, afterward, using the optimization to allocate this staff (Rezaeiahari and Khasawneh 2020).
• Optimization for configuring simulation: Here, the simulation is employed to evaluate the feasibility of a solution found by the optimization (Yang et al. 2019).

A review of the literature that includes all the aforementioned can be found in Hussain et al. (2019). Moreover, some good introductory books regarding the field are Talbi (2009) and Luke (2013). As shown in Figure 2, the application of the combination of these techniques in the Business Economics and Operations Research/Management Science fields has increased over time. Furthermore, looking at Figure 3, one can conclude that the application of simulation is widely extended. Moreover, the trend in its widespread within the academia is growing for the three fields, i.e.: simulation, metaheuristics, and their combination.

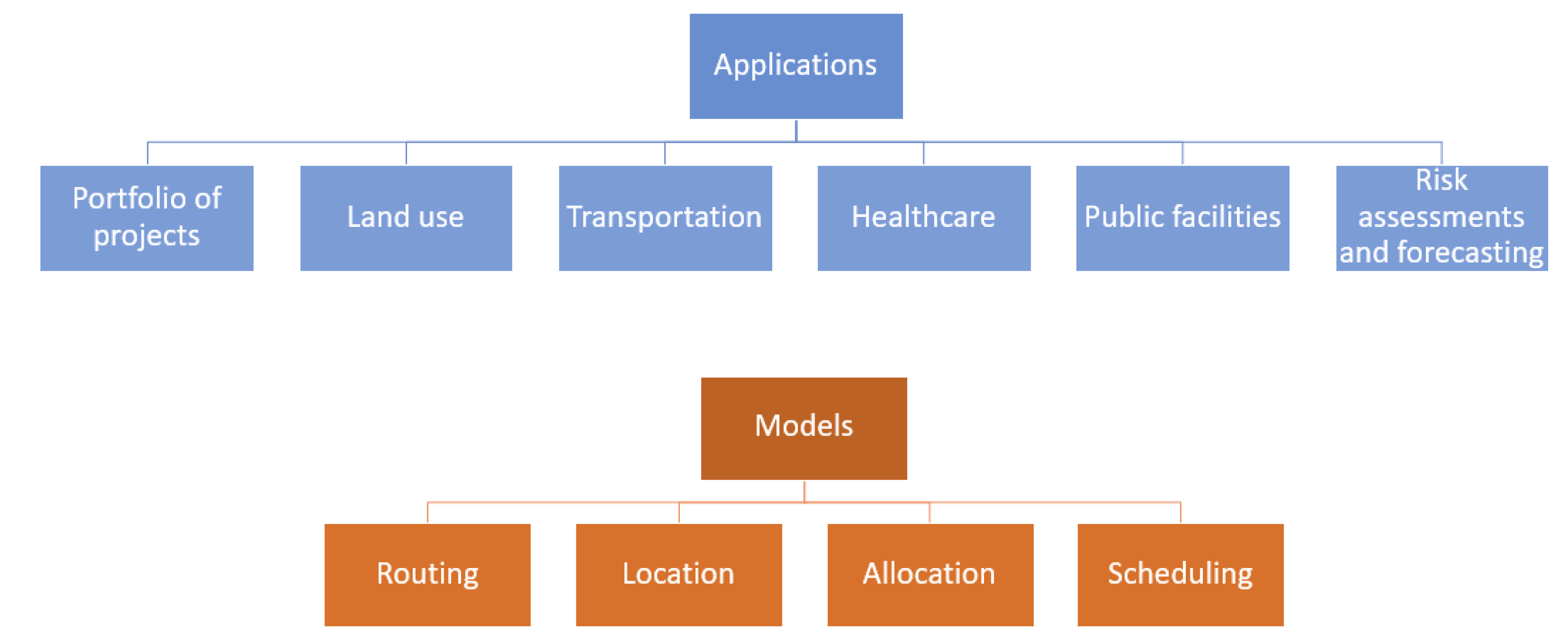
4. Applications in Competitive Markets

This section will review works in which firms benefit from the application of optimization and simulation techniques to improve their competitiveness. The existing literature provides many examples of applications. However, a series of challenges can also be identified. To limit the scope, the references will focus on recent articles in the services sector, the manufacturing sector, and the power generation markets. A common trend facing organizations is that managerial decisions are becoming increasingly complex, as they need to consider various parameters simultaneously (e.g., different types of resources) and are affected by multiple economic indicators. This is especially true for almost any decision-making exercise in collaborative networks, where metaheuristic algorithms and simulations help to suggest and provide solutions with possible better utilization of the available resources. In fact, one of the main factors that condition a firm’s success is its ability to build and maintain an effective collaboration network itself. This is especially critical for companies in the Information Technology industry, for which the creation of a competitive system requires the integration of numerous resources, platforms, and skills (Brass et al. 2004). In this regard, Salamat et al. (2016) design and implement an optimization model, based on the analytic hierarchy process (AHP) and on multi-objective programming, for the decision-making process involved in the creation of a collaborative network. The idea is to use the transaction cost theory (TCT) for short-term decisions and the resource-based view for long-term decisions. The results show that the application of optimization techniques contributes to make the selection process more efficient in terms of cost, time, and development speed. Further, the designed framework provides analytical solutions and can be used as an effective tool in selecting network alternatives according to the managerial requirements. Crispim et al. (2015) advocate that the success of a virtual enterprise depends on its composition, and the selection of partners. These authors remark the inherent difficulty in this last decision, which is due to the uncertainties related to information, market dynamics, customer expectations, and technology speed-up, with a strongly stochastic decision-making context. They propose a two-stage model for cooping business environments with uncertainty: a chance-constraint multi-objective directional TS metaheuristic complemented with a 2-tuple fuzzy linguistic representation model. The results show the potential of this approach for handling partner selection problems under different scenarios.

In addition to their widespread use in companies from the service sector, metaheuristics and simulation are also frequently employed in the manufacturing industry. Being a very competitive business environment (Wang and Cao 2008), managers often seek new strategies to reduce costs, without sacrificing product quality and the reliability of the designed system or product. Ma and Lv (2019) tackle the problem of finding a solution for optimal production and scheduling with the objective of minimizing the cost per unit time in a competitive environment. They design and implemented an approach speeding up the Monte Carlo simulation to calculate the objective function, as well as to corroborate the feasibility in order to optimize the objective function by metaheuristic algorithms. To address the same problem, Lian et al. (2012) proposes a solving approach inspired by the imperialist competitive algorithm (ICA). The procedure is based on the initial population, and includes different stages: assimilation, position exchange, imperialistic competition, and elimination.

Another main goal to improve the production system is to reduce the total makespan in scheduling problems. In these cases, the use of procedures that integrate simulation and metaheuristics is widely contrasted and quite versatile, regardless of the manufacturing industry of application (from the chemical industry to the textile manufacturing one). In the case of job-shop problems, some of the most relevant manuscripts in recent years are the ones by Amelian et al. (2019) and Belkaid et al. (2016). With the main objective of enhancing competitiveness and improving effectiveness, many countries have decided to change from a monopoly-based electric power generation to one of perfect competition (Section 5). It is expected that a more competitive market helps to reduce the marginal cost (Wen and David 2001). Associated with the concept of competitiveness, the development of bidding strategies for the maximization of profits in public-service companies is inevitable. With this purpose in mind, an optimal bidding structure is needed (David and Wen 2000). In recent years, different models have been developed and implemented for bidding competitive markets based on optimization, gaming theory, and multi-agent models (Mathur et al. 2017). Thus, for example, Mousavi et al. (2015) develop and compare different metaheuristic algorithms (a GA, a SA, and a hybrid SA-GA) for optimizing bidding strategy. The authors address the problem of computing a pure Nash equilibrium for electricity markets with many players. Baringo and Amaro (2017) formulate the same problem by using a stochastic robust optimization model that takes into account uncertainties in the market prices and in the driving requirements of electric vehicles. Usually, the supplier actors of the power market are modeled as adaptive agents who can learn how to bid strategically, so they can optimize their profit through indirect interaction with other actors within the market (Azadeh et al. 2010). Following this line, Tang et al. (2017) propose a game-theoretic bidding optimization method based on bi-level programming, where the multiple power producers are formulated as a non-cooperative game with different bidding curves as strategies, while pricing is optimized simultaneously. Moreover, a distributed algorithm is implemented in order to search the solution of the generalized Nash equilibrium. Further, for verifying the feasibility and the effectiveness of the proposed optimization approach, a simulation is performed and discussed. Sadeghi and Zandieh (2011) studied a product portfolio identification problem, which was based on a customer engineering interaction model in a competitive environment. These authors approached the problem as a 2-person non-cooperative game with a Nash equilibrium point.

In the area of production scheduling, Pan et al. (2019) compared seven solving approaches, including a mixed integer linear programming model, three constructive heuristics, two variant neighborhood descent algorithms, and an iterated greedy algorithm. As they indicated, the seven algorithms were found to be effective against the sixteen algorithms presented in the existing literature. Lin et al. (2020) worked on a non-linear zero-one programming model for the courier delivery network design. The objective was to minimize the total cost including accumulation cost, transportation cost, and transfer cost, while considering facilities with a limited capacity. A simulated annealing algorithm was developed for achieving near-optimal solutions. This problem has applications in optimizing transportation routes, either to deliver courier directly or through a transfer facility. In another study for a multi-period facility location problem, Sauvey et al. (2020) coped with the problem of finding optimal locations and facilities. These need to have sufficient capacities to satisfy customers while keeping the cost as low as possible. Also, some customers required the product delivery in time, whereas other accepted a delayed delivery within a given time window. Tsao et al. (2020) worked in the context of globally competitive apparel industry to minimize the total cost considering the length of used fabric and the number of operative sections in the manufacturing process. The cut order planning problem was modeled as a mixed-integer programming model. Seven garment sizes were considered along nine cases. Several metaheuristic techniques were employed to solve the aforementioned problem, including: SA, GA, TS, a hybrid SA-GA, and a hybrid TS-GA.

5. Applications in Imperfect Markets

Imperfect competition refers to any economic market that does not meet the rigorous standards of a purely competitive market (Krugman et al. 2007). It comprises the following types of market structures: monopolies, monopsonies, monopolistic competition, oligopolies, and oligopsonies. All firms operating in different market structures face complex problems with changing consumer preferences with time, new government policies, technological advancements, scarcity of resources, and competitive landscape changing with different players entering the market with new offers. In this environment, we may find companies, for instance, that sell different products and services, set their own individual prices, fight for market share, and are protected by entry and/or exit barriers. There are such dynamic challenging situations across industries and firms operating in different market structures.

5.1. Monopolies and Monopsonies

There are different types of monopolies: (i) a pure monopoly, in which there is a single seller in the market; (ii) a soft monopoly, where the market includes several sellers but one has a very high percentage of it; and (iii) a situation in which there are several sellers but they set prices and outputs in concert (i.e., cartels). In addition, monopolies can be classified according to the factors that make possible that situation, e.g., (i) a key resource is owned by a single company; (ii) a company owns a patent to produce a good; (iii) the government grants a company the exclusive right to produce a good; and (iv) a natural monopoly, where production costs make a single producer more efficient than many (e.g., water distribution). The decisions for a monopolist are mainly related to prices and outputs, but there are plenty of options regarding strategic entry barriers. These barriers refer to any action taken by incumbent companies in a given market with the aim of discouraging potential entrants from entering. Hostile takeovers and predatory pricing are popular examples. In a similar way in which a monopolist can influence the price for its buyers in a monopoly, in a monopsony a single entity has a strong influence over sellers. Thus, the monopsonist has also decisions to make regarding price, quantity, and behavior.

Lu et al. (2010) presents a two-stage model to investigate the location strategy and the commodity pricing strategy for a retail firm. This firm wants to enter a spatial market with multiple facilities, where a competitor firm is already operating as a monopoly. Expected market shares are calculated based on the stochastic customer behavior. The authors proof the existence and uniqueness of the pure strategy Nash equilibrium price with a specified utility function. A TS is proposed to search the optimal location-price solution. Panin et al. (2014) present a series of studies in the field of optimal facility location and pricing and propose a mathematical model for the corresponding Stackelberg game. On a different application field Zhou and Huang (2016) discussed two types of contracts for energy-saving products in a monopoly with the government’s budget constraint. In this study the authors modeled a three-stage game and gave optimal design of the contracts according to the goal of minimizing the total and the average energy consumption. In a monopolistic scenario, Raza et al. (2019) presents a multi-objective model considering pricing, production, and quality decisions in a multi-objective context when the manufacturing firm experiences a demand leakage in simultaneously observed price-dependent stochastic demand. A goal programming approach combined with a simulation based optimization and a multi-objective genetic algorithm are proposed.

5.2. Monopolistic Competition

Monopolistic competition (Parenti et al. 2017) represents a popular mixture of monopoly and perfect competition. In this case, firms compete selling products that differ slightly from one another. This feature means that competing companies have some control over price. Since the demand is relatively elastic, the company may raise price without losing its entire market to competitors. There are two types of differentiation: vertical and horizontal (Besanko et al. 2009). In the first case, it can be objectively stated that the product is better or worse than the products of the competitors. Consider, for example, a producer of household appliances that uses accessories to improve the durability; all consumers appreciate the improvement, but they may not agree on its value (willingness to pay). In the case of horizontal differentiation, although the price would be the same, only a proportion of consumers would prefer a given product. Classic examples are clothing and fast food.

Feenstra (2010) states that there are three sources of gains from monopolistic competition that are not present in traditional models. The first one is the consumer gain due to the fact that she has access to new import varieties of differentiated products. Then, a second source of gains coming from self-selection of efficient firms into export markets. Last, the monopolistic competition model, allows a reduction in firm’s markups due to import competition. In a scenario of monopolistic competitive markets, Kumar and Chatterjee (2015) present a mathematical programming formulation that models an entrant firm’s problem, which consists in deciding on the market segments to enter and the corresponding product designs to offer. The firm’s aim is to maximize its profit. The resulting non-linear programming problem is addressed by means of a heuristic. A commercial solver is used to solve a small example and compare results. Annicchiarico and Marvasi (2019) have developed a tool to understand how the underlying structure of preferences affects trade policy decisions in an environoment where lobbies have their own interests that may not be the same as the ones of consumers. They show that the trade policy emerging in the political equilibrium may be either protectionist or liberal.

5.3. Oligopolies and Oligopsonies

So far, we have discussed competitive markets and monopolies. However, they constitute extreme options of market structure and there are many relevant positions between them. Oligopoly refers to the market consisting of a small number of companies. Competitive strategies are particularly important in oligopolies: in a pure monopoly there are no competitors to worry about; in competitive markets, price and output are set by supply and demand; in contrast, in oligopolies firms must correctly anticipate the actions and reactions of its rivals and respond accordingly. In fact, oligopoly market structures provide more challenging aspects to remain differentiated from each other with simultaneously following rules of the game among the competing firms –which may be governed by the leading player–, as well as the uncertainties of the environment (Robbins and Lunday 2016).

In many countries, the electricity market is no longer a monopoly, but is far from being a perfect market yet. The size of investments needed in the market represents a relevant entry barrier. Thus, producers can influence the prices by behaving strategically. In this context, Ladjici et al. (2014) presents a two settlement model consisting of a spot and a forward market. Agents aim to maximize their profit and can take part in both spot and forward transactions. The strategic interactions of the agents are modeled as a non-cooperative game. A competitive co-evolutionary algorithm is developed to calculate the Nash Equilibrium strategies ensuring the best outcome for each agent. Also in the context of the electricity market, Bhattacharya et al. (2017) develops an optimization method for bidding strategies. This method aims to maximize profits and combines GA, adaptive metropolis search, PSO and differential evolution (DE) methods. Rego et al. (2014) presents an approach designed to recommend the number, size, and composition of purchasing groups for a set of hospitals willing to cooperate. The aim is to minimize their shared supply chain costs. A hybrid variable neighbourhood search (VNS) - TS metaheuristic is put forward, while preliminary computational results are carried out for illustrative purposes and to show the potential of their approach. Robbins and Lunday (2016) studies the characterization of optimal pricing strategies for a pediatric vaccine manufacturing firm operating in an oligopolistic market. Variants of three heuristics are proposed and tested to identify the pricing scheme that maximize a manufacturer’s profit: a Latin Hypercube Sampling (LHS) of the upper-level feasible region, an LHS enhanced by a Nelder–Meade search from each price point, and an LHS enhanced by a custom implementation of the Cyclic Coordinate Method from each price point. Cai et al. (2011) relate the concept of oligopoly to the study of beef packing margins. Their results show that after mandatory price regimes took effect, cooperative regimes were longer and oligopsonistic rent, as measured by average economic profit, experimented a remarkable rise. Other studies Alvarez et al. (2000) present a conceptual and empirical analysis of buyer oligopsony power in a spatial markets setting. Results show that firms may set prices above the monopsony level to minimize direct competition among them.

6. Public Sector and Public-Private Partnerships

Most economies have both private markets and a public sector. Private markets tend to offer a large number of different goods and services, but there are other things that they can not efficiently offer. Non-profit organizations will have similar offers but the need is to make decisions to have regular demand/acceptance of their services with minimum usage of resources. Government agencies providing public utilities need an optimal utilization of scarce resources to meet large scale demand (Memmah et al. 2015). National security or educational systems constitute two illustrative examples. While in private markets the optimization criteria are mainly profit and market capture maximization, the public sector has a wider range of goals, such as social cost minimization, access, efficiency, and equity. According to Samuelson and Marks (2015), the government has two main roles: (i) to regulate private markets by providing basic rules and by correcting market failures; and (ii) to provide certain desirable public goods and services that are not, or cannot, be provided via private markets. Generally, there are three causes for market failure, which we show in the following list linked to the main government responses:

• Monopoly power: (a) breaking up existing monopolies, (b) preventing monopolistic practices, (c) preventing mergers that reduce competition, and (d) preventing collusion.
• Negative externalities: (a) taxes, (b) government standards, (c) permits (either tradable or not), (d) liability rules, and $\left(e\right)$ bargaining among affected parties.
• Positive externalities: (a) promoting literacy and education, $(b$) improving health, (c) promoting research, (d) patent system, and $\left(e\right)$ copyright.
• Imperfect information: (a) banning some drugs, (b) taxing unhealthy products, (c) mandating compulsory education, and (d) requiring producers to provide information (e.g., warning labels on cigarettes).

The rest of this section describes recent works classified by field of application. We also review the models and methodologies proposed in each work, which are summarized in Figure 4.

6.1. Regulation

In the field of project portfolio, Manavizadeh et al. (2017) formulates and solves a multi-objective portfolio selection problem with an exact method for small instances and a non-dominated sorting GA for large sized instances. The aim is to determine the optimal portfolio for financing projects of renewable energies. The approach minimizes both the weighted cost of capital of the investors and the greenhouse gas emissions. Moreover, it maximizes net present value and job generation for urban, rural, and remote areas. Three ways to cover the required budget are considered: bonds, common stocks, and bank loans. Fernandez et al. (2013) applies a multi-criteria analysis to the problem of allocating public funds to competing programs, projects, or policies, with the subjective aim of maximizing the portfolio social return (based on either an individual or a collective decision-maker). The extended non-outranked sorting genetic algorithm (NOSGA-II) is applied for addressing this problem. The methodology is tested through two real size problems. Fonseca et al. (2015) focuses on foundations that provide grants for research projects (either public or private), which face the responsibility of selecting projects. The authors propose a TS to support the decision-making process of grant allocation, with the aim of maximizing the overall cost-benefit relation. Balderas et al. (2019) addresses the project portfolio as a multi-objective problem. The authors propose an interval-based method that considers imperfect knowledge of the contribution of projects to a portfolio, the project requirements, available resources, and preference parameters in the model. An evolutionary algorithm is used to deal with the problem. The proposal is tested both on an example from the literature and a public project portfolio with nine objective functions and large number of applicant projects.

In the field of land use optimization, Memmah et al. (2015) reviews metaheuristic algorithms for agricultural land use optimization. Land use optimization consists in allocating different species and activities to different areas in agricultural landscapes. Combining optimization techniques and simulation allow decision-makers (from private and/or public sector) to explore a large number of land use combinations. This optimization usually involve many stakeholders and decision-makers, many spatial factors, attributes and constraints, and multiple conflicting objectives (environmental, economical, and technical). Metaheuristics are quite successful in this context for several reasons: (i) the existence of a high number of integer variables; (ii) a need to take into account the points of view of many stakeholders and decision-makers; (iii) a large number of nonlinear objectives and constraints; and (iv) the need for interactive decision-support systems, which requires from fast algorithms.

6.2. Public Goods

Public transportation is a field with a large range of complex optimization problems. Because of the huge impact of public transportation, both national and local city economies, pollution reduction, and people welfare in general, many approaches have been proposed. Indeed, there are approaches for repositioning bicycles in a public bike-sharing system (Luong et al. 2014), design of feeder bus networks (Ciaffi et al. 2012), design of crew rostering problem in public bus transit (Xie et al. 2017), multi-variant optimization of traffic management (control of traffic lights) (Turek et al. 2017), disaster relief operation planning—which consists in the delivery of basic items in a post-natural-disaster scenario (Nolz et al. 2010), and design of electric transit route networks (Iliopoulou et al. 2019), among many others. Iliopoulou et al. (2019) reviews applications of metaheuristics for solving the transit route network design problem and compares them according to a benchmark network. In addition to highlight algorithmic components, solution representations and methods that tend to provide high-quality solutions, the paper identifies gaps in research and opportunities for future research. Uvaraja and Lee (2017) reviews metaheuristic approaches for urban transit scheduling, that is, for deriving useful set of routes, manageable timetabling for each transit route and transit scheduling based on available resources. They conclude that there is scarce work on parallel approaches, solving sub-problems concurrently, multi-objective approaches, and considering working preferences of the transit driver. Rodriguez et al. (2019) proposes a hyper-heuristics, which consists of a parallel combination of three metaheuristics: SA, GA, and ACO. This strategy is applied to design transport networks. Information exchanges take place between the metaheuristics and speed up the search process. The parallel implementation makes it possible for metaheuristics to run simultaneously. The hyper-heuristics achieves low computational times as well as high solution quality. Xu and Ying (2019) addresses the re-balancing problem in public bicycle systems, i.e., the problem of meeting the fluctuating demand for bicycles and for vacant lockers at each station, by actively shifting bicycles between stations with a fleet of vehicles. The authors propose a greedy randomized adaptive search procedure with a path-relinking, which is enhanced with a data mining process that makes it adaptive. This approach has been implemented in a populous city. Finally, Zhang et al. (2020) puts forward a model of transit route network design for low-mobility individuals and proposes a solving methodology. The objective function prioritizes the transit demands of low-mobility individuals followed by those of general public, and aims to minimize the weighted sum of direct traveler, transfer, and unsatisfied demand costs. A hybrid ACO-GA approach is formulated to solve the proposed model in accordance with current conditions (i.e., existing routes). Many authors have explored the use of hybrid approaches combining metaheuristics and simulation in public transportation. For instance, Fikar et al. (2016) proposes a discrete-event driven metaheuristic for dynamic home service routing with synchronized trip sharing. It is applied to home health care operations, where nurses are scheduled and routed to perform various services at clients’ homes. The authors propose facilitating trip sharing and walking policies to reduce the number of required vehicles, while taking into account that, in real life, cancellations or new requests can happen at any time. Another challenging and increasingly relevant application, particularly in smart cities, is the waste collection management under uncertainty of waste levels. In this context, Gruler et al. (2017) proposes a simheuristic algorithm integrating MCS into a VNS. MCS is used to assess promising solutions and guide the search of the VNS. Hamid et al. (2019) addresses a a stochastic multi-objective and multi-period hub location problem, and applies it in public transportation. Their approach aims to minimize: (a) the total costs considering the possibility of investing the unused budget at each period; (b) the total processing time in the hub network at each period; and (c) the maximum distance between each pair of origin-destination nodes in the network. Three population-based metaheuristics are proposed and compared. The stochasticity in this problem resides in the fact that many types of disruptions may affect the capacity of hubs: computer-telecommunication network equipment failure, terrorist incidents, social strikes, natural disasters, etc.

In the area of public healthcare systems, Mendoza-Gómez et al. (2018) describes a problem arising in the planning of specialized diagnostic services. In particular, the problem consists in deciding which hospitals will provide the service and their capacity levels, the allocation of demand in each institution, and the reallocation of uncovered demand to other institutions or private providers. The aim is to minimize the total equivalent annual cost of investment and operating cost required to satisfy all the demand. The proposed methodology is a hybrid metaheuristic framework combining iterated greedy and variable neighborhood descent components. Marynissen and Demeulemeester (2019) reviews documents on multi-appointment scheduling problems in hospitals, in which patients need to sequentially visit multiple resource types to receive treatment or be diagnosed. Each patient is assigned a specific path over a subset of the resources and each step has to be scheduled. The aim is to let each patient visit the resources within the allotted time to receive timely care, thus avoiding a delayed diagnosis or treatment, which could result in adverse health effects. The review shows that these problems are becoming increasingly popular. For instance, Khalfalli et al. (2019) deals with the generation of a daily operating theater schedule, aiming to minimize completion time and maximum overtime while integrating real-life surgeon constraints (role, specialty, qualification, and availability). Also in the context of surgery departments, Aringhieri et al. (2015) considers the problem of determining the allocation of operating-rooms time blocks to specialties together with the subsets of patients to be scheduled within each time block. The aim is to reduce both waiting time cost and production costs measured in terms of the number of weekend stay beds required by the surgery planning. The authors propose a two level metaheuristic to address this problem.

Regarding the design and location of public facilities, Li and Li (2019) formulate the life-cycle analysis in seismic design of bridges as an interactive multi-objective optimization problem. The authors apply an evolutionary multi-objective optimization (EMO) algorithm to the seismic design of a reinforced concrete pier with four objectives: flexural strength coefficient, shear strength coefficient, reliability index of drift, and life-cycle cost coefficient. There are plenty of manuscripts on facility location in the public sector, and many of them propose heuristics/metaheuristics as solving methodologies. Haase et al. (2019) reviews recent works, highlighting the main applications: bike sharing systems, simultaneous bus scheduling and depot location planning, electric vehicle charging station planning, healthcare facility location planning, and school location planning. Hence, regarding education Xavier et al. (2020) propose location models to determine the best distribution of higher education facilities in the Amazonas State (Brazil). Castillo-López and López-Ospina (2015) present a model of location and modification of school capacity aiming to increase the efficiency of schools located in rural zones of Chile. Another interesting application is proposed by Gupta et al. (2019). It deals with the problem of setting up tele-centers (popularly known as the rural kiosks) at appropriate locations. This work proposes the combination of several metaheuristic algorithms (PSO, bat algorithm, and ACO) with traditional clustering approaches (K-means and fuzzy C-means) for the location allocation problem. The objective is that the maximum number of people can use the services with minimum travel and cost. A case study is performed with data from the Indian region. Finally, Miskovic and Stanimirovic (2016) addresses the problem of establishing the network of emergency service units, that is, locating a certain number of units at given discrete points of the region and to allocate cities to established units, aiming to balance the load of established emergency units. The authors consider a multi-period model as well as the uncertainty of the number of incidents. Another interesting contribution is provided by Lopez-Garcia et al. (2016). The authors present a hybrid technique combining a GA with a cross entropy method to optimize fuzzy rule-based systems. This technique is applied to traffic congestion datasets in order to determine their performance in this area.

In the field of risk assessments and forecasting, Moayedi et al. (2020) address the spatial analysis of landslide susceptibility and describes a case study based on the Ardabil province of Iran. Similarly, Jaafari et al. (2019) present two predictive models that rely on an adaptive neuro-fuzzy inference system and two metaheuristic optimization algorithms for the spatially explicit prediction of wildfire probabilities. Finally, Pourghasemi et al. (2020) develop and compares four ensemble metaheuristic approaches, including the combinations of an adaptive neuro-fuzzy inference system with a GA, a SA, an ICA, and a DE. It can be concluded from these articles that metaheuristics can be useful when developing predictive models, e.g., for landslide susceptibility assessment (which can help to alleviate damages caused by this natural hazard), wildfire probabilities (which may help to effectively guide fire management plans and on-the-ground decisions on firefighting strategies), and flood assessment (that can improve flood hazard management and land use planning). As Figure 5 shows, the public sector has to deal with different applications and models to provide goods and services.

7. Common Trends and Open Challenges

The following research challenges and opportunities have been identified regarding the utilization of metaheuristics and simulation in the management field:

• The first challenge is the adaptability of the used techniques. In fact, a particular decision-making problem can be answered by different methodologies (Tsao et al. 2020) and, in other cases, a particular methodology can provide a solution for different sets of decision-making requirements. That is, within the same industry, firms are most likely to face similar problems or have similar goals. However, and independently of their goals, their necessities cannot be answered by the same methodology, since the firm environment can be diametrically opposite and can vary over time (Salamat et al. 2016). For example, collaborators (i.e., they may be based in local, national, or international region), target customers (i.e., with different demographics and living patterns) and market environment (i.e., perfect or imperfect competition), among others. Thus, it is in these cases where an intelligent design that allows adaptation and evolution of decision-making mechanisms play a fundamental role in the competitiveness of firms. In a similar line, it is also necessary to develop dynamic procedures that include uncertainty (Kumar and Chatterjee 2015; Mathur et al. 2017).
• The second challenge is the reliability of some of the simulation outputs. Some authors, like Zhang et al. (2019), point out about the discrepancies between the simulation outputs and the observed data in practice, due to multiple nuances that were not incorporated in the models in complex environments. This statement is particularly true in those cases where consumers’ behavior may intervene (e.g., hospitals). As a consequence, the aforementioned discrepancies in output may affect the reliability of the model insights, especially when those insights are implemented in high-risk practice.
• The third challenge is the applicability, i.e., the horizon of repercussion to which the decision to make belongs. The previous literature review shows that firms and researchers are making an attempt to design and implement possible simulation and metaheuristic algorithms for better decision, but in most of the studies referenced in this work, the utilization of the aforementioned techniques is limited to the strategic decision level (considering the importance of these decisions for the survival of the firm). However, there is no impediment to use them as a support system in all decision making processes. Reinforcing this idea, some authors, such as Mendoza-Gómez et al. (2018), advocate its massive implementation as a support technique in the decision-making process in regular basis (i.e., tactical and operational levels).
• Finally, the fourth challenge refers to the dissemination of these techniques as a decision tool, the uniqueness in the solution. The procedures described in this study can provide more than one good and feasible solution, such that, according to Tang et al. (2017) this can generate controversy when making a decision. It is possible that in this scenario, in which two equally good solutions are available, the managers of the firms doubt the effectiveness of these tools and dismiss it as effective tools by not providing a single solution.

8. Potential use of Simheuristics and Learnheuristics

Decision-making processes related to ME/BE scenarios are becoming increasingly complex due to trends such as globalization, increasing scale of enterprise operations, information technologies capable of provide real-time data that needs to be analyzed, and the availability of an increasing amount of data that allows us to make more informed decisions than ever but also requires from a deeper analysis of the economical and managerial environments. Hence, there are many times in which these decision-making processes have to be done under uncertainty and/or dynamic conditions.

A concept combining simulation with metaheuristic optimization is that of simheuristics (Rabe et al. 2020). Simheuristics can be seen as an extension of metaheuristics, since a simulation module is integrated inside the metaheuristic framework to efficiently deal with NP-hard and large-scale stochastic optimization problems (Ferone et al. 2019). Notice that simheuristics might employ any type of simulation, e.g., discrete-event, agent-based, or MCS. These algorithms have also been used recently in multiple sectors, including: flow-shop scheduling (Gonzalez-Neira et al. 2017; Hatami et al. 2018), waste collection management (Gruler et al. 2017), arc routing (Gonzalez-Martin et al. 2018), Internet computing (Cabrera et al. 2014), finance (Panadero et al. 2020), e-commerce (Pages-Bernaus et al. 2019), and inventory routing (Gruler et al. 2018, 2020). All in all, simheuristics illustrate the extraordinary potential that simulation has when combined with heuristics and metaheuristics, specially when solving stochastic versions of NP-hard optimization problems. While simheuristics are designed to cope with NP-hard optimization problems under stochastic environments, learnheuristics combine metaheuristics with machine learning methods in order to deal with NP-hard optimization problems under dynamic conditions, e.g., problems in which the inputs are not static but change over time or as in response to managerial decisions while the solution plan is built (Calvet et al. 2017). Thus, for instance, Calvet et al. (2016) consider how managerial decisions might dynamically influence consumers’ willingness to spend (and the impact over the firm’s revenues) while building a plan to assign customers to retail centers. Similarly, Arnau et al. (2018) consider dynamic travel times while optimizing delivery plans for a transportation company.

All in all, many of the ME/BE-related challenges discussed in Section 7 might consider uncertainty and/or dynamic scenarios. Therefore, they clearly require from flexible tools, like simheuristics and learnheuristics, to efficiently deal with them. Indeed, most real-life applications related to ME/BE are characterized by a high degree of uncertainty and dynamism. Some examples are described next.

• Pricing strategies in oligopolies or monopolistic competition usually are subject to incomplete/ uncertain information, such as the pricing strategies and cost of competitors or characteristics of potential entrants. Taking into account this uncertainty is key for the economical sustainability of an organization.
• The best market segment strategy may depend on the strategies of the competitors, current and future technologies, and customer demands, among many other factors. All these factors are impossible to predict perfectly and may change over time very fast.
• Public transportation has many relevant positive externalities. To design efficient systems is required to estimate the number of users, but such predictions tend to have a high margin error. Moreover, the number of users of a given system, for instance a shuttle bus service, may depend on many factors that may change over time: prices in the car market, environmental awareness, characteristics of other public alternatives, etc.
• Public/private portfolio design is usually a multiobjective optimization problem with many restrictions. Completion times, cost and even the preferences of decision-makers and available funding may be fuzzy and change over time.

9. Conclusions

Managerial or business economics deals with the efficient assignment of scarce resources in order to enhance the performance of a firm or organization. In a context of globalization and access to huge amount of data, now more than ever only firms and organizations that are able to make an efficient use of their limited resources will be able to reach a sustainable condition (in a general sense that includes economic, environmental, and social dimensions of sustainability). In this framework, we have reviewed the applications of metaheuristic optimization algorithms and simulation methods to support informed decision-making. Hence, different recent and representative examples related to competitive markets, imperfect markets (monopolies and monopsonies, monopolitistic competition, and oligopies and oligopsonies), as well as public sector and public-private partnerships (considering works related to regulations and public goods) have been introduced and discussed. It can be concluded that the use of these methods is very extended and a high number of applications are related to routing, location, allocation, and scheduling decisions. From these examples, a series of open research challenges have been also identified, which are: (i) adaptability of the used techniques; (ii) reliability of simulation outputs; (iii) applicability (that is, implementation to support decision-making process in a more regular basis); and (iv) uniqueness of the solution (giving more than one solution may generate controversy). Finally, the paper discusses how hybrid flexible tools, combining metaheuristic optimization, simulation, and machine learning methods, can be employed to cope with increasingly complex decision-making process, under uncertainty and/or dynamic conditions. In addition, realistic examples are provided.

The use of metaheuristics and simulation methods is becoming increasingly popular due to the need of support in the complex decision-making processes of intensely competitive markets. The increasing availability of data and the unstoppable technological development is leading to a culture (both in private markets and the public sector) for evidence-based decision-making. Undoubtedly, a more efficient management represents a competitive advantage. Focusing on public sector and public-private partnerships, the existing works reviewed have shown a diverse range of applications, mainly: portfolio of projects, land use, transportation, healthcare, public facilities, and risk assessments and forecasting. This means that public policy-makers have powerful methods to support decision making processes and previous works as examples. Although most works come from the private sector, knowledge transfer could help to make better and faster decisions in the public sector. Indeed, most of the software/platforms used in the private companies could be directly applied by the public sector. However, applications in the public sector tend to have more agents involved and dissimilar and even competing objectives. Thus, multi-objective optimization approaches for the public sector represent an open, interesting and challenging line of research.

As future research lines, we plan to tackle the following ME/BE problems that have caught our eye: (i) segment discrimination and mixed bundling in e-commerce; (ii) randomized strategies in situations in which Nash equilibrium strategies cannot be easily achieved; (iii) risk analysis in lending and insurance under imperfect information; and (iv) auction methods under dynamic price conditions.