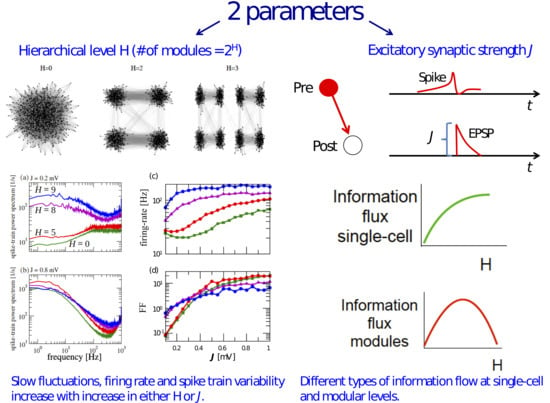
Optimal Interplay between Synaptic Strengths and Network Structure Enhances Activity Fluctuations and Information Propagation in Hierarchical Modular Networks
Abstract
:1. Introduction
2. Methods
2.1. Neuron Model
2.2. Network
- Randomly divide each module of the network into two modules of equal size;
- With probability , replace each intermodular connection by a new connection between i and k where k is a randomly chosen neuron from (the same module as i;
- Recursively apply Steps 1 and 2 to build networks of higher (H = 2, 3…) hierarchical levels. A network with hierarchical level H has modules.
2.3. Simulation Protocol
2.4. Statistics
3. Results
3.1. Information Transfer is Enhanced When Both Modularity and Synaptic Strength Increase
3.2. Effects of J and H on the Autocorrelation and Cross-Correlation of Single-Neuron Spike-Trains
3.3. Information Flow at the Population Level
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Paxinos, G.; Huang, X.; Toga, A.W. The Rhesus Monkey Brain in Stereotaxic Coordinates; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Sporns, O.; Tononi, G.; Ko¨tter, R. The human connectome: A structural description of the human brain. PLoS Comput. Biol. 2005, 1, e42. [Google Scholar] [CrossRef]
- Bullmore, E.T.; Bassett, D.S. Brain graphs: Graphical models of the human brain connectome. Annu. Rev. Clin. Psycho. 2011, 7, 113–140. [Google Scholar] [CrossRef] [Green Version]
- Sporns, O. The Non-Random Brain: Efficiency, Economy, and Complex Dynamics. Front. Comput. Neurosci. 2011, 5, 5. [Google Scholar] [CrossRef] [Green Version]
- Alivisatos, A.P.; Chun, M.; Church, G.M.; Deisseroth, K.; Donoghue, J.P.; Greenspan, R.J.; McEuen, P.L.; Roukes, M.L.; Sejnowski, T.J.; Weiss, P.S.; et al. The brain activity map. Science 2013, 339, 1284–1285. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- da Costa, N.M.; Martin, K.A. Sparse reconstruction of brain circuits: Or, how to survive without a microscopic connectome. Neuroimage 2013, 80, 27–36. [Google Scholar] [CrossRef]
- Stephan, K.E. The history of CoCoMac. Neuroimage 2013, 80, 46–52. [Google Scholar] [CrossRef] [Green Version]
- Szalkai, B.; Kerepesi, C.; Varga, B.; Grolmusz, V. High-resolution directed human connectomes and the Consensus Connectome Dynamics. PLoS ONE 2019, 14, e0215473. [Google Scholar] [CrossRef] [PubMed]
- Potjans, T.C.; Diesmann, M. The cell-type specific cortical microcircuit: Relating structure and activity in a full-scale spiking network model. Cereb. Cortex 2014, 24, 785–806. [Google Scholar] [CrossRef]
- Schuecker, J.; Schmidt, M.; van Albada, S.; Diesmann, M.; Helias, M. Fundamental activity constraints lead to specific interpretations of the connectome. PLoS Comput. Biol. 2017, 13, e1005179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamamoto, H.; Moriya, S.; Ide, K.; Hayakawa, T.; Akima, H.; Sato, S.; Kubota, S.; Tanii, T.; Niwano, M.; Teller, S.; et al. Impact of modular organization on dynamical richness in cortical networks. Sci. Adv. 2018, 4, eaau4914. [Google Scholar] [CrossRef] [Green Version]
- Avena-Koenigsberger, A.; Misic, B.; Sporns, O. Communication dynamics in complex brain networks. Nat. Rev. Neurosci. 2018, 19, 17. [Google Scholar] [CrossRef] [PubMed]
- Laughlin, S.B.; Sejnowski, T.J. Communication in neuronal networks. Science 2003, 301, 1870–1874. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tkačik, G.; Bialek, W. Information processing in living systems. Annu. Rev. Condens. Matter Phys. 2016, 7, 89–117. [Google Scholar] [CrossRef] [Green Version]
- Friston, K.J. Functional and effective connectivity: A review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef]
- Van Den Heuvel, M.P.; Pol, H.H. Exploring the brain network: A review on resting-state fMRI functional connectivity. Eur. Neuropsychopharm. 2010, 20, 519–534. [Google Scholar] [CrossRef]
- Mountcastle, V.B. The columnar organization of the neocortex. Brain 1997, 120, 701–722. [Google Scholar] [CrossRef] [Green Version]
- Hagmann, P.; Cammoun, L.; Gigandet, X.; Meuli, R.; Honey, C.J.; Wedeen, V.J.; Sporns, O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008, 6, e159. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186. [Google Scholar] [CrossRef]
- Kaiser, M.; Hilgetag, C.C. Optimal hierarchical modular topologies for producing limited sustained activation of neural networks. Front. Neuroinform. 2010, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Meunier, D.; Lambiotte, R.; Bullmore, E.T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 2010, 4, 200. [Google Scholar] [CrossRef] [Green Version]
- Shafi, R. Understanding the Hierarchical Organization of Large-Scale Networks Based on Temporal Modulations in Patterns of Neural Connectivity. J. Neurosci. 2018, 38, 3154–3156. [Google Scholar] [CrossRef]
- Wang, S.-J.; Hilgetag, C.; Zhou, C. Sustained activity in hierarchical modular neural networks: Self-organized criticality and oscillations. Front. Comput. Neurosci. 2011, 5, 30. [Google Scholar] [CrossRef] [Green Version]
- Tomov, P.; Pena, R.F.O.; Zaks, M.A.; Roque, A.C. Sustained oscillations, irregular firing, and chaotic dynamics in hierarchical modular networks with mixtures of electrophysiological cell types. Front. Comput. Neurosci. 2014, 8, 103. [Google Scholar] [CrossRef] [PubMed]
- Tomov, P.; Pena, R.F.O.; Roque, A.C.; Zaks, M.A. Mechanisms of self-sustained oscillatory states in hierarchical modular networks with mixtures of electrophysiological cell types. Front. Comput. Neurosci. 2016, 10, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ostojic, S. Two types of asynchronous activity in networks of excitatory and inhibitory spiking neurons. Nat. Neurosci. 2014, 17, 594–600. [Google Scholar] [CrossRef] [PubMed]
- Buehlmann, A.; Deco, G. Optimal information transfer in the cortex through synchronization. PLoS Comput. Biol. 2010, 6, e1000934. [Google Scholar] [CrossRef] [Green Version]
- Lukoševičius, M.; Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comput. Sci. Rev. 2009, 3, 127–149. [Google Scholar] [CrossRef]
- Rodriguez, N.; Izquierdo, E.; Ahn, Y.Y. Optimal modularity and memory capacity of neural reservoirs. Netw. Neurosci. 2019, 3, 551–566. [Google Scholar] [CrossRef]
- Zajzon, B.; Mahmoudian, S.; Morrison, A.; Duarte, R. Passing the message: Representation transfer in modular balanced networks. Front. Comput. Neurosci. 2019, 13, 79. [Google Scholar] [CrossRef] [Green Version]
- Shih, C.; Sporns, O.; Yuan, S.; Su, T.; Lin, Y.; Chuang, C.; Wang, T.; Lo, C.; Greenspan, R.J.; Chiang, A. Connectomics-based analysis of information flow in the Drosophila brain. Curr. Biol. 2015, 25, 1249–1258. [Google Scholar] [CrossRef] [Green Version]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Hilgetag, C.; Burns, G.; O’Neill, M.; Scannell, J.; Young, M. Anatomical connectivity defines the organization of clusters of cortical areas in the macaque monkey and the cat. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2000, 355, 91–101. [Google Scholar] [CrossRef]
- Hilgetag, C.; Kaiser, M. Clustered organization of cortical connectivity. Neuroinformatics 2004, 2, 353–360. [Google Scholar] [CrossRef]
- Hendry, S.H.; Schwark, H.D.; Jones, E.G.; Yan, J. Numbers and proportions of GABA-immunoreactive neurons in different areas of monkey cerebral cortex. J. Neurosci. 1987, 7, 1503–1519. [Google Scholar] [CrossRef]
- Markram, H.; Toledo-Rodriguez, M.; Wang, Y.; Gupta, A.; Silberberg, G.; Wu, C. Interneurons of the neocortical inhibitory system. Nat. Rev. Neurosci. 2004, 5, 793–807. [Google Scholar] [CrossRef] [PubMed]
- Isaacson, J.S.; Scanziani, M. How inhibition shapes cortical activity. Neuron 2011, 72, 231–243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fishell, G.; Kepecs, A. Interneuron types as attractors and controllers. Annu. Rev. Neurosci. 2020, 43, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Grün, S.; Rotter, S. Analysis of Parallel Spike Trains; Springer: Boston, MA, USA, 2010; Volume 7. [Google Scholar]
- Pena, R.F.O.; Vellmer, S.; Bernardi, D.; Roque, A.C.; Lindner, B. Self-consistent scheme for spike-train power spectra in heterogeneous sparse networks. Front. Comput. Neurosci. 2018, 12, 9. [Google Scholar] [CrossRef] [Green Version]
- Neiman, A.B.; Yakusheva, T.A.; Russell, D.F. Noise-induced transition to bursting in responses of paddlefish electroreceptor afferents. J. Neurophysiol. 2007, 98, 2795–2806. [Google Scholar] [CrossRef] [PubMed]
- Wieland, S.; Bernardi, D.; Schwalger, T.; Lindner, B. Slow fluctuations in recurrent networks of spiking neurons. Phys. Rev. E 2015, 92, 040901. [Google Scholar] [CrossRef] [Green Version]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef] [Green Version]
- Palmigiano, A.; Geisel, T.; Wolf, F.; Battaglia, D. Flexible information routing by transient synchrony. Nat. Neurosci. 2017, 20, 1014–1022. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Hansen, M.E.; Heiland, R.; Lumsdaine, A.; Litke, A.M.; Beggs, J.M. Extending transfer entropy improves identification of effective connectivity in a spiking cortical network model. PLoS ONE 2011, 6, e27431. [Google Scholar] [CrossRef] [PubMed]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from brains for biologically inspired computing. Front. Robot. AI 2015, 2, 5. [Google Scholar] [CrossRef] [Green Version]
- de Abril, I.M.; Yoshimoto, J.; Doya, K. Connectivity inference from neural recording data: Challenges, mathematical bases and research directions. Neural Netw. 2018, 102, 120–137. [Google Scholar]
- Wibral, M.; Pampu, N.; Priesemann, V.; Siebenhühner, F.; Seiwert, H.; Lindner, M.; Lizier, J.T.; Vicente, R. Measuring information-transfer delays. PLoS ONE 2013, 8, e55809. [Google Scholar] [CrossRef] [PubMed]
- Stimberg, M.; Brette, R.; Goodman, D. Brian 2: An intuitive and efficient neural simulator. eLife 2019, 8, e47314. [Google Scholar] [CrossRef]
- Repositories: InfoPy, and HMnetwork. Available online: github.com/ViniciusLima94 (accessed on 9 April 2020).
- Bair, W.; Koch, C.; Newsome, W.; Britten, K. Power spectrum analysis of bursting cells in area mt in the behaving monkey. J. Neurosci. 1994, 14, 2870–2892. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brunel, M. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J. Comput. Neurosci. 2000, 8, 183–208. [Google Scholar] [CrossRef]
- Renart, A.; Rocha, J.D.L.; Bartho, P.; Hollender, L.; Parga, N.; Reyes, A.; Harris, K.D. The Asynchronous State in Cortical Circuits. Science 2010, 327, 587. [Google Scholar] [CrossRef] [Green Version]
- Pena, R.F.O.; Zaks, M.A.; Roque, A.C. Dynamics of spontaneous activity in random networks with multiple neuron subtypes and synaptic noise. J. Comput. Neurosci. 2018, 45, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Litwin-Kumar, A.; Doiron, B. Slow dynamics and high variability in balanced cortical networks with clustered connections. Nat. Neurosci. 2012, 15, 1498. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sporns, O.; Chialvo, D.R.; Kaiser, M.; Hilgetag, C.C. Organization, development and function of complex brain networks. Trends Cogn. Sci. 2004, 8, 418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reijneveld, J.C.; Ponten, S.C.; Berendse, H.W.; Stam, C.J. The application of graph theoretical analysis to complex networks in the brain. Clin. Neurophysiol. 2007, 118, 2317–2331. [Google Scholar] [CrossRef] [PubMed]
- Kinouchi, O.; Copelli, M. Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2006, 2, 348. [Google Scholar] [CrossRef] [Green Version]
- Galán, R.F.; Fourcaud-Trocme, N.; Ermentrout, G.B.; Urban, N.N. Correlation-induced synchronization of oscillations in olfactory bulb neurons. J. Neurosci. 2006, 26, 3646. [Google Scholar] [CrossRef] [Green Version]
- Moreno-Bote, R.; Renart, A.; Parga, N. Theory of input spike auto- and cross-correlations and their effect on the response of spiking neurons. Neural Comput. 2008, 20, 1651. [Google Scholar] [CrossRef]
- Barreiro, A.K.; Ly, C. Investigating the correlation–firing rate relationship in heterogeneous recurrent networks. J. Math. Neurosci. 2018, 8, 8. [Google Scholar] [CrossRef] [Green Version]
- Sporns, O.; Tononi, G.; Edelman, G.M. Theoretical neuroanatomy: Relating anatomical and functional connectivity in graphs and cortical connection matrices. Cereb. Cortex 2000, 10, 127–141. [Google Scholar] [CrossRef] [Green Version]
- Vincent, B.T.; Baddeley, R.J. Synaptic energy efficiency in retinal processing. Vis. Res. 2003, 43, 1285–1292. [Google Scholar] [CrossRef] [Green Version]
- Harris, J.J.; Jolivet, R.; Attwell, D. Synaptic energy use and supply. Neuron 2012, 75, 762–777. [Google Scholar] [CrossRef] [Green Version]







| PARAMETERS | ||
|---|---|---|
| Neuron parameters | ||
| Name | Value | Description |
| 20 ms | Membrane time constant | |
| 20 mV | Firing threshold | |
| 10 mV | Reset potential | |
| 0.5 ms | Refractory period | |
| 30 mV | External input | |
| Network connectivity parameters | ||
| Name | Value | Description |
| N | Size of excitatory population | |
| Connectivity | ||
| Excitatory rewiring probability | ||
| 1 | Inhibitory rewiring probability | |
| Synaptic parameters | ||
| Name | Value | Description |
| J | mV | Excitatory synaptic strength |
| g | 5 | Relative inhibitory synaptic strength |
| ms | Synaptic delay | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pena, R.F.O.; Lima, V.; O. Shimoura, R.; Paulo Novato, J.; Roque, A.C. Optimal Interplay between Synaptic Strengths and Network Structure Enhances Activity Fluctuations and Information Propagation in Hierarchical Modular Networks. Brain Sci. 2020, 10, 228. https://doi.org/10.3390/brainsci10040228
Pena RFO, Lima V, O. Shimoura R, Paulo Novato J, Roque AC. Optimal Interplay between Synaptic Strengths and Network Structure Enhances Activity Fluctuations and Information Propagation in Hierarchical Modular Networks. Brain Sciences. 2020; 10(4):228. https://doi.org/10.3390/brainsci10040228
Chicago/Turabian StylePena, Rodrigo F. O., Vinicius Lima, Renan O. Shimoura, João Paulo Novato, and Antonio C. Roque. 2020. "Optimal Interplay between Synaptic Strengths and Network Structure Enhances Activity Fluctuations and Information Propagation in Hierarchical Modular Networks" Brain Sciences 10, no. 4: 228. https://doi.org/10.3390/brainsci10040228
APA StylePena, R. F. O., Lima, V., O. Shimoura, R., Paulo Novato, J., & Roque, A. C. (2020). Optimal Interplay between Synaptic Strengths and Network Structure Enhances Activity Fluctuations and Information Propagation in Hierarchical Modular Networks. Brain Sciences, 10(4), 228. https://doi.org/10.3390/brainsci10040228