Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain
Abstract
:1. Introduction
2. Materials and Methods
3. Results
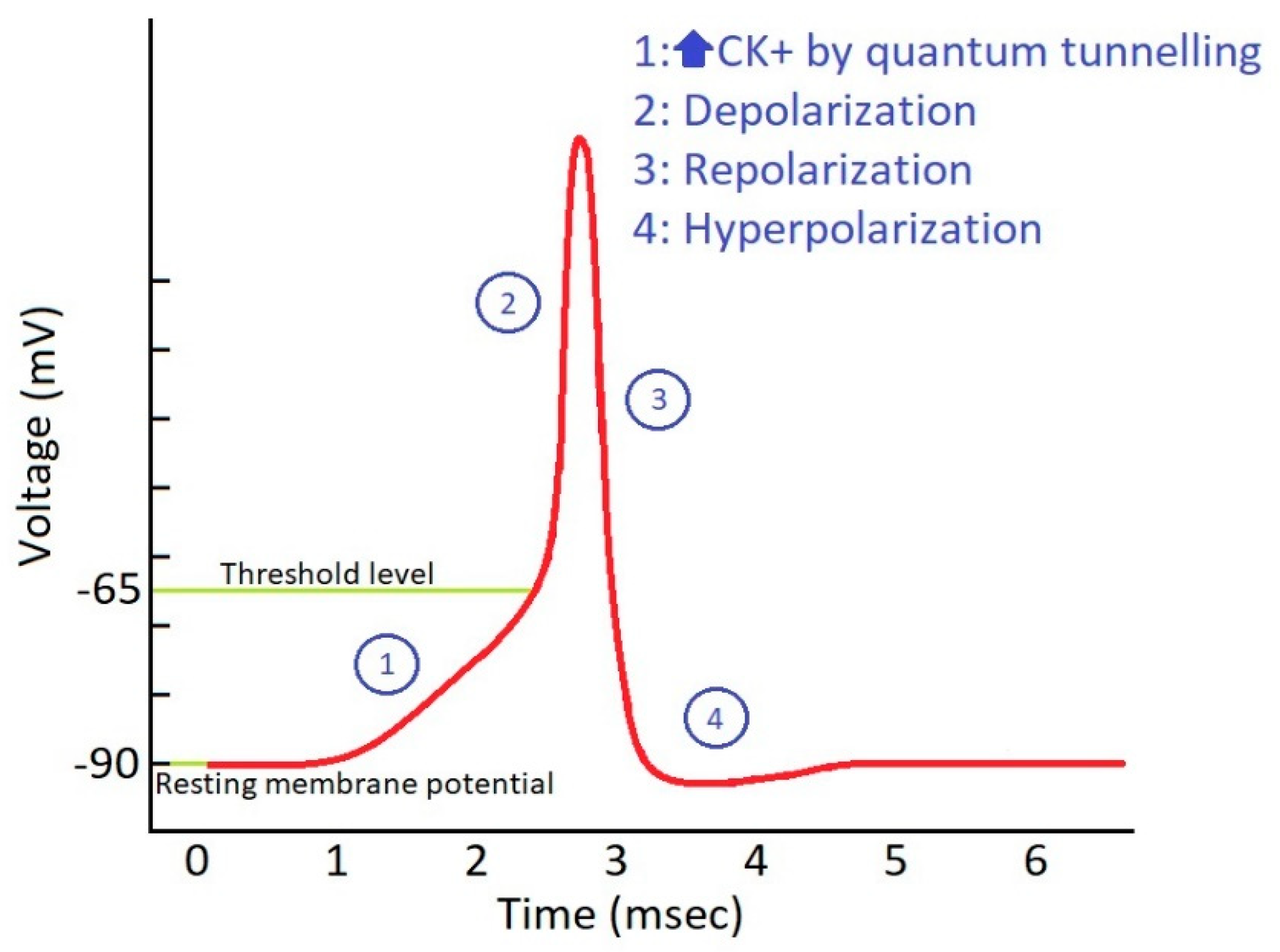
3.1. Repetitive Increases in Extracellular Potassium Concentration during Action Potential
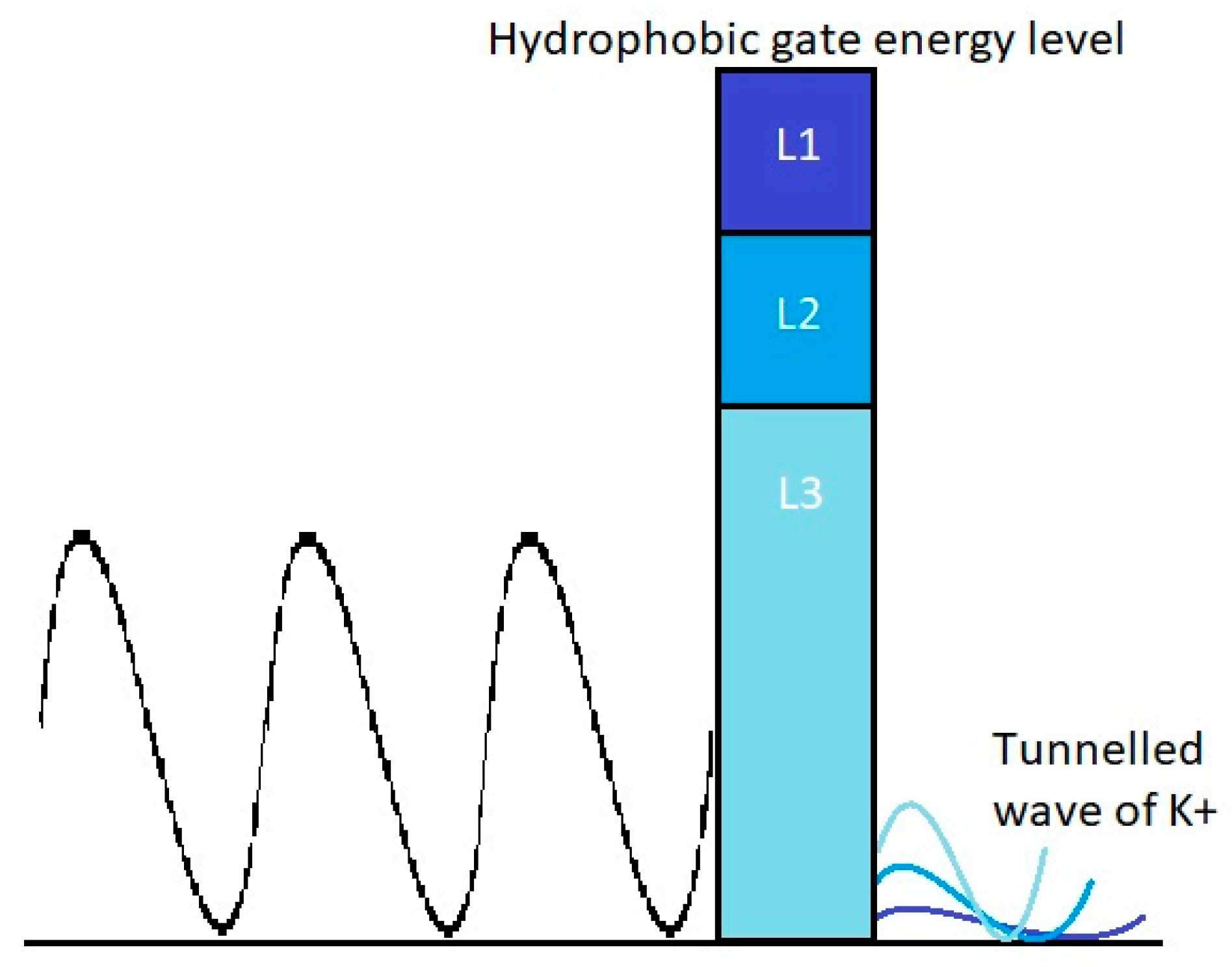
3.2. The Tunneling Probability of Potassium Ions through the Closed Gate of the Channels and Quantum Conductance
3.3. The Effect of Quantum Membrane Conductance of Potassium Ions on the Resting Membrane Potential
3.4. The Threshold Value of Quantum Conductance and Quantum Tunneling to Induce Action Potential
3.5. The Probability of Inducing an Action Potential in Phantom Limb Neurons
- When action potential happens, there will be ions/µm2 [48] and there are 50 channels/µm2. Therefore, on average, there will be potassium ions trying to tunnel each channel [47]. Additionally, the tunneling probability, which represents the probability of success in passing the closed channel (P), is . However, in section D, the threshold tunneling probability to induce an action potential is which also represents the sufficient fraction of potassium ions that must tunnel to induce action potential. Therefore, if one of the 87 potassium ions tunneled, there will be a fraction of 1/87 = , which is higher than threshold, and will be enough to induce an action potential. Therefore, the probability that at least one of the 87 potassium ions will tunnel through the closed channel is:
- Furthermore, for the sake of simplicity, it is assumed that one channel is enough to induce the action potential. Therefore, the probability that at least one channel from the 50 channels/µm2 in the membrane of unmyelinated neurons will be tunneled by a sufficient fraction of potassium ions is calculated as the following:
- Finally, the probability will depend on the surface area available for quantum tunneling; the larger the surface area, the higher the probability of inducing an action potential. For a surface area of 1 mm2, there will be 106 times of (1) µm2. If one of these areas was tunneled by a sufficient fraction of potassium ions, action potential will be induced and propagated along the axon to be transmitted to the brain and perceived as PLP. Therefore, stimulation of at least one area will be enough to transmit the action potential to the brain. Thus, the probability that at least one area is stimulated by quantum tunneling is:
4. Discussion
4.1. Scope and Rationale
4.2. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weeks, S.; Anderson-Barnes, V.; Tsao, J. Phantom limb pain: Theories and therapies. Neurologist 2010, 16, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Weinstein, S. Phantom limb pain and related disorders. Neurol. Clin. 1998, 16, 919–935. [Google Scholar] [CrossRef]
- Probstner, D.; Thuler, L.; Ishikawa, N.; Alvarenga, R. Phantom limb phenomena in cancer amputees. Pain Pract. 2010, 10, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Subedi, B.; Grossberg, G. Phantom limb pain: Mechanisms and treatment approaches. Pain Res. Treat 2011, 2011, 864605. [Google Scholar] [CrossRef]
- Richardson, C.; Glenn, S.; Nurmikko, T.; Horgan, M. Incidence of phantom phenomena including phantom limb pain 6 months after major lower limb amputation in patients with peripheral vascular disease. Clin. J. Pain 2006, 22, 353–358. [Google Scholar] [CrossRef]
- Davidson, J.; Khor, K.; Jones, L. A cross-sectional study of post-amputation pain in upper and lower limb amputees, experience of a tertiary referral amputee clinic. Disabil. Rehabil. 2010, 32, 1855–1862. [Google Scholar] [CrossRef]
- De Broglie, L. The wave nature of the electron. Nobel Lect. 1929, 12, 244–256. [Google Scholar]
- Birbaumer, N.; Lutzenberger, W.; Montoya, P.; Larbig, W.; Unertl, K.; Töpfner, S.; Grodd, W.; Taub, E.; Flor, H. Effects of regional anesthesia on phantom limb pain are mirrored in changes in cortical reorganization. J. Neurosci. 1997, 17, 5503–5508. [Google Scholar] [CrossRef]
- Flor, H.; Elbert, T.; Knecht, S.; Wienbruch, C.; Pantev, C.; Birbaumer, N.; Larbig, W.; Taub, E. Phantom-limb pain as a perceptual correlate of cortical reorganization following arm amputation. Nature 1995, 375, 482–484. [Google Scholar] [CrossRef]
- Jiang, G.; Yin, X.; Li, C.; Li, L.; Zhao, L.; Evans, A.; Jiang, T.; Wu, J.; Wang, J. The plasticity of brain grey matter and white matter following lower limb amputation. Neural. Plast 2015, 2015, 823185. [Google Scholar] [CrossRef] [Green Version]
- Merzenich, M.; Kaas, J.; Wall, J.; Nelson, R.; Sur, M.; Felleman, D. Topographic reorganization of somatosensory cortical areas 3b and 1 in adult monkeys following restricted deafferentation. Neuroscience 1983, 8, 33–55. [Google Scholar] [CrossRef]
- Vartiainen, N.; Kirveskari, E.; Kallio-Laine, K.; Kalso, E.; Forss, N. Cortical reorganization in primary somatosensory cortex in patients with unilateral chronic pain. J. Pain 2009, 10, 854–859. [Google Scholar] [CrossRef] [PubMed]
- Botvinick, M.; Cohen, J. Rubber hands ‘feel’touch that eyes see. Nature 1998, 391, 756. [Google Scholar] [CrossRef]
- Flor, H. Phantom-limb pain: Characteristics, causes, and treatment. Lancet Neurol. 2002, 1, 182–189. [Google Scholar] [CrossRef]
- Melzack, R. Pain and the neuromatrix in the brain. J. Dent. Educ. 2001, 65, 1378–1382. [Google Scholar] [PubMed]
- Anderson-Barnes, V.; McAuliffe, C.; Swanberg, K.; Tsao, J. Phantom limb pain–a phenomenon of proprioceptive memory? Med. Hypotheses 2009, 73, 555–558. [Google Scholar] [CrossRef] [PubMed]
- Gentili, M.; Verton, C.; Kinirons, B.; Bonnet, F. Clinical perception of phantom limb sensation in patients with brachial plexus block. Eur. J. Anaesthesiol. 2002, 19, 105–108. [Google Scholar] [CrossRef]
- Ramachandran, V.; Hirstein, W. The perception of phantom limbs. The DO Hebb lecture. Brain J. Neurol. 1998, 121, 1603–1630. [Google Scholar] [CrossRef] [Green Version]
- Woolf, C.; Thompson, S. The induction and maintenance of central sensitization is dependent on N-methyl-D-aspartic acid receptor activation; implications for the treatment of post-injury pain hypersensitivity states. Pain 1991, 44, 293–299. [Google Scholar] [CrossRef]
- Koga, K.; Li, S.; Zhuo, M. Metabotropic glutamate receptor dependent cortical plasticity in chronic pain. Curr. Neuropharmacol. 2016, 14, 427–434. [Google Scholar] [CrossRef] [Green Version]
- Baron, R. Mechanisms of disease: Neuropathic pain—A clinical perspective. Nat. Clin. Pr. Neurol. 2006, 2, 95–106. [Google Scholar] [CrossRef] [PubMed]
- Govrin-Lippmann, R.; Devor, M. Ongoing activity in severed nerves: Source and variation with time. Brain Res. 1978, 159, 406–410. [Google Scholar] [CrossRef]
- Nikolajsen, L.; Jensen, T. Phantom limb pain. Br. J. Anaesth. 2001, 87, 107–116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dickinson, B.; Head, C.; Gitlow, S.; Osbahr, A., III. Maldynia: Pathophysiology and management of neuropathic and maladaptive pain—A report of the AMA Council on Science and Public Health. Pain Med. 2010, 11, 1635–1653. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Wall, P.; Ben-Dor, E.; Michaelis, M.; Amir, R.; Devor, M. Tactile allodynia in the absence of C-fiber activation: Altered firing properties of DRG neurons following spinal nerve injury. Pain 2000, 85, 503–521. [Google Scholar] [CrossRef]
- Wall, P.; Devor, M. Sensory afferent impulses originate from dorsal root ganglia as well as from the periphery in normal and nerve injured rats. Pain 1983, 17, 321–339. [Google Scholar] [CrossRef]
- Bannister, K.; Kucharczyk, M.; Dickenson, A. Hopes for the future of pain control. Pain 2017, 6, 117–128. [Google Scholar] [CrossRef] [Green Version]
- Basbaum, A.; Bautista, D.; Scherrer, G.; Julius, D. Cellular and molecular mechanisms of pain. Cell 2009, 139, 267–284. [Google Scholar] [CrossRef] [Green Version]
- Linley, J.; Rose, K.; Ooi, L.; Gamper, N. Understanding inflammatory pain: Ion channels contributing to acute and chronic nociception. Pflugers Arch. 2010, 459, 657–669. [Google Scholar] [CrossRef]
- Karanikolas, M.; Aretha, D.; Tsolakis, I.; Monantera, G.; Kiekkas, P.; Papadoulas, S.; Swarm, R.; Filos, K. Optimized Perioperative Analgesia Reduces Chronic Phantom Limb Pain Intensity, Prevalence, and FrequencyA Prospective, Randomized, Clinical Trial. Anesthesiology 2011, 114, 1144–1154. [Google Scholar] [CrossRef]
- Burchiel, K.; Russell, L. Effects of potassium channel-blocking agents on spontaneous discharges from neuromas in rats. J. Neurosurg. 1985, 63, 246–249. [Google Scholar] [CrossRef] [PubMed]
- Devor, M. Potassium channels moderate ectopic excitability of nerve-end neuromas in rats. Neurosci. Lett. 1983, 40, 181–186. [Google Scholar] [CrossRef]
- Du, X.; Gamper, N. Potassium channels in peripheral pain pathways: Expression, function and therapeutic potential. Curr. Neuropharmacol. 2013, 11, 621–640. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Klein, C.; Lennon, V.; Aston, P.; McKeon, A.; Pittock, S. Chronic pain as a manifestation of potassium channel-complex autoimmunity. Neurology 2012, 79, 1136–1144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Devor, M. Neuropathic pain: What do we do with all these theories? Acta Anaesthesiol. Scand. 2001, 45, 1121–1127. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Hao, H.; Yang, Y.; Huang, S.; Wang, C.; Gigout, S.; Ramli, R.; Li, X.; Jaworska, E.; Edwards, I.; et al. Local GABAergic signaling within sensory ganglia controls peripheral nociceptive transmission. J. Clin. Investig. 2017, 127, 1741–1756. [Google Scholar] [CrossRef] [Green Version]
- Kajander, K.; Wakisaka, S.; Bennett, G. Spontaneous discharge originates in the dorsal root ganglion at the onset of a painful peripheral neuropathy in the rat. Neurosci. Lett. 1992, 138, 225–228. [Google Scholar] [CrossRef]
- Navarro, X.; Meritxell, V.; Antoni, V. Neural plasticity after peripheral nerve injury and regeneration. Prog. Neurobiol. 2007, 82, 163–201. [Google Scholar] [CrossRef]
- Pagadala, P.; Park, C.; Bang, S.; Xu, Z.; Xie, R.; Liu, T.; Han, B.; Tracey, W.; Wang, F.; Ji, R. Loss of NR1 subunit of NMDARs in primary sensory neurons leads to hyperexcitability and pain hypersensitivity: Involvement of Ca2+-activated small conductance potassium channels. J. Neurosci. 2013, 33, 13425–13430. [Google Scholar] [CrossRef]
- Zhang, X.; Albers, K.; Gold, M. Inflammation-induced increase in nicotinic acetylcholine receptor current in cutaneous nociceptive DRG neurons from the adult rat. Neuroscience 2015, 284, 483–499. [Google Scholar] [CrossRef] [Green Version]
- Kaur, A.; Guan, Y. Phantom limb pain: A literature review. Chin. J. Traumatol. 2018, 21, 366–368. [Google Scholar] [CrossRef] [PubMed]
- Barjas, A. Quantum Tunneling of Ions through the Closed Voltage-Gated Channels of the Biological Membrane: A Mathematical Model and Implications. Quantum Rep. 2019, 1, 219–225. [Google Scholar] [CrossRef] [Green Version]
- Merali, Z. Solving Biology’s Mysteries Using Quantum Mechanics; Discover: Riverwoods, IL, USA, 2014. [Google Scholar]
- Trixler, F. Quantum tunnelling to the origin and evolution of life. Curr. Org. Chem. 2013, 17, 1758–1770. [Google Scholar] [CrossRef] [PubMed]
- Stroscio, J.; Kaiser, W. Scanning Tunneling Microscopy; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Qaswal, A. A Theoretical Study to Explain the Referred Pain Phenomenon and Its Characteristics via Quantum Tunneling of Potassium Ions Through the Channels of Neuronal Membrane. NeuroQuantology 2019, 17, 43–52. [Google Scholar]
- Barjas, A. The Myelin Sheath Maintains the Spatiotemporal Fidelity of Action Potentials by Eliminating the Effect of Quantum Tunneling of Potassium Ions through the Closed Channels of the Neuronal Membrane. Quantum Rep. 2019, 1, 287–294. [Google Scholar] [CrossRef] [Green Version]
- Labro, A.; Snyders, D. Being flexible: The voltage-controllable activation gate of Kv channels. Front Pharm. 2012, 3, 168. [Google Scholar] [CrossRef] [Green Version]
- Serway, R.; Moses, C.; Moyer, C. Modern Physics; Cengage Learning: Boston, MA, USA, 2004. [Google Scholar]
- Hall, J. Guyton & Hall Physiology Review; Elsevier: Amsterdam, The Netherlands, 2015; pp. 57–71. [Google Scholar]
- Chen, F.; Hihath, J.; Huang, Z.; Li, X.; Tao, N. Measurement of single-molecule conductance. Annu. Rev. Phys. Chem. 2007, 58, 535–564. [Google Scholar] [CrossRef] [Green Version]
- Caldwell, J.H. Action Potential Initiation and Conduction in Axons; Elsevier: Amsterdam, The Netherlands, 2009; pp. 23–29. [Google Scholar]
- Grammer, G.; Williams-Joseph, S.; Cesar, A.; Adkinson, D.; Spevak, C. Significant reduction in phantom limb pain after low-frequency repetitive transcranial magnetic stimulation to the primary sensory cortex. Mil. Med. 2015, 180, e126–e128. [Google Scholar] [CrossRef] [Green Version]
- Karl, A.; Mühlnickel, W.; Kurth, R.; Flor, H. Neuroelectric source imaging of steady-state movement-related cortical potentials in human upper extremity amputees with and without phantom limb pain. Pain 2004, 110, 90–102. [Google Scholar] [CrossRef]
- Makin, T.; Scholz, J.; Henderson, D.; Johansen-Berg, H.; Tracey, I. Reassessing cortical reorganization in the primary sensorimotor cortex following arm amputation. Brain 2015, 138, 2140–2146. [Google Scholar] [CrossRef] [Green Version]
- Penfield, W.; Faulk, M., Jr. The insula: Further observations on its function. Brain 1955, 78, 445–470. [Google Scholar] [CrossRef] [PubMed]
- Yanagisawa, T.; Fukuma, R.; Seymour, B.; Hosomi, K.; Kishima, H.; Shimizu, T.; Yokoi, H.; Hirata, M.; Yoshimine, T.; Kamitani, Y.; et al. Induced sensorimotor brain plasticity controls pain in phantom limb patients. Nat. Commun. 2016, 7, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sahin, S.; Colak, A.; Arar, C.; Tutunculer, E.; Sut, N.; Yılmaz, B.; Birtane, M. A retrospective trial comparing the effects of different anesthetic techniques on phantom pain after lower limb amputation. Curr. Res. 2011, 72, 127–137. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carlen, P.; Wall, P.; Nadvorna, H.; Steinbach, T. Phantom limbs and related phenomena in recent traumatic amputations. Neurology 1978, 28, 211. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.; Kiss, Z.; Luo, L.; Tasker, R.; Lozano, A.; Dostrovsky, J. Phantom sensations generated by thalamic microstimulation. Nature 1998, 391, 385–387. [Google Scholar] [CrossRef] [PubMed]
- Devor, M. Neuropathic Pain: Pathophysiological Response of Nerves to Injury. In Wall and Melzack’s Textbook of Pain; Elsevier: Amsterdam, The Netherlands, 2013; pp. 861–888. [Google Scholar]
- Jensen, T.; Krebs, B.; Nielsen, J.; Rasmussen, P. Immediate and long-term phantom limb pain in amputees: Incidence, clinical characteristics and relationship to pre-amputation limb pain. Pain 1985, 21, 267–278. [Google Scholar] [CrossRef]
- Livingston, K. The phantom limb syndrome. A discussion of the role of major peripheral nerve neuromas. J. Neurosurg. 1945, 2, 251–255. [Google Scholar] [CrossRef]
- Livingston, W. Fantom Limb Pain: A Report of Ten Cases in Which It Was Treated by Injections of Procaine Hydrochloride Near the Thoracic Sympathetic Ganglions. Arch. Surg. 1938, 37, 353–370. [Google Scholar] [CrossRef]
- Mitchell, S. Injuries of Nerves and Their Consequences; JB Lippincott: Philadelphia, PA, USA, 1872; pp. 94–108. [Google Scholar]
- Molotkoff, A. The source of pain in amputation stumps in relation to the rational treatment. JBJS 1935, 17, 419–423. [Google Scholar]
- Lopez, G.; Ian, Y.; Ian, L. Hydrophobic substitution mutations in the S4 sequence alter voltage-dependent gating in Shaker K+ channels. Neuron 1991, 7, 327–336. [Google Scholar] [CrossRef]
- Hanley, M.; Jensen, M.; Smith, D.; Ehde, D.; Edwards, W.; Robinson, L. Preamputation pain and acute pain predict chronic pain after lower extremity amputation. J. Pain 2007, 8, 102–109. [Google Scholar] [CrossRef] [PubMed]
- Bach, S.; Noreng, M.; Tjéllden, N. Phantom limb pain in amputees during the first 12 months following limb amputation, after preoperative lumbar epidural blockade. Pain 1988, 33, 297–301. [Google Scholar] [CrossRef]
- Nikolajsen, L.; Ilkjær, S.; Krøner, K.; Christensen, J.; Jensen, T. The influence of preamputation pain on postamputation stump and phantom pain. Pain 1997, 72, 393–405. [Google Scholar] [CrossRef]
- Weiss, S.; Lindell, B. Phantom limb pain and etiology of amputation in unilateral lower extremity amputees. J. Pain Symptom. Manag. 1996, 11, 3–17. [Google Scholar] [CrossRef]
- Kooijman, C.; Dijkstra, P.; Geertzen, J.; Elzinga, A.; van der Schans, C. Phantom pain and phantom sensations in upper limb amputees: An epidemiological study. Pain 2000, 87, 33–41. [Google Scholar] [CrossRef]
- Schley, M.; Wilms, P.; Toepfner, S.; Schaller, H.; Schmelz, M.; Konrad, C.; Birbaumer, N. Painful and nonpainful phantom and stump sensations in acute traumatic amputees. J. Trauma Acute Care Surg. 2008, 65, 858–864. [Google Scholar] [CrossRef]
- Srivastava, D. Chronic post-amputation pain: Peri-operative management–review. Br. J. Pain 2017, 11, 192–202. [Google Scholar] [CrossRef]
- Houghton, A.; Nicholls, G.; Houghton, A.; Saadah, E.; McColl, L. Phantom pain: Natural history and association with rehabilitation. Ann. R. Coll. Surg. Engl. 1994, 76, 22. [Google Scholar]
- Wartan, S.; Hamann, W.; Wedley, J.; McColl, I. Phantom pain and sensation among British veteran amputees. Br. J. Anaesth. 1997, 78, 652–659. [Google Scholar] [CrossRef]
- Katz, J.; Melzack, R. Pain ‘memories’ in phantom limbs: Review and clinical observations. Pain 1990, 43, 319–336. [Google Scholar] [CrossRef] [Green Version]
- Coleman, M.; Freeman, M. Wallerian degeneration, wlds, and nmnat. Annu. Rev. Neurosci. 2010, 33, 245–267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Devor, M. Sodium channels and mechanisms of neuropathic pain. J. Pain 2006, 7, S3–S12. [Google Scholar] [CrossRef] [PubMed]
- Flor, H.; Nikolajsen, L.; Jensen, T. Phantom limb pain: A case of maladaptive CNS plasticity? Nat. Rev. Neurosci. 2006, 7, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Waxman, S.; Cummins, T.; Dib-Hajj, S.; Black, J. Voltage-gated sodium channels and the molecular pathogenesis of pain: A review. J. Rehabil. Res. Dev. 2000, 37, 517–528. [Google Scholar]
- Waxman, S.; Dib-Hajj, S.; Cummins, T.; Black, J. Sodium channels and pain. Proc. Natl. Acad. Sci. USA 1999, 96, 7635–7639. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Cendan, C.; Roza, C.; Okuse, K.; Cramer, R.; Timms, J.; Wood, J. Proteomic profiling of neuromas reveals alterations in protein composition and local protein synthesis in hyper-excitable nerves. Mol. Pain 2008, 4, 33. [Google Scholar] [CrossRef] [Green Version]
- Nassar, M.; Baker, M.; Levato, A.; Ingram, R.; Mallucci, G.; McMahon, S.; Wood, J. Nerve injury induces robust allodynia and ectopic discharges in Nav1. 3 null mutant mice. Mol. Pain 2006, 2, 1744–8069. [Google Scholar] [CrossRef] [Green Version]
- Tsantoulas, C.; Zhu, L.; Shaifta, Y.; Grist, J.; Ward, J.; Raouf, R.; Michael, G.; McMahon, S. Sensory neuron downregulation of the Kv9. 1 potassium channel subunit mediates neuropathic pain following nerve injury. J. Neurosci. 2012, 32, 17502–17513. [Google Scholar] [CrossRef] [Green Version]
- Abdulla, F.; Smith, P. Axotomy-and autotomy-induced changes in Ca2+ and K+ channel currents of rat dorsal root ganglion neurons. J. Neurophysiol. 2001, 85, 644–658. [Google Scholar] [CrossRef] [Green Version]
- Everill, B.; Kocsis, J. Reduction in potassium currents in identified cutaneous afferent dorsal root ganglion neurons after axotomy. J. Neurophysiol. 1999, 82, 700–708. [Google Scholar] [CrossRef] [Green Version]
- Rae, A. Quantum Physics: A Beginner’s Guide; Oneworld Publications: London, UK, 2005; pp. 27–49. [Google Scholar]
- Wilkins, K.; McGrath, P.; Finley, G.; Katz, J. Phantom limb sensations and phantom limb pain in child and adolescent amputees. Pain 1998, 78, 7–12. [Google Scholar] [CrossRef] [Green Version]
- Pazzaglia, M.; Leemhuis, E.; Giannini, A.M.; Haggard, P. The homuncular jigsaw: Investigations of phantom limb and body awareness following brachial plexus block or avulsion. J. Clin. Med. 2019, 8, 182. [Google Scholar] [CrossRef] [PubMed] [Green Version]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrabayah, M.; Qaswal, A.B.; Suleiman, A.; Khreesha, L. Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain. Brain Sci. 2020, 10, 241. https://doi.org/10.3390/brainsci10040241
Alrabayah M, Qaswal AB, Suleiman A, Khreesha L. Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain. Brain Sciences. 2020; 10(4):241. https://doi.org/10.3390/brainsci10040241
Chicago/Turabian StyleAlrabayah, Mustafa, Abdallah Barjas Qaswal, Aiman Suleiman, and Lubna Khreesha. 2020. "Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain" Brain Sciences 10, no. 4: 241. https://doi.org/10.3390/brainsci10040241
APA StyleAlrabayah, M., Qaswal, A. B., Suleiman, A., & Khreesha, L. (2020). Role of Potassium Ions Quantum Tunneling in the Pathophysiology of Phantom Limb Pain. Brain Sciences, 10(4), 241. https://doi.org/10.3390/brainsci10040241





