Quantifying the Child–Therapist Interaction in ASD Intervention: An Observational Coding System
Abstract
1. Introduction
Aims and Hypotheses
2. Materials and Methods
2.1. Participants
2.2. Measures
2.2.1. Observational Coding Scheme
Interaction Units
2.2.2. Griffith Mental Development Scales—Edition Revised
2.2.3. Autism Diagnostic Observation Schedule—Second Edition
2.2.4. Emotional Availability Scales
2.3. Early Developmental Intervention
2.4. Procedure
2.5. Data Extraction
2.6. Statistical Analysis
3. Results
3.1. Demographic and General Statistics
3.2. Analytic Plan
3.3. Hypothesis 1: Longitudinal Changes
3.3.1. Interaction Structure
3.3.2. Interaction Dynamics
3.3.3. Longitudinal Changes in Developmental Trajectories and Symptoms Severity
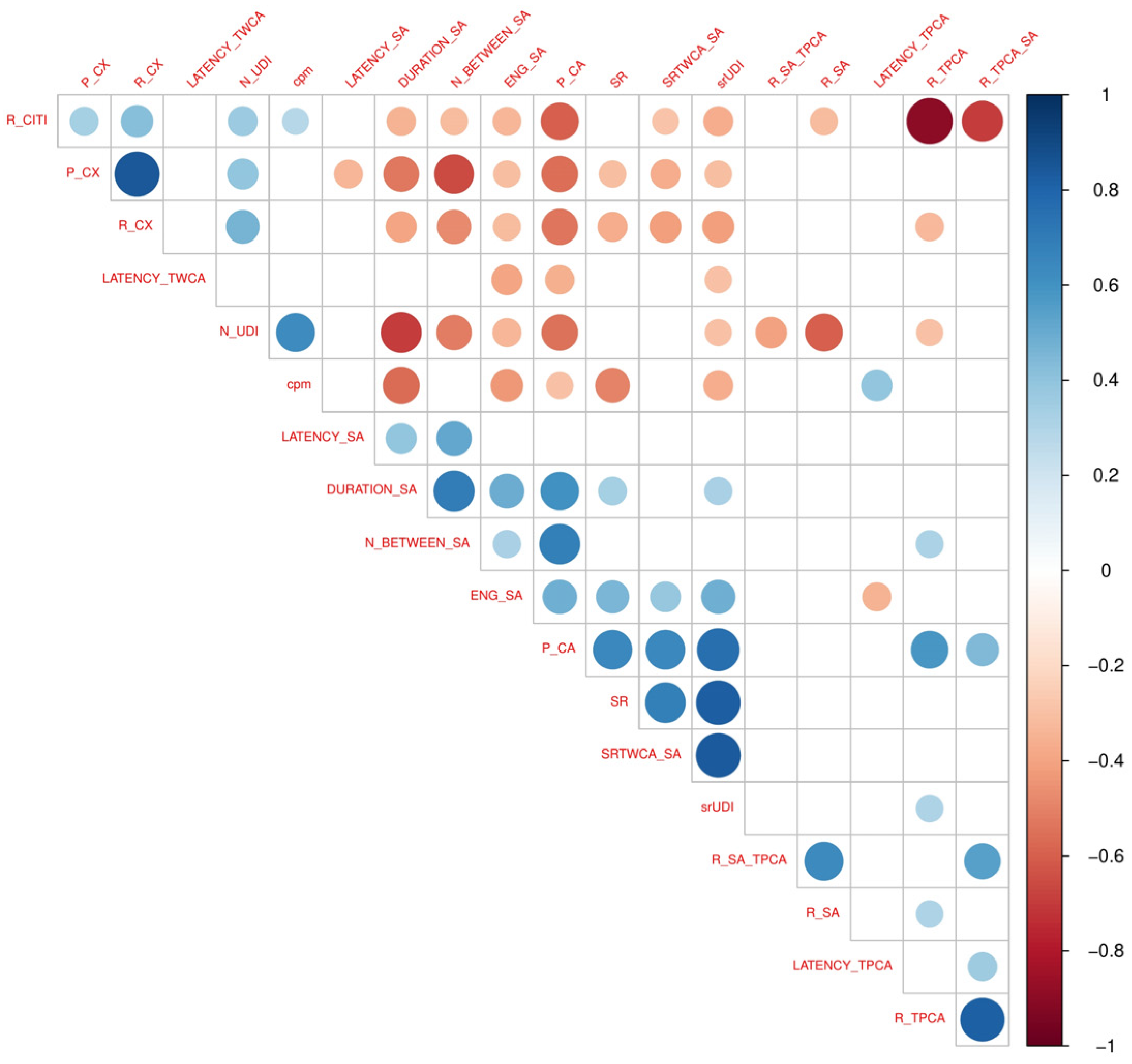
3.4. Hypothesis 2: Convergent Validity
3.5. Hypothesis 3: Outcome Models
3.5.1. Predictive Validity: Relations between Developmental Outcomes, Symptoms Severity and Behavioral Descriptors
3.5.2. Longitudinal Validity
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Apicella, F.; Chericoni, N.; Costanzo, V.; Baldini, S.; Billeci, L.; Cohen, D.; Muratori, F. Reciprocity in Interaction: A Window on the First Year of Life in Autism. Autism Res. Treat. 2013, 2013, 705895. [Google Scholar] [CrossRef]
- Cohen, D. Enfance et Psychopathologie, 9th ed.; Marcelli, D., Ed.; Elsevier Masson: Paris, France, 2012. [Google Scholar] [CrossRef]
- Chorney, J.M.; McMurtry, C.M.; Chambers, C.T.; Bakeman, R. Developing and Modifying Behavioral Coding Schemes in Pediatric Psychology: A Practical Guide. J. Pediatric Psychol. 2015, 40, 154–164. [Google Scholar] [CrossRef]
- Goodwin, C.J. Research in Psychology: Methods and Design; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ramchandani, P.G.; Domoney, J.; Sethna, V.; Psychogiou, L.; Vlachos, H.; Murray, L. Do Early Father-Infant Interactions Predict the Onset of Externalising Behaviours in Young Children? Findings from a Longitudinal Cohort Study. J. Child Psychol. Psychiatry Allied Discip. 2013, 54, 56–64. [Google Scholar] [CrossRef] [PubMed]
- Wan, M.W.; Green, J.; Elsabbagh, M.; Johnson, M.; Charman, T.; Plummer, F.; Basis Team. Quality of Interaction between At-Risk Infants and Caregiver at 12-15 Months Is Associated with 3-Year Autism Outcome. J. Child Psychol. Psychiatryand Allied Discip. 2013, 54, 763–771. [Google Scholar] [CrossRef] [PubMed]
- Anglemyer, A.; Horvath, H.T.; Bero, L. Healthcare Outcomes Assessed with Observational Study Designs Compared with Those Assessed in Randomized Trials. Cochrane Database Syst. Rev. 2014. [Google Scholar] [CrossRef] [PubMed]
- Elm, E.; Altman, D.G.; Egger, M.; Pocock, S.J.; Gøtzsche, P.C.; Vandenbroucke, J.P.; Strobe Initiative. The Strengthening the Reporting of Observational Studies in Epidemiology (STROBE) Statement: Guidelines for Reporting Observational Studies. PLoS Med. 2007, 4, e296. [Google Scholar] [CrossRef]
- Vandenbroucke, J.P. Observational Research, Randomised Trials, and Two Views of Medical Science. PLoS Med. 2008, 5, e67. [Google Scholar] [CrossRef]
- Booth, C.; Tannock, I. Randomised controlled trials and population-based observational research: Partners in the evolution of medical evidence. Br. J. Cancer 2014, 110, 551–555. [Google Scholar] [CrossRef]
- Mann, C.J. Observational Research Methods. Research Design II: Cohort, Cross Sectional, and Case-Control Studies. Emerg. Med. J. 2003, 20, 54–60. [Google Scholar] [CrossRef]
- Little, T.D. The Oxford Handbook of Quantitative Methods in Psychology; Oxford University Press: Oxford, UK, 2013; Volume 1. [Google Scholar]
- Nigam, S.; Singh, R.; Misra, A.K. A Review of Computational Approaches for Human Behavior Detection. Arch Comput. Methods Eng. 2019, 26, 831–863. [Google Scholar] [CrossRef]
- Washington, P.; Park, N.; Srivastava, P.; Voss, C.; Kline, A.; Varma, M.; Tariq, Q.; Kalantarian, H.; Schwartz, J.; Patnaik, R.; et al. Data-Driven Diagnostics and the Potential of Mobile Artificial Intelligence for Digital Therapeutic Phenotyping in Computational Psychiatry. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2019, 5, 759–769. [Google Scholar] [CrossRef] [PubMed]
- Jacob, S.; Wolff, J.J.; Steinbach, M.S. Neurodevelopmental Heterogeneity and Computational Approaches for Understanding Autism. Transl. Psychiatry 2019, 9, 63. [Google Scholar] [CrossRef] [PubMed]
- Sameroff, A. The Transactional Model. In The Transactional Model of Development: How Children and Contexts Shape Each Other; Sameroff, A., Ed.; American Psychological Association: Washington, DC, USA, 2009; pp. 3–21. [Google Scholar] [CrossRef]
- Meltzoff, A.N.; Kuhl, P.K.; Movellan, J.; Sejnowski, T.J. Foundations for a New Science of Learning. Science 2009, 325, 284–288. [Google Scholar] [CrossRef]
- Venuti, P.; Bentenuto, A.; Cainelli, S.; Landi, I.; Suvini, F.; Tancredi, R.; Muratori, F. A Joint Behavioral and Emotive Analysis of Synchrony in Music Therapy of Children with Autism Spectrum Disorders. Health Psychol. Rep. 2017, 5, 162–172. [Google Scholar] [CrossRef]
- Feldman, R. Parent–Infant Synchrony: Biological Foundations and Developmental Outcomes. Curr. Dir. Psychol. Sci. 2007, 16, 340–345. [Google Scholar] [CrossRef]
- Beebe, B.; Messinger, D.; Bahrick, L.E.; Margolis, A.; Buck, K.A.; Chen, H. A Systems View of Mother-Infant Face-to-Face Communication. Dev. Psychol. 2016, 52, 556–571. [Google Scholar] [CrossRef] [PubMed]
- Bloch, C.; Vogeley, K.; AL, G.; Falter-Wagner, C.M. INTRApersonal Synchrony as Constituent of INTERpersonal Synchrony and Its Relevance for Autism Spectrum Disorder. Front. Robot. AI 2019, 6. [Google Scholar] [CrossRef]
- Noel, J.P.; De Niear, N.S.; Lazzara, M.A.; Wallace, M.T. Uncoupling Between Multisensory Temporal Function and Nonverbal Turn-Taking in Autism Spectrum Disorder. IEEE Trans. Cogn. Dev. Syst. 2018, 10, 973–982. [Google Scholar] [CrossRef]
- Fitzpatrick, P.; Romero, V.; Amaral, J.L.; Duncan, A.; Barnard, H.; Richardson, M.J.; Schmidt, R.C. Evaluating the Importance of Social Motor Synchronization and Motor Skill for Understanding Autism. Autism Res. Off. J. Int. Soc. Autism Res. 2017, 10, 1687–1699. [Google Scholar] [CrossRef]
- Delaherche, E.; Chetouani, M.; Bigouret, F.; Xavier, J.; Plaza, M.; Cohen, D. Assessment of the Communicative and Coordination Skills of Children with Autism Spectrum Disorders and Typically Developing Children Using Social Signal Processing. Res. Autism Spectr. Disord. 2013, 7, 741–756. [Google Scholar] [CrossRef]
- Esposito, G.; Venuti, P.; Maestro, S.; Muratori, F. An exploration of symmetry in early autism spectrum disorders: Analysis of lying. Brain Dev. 2009, 31, 131–138. [Google Scholar] [CrossRef]
- Esposito, G.; Venuti, P. Comparative Analysis of Crying in Children with Autism, Developmental Delays, and Typical Development. Focus Autism Other Dev. Disabil. 2009, 24, 240–247. [Google Scholar] [CrossRef]
- Siller, M.; Sigman, M. The Behaviors of Parents of Children with Autism Predict the Subsequent Development of Their Children’s Communication. J. Autism Dev. Disord. 2002, 32, 77–89. [Google Scholar] [CrossRef] [PubMed]
- de Falco, S.; Venuti, P.; Esposito, G.; Bornstein, M.H. Mother–Child and Father–Child Emotional Availability in Families of Children with Down Syndrome. Parent. Sci. Pract. 2009, 9, 198–215. [Google Scholar] [CrossRef]
- Ouss, L.; Palestra, G.; Saint-Georges, C.; Leitgel Gille, M.; Afshar, M.; Pellerin, H.; Bailly, K.; Chetouani, M.; Robel, L.; Golse, B.; et al. Behavior and Interaction Imaging at 9 Months of Age Predict Autism/Intellectual Disability in High-Risk Infants with West Syndrome. Transl. Psychiatry 2020, 10, 54. [Google Scholar] [CrossRef] [PubMed]
- Wan, M.W.; Green, J.; Scott, J. A Systematic Review of Parent–Infant Interaction in Infants at Risk of Autism. Autism 2019, 23, 811–820. [Google Scholar] [CrossRef] [PubMed]
- Leclère, C.; Avril, M.; Viaux-Savelon, S. Interaction and Behaviour Imaging: A Novel Method to Measure Mother–Infant Interaction Using Video 3D Reconstruction. Transl. Psychiatry 2016, 6, 816. [Google Scholar] [CrossRef] [PubMed]
- Robertson, C.E.; Baron-Cohen, S. Sensory Perception in Autism. Nat Rev Neurosci 2017, 18, 671–684. [Google Scholar] [CrossRef] [PubMed]
- Landa, R.J.; Holman, K.C.; O’Neill, A.H.; Stuart, E.A. Intervention Targeting Development of Socially Synchronous Engagement in Toddlers with Autism Spectrum Disorder: A Randomized Controlled Trial. J. Child Psychol. Psychiatryand Allied Discip. 2011, 52, 13–21. [Google Scholar] [CrossRef]
- Ng, M.Y.; Weisz, J.R. Annual Research Review: Building a Science of Personalized Intervention for Youth Mental Health. J. Child Psychol. Psychiatryand Allied Discip. 2016, 57, 216–236. [Google Scholar] [CrossRef]
- Lotzin, A.; Lu, X.; Kriston, L.; Schiborr, J.; Musal, T.; Romer, G.; Ramsauer, B. Observational Tools for Measuring Parent–Infant Interaction: A Systematic Review. Clin. Child Fam. Psychol. Rev. 2015, 18, 99–132. [Google Scholar] [CrossRef] [PubMed]
- Biringen, Z.; Derscheid, D.; Vliegen, N.; Closson, L.; Easterbrooks, M.A. Emotional Availability (EA): Theoretical Background, Empirical Research Using the EA Scales, and Clinical Applications. Dev. Rev. 2014, 34, 114–167. [Google Scholar] [CrossRef]
- Biringen, Z.; Robinson, J. Emotional availability in mother-child interactions: A reconceptualization for research. Am. J. Orthopsychiatry 1991, 61, 258–271. [Google Scholar] [CrossRef]
- Emde, R.N.; Easterbrooks, M.A. Assessing Emotional Availability in Early Development. In Early Identification of Children at Risk; Springer: Berlin/Heidelberg, Germany, 1985; pp. 79–101. [Google Scholar]
- Biringen, Z. The Emotional Availability (EA) Scales Manual: Part 1, Infancy/Early Childhood Version; 2008. Available online: http://www.emotionalavailability.com/wp-content/uploads/2009/08/Emotional-Availability-Trainings-Description.pdf (accessed on 12 March 2021).
- Perzolli, S.; Bertamini, G.; Falco, S.D.; Venuti, P.; Bentenuto, A. Emotional Availability and Play in Mother–Child Dyads with ASD: Changes during a Parental Based Intervention. Brain Sci. 2020, 10, 904. [Google Scholar] [CrossRef] [PubMed]
- Bentenuto, A.; Perzolli, S.; de Falco, S.; Venuti, P. The emotional availability in mother-child and father-child interactions in families with children with Autism Spectrum Disorder. Res. Autism Spectr. Disord. 2020, 75, 101569. [Google Scholar] [CrossRef]
- Dolev, S.; Oppenheim, D.; Koren-Karie, N.; Yirmiya, N. Emotional Availability in Mother-Child Interaction: The Case of Children with Autism Spectrum Disorders. Parent. Sci. Pract. 2009, 9, 183–197. [Google Scholar] [CrossRef]
- Bakeman, R.; Quera, V. Sequential Analysis and Observational Methods for the Behavioral Sciences; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Cicchetti, D.V.; Klin, A.; Volkmar, F.R. Assessing Binary Diagnoses of Bio-Behavioral Disorders: The Clinical Relevance of Cohen’s Kappa. J. Nerv. Ment. Dis. 2017, 205, 58–65. [Google Scholar] [CrossRef]
- Liljequist, D.; Elfving, B.; Skavberg Roaldsen, K. Intraclass Correlation—A Discussion and Demonstration of Basic Features. PLoS ONE 2019, 14, e0219854. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, M.; Capozzoli, M.; McSweeney, L.; Sinha, D. Beyond Kappa: A Review of Interrater Agreement Measures. Can. J. Stat. 1999, 27, 3–23. [Google Scholar] [CrossRef]
- Kazdin, A.E. Research Design in Clinical Psychology, 3rd ed.; Allyn & Bacon: Boston, MA, USA, 2003. [Google Scholar]
- Yoder, P.; Symons, F. Observational Measurement of Behavior; Springer Publishing Co.: New York, NY, USA, 2010. [Google Scholar]
- Delaherche, E.; Chetouani, M.; Mahdhaoui, A.; Saint-Georges, C.; Viaux, S.; Cohen, D. Interpersonal Synchrony: A Survey of Evaluation Methods across Disciplines. IEEE Trans. Affect. Comput. 2012, 3, 349–365. [Google Scholar] [CrossRef]
- Su, W.C.; Culotta, M.; Mueller, J.; Tsuzuki, D.; Pelphrey, K.; Bhat, A. Differences in Cortical Activation Patterns during Action Observation, Action Execution, and Interpersonal Synchrony between Children with or without Autism Spectrum Disorder (ASD): An FNIRS Pilot Study. PLoS ONE 2020, 15, e0240301. [Google Scholar]
- Baltrušaitis, T.; Ahuja, C.; Morency, L. Multimodal Machine Learning: A Survey and Taxonomy. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 41, 423–443. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, J.M.; Bargh, J.A. Two to Tango: Automatic Social Coordination and the Role of Felt Effort. In Effortless Attention: A New Perspective in the Cognitive Science of Attention and Action; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Bernieri, F.J.; Rosenthal, R. Interpersonal Coordination: Behavior Matching and Interactional Synchrony. In Studies in Emotion & Social Interaction. Fundamentals of Nonverbal Behavior; Cambridge University Press: Cambridge, UK, 1991; pp. 401–432. [Google Scholar]
- Chartrand, T.L.; Lakin, J.L. The Antecedents and Consequences of Human Behavioral Mimicry. Annu. Rev. Psychol. 2013, 64, 285–308. [Google Scholar] [CrossRef] [PubMed]
- Dahan, A.; Noy, L.; Hart, Y.; Mayo, A.; Alon, U. Exit from Synchrony in Joint Improvised Motion. PLoS ONE 2016, 11, e0160747. [Google Scholar] [CrossRef] [PubMed]
- Ahn, S.; Cho, H.; Kwon, M.; Kim, K.; Kwon, H.; Kim, B.S.; Chang, W.S.; Chang, J.W.; Jun, S.C. Interbrain Phase Synchronization during Turn-taking Verbal Interaction—A Hyperscanning Study Using Simultaneous EEG/MEG. Hum. Brain Mapp. 2018, 39, 171–188. [Google Scholar] [CrossRef]
- Palumbo, R.V.; Marraccini, M.E.; Weyandt, L.L. Interpersonal Autonomic Physiology: A Systematic Review of the Literature. Pers. Soc. Psychol. Rev. 2017, 21, 99–141. [Google Scholar] [CrossRef] [PubMed]
- Mayo, O.; Gordon, I. In and out of Synchrony—Behavioral and Physiological Dynamics of Dyadic Interpersonal Coordination. Psychophysiology 2020, 57, e13574. [Google Scholar] [CrossRef] [PubMed]
- Chetouani, M.; Delaherche, E.; Dumas, G.; Cohen, D. Interpersonal Synchrony: From Social Perception to Social Interaction. In Social Signal Processing; Burgoon, J., Magnenat-Thalmann, N., Pantic, M., Vinciarelli, A., Eds.; Cambridge University Press: Cambridge, UK, 2017; pp. 202–212. [Google Scholar] [CrossRef]
- Galbusera, L.; Finn, M.T.M.; Tschacher, W. Interpersonal Synchrony Feels Good but Impedes Self-Regulation of Affect. Sci. Rep. 2019, 9, 14691. [Google Scholar] [CrossRef]
- Butler, E.A. Emotions are temporal interpersonal systems. Curr. Opin. Psychol. 2017, 17, 129–134. [Google Scholar] [CrossRef]
- Butler, E.A. Interpersonal Affect Dynamics: It Takes Two (and Time) to Tango. Emot. Rev. 2015, 7, 336–341. [Google Scholar] [CrossRef]
- Koehne, S.; Hatri, A.; Cacioppo, J.T.; Dziobek, I. Perceived Interpersonal Synchrony Increases Empathy: Insights from Autism Spectrum Disorder. Cognition 2016, 146, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.K.; Fenning, R.M.; Howland, M.A.; Baucom, B.R.; Moffitt, J.; Erath, S.A. Brief Report: A Pilot Study of Parent–Child Biobehavioral Synchrony in Autism Spectrum Disorder. J. Autism Dev. Disord. 2015, 45, 4140–4146. [Google Scholar] [CrossRef]
- Feldman, R. The Neurobiology of Human Attachments. Trends Cogn. Sci. 2017, 21, 80–99. [Google Scholar] [CrossRef]
- Baldwin, M.M.; Xiao, Z.; Murray, A.L. Temporal Synchrony in Autism: A Systematic Review. PsyArXiv 2020. [Google Scholar] [CrossRef]
- McNaughton, K.A.; Redcay, E. Interpersonal Synchrony in Autism. Curr. Psychiatry Rep. 2020, 22, 12. [Google Scholar] [CrossRef] [PubMed]
- Wetherby, A.M.; Woods, J.; Guthrie, W.; Delehanty, A.; Brown, J.A.; Morgan, L.; Holland, R.D.; Schatschneider, C.; Lord, C. Changing Developmental Trajectories of Toddlers With Autism Spectrum Disorder: Strategies for Bridging Research to Community Practice. J. Speech Lang. Hear. Res. 2018, 61, 2615–2628. [Google Scholar] [CrossRef] [PubMed]
- Coronato, A.; Naeem, M.; De Pietro, G.; Paragliola, G. Reinforcement Learning for Intelligent Healthcare Applications: A Survey. Artif. Intell. Med. 2020, 109, 101964. [Google Scholar] [CrossRef]
- Rudovic, O.O. Personalized Machine Learning for Human-Centered Machine Intelligence. In Proceedings of the 1st International on Multimodal Sentiment Analysis in Real-Life Media Challenge and Workshop, MuSe’20, Seattle, WA, USA, 16 October 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 3–4. [Google Scholar] [CrossRef]
- Chu, W.-S.; De la Torre, F.; Cohn, J.F.; Messinger, D.S. A Branch-and-Bound Framework for Unsupervised Common Event Discovery. Int. J. Comput. Vis. 2017, 123, 372–391. [Google Scholar] [CrossRef] [PubMed]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Pub.: Washington, DC, USA, 2014. [Google Scholar]
- Lord, C.; Rutter, M.; Di Lavore, P.C.; Risi, S.; Gotham, K.; Bishop, S. Autism Diagnostic Observation Schedule—Second Edition (ADOS-2). Man. Part I Modul. 2012, 1, 4. [Google Scholar]
- Frost, K.M.; Brian, J.; Gengoux, G.W.; Hardan, A.; Rieth, S.R.; Stahmer, A.; Ingersoll, B. Identifying and Measuring the Common Elements of Naturalistic Developmental Behavioral Interventions for Autism Spectrum Disorder: Development of the NDBI-Fi. Autism 2020, 24, 2285–2297. [Google Scholar] [CrossRef] [PubMed]
- Hollingshead, A.B. Four Factor Index of Social Status. Yale J. Sociol. 1975, 8, 21–51. [Google Scholar]
- Leclère, C.; Viaux, S.; Avril, M.; Achard, C.; Chetouani, M.; Missonnier, S. Why Synchrony Matters during Mother-Child Interactions: A Systematic Review. PLoS ONE 2014, 9, e113571. [Google Scholar] [CrossRef]
- Minjarez, M.B.; Bruinsma, Y.; Stahmer, A.C. Considering NDBI Models. In Naturalistic Developmental Behavioral Interventions for Autism Spectrum Disorder; Paul H. Brookes Publishing Co.: Baltimore, MD, USA, 2020; pp. 21–42. [Google Scholar]
- Wong, V.; Fuller, E.A.; Rogers, S.J. Time to make a change. Early Start Denver Model for Young Children with ASD. Enfance 2019, 1, 83–98. [Google Scholar] [CrossRef]
- Vivanti, G.; Bottema-Beutel, K.; Turner-Brown, L. Clinical Guide to Early Interventions for Children with Autism; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Mazefsky, C.A.; Herrington, J.; Siegel, M.; Scarpa, A.; Maddox, B.B.; Scahill, L.; White, S.W. The Role of Emotion Regulation in Autism Spectrum Disorder. J. Am. Acad. Child Adolesc. Psychiatry 2013, 52, 679–688. [Google Scholar] [CrossRef] [PubMed]
- Zwaigenbaum, L.; Bauman, M.L.; Choueiri, R.; Kasari, C.; Carter, A.; Granpeesheh, D.; Pierce, K. Early Intervention for Children with Autism Spectrum Disorder under 3 Years of Age: Recommendations for Practice and Research. Pediatrics 2015, 136 (Suppl. 1), 60–81. [Google Scholar] [CrossRef]
- Luiz, D.; Barnard, A.; Knoesen, N.; Kotras, N.; Horrocks, S.; McAlinden, P.; O’Connell, R. Griffiths Mental Development Scales–Extended Revised. Two to Eight Years; Cianchetti, C., Fancello, G.S., Eds.; Administration Manual; Hogrefe: Oxford, UK, 2006. (In Italian) [Google Scholar]
- Klintwall, L.; Eldevik, S.; Eikeseth, S. Narrowing the Gap: Effects of Intervention on Developmental Trajectories in Autism. Autism 2015, 19, 53–63. [Google Scholar] [CrossRef]
- Venuti, P. Intervento e Riabilitazione nei Disturbi Dello Spettro Autistico; Carocci: Roma, Italy, 2012. [Google Scholar]
- Istituto Superiore di Sanità. Il Trattamento dei Disturbi dello Spettro Autistico nei Bambini e Negli Adolescenti; Linea Guida 21, Sistema Nazionale per le Linee Guida; Ministero della Salute: Roma, Italy, 2011.
- Kim, S.H.; Grzadzinski, R.; Martinez, K.; Lord, C. Measuring Treatment Response in Children with Autism Spectrum Disorder: Applications of the Brief Observation of Social Communication Change to the Autism Diagnostic Observation Schedule. Autism 2018, 23, 1176–1185. [Google Scholar] [CrossRef]
- World Medical Association Declaration of Helsinki: Ethical Principles for Medical Research Involving Human Subjects. JAMA 2013, 310, 2191–2194. [CrossRef]
- Friard, O.; Gamba, M. BORIS: A Free, Versatile Open-Source Event-Logging Software for Video/Audio Coding and Live Observations. Methods Ecol. Evol. 2016, 7, 1325–1330. [Google Scholar] [CrossRef]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Uttley, J. Power Analysis, Sample Size, and Assessment of Statistical Assumptions—Improving the Evidential Value of Lighting Research. LEUKOS 2019, 15, 143–162. [Google Scholar] [CrossRef]
- Derrick, B.; Toher, D.; White, P. Why Welch’s Test Is Type I Error Robust. Quant. Methods Psychol. 2016, 12, 30–38. [Google Scholar] [CrossRef]
- Delacre, M.; Lakens, D.; Leys, C. Why Psychologists Should by Default Use Welch’s t-Test Instead of Student’s t-Test. Int. Rev. Soc. Psychol. 2017, 30, 92–101. [Google Scholar] [CrossRef]
- Kerby, D.S. The Simple Difference Formula: An Approach to Teaching Nonparametric Correlation. Compr. Psychol. 2014. [Google Scholar] [CrossRef]
- Liang, F.; Paulo, R.; Molina, G.; Clyde, M.A.; Berger, J.O. Mixtures of g Priors for Bayesian Variable Selection. J. Am. Stat. Assoc. 2008, 103, 410–423. [Google Scholar] [CrossRef]
- Lee, M.D.; Wagenmakers, E.-J. Bayesian Cognitive Modeling: A Practical Course; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance Inflation Factor: As a Condition for the Inclusion of Suppressor Variable(s) in Regression Analysis. OJS 2015, 05, 754–767. [Google Scholar] [CrossRef]
- Heinze, G.; Wallisch, C.; Dunkler, D. Variable Selection—A Review and Recommendations for the Practicing Statistician. Biom. J. Biom. Z. 2018, 60, 431–449. [Google Scholar] [CrossRef] [PubMed]
- Pham, H. A New Criterion for Model Selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S. Gene Selection for Cancer Classification Using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Tomaschek, F.; Hendrix, P.; Baayen, R.H. Strategies for Addressing Collinearity in Multivariate Linguistic Data. J. Phon. 2018, 71, 249–267. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Furlanello, C.; Serafini, M.; Merler, S.; Jurman, G. Entropy-Based Gene Ranking without Selection Bias for the Predictive Classification of Microarray Data. BMC Bioinform. 2003, 4, 54. [Google Scholar] [CrossRef] [PubMed]
- Fuller, E.A.; Kaiser, A.P. The Effects of Early Intervention on Social Communication Outcomes for Children with Autism Spectrum Disorder: A Meta-Analysis. J. Autism Dev. Disord. 2020, 50, 1683–1700. [Google Scholar] [CrossRef]
- Tupou, J. Meta-Analysis Supports Naturalistic Developmental Behavioral Interventions as a Promising Approach for Improving a Range of Outcomes for Children with Autism Spectrum Disorder. Evid. Based Commun. Assess. Interv. 2020, 14, 206–210. [Google Scholar] [CrossRef]
- Tiede, G.; Walton, K.M. Meta-Analysis of Naturalistic Developmental Behavioral Interventions for Young Children with Autism Spectrum Disorder. Autism 2019, 23, 2080–2095. [Google Scholar] [CrossRef]
- Schreibman, L.; Dawson, G.; Stahmer, A.C.; Landa, R.; Rogers, S.J.; McGee, G.G.; Halladay, A. Naturalistic Developmental Behavioral Interventions: Empirically Validated Treatments for Autism Spectrum Disorder. J. Autism Dev. Disord. 2015, 45, 2411–2428. [Google Scholar] [CrossRef]
- Vivanti, G.; Zhong, H.N. Naturalistic Developmental Behavioral Interventions for Children with Autism. In Clinical Guide to Early Interventions for Children with Autism; Vivanti, G., Bottema-Beutel, K., Turner-Brown, L., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 93–130. [Google Scholar] [CrossRef]
- Dawson, G.; Sapiro, G. Potential for Digital Behavioral Measurement Tools to Transform the Detection and Diagnosis of Autism Spectrum Disorder. JAMA Pediatr. 2019, 173, 305–306. [Google Scholar] [CrossRef] [PubMed]
- Kleinspehn-Ammerlahn, A.; Riediger, M.; Schmiedek, F.; Oertzen, T.; Li, S.-C.; Lindenberger, U. Dyadic Drumming across the Lifespan Reveals a Zone of Proximal Development in Children. Dev. Psychol. 2011, 47, 632–644. [Google Scholar] [CrossRef]
- Fountain, C.; Winter, A.S.; Bearman, P.S. Six Developmental Trajectories Characterize Children with Autism. Pediatrics 2012, 129, 1112–1120. [Google Scholar] [CrossRef]
- Vivanti, G.; Kasari, C.; Green, J.; Mandell, D.; Maye, M.; Hudry, K. Implementing and Evaluating Early Intervention for Children with Autism: Where Are the Gaps and What Should We Do? Autism Res 2018, 11, 16–23. [Google Scholar] [CrossRef]

| Code | Description | ICC (Alternative Hypothesis r0 > 0.8) |
|---|---|---|
| TP * | Therapist proposes | 0.958; F(9,5.100) = 5.400; p = 0.038 (0.764–0.990) |
| TW * | Therapist widens | 0.953; F(9,9.090) = 4.620; p = 0.016 (0.824–0.988) |
| CA * | Child accepts | 0.952; F(9,5.580) = 4.600; p = 0.039 (0.765–0.989) |
| CR | Child refuses | 0.627; F(9,9.49) = 0.477; p = 0.858 (0.096–0.889) |
| CI * | Child’s signal of intentionality | 0.940; F(9,7.990) = 3.640; p = 0.042 (0.766–0.985) |
| TI * | Therapist recognizes intentionality | 0.957; F(9,5.820) = 5.250; p = 0.030 (0.786–0.990) |
| CP | Child proposes | 1 |
| TA | Therapist shares | 1 |
| SA | Social interplay/Shared activity | 1 |
| CX *** | Child’s withdrawal to interrupt the sharing | 0.992; F(9,10) = 28.800; p < 0.001 (0.971–0.998) |
| TE | Therapist ends activity | 1 |
| CE ** | Child ends the activity | 0.975; F(9,10) = 8.700; p = 0.001 (0.908–0.994) |
| CD | Child’s signals of dysregulation | 0.571; F(9,9.870) = 0.401; p = 0.907 (0.014–0.869) |
| TR | Therapist recognizes child’s emotional/activation state | 0.667; F(9,9.960) = 0.556; p = 0.805 (0.138–0.904) |
| ENG | 1—low engagement | 0.943; F(9,5.91) = 3.9; p = 0.057 |
| 2—medium engagement | 0.741; F(9,6.56) = 0.738; p = 0.672 | |
| 3—high engagement | 1 |
| Index | Description |
|---|---|
| N_TOT | Total number of behavioral events |
| N_SYNC | Total number of synchrony pairs |
| N_UDI | Total number of IUs (TP-CA; CP-TA; CI-TI) |
| P_CA a | Proportional frequency of child’s acceptance |
| P_CX a | Proportional frequency of child’s withdrawals |
| P_SA | Proportional frequency of shared activities |
| R_TPCA a | Rate of therapist’s proposals over the total number of IUs |
| R_CITI a | Rate of child’s intentionality signals over the total number of IUs |
| R_SYNC a | Rate of synchrony code pairs over total code pairs |
| SR_TPCA | Rate of therapist’s proposals accepted by the child over the total number of therapist’s proposals |
| SR_CITI | Rate of child’s intentionality signals recognized by the therapist |
| R_SA a | Rate of IUs that actually led to the initiation of a shared activity |
| R_SA_TPCA a | Rate of therapist’s proposals that actually allowed for the initiation of a shared activity |
| LATENCY_TPCA a (s) | Mean latency between therapist’s proposals child’s acceptances |
| LATENCY_SA a (s) | Mean latency between IUs and the actual start of the shared activity |
| LATENCY_TWCA a (s) | Mean latency between therapist’s widenings and child’s acceptances |
| DURATION_SA a (s) | Mean duration of shared activities |
| R_CX a | Rate of shared activities interrupted by child’s withdrawal |
| SRTWCA_SA a | Rate of therapist’s widenings accepted by the child |
| N_BETWEEN_SA a | Mean number of mid codes during shared activities (i.e., therapists widenings) |
| CPM a | Codes per minute |
| SR_UDI a | Rate of child’s acceptances over the total number of therapist’s proposals and widenings |
| ENG a | Mean engagement level during shared activities |
| T0 Mean (SD) [Range] | T1 Mean (SD) [Range] | |
|---|---|---|
| Chronological age (months) | 38.250 (9.988) (23–56) | 53.583 (12.233) (33–75) |
| Mental age (months) | 26.500 (7.223) (14–45) | 39.33 (11.224) (18–63) |
| Socioeconomic Status (SES) | 35.833 (13.230) (12.500–59.500) | |
| Time between T0 and T1 assessments (months) | 14.333 (3.886) (8–23) | |
| Coding time (seconds) | 1270 (109) (1184–1642) | 1313 (122) (1133–1606) |
| V = 98; p = 0.143; r2 = 0.303; BF = 0.408 | ||
| Frequency Distributions | |||
|---|---|---|---|
| Code | T0 Mean (SD) [Range] | T1 Mean (SD) [Range] | |
| Total * (TOT) | 94.250 (27.227) (46–154) | 74.708 (22.383) (35–123) | t(23) = 2.669; p = 0.014; R2 = 0.236; BF = 3.717 |
| Proportional frequencies | |||
| T. Proposes (TP) | 0.123 (0.055) (0.022–0.222) | 0.115 (0.057) (0.017–0.243) | t(23) = 0.687; p = 0.499; R2 = 0.020; BF = 0.266 |
| T. Widens (TW) | 0.253 (0.084) (0.126–0.391) | 0.278 (0.094) (0.094–0.470) | t(23) = −1.027; p = 0.315; R2 = 0.043; BF = 0.344 |
| C. Accepts ** (CA) | 0.240 (0.061) (0.117–0.359) | 0.299 (0.064) (0.186–0.424) | t(23) = −4.059; p < 0.001; R2 = 0.417; BF = 66.245 |
| C. Rejects (CR) | 0.021 (0.018) (0–0.067) | 0.010 (0.015) (0–0.043) | - |
| C. Intentionality (CI) | 0.074 (0.045) (0–0.181) | 0.054 (0.039) (0–0.172) | t(23) = 1.764; p = 0.091; R2 = 0.119; BF = 0.819 |
| T. Intentionality (TI) | 0.070 (0.040) (0–0.149) | 0.049 (0.036) (0–0.156) | t(23) = 1.940; p = 0.065; R2 = 0.141;BF = 1.063 |
| C. Proposes (CP) | 0.011 (0.015) (0–0.050) | 0.014 (0.023) (0–0.105) | - |
| T. Accepts (TA) | 0.011 (0.015) (0–0.050) | 0.013 (0.023) (0–0.105) | - |
| C. Dysregulation (CD) | 0.032 (0.043) (0–0.167) | 0.021 (0.029) (0–0.110) | - |
| T. Recognizes (TR) | 0.018 (0.024) (0–0.081) | 0.016 (0.023) (0–0.090) | - |
| Shared Activity (SA) | 0.074 (0.018) (0.029–0.097) | 0.065 (0.022) (0.030–0.115) | t(23) = 1.794; p = 0.086; R2 = 0.123; BF = 0.855 |
| C. Withdrawal * (CX) | 0.060 (0.025) (0.011–0.097) | 0.039 (0.026) (0–0.096) | t(23) = 3.305; p = 0.003; R2 = 0.322; BF = 13.142 |
| C. Ends (CE) | 0.005 (0.012) (0–0.045) | 0.010 (0.012) (0–0.035) | - |
| T. Ends (TE) | 0.009 (0.009) (0–0.031) | 0.016 (0.021) (0–0.093) | - |
| Longitudinal Changes | |||
|---|---|---|---|
| T0 Mean (SD) [Range] | T1 Mean (SD) [Range] | Statistics | |
| Behavioral Descriptors | |||
| N_TOT * | 94.250 (27.227) (46–154) | 74.708 (22.383) (35–123) | t(23) = 2.669; p = 0.014; R2 = 0.236; BF = 3.717 |
| N_SYNC | 31.083 (90.12) (18–52) | 27.958 (8.312) (11–44) | t(23) = 1.406; p = 0.173; R2 = 0.08; BF = 0.512 |
| N_UDI | 14.500 (6.228) (6–31) | 10.792 (5.283) (1–19) | t(23) = 1.875; p = 0.074; R2 = 0.133; BF = 0.963 |
| P_CA *** | 0.240 (0.061) (0.117–0.359) | 0.299 (0.064) (0.186–0.424) | t(23) = −4.059; p < 0.001; R2 = 0.417; BF = 66.245 |
| P_CX ** | 0.060 (0.025) (0.011–0.097) | 0.039 (0.026) (0–0.096) | t(23) = 3.305; p = 0.003; R2 = 0.322; BF = 13.142 |
| P_SA | 0.074 (0.018) (0.030–0.115) | 0.065 (0.022) (0.030–0.115) | t(23) = 1.794; p = 0.086; R2 = 0.123; BF = 0.855 |
| R_TPCA * | 0.504 (0.249) (0.037–1) | 0.616 (0.225) (0.143–1) | t(23) = −2.147; p = 0.043; R2 = 0.167; BF = 1.478 |
| R_CITI * | 0.424 (0.213) (0–0.815) | 0.311 (0.185) (0–0.571) | t(23) = 2.355; p = 0.027; R2 = 0.194; BF = 2.102 |
| R_SYNC *** | 0.715 (0.092) (0.469–0.849) | 0.836 (0.088) (0.600–0.967) | t(23) = −4.140; p < 0.001; R2 = 0.427; BF = 79.093 |
| SR_TPCA ** | 0.618 (0.178) (0.250–1) | 0.791 (0.174) (0.333–1) | t(23) = −3.483; p = 0.002; R2 = 0.345; BF = 19.07 |
| SR_CITI | 0.919 (0.125) (0.600–1) | 0.878 (0.246) (0–1) | V = 77; p = 0.660; R2 = 0.069; BF = 0.272 |
| R_SA | 0.488 (0.163) (0.194–0.833) | 0.506 (0.227) (0.211–1) | t(23) = −0.301; p = 0.766; R2 = 0.004; BF = 0.224 |
| R_SA_TPCA | 0.540 (0.282) (0–1) | 0.538 (0.308) (0–1) | t(23) = 0.028; p = 0.978; R2 < 0.001; BF = 0.215 |
| LATENCY_TPCA | 2.747 (1.292) (0.280–6.091) | 2.158 (1.114) (0.300–6.037) | t(23) = 1.786; p = 0.087; R2 = 0.122; BF = 0.846 |
| LATENCY_SA | 12.536 (5.491) (4.143–26.500) | 14.234 (10.072) (2.33–46) | t(23) = −0.716; p = 0.481; R2 = 0.02; BF = 0.271 |
| LATENCY_TWCA * | 2.817 (0.854) (1.593–4.357) | 2.291 (0.987) (0.712–4.522) | t(23) = 2.162; p = 0.041; R2 = 0.169; BF = 1.513 |
| DURATION_SA * | 144.328 (98.640) (47.533–523) | 233.476 (140.148) (109–645) | V = 64; p = 0.013; R2 = 0.502; BF = 2.415 |
| R_CX * | 0.795 (0.237) (0.167–1) | 0.584 (0.277) (0–1) | V = 205; p = 0.011; R2 = 0.540; BF = 5.336 |
| SRTWCA_SA *** | 0.572 (0.251) (0–1) | 0.776 (0.185) (0.250–1) | t(23) = −3.982; p < 0.001; R2 = 0.408; BF = 55.914 |
| N_BETWEEN_SA * | 5.338 (4.447) (0.571–21.750) | 8.145 (6.322) (2–28) | V = 74; p = 0.029; R2 = 0.44; BF = 1.857 |
| CPM ** | 4.464 (1.276) (2.319–6.591) | 3.421 (0.966) (1.307–5.390) | t(23) = 0.321; p = 0.004; R2 = 0.309; BF = 10.726 |
| SR_UDI *** | 0.635 (0.114) (0.383–0.791) | 0.767 (0.141) (0.419–0.944) | t(23) = −3.788; p < 0.001; R2 = 0.384; BF = 36.647 |
| ENG *** | 1.117 (0.170) (1–1.500) | 1.694 (0.297) (1–2) | V = 0; p < 0.001; R2 = 0.872; BF > 100 |
| Longitudinal Changes | |||
|---|---|---|---|
| T0 Mean (SD) [Range] | T1 Mean (SD) [Range] | Statistics | |
| Developmental outcomes and symptoms severity | |||
| Language Quotient * | 55.417 (26.090) (25–120) | 71.667 (34.949) (21–35) | V = 60.5; p = 0.0191; R2 = 0.473; BF = 7.637 |
| rMC (mental age/chronological age) ** | 0.718 (0.199) (0.375–1.304) | 0.782(0.276) (0.378–1.576) | t(23) = −2.862; p = 0.009; R2 = 0.263 |
| Ados-2 Social Affect (SA) ** | 12.333 (3.319) (6–19) | 10.458 (2.978) (6–16) | t(23) = 2.828; p = 0.010; R2 = 0.258; BF = 5.041 |
| Ados-2 Restricted Repetitive Behaviors (RRB) | 3.917 (1.640) (1–7) | 3.667 (1.711) (1–7) | t(23) = 0.655; p = 0.519; R2 = 0.018; BF = 0.261 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bertamini, G.; Bentenuto, A.; Perzolli, S.; Paolizzi, E.; Furlanello, C.; Venuti, P. Quantifying the Child–Therapist Interaction in ASD Intervention: An Observational Coding System. Brain Sci. 2021, 11, 366. https://doi.org/10.3390/brainsci11030366
Bertamini G, Bentenuto A, Perzolli S, Paolizzi E, Furlanello C, Venuti P. Quantifying the Child–Therapist Interaction in ASD Intervention: An Observational Coding System. Brain Sciences. 2021; 11(3):366. https://doi.org/10.3390/brainsci11030366
Chicago/Turabian StyleBertamini, Giulio, Arianna Bentenuto, Silvia Perzolli, Eleonora Paolizzi, Cesare Furlanello, and Paola Venuti. 2021. "Quantifying the Child–Therapist Interaction in ASD Intervention: An Observational Coding System" Brain Sciences 11, no. 3: 366. https://doi.org/10.3390/brainsci11030366
APA StyleBertamini, G., Bentenuto, A., Perzolli, S., Paolizzi, E., Furlanello, C., & Venuti, P. (2021). Quantifying the Child–Therapist Interaction in ASD Intervention: An Observational Coding System. Brain Sciences, 11(3), 366. https://doi.org/10.3390/brainsci11030366








