Use of Empirical Mode Decomposition in ERP Analysis to Classify Familial Risk and Diagnostic Outcomes for Autism Spectrum Disorder
Abstract
1. Introduction
2. Method
2.1. Participants
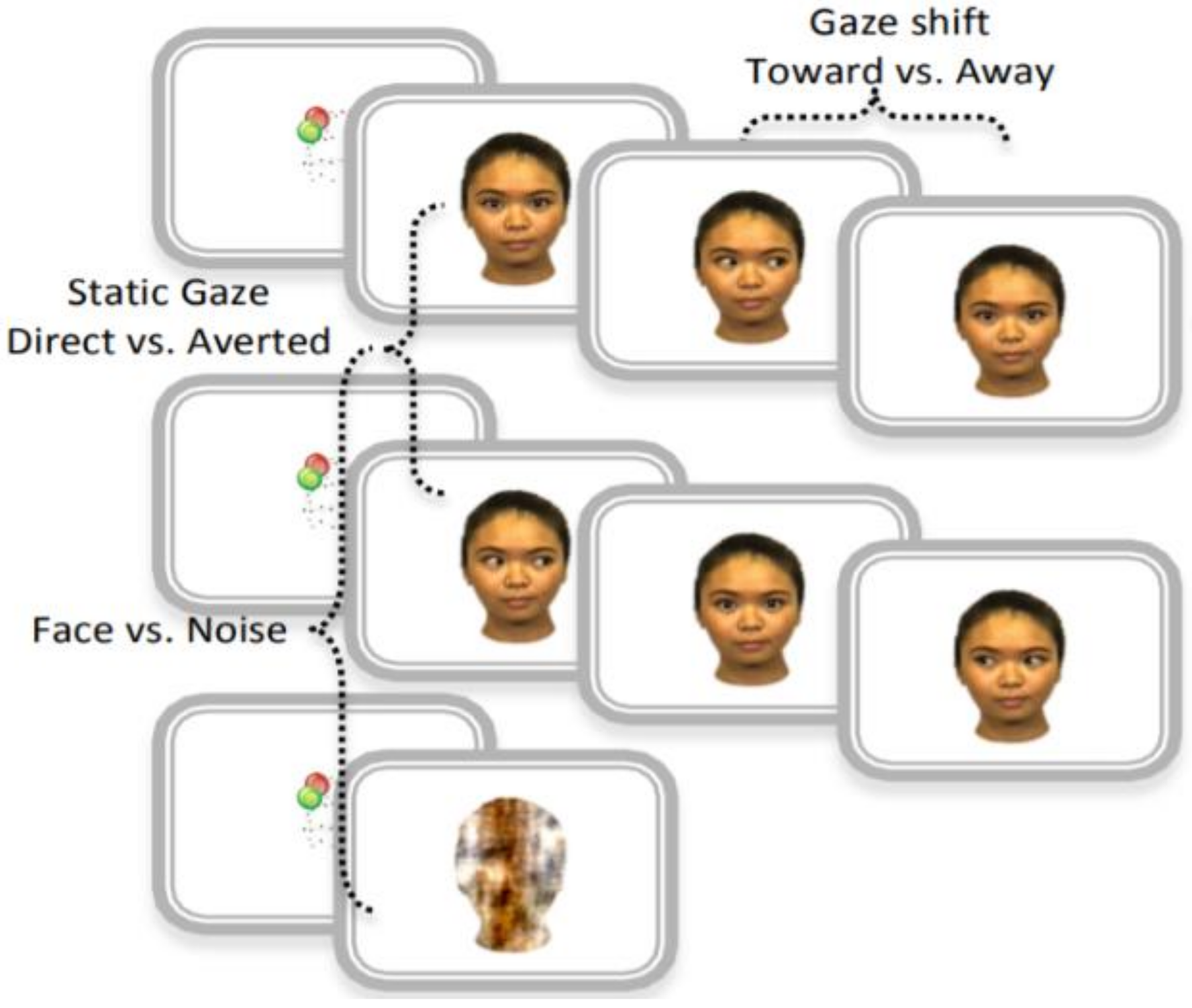
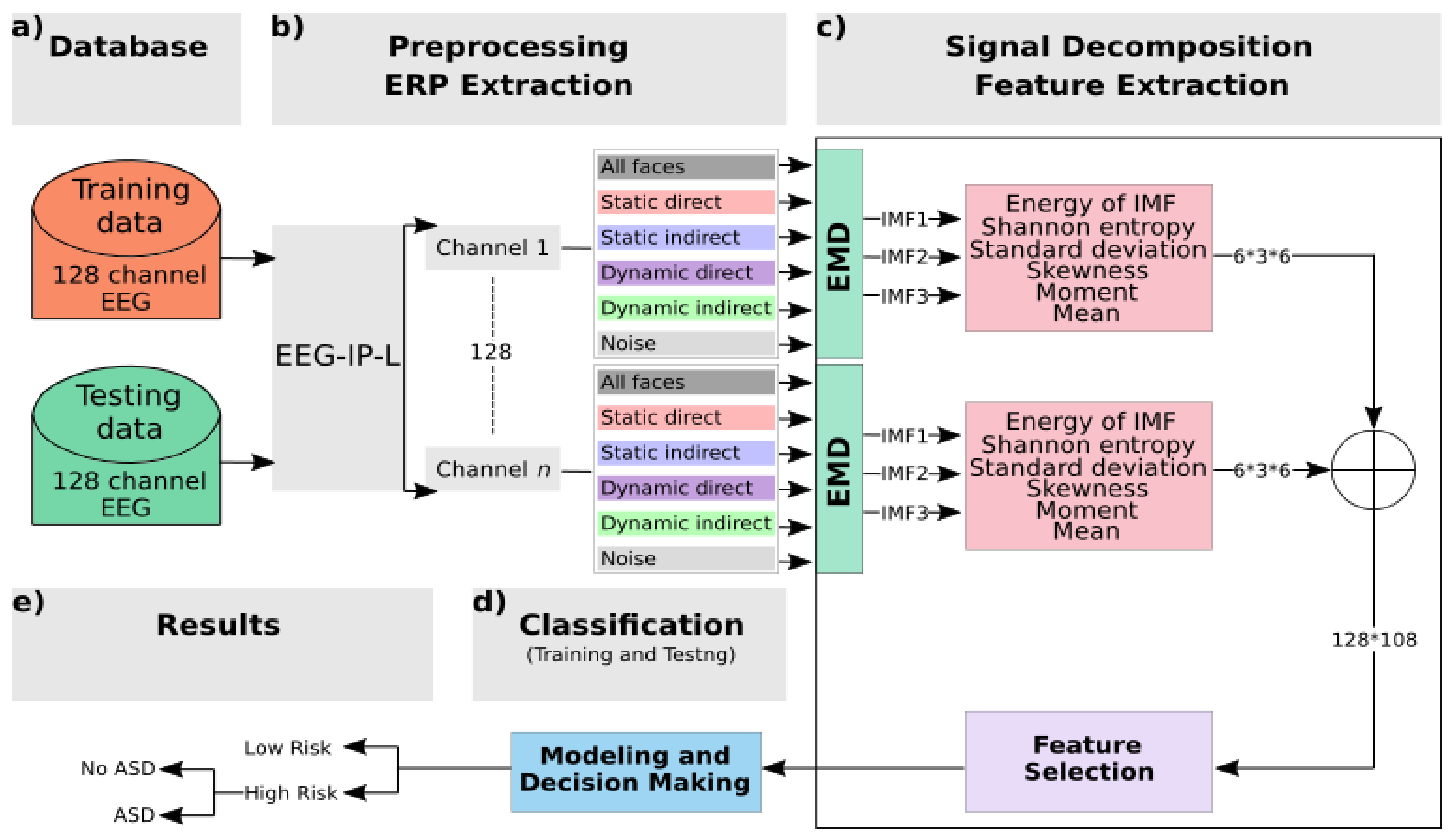
2.2. Analysis Framework
- The EEG data were preprocessed to isolate and flag artifact for removal. The retained data were segmented into −200 to 800 ms epochs and averaged within condition to generate the ERP waveforms.
- The single-channel ERP for each condition was decomposed to the first three IMFs using the EMD technique.
- Energy and Shannon entropy were extracted along with four statistical parameters from each IMF: standard deviation, skewness, moment, and mean.
- The maximum value, across all channels, for each of these six features was used in a selection step to determine the strongest features based on their weight correlation.
- During the training stage, the vector of selected features that was extracted using an input signal from the training database was then fed into two classifiers to train and create models.
- During the testing stage, the input vector chosen from the testing database was classified using trained models in order to associate the unknown input to one class.
2.2.1. EEG Preprocessing
2.2.2. ERP Extraction
2.2.3. Signal Decomposition
- The original signal and the extracted IMF cannot differ by more than one with respect to the number of zero-crossing rates and extrema.
- The mean value of the envelope representing the local maxima and the envelope representing the local minima must be zero at each time point.
- Identify local maxima and local minima, so-called extrema, in the observed
- Generate the lower envelope by interpolating local minima
- Generate the upper envelope by interpolating local maxima
- Calculate the mean of the lower and upper envelopes as
- Retrieve the detail from the original signal
2.2.4. Feature Extraction and Selection
- IMF energy describes the weight of oscillation. It provides a quantitative measure of the strength of the oscillation over a finite period. It is defined as the sum of squared absolute values of IMFs and is calculated as follows:
- Shannon entropy describes the measure of the impurity or the complexity of the time series signal. The concept is introduced in “A mathematical theory of communication” (1948) by Shannon. In this study, Shannon entropy is computed for each IMF to evaluate its complexities. The formula of entropy calculation is as follows:
- Four statistical parameters were derived from IMF signals: mean, standard deviation, skewness, and moment. These parameters were extracted directly from each IMF per channel to represent its statistical distribution.
2.2.5. Classification: Modeling and Decision-Making
2.2.6. Performance Evaluation
3. Results
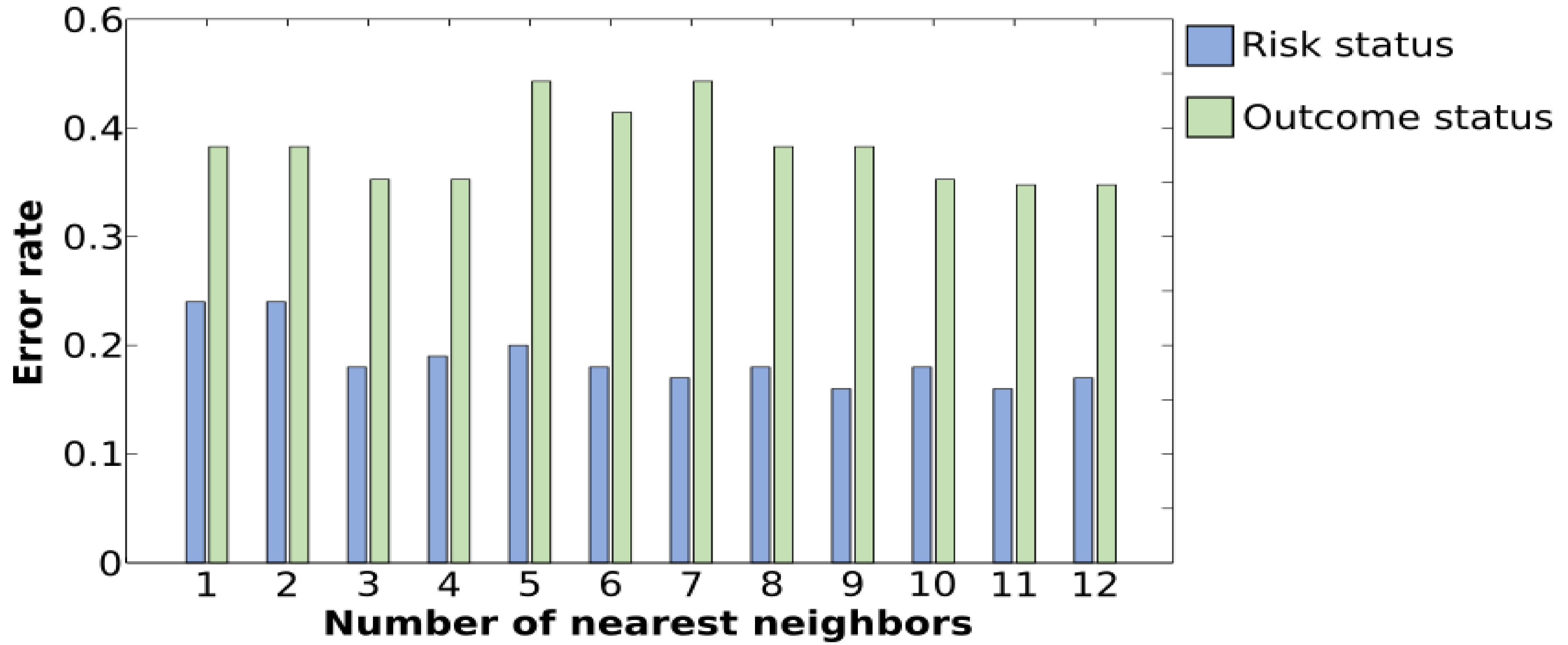
3.1. Classification of HR vs. Control Using k-NN
3.2. Classification of HR and Control Using SVM
3.3. Classification of HR-ASD and HR-noASD Using k-NN
3.4. Classification of HR-ASD and HR-noASD Using SVM
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ozonoff, S.; Young, G.S.; Carter, A.; Messinger, D.; Yirmiya, N.; Zwaigenbaum, L.; Bryson, S.; Carver, L.J.; Constantino, J.N.; Dobkins, K.; et al. Recurrence Risk for Autism Spectrum Disorders: A Baby Siblings Research Consortium Study. Pediatrics 2011, 128, e488–e495. [Google Scholar] [CrossRef]
- Elsabbagh, M.; Volein, A.; Csibra, G.; Holmboe, K.; Garwood, H.; Tucker, L.; Krljes, S.; Baron-Cohen, S.; Bolton, P.; Charman, T.; et al. Neural Correlates of Eye Gaze Processing in the Infant Broader Autism Phenotype. Biol. Psychiatry 2009, 65, 31–38. [Google Scholar] [CrossRef] [PubMed]
- Jeste, S.S.; Frohlich, J.; Loo, S.K. Electrophysiological biomarkers of diagnosis and outcome in neurodevelopmental disorders. Curr. Opin. Neurol. 2015, 28, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Bussu, G.; Jones, E.J.H.; Charman, T.; Johnson, M.H.; Buitelaar, J.K.; Baron-Cohen, S.; Bedford, R.; Bolton, P.; Blasi, A.; Chandler, S.; et al. Prediction of Autism at 3 Years from Behavioural and Developmental Measures in High-Risk Infants: A Longitudinal Cross-Domain Classifier Analysis. J. Autism Dev. Disord. 2018, 48, 2418–2433. [Google Scholar] [CrossRef] [PubMed]
- O’Reilly, C.; Lewis, J.D.; Elsabbagh, M. Is functional brain connectivity atypical in autism? A systematic review of EEG and MEG studies. PLoS ONE 2017, 12, e0175870. [Google Scholar] [CrossRef] [PubMed]
- Elsabbagh, M.; Mercure, E.; Hudry, K.; Chandler, S.; Pasco, G.; Charman, T.; Pickles, A.; Baron-Cohen, S.; Bolton, P.; Johnson, M.H. Infant neural sensitivity to dynamic eye gaze is associated with later emerging autism. Curr. Biol. 2012, 22, 338–342. [Google Scholar] [CrossRef] [PubMed]
- Dawson, G.; Carver, L.; Meltzoff, A.N.; Panagiotides, H.; McPartland, J.; Webb, S.J. Neural correlates of face and object recognition in young children with autism spectrum disorder, developmental delay, and typical development. Child Dev. 2002, 73, 700–717. [Google Scholar] [CrossRef] [PubMed]
- McPartland, J.; Dawson, G.; Webb, S.J.; Panagiotides, H.; Carver, L.J. Event-related brain potentials reveal anomalies in temporal processing of faces in autism spectrum disorder. J. Child Psychol. Psychiatry Allied Discip. 2004, 45, 1235–1245. [Google Scholar] [CrossRef] [PubMed]
- Luck, S.J. An Introduction to Event-Related Potentials and Their Neural Origins. Introd. Event-Relat. Potential Tech. 2005, 11. [Google Scholar] [CrossRef]
- McCleery, J.P.; Akshoomoff, N.; Dobkins, K.R.; Carver, L.J. Atypical Face Versus Object Processing and Hemispheric Asymmetries in 10-Month-Old Infants at Risk for Autism. Biol. Psychiatry 2009, 66, 950–957. [Google Scholar] [CrossRef]
- Key, A.P.F.; Stone, W.L. Processing of novel and familiar faces in infants at average and high risk for autism. Dev. Cogn. Neurosci. 2012, 2, 244–255. [Google Scholar] [CrossRef]
- Zhang, F.; Savadjiev, P.; Cai, W.; Song, Y.; Rathi, Y.; Tunç, B.; Parker, D.; Kapur, T.; Schultz, R.T.; Makris, N.; et al. Whole brain white matter connectivity analysis using machine learning: An application to autism. NeuroImage 2018, 172, 826–837. [Google Scholar] [CrossRef]
- Usta, M.B.; Karabekiroglu, K.; Sahin, B.; Aydin, M.; Bozkurt, A.; Karaosman, T.; Aral, A.; Cobanoglu, C.; Kurt, A.D.; Kesim, N.; et al. Use of machine learning methods in prediction of short-term outcome in autism spectrum disorders. Psychiatry Clin. Psychopharmacol. 2019, 320–325. [Google Scholar] [CrossRef]
- Bosl, W.J.; Tager-Flusberg, H.; Nelson, C.A. EEG Analytics for Early Detection of Autism Spectrum Disorder: A data-driven approach. Sci. Rep. 2018, 29, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Grossi, E.; Olivieri, C.; Buscema, M. Diagnosis of autism through EEG processed by advanced computational algorithms: A pilot study. Comput. Methods Programs Biomed. 2017, 142, 73–79. [Google Scholar] [CrossRef] [PubMed]
- Jamal, W.; Das, S.; Oprescu, I.A.; Maharatna, K.; Apicella, F.; Sicca, F. Classification of autism spectrum disorder using supervised learning of brain connectivity measures extracted from synchrostates. J. Neural Eng. 2014, 11, 046019. [Google Scholar] [CrossRef] [PubMed]
- Bone, D.; Bishop, S.L.; Black, M.P.; Goodwin, M.S.; Lord, C.; Narayanan, S.S. Use of machine learning to improve autism screening and diagnostic instruments: Effectiveness, efficiency, and multi-instrument fusion. J. Child Psychol. Psychiatry Allied Discip. 2016, 27, 927–937. [Google Scholar] [CrossRef] [PubMed]
- Bosl, W.; Tierney, A.; Tager-Flusberg, H.; Nelson, C. EEG complexity as a biomarker for autism spectrum disorder risk. BMC Med. 2011, 9, 18. [Google Scholar] [CrossRef] [PubMed]
- Stahl, D.; Pickles, A.; Elsabbagh, M.; Johnson, M.H. Novel machine learning methods for ERP analysis: A validation from research on infants at risk for autism. Dev. Neuropsychol. 2012, 37, 274–298. [Google Scholar] [CrossRef] [PubMed]
- Martis, R.J.; Acharya, U.R.; Tan, J.H.; Petznick, A.; Yanti, R.; Chua, C.K.; Ng, E.Y.K.; Tong, L. Application of empirical mode decomposition (EMD) for automated detection of epilepsy using EEG signals. Int. J. Neural Syst. 2012, 22, 1250027. [Google Scholar] [CrossRef]
- Pachori, R.B. Discrimination between Ictal and Seizure-Free EEG Signals Using Empirical Mode Decomposition. Res. Lett. Signal Process. 2008, 2008, 293056. [Google Scholar] [CrossRef]
- Sharma, R.; Pachori, R.B. Classification of epileptic seizures in EEG signals based on phase space representation of intrinsic mode functions. Expert Syst. Appl. 2015, 42, 1106–1117. [Google Scholar] [CrossRef]
- Fu, K.; Qu, J.; Chai, Y.; Dong, Y. Classification of seizure based on the time-frequency image of EEG signals using HHT and SVM. Biomed. Signal Process. Control 2014, 13, 15–22. [Google Scholar] [CrossRef]
- Desjardins, J.A.; van Noordt, S.; Huberty, S.; Segalowitz, S.J.; Elsabbagh, M. EEG Integrated Platform Lossless (EEG-IP-L) pre-processing pipeline for objective signal quality assessment incorporating data annotation and blind source separation. J. Neurosci. Methods 2021, 347, 108961. [Google Scholar] [CrossRef]
- Winkler, I.; Debener, S.; Muller, K.R.; Tangermann, M. On the influence of high-pass filtering on ICA-based artifact reduction in EEG-ERP. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015; Volume 2015, pp. 4101–4105. [Google Scholar]
- Pion-Tonachini, L.; Kreutz-Delgado, K.; Makeig, S. The ICLabel dataset of electroencephalographic (EEG) independent component (IC) features. Data Brief 2019, 198, 181–197. [Google Scholar] [CrossRef] [PubMed]
- Pion-Tonachini, L.; Kreutz-Delgado, K.; Makeig, S. ICLabel: An automated electroencephalographic independent component classifier, dataset, and website. NeuroImage 2019, 198, 181–197. [Google Scholar] [CrossRef] [PubMed]
- van Noordt, S.; Desjardins, J.A.; Huberty, S.; Abou-Abbas, L.; Webb, S.J.; Levin, A.R.; Segalowitz, S.J.; Evans, A.C.; Elsabbagh, M. EEG-IP: An international infant EEG data integration platform for the study of risk and resilience in autism and related conditions. Mol. Med. 2020, 26, 40. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E. New method for nonlinear and nonstationary time series analysis: Empirical mode decomposition and Hilbert spectral analysis. In Proceedings of the Wavelet Applications VII; Szu, H.H., Vetterli, M., Campbell, W.J., Buss, J.R., Eds.; SPIE: Bellingham, WA, USA, 2000; Volume 4056, pp. 197–209. [Google Scholar]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Calderon, J.; Luck, S.J. ERPLAB: An open-source toolbox for the analysis of event-related potentials. Front. Hum. Neurosci. 2014, 8, 213. [Google Scholar] [CrossRef]
- Cover, T.M.; Hart, P.E. Nearest Neighbor Pattern Classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 273–297. [Google Scholar] [CrossRef]
- Behnam, H.; Sheikhani, A.; Mohammadi, M.R.; Noroozian, M.; Golabi, P. Analyses of EEG background activity in Autism disorders with fast Fourier transform and short time Fourier measure. In Proceedings of the 2007 International Conference on Intelligent and Advanced Systems, ICIAS 2007, Kuala Lumpur, Malaysia, 25–28 November 2007; pp. 1240–1244. [Google Scholar]
- Subha, D.P.; Joseph, P.K.; Acharya, U.R.; Lim, C.M. EEG signal analysis: A survey. J. Med. Syst. 2010, 34, 195–212. [Google Scholar] [CrossRef] [PubMed]
- Sheikhani, A.; Behnam, H.; Mohammadi, M.R.; Noroozian, M.; Mohammadi, M. Detection of abnormalities for diagnosing of children with autism disorders using of quantitative electroencephalography analysis. J. Med. Syst. 2012, 36, 957–963. [Google Scholar] [CrossRef] [PubMed]
- Alam, S.M.S.; Bhuiyan, M.I.H. Detection of seizure and epilepsy using higher order statistics in the EMD domain. IEEE J. Biomed. Health Inform. 2013, 17, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Orosco, L.; Laciar, E.; Correa, A.G.; Torres, A.; Graffigna, J.P. An epileptic seizures detection algorithm based on the empirical mode decomposition of EEG. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society: Engineering the Future of Biomedicine, EMBC 2009, Minneapolis, MN, USA, 2–6 September 2009; pp. 2651–2654. [Google Scholar]
- Oweis, R.J.; Abdulhay, E.W. Seizure classification in EEG signals utilizing Hilbert-Huang transform. Biomed. Eng. Online 2011, 10, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Tierney, A.L.; Gabard-Durnam, L.; Vogel-Farley, V.; Tager-Flusberg, H.; Nelson, C.A. Developmental trajectories of resting eeg power: An endophenotype of autism spectrum disorder. PLoS ONE 2012, 7, e39127. [Google Scholar] [CrossRef]


| Control | HR-noASD | HR-ASD | All | |
|---|---|---|---|---|
| Male | 15 (43%) | 9 (26%) | 11 (31%) | 35 (37%) |
| Female | 29 (49%) | 24 (41%) | 6 (10%) | 59 (63%) |
| Total | 44 (47%) | 33 (35%) | 17 (18%) | 94 (100%) |
| Classification of HR and Control | ||||||||
|---|---|---|---|---|---|---|---|---|
| Condition | Component | Number of Features after Reduction | k-NN Performance | SVM Performance | ||||
| Accuracy Rate | Sensitivity | Specificity | Accuracy Rate | Sensitivity | Specificity | |||
| Direct gaze | IMF1–3 | 18 | 76.60% | 72.00% | 82.00% | 77.70% | 82.00% | 73.00% |
| Averted gaze | IMF1–3 | 18 | 70.20% | 74.00% | 66.00% | 74.50% | 76.00% | 73.00% |
| Static direct | IMF1–3 | 18 | 60.60% | 68.00% | 52.00% | 62.80% | 68.00% | 57.00% |
| Static averted | IMF1–3 | 18 | 73.40% | 68.00% | 80.00% | 74.50% | 86.00% | 61.00% |
| Face | IMF1–3 | 18 | 71.30% | 72.00% | 70.00% | 74.50% | 78.00% | 70.00% |
| Noise | IMF1–3 | 18 | 68.10% | 72.00% | 64.00% | 63.80% | 72.00% | 55.00% |
| All | IMF1 | 36 | 63.80% | 56.00% | 73.00% | 68.10% | 68.00% | 68.00% |
| All | IMF2 | 36 | 77.70% | 80.00% | 75.00% | 80.90% | 78.00% | 84.00% |
| All | IMF3 | 36 | 74.50% | 76.00% | 73.00% | 76.60% | 68.00% | 86.00% |
| All | IMF1–3 | 11 | 86.22% | 80.00% | 93.18% | - | - | - |
| 30 | - | - | - | 88.44% | 84.00% | 93.18% | ||
| Classification of HR-ASD and HR-noASD | ||||||||
|---|---|---|---|---|---|---|---|---|
| Condition | Component | Number of Features after Reduction | k-NN Performance | SVM Performance | ||||
| Accuracy Rate | Sensitivity | Specificity | Accuracy Rate | Sensitivity | Specificity | |||
| Direct gaze | IMF1–3 | 18 | 64.70% | 53.00% | 76.00% | 64.70% | 53.00% | 76.00% |
| Averted gaze | IMF1–3 | 18 | 47.10% | 29.00% | 65.00% | 50.00% | 41.00% | 59% |
| Static direct | IMF1–3 | 18 | 55.90% | 59.00% | 53.00% | 67.60% | 71.00% | 65.00% |
| Static averted | IMF1–3 | 18 | 55.90% | 65.00% | 47.00% | 50.00% | 47.00% | 53.00% |
| Face | IMF1–3 | 18 | 52.90% | 29.00% | 76.00% | 55.90% | 53.00% | 59.00% |
| Noise | IMF1–3 | 18 | 73.50% | 53.00% | 94.00% | 67.60% | 76.00% | 59.00% |
| All | IMF1 | 36 | 64.70% | 47.00% | 82.00% | 67.60% | 59.00% | 76.00% |
| All | IMF2 | 36 | 47.10% | 47.00% | 47.00% | 58.80% | 53.00% | 65.00% |
| All | IMF3 | 36 | 55.90% | 53.00% | 59.00% | 61.80% | 47.00% | 76.00% |
| All | IMF1–3 | 11 | 74.00% | 78.00% | 70.00% | 70.48% | 76.47% | 64.71% |
| HR vs. Control | HR-ASD vs. HR-noASD | |||||
|---|---|---|---|---|---|---|
| Condition | Component | Number of Features | Best Classifier | Accuracy Rate | Best Classifier(s) | Accuracy Rate |
| Direct gaze | IMF1–3 | 18 | SVM | 77.7 | k-NN and SVM | 64.70 |
| Averted gaze | IMF1–3 | 18 | SVM | 74.5 | SVM | 50.00 |
| Static direct | IMF1–3 | 18 | SVM | 62.8 | SVM | 67.60 |
| Static averted | IMF1–3 | 18 | SVM | 74.50 | k-NN | 55.90 |
| Face | IMF1–3 | 18 | SVM | 74.50 | SVM | 55.90 |
| Noise | IMF1–3 | 18 | k-NN | 68.10 | k-NN | 73.50 |
| All | IMF1 | 36 | SVM | 68.1 | SVM | 67.60 |
| All | IMF2 | 36 | SVM | 80.9 | SVM | 58.80 |
| All | IMF3 | 36 | SVM | 76.6 | SVM | 61.80 |
| All | IMF1–3 | 30/11 | SVM | 88.44 | k-NN | 74.00 |
| Prediction Importance Target: Familial Risk | |||
|---|---|---|---|
| Rank | Feature | IMF# | Stimulus |
| 1 | Skewness | IMF3 | Averted gaze |
| 2 | Skewness | IMF1 | Face |
| 3 | Std | IMF2 | Static direct |
| 4 | Std | IMF1 | Noise |
| 5 | Std | IMF2 | Face |
| 6 | Skewness | IMF2 | Direct gaze |
| 7 | Shannon entropy | IMF1 | Direct gaze |
| 8 | Std | IMF2 | Static averted |
| 9 | Mean | IMF2 | Noise |
| 10 | Moment | IMF1 | Noise |
| Prediction Importance Target: HR-ASD and HR-noASD | |||
|---|---|---|---|
| Rank | Feature | IMF# | Stimulus |
| 1 | Skewness | IMF2 | Noise |
| 2 | Skewness | IMF3 | Noise |
| 3 | Energy | IMF2 | Static direct |
| 4 | Shannon entropy | IMF1 | Static direct |
| 5 | Moment | IMF3 | Static direct |
| 6 | Skewness | IMF3 | Static direct |
| 7 | Skewness | IMF1 | Static averted |
| 8 | Skewness | IMF3 | Averted gaze |
| 9 | Skewness | IMF3 | Static averted |
| 10 | Skewness | IMF1 | Static direct |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abou-Abbas, L.; van Noordt, S.; Desjardins, J.A.; Cichonski, M.; Elsabbagh, M. Use of Empirical Mode Decomposition in ERP Analysis to Classify Familial Risk and Diagnostic Outcomes for Autism Spectrum Disorder. Brain Sci. 2021, 11, 409. https://doi.org/10.3390/brainsci11040409
Abou-Abbas L, van Noordt S, Desjardins JA, Cichonski M, Elsabbagh M. Use of Empirical Mode Decomposition in ERP Analysis to Classify Familial Risk and Diagnostic Outcomes for Autism Spectrum Disorder. Brain Sciences. 2021; 11(4):409. https://doi.org/10.3390/brainsci11040409
Chicago/Turabian StyleAbou-Abbas, Lina, Stefon van Noordt, James A. Desjardins, Mike Cichonski, and Mayada Elsabbagh. 2021. "Use of Empirical Mode Decomposition in ERP Analysis to Classify Familial Risk and Diagnostic Outcomes for Autism Spectrum Disorder" Brain Sciences 11, no. 4: 409. https://doi.org/10.3390/brainsci11040409
APA StyleAbou-Abbas, L., van Noordt, S., Desjardins, J. A., Cichonski, M., & Elsabbagh, M. (2021). Use of Empirical Mode Decomposition in ERP Analysis to Classify Familial Risk and Diagnostic Outcomes for Autism Spectrum Disorder. Brain Sciences, 11(4), 409. https://doi.org/10.3390/brainsci11040409






