EEG Microstate Features as an Automatic Recognition Model of High-Density Epileptic EEG Using Support Vector Machine
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects and EEG Recording and Preprocessing
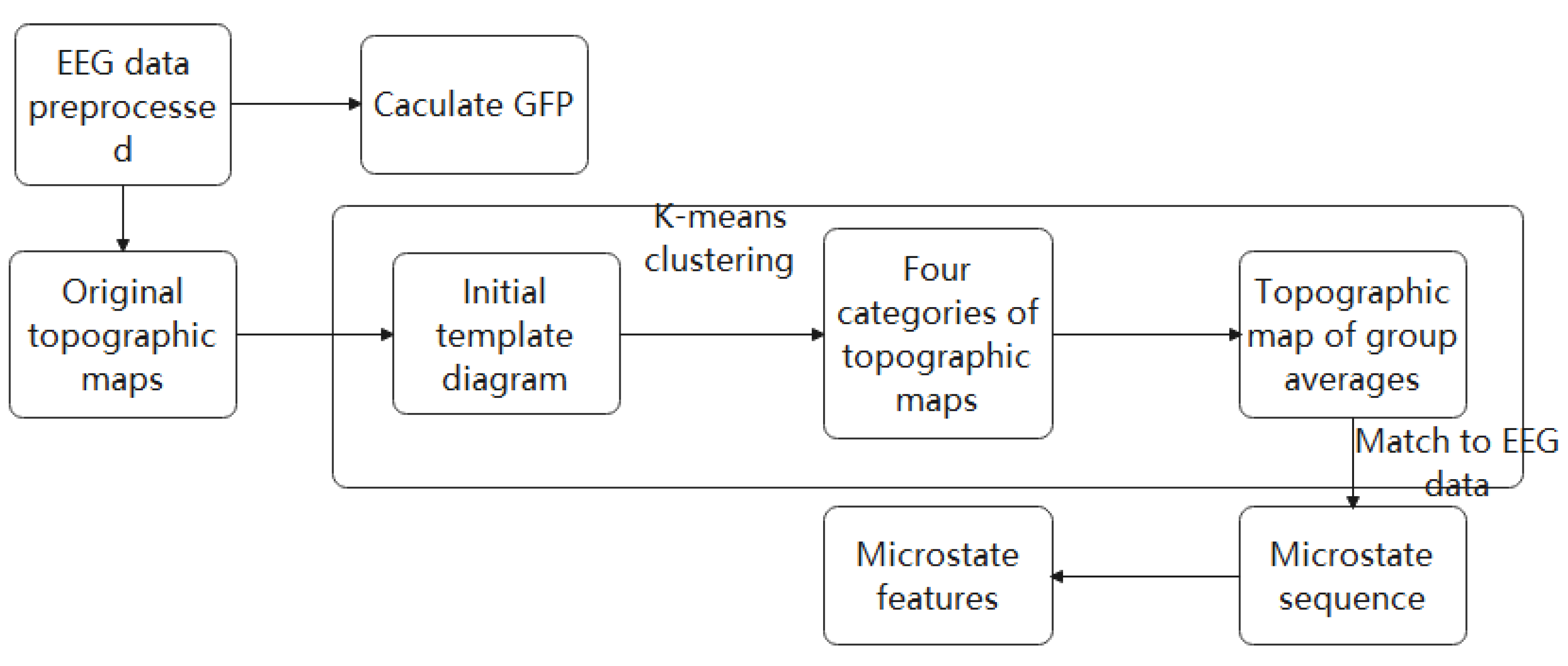
2.2. Microstate Analysis
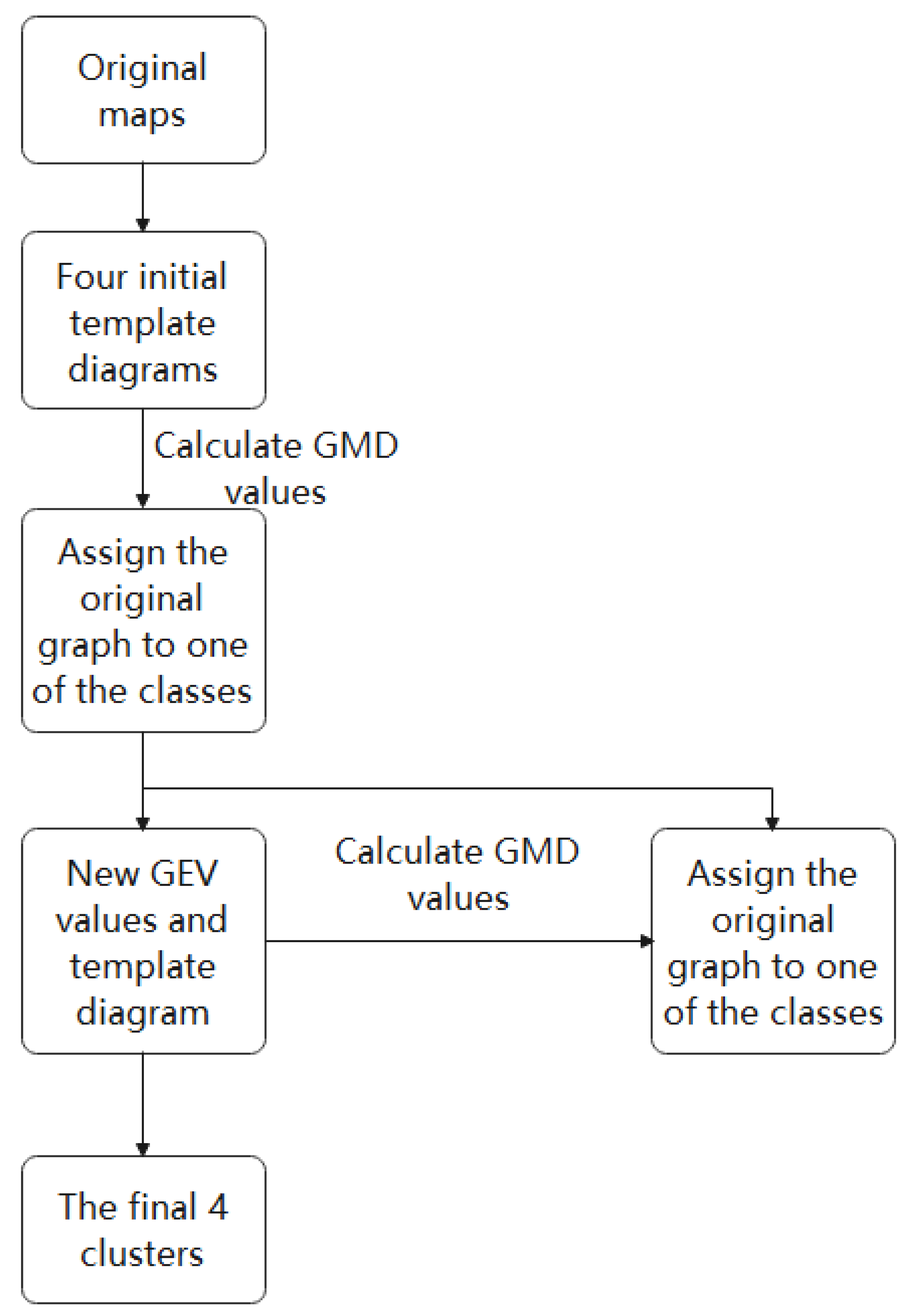
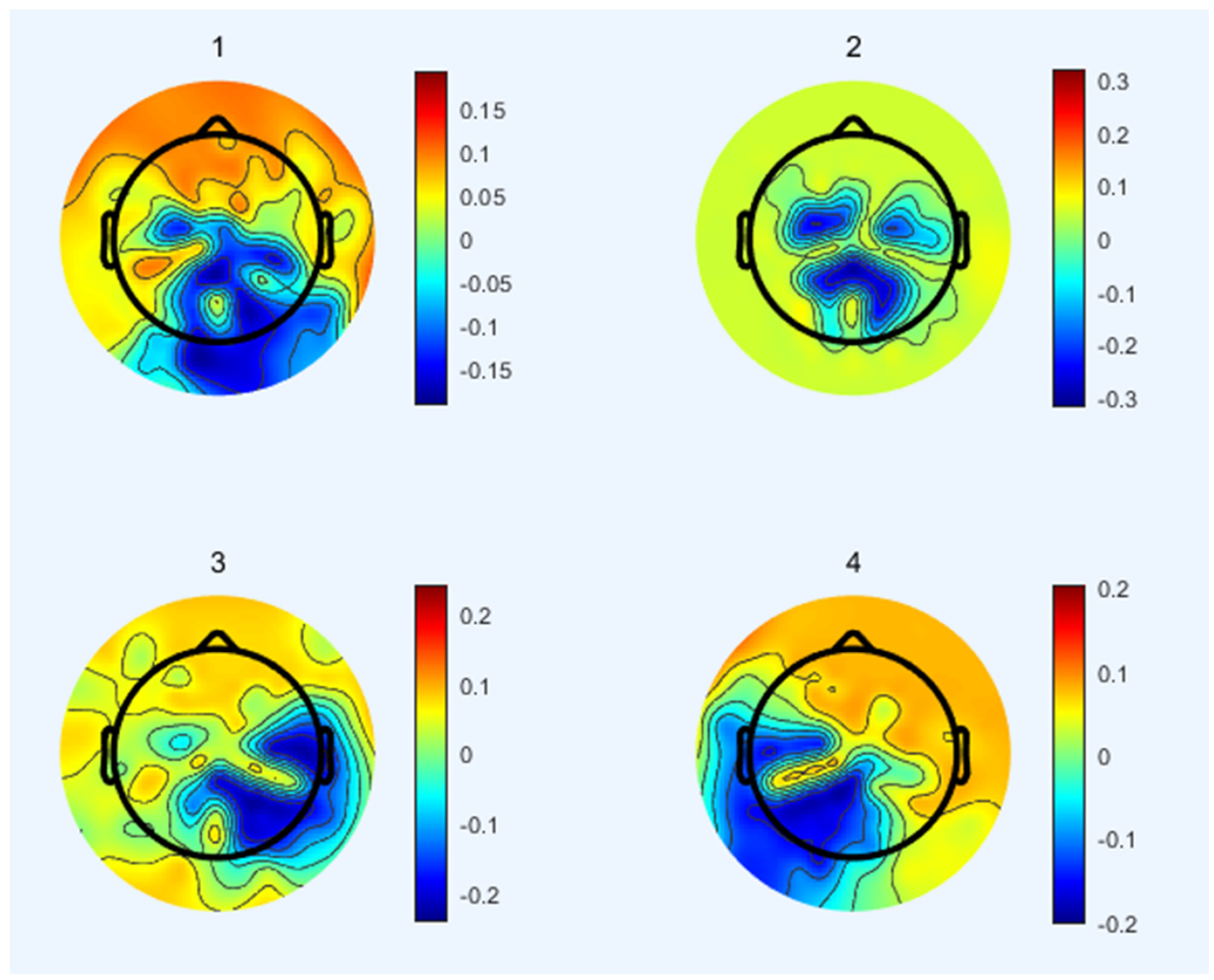
2.2.1. K-Means Clustering
2.2.2. EEG Microstate Parameters
2.3. Feature Extraction
2.3.1. Linear Feature Extraction
2.3.2. Nonlinear Feature Extraction
PFD
LZC
Entropy
2.4. Training/Test Set Split
2.5. EEG Signal Classification
2.6. Evaluation of Classifier
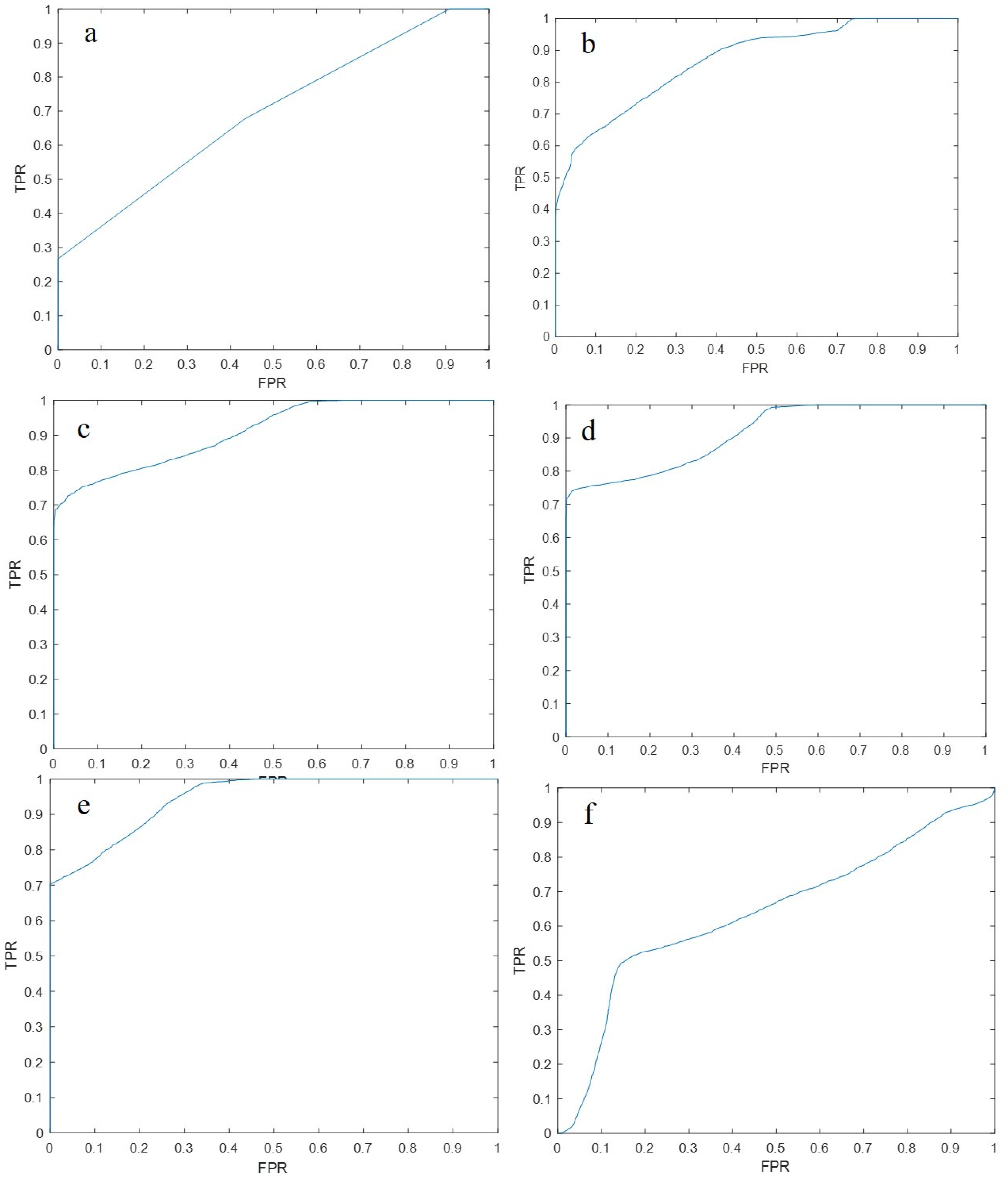
3. Results
3.1. Participants’ Information
3.2. EEG Microstates Parameters’ Classification
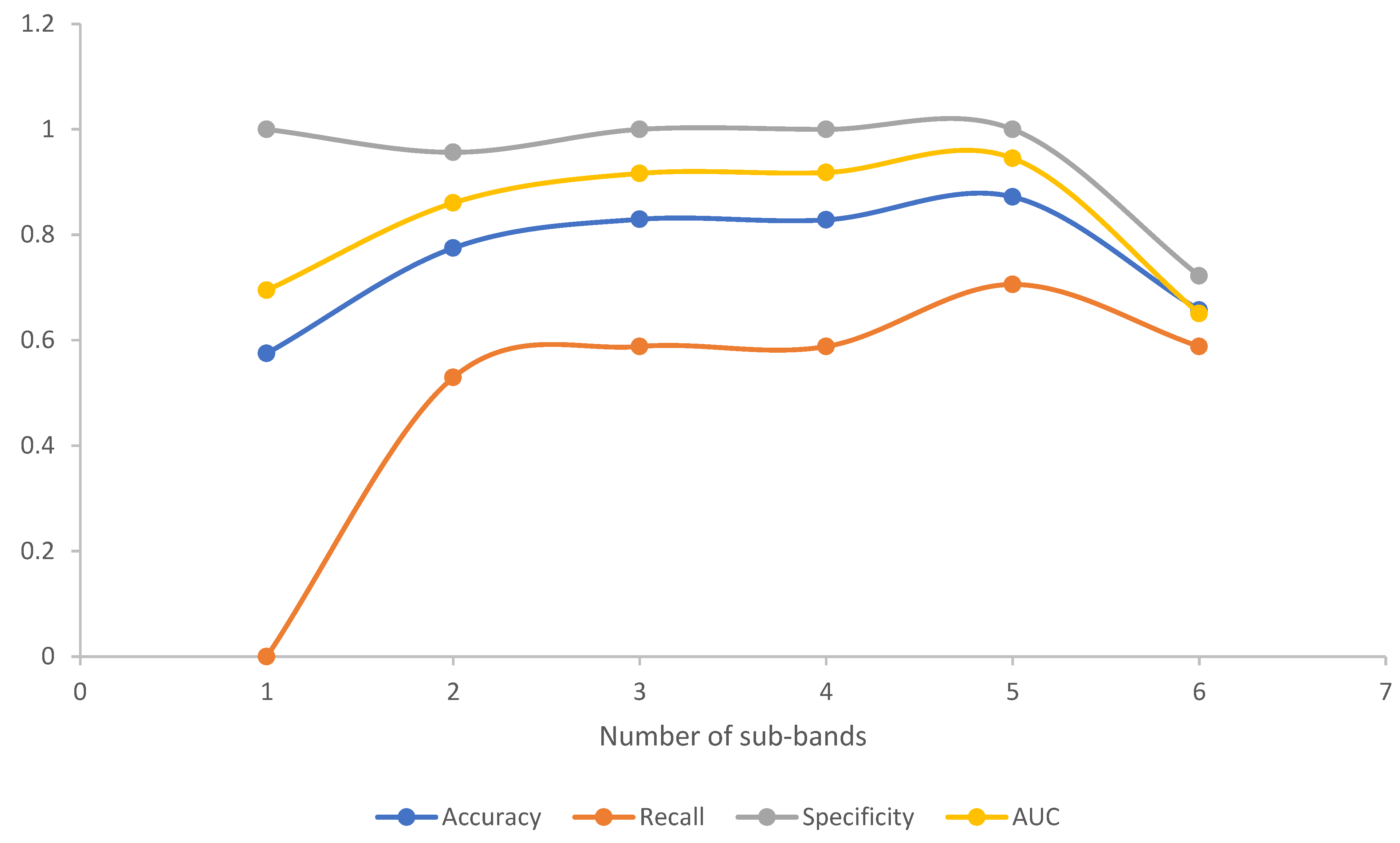
3.3. EEG Feature Set Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VEEG | Video electroencephalogram |
| EEG | Electroencephalogram |
| PWEs | Patients with epilepsy |
| SVM | Support vector machines |
| PFD | Petrosian fractal dimension |
| ApEn | Approximate entropy |
| LZC | Lempel–Ziv complexity |
| AUC | Area under the curve |
| ILAE | International League Against Epilepsy |
| IEDs | Ictal epileptiform discharges |
| Ms | Millisecond |
| GFP | Global field power |
| Hz | Hertz |
| GMD | Global map dissimilarity |
| GEV | Global explained variance |
| TP | True positive |
| FP | False positive |
| FN | False negative |
| TN | True negative |
| ROC | Receiver operating characteristic |
| aEEG | Amplitude-integrated electroencephalography |
| CDSA | Compress spectrum array |
References
- Koutroumanidis, M.; Arzimanoglou, A.; Caraballo, R.; Goyal, S.; Kaminska, A.; Laoprasert, P.; Oguni, H.; Rubboli, G.; Tatum, W.; Thomas, P.; et al. The Role of EEG in the Diagnosis and Classification of the Epilepsy Syndromes: A Tool for Clinical Practice by the ILAE Neurophysiology Task Force (Part 1). Epileptic. Disord. 2017, 19, 233–298. [Google Scholar] [CrossRef] [PubMed]
- Koutroumanidis, M.; Arzimanoglou, A.; Caraballo, R.; Goyal, S.; Kaminska, A.; Laoprasert, P.; Oguni, H.; Rubboli, G.; Tatum, W.; Thomas, P.; et al. The Role of EEG in the Diagnosis and Classification of the Epilepsy Syndromes: A Tool for Clinical Practice by the ILAE Neurophysiology Task Force (Part 2). Epileptic. Disord. 2017, 19, 385–437. [Google Scholar] [CrossRef] [PubMed]
- Thangavel, P.; Thomas, J.; Sinha, N.; Peh, W.Y.; Yuvaraj, R.; Cash, S.S.; Chaudhari, R.; Karia, S.; Jin, J.; Rathakrishnan, R.; et al. Improving Automated Diagnosis of Epilepsy from EEGs beyond IEDs. J. Neural Eng. 2022, 19, 066017. [Google Scholar] [CrossRef] [PubMed]
- Nhu, D.; Janmohamed, M.; Antonic-Baker, A.; Perucca, P.; O’Brien, T.J.; Gilligan, A.K.; Kwan, P.; Tan, C.W.; Kuhlmann, L. Deep Learning for Automated Epileptiform Discharge Detection from Scalp EEG: A Systematic Review. J. Neural Eng. 2022, 19, 051002. [Google Scholar] [CrossRef]
- Phadikar, S.; Sinha, N.; Ghosh, R.; Ghaderpour, E. Automatic Muscle Artifacts Identification and Removal from Single-Channel EEG Using Wavelet Transform with Meta-Heuristically Optimized Non-Local Means Filter. Sensors 2022, 22, 2948. [Google Scholar] [CrossRef]
- Zorzos, I.; Kakkos, I.; Ventouras, E.M.; Matsopoulos, G.K. Advances in Electrical Source Imaging: A Review of the Current Approaches, Applications and Challenges. Signals 2021, 2, 378–391. [Google Scholar] [CrossRef]
- Barkley, G.L.; Baumgartner, C. MEG and EEG in Epilepsy. J. Clin. Neurophysiol. 2003, 20, 163–178. [Google Scholar] [CrossRef]
- Rajagopalan, S.S.; Bhardwaj, S.; Panda, R.; Reddam, V.R.; Ganne, C.; Kenchaiah, R.; Mundlamuri, R.C.; Kandavel, T.; Majumdar, K.K.; Parthasarathy, S.; et al. Machine Learning Detects EEG Microstate Alterations in Patients Living with Temporal Lobe Epilepsy. Seizure 2018, 61, 8–13. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, M.Z.I.; Sinha, N.; Phadikar, S.; Ghaderpour, E. Automated Feature Extraction on AsMap for Emotion Classification Using EEG. Sensors 2022, 22, 2346. [Google Scholar] [CrossRef]
- Lehmann, D. Past, Present and Future of Topographic Mapping. Brain Topogr. 1990, 3, 191–202. [Google Scholar] [CrossRef]
- Lehmann, D.; Ozaki, H.; Pal, I. EEG Alpha Map Series: Brain Micro-States by Space-Oriented Adaptive Segmentation. Electroencephalogr. Clin. Neurophysiol. 1987, 67, 271–288. [Google Scholar] [CrossRef] [PubMed]
- Koenig, T.; Prichep, L.; Lehmann, D.; Sosa, P.V.; Braeker, E.; Kleinlogel, H.; Isenhart, R.; John, E.R. Millisecond by Millisecond, Year by Year: Normative EEG Microstates and Developmental Stages. NeuroImage 2002, 16, 41–48. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Duc, N.T.; Choi, M.; Lee, B. EEG Microstate Features for Schizophrenia Classification. PLoS ONE 2021, 16, e0251842. [Google Scholar] [CrossRef]
- Chu, C.; Wang, X.; Cai, L.; Zhang, L.; Wang, J.; Liu, C.; Zhu, X. Spatiotemporal EEG Microstate Analysis in Drug-Free Patients with Parkinson’s Disease. NeuroImage Clin. 2019, 25, 102132. [Google Scholar] [CrossRef] [PubMed]
- Faber, P.L.; Milz, P.; Reininghaus, E.Z.; Mörkl, S.; Holl, A.K.; Kapfhammer, H.-P.; Pascual-Marqui, R.D.; Kochi, K.; Achermann, P.; Painold, A. Fundamentally Altered Global- and Microstate EEG Characteristics in Huntington’s Disease. Clin. Neurophysiol. 2021, 132, 13–22. [Google Scholar] [CrossRef]
- Musaeus, C.S.; Nielsen, M.S.; Høgh, P. Microstates as Disease and Progression Markers in Patients With Mild Cognitive Impairment. Front. Neurosci. 2019, 13, 563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Britz, J.; Van De Ville, D.; Michel, C.M. BOLD Correlates of EEG Topography Reveal Rapid Resting-State Network Dynamics. NeuroImage 2010, 52, 1162–1170. [Google Scholar] [CrossRef]
- Alazrai, R.; Homoud, R.; Alwanni, H.; Daoud, M.I. EEG-Based Emotion Recognition Using Quadratic Time-Frequency Distribution. Sensors 2018, 18, 2739. [Google Scholar] [CrossRef] [Green Version]
- Yousefzadeh, F.; Pirzad Jahromi, G.; Mokari Manshadi, E.; Hatef, B. The Effect of Prostration (Sajdah) on the Prefrontal Brain Activity: A Pilot Study. Basic Clin. Neurosci. 2019, 10, 257–268. [Google Scholar] [CrossRef]
- Abásolo, D.; James, C.J.; Hornero, R. Non-Linear Analysis of Intracranial Electroencephalogram Recordings with Approximate Entropy and Lempel-Ziv Complexity for Epileptic Seizure Detection. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1953–1956. [Google Scholar] [CrossRef]
- Bruhn, J.; Röpcke, H.; Hoeft, A. Approximate Entropy as an Electroencephalographic Measure of Anesthetic Drug Effect during Desflurane Anesthesia. Anesthesiology 2000, 92, 715–726. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological Time-Series Analysis Using Approximate Entropy and Sample Entropy. Am. J. Physiol.-Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahmadi, N.; Pei, Y.; Carrette, E.; Aldenkamp, A.P.; Pechenizkiy, M. EEG-Based Classification of Epilepsy and PNES: EEG Microstate and Functional Brain Network Features. Brain Inform. 2020, 7, 6. [Google Scholar] [CrossRef] [PubMed]
- Purushothaman, G.; Vikas, R. Identification of a Feature Selection Based Pattern Recognition Scheme for Finger Movement Recognition from Multichannel EMG Signals. Australas. Phys. Eng. Sci. Med. 2018, 41, 549–559. [Google Scholar] [CrossRef] [PubMed]
- Merry, K.J.; Macdonald, E.; MacPherson, M.; Aziz, O.; Park, E.; Ryan, M.; Sparrey, C.J. Classifying Sitting, Standing, and Walking Using Plantar Force Data. Med. Biol. Eng. Comput. 2021, 59, 257–270. [Google Scholar] [CrossRef]
- Thomas, J.; Thangavel, P.; Peh, W.Y.; Jing, J.; Yuvaraj, R.; Cash, S.S.; Chaudhari, R.; Karia, S.; Rathakrishnan, R.; Saini, V.; et al. Automated Adult Epilepsy Diagnostic Tool Based on Interictal Scalp Electroencephalogram Characteristics: A Six-Center Study. Int. J. Neural Syst. 2021, 31, 2050074. [Google Scholar] [CrossRef]
- Zhang, F.; Petersen, M.; Johnson, L.; Hall, J.; O’Bryant, S.E. Recursive Support Vector Machine Biomarker Selection for Alzheimer’s Disease. J. Alzheimers Dis. 2021, 79, 1691–1700. [Google Scholar] [CrossRef]
- Rice, M.E.; Harris, G.T. Comparing Effect Sizes in Follow-up Studies: ROC Area, Cohen’s d, and r. Law Hum. Behav. 2005, 29, 615–620. [Google Scholar] [CrossRef]
- Acharya, U.R.; Faust, O.; Kannathal, N.; Chua, T.; Laxminarayan, S. Non-Linear Analysis of EEG Signals at Various Sleep Stages. Comput. Methods Programs Biomed. 2005, 80, 37–45. [Google Scholar] [CrossRef]
- Diykh, M.; Li, Y.; Wen, P. Classify Epileptic EEG Signals Using Weighted Complex Networks Based Community Structure Detection. Expert Syst. Appl. 2017, 90, 87–100. [Google Scholar] [CrossRef]
- Abend, N.S.; Dlugos, D.; Herman, S. Neonatal Seizure Detection Using Multichannel Display of Envelope Trend. Epilepsia 2008, 49, 349–352. [Google Scholar] [CrossRef]
- Li, Q.; Gao, J.; Huang, Q.; Wu, Y.; Xu, B. Distinguishing Epileptiform Discharges From Normal Electroencephalograms Using Scale-Dependent Lyapunov Exponent. Front. Bioeng. Biotechnol. 2020, 8, 1006. [Google Scholar] [CrossRef] [PubMed]
- Falco-Walter, J. Epilepsy—Definition, Classification, Pathophysiology, and Epidemiology. Semin. Neurol. 2020, 40, 617–623. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Kiral-Kornek, I.; Harrer, S. Deep Learning Enabled Automatic Abnormal EEG Identification. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 2756–2759. [Google Scholar] [CrossRef]
- Liu, H.; Tang, H.; Wei, W.; Wang, G.; Du, Y.; Ruan, J. Altered Peri-Seizure EEG Microstate Dynamics in Patients with Absence Epilepsy. Seizure 2021, 88, 15–21. [Google Scholar] [CrossRef] [PubMed]

| Formula | |
|---|---|
| Median | , N is an odd , N is an even |
| Mean | |
| Skewness | |
| Kurtosis |
| Group | N | Gender (n) b | Age (Years) a | Education Level b | ||||
|---|---|---|---|---|---|---|---|---|
| Male | Female | Mean ± SD | Primary School | Junior High School | High School | University Graduate | ||
| PWEs | 27 | 7 | 20 | 1 | 6 | 7 | 13 | |
| CONs | 17 | 5 | 12 | 2 | 1 | 0 | 14 | |
| p value | 0.803 | 0.288 | 0.084 | |||||
| Number | Gender | Age (Yds) | Course of Epilepsy (Yds) | Abnormal Focus of VEEG |
|---|---|---|---|---|
| 01 | Female | 40 | 10 | Frontal lobe |
| 02 | Male | 20 | 5 | Anterior temporal area |
| 03 | Female | 27 | 1.5 | Anterior temporal area |
| 04 | Female | 38 | 34 | - |
| 05 | Male | 20 | 6 | Frontal lobe |
| 06 | Female | 31 | 8 | Frontal pole |
| 07 | Male | 19 | 4 | Central frontal area |
| 08 | Female | 32 | 8 | Middle temporal area |
| 09 | Female | 44 | 28 | Temporal lobe |
| 10 | Female | 21 | 3 | Frontal lobe |
| 11 | Female | 30 | 4 | Anterior temporal area |
| 12 | Female | 50 | 7 | Anterior temporal area |
| 13 | Female | 21 | 3 | Anterior temporal area |
| 14 | Female | 16 | 1 | Frontal lobe |
| 15 | Female | 20 | 12 | Central frontal area |
| 16 | Female | 23 | 3 | Anterior temporal area |
| 17 | Female | 18 | 10 | Right frontal lobe |
| 18 | Female | 18 | 9 | Frontal lobe |
| 19 | Male | 40 | 40 | Anterior temporal area |
| 20 | Female | 18 | 3.5 | Frontal pole |
| 21 | Female | 18 | 3.5 | Central frontal area |
| 22 | Female | 32 | 1 | Central frontal area |
| 23 | Male | 19 | 11 | Frontal lobe |
| 24 | Female | 23 | 5 | Anterior-middle temporal area |
| 25 | Female | 15 | 11 | - |
| 26 | Male | 26 | 6 | Anterior temporal area |
| 27 | Male | 21 | 0.5 | Anterior-middle temporal area |
| Number | Sub-Band | Accuracy | Recall | Specificity | AUC |
|---|---|---|---|---|---|
| 1 | δ (0.5~4 Hz) | 0.5750 | 0 | 1 | 0.6947 |
| 2 | θ (4~8 Hz) | 0.7750 | 0.5294 | 0.9565 | 0.8605 |
| 3 | α (8~13 Hz) | 0.8293 | 0.5882 | 1 | 0.9165 |
| 4 | β (13~30 Hz) | 0.8283 | 0.5882 | 1 | 0.9182 |
| 5 | γ (30~45 Hz) | 0.8718 | 0.7059 | 1 | 0.9452 |
| 6 | 45~80 Hz | 0.6571 | 0.5882 | 0.7222 | 0.6508 |
| EEG Signal Features Set | Classification Accuracy (%) | Recall (%) | Specificity (%) |
|---|---|---|---|
| Median, second quartile, mean, kurtosis, skewness, fuzzy entropy, PFD, ApEn, SampEn, LZC | 79.55 | 81.84 | 76.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; He, J.; Liu, D.; Zheng, W.; Song, Z. EEG Microstate Features as an Automatic Recognition Model of High-Density Epileptic EEG Using Support Vector Machine. Brain Sci. 2022, 12, 1731. https://doi.org/10.3390/brainsci12121731
Yang L, He J, Liu D, Zheng W, Song Z. EEG Microstate Features as an Automatic Recognition Model of High-Density Epileptic EEG Using Support Vector Machine. Brain Sciences. 2022; 12(12):1731. https://doi.org/10.3390/brainsci12121731
Chicago/Turabian StyleYang, Li, Jiaxiu He, Ding Liu, Wen Zheng, and Zhi Song. 2022. "EEG Microstate Features as an Automatic Recognition Model of High-Density Epileptic EEG Using Support Vector Machine" Brain Sciences 12, no. 12: 1731. https://doi.org/10.3390/brainsci12121731
APA StyleYang, L., He, J., Liu, D., Zheng, W., & Song, Z. (2022). EEG Microstate Features as an Automatic Recognition Model of High-Density Epileptic EEG Using Support Vector Machine. Brain Sciences, 12(12), 1731. https://doi.org/10.3390/brainsci12121731





