Discerning Developmental Dyscalculia and Neurodevelopmental Models of Numerical Cognition in a Disadvantaged Educational Context
Abstract
1. Introduction
1.1. Challenges for Prevalence Studies
1.2. Neurodevelopmental Models of Numerical Cognition
2. Materials and Methods
2.1. Participants
2.2. Screening and Domain-Specific Measures
2.3. Procedures
2.4. Data Analysis
3. Results
3.1. Prevalence Criteria
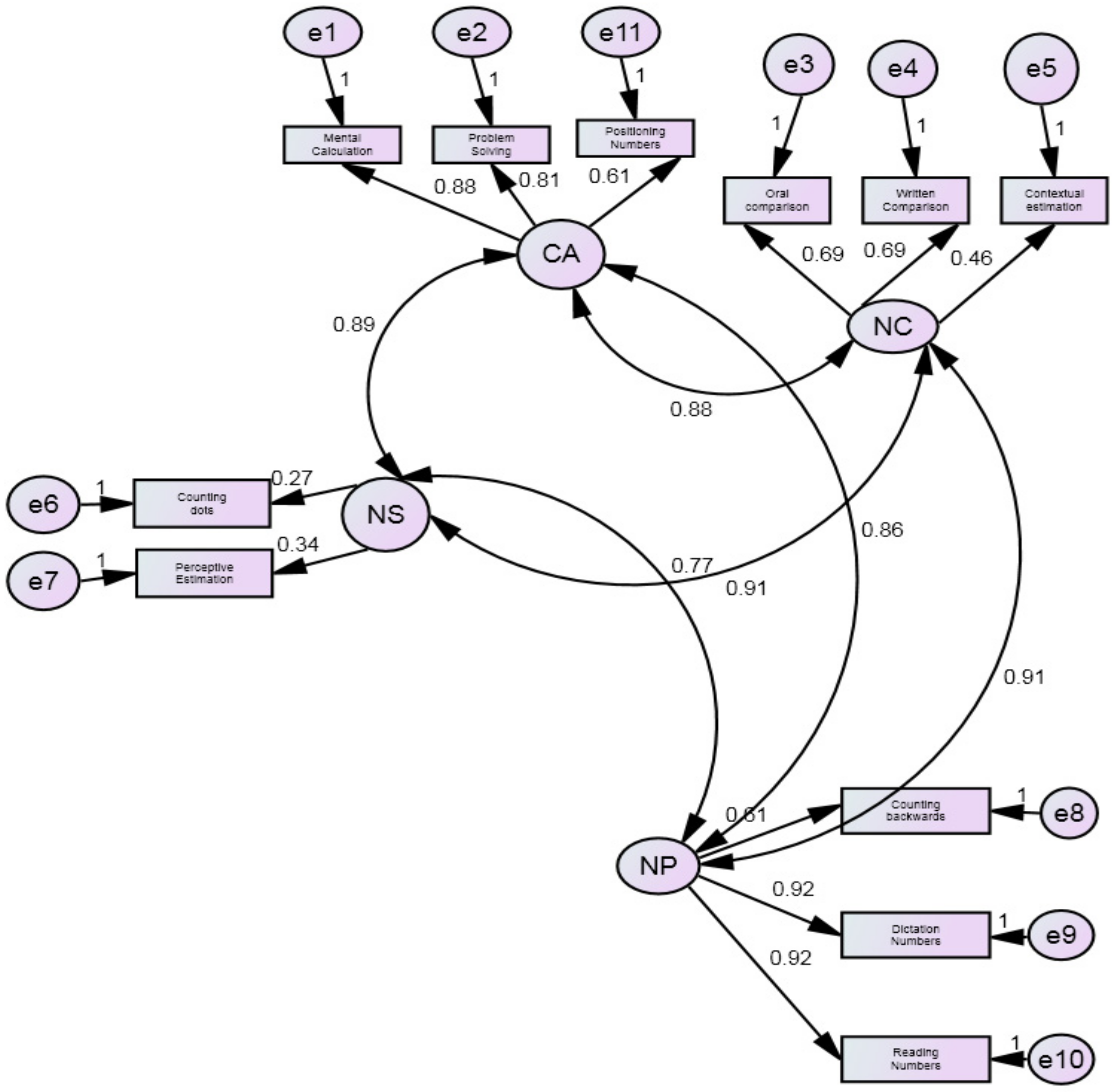
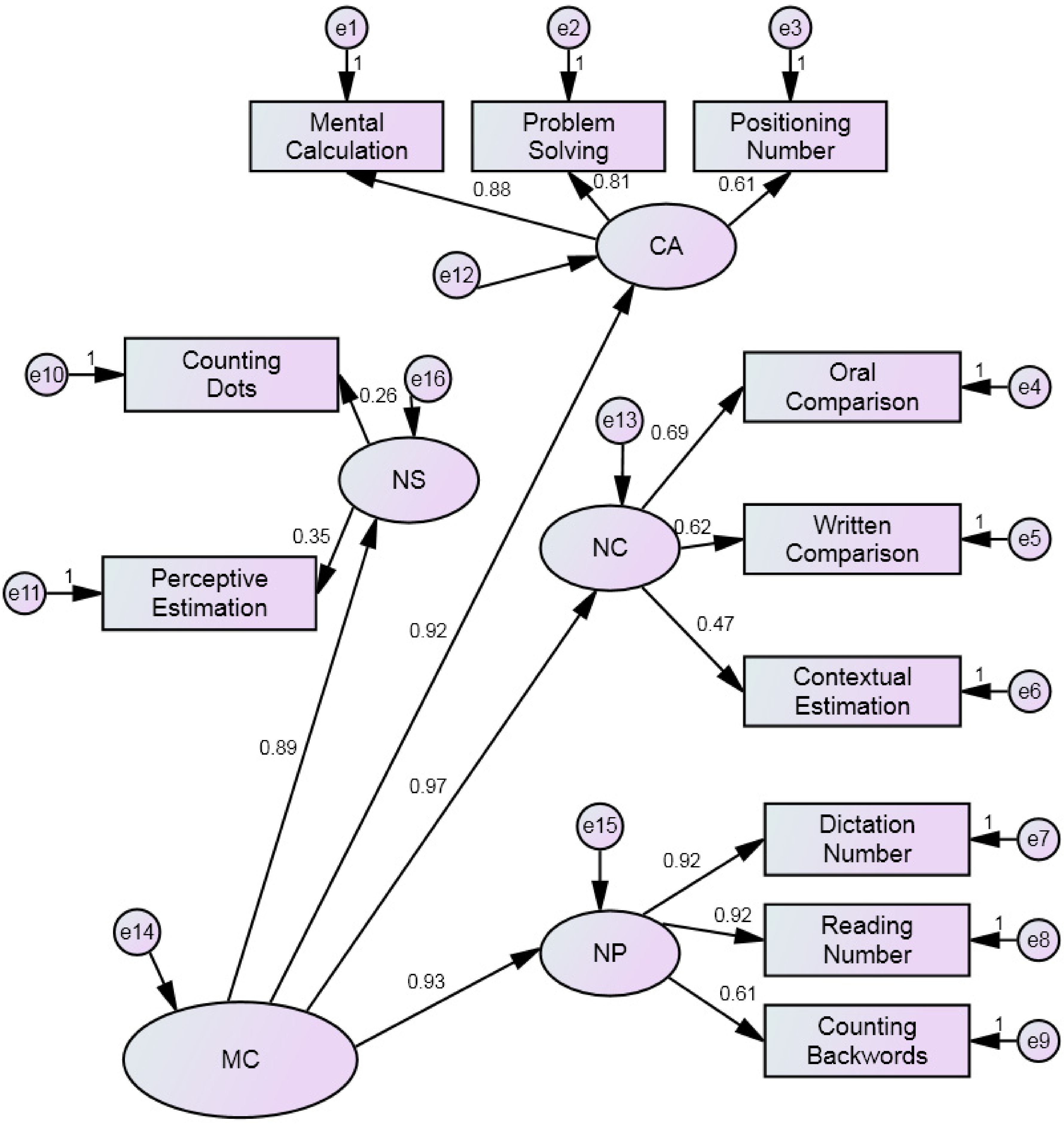
3.2. Dimensionality
3.3. Gender Invariance
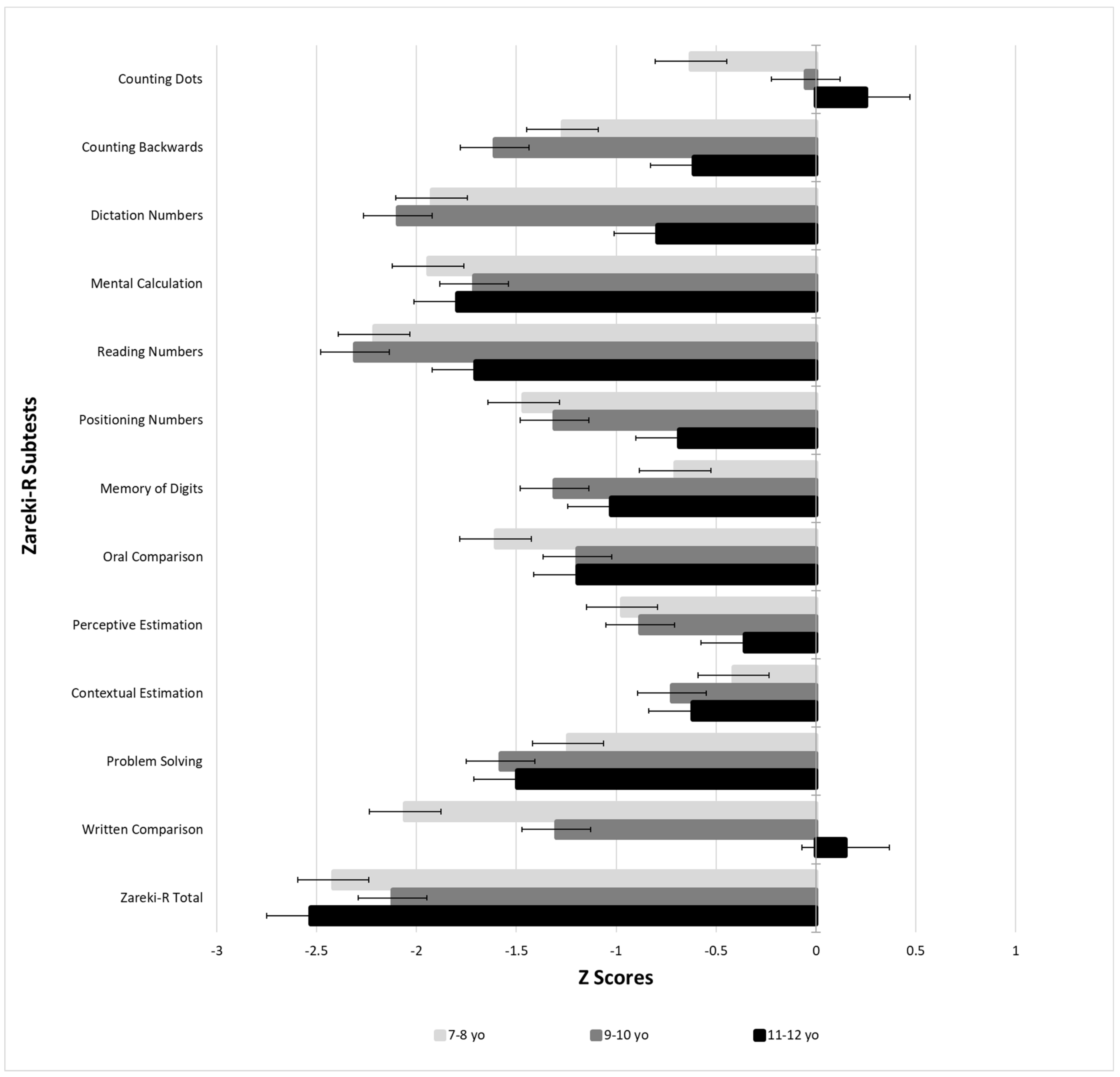
3.4. Gender Differences
3.5. Reliability
3.6. Criterion-Related Validity
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Age 7 N = 36 | Age 8 N = 81 | Age 9 N = 75 | Age 10 N = 51 | Age 11 N = 28 | Age 12 N = 33 | Z-Score | Category | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Counting dots | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | ≥1.5 | High |
| 34 | 2.0–4.0 | 78 | 2.0–4.00 | 65 | 2.0–4.00 | 45 | 3.0–4.00 | 25 | 3.0–4.00 | 31 | 3.0–4.00 | −1.49–+1.49 | Expected | |
| 2 | ≤1.0 | 3 | ≤1.0 | 10 | ≤2.0 | 6 | ≤2.0 | 3 | ≤2.0 | 2 | ≤2.0 | ≤−1.5 | Low | |
| Counting Backwards | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | ≥1.5 | High |
| 36 | 0–4.0 | 73 | 1.0–4.0 | 63 | 1.0–4.0 | 50 | 2.0–4.0 | 26 | 2.0–4.0 | 30 | 2.0–4.0 | −1.49–+1.49 | Expected | |
| -- | NA | 8 | 0 | 12 | 0 | 1 | ≤1.0 | 2 | ≤1.0 | 3 | ≤1.0 | ≤−1.5 | Low | |
| Dictation of Numbers | 2 | ≥13.0 | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | ≥1.5 | High |
| 32 | 1–12.0 | 73 | 7.0–16.0 | 67 | 8.0–16.0 | 51 | 14.0–16.0 | 25 | 13.0–16.0 | 32 | 13.0 –16.0 | −1.49–+1.49 | Expected | |
| 2 | 0 | 8 | ≤6.0 | 8 | ≤7.0 | -- | ≤13.0 | 3 | ≤12.0 | 1 | ≤12.0 | ≤−1.5 | Low | |
| Mental Calculation | 2 | ≥27 | 1 | ≥40 | -- | NA | -- | NA | -- | NA | -- | 44 | ≥1.5 | High |
| 34 | 0–26.0 | 74 | 9.0–39 | 69 | 14.0–44.0 | 51 | 25.0–44.0 | 26 | 21.0–44.0 | 30 | 20.0–43.0 | −1.49–+1.49 | Expected | |
| -- | NA | 6 | ≤8.0 | 6 | ≤13.0 | -- | ≤24.0 | 2 | ≤20.0 | 3 | ≤19.0 | ≤−1.5 | Low | |
| Reading Numbers | 2 | 16 | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | ≥1.5 | High |
| 33 | 1.0–15.0 | 74 | 9.0–16.0 | 67 | 10.0–16.0 | 51 | 15.0–16.0 | 27 | 15.0–16.0 | 31 | 14.0–16.0 | −1.49–+1.49 | Expected | |
| 1 | 0 | 7 | ≤8.0 | 8 | ≤9.0 | -- | ≤14.0 | 1 | ≤14.0 | 2 | ≤13.0 | ≤−1.5 | Low | |
| Positioning Numbers | 1 | ≥21.0 | 5 | 24.0 | -- | NA | -- | 24.0 | -- | NA | 2 | ≥23.0 | ≥1.5 | High |
| 32 | 2.0–20.0 | 68 | 9.0–23.0 | 68 | 9.0–24.0 | 50 | 14.0–23.0 | 25 | 12.0–24.0 | 29 | 13.0–22.0 | −1.49–+1.49 | Expected | |
| 3 | ≤1.0 | 8 | ≤8.0 | 7 | ≤8.0 | 1 | ≤13.0 | 3 | ≤11.0 | 2 | ≤12.0 | ≤−1.5 | Low | |
| Oral Comparison | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | ≥1.5 | High |
| 35 | 6.0–16.0 | 77 | 8.0–16.0 | 70 | 12.0–16.0 | 50 | 12.0–16.0 | 26 | 13.0–16.0 | 29 | 13.0–16.0 | −1.49–+1.49 | Expected | |
| 1 | ≤5.0 | 4 | ≤7.0 | 5 | ≤11.0 | 1 | ≤11.0 | 2 | ≤12.0 | 4 | ≤12.0 | ≤−1.5 | Low | |
| Perceptual Estimation | 1 | 10 | 10 | 10 | -- | NA | -- | NA | 1 | 10 | -- | NA | ≥1.5 | High |
| 34 | 2.0–9.0 | 65 | 3.0–9.0 | 69 | 3.0–10.0 | 48 | 4.0–10.0 | 24 | 4.0–9.0 | 32 | 4.0–10.0 | −1.49–+1.49 | Expected | |
| 1 | ≤1.0 | 6 | ≤2.0 | 6 | ≤2.0 | 3 | ≤3.0 | 3 | ≤3.0 | 1 | ≤3.0 | ≤−1.5 | Low | |
| Contextual Estimation | 1 | ≥15.0 | 6 | ≥18.0 | 4 | 20.0 | 6 | 20.0 | -- | NA | -- | NA | ≥1.5 | High |
| 35 | 2.0–14 | 75 | 3.0 –17.0 | 70 | 4.0–19.0 | 45 | 7.0–19.0 | 25 | 8.0–20.0 | 31 | 11.0–20.0 | −1.49–+1.49 | Expected | |
| -- | ≤1.0 | -- | ≤2.0 | 1 | ≤3.0 | 0 | ≤6.0 | 3 | ≤7.0 | 2 | ≤10.0 | ≤−1.5 | Low | |
| Problem Solving | 4 | ≥9.0 | 3 | ≥12.0 | -- | NA | -- | 14 | 3 | 14.0 | 1 | 14 | ≥1.5 | High |
| 32 | 0–8.0 | 78 | 0–11.0 | 70 | 2.0 –14.0 | 51 | 5.0–13.0 | 23 | 5.0–13.0 | 30 | 6.0–13.0 | −1.49–+1.49 | Expected | |
| -- | NA | -- | NA | 5 | ≤1.0 | -- | ≤4.0 | 2 | ≤4.0 | 2 | ≤5.0 | ≤−1.5 | Low | |
| Written Comparison | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | -- | NA | ≥1.5 | High |
| 34 | 12.0–20.0 | 75 | 15.0–20.0 | 68 | 17.0–20.0 | 49 | 17.0–20.0 | 22 | 18.0–20.0 | 31 | 17.0–20.0 | −1.49–+1.49 | Expected | |
| 2 | ≤11.0 | 6 | ≤14.0 | 7 | ≤16.0 | 2 | ≤16.0 | 6 | ≤17.0 | 2 | ≤16.0 | ≤−1.5 | Low | |
| Zareki-R Total | 2 | ≥127.0 | 2 | ≥164.0 | 0 | ≥181.0 | 0 | ≥178.0 | 0 | ≥180.0 | 1 | ≥177.0 | ≥1.5 | High |
| 33 | 48.0–126.0 | 74 | 87.0–163 | 66 | 100.0–180.0 | 48 | 135.0–177.0 | 26 | 132.0–179.0 | 30 | 130.0–176.0 | −1.49–+1.49 | Expected | |
| 1 | ≤47.0 | 5 | ≤86.0 | 9 | ≤99.0 | 3 | ≤134.0 | 2 | ≤131.0 | 2 | ≤129.0 | ≤−1.5 | Low | |
| Classification | p/z | p/z | p/z | p/z | p/z | Z | p/z | p/z | p/z | p/z | z | z | z | z | z | p/z | p/z | p/z | p/z | z | p/z | Z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age | 7 | 8 | 8 | 8 | 8 | 8 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 9 | 10 | 10 | 10 | 11 | 11 | 12 | 12 |
| Gender | F | M | M | M | M | M | F | M | M | M | F | M | F | F | F | F | F | F | F | M | M | F |
| Counting dots | 1 | 4 | 1 | 4 | 3 † | 3 † | 3 | 4 | 2 † | 3 | 4 | 1 | 4 | 4 | 2 † | 3 † | 4 | 4 | 4 † | 4 † | 4 † | 4 † |
| Counting backwards | 0 † | 0 | 0 | 2 | 1 † | 3 | 1 † | 0 | 1 † | 0 | 3 | 2 | 2 | 0 | 1 † | 1 | 4 | 3 † | 4 | 3 † | 1 | 3 † |
| Dictation of numbers | 4 † | 6 | 0 | 2 | 5 | 10 † | 4 | 8 † | 4 | 6 | 4 | 15 | 4 | 4 | 5 | 14 † | 16 | 10 | 14 † | 16 | 10 | 13 † |
| Mental calculation | 2 † | 10 † | 0 | 2 | 0 | 2 | 0 | 4 | 15 † | 4 | 26 | 13 | 6 | 24 | 12 | 16 | 20 | 20 | 6 | 18 | 13 | 16 |
| Reading numbers | 2 † | 4 | 2 | 12 | 4 | 8 † | 5 | 8 | 12 | 6 | 12 | 10 † | 8 | 8 | 4 | 12 | 16 | 15 † | 14 | 16 † | 11 | 13 † |
| Positioning numbers | 0 | 4 | 5 | 12 † | 15 | 12 † | 12 | 4 | 16 | 4 | 3 | 11 † | 16 | 4 | 20 | 10 | 19 † | 20 | 12 † | 17 | 13 † | 16 |
| Memory of Digits | 26 † | 18 † | 12 | 18 † | 14 | 20 | 18 | 20 | 8 | 20 | 12 | 10 † | 14 | 16 | 18 | 18 † | 22 | 14 | 20 † | 16 | 16 | 16 |
| Oral comparison | 6 † | 4 | 4 | 12 | 9 † | 10 | 10 | 16 | 8 | 12 † | 10 | 15 | 14 | 14 | 12 † | 12 † | 9 | 14 | 14 † | 14 † | 11 | 16 † |
| Perceptual estimation | 0 | 2 | 6 † | 6 † | 8 | 0 | 2 | 6 | 4 † | 6 | 6 | 2 | 6 | 4 † | 4 † | 2 | 6 † | 4 | 6 † | 7 | 6 † | 10 |
| Contextual estimation | 4 † | 16 † | 4 † | 6 † | 8 † | 10 † | 12 † | 10 † | 4 † | 8 † | 4 † | 4 † | 8 † | 6 † | 14 † | 18 † | 6 | 12 † | 10 | 4 | 16 † | 12 † |
| Problem-solving | 0 † | 2 † | 0 † | 0 † | 1 | 0 † | 0 | 2 † | 2 † | 0 | 4 | 0 | 0 | 4 | 2 † | 4 | 4 | 2 | 2 | 6 † | 2 | 8 † |
| Written comparison | 12 † | 10 | 12 | 12 | 14 | 18 † | 16 | 18 † | 16 | 18 † | 16 | 18 † | 18 † | 16 | 20 | 18 † | 20 | 18 † | 20 † | 20 † | 20 † | 20 † |
| Zareki-R Total | 31 | 62 | 34 | 70 | 68 | 76 | 65 | 80 | 84 | 67 | 92 | 91 | 86 | 88 | 96 | 110 | 124 | 122 | 106 | 125 | 107 | 131 |
References
- Santos, F.H. Discalculia do Desenvolvimento; Pearson Clinical Brasil: São Paulo, Brazil, 2017. [Google Scholar]
- Von Aster, M.; Shalev, R.S. Number development and developmental dyscalculia. Dev. Med. Child Neurol. 2007, 49, 868–873. [Google Scholar] [CrossRef] [PubMed]
- Rubinsten, O.; Henik, A. Developmental dyscalculia: Heterogeneity might not mean different mechanisms. Trends Cogn. Sci. 2009, 13, 92–99. [Google Scholar] [CrossRef] [PubMed]
- Kosc, L. Developmental Dyscalculia. J. Learn. Disabil. 1974, 7, 164–177. [Google Scholar] [CrossRef]
- Von Aster, M.; Schweiter, M.; Weinhold-Zulauf, M. Rechenstörungen bei Kindern. Z. Entwickl. Pädagogische Psychol. 2007, 39, 85–96. [Google Scholar] [CrossRef]
- Murphy, M.M.; Mazzocco, M.M.; Hanich, L.B.; Early, M.C. Cognitive characteristics of children with mathematics learning disability (MLD) vary as a function of the cutoff criterion used to define MLD. J. Learn. Disabil. 2007, 40, 458–478. [Google Scholar] [CrossRef] [PubMed]
- Desoete, A.; Ceulemans, A.; De Weerdt, F.; Pieters, S. Can we predict mathematical learning disabilities from symbolic and non symbolic comparison tasks in kindergarten? Findings from a longitudinal study. Br. J. Educ. Psychol. 2012, 82, 64–81. [Google Scholar] [CrossRef] [PubMed]
- Geary, D.C.; Hoard, M.K.; Byrd Craven, J.; Nugent, L.; Numtee, C. Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Dev. 2007, 78, 1343–1359. [Google Scholar] [CrossRef]
- Kaufmann, L.; Mazzocco, M.; Dowker, A.; von Aster, M.; Göbel, S.M.; Grabner, R.H.; Rubinsten, O. Dyscalculia from a developmental and differential perspective. Front. Psychol. 2013, 4, 516. [Google Scholar] [CrossRef]
- Ribeiro, F.S.; Tonoli, M.C.; Ribeiro, D.P.S.A.; Santos, F.H. Numeracy deficits scrutinized: Evidences of primary developmental dyscalculia. Psychol. Neurosci. 2017, 10, 189–200. [Google Scholar] [CrossRef]
- Koumoula, A.; Tsironi, V.; Stamouli, V.; Bardani, I.; Siapati, S.; Graham, A.; von Aster, M. An epidemiological study of number processing and mental calculation in Greek schoolchildren. J. Learn. Disabil. 2004, 37, 377–388. [Google Scholar] [CrossRef]
- Landerl, K.; Moll, K. Comorbidity of learning disorders: Prevalence and familial transmission. J. Child Psychol. Psychiatry 2010, 51, 287–294. [Google Scholar] [CrossRef] [PubMed]
- Kißler, C.; Schwenk, C.; Kuhn, J.-T. Two Dyscalculia Subtypes With Similar, Low Comorbidity Profiles: A Mixture Model Analysis. Front. Psychol. 2021, 12, 589506. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. The ICD-11 Classification of Mental and Behavioural Disorders: Diagnostic Criteria for Research; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Devine, A.; Soltész, F.; Nobes, A.; Goswami, U.; Szücs, D. Gender differences in developmental dyscalculia depend on diagnostic criteria. Learn. Instr. 2013, 27, 31–39. [Google Scholar] [CrossRef] [PubMed]
- Tannock, R. Rethinking ADHD and LD in DSM-5: Proposed Changes in Diagnostic Criteria. J. Learn. Disabil. 2013, 46, 5–25. [Google Scholar] [CrossRef]
- Butterworth, B. Developmental dyscalculia. In Handbook of Mathematical Cognition; Campbell, J.I., Ed.; Psychology Press: New York, NY, USA, 2005; pp. 455–467. [Google Scholar]
- Mazzocco, M.M.M.; Myers, G.F. Complexities in identifying and defining mathematics learning disability in the primary school age years. Ann. Dyslexia 2003, 53, 218–253. [Google Scholar] [CrossRef]
- Shalev, R.S.; Manor, O.; Gross-Tsur, V. Developmental dyscalculia: A prospective six-year follow-up. Dev. Med. Child Neurol. 2005, 47, 121–125. [Google Scholar] [CrossRef]
- Hoard, M.K.; Geary, D.C.; Hamson, C.O. Numerical and arithmetical cognition: Performance of low- and average-IQ children. Math. Cogn. 1999, 5, 65–91. [Google Scholar] [CrossRef]
- Shalev, R.S.; Manor, O.; Auerbach, J.; Gross-Tsur, V. Persistence of developmental dyscalculia: What counts? Results from a 3-year prospective follow-up study. J. Pediatr. 1998, 133, 358–362. [Google Scholar] [CrossRef]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; American Psychiatric Publishing: Arlington, VA, USA, 2013. [Google Scholar]
- Freitas-Feldberg, S.C.; Silva Gusmão Cardoso, T.; Santos, F.H.; Muszkat, M.; Bueno, O.F.; Berlim-Mello, C. Numerical cognition in children with cerebral palsy. Res. Develop. Disabil. 2021, 119, 104086. [Google Scholar] [CrossRef]
- Simms, V.; Gilmore, C.; Cragg, L. Nature and origins of mathematics difficulties in very preterm children: A different etiology than developmental dyscalculia. Pediatr. Res. 2015, 77, 389–395. [Google Scholar] [CrossRef]
- Castaldi, E.; Piazza, M.; Iuculano, T. Learning disabilities: Developmental dyscalculia. Handb. Clin. Neurol. 2020, 174, 61–75. [Google Scholar] [CrossRef] [PubMed]
- Devine, A.; Hill, F.; Carey, E.; Szucs, D. Cognitive and emotional math problems largely dissociate: Prevalence of developmental dyscalculia and mathematics anxiety. J. Educ. Psychol. 2018, 110, 431–444. [Google Scholar] [CrossRef]
- Szücs, D. Subtypes and comorbidity in mathematical learning disabilities: Multidimensional study of verbal and visual memory processes is key to understanding. Prog. Brain Res. 2016, 227, 277–304. [Google Scholar] [CrossRef] [PubMed]
- World Bank. World Development Report 2018: Learning to Realize Education’s Promise; License: Creative Commons Attribution CC BY 3.0 IGO; World Bank: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Economist Intelligence Unit. The Learning Curve; Pearson: London, UK, 2012; Available online: http://thelearningcurve.pearson.com/the-report (accessed on 30 October 2013).
- OECD. OECD Environmental Performance Reviews: Brazil 2015; OECD Publishing: Paris, France, 2015. [Google Scholar] [CrossRef]
- INEP—Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Ministério da Educação. 2018. Available online: http://ideb.inep.gov.br/ (accessed on 30 May 2021).
- OECD. Brazil—Country Note—PISA 2018 Results. 2019. Available online: https://www.oecd.org/pisa/publications/PISA2018_CN_BRA.PDF (accessed on 6 April 2021).
- Unesco. Regional Report about Education for All in Latin America and the Caribbean: Global Education for All Meeting Muscat, Oman 12th and 14th of 2014. 2014. Available online: https://unesdoc.unesco.org/ark:/48223/pf0000232701 (accessed on 7 June 2021).
- Ribeiro, F.S.; Santos, F.H. Enhancement of Numeric Cognition in Children with Numeracy Deficits after a Non-Instrumental Musical Training. Res. Devel. Disabil. 2017, 62, 26–39. [Google Scholar] [CrossRef]
- Fortes, I.S.; Paula, C.S.; Oliveira, M.C.; Bordin, I.A.; de Jesus Mari, J.; Rohde, L.A. A cross-sectional study to assess the prevalence of DSM-5 specific learning disorders in representative school samples from the second to sixth grade in Brazil. Eur. Child Adolesc. Psychiatry 2015, 25, 195–207. [Google Scholar] [CrossRef]
- Bastos, J.A.; Cecato, A.M.T.; Martins, M.R.I.; Grecca, K.R.R.; Pierini, R. The prevalence of developmental dyscalculia in Brazilian public school system. Arq. Neuropsiquiatr. 2016, 74, 201–206. [Google Scholar] [CrossRef][Green Version]
- Badian, N. Dyscalculia and nonverbal disorders of learning. In Progress in Learning Disabilities; Myklebust, H.R., Ed.; Grune & Stratton: New York, NY, USA, 1983; pp. 235–264. [Google Scholar]
- Guiso, L.; Monte, F.; Sapienza, P.; Zingales, L. Culture, gender, and math. Science 2008, 320, 1164–1165. [Google Scholar] [CrossRef]
- Devine, A.; Fawcett, K.; Szücs, D.; Dowker, A. Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behav. Brain Funct 2012, 8, 33. [Google Scholar] [CrossRef]
- Kovas, Y.; Haworth, C.M.; Petrill, S.A.; Plomin, R. Mathematical ability of 10-year-old boys and girls: Genetic and environmental etiology of typical and low performance. J. Learn. Disabil. 2007, 40, 554–567. [Google Scholar] [CrossRef]
- McCoy, S.; Byrne, D.; O’Connor, P. Gender stereotyping in mothers’ and teachers’ perceptions of boys’ and girls’ mathematics performance in Ireland. Oxf. Rev. Educ. 2021, 48, 341–363. [Google Scholar] [CrossRef]
- Caviola, S.; Colling, L.J.; Mammarella, I.C.; Szűcs, D. Predictors of mathematics in primary school: Magnitude comparison, verbal and spatial working memory measures. Dev. Sci. 2020, 23, e12957. [Google Scholar] [CrossRef] [PubMed]
- Mammarella, I.C.; Toffalini, E.; Caviola, S.; Colling, L.; Szűcs, D. No evidence for a core deficit in developmental dyscalculia or mathematical learning disabilities. J. Child Psychol. Psychiatry Allied Discip. 2021, 62, 704–714. [Google Scholar] [CrossRef]
- Von Aster, M.G.; Dellatolas, G. ZAREKI-R: Batterie Pour L’évaluation du Traitement des Nombres et du Calcul Chez L’enfant. Adaptation Française; Les Editions du Centre de Psychologie Appliquée: Paris, France, 2006. [Google Scholar]
- Rotzer, S.; Loenneker, T.; Kucian, K.; Martin, E.; Klaver, P.; von Aster, M. Dysfunctional neural network of spatial working memory contributes to developmental dyscalculia. Neuropsychologia 2009, 47, 2859–2865. [Google Scholar] [CrossRef] [PubMed]
- Labrell, F.; Mikaeloff, Y.; Perdry, H.; Dellatolas, G. Time knowledge acquisition in children aged 6 to 11 years and its relationship with numerical skills. J. Exp. Child Psychol. 2016, 143, 1–13. [Google Scholar] [CrossRef] [PubMed]
- DeClercq-Quaegebeur, M.D.; Casalis, S.; Vilette, B.; Lemaitre, M.P.; Vallée, L. Arithmetic abilities in children with developmental dyslexia. Performance on French ZAREKI-R Test. J. Learn. Disabil. 2017, 51, 236–249. [Google Scholar] [CrossRef]
- Dellatolas, G.; von Aster, M.; Braga, L.W.; Meier, M.; Deloche, G. Number processing and mental calculation in school children aged 7 to 10 years: A transcultural comparison. Eur. Child Adolesc. Psychiatry 2000, 9, 102–110. [Google Scholar] [CrossRef]
- Santos, F.H.; Silva, P.A.; Ribeiro, F.S.; Dias, A.L.R.P.; Frigério, M.C.; Dellatolas, G.; von Aster, M. Number representation in Brazilian children number processing and calculation in Brazilian children aged 7–12 years. Span. J. Psychol. 2012, 15, 513–525. [Google Scholar] [CrossRef]
- Lahmer, M. Développement des données normatives adaptées pour la batterie Zareki-R en Algérie. Glossa 2021, 130, 41–57. [Google Scholar]
- Dehaene, S. Varieties of numerical abilities. Cognition 1992, 44, 1–42. [Google Scholar] [CrossRef]
- Hubbard, E.; Piazza, M.; Pinel, P.; Dehaene, S. Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 2005, 6, 435–448. [Google Scholar] [CrossRef]
- Feigenson, L.; Dehaene, S.; Spelke, E. Core systems of number. Trends Cogn. Sci. 2004, 8, 307–314. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Li, F.; Zhao, L.; Xie, L.; Zhao, H. The Developmental Changes of Number Processing and Calculation Abilities in Chinese Primary School Students. Eurasia J. Math. Sci. Technol. Educ. 2018, 14, 2745–2756. [Google Scholar] [CrossRef]
- Sella, F.; Hartwright, C.; Cohen Kadosh, R. The Neurocognitive Bases of Numerical Cognition. In Stevens’ Handbook of Experimental Psychology and Cognitive Neuroscience; John Wiley & Sons, 2018; pp. 1–47. [Google Scholar] [CrossRef]
- Kucian, K.; Kaufmann, L. A developmental model of number representation. Behav. Brain Sci. 2009, 32, 340. [Google Scholar] [CrossRef]
- Kaufmann, L.; Wood, G.; Rubinsten, O.; Henik, A. Meta-analyses of developmental fMRI studies investigating typical and atypical trajectories of number processing and calculation. Dev. Neuropsychol. 2011, 36, 763–787. [Google Scholar] [CrossRef]
- Dehaene, S.; Piazza, M.; Pinel, P.; Cohen, L. Three parietal circuits for number processing. Cogn. Neuropsychol. 2003, 20, 487–506. [Google Scholar] [CrossRef]
- McCaskey, U.; von Aster, M.; O’Gorman, R.; Kucian, K. Persistent Differences in Brain Structure in Developmental Dyscalculia: A Longitudinal Morphometry Study. Front. Hum. Neurosci. 2020, 14, 272. [Google Scholar] [CrossRef]
- Siemann, J.; Petermann, F. Evaluation of the Triple Code Model of numerical processing—Reviewing past neuroimaging and clinical findings. Res. Dev. Disabil. 2017, 72, 106–117. [Google Scholar] [CrossRef]
- Santos, F.H.; Silva, P.A.; Ribeiro, F.S.; Dellatolas, G.; von Aster, M. Development of numerical cognition among Brazilian school-aged children. Int. J. Stud. Math. Edu. 2012, 5, 44–64. [Google Scholar]
- World Health Organization. The World Health Organization Quality of Life Assessment; World Health Organization: Geneva, Switzerland, 1995. [Google Scholar]
- Wang, Y.; Chen, H. Use of Percentiles and Z -Scores in Anthropometry. In Handbook of Anthropometry: Physical Measures of Human Form in Health and Disease; Preedy, V.R., Ed.; Springer: New York, NY, USA, 2012; pp. 29–48. [Google Scholar] [CrossRef]
- Byrne, B.M. Testing for multigroup invariance using AMOS Graphics: A road less traveled. Struct. Equ. Modeling A Multidiscip. J. 2004, 11, 272–300. [Google Scholar] [CrossRef]
- Dimitrov, D.M. Testing for factorial invariance in the context of construct validation. Meas. Eval. Couns. Dev. 2010, 43, 121–149. [Google Scholar] [CrossRef]
- Vandenberg, R.J.; Lance, C.E. A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Org. Res. Methods 2000, 3, 4–70. [Google Scholar] [CrossRef]
- Angelini, A.L.; Alves, I.C.B.; Custódio, E.M.; Duarte, W.F.; Duarte, J.L.M. Manual: Matrizes Progressivas Coloridas de Raven; Centro Editor de Testes e Pesquisas em Psicologia: São Paulo, Brazil, 1999. [Google Scholar]
- Wechsler, D. WISC-III: Escala de Inteligência Wechsler Para Crianças: Manual, 3rd ed.; Casa do Psicólogo: São Paulo, Brazil, 2002. [Google Scholar]
- Stein, L.M. TDE—Teste de Desempenho Escolar; Casa do Psicólogo: São Paulo, Brazil, 1994. [Google Scholar]
- Girard, C.; Bastelica, T.; Léone, J.; Epinat-Duclos, J.; Longo, L.; Prado, J. The relation between home numeracy practices and a variety of math skills in elementary school children. PLoS ONE 2021, 16, e0255400. [Google Scholar] [CrossRef] [PubMed]
- Santos, F.H. Memória Operacional de Crianças Normais e com Lesões Congênitas: Desenvolvimento Cognitivo e Reorganização Cerebral. Ph.D. Thesis, Universidade Federal de São Paulo, São Paulo, Brazil, 2002. Available online: https://pesquisa.bvsalud.org/portal/resource/pt/lil-330816 (accessed on 9 September 2021).
- Muthén, L.K.; Muthén, B.O. Mplus: The Comprehensive Modeling Program for Applied Researchers: User’s Guide, 3rd ed.; Muthén & Muthén: Los Angeles, CA, USA, 2004. [Google Scholar]
- Satorra, A.; Bentler, P.M. A scaled difference chi-square test statistic for moment structure analysis. Psychometrika 2001, 66, 507–514. [Google Scholar] [CrossRef]
- Bentler, P.M.; Dudgeon, P. Covariance structure analysis: Statistical practice, theory and directions. Ann. Rev. Psychol. 1996, 47, 541–570. [Google Scholar] [CrossRef] [PubMed]
- Bentler, P.M. Comparative fit indexes in structural models. Psychol. Bull. 1990, 107, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Tucker, L.R.; Lewis, C. A reliability coefficient for maximum likelihood factor analysis. Psychometrika 1973, 38, 1–10. [Google Scholar] [CrossRef]
- Steiger, J.H.; Lind, J.C. Statistically-based tests for the number of common factors. In Proceedings of the Annual Spring Meeting of the Psychometric Society, Iowa City, CA, USA, April 1980. [Google Scholar]
- Schermelleh-Engel, K.; Moosbrugger, H.; Müller, H. Evaluating the fit of structural equation models: Tests of significance and descriptive goodness-of-fit measures. Methods Psychol. Res. Online 2003, 8, 23–74. [Google Scholar]
- Hu, L.T.; Bentler, P.M. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Modeling A Multidiscip. J. 1999, 6, 1–55. [Google Scholar] [CrossRef]
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 3rd ed.; Guilford Press: New York, NY, USA, 2010. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228–243. [Google Scholar] [CrossRef] [PubMed]
- Meade, A.W.; Johnson, E.C.; Braddy, P.W. Power and sensitivity of alternative fit indices in tests of measurement invariance. J. Appl. Psychol. 2008, 93, 568–592. [Google Scholar] [CrossRef] [PubMed]
- Cheung, G.W.; Rensvold, R.B. Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equ. Modeling 2002, 9, 233–255. [Google Scholar] [CrossRef]
- Little, T.D. Mean and covariance structures (MACS) analyses of cross-cultural data: Practical and theoretical issues. Multivar. Behav. Res. 1997, 32, 53–76. [Google Scholar] [CrossRef] [PubMed]
- Molina, J.; Ribeiro, F.S.; Santos, F.H.; Aster, M. Cognição numérica de crianças pré-escolares brasileiras pela ZAREKI-K. Temas Em Psicol. 2015, 23, 123–135. [Google Scholar] [CrossRef]
- Brazil. Ministry of Education. Education for All 2015 National Review Report: Brazil. 2014. Available online: http://unesdoc.unesco.org/images/0023/002300/230021e.pdf (accessed on 3 May 2022).
- Else-Quest, N.; Hyde, J.; Linn., M. Cross-national patterns of gender differences in mathematics: A meta-analysis. Psychol. Bull. 2010, 136, 103–127. [Google Scholar] [CrossRef]
- Cowan, R.; Donlan, C.; Shepherd, D.L.; Cole-Fletcher, R.; Saxton, M.; Hurry, J. Basic calculation proficiency and mathematics achievement in elementary school children. J. Educ. Psych. 2011, 103, 786–803. [Google Scholar] [CrossRef]
- Dowker, A. Individual differences in numerical abilities in preschoolers. Dev. Sci. 2008, 11, 650–654. [Google Scholar] [CrossRef]
- Dowker, A. Individual differences in arithmetical abilities. The componential nature of arithmetic. In The Oxford Handbook of Mathematical Cognition; Cohen Kadosh, R., Dowker, A., Eds.; Oxford University Press: Oxford, UK, 2015; pp. 862–878. [Google Scholar]
- Jordan, J.A.; Mulhern, G.; Wylie, J. Individual differences in trajectories of arithmetical development in typically achieving 5-7-year-olds. J. Exp. Child Psychol. 2009, 103, 455–468. [Google Scholar] [CrossRef]
- Dowker, A. What can intervention tell us about the development of arithmetic? Educ. Child Psychol. 2007, 24, 64–82. [Google Scholar]
- Gifford, S.; Rockliffe, F. Mathematics difficulties: Does one approach fit all? J. Res. Math. Educ. 2012, 14, 1–16. [Google Scholar] [CrossRef]
- Kaufmann, L.; von Aster, M. The diagnosis and management of dyscalculia. Dtsch. Ärzteblatt Int. 2012, 109, 767–778. [Google Scholar] [CrossRef] [PubMed]
- Dowker, A. Interventions for primary school children with difficulties in mathematics. Adv. Child Dev. Behav. 2017, 53, 255–287. [Google Scholar] [CrossRef] [PubMed]
- Holmes, W.; Dowker, A.D. Catch Up Numeracy: A targeted intervention for children who are low attaining in mathematics. J. Res. Math. Educ. 2013, 15, 249–265. [Google Scholar] [CrossRef]
- Mazzocco, M.M.M.; Räsänen, P. Contributions of longitudinal studies to evolving definitions and knowledge of developmental dyscalculia. Trends Neurosci. Educ. 2013, 2, 65–73. [Google Scholar] [CrossRef]
- Karagiannis, G.N.; Coorman, A. Focused MLD intervention based on the classification of MLD subtypes. In The Routledge International Handbook of Dyscalculia and Mathematical Learning Difficulties; Chinn, S., Ed.; Routledge: London, UK, 2014; pp. 265–289. [Google Scholar]
- Santos, F.H. Interventions for Children with Developmental Dyscalculia: Parents, teachers and neuropsychologists working together. In Understanding Dyscalculia: A Guide to Symptoms, Management and Treatment; Lucangeli, D., Ed.; Routledge: London, UK, 2021; pp. 65–92. [Google Scholar]
- Reigosa-Crespo, V.; Valdes-Sosa, M.; Butterworth, B.; Estevez, N.; Rodriguez, M.; Santos, E.; Torres, P.; Suarez, R.; Lage, A. Basic numerical abilities and prevalence of Developmental dyscalculia: The Havana survey. Dev. Psychol. 2012, 48, 123–135. [Google Scholar] [CrossRef]
- Ribeiro, F.S.; Santos, F.H. Persistent Effects of Musical Training on Mathematical Skills of Children with Developmental Dyscalculia. Front. Psychol. 2020, 10, 2888. [Google Scholar] [CrossRef]
- Kohn, J.; Rauscher, L.; Kucian, K.; Käser, T.; Wyschkon, A.; Esser, G.; von Aster, M. Efficacy of a Computer-Based Learning Program in Children with Developmental Dyscalculia. What Influences Individual Responsiveness? Front. Psychol. 2020, 11, 1115. [Google Scholar] [CrossRef]

| Age 7 | N (36) | Age 8 | N (81) | Age 9 | N (75) | Age 10 | N (51) | Age 11 | N (28) | Age 12 | N (33) | Percentile | Classification |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| >138.95 | 1 | >160 | 3 | >174.8 | 4 | >176.1 | 3 | >173 | 2 | >174.35 | 1 | >95 | High |
| 104.2–135.0 | 8 | 144.2–159.8 | 17 | 158.0–174.2 | 15 | 165.0–175.4 | 10 | 168.1–173.0 | 5 | 165.2–172.9 | 9 | 75–94 | High average |
| 65.9–103.1 | 18 | 111.6–143.8 | 40 | 127.8–157.2 | 37 | 149.8–164.7 | 25 | 148.1–167.7 | 14 | 143.9–165.1 | 15 | 26–74 | Average |
| 48.2–64.6 | 8 | 75.5–111.2 | 17 | 85.1–127 | 15 | 125.0–149.5 | 10 | 119.6–147.5 | 6 | 131.2–143.75 | 7 | 6–25 | Low average |
| <45.4 | 1 | <75.0 | 4 | <84 | 4 | <122.7 | 3 | <114.1 | 1 | <123.6 | 1 | <5 | Low |
| Model | χ2 (df) | CFI | Model Comparison | Δχ2 | Δdf | p | ΔCFI |
|---|---|---|---|---|---|---|---|
| 1. Invariance of model configuration | 116.22 (62) | 0.961 | - | - | - | - | - |
| 2. Invariance of first-order factor loadings | 125.34 (68) | 0.959 | Model 1–Model 2 | 9.12 | 6 | 0.167 | 0.002 |
| 3. Invariance of intercepts | 141.78 (78) | 0.954 | Model 2–Model 3 | 16.44 | 10 | 0.088 | 0.005 |
| 4. Invariance of second-order factor loadings | 144.36 (81) | 0.954 | Model 3–Model 4 | 2.58 | 3 | 0.462 | 0.000 |
| 5. Invariance of structural variances/covariances | 150.11 (86) | 0.954 | Model 4–Model 5 | 5.75 | 5 | 0.331 | 0.000 |
| 6. Invariance of measurement error variances/covariances | 159.78 (96) | 0.954 | Model 5–Model 6 | 9.67 | 10 | 0.470 | 0.000 |
| Girls (n = 143) | Boys (n = 161) | Age 7 (n = 36) | Age 8 (n = 81) | Age 9 (n = 75) | Age 10 (n= 51) | Age 11 (n = 28) | Age 12 (n= 33) | F (5398) | p | ηp2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Counting dots | 3.44 (0.77) | 3.42 (0.83) | 3.36 (0.93) | 3.21 (0.86) | 3.37 (0.78) | 3.61 (0.69) | 3.68 (0.67) | 3.70 (0.64) | 3.24 | 0.007 | 0.05 |
| Counting backwards a | 2.99 (1.25) | 3.08 (1.18) | 2.03 (1.36) | 2.84 (1.34) | 3.05 (1.21) | 3.57 (0.73) | 3.50 (0.88) | 3.36 (0.82) | 9.88 | <0.001 | 0.14 |
| Dictation of numbers b | 12.59 (4.29) | 13.42 (3.74) | 6.33 (3.90) | 12.48 (3.60) | 13.66 (3.66) | 15.28 (1.12) | 15.21 (1.26) | 14.94 (1.39) | 45.40 | <0.001 | 0.44 |
| Mental calculation c | 26.54 (11.12) | 28.40 (11.65) | 12.19 (9.00) | 23. 95 (10.06) | 29.11 (10.26) | 35.26 (6.52) | 34.68 (8.85) | 31.46 (7.75) | 35.16 | <0.001 | 0.37 |
| Reading numbers d | 13.66 (3.77) | 14.32 (3.45) | 7.92 (4.63) | 13.72 (3.22) | 14.65 (2.84) | 15.78 (0.67) | 15.93 (0.38) | 15.55 (1.06) | 45.72 | <0.001 | 0.43 |
| Memory of Digits | 23.44 (6.21) | 23.56 (6.57) | 21.34 (5.64) | 23.63 (6.72) | 22.59 (5.71) | 24.90 (6.90) | 23.86 (6.88) | 25.21 (6.02) | 2.16 | <0.06 | 0.03 |
| Positioning numberse | 16.04 (5.06) | 16.61 (4.85) | 11.13 (5.88) | 15.93 (4.67) | 16.81 (5.25) | 18.28 (2.91) | 17.95 (3.82) | 17.65 (3.01) | 13.00 | <0.001 | 0.18 |
| Oral comparison f | 13.23 (2.84) | 14.06 (2.45) | 10.92 (3.42) | 12.52 (2.88) | 14.52 (1.83) | 14.57 (1.66) | 15.04 (1.23) | 15.00 (1.50) | 22.24 | <0.001 | 0.27 |
| Perceptual estimation | 6.10 (2.27) | 6.71 (2.29) | 5.50 (2.36) | 6.05 (2.36) | 6.56 (2.41) | 6.90 (2.05) | 6.54 (1.90) | 7.21 (2.13) | 2.97 | 0.01 | 0.05 |
| Contextual estimation g | 11.80 (4.89) | 11.90 (5.11) | 8.39 (3.99) | 10.05 (4.53) | 11.39 (5.00) | 14.12 (4.81) | 14.21 (3.86) | 15.64 (3.41) | 15.98 | <0.001 | 0.21 |
| Problem-solving h | 6.41 (3.91) | 7.56 (3.92) | 2.81 (3.25) | 5.30 (3.57) | 7.81 (3.97) | 8.92 (2.63) | 9.14 (2.86) | 9.30 (2.47) | 25.32 | <0.001 | 0.30 |
| Written comparison j | 18.73 (2.12) | 18.88 (2.14) | 16.72 (3.03) | 18.57 (2.49) | 19.05 (1.32) | 19.49 (1.59) | 19.57 (0.84) | 19.39 (1.37) | 11.21 | <0.001 | 0.16 |
| Zareki-R Total c | 140.27 (38.52) | 149.20 (37.68) | 87.31 (26.11) | 124.75 (25.46) | 140.00 (26.8) | 155.78 (13.87) | 155.54 (15.9) | 153.26 (15.17) | 53.47 | <0.001 | 0.47 |
| Score A c | 91.16 (23.31) | 96.63 (23.46) | 56.89 (20.38) | 86.53 (19.59) | 98.80 (19.67) | 109.29 (10.42) | 109.57 (12.22) | 105.64 (11.83) | 52.97 | <0.001 | 0.47 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, F.H.; Ribeiro, F.S.; Dias-Piovezana, A.L.; Primi, C.; Dowker, A.; von Aster, M. Discerning Developmental Dyscalculia and Neurodevelopmental Models of Numerical Cognition in a Disadvantaged Educational Context. Brain Sci. 2022, 12, 653. https://doi.org/10.3390/brainsci12050653
Santos FH, Ribeiro FS, Dias-Piovezana AL, Primi C, Dowker A, von Aster M. Discerning Developmental Dyscalculia and Neurodevelopmental Models of Numerical Cognition in a Disadvantaged Educational Context. Brain Sciences. 2022; 12(5):653. https://doi.org/10.3390/brainsci12050653
Chicago/Turabian StyleSantos, Flavia H., Fabiana S. Ribeiro, Ana Luiza Dias-Piovezana, Caterina Primi, Ann Dowker, and Michael von Aster. 2022. "Discerning Developmental Dyscalculia and Neurodevelopmental Models of Numerical Cognition in a Disadvantaged Educational Context" Brain Sciences 12, no. 5: 653. https://doi.org/10.3390/brainsci12050653
APA StyleSantos, F. H., Ribeiro, F. S., Dias-Piovezana, A. L., Primi, C., Dowker, A., & von Aster, M. (2022). Discerning Developmental Dyscalculia and Neurodevelopmental Models of Numerical Cognition in a Disadvantaged Educational Context. Brain Sciences, 12(5), 653. https://doi.org/10.3390/brainsci12050653







