Decoding Task-Based fMRI Data with Graph Neural Networks, Considering Individual Differences
Abstract
:1. Introduction
- We propose an end-to-end GCN framework to classify task-evoked fMRI data. The objective is to examine the performance of various node embeddings to generate topological embeddings of the graph’s nodes. To our knowledge, this is the first investigation of different node embeddings on task fMRI classification performance. The code is available at https://github.com/krzysztoffiok/gnn-classification-pipeline, accessed on 20 February 2022.
- We demonstrate the performance of the proposed GCN framework according to individual differences (i.e., gender and fluid intelligence). To this end, we constructed four small sub-datasets of gender and gF score (LM-gF/HM-gF) with replacement.
2. Background
3. Materials and Methods
3.1. fMRI Dataset and Preprocessing
3.2. Graph Convolutional Network: Spectral
3.2.1. Notation
3.2.2. Spectral-Based GCN
3.3. Functional Graph
3.4. Feature Engineering and Node Embedding Algorithms
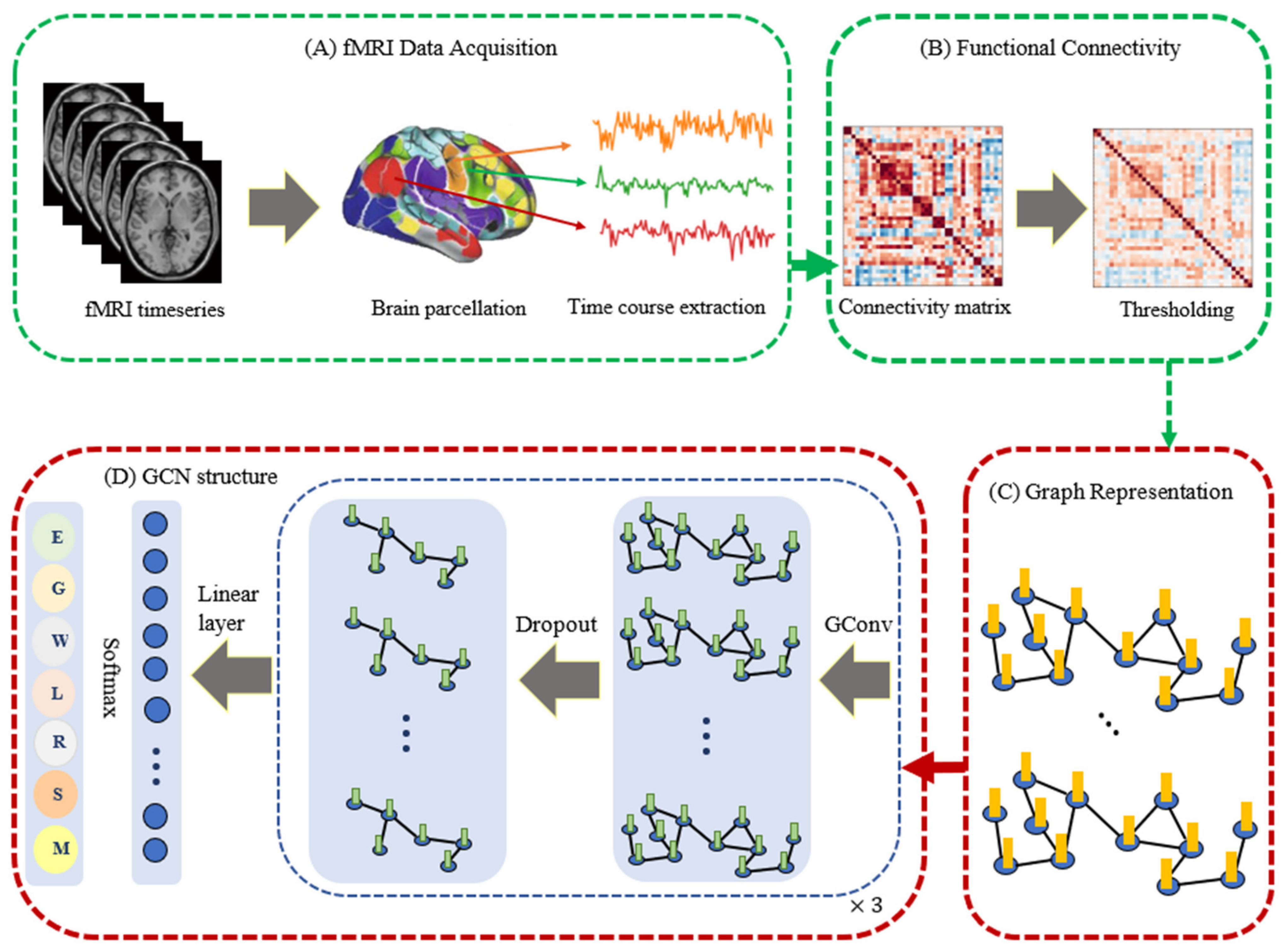
3.5. Proposed Model
3.5.1. Modular Architecture
3.5.2. Training and Testing
3.5.3. Evaluation Metrics
4. Results
4.1. Classification of Task fMRI Data
Performance Comparison
4.2. Effects of Group Membership on Classification
4.2.1. Gender Predictions
4.2.2. Fluid Intelligence Level Discrepancy
5. Discussion
5.1. Overview
5.2. Effects of Individual Differences
5.3. Effects of Batch Size
5.4. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goense, J.; Bohraus, Y.; Logothetis, N.K. fMRI at high spatial resolution implications for BOLD-models. Front. Comput. Neurosci. 2016, 10, 66. [Google Scholar] [CrossRef] [PubMed]
- Logothetis, N.K.; Pauls, J.; Augath, M.; Trinath, T.; Oeltermann, A. Neurophysiological investigation of the basis of the fMRI signal. Nature 2001, 412, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Kriegeskorte, N.; Douglas, P.K. Interpreting encoding and decoding models. Curr. Opin. Neurobiol. 2019, 55, 167–179. [Google Scholar] [CrossRef] [PubMed]
- Douglas, P.K.; Lau, E.; Anderson, A.; Head, A.; Kerr, W.; Wollner, M.A.; Moyer, D.; Li, W.; Durnhofer, M.; Bramen, J.; et al. Single trial decoding of belief decision making from EEG and fMRI data using independent components features. Front. Hum. Neurosci. 2013, 7, 392. [Google Scholar] [CrossRef]
- Colby, J.B.; Rudie, J.D.; Brown, J.A.; Douglas, P.K.; Cohen, M.S.; Shehzad, Z. Insights into multimodal imaging classification of ADHD. Front. Syst. Neurosci. 2012, 6, 59. [Google Scholar] [CrossRef]
- Zhang, Y.; Tetrel, L.; Thirion, B.; Bellec, P. Functional annotation of human cognitive states using deep graph convolution. NeuroImage 2021, 231, 117847. [Google Scholar] [CrossRef]
- Li, X.; Dvornek, N.C.; Zhou, Y.; Zhuang, J.; Ventola, P.; Duncan, J.S. Graph Neural Network for Interpreting Task-fMRI Biomarkers. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; Volume 11768, pp. 485–493. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Dvornek, N.; Zhang, M.; Gao, S.; Zhuang, J.; Scheinost, D.; Staib, L.H.; Ventola, P.; Duncan, J.S. BrainGNN: Interpretable Brain Graph Neural Network for fMRI Analysis. Med. Image Anal. 2021, 74, 102233. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Dvornek, N.C.; Zhang, M.; Zhuang, J.; Ventola, P.; Duncan, J.S. Pooling Regularized Graph Neural Network for fMRI Biomarker Analysis. In Alzheimer’s Disease and Frontotemporal Dementia; Humana Press: Totowa, NJ, USA, 2020; Volume 12267, pp. 625–635. [Google Scholar] [CrossRef]
- Kim, B.-H.; Ye, J.C.; Kim, J.-J. Learning Dynamic Graph Representation of Brain Connectome with Spatio-Temporal Attention. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Virtual Event, 6–14 December 2021. [Google Scholar]
- Li, X.; Dvornek, N.C.; Zhuang, J.; Ventola, P.; Duncan, J. Graph embedding using Infomax for ASD classification and brain functional difference detection. In Proceedings of the Medical Imaging 2020: Biomedical Applications in Molecular, Structural, and Functional Imaging, Houston, TX, USA, 15–20 February 2020; Volume 11317, p. 1131702. [Google Scholar] [CrossRef]
- Xu, K.; Jegelka, S.; Hu, W.; Leskovec, J. How Powerful are Graph Neural Networks? arXiv 2018, arXiv:1810.00826. [Google Scholar] [CrossRef]
- Goyal, P.; Ferrara, E. Graph embedding techniques, applications, and performance: A survey. Knowl.-Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef]
- Van Essen, D.C.; Smith, S.M.; Barch, D.M.; Behrens, T.E.J.; Yacoub, E.; Ugurbil, K. The WU-Minn Human Connectome Project: An overview. NeuroImage 2013, 80, 62–79. [Google Scholar] [CrossRef]
- Tomasi, D.; Volkow, N.D. Gender differences in brain functional connectivity density. Hum. Brain Mapp. 2011, 33, 849–860. [Google Scholar] [CrossRef]
- Bruzzone, S.E.P.; Lumaca, M.; Brattico, E.; Vuust, P.; Kringelbach, M.L.; Bonetti, L. Dissociated brain functional connectivity of fast versus slow frequencies underlying individual differences in fluid intelligence: A DTI and MEG study. Sci. Rep. 2022, 12, 4746. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, M.; Qin, W.; Wan, B.; Yu, C.; Ming, D. Gender Differences Are Encoded Differently in the Structure and Function of the Human Brain Revealed by Multimodal MRI. Front. Hum. Neurosci. 2020, 14, 244. [Google Scholar] [CrossRef]
- Santarnecchi, E.; Emmendorfer, A.; Tadayon, S.; Rossi, S.; Rossi, A.; Pascual-Leone, A. Network connectivity correlates of variability in fluid intelligence performance. Intelligence 2017, 65, 35–47. [Google Scholar] [CrossRef]
- Jiang, R.; Calhoun, V.D.; Fan, L.; Zuo, N.; Jung, R.; Qi, S.; Lin, D.; Li, J.; Zhuo, C.; Song, M.; et al. Gender Differences in Connectome-based Predictions of Individualized Intelligence Quotient and Sub-domain Scores. Cereb. Cortex 2019, 30, 888–900. [Google Scholar] [CrossRef]
- Farahani, F.V.; Fafrowicz, M.; Karwowski, W.; Douglas, P.K.; Domagalik, A.; Beldzik, E.; Oginska, H.; Marek, T. Effects of chronic sleep restriction on the brain functional network, as revealed by graph theory. Front. Neurosci. 2019, 13, 1087. [Google Scholar] [CrossRef]
- Sen, B.; Parhi, K.K. Predicting Male vs. Female from Task-fMRI Brain Connectivity. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 4089–4092. [Google Scholar] [CrossRef]
- Anderson, A.E.; Diaz-Santos, M.; Frei, S.; Dang, B.H.; Kaur, P.; Lyden, P.; Buxton, R.; Douglas, P.K.; Bilder, R.M.; Esfandiari, M.; et al. Hemodynamic latency is associated with reduced intelligence across the lifespan: An fMRI DCM study of aging, cerebrovascular integrity, and cognitive ability. Brain Struct. Funct. 2020, 225, 1705–1717. [Google Scholar] [CrossRef]
- Betzel, R.F.; Byrge, L.; He, Y.; Goñi, J.; Zuo, X.-N.; Sporns, O. Changes in structural and functional connectivity among resting-state networks across the human lifespan. NeuroImage 2014, 102, 345–357. [Google Scholar] [CrossRef]
- Christov-Moore, L.; Reggente, N.; Douglas, P.K.; Feusner, J.D.; Iacoboni, M. Predicting Empathy from Resting State Brain Connectivity: A Multivariate Approach. Front. Integr. Neurosci. 2020, 14, 3. [Google Scholar] [CrossRef]
- Friston, K.J.; Holmes, A.P.; Worsley, K.J.; Poline, J.-P.; Frith, C.D.; Frackowiak, R.S.J. Statistical parametric maps in functional imaging: A general linear approach. Hum. Brain Mapp. 1995, 2, 189–210. [Google Scholar] [CrossRef]
- Barch, D.M.; Burgess, G.C.; Harms, M.; Petersen, S.E.; Schlaggar, B.L.; Corbetta, M.; Glasser, M.F.; Curtiss, S.; Dixit, S.; Feldt, C.; et al. Function in the human connectome: Task-fMRI and individual differences in behavior. NeuroImage 2013, 80, 169–189. [Google Scholar] [CrossRef]
- Hu, X.; Lv, C.; Cheng, G.; Lv, J.; Guo, L.; Han, J.; Liu, T. Sparsity-Constrained fMRI Decoding of Visual Saliency in Naturalistic Video Streams. IEEE Trans. Auton. Ment. Dev. 2015, 7, 65–75. [Google Scholar] [CrossRef]
- Lv, J.; Lin, B.; Li, Q.; Zhang, W.; Zhao, Y.; Jiang, X.; Guo, L.; Han, J.; Hu, X.; Guo, C.; et al. Task fMRI data analysis based on supervised stochastic coordinate coding. Med. Image Anal. 2017, 38, 1–16. [Google Scholar] [CrossRef]
- Zhang, W.; Lv, J.; Li, X.; Zhu, D.; Jiang, X.; Zhang, S.; Zhao, Y.; Guo, L.; Ye, J.; Hu, D.; et al. Experimental Comparisons of Sparse Dictionary Learning and Independent Component Analysis for Brain Network Inference From fMRI Data. IEEE Trans. Biomed. Eng. 2018, 66, 289–299. [Google Scholar] [CrossRef]
- Anderson, A.; Han, D.; Douglas, P.K.; Bramen, J.; Cohen, M.S. Real-time functional MRI classification of brain states using Markov-SVM hybrid models: Peering inside the rt-fMRI black box. In Machine Learning and Interpretation in Neuroimaging; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7263, pp. 242–255. [Google Scholar] [CrossRef]
- Beckmann, C.F.; DeLuca, M.; Devlin, J.T.; Smith, S.M. Investigations into resting-state connectivity using independent component analysis. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 1001–1013. [Google Scholar] [CrossRef]
- Calhoun, V.D.; Liu, J.; Adali, T. A review of group ICA for fMRI data and ICA for joint inference of imaging, genetic, and ERP data. Neuroimage 2009, 45, S163–S172. [Google Scholar] [CrossRef]
- Calhoun, V.D.; Adali, T. Multisubject Independent Component Analysis of fMRI: A Decade of Intrinsic Networks, Default Mode, and Neurodiagnostic Discovery. IEEE Rev. Biomed. Eng. 2012, 5, 60–73. [Google Scholar] [CrossRef]
- Douglas, P.; Harris, S.; Yuille, A.; Cohen, M.S. Performance comparison of machine learning algorithms and number of independent components used in fMRI decoding of belief vs. disbelief. NeuroImage 2011, 56, 544–553. [Google Scholar] [CrossRef]
- Anderson, A.; Douglas, P.; Kerr, W.; Haynes, V.S.; Yuille, A.L.; Xie, J.; Wu, Y.N.; Brown, J.A.; Cohen, M.S. Non-negative matrix factorization of multimodal MRI, fMRI and phenotypic data reveals differential changes in default mode subnetworks in ADHD. NeuroImage 2013, 102, 207–219. [Google Scholar] [CrossRef]
- Sen, B.; Parhi, K.K. Extraction of common task signals and spatial maps from group fMRI using a PARAFAC-based tensor decomposition technique. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 1113–1117. [Google Scholar] [CrossRef]
- Sen, B.; Parhi, K.K. Predicting Tasks from Task-fMRI Using Blind Source Separation. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 3–6 November 2019; pp. 2201–2205. [Google Scholar] [CrossRef]
- Kriegeskorte, N.; Douglas, P. Cognitive computational neuroscience. Nat. Neurosci. 2018, 21, 1148–1160. [Google Scholar] [CrossRef]
- Xu, M. Understanding Graph Embedding Methods and Their Applications. SIAM Rev. 2021, 63, 825–853. [Google Scholar] [CrossRef]
- Huang, X.; Xiao, J.; Wu, C. Design of Deep Learning Model for Task-Evoked fMRI Data Classification. Comput. Intell. Neurosci. 2021, 2021, 6660866. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liang, X.; Jiang, Z.; Nguchu, B.A.; Zhou, Y.; Wang, Y.; Wang, H.; Li, Y.; Zhu, Y.; Wu, F.; et al. Decoding and mapping task states of the human brain via deep learning. Hum. Brain Mapp. 2019, 41, 1505–1519. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Hu, X.; Zhao, Y.; Makkie, M.; Dong, Q.; Zhao, S.; Guo, L.; Liu, T. Modeling Task fMRI Data Via Deep Convolutional Autoencoder. IEEE Trans. Med. Imaging 2017, 37, 1551–1561. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Hu, X.; Dong, Q.; Zhao, S.; Zhang, S.; Zhao, Y.; Quo, L.; Liu, T. Modeling task fMRI data via mixture of deep expert networks. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 82–86. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, X.; Huang, H.; Zhang, W.; Zhao, S.; Makkie, M.; Zhang, M.; Li, Q.; Liu, T. Four-Dimensional Modeling of fMRI Data via Spatio–Temporal Convolutional Neural Networks (ST-CNNs). IEEE Trans. Cogn. Dev. Syst. 2019, 12, 451–460. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhao, S.; Dong, Q.; Cui, Y.; Chen, Y.; Han, J.; Xie, L.; Liu, T. Recognizing Brain States Using Deep Sparse Recurrent Neural Network. IEEE Trans. Med. Imaging 2018, 38, 1058–1068. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Dong, Q.; Ge, F.; Qiang, N.; Wu, X.; Liu, T. Simultaneous spatial-temporal decomposition for connectome-scale brain networks by deep sparse recurrent auto-encoder. Brain Imaging Behav. 2021, 15, 2646–2660. [Google Scholar] [CrossRef]
- Hjelm, R.D.; Calhoun, V.D.; Salakhutdinov, R.; Allen, E.A.; Adali, T.; Plis, S.M. Restricted Boltzmann machines for neuroimaging: An application in identifying intrinsic networks. NeuroImage 2014, 96, 245–260. [Google Scholar] [CrossRef]
- Jang, H.; Plis, S.M.; Calhoun, V.D.; Lee, J.-H. Task-specific feature extraction and classification of fMRI volumes using a deep neural network initialized with a deep belief network: Evaluation using sensorimotor tasks. NeuroImage 2016, 145, 314–328. [Google Scholar] [CrossRef]
- Dong, Q.; Ge, F.; Ning, Q.; Zhao, Y.; Lv, J.; Huang, H.; Yuan, J.; Jiang, X.; Shen, D.; Liu, T.; et al. Modeling Hierarchical Brain Networks via Volumetric Sparse Deep Belief Network. IEEE Trans. Biomed. Eng. 2019, 67, 1739–1748. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Bi, X.; Liu, Z.; He, Y.; Zhao, X.; Sun, Y.; Liu, H. GNEA: A Graph Neural Network with ELM Aggregator for Brain Network Classification. Complexity 2020, 2020, 8813738. [Google Scholar] [CrossRef]
- Zhu, S.; Pan, S.; Zhou, C.; Wu, J.; Cao, Y.; Wang, B. Graph geometry interaction learning. In Proceedings of the Advances in Neural Information Processing Systems 33 (NeurIPS 2020), Virtual Event, 6–12 December 2020. [Google Scholar]
- Ning, L.; Bonet-Carne, E.; Grussu, F.; Sepehrband, F.; Kaden, E.; Veraart, J.; Blumberg, S.B.; Khoo, C.S.; Palombo, M.; Kokkinos, I.; et al. Cross-scanner and cross-protocol multi-shell diffusion MRI data harmonization: Algorithms and results. NeuroImage 2020, 221, 117128. [Google Scholar] [CrossRef]
- Glasser, M.F.; Sotiropoulos, S.N.; Wilson, J.A.; Coalson, T.S.; Fischl, B.; Andersson, J.L.; Xu, J.; Jbabdi, S.; Webster, M.; Polimeni, J.R.; et al. The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage 2013, 80, 105–124. [Google Scholar] [CrossRef]
- Beckmann, C.F.; Smith, S.M. Probabilistic Independent Component Analysis for Functional Magnetic Resonance Imaging. IEEE Trans. Med. Imaging 2004, 23, 137–152. [Google Scholar] [CrossRef]
- Gross, J.L.; Yellen, J.; Anderson, M. Graph Theory and Its Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. arXiv 2014, arXiv:1312.6203. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. In Proceedings of the Advances in Neural Information Processing Systems 29 (NIPS 2016), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Ma, Y.; Hao, J.; Yang, Y.; Alibaba, H.L.; Alibaba, J.J.; Tencent, G.C. Spectral-based Graph Convolutional Network for Directed Graphs. arXiv 2019, arXiv:1907.08990. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, ICLR 2017—Conference Track Proceedings, Toulon, France, 24–26 April 2017. [Google Scholar]
- Salimi-Khorshidi, G.; Douaud, G.; Beckmann, C.F.; Glasser, M.F.; Griffanti, L.; Smith, S.M. Automatic denoising of functional MRI data: Combining independent component analysis and hierarchical fusion of classifiers. NeuroImage 2014, 90, 449–468. [Google Scholar] [CrossRef]
- Glasser, M.F.; Coalson, T.S.; Robinson, E.C.; Hacker, C.D.; Harwell, J.; Yacoub, E.; Ugurbil, K.; Andersson, J.; Beckmann, C.F.; Jenkinson, M.; et al. A multi-modal parcellation of human cerebral cortex. Nature 2016, 536, 171–178. [Google Scholar] [CrossRef]
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time Series FeatuRe Extraction on basis of Scalable Hypothesis tests (tsfresh—A Python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Christ, M.; Kempa-Liehr, A.W.; Feindt, M. Distributed and parallel time series feature extraction for industrial big data applications. arXiv 2016, arXiv:1610.07717. [Google Scholar] [CrossRef]
- Benjamini, Y.; Yekutieli, D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat. 2001, 29, 1165–1188. [Google Scholar] [CrossRef]
- Cai, H.; Zheng, V.W.; Chang, K.C.-C. A Comprehensive Survey of Graph Embedding: Problems, Techniques, and Applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Rozemberczki, B.; Kiss, O.; Sarkar, R. Karate Club: An API Oriented Open-Source Python Framework for Unsupervised Learning on Graphs. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Atlanta, GA, USA, 17–21 October 2020; pp. 3125–3132. [Google Scholar] [CrossRef]
- Perozzi, B.; Kulkarni, V.; Chen, H.; Skiena, S. Don’t walk, skip! online learning of multi-scale network embeddings. In Proceedings of the 2017 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2017, Sydney, Australia, 31 July–3 August 2017; pp. 258–265. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. Node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2022. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Y.; Ma, H.; Li, J.; Wang, K.; Tang, J. Network embedding as matrix factorization: Unifying DeepWalk, LINE, PTE, and node2vec. In Proceedings of the WSDM 2018: The Eleventh ACM International Conference on Web Search and Data Mining, Marina Del Rey, CA, USA, 5–9 February 2018; pp. 459–467. [Google Scholar] [CrossRef]
- Zhang, Z.; Cui, P.; Li, H.; Wang, X.; Zhu, W. Billion-Scale Network Embedding with Iterative Random Projection. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 787–796. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. DeepWalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar] [CrossRef]
- Dalmia, A.; Ganesh, J.; Gupta, M. Towards Interpretation of Node Embeddings. In Proceedings of the WWW’18: Companion Proceedings of the Web Conference 2018, Lyon, France, 23–27 April 2013; pp. 945–952. [Google Scholar] [CrossRef]
- Yu, B.; Lu, B.; Zhang, C.; Li, C.; Pan, K. Node proximity preserved dynamic network embedding via matrix perturbation. Knowl.-Based Syst. 2020, 196, 105822. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar] [CrossRef]
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 1–13. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly: Sebastopol, CA, USA, 2017. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Dong, G.; Cai, L.; Datta, D.; Kumar, S.; Barnes, L.E.; Boukhechba, M. Influenza-like symptom recognition using mobile sensing and graph neural networks. In Proceedings of the Conference on Health, Inference, and Learning, Virtual Event, 8–10 April 2021; Volume 21, pp. 291–300. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, H. New Graph-Blind Convolutional Network for Brain Connectome Data Analysis. In Proceedings of the 26th International Conference, IPMI 2019, Hong Kong, China, 2–7 June 2019; Volume 11492, pp. 669–681. [Google Scholar] [CrossRef]
- Yu, S.; Yue, G.; Elazab, A.; Song, X.; Wang, T.; Lei, B. Multi-scale Graph Convolutional Network for Mild Cognitive Impairment Detection. In Proceedings of the Graph Learning in Medical Imaging, GLMI 2019, Shenzhen, China, 13–17 October 2019; Volume 11849, pp. 79–87. [Google Scholar] [CrossRef]
- Yu, S.; Wang, S.; Xiao, X.; Cao, J.; Yue, G.; Liu, D.; Wang, T.; Xu, Y.; Lei, B. Multi-scale Enhanced Graph Convolutional Network for Early Mild Cognitive Impairment Detection. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2020, Lima, Peru, 4–8 October 2020; Volume 12267, pp. 228–237. [Google Scholar] [CrossRef]
- Xing, X.; Li, Q.; Wei, H.; Zhang, M.; Zhan, Y.; Zhou, X.S.; Xue, Z.; Shi, F. Dynamic spectral graph convolution networks with assistant task training for early MCI diagnosis. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; Volume 11767, pp. 639–646. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Martin, C.; Riebeling, M. A Process for the Evaluation of Node Embedding Methods in the Context of Node Classification. arXiv 2020, arXiv:2005.14683. [Google Scholar] [CrossRef]
- Douglas, P.K.; Farahani, F.V. On the Similarity of Deep Learning Representations Across Didactic and Adversarial Examples. arXiv 2020, arXiv:2002.06816. [Google Scholar] [CrossRef]





| Groups | Number of Participants | ||
|---|---|---|---|
| Female | - | ||
| Male | - | ||
| LM-gF | |||
| HM-gF |
| Batch Size | Node Embeddings | Metrics | ||
|---|---|---|---|---|
| Accuracy | F1 Macro | MCC | ||
| 16 | Walklets | 0.886 | 0.89 | 0.867 |
| Node2Vec | 0.854 | 0.863 | 0.831 | |
| RandNE | 0.939 | 0.941 | 0.928 | |
| NetMF | 0.933 | 0.936 | 0.921 | |
| 32 | Walklets | 0.911 | 0.915 | 0.895 |
| Node2Vec | 0.873 | 0.886 | 0.854 | |
| RandNE | 0.969 | 0.97 | 0.954 | |
| NetMF | 0.974 | 0.976 | 0.97 | |
| 48 | Walklets | 0.915 | 0.92 | 0.901 |
| Node2Vec | 0.898 | 0.9 | 0.882 | |
| RandNE | 0.971 | 0.973 | 0.966 | |
| NetMF | 0.976 | 0.977 | 0.971 | |
| 64 | Walklets | 0.932 | 0.936 | 0.922 |
| Node2Vec | 0.902 | 0.908 | 0.886 | |
| RandNE | 0.975 | 0.976 | 0.971 | |
| NetMF | 0.977 | 0.978 | 0.974 | |
| Batch Size | Node Embeddings | Female Dataset | Male Dataset | ||||
|---|---|---|---|---|---|---|---|
| Metrics | Metrics | ||||||
| Accuracy | F1 Macro | MCC | Accuracy | F1 Macro | MCC | ||
| 16 | Walklets | 0.881 | 0.882 | 0.862 | 0.849 | 0.85 | 0.823 |
| Node2Vec | 0.792 | 0.795 | 0.764 | 0.841 | 0.845 | 0.817 | |
| RandNE | 0.916 | 0.916 | 0.902 | 0.907 | 0.909 | 0.891 | |
| NetMF | 0.927 | 0.928 | 0.915 | 0.908 | 0.911 | 0.892 | |
| 32 | Walklets | 0.919 | 0.919 | 0.905 | 0.879 | 0.882 | 0.859 |
| Node2Vec | 0.835 | 0.837 | 0.807 | 0.878 | 0.879 | 0.856 | |
| RandNE | 0.938 | 0.939 | 0.927 | 0.949 | 0.951 | 0.94 | |
| NetMF | 0.959 | 0.959 | 0.952 | 0.939 | 0.941 | 0.928 | |
| 48 | Walklets | 0.931 | 0.932 | 0.92 | 0.887 | 0.889 | 0.862 |
| Node2Vec | 0.871 | 0.869 | 0.851 | 0.852 | 0.857 | 0.827 | |
| RandNE | 0.952 | 0.952 | 0.944 | 0.955 | 0.957 | 0.947 | |
| NetMF | 0.967 | 0.967 | 0.961 | 0.962 | 0.964 | 0.953 | |
| 64 | Walklets | 0.928 | 0.928 | 0.916 | 0.871 | 0.874 | 0.844 |
| Node2Vec | 0.859 | 0.861 | 0.837 | 0.845 | 0.849 | 0.817 | |
| RandNE | 0.971 | 0.972 | 0.966 | 0.958 | 0.961 | 0.951 | |
| NetMF | 0.979 | 0.979 | 0.974 | 0.962 | 0.965 | 0.953 | |
| Batch Size | Node Embeddings | LM-gF Dataset | HM-gF Dataset | ||||
|---|---|---|---|---|---|---|---|
| Metrics | Metrics | ||||||
| Accuracy | F1 Macro | MCC | Accuracy | F1 Macro | MCC | ||
| 16 | Walklets | 0.869 | 0.873 | 0.847 | 0.876 | 0.876 | 0.855 |
| Node2Vec | 0.895 | 0.896 | 0.877 | 0.876 | 0.878 | 0.855 | |
| RandNE | 0.936 | 0.937 | 0.925 | 0.945 | 0.944 | 0.936 | |
| NetMF | 0.906 | 0.908 | 0.89 | 0.921 | 0.921 | 0.909 | |
| 32 | Walklets | 0.899 | 0.902 | 0.882 | 0.901 | 0.901 | 0.883 |
| Node2Vec | 0.891 | 0.893 | 0.869 | 0.92 | 0.92 | 0.907 | |
| RandNE | 0.977 | 0.977 | 0.973 | 0.98 | 0.979 | 0.975 | |
| NetMF | 0.93 | 0.93 | 0.918 | 0.942 | 0.942 | 0.932 | |
| 48 | Walklets | 0.908 | 0.91 | 0.891 | 0.92 | 0.919 | 0.906 |
| Node2Vec | 0.9 | 0.902 | 0.883 | 0.915 | 0.915 | 0.901 | |
| RandNE | 0.991 | 0.991 | 0.989 | 0.988 | 0.988 | 0.983 | |
| NetMF | 0.934 | 0.934 | 0.922 | 0.948 | 0.947 | 0.939 | |
| 64 | Walklets | 0.899 | 0.901 | 0.881 | 0.92 | 0.918 | 0.907 |
| Node2Vec | 0.901 | 0.903 | 0.885 | 0.906 | 0.905 | 0.891 | |
| RandNE | 0.991 | 0.991 | 0.99 | 0.988 | 0.988 | 0.986 | |
| NetMF | 0.936 | 0.938 | 0.925 | 0.944 | 0.943 | 0.935 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeidi, M.; Karwowski, W.; Farahani, F.V.; Fiok, K.; Hancock, P.A.; Sawyer, B.D.; Christov-Moore, L.; Douglas, P.K. Decoding Task-Based fMRI Data with Graph Neural Networks, Considering Individual Differences. Brain Sci. 2022, 12, 1094. https://doi.org/10.3390/brainsci12081094
Saeidi M, Karwowski W, Farahani FV, Fiok K, Hancock PA, Sawyer BD, Christov-Moore L, Douglas PK. Decoding Task-Based fMRI Data with Graph Neural Networks, Considering Individual Differences. Brain Sciences. 2022; 12(8):1094. https://doi.org/10.3390/brainsci12081094
Chicago/Turabian StyleSaeidi, Maham, Waldemar Karwowski, Farzad V. Farahani, Krzysztof Fiok, P. A. Hancock, Ben D. Sawyer, Leonardo Christov-Moore, and Pamela K. Douglas. 2022. "Decoding Task-Based fMRI Data with Graph Neural Networks, Considering Individual Differences" Brain Sciences 12, no. 8: 1094. https://doi.org/10.3390/brainsci12081094
APA StyleSaeidi, M., Karwowski, W., Farahani, F. V., Fiok, K., Hancock, P. A., Sawyer, B. D., Christov-Moore, L., & Douglas, P. K. (2022). Decoding Task-Based fMRI Data with Graph Neural Networks, Considering Individual Differences. Brain Sciences, 12(8), 1094. https://doi.org/10.3390/brainsci12081094







