High-Level Visual Encoding Model Framework with Hierarchical Ventral Stream-Optimized Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. fMRI Data
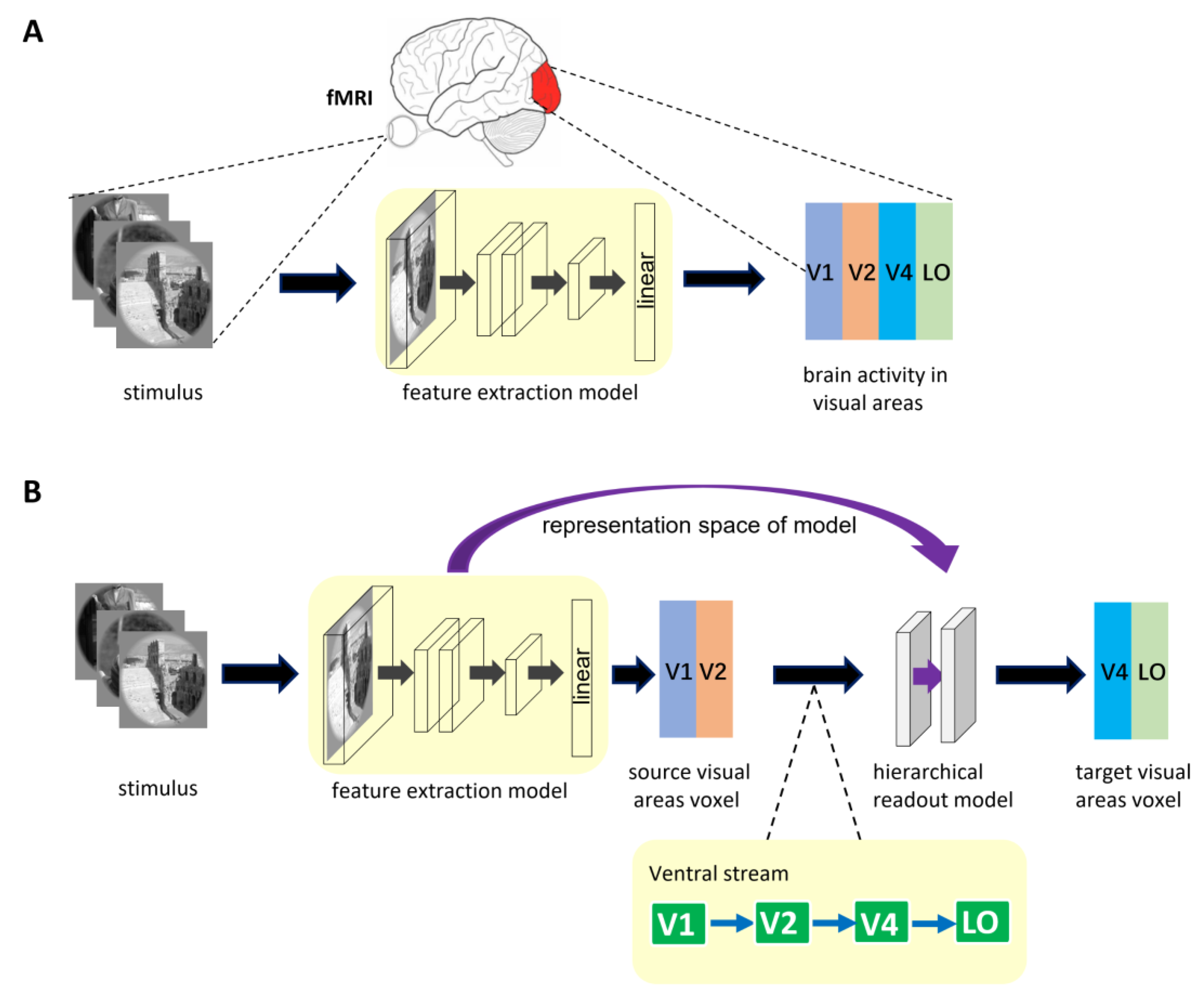
2.2. Encoding Model Framework
2.2.1. General Encoding Model from Stimulus to Voxel
2.2.2. Encoding Model with Hierarchical Ventral Stream-Optimized Neural Networks
2.3. Predictive Models
2.3.1. S2V-EM
2.3.2. S2V2V-EM
2.3.3. S2F2V-EM
2.4. Control Models
2.4.1. GaborNet-VE
2.4.2. CNN-EM
2.5. Prediction Accuracy, Model Effectiveness Evaluation, and Training Strategy
2.6. Analysis of the Role of the Hierarchy of Representations in Encoding Different Visual Areas
3. Results
3.1. Comparison of Prediction Accuracy between S2V2V-EM and Control Models
3.2. Comparison of Prediction Accuracy between S2F2V-EM and Control Models
3.3. The Proportion of Best-Encoded Voxels for Different Encoding Models
4. Discussion
4.1. Advantages of the Encoding Model Framework
4.2. The Effects of Hierarchical Information Conveyance Perspectives on Model Encoding Performance
4.3. The Encoding Contribution of Different Low-Level Visual Areas to the High-Level Visual Area
4.4. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, M.C.-K.; David, S.V.; Gallant, J.L. Complete functional characterization of sensory neurons by system identification. Annu. Rev. Neurosci. 2006, 29, 477–505. [Google Scholar] [CrossRef] [PubMed]
- Naselaris, T.; Kay, K.N.; Nishimoto, S.; Gallant, J.L. Encoding and Decoding in FMRI. NeuroImage 2011, 56, 400–410. [Google Scholar] [CrossRef] [PubMed]
- Sharkawy, A.-N. Principle of Neural Network and Its Main Types: Review. J. Adv. Appl. Comput. Math. 2020, 7, 8–19. [Google Scholar] [CrossRef]
- Mishkin, M.; Ungerleider, L.G.; Macko, K.A. Object Vision and Spatial Vision: Two Cortical Pathways. Trends Neurosci. 1983, 6, 414–417. [Google Scholar] [CrossRef]
- Grill-Spector, K.; Kourtzi, Z.; Kanwisher, N. The Lateral Occipital Complex and Its Role in Object Recognition. Vis. Res. 2001, 41, 1409–1422. [Google Scholar] [CrossRef]
- Guclu, U.; van Gerven, M.A.J. Deep Neural Networks Reveal a Gradient in the Complexity of Neural Representations across the Ventral Stream. J. Neurosci. 2015, 35, 10005–10014. [Google Scholar] [CrossRef]
- Wang, H.; Huang, L.; Du, C.; Li, D.; Wang, B.; He, H. Neural Encoding for Human Visual Cortex With Deep Neural Networks Learning “What” and “Where”. IEEE Trans. Cogn. Dev. Syst. 2021, 13, 827–840. [Google Scholar] [CrossRef]
- Shi, J.; Wen, H.; Zhang, Y.; Han, K.; Liu, Z. Deep Recurrent Neural Network Reveals a Hierarchy of Process Memory during Dynamic Natural Vision. Hum. Brain Mapp. 2018, 39, 2269–2282. [Google Scholar] [CrossRef]
- Cadena, S.A.; Denfield, G.H.; Walker, E.Y.; Gatys, L.A.; Tolias, A.S.; Bethge, M.; Ecker, A.S. Deep Convolutional Models Improve Predictions of Macaque V1 Responses to Natural Images. PLoS Comput. Biol. 2019, 15, e1006897. [Google Scholar] [CrossRef]
- Zhang, C.; Qiao, K.; Wang, L.; Tong, L.; Hu, G.; Zhang, R.-Y.; Yan, B. A Visual Encoding Model Based on Deep Neural Networks and Transfer Learning for Brain Activity Measured by Functional Magnetic Resonance Imaging. J. Neurosci. Methods 2019, 325, 108318. [Google Scholar] [CrossRef]
- Zhuang, C.; Yan, S.; Nayebi, A.; Schrimpf, M.; Frank, M.C.; DiCarlo, J.J.; Yamins, D.L.K. Unsupervised Neural Network Models of the Ventral Visual Stream. Proc. Natl. Acad. Sci. USA 2021, 118, e2014196118. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, C.; Wang, L.; Ding, P.; Hu, L.; Yan, B.; Tong, L. A Visual Encoding Model Based on Contrastive Self-Supervised Learning for Human Brain Activity along the Ventral Visual Stream. Brain Sci. 2021, 11, 1004. [Google Scholar] [CrossRef] [PubMed]
- Cichy, R.M.; Khosla, A.; Pantazis, D.; Torralba, A.; Oliva, A. Comparison of Deep Neural Networks to Spatio-Temporal Cortical Dynamics of Human Visual Object Recognition Reveals Hierarchical Correspondence. Sci. Rep. 2016, 6, 27755. [Google Scholar] [CrossRef] [PubMed]
- Güçlü, U.; van Gerven, M.A.J. Increasingly Complex Representations of Natural Movies across the Dorsal Stream Are Shared between Subjects. NeuroImage 2017, 145, 329–336. [Google Scholar] [CrossRef] [PubMed]
- Eickenberg, M.; Gramfort, A.; Varoquaux, G.; Thirion, B. Seeing It All: Convolutional Network Layers Map the Function of the Human Visual System. NeuroImage 2017, 152, 184–194. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; IEEE: Las Vegas, NV, USA, 2016; pp. 770–778. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Bergelson, E.; Swingley, D. At 6–9 Months, Human Infants Know the Meanings of Many Common Nouns. Proc. Natl. Acad. Sci. USA 2012, 109, 3253–3258. [Google Scholar] [CrossRef]
- Bergelson, E.; Aslin, R.N. Nature and Origins of the Lexicon in 6-Mo-Olds. Proc. Natl. Acad. Sci. USA 2017, 114, 12916–12921. [Google Scholar] [CrossRef]
- Baker, N.; Lu, H.; Erlikhman, G.; Kellman, P.J. Deep Convolutional Networks Do Not Classify Based on Global Object Shape. PLoS Comput. Biol. 2018, 14, e1006613. [Google Scholar] [CrossRef]
- Geirhos, R.; Michaelis, C.; Wichmann, F.A.; Rubisch, P.; Bethge, M.; Brendel, W. Imagenet-trained cnns are biased towards texture; increasing shape bias improves accuracy and robustness. arXiv 2018, arXiv:1811.12231. [Google Scholar]
- Biederman, I. Recognition-by-Components: A Theory of Human Image Understanding. Psychol. Rev. 1987, 94, 115–147. [Google Scholar] [CrossRef] [PubMed]
- Kucker, S.C.; Samuelson, L.K.; Perry, L.K.; Yoshida, H.; Colunga, E.; Lorenz, M.G.; Smith, L.B. Reproducibility and a Unifying Explanation: Lessons from the Shape Bias. Infant Behav. Dev. 2019, 54, 156–165. [Google Scholar] [CrossRef] [PubMed]
- Pasupathy, A.; Kim, T.; Popovkina, D.V. Object Shape and Surface Properties Are Jointly Encoded in Mid-Level Ventral Visual Cortex. Curr. Opin. Neurobiol. 2019, 58, 199–208. [Google Scholar] [CrossRef] [PubMed]
- Güçlü, U.; van Gerven, M.A.J. Modeling the Dynamics of Human Brain Activity with Recurrent Neural Networks. Front. Comput. Neurosci. 2017, 11, 7. [Google Scholar] [CrossRef] [PubMed]
- Klindt, D.; Ecker, A.S.; Euler, T.; Bethge, M. Neural System Identification for Large Populations Separating “What” and “Where”. Adv. Neural Inf. Processing Syst. 2017, 30, 11. [Google Scholar]
- St-Yves, G.; Naselaris, T. The Feature-Weighted Receptive Field: An Interpretable Encoding Model for Complex Feature Spaces. NeuroImage 2018, 180, 188–202. [Google Scholar] [CrossRef] [PubMed]
- Tripp, B. Approximating the Architecture of Visual Cortex in a Convolutional Network. Neural Comput. 2019, 31, 1551–1591. [Google Scholar] [CrossRef]
- Qiao, K.; Zhang, C.; Chen, J.; Wang, L.; Tong, L.; Yan, B. Effective and Efficient ROI-Wise Visual Encoding Using an End-to-End CNN Regression Model and Selective Optimization. In Human Brain and Artificial Intelligence; Wang, Y., Ed.; Communications in Computer and Information Science; Springer: Singapore, 2021; Volume 1369, pp. 72–86. ISBN 9789811612879. [Google Scholar]
- Seeliger, K.; Ambrogioni, L.; Güçlütürk, Y.; van den Bulk, L.M.; Güçlü, U.; van Gerven, M.A.J. End-to-End Neural System Identification with Neural Information Flow. PLoS Comput. Biol. 2021, 17, e1008558. [Google Scholar] [CrossRef]
- Cui, Y.; Qiao, K.; Zhang, C.; Wang, L.; Yan, B.; Tong, L. GaborNet Visual Encoding: A Lightweight Region-Based Visual Encoding Model With Good Expressiveness and Biological Interpretability. Front. Neurosci. 2021, 15, 614182. [Google Scholar] [CrossRef]
- Hubel, D.H.; Wiesel, T.N. Ferrier Lecture. Functional Architecture of Macaque Monkey Visual Cortex. Proc. R. Soc. B Biol. Sci. 1977, 198, 1–59. [Google Scholar] [CrossRef]
- Felleman, D.J.; Van Essen, D.C. Distributed Hierarchical Processing in the Primate Cerebral Cortex. Cerebral Cortex 1991, 1, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Himberger, K.D.; Chien, H.-Y.; Honey, C.J. Principles of Temporal Processing Across the Cortical Hierarchy. Neuroscience 2018, 389, 161–174. [Google Scholar] [CrossRef] [PubMed]
- Joukes, J.; Hartmann, T.S.; Krekelberg, B. Motion Detection Based on Recurrent Network Dynamics. Front. Syst. Neurosci. 2014, 8, 239. [Google Scholar] [CrossRef]
- Antolík, J.; Hofer, S.B.; Bednar, J.A.; Mrsic-Flogel, T.D. Model Constrained by Visual Hierarchy Improves Prediction of Neural Responses to Natural Scenes. PLoS Comput. Biol. 2016, 12, e1004927. [Google Scholar] [CrossRef]
- Batty, E.; Merel, J.; Brackbill, N.; Heitman, A.; Sher, A.; Litke, A.; Chichilnisky, E.J.; Paninski, L. Multilayer recurrent network models of pri- mate retinal ganglion cell responses. In Proceedings of the 5th International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Kietzmann, T.C.; Spoerer, C.J.; Sörensen, L.K.A.; Cichy, R.M.; Hauk, O.; Kriegeskorte, N. Recurrence Is Required to Capture the Representational Dynamics of the Human Visual System. Proc. Natl. Acad. Sci. USA 2019, 116, 21854–21863. [Google Scholar] [CrossRef] [PubMed]
- Qiao, K.; Chen, J.; Wang, L.; Zhang, C.; Zeng, L.; Tong, L.; Yan, B. Category Decoding of Visual Stimuli From Human Brain Activity Using a Bidirectional Recurrent Neural Network to Simulate Bidirectional Information Flows in Human Visual Cortices. Front. Neurosci. 2019, 13, 692. [Google Scholar] [CrossRef]
- Laskar, M.N.U.; Sanchez Giraldo, L.G.; Schwartz, O. Deep Neural Networks Capture Texture Sensitivity in V2. J. Vis. 2020, 20, 21. [Google Scholar] [CrossRef]
- Zhong, H.; Wang, R. A New Discovery on Visual Information Dynamic Changes from V1 to V2: Corner Encoding. Nonlinear Dyn. 2021, 105, 3551–3570. [Google Scholar] [CrossRef]
- Mell, M.M.; St-Yves, G.; Naselaris, T. Voxel-to-Voxel Predictive Models Reveal Unexpected Structure in Unexplained Variance. NeuroImage 2021, 238, 118266. [Google Scholar] [CrossRef]
- Kay, K.N.; Naselaris, T.; Prenger, R.J.; Gallant, J.L. Identifying Natural Images from Human Brain Activity. Nature 2008, 452, 352–355. [Google Scholar] [CrossRef]
- Naselaris, T.; Prenger, R.J.; Kay, K.N.; Oliver, M.; Gallant, J.L. Bayesian Reconstruction of Natural Images from Human Brain Activity. Neuron 2009, 63, 902–915. [Google Scholar] [CrossRef] [PubMed]
- Wallisch, P.; Movshon, J.A. Structure and Function Come Unglued in the Visual Cortex. Neuron 2008, 60, 195–197. [Google Scholar] [CrossRef] [PubMed]
- Ponce, C.R.; Lomber, S.G.; Born, R.T. Integrating Motion and Depth via Parallel Pathways. Nat. Neurosci. 2008, 11, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Lennie, P. Single Units and Visual Cortical Organization. Perception 1998, 27, 889–935. [Google Scholar] [CrossRef] [PubMed]
- Young, M.P. Objective Analysis of the Topological Organization of the Primate Cortical Visual System. Nature 1992, 358, 152–155. [Google Scholar] [CrossRef]




| Source | Target | Top-300 AA |
|---|---|---|
| V1 | V2 | 0.6284 |
| V2 | 0.6561 | |
| V1 | V4 | 0.3731 |
| V2 | 0.3761 | |
| V4 | 0.3540 | |
| V1 | LO | 0.2647 |
| V2 | 0.2594 | |
| V4 | 0.2626 | |
| LO | 0.2234 |
| Source | Target | Top-300 AA |
|---|---|---|
| V1 | V2 | 0.6411 |
| V2 | 0.6561 | |
| V1 | V4 | 0.3717 |
| V2 | 0.3771 | |
| V4 | 0.3540 | |
| V1 | LO | 0.2673 |
| V2 | 0.2645 | |
| V4 | 0.2577 | |
| LO | 0.2234 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, W.; Li, J.; Zhang, C.; Wang, L.; Chen, P.; Yu, Z.; Tong, L.; Yan, B. High-Level Visual Encoding Model Framework with Hierarchical Ventral Stream-Optimized Neural Networks. Brain Sci. 2022, 12, 1101. https://doi.org/10.3390/brainsci12081101
Xiao W, Li J, Zhang C, Wang L, Chen P, Yu Z, Tong L, Yan B. High-Level Visual Encoding Model Framework with Hierarchical Ventral Stream-Optimized Neural Networks. Brain Sciences. 2022; 12(8):1101. https://doi.org/10.3390/brainsci12081101
Chicago/Turabian StyleXiao, Wulue, Jingwei Li, Chi Zhang, Linyuan Wang, Panpan Chen, Ziya Yu, Li Tong, and Bin Yan. 2022. "High-Level Visual Encoding Model Framework with Hierarchical Ventral Stream-Optimized Neural Networks" Brain Sciences 12, no. 8: 1101. https://doi.org/10.3390/brainsci12081101
APA StyleXiao, W., Li, J., Zhang, C., Wang, L., Chen, P., Yu, Z., Tong, L., & Yan, B. (2022). High-Level Visual Encoding Model Framework with Hierarchical Ventral Stream-Optimized Neural Networks. Brain Sciences, 12(8), 1101. https://doi.org/10.3390/brainsci12081101






