Case-Based and Quantum Classification for ERP-Based Brain–Computer Interfaces
Abstract
:1. Introduction
2. Algorithms
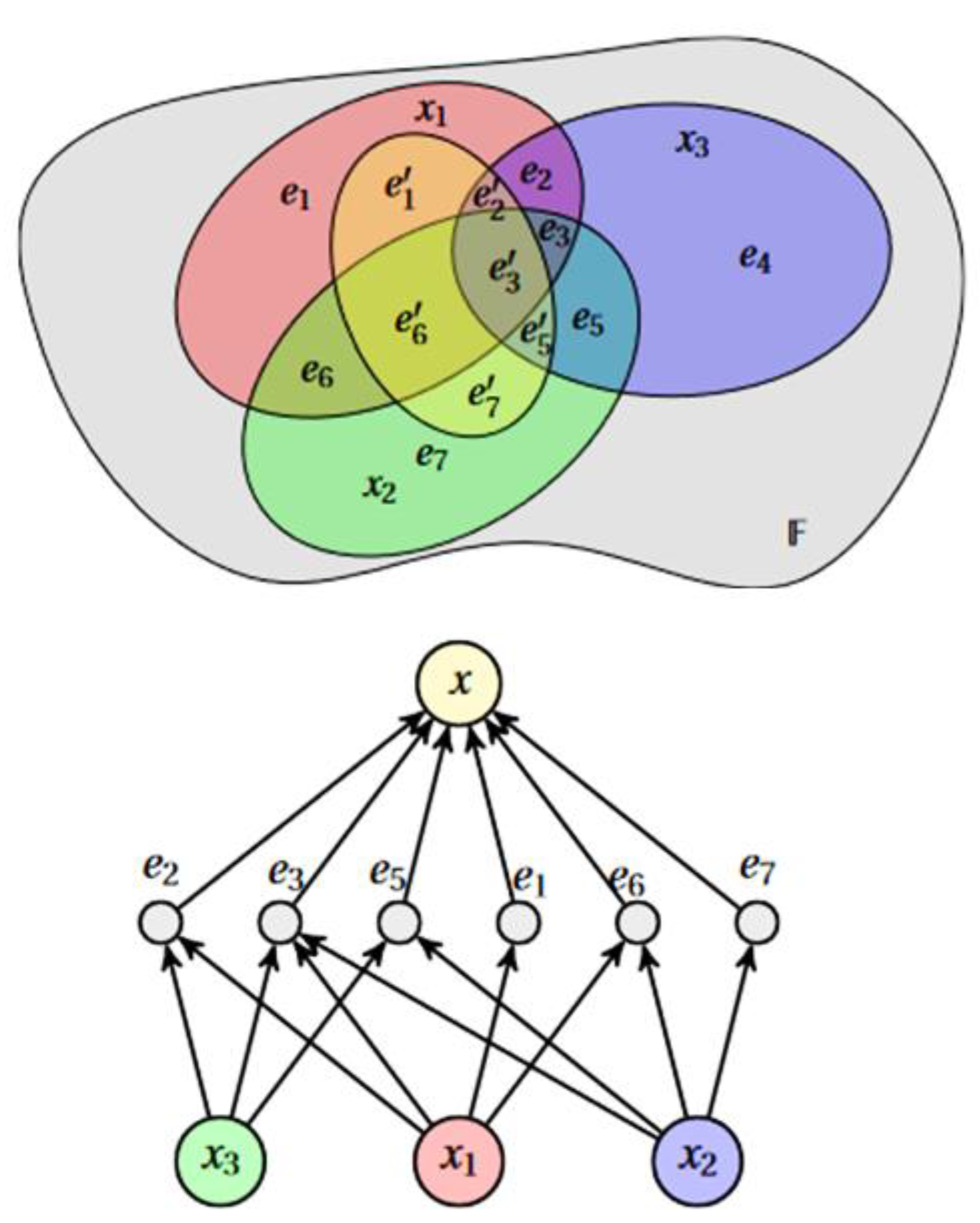
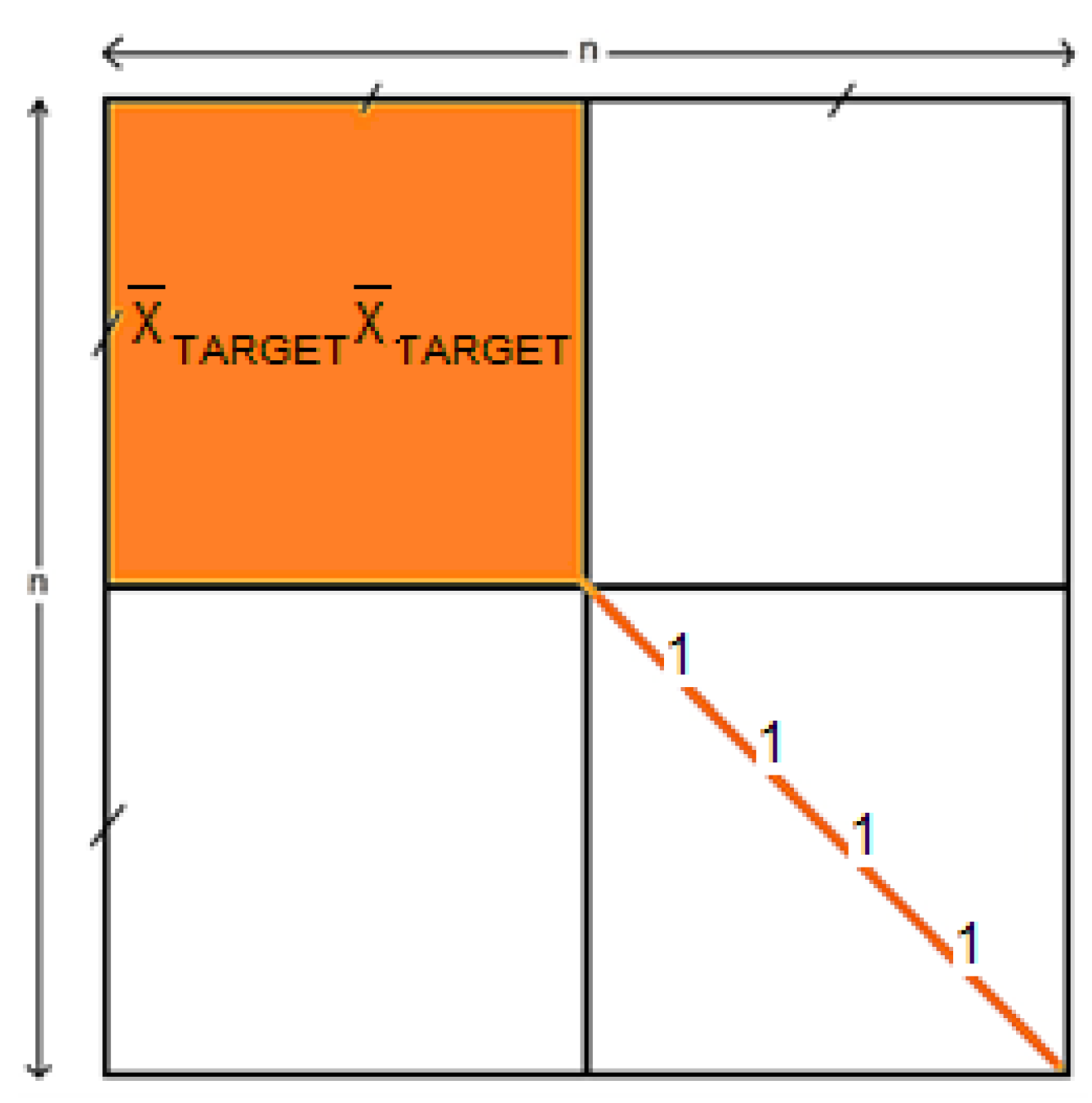
2.1. Hypergraph Case-Based Reasoning
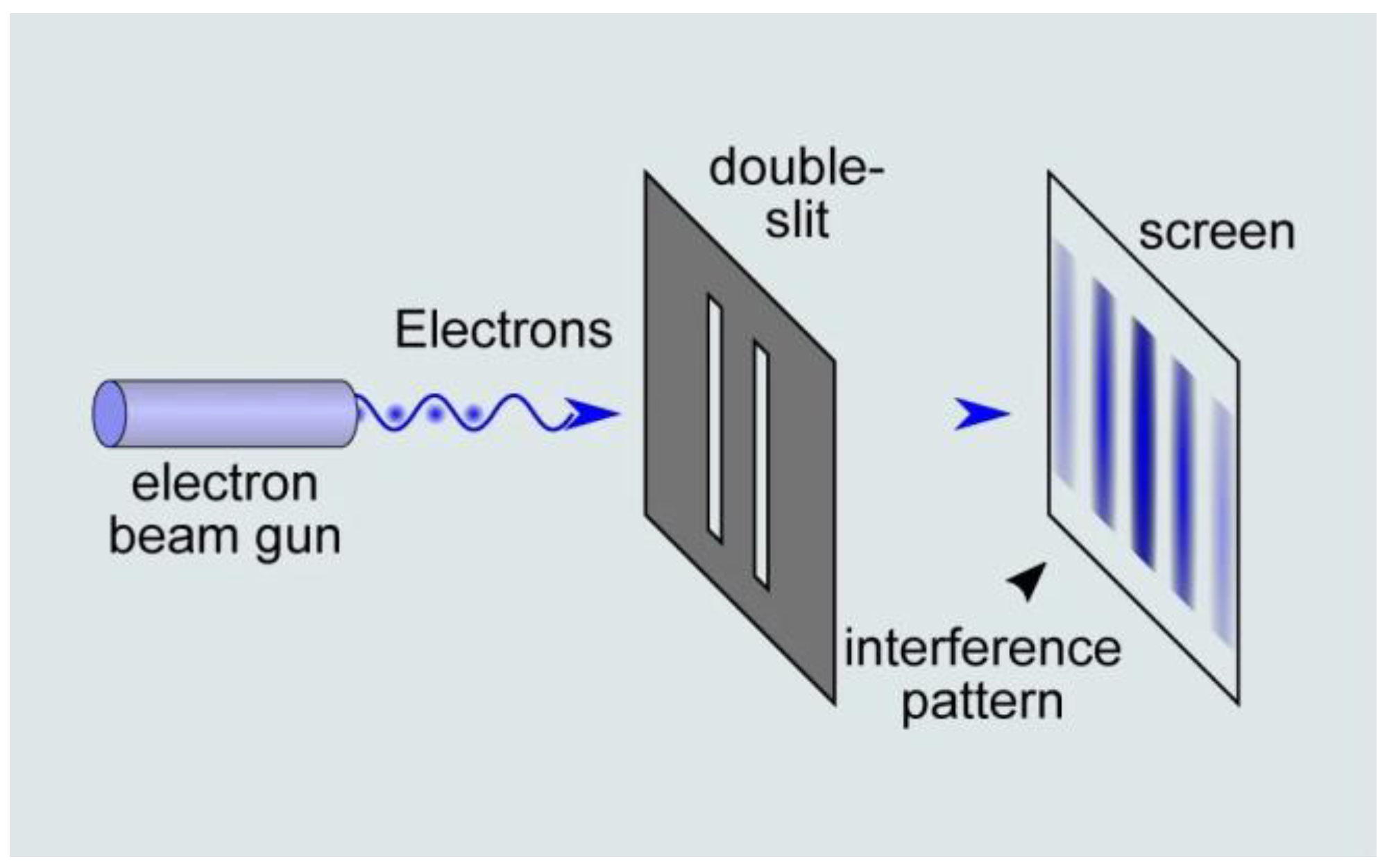
2.2. Foundation of Quantum Computation
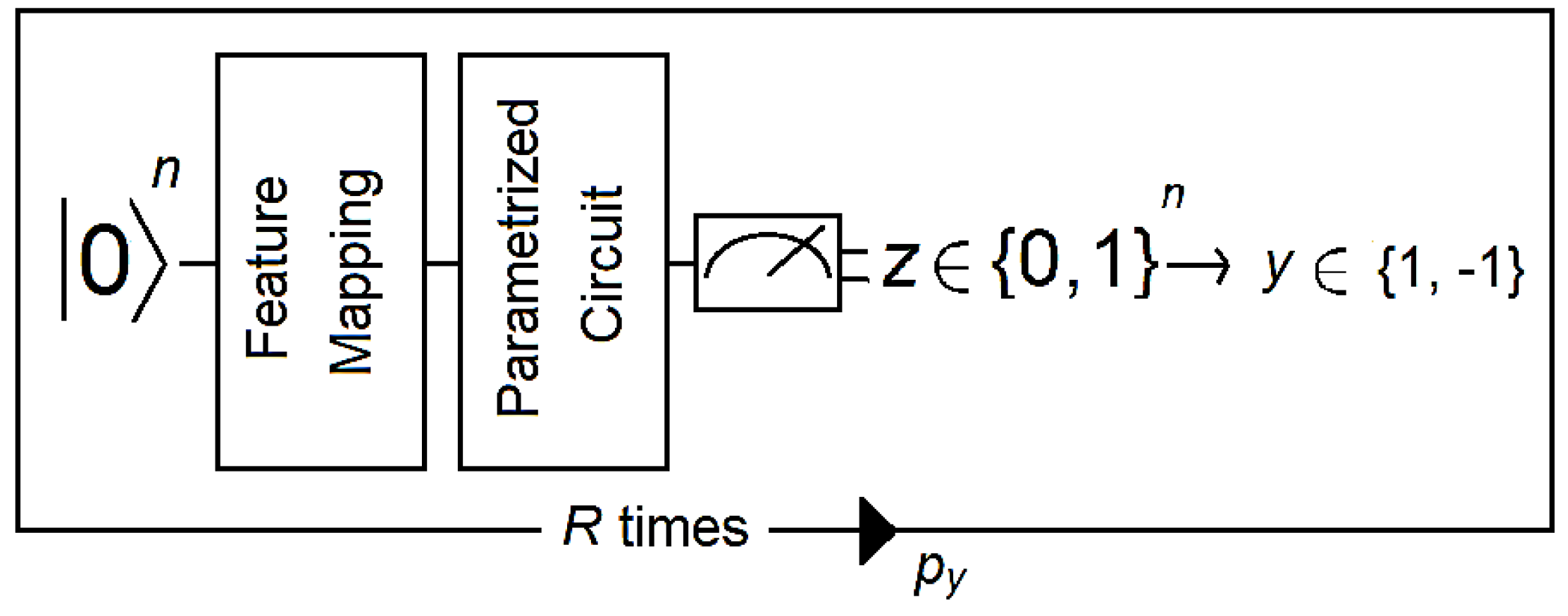
2.3. SVM-like Quantum Classification
- (1).
- A reference quantum vector is associated with the data using a nonlinear feature map.
- (2).
- A discriminator that corresponds to a short-depth circuit with one to four layers is applied to the data. Short-depth circuits are algorithms that are suitable for error-mitigation techniques because quantum decoherence increases with the depth of the circuit (e.g., see [42]).
- (3).
- The output of the discriminator circuit is measured and mapped to a label that corresponds to the class of the binary classifier.
- (4).
- An empirical distribution is generated by repeating steps 1 to 3 R times (where R is the number of shots). Then, labels are assigned according to whether (where b is a bias parameter).
- (5).
- The circuit becomes a binary classifier after the convergence of the algorithm, which determines the correct weights for the discriminator circuit as well as the bias parameter.
2.4. Complexity of Quantum SVMs
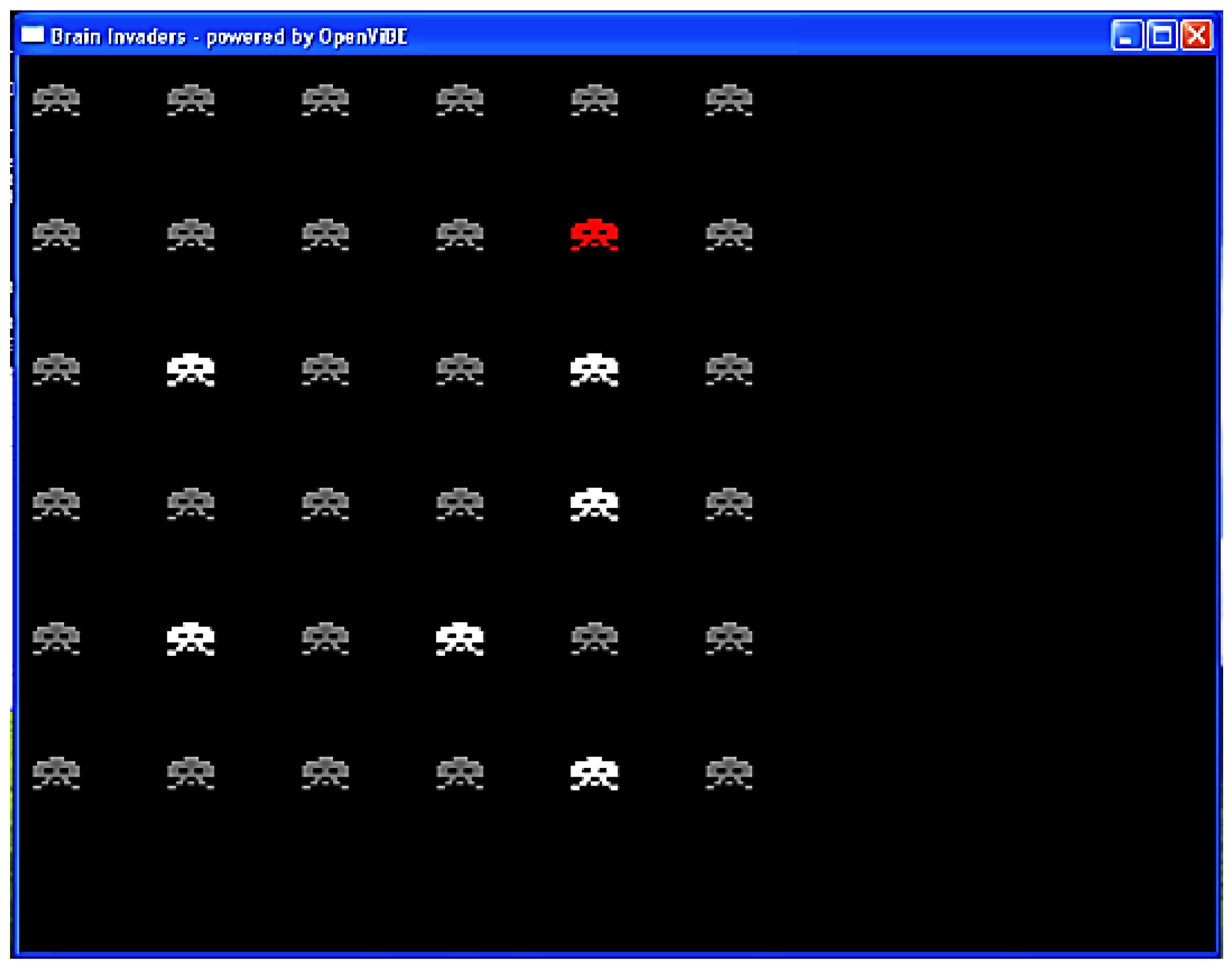
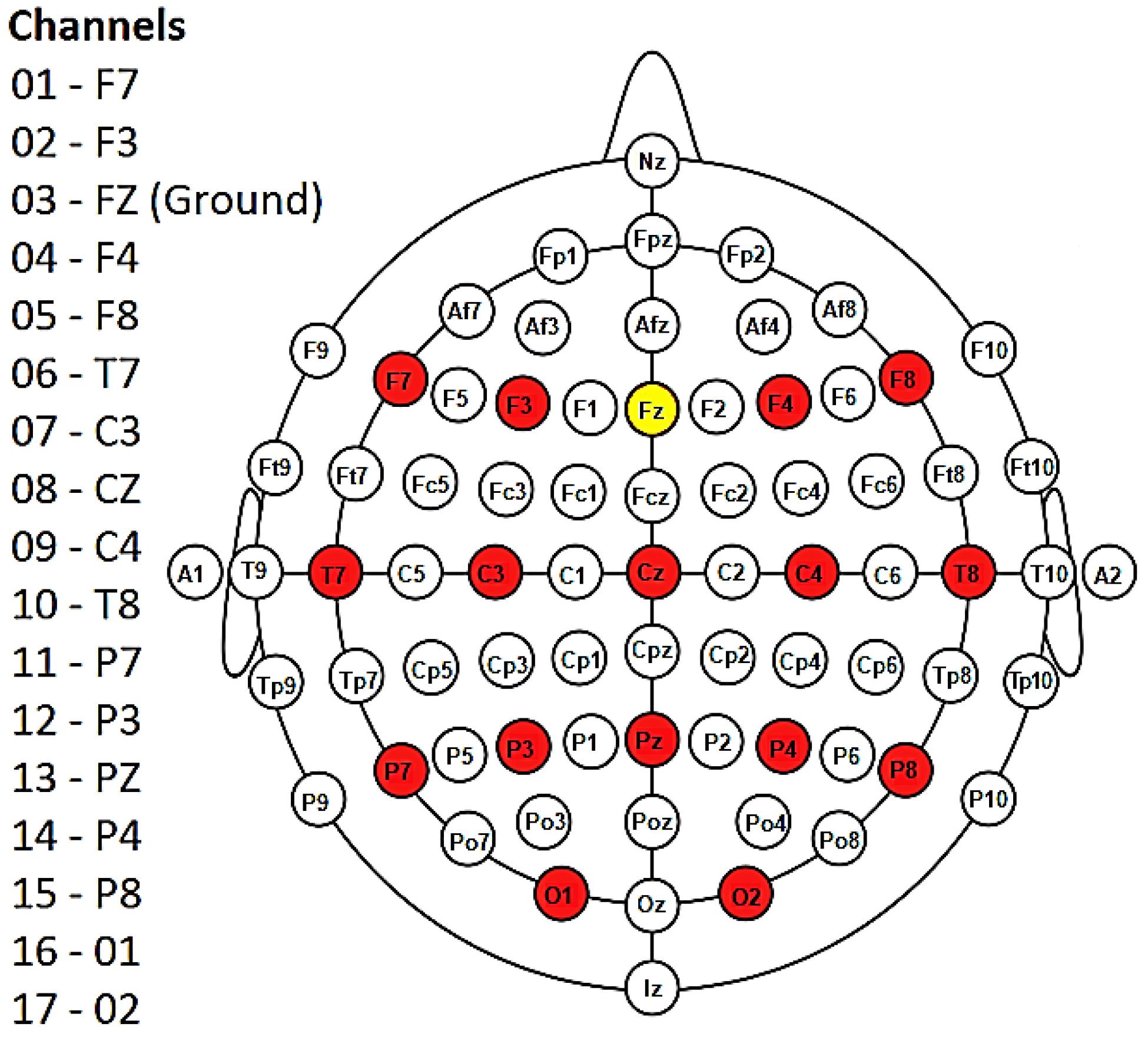
3. Data
4. Method
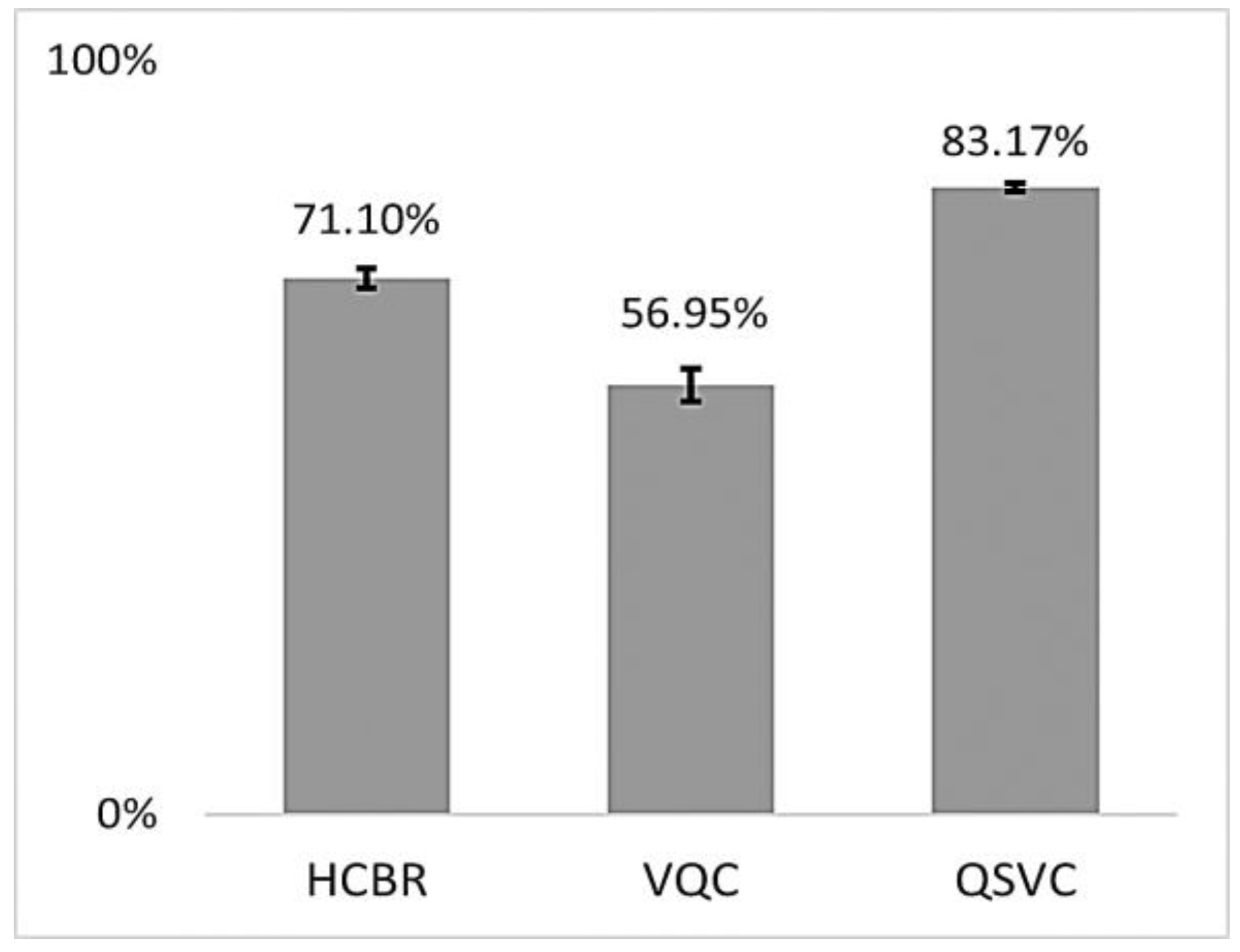
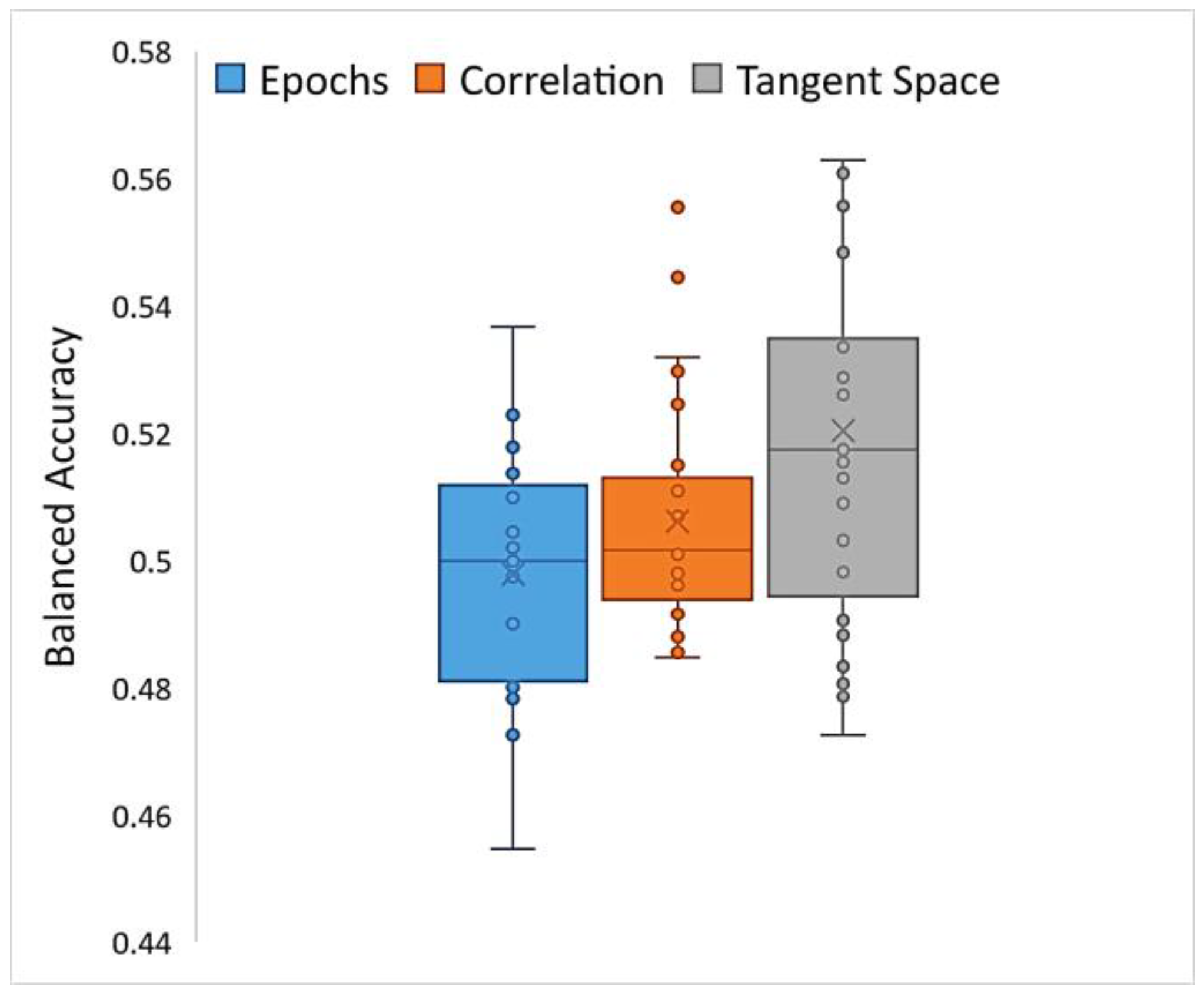
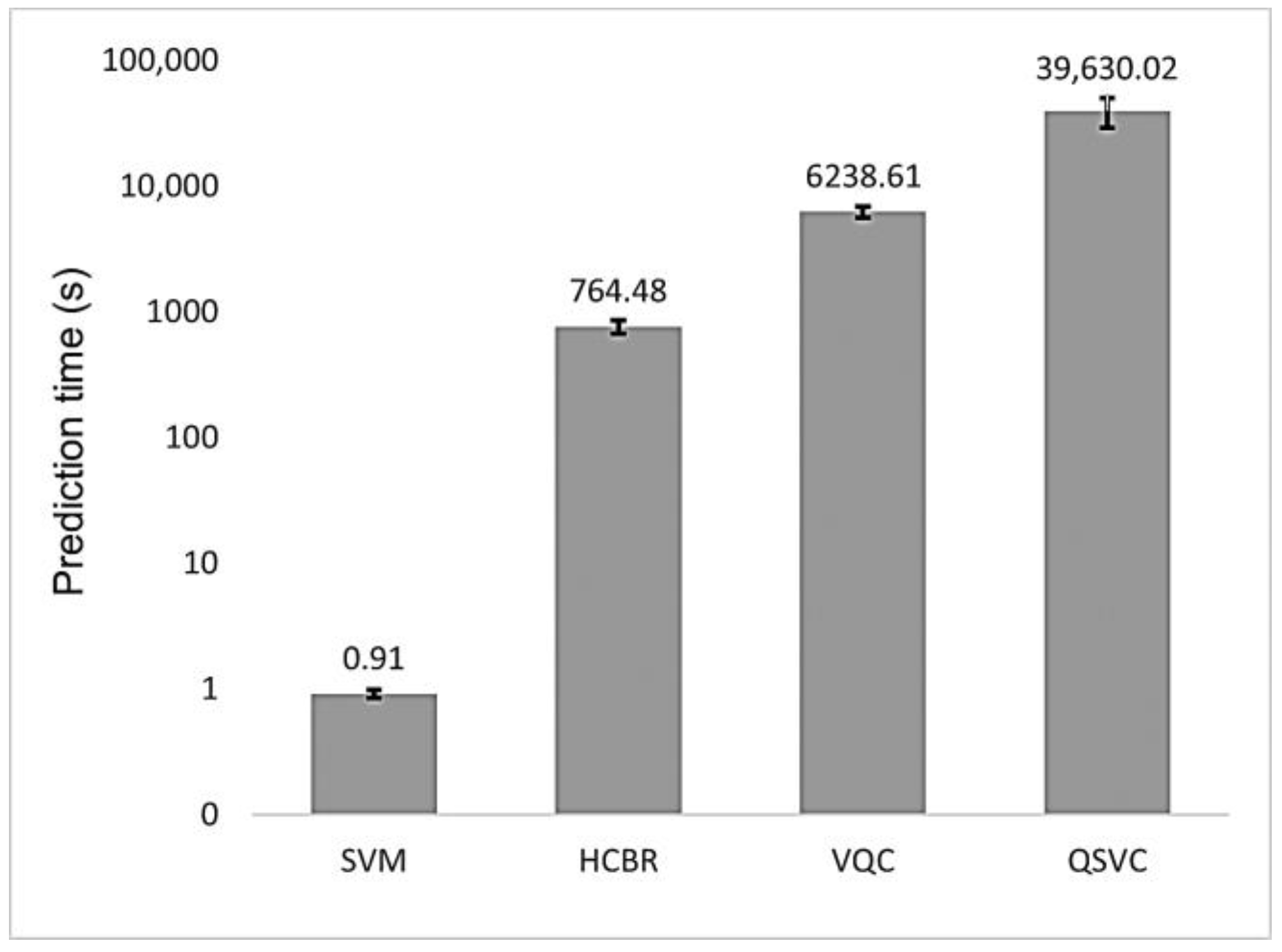
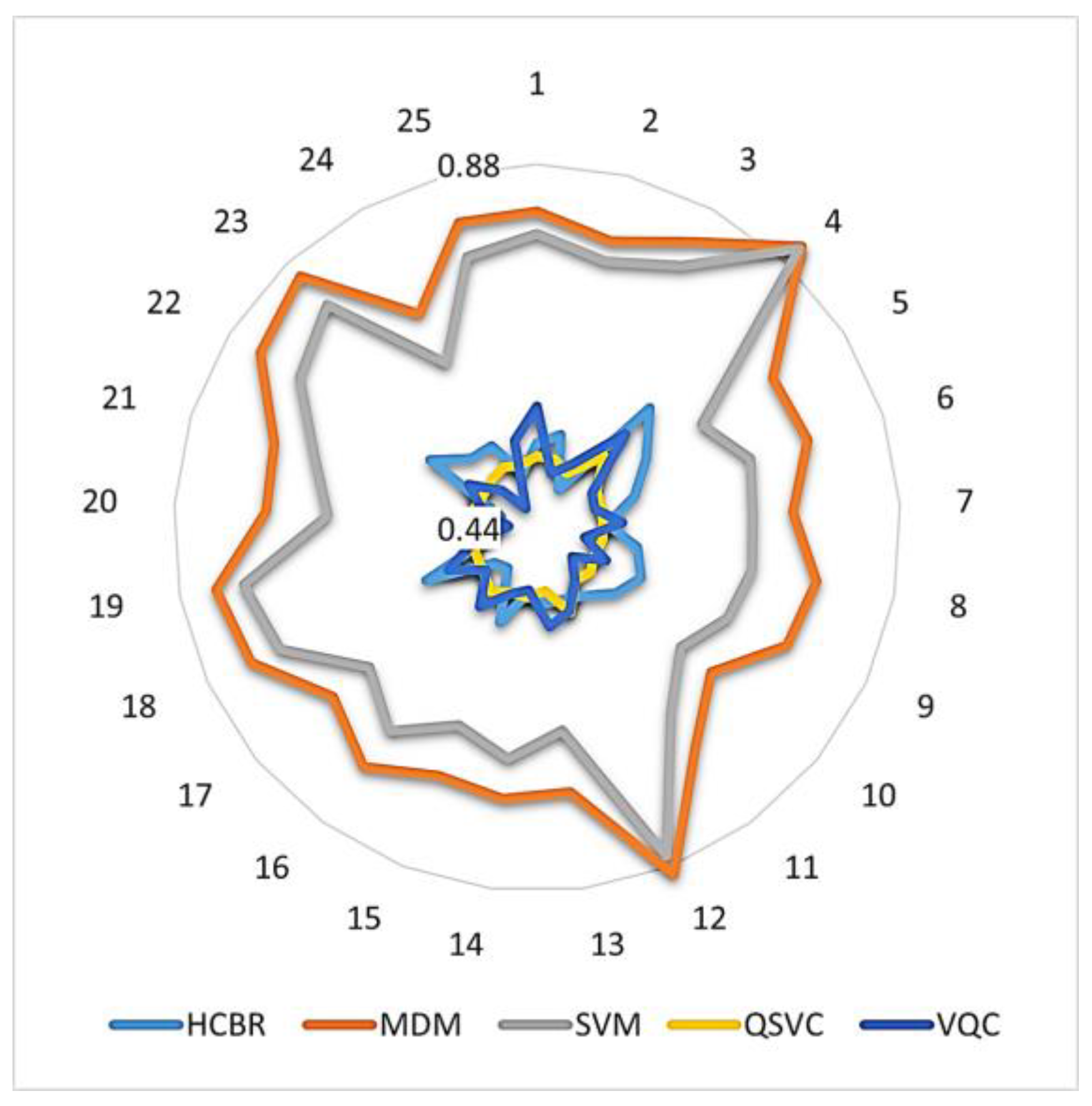
5. Results
6. Discussion and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vidal, J.J. Toward Direct Brain-Computer Communication. Annu. Rev. Biophys. Bioeng. 1973, 2, 157–180. [Google Scholar] [CrossRef]
- Guy, V.; Soriani, M.-H.; Bruno, M.; Papadopoulo, T.; Desnuelle, C.; Clerc, M. Brain computer interface with the P300 speller: Usability for disabled people with amyotrophic lateral sclerosis. Ann. Phys. Rehabilit. Med. 2018, 61, 5–11. [Google Scholar] [CrossRef] [PubMed]
- Norcia, A.M.; Appelbaum, L.G.; Ales, J.M.; Cottereau, B.R.; Rossion, B. The steady-state visual evoked potential in vision research: A review. J. Vis. 2015, 15, 4. [Google Scholar] [CrossRef] [PubMed]
- Sepulveda, F. Brain-actuated Control of Robot Navigation. In Advances in Robot Navigation; IntechOpen: London, UK, 2011; Volume 8, Available online: http://www.intechopen.com/books/advances-in-robot-navigation/brain-actuated-control-of-robot-navigation (accessed on 4 August 2017).
- Ahn, M.; Cho, H.; Ahn, S.; Jun, S.C. High Theta and Low Alpha Powers May Be Indicative of BCI-Illiteracy in Motor Imagery. PLoS ONE 2013, 8, e80886. [Google Scholar] [CrossRef] [PubMed]
- Thompson, M.C. Critiquing the Concept of BCI Illiteracy. Sci. Eng. Ethics 2018, 25, 1217–1233. [Google Scholar] [CrossRef]
- Volosyak, I.; Rezeika, A.; Benda, M.; Gembler, F.; Stawicki, P. Towards solving of the Illiteracy phenomenon for VEP-based brain-computer interfaces. Biomed. Phys. Eng. Express 2020, 6, 035034. [Google Scholar] [CrossRef]
- Polich, J. Clinical application of the P300 event-related brain potential. Phys. Med. Rehabilit. Clin. N. Am. 2004, 15, 133–161. [Google Scholar] [CrossRef] [PubMed]
- Lopes-Dias, C.; Sburlea, A.I.; Breitegger, K.; Wyss, D.; Drescher, H.; Wildburger, R.; Müller-Putz, G.R. Online asynchronous detection of error-related potentials in participants with a spinal cord injury using a generic classifier. J. Neural Eng. 2020, 18, 046022. [Google Scholar] [CrossRef]
- Müller-Putz, G.R.; Kobler, R.J.; Pereira, J.; Lopes-Dias, C.; Hehenberger, L.; Mondini, V.; Martínez-Cagigal, V.; Srisrisawang, N.; Pulferer, H.; Batistić, L.; et al. Feel Your Reach: An EEG-Based Framework to Continuously Detect Goal-Directed Movements and Error Processing to Gate Kinesthetic Feedback Informed Artificial Arm Control. Front. Hum. Neurosci. 2022, 16. Available online: https://www.frontiersin.org/article/10.3389/fnhum.2022.841312 (accessed on 20 May 2022). [CrossRef]
- Cattan, G. The Use of Brain–Computer Interfaces in Games Is Not Ready for the General Public. Front. Comput. Sci. 2021, 3, 628773. [Google Scholar] [CrossRef]
- Cattan, G.; Andreev, A.; Visinoni, E. Recommendations for Integrating a P300-Based Brain–Computer Interface in Virtual Reality Environments for Gaming: An Update. Computers 2020, 9, 92. [Google Scholar] [CrossRef]
- Nijholt, A. BCI for Games: A ‘State of the Art’ Survey. In Proceedings of the ICEC 2008: Entertainment Computing-ICEC 2008, Pittsburgh, PA, USA, 25–27 September 2008; pp. 225–228. [Google Scholar] [CrossRef]
- Lotte, F. Les interfaces cerveau-ordinateur. Conception et utilisation en réalité virtuelle. Tech. Sci. Inform. 2012, 31, 289–310. [Google Scholar] [CrossRef]
- Lotte, F.; Congedo, M.; Lécuyer, A.; Lamarche, F.; Arnaldi, B. A review of classification algorithms for EEG-based brain–computer interfaces. J. Neural Eng. 2007, 4, R1–R13. [Google Scholar] [CrossRef] [PubMed]
- Steyrl, D.; Scherer, R.; Faller, J.; Müller-Putz, G.R. Random forests in non-invasive sensorimotor rhythm brain-computer interfaces: A practical and convenient non-linear classifier. Biomed. Eng./Biomed. Tech. 2015, 61, 77–86. [Google Scholar] [CrossRef]
- Congedo, M.; Barachant, A.; Bhatia, R. Riemannian geometry for EEG-based brain-computer interfaces; a primer and a review. Brain-Comput. Interfaces 2017, 4, 155–174. [Google Scholar] [CrossRef]
- Jia, Z.; Ji, J.; Zhou, X.; Zhou, Y. Hybrid spiking neural network for sleep electroencephalogram signals. Sci. China Inf. Sci. 2022, 65, 140403. [Google Scholar] [CrossRef]
- Jia, Z.; Cai, X.; Jiao, Z. Multi-Modal Physiological Signals Based Squeeze-and-Excitation Network with Domain Adversarial Learning for Sleep Staging. IEEE Sensors J. 2022, 22, 3464–3471. [Google Scholar] [CrossRef]
- Lee, M.-H.; Fazli, S.; Mehnert, J.; Lee, S.-W. Subject-dependent classification for robust idle state detection using multi-modal neuroimaging and data-fusion techniques in BCI. Pattern Recognit. 2015, 48, 2725–2737. [Google Scholar] [CrossRef]
- Abdi-Sargezeh, B.; Foodeh, R.; Shalchyan, V.; Daliri, M.R. EEG artifact rejection by extracting spatial and spatio-spectral common components. J. Neurosci. Methods 2021, 358, 109182. [Google Scholar] [CrossRef]
- Barthelemy, Q.; Mayaud, L.; Ojeda, D.; Congedo, M. The Riemannian Potato Field: A Tool for Online Signal Quality Index of EEG. IEEE Trans. Neural Syst. Rehabilit. Eng. 2019, 27, 244–255. [Google Scholar] [CrossRef]
- Shahbakhti, M.; Beiramvand, M.; Rejer, I.; Augustyniak, P.; Broniec-Wojcik, A.; Wierzchon, M.; Marozas, V. Simultaneous Eye Blink Characterization and Elimination from Low-Channel Prefrontal EEG Signals Enhances Driver Drowsiness Detection. IEEE J. Biomed. Heal. Informatics 2021, 26, 1001–1012. [Google Scholar] [CrossRef] [PubMed]
- Congedo, M. EEG Source Analysis. Ph.D. Thesis, Université de Grenoble, Grenoble, France, 2013. Available online: https://tel.archives-ouvertes.fr/tel-00880483 (accessed on 30 November 2021).
- Corsi, M.-C.; Yger, F.; Chevallier, S.; Nous, C. Riemannian Geometry on Connectivity for Clinical BCI. In Proceedings of the ICASSP 2021—2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 6–11 June 2021; pp. 980–984. [Google Scholar] [CrossRef]
- Quemy, A. Binary classification in unstructured space with hypergraph case-based reasoning. Inf. Syst. 2019, 85, 92–113. [Google Scholar] [CrossRef]
- Havenstein, C.; Thomas, D.; Chandrasekaran, S. Comparisons of Performance between Quantum and Classical Machine Learning. SMU Data Sci. Rev 2019, 1. Available online: https://scholar.smu.edu/datasciencereview/vol1/iss4/11 (accessed on 29 August 2020).
- Rebentrost, P.; Mohseni, M.; Lloyd, S. Quantum Support Vector Machine for Big Data Classification. Phys. Rev. Lett. 2014, 113, 130503. [Google Scholar] [CrossRef]
- Blance, A.; Spannowsky, M. Quantum machine learning for particle physics using a variational quantum classifier. J. High Energy Phys. 2021, 2021, 212. [Google Scholar] [CrossRef]
- Aletras, N.; Tsarapatsanis, D.; Preoţiuc-Pietro, D.; Lampos, V. Predicting judicial decisions of the European Court of Human Rights: A Natural Language Processing perspective. PeerJ Comput. Sci. 2016, 2, e93. [Google Scholar] [CrossRef]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Everett, I.H. “Relative State” Formulation of Quantum Mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef]
- LaPierre, R. Shor Algorithm. In Introduction to Quantum Computing; LaPierre, R., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 177–192. [Google Scholar] [CrossRef]
- Nanda, A.; Puthal, D.; Mohanty, S.P.; Choppali, U. A Computing Perspective of Quantum Cryptography [Energy and Security]. IEEE Consum. Electron. Mag. 2018, 7, 57–59. [Google Scholar] [CrossRef]
- McClean, J.R.; Rubin, N.C.; Lee, J.; Harrigan, M.P.; O’Brien, T.E.; Babbush, R.; Huggins, W.J.; Huang, H.-Y. What the foundations of quantum computer science teach us about chemistry. J. Chem. Phys. 2021, 155, 150901. [Google Scholar] [CrossRef]
- Harwood, S.; Gambella, C.; Trenev, D.; Simonetto, A.; Neira, D.B.; Greenberg, D. Formulating and Solving Routing Problems on Quantum Computers. IEEE Trans. Quantum Eng. 2021, 2, 3100118. [Google Scholar] [CrossRef]
- Lamata, L. Quantum machine learning and quantum biomimetics: A perspective. Mach. Learn. Sci. Technol. 2020, 1, 033002. [Google Scholar] [CrossRef]
- Barzen, J.; Leymann, F.; Falkenthal, M.; Vietz, D.; Weder, B.; Wild, K. Relevance of Near-Term Quantum Computing in the Cloud: A Humanities Perspective. In Cloud Computing and Services Science; Springer International Publishing: Cham, Switzerland, 2021; pp. 25–58. [Google Scholar] [CrossRef]
- Mehrpoo, M.; Patra, B.; Gong, J.; Hart, P.A.; van Dijk, J.P.G.; Homulle, H.; Kiene, G.; Vladimirescu, A.; Sebastiano, F.; Charbon, E. Benefits and Challenges of Designing Cryogenic CMOS RF Circuits for Quantum Computers. In Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS), Sapporo, Japan, 26–29 May 2019. [Google Scholar] [CrossRef]
- Havlíček, V.; Córcoles, A.D.; Temme, K.; Harrow, A.W.; Kandala, A.; Chow, J.M.; Gambetta, J.M. Supervised learning with quantum-enhanced feature spaces. Nature 2019, 567, 209–212. [Google Scholar] [CrossRef] [PubMed]
- Abraham, H.; Alexander, T.; Barkoutsos, P.; Bello, L.; Ben-Haim, Y.; Bucher, D.; Cabrera-Hernández, F.J.; Carballo-Franquis, J.; Chen, A.; Chen, C.-F.; et al. Qiskit: An Open-source Framework for Quantum Computing. Zenodo 2019. [Google Scholar] [CrossRef]
- Temme, K.; Bravyi, S.; Gambetta, J.M. Error Mitigation for Short-Depth Quantum Circuits. Phys. Rev. Lett. 2017, 119, 180509. [Google Scholar] [CrossRef] [PubMed]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Chang, C.; Lin, C. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2013, 2, 1–39. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Shalev-Shwartz, S.; Singer, Y.; Srebro, N.; Cotter, A. Pegasos: Primal estimated sub-gradient solver for SVM. Math. Program. 2010, 127, 3–30. [Google Scholar] [CrossRef]
- Gentinetta, G.; Thomsen, A.; Sutter, D.; Woerner, S. The complexity of quantum support vector machines. arXiv 2022, arXiv:2203.00031. [Google Scholar] [CrossRef]
- Liu, Y.; Arunachalam, S.; Temme, K. A rigorous and robust quantum speed-up in supervised machine learning. Nat. Phys. 2021, 17, 1013–1017. [Google Scholar] [CrossRef]
- Luck, S.J. Event-related potentials. In APA Handbook of Research Methods in Psychology, Vol 1: Foundations, Planning, Measures, and Psychometrics; American Psychological Association: Washington, DC, USA, 2012; pp. 523–546. [Google Scholar] [CrossRef]
- Van Veen, G.F.P.; Barachant, A.; Andreev, A.; Cattan, G.; Rodrigues, P.L.C.; Congedo, M. Building Brain Invaders: EEG Data of an Experimental Validation, Research Report 1. GIPSA-lab. 2019. Available online: https://hal.archives-ouvertes.fr/hal-02126068 (accessed on 30 November 2021).
- Rivet, B.; Souloumiac, A. Optimal linear spatial filters for event-related potentials based on a spatio-temporal model: Asymptotical performance analysis. Signal Process. 2013, 93, 387–398. [Google Scholar] [CrossRef]
- Barachant, A.; Bonnet, S.; Congedo, M.; Jutten, C. Classification of covariance matrices using a Riemannian-based kernel for BCI applications. Neurocomputing 2013, 112, 172–178. [Google Scholar] [CrossRef]
- Spall, J. Adaptive stochastic approximation by the simultaneous perturbation method. IEEE Trans. Autom. Control 2000, 45, 1839–1853. [Google Scholar] [CrossRef]
- Spall, J.C. A one-measurement form of simultaneous perturbation stochastic approximation. Automatica 1997, 33, 109–112. [Google Scholar] [CrossRef]
- IBM Q Team. IBM Q 16 Melbourne Backend Specification. Qiskit. 2018. Available online: https://github.com/Qiskit/ibmq-device-information (accessed on 6 February 2021).
- Gramfort, A.; Luessi, M.; Larson, E.; Engemann, D.A.; Strohmeier, D.; Brodbeck, C.; Parkkonen, L.; Hämäläinen, M.S. MNE software for processing MEG and EEG data. Neuroimage 2014, 86, 446–460. [Google Scholar] [CrossRef] [PubMed]
- Barachant, A. pyRiemann. pyRiemann. 2015. Available online: https://github.com/pyRiemann/pyRiemann (accessed on 20 December 2022).
- Cattan, G.; Barthélemy, Q.; Andreev, A.; Chevallier, S. pyRiemann-qiskit. pyRiemann. 2021. Available online: https://github.com/pyRiemann/pyRiemann-qiskit (accessed on 1 February 2022).
- Quemy, A. HCBR. 17 September 2020. Available online: https://github.com/aquemy/HCBR (accessed on 2 June 2021).
- Maris, E.; Oostenveld, R. Nonparametric statistical testing of EEG- and MEG-data. J. Neurosci. Methods 2007, 164, 177–190. [Google Scholar] [CrossRef] [PubMed]
- Mueller-Putz, G.; Scherer, R.; Brunner, C.; Leeb, R.; Pfurtscheller, G. (Eds.) Better than random: A closer look on BCI results. Int. J. Bioelectromagn. 2008, 10, 52–55. [Google Scholar]
- Rodrigues, P.L.C.; Jutten, C.; Congedo, M. Riemannian Procrustes Analysis: Transfer Learning for Brain–Computer Interfaces. IEEE Trans. Biomed. Eng. 2019, 66, 2390–2401. [Google Scholar] [CrossRef]
- Zhao, K.; Wiliem, A.; Chen, S.; Lovell, B.C. Convex class model on symmetric positive definite manifolds. Image Vis. Comput. 2019, 87, 57–67. [Google Scholar] [CrossRef]
- Van Apeldoorn, J.; Gilyén, A.; Gribling, S.; De Wolf, R. Convex optimization using quantum oracles. Quantum 2020, 4, 220. [Google Scholar] [CrossRef]
| Number of Decimal Digits | ||||
|---|---|---|---|---|
| 4 | 6 | 8 | ||
| Number of filters | 1 | 0.5367 | 0.5087 | 0.4976 |
| 2 | 0.4914 | 0.4625 | 0.5030 | |
| 4 | 0.4950 | 0.4567 | 0.4982 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cattan, G.H.; Quemy, A. Case-Based and Quantum Classification for ERP-Based Brain–Computer Interfaces. Brain Sci. 2023, 13, 303. https://doi.org/10.3390/brainsci13020303
Cattan GH, Quemy A. Case-Based and Quantum Classification for ERP-Based Brain–Computer Interfaces. Brain Sciences. 2023; 13(2):303. https://doi.org/10.3390/brainsci13020303
Chicago/Turabian StyleCattan, Grégoire H., and Alexandre Quemy. 2023. "Case-Based and Quantum Classification for ERP-Based Brain–Computer Interfaces" Brain Sciences 13, no. 2: 303. https://doi.org/10.3390/brainsci13020303
APA StyleCattan, G. H., & Quemy, A. (2023). Case-Based and Quantum Classification for ERP-Based Brain–Computer Interfaces. Brain Sciences, 13(2), 303. https://doi.org/10.3390/brainsci13020303







