The Roles of Potassium and Calcium Currents in the Bistable Firing Transition
Abstract
:1. Introduction
2. Materials and Methods
2.1. Neural Model
2.2. Description of Ionic Currents
2.2.1. Sodium and Potassium Currents
2.2.2. Slow Potassium Current
2.2.3. Calcium Currents
2.2.4. Neuronal Network
2.3. Measures
2.3.1. Firing Rate
2.3.2. Coefficient of Variation
2.3.3. Synchronization
3. Results
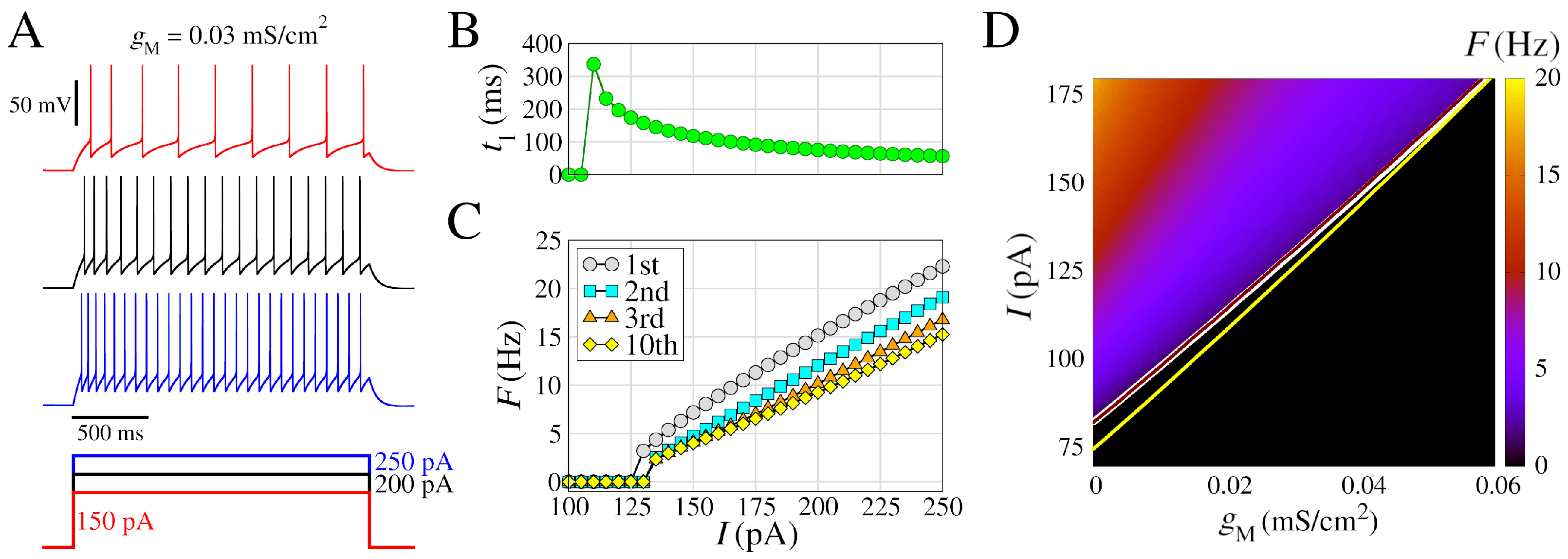
3.1. Neuron Dynamics
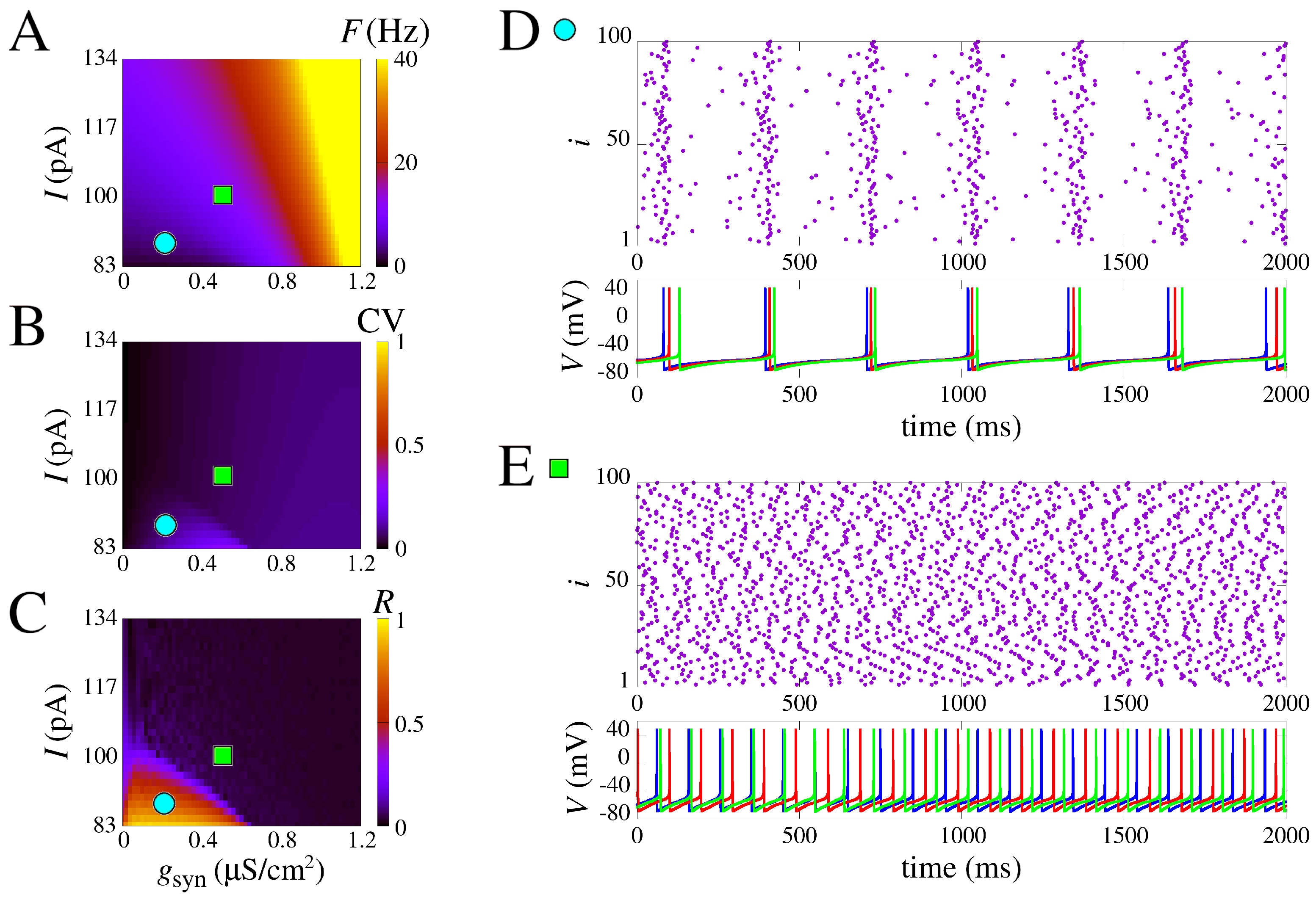
3.2. Neuron Networks
3.3. Bistable Regime
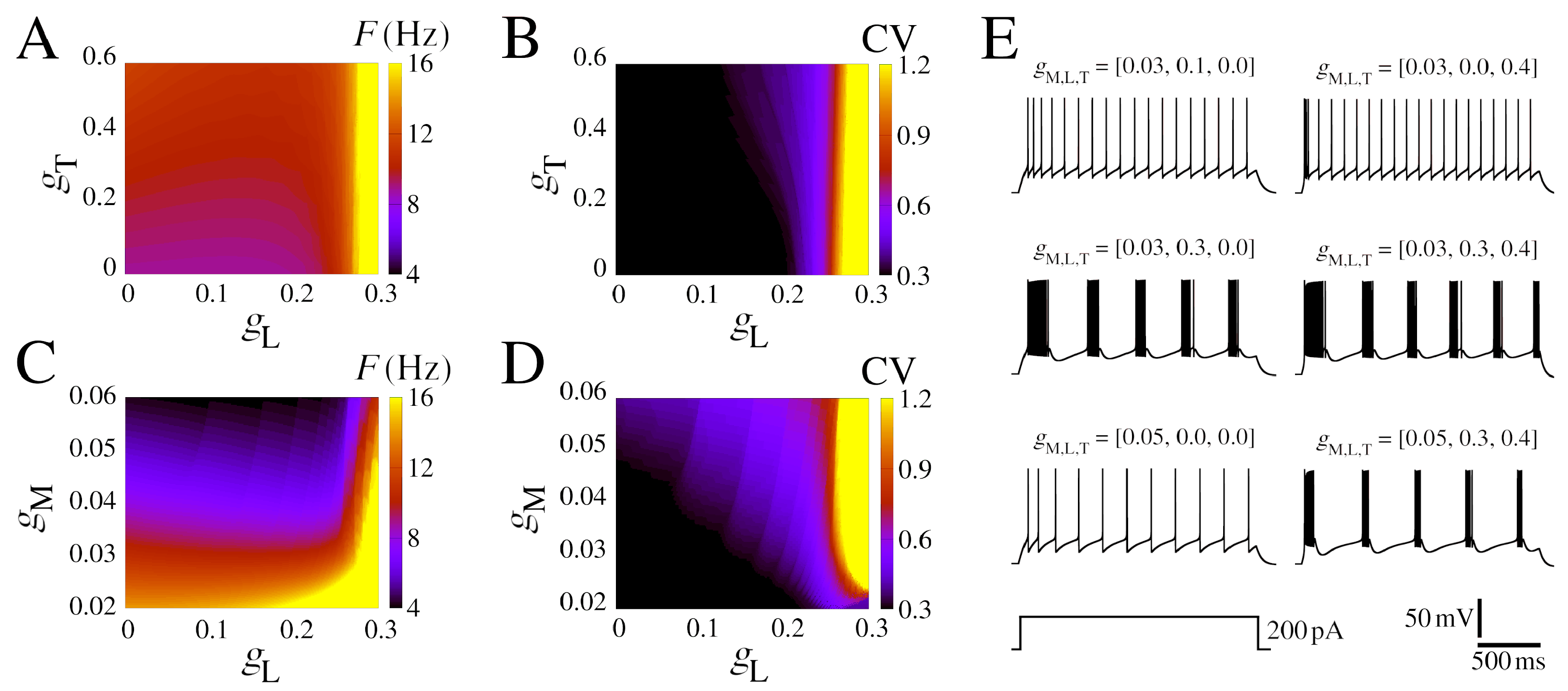
3.4. Calcium Effects in the Bistability
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Dalla Porta, L.; Barbero-Castillo, A.; Sanchez-Sanchez, J.M.; Sanchez-Vives, M.V. M-current modulation of cortical slow oscillations: Network dynamics and computational modeling. PLoS Comput. Biol. 2023, 19, e1011246. [Google Scholar] [CrossRef] [PubMed]
- Burke, K.J., Jr.; Bender, K.J. Modulation of ion channells in the axon: Mechanism and function. Front. Cell. Neurosci. 2019, 13, 221. [Google Scholar] [CrossRef]
- Ranjan, R.; Logette, E.; Marani, M.; Herzog, M.; Tâche, V.; Scantamburlo, E.; Buchillier, V.; Markram, H. A kinetic map of the homomeric voltage-gated potassium channel (Kv) family. Front. Cell. Neurosci. 2019, 13, 358. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.S.; Walsh, C.A. Ion channel functions in early brain development. Trends Neurosci. 2020, 43, 103–114. [Google Scholar] [CrossRef] [PubMed]
- Bando, Y.; Ishibashi, M.; Yamagishi, S.; Fukuda, A.; Sato, K. Orchestration of ion channels and transporters in neocortical development and neurological disorders. Front. Neurosci. 2022, 16, 827284. [Google Scholar] [CrossRef]
- Hou, P.; Du, X.; An, H. Editorial: Ion channels: Therapeutic targets for neurological disease. Front. Mol. Neurosci. 2021, 14, 797327. [Google Scholar] [CrossRef]
- Hübner, C.; Jentsch, T.J. Ion channel diseases. Hum. Mol. Genet. 2002, 11, 2435–2445. [Google Scholar] [CrossRef]
- Kecskes, M.; Peigneur, S.; Held, K. Editorial: Contribution of ion channels to neuropathologies. Front. Cell Dev. Biol. 2023, 11, 1179663. [Google Scholar] [CrossRef]
- Podlaski, W.F.; Seeholzer, A.; Groschner, L.N.; Miesenöck, G.; Ranjan, R.; Vogels, T.P. Mapping the function of neuronal ion channels in model and experiment. eLife 2017, 6, e22152. [Google Scholar] [CrossRef]
- Nayak, L.; Dasgupta, A.; Das, R.; Ghosh, K.; De, R.K. Computational neuroscience and neuroinformatics: Recent progress and resources. J. Biosci. 2018, 43, 1037–1054. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.; Majhi, S.K. A comprehensive survey of recent developments in neuronal communication and computational neuroscience. J. Ind. Inf. Integration 2019, 13, 40–54. [Google Scholar] [CrossRef]
- Barbulescu, R.; Mestre, G.; Oliveira, A.L.; Silveira, L.M. Learning the dynamics of realistic models of C. elegans nervous system with recurrent neural networks. Sci. Rep. 2023, 13, 467. [Google Scholar] [CrossRef]
- Cannon, R.C.; D’Alessandro, G. The ion channel inverse problem: Neuroinformatics meets biophysics. PLoS Comput. Biol. 2006, 2, e91. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Chen, P.-H.; Lin, H.-H.; Huang, W.-M. U(1) dynamics in neuronal activities. Sci. Rep. 2022, 12, 17629. [Google Scholar] [CrossRef]
- Hansen, M.; Protachevicz, P.R.; Iarosz, K.C.; Caldas, I.L.; Batista, A.M.; Macau, E.E. Dynamics of uncoupled and coupled neurons under external pulsed currents. Chaos Solit. Fractals 2022, 155, 11734. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Dynamical Systems in Neuroscience; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Borges, F.S.; Protachevicz, P.R.; Lameu, E.L.; Bonetti, R.C.; Iarosz, K.C.; Caldas, I.L.; Baptista, M.S.; Batista, A.M. Synchronous behaviour in network model based on human cortico-cortical connections. Neural Netw. 2017, 90, 074006. [Google Scholar]
- Protachevicz, P.R.; Borges, R.R.; Reis, A.S.; Borges, F.S.; Iarosz, K.C.; Caldas, I.L.; Lameu, E.L.; Macau, E.E.N.; Viana, R.L.; Sokolov, I.M.; et al. Synchronous behaviour in network model based on human cortico-cortical connections. Physiol. Meas. 2018, 39, 7. [Google Scholar] [CrossRef]
- Jiao, X.; Wang, R. Synchronous firing patterns of neuronal population with excitatory and inhibitory connections. Int. J. Non Linear Mech. 2010, 45, 647–651. [Google Scholar] [CrossRef]
- Wang, H.; Ma, J.; Chen, Y.; Chen, Y. Effect of an autapse on the firing pattern transition in a bursting neuron. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3242–3254. [Google Scholar] [CrossRef]
- Santos, M.S.; Protachevicz, P.R.; Iarosz, K.C.; Caldas, I.L.; Viana, R.L.; Borges, F.S.; Ren, H.-P.; Szezech, J.D.; Batista, A.M.; Grebogi, C. Spike-burst chimera states in an adaptive exponential integrate-and-fire neuronal network. Chaos 2019, 29, 4. [Google Scholar] [CrossRef]
- Protachevicz, P.R.; Iarosz, K.C.; Caldas, I.L.; Antonopoulos, C.G.; Batista, A.M.; Kurths, J. Influence of autapses on synchronization in neural networks with chemical synapses. Front. Syst. Neurosci. 2020, 14, 604563. [Google Scholar] [CrossRef]
- Protachevicz, P.R.; Hansen, M.; Iarosz, K.C.; Caldas, I.L.; Batista, A.M.; Kurths, J. Emergence of neuronal synchronization in coupled areas. Front. Comput. Neurosci. 2021, 15, 663408. [Google Scholar] [CrossRef]
- Pena, R.F.O.; Lima, V.; Shimoura, R.O.; Paulo Novato, J.; Roque, A.C. Optimal Interplay between Synaptic Strengths and Network Structure Enhances Activity Fluctuations and Information Propagation in Hierarchical Modular Networks. Brain Sci. 2020, 10, 228. [Google Scholar] [CrossRef]
- Huang, S.; Zhang, J.; Wang, M.; Hu, C.-H. Firing patterns transitions and desynchronization induced by time delay in neural networks. Physica A 2018, 499, 88–97. [Google Scholar] [CrossRef]
- Protachevicz, P.R.; Borges, F.S.; Iarosz, K.C.; Baptista, M.S.; Lameu, E.L.; Hansen, M.; Caldas, I.L.; Szezech, J.D., Jr.; Batista, A.M.; Kurths, J. Influence of delayed conductance on neuronal synchronization. Front. Physiol. 2020, 11, 1053. [Google Scholar] [CrossRef] [PubMed]
- Pena, R.F.O.; Zaks, M.A.; Roque, A.C. Dynamics of spontaneous activity in random networks with multiple neuron subtypes and synaptic noise. J. Comput. Neurosci. 2018, 45, 1–28. [Google Scholar] [CrossRef]
- Protachevicz, P.R.; Bonin, C.A.; Iarosz, K.C.; Caldas, I.L.; Batista, A.M. Large coefficient of variation of inter-spike intervals induced by noise current in the resonate-and-fire model neuron. Cogn. Neurodyn. 2022, 16, 1461–1470. [Google Scholar] [CrossRef]
- Protachevicz, P.R.; Santos, M.S.; Seifert, E.G.; Gabrick, E.C.; Borges, F.S.; Borges, R.R.; Trobia, J.; Szezech, J.D., Jr.; Iarosz, K.C.; Caldas, I.L.; et al. Noise induces continuous and non-continuous transitions in neuronal interspike interval range. Indian Acad. Sci. Conf. Ser. 2020, 3, 1. [Google Scholar]
- Lowet, E.; Sheehan, D.J.; Chialva, U.; Pena, R.D.O.; De Mount, R.A.; Xiao, S.; Zhou, S.L.; Tseng, H.; Gritton, H.; Shroff, S.; et al. Theta and gamma rhythmic coding through two spike output modes in the hippocampus during spatial navigation. Cell Rep. 2023, 42, 112906. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Pan, B.; Xu, J. Experimental observation of spike, burst, and chaos synchronization of calcium concentration oscillations. Europhys. Lett. 2014, 106, 50003. [Google Scholar] [CrossRef]
- Århem, P.; Klement, G.; Blomberg, C. Channel density regulation of firing patterns in a cortical neuron model. Biophys. J. 2006, 90, 4392–4404. [Google Scholar] [CrossRef] [PubMed]
- Protachevicz, P.R.; Borges, F.S.; Lameu, E.L.; Ji, P.; Iarosz, K.C.; Kihara, A.L.; Caldas, I.L.; Szezech, J.D., Jr.; Baptista, M.S.; Macau, E.E.N.; et al. Bistable firing patterns in a neural network model. Front. Comput. Neurosci. 2019, 13, 19. [Google Scholar] [CrossRef] [PubMed]
- Cooper, D.C.; Chung, S.; Spruston, N. Output-mode transitions are controlled by prolonged inactivation of sodium channels in pyramidal neurons of subiculum. PLoS Biol. 2005, 3, e175. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Fu, W.-L.; Cao, L.-H. Modulation of neuronal dynamic range using two different adaptation mechanisms. Neural Regen. Res. 2017, 12, 3. [Google Scholar] [CrossRef]
- Benda, J. Neural adaptation. Curr. Biol. 2021, 31, R110–R116. [Google Scholar] [CrossRef]
- Trinh, A.; Girardi-Schappo, M.; Béïque, J.; Longtin, A.; Maler, L. Dentate gyrus mossy cells exhibit sparse coding via adaptive spike threshold dynamics. bioRxiv 2022, bioRxiv483263. [Google Scholar]
- Ha, G.E.; Cheong, E. Spike frequency adaptation in neuron of the central nervous system. Exp. Neurobiol. 2017, 26, 179. [Google Scholar] [CrossRef]
- Pospischil, M.; Toledo-Rodriguez, M.; Monier, C.; Piwkowska, Z.; Bal, T.; Frégnac, Y.; Destexhe, A. Minimal Hodgkin–Huxley type models for different classes of cortical and thalamic neurons. Biol. Cybern. 2008, 99, 427–441. [Google Scholar] [CrossRef]
- Wang, J.; Deng, B.; Gao, T.; Jiang, W.; Hong, T. Spike-frequency adaptation inhibits the pairwise spike correlation. Front. Neurosci. 2023, 17, 1193930. [Google Scholar] [CrossRef]
- Berger, S.D.; Crook, S.M. Modeling the influence of ion channels on neuron dynamics in Drosophila. Front. Comput. Neurosci. 2015, 9, 139. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Wade, K.; Hong, H.; Sanchez, J.T. Ion channel mechanisms underlying frequency-firing patterns of the avian nucleous magnocellularis: A computational model. Channels 2017, 11, 444–458. [Google Scholar] [CrossRef] [PubMed]
- Landisman, C.E.; Long, M.A.; Beierlein, M.; Deans, M.R.; Paul, D.L.; Connors, B.W. Electrical synapses in the thalamic reticular nucleos. J. Neurosci. 2002, 22, 1002–1009. [Google Scholar] [CrossRef] [PubMed]
- Svirskis, G.; Rinzel, J. Influence of temporal correlation of synaptic input on the rate and variability of firing in neurons. Biophys. J. 2000, 79, 629–637. [Google Scholar] [CrossRef] [PubMed]
- Borges, F.S.; Moreira, J.V.S.; Takarabe, L.M.; Lytton, W.W.; Dura-Bernal, S. Large-scale biophysically detailed model of somatosensory thalamocortical circuits in NetPyNE. Front. Neuroinform. 2022, 16, 884245. [Google Scholar] [CrossRef]
- Lu, Q.; Yang, Z.; Duan, L.; Gu, H.; Ren, W. Dynamics and transitions of firing patterns in deterministic and stochastic neuronal systems. Chaos Solit. Fractals 2009, 40, 577–597. [Google Scholar] [CrossRef]
- Maisel, B.; Lindenberg, K. Channel noise effects on neural synchronization. Phys. A Stat. Mech. Appl. 2020, 552, 123186. [Google Scholar] [CrossRef]
- Schmid, G.; Goychuk, I.; Hänggi, P. Channel noise and synchronization in excitable membranes. Phys. A Stat. Mech. Appl. 2003, 325, 165–175. [Google Scholar] [CrossRef]
- Boaretto, B.R.R.; Manchein, C.; Prado, T.L.; Lopes, S.R. The role of individual neuron ion conductance in the synchronization processes of neuron networks. Neural Netw. 2021, 137, 97–105. [Google Scholar] [CrossRef]
- Ladenbauer, J.; Augustin, M.; Shiau, L.; Obermayer, K. Impact of adaptation currents on synchronization of coupled exponential integrate-and-fire neurons. PLoS Comput. Biol. 2012, 8, e1002478. [Google Scholar] [CrossRef]
- Avoli, M. Mechanism of epileptiform synchronization in cortical neuronal networks. Curr. Med. Chem. 2014, 21, 653–662. [Google Scholar] [CrossRef]
- Traub, R.D.; Wong, R.K.S. Cellular mechanism of neuronal synchronization in epilepsy. Science 1982, 216, 745–747. [Google Scholar] [CrossRef] [PubMed]
- Hofer, K.T.; Kandrás, A.; Tóth, K.; Hajnal, B.; Bokodi, V.; Tóth, E.Z.; Eros, L.; Entz, L.; Bagó, A.G.; Fabó, D.; et al. Bursting of excitatory cells is linked to interictal epileptic discharge generation in humans. Nature 2022, 12, 6280. [Google Scholar] [CrossRef] [PubMed]
- Jiruska, P.; de Curtis, M.; Jefferys, J.G.; Schevon, C.A.; Schiff, S.J.; Schindler, K. Synchronization and desynchronization in epilepsy: Controversies and hypotheses. J. Physiol. 2013, 591, 787–797. [Google Scholar] [CrossRef]
- Chen, C.; Chen, L.; Lin, Y.; Zeng, S.; Luo, Q. The origin of spontaneous synchronized burst in cultured neuronal networks based on multi-electrode arrays. Biosystems 2006, 85, 137–143. [Google Scholar] [CrossRef]
- Matsumoto-Makidono, Y.; Nakayama, H.; Yamasaki, M.; Miyazaki, T.; Kobayashi, K.; Watanabe, M.; Hashimoto, K. Ionic basis for membrane potential resonance in neurons of the inferior olive. Cell Rep. 2016, 16, 994–1004. [Google Scholar] [CrossRef] [PubMed]
- Graef, J.; Nordskog, B.K.; Wiggins, W.F.; Godwin, S.W. An acquired channelopathy involving thalamic T-type Ca2+ channels after status epilepticus. J. Neurosci. 2009, 29, 4430–4441. [Google Scholar] [CrossRef]
- Becker, A.J.; Pitsch, J.; Sochivko, D.; Opitz, T.; Staniek, M.; Chen, C.-C.; Campbell, K.P.; Schoch, S.; Yaari, Y.; Beck, H. Transcriptional upregulation of Cav3.2 mediates epileptogenesis in pilocarpine model of epilepsy. J. Neurosci. 2008, 28, 13341–13353. [Google Scholar] [CrossRef]
- Su, H.; Sochivko, D.; Becker, A.; Chen, J.; Jiang, Y.; Yaari, Y.; Becker, H. Upregulation of a T-type Ca2+ channel causes a long-lasting modification of neuronal firing mode after status epilepticus. J. Neurosci. 2002, 22, 3645–3655. [Google Scholar] [CrossRef]
- Dovzhenok, A.; Kuznetsov, A.S. Exploring neuronal bistability at the depolatization block. PLoS ONE 2012, 7, e42811. [Google Scholar] [CrossRef]
- Tartaglia, E.M.; Brunel, N. Bistability and up/down state alternations in inhibition-dominated randomly connected networks of LIF neurons. Sci. Rep. 2017, 7, 11916. [Google Scholar] [CrossRef] [PubMed]
- Compte, A.; Sanchez-Vives, M.V.; McCormick, D.A.; Wang, X.-J. Cellular and Network Mechanism of slow oscillatory activity (1< Hz) and wave propagation in a cortical network model. J. Neurophysiol. 2003, 89, 5. [Google Scholar]
- Boaretto, B.R.R.; Budzinski, R.C.; Rossi, K.L.; Manchein, C.; Prado, T.L.; Feudel, U.; Lopes, S.R. Bistability in synchronization of identical neurons. Phys. Rev. E 2021, 104, 0240204. [Google Scholar] [CrossRef] [PubMed]
- Akcay, Z.; Xinxian, H.; Nadim, F.; Bose, A. Phase-locking and bistability in neuronal networks with synaptic depression. Phys. D Nonlinear Phenom. 2018, 364, 8–21. [Google Scholar] [CrossRef]
- Lu, Y.; Xin, X.; Rinzel, J. Bistability at the onset of neuronal oscillations. Biol. Cybern. 2023, 117, 61–79. [Google Scholar] [CrossRef]
- Fröhlich, F.; Bazhenov, M. Coexistence of tonic firing and bursting in cortical neurons. Phys. Rev. E 2006, 74, 031922. [Google Scholar] [CrossRef]
- Meng, J.H.; Riecke, H. Synchronization by uncorrelated noise: Interacting rhythms in interconnected oscillator networks. Sci. Rep. 2018, 8, 6949. [Google Scholar] [CrossRef]
- Kelso, J.A.S. Multistability and metastability: Understanding dynamic coordination in the brain. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 906–918. [Google Scholar] [CrossRef]
- Silva, F.L.; Blanes, W.; Kalitzin, S.N.; Parra, J.; Suffczynski, P.; Velos, D.N. Epilepsies as dynamical diseases of brain systems: Basic models of the transition between normal and epileptic activity. Epilepsia 2003, 44, 72–83. [Google Scholar] [CrossRef]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural; MIT Press: Cambridge, MA, USA, 2005; pp. 160–162. [Google Scholar]
- Traub, R.D.; Miles, R. Neuronal Networks of the Hippocampus; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Yamada, W.M.; Koch, C.; Adams, P.R. Multiple Channels and Calcium Dynamics, Methods in Neuronal Modeling: From Synapses to Networks; MIT Press: Cambridge, MA, USA, 1989; pp. 97–134. [Google Scholar]
- Destexhe, A.; Neubig, M.; Ulrich, D.; Huguenard, J. Dendritic low-threshold calcium currents in thalamic relay cells. J. Neurosci. 1998, 18, 3574–3588. [Google Scholar] [CrossRef]
- Reuveni, I.; Friedman, A.; Amitai, Y.; Gutnick, M.J. Stepwise repolarization from Ca2+ plateaus in neocortical pyramidal cells: Evidence for nonhomogeneous distribution of HVA Ca2+ channels in dendrites. J. Neurosci. 1993, 13, 4609–4621. [Google Scholar] [CrossRef] [PubMed]
- Destexhe, A.; Bal, T.; McCormick, D.A.; Sejnowski, T.J. Ionic mechanisms underlying synchronized oscillations and propagating waves in a model of ferret thalamic slices. J. Neurophysiol. 1996, 76, 2049–2070. [Google Scholar] [CrossRef] [PubMed]
- Huguenard, J.R.; McCormick, D.A. Simulation of the currents involved in rhythmic oscillations in thalamic relay neurons. J. Neurophysiol. 1992, 68, 1373–1383. [Google Scholar] [CrossRef]
- Noback, C.R.; Ruggiero, D.A.; Strominger, N.L.; Demarest, R.J. The Human Nervous System: Structure and Function; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; p. 744. [Google Scholar]
- Borges, F.S.; Protachevicz, P.R.; Pena, R.F.O.; Lameu, E.L.; Higa, G.S.V.; Kihara, A.H.; Matias, F.S.; Antonopoulos, C.G.; de Pasquale, R.; Roque, A.C.; et al. Self-sustained activity of low firing rate in balanced networks. Phys. A Stat. Mech. Appl. 2020, 537, 122671. [Google Scholar] [CrossRef]
- Kuramoto, Y. Chemical Oscillations, Waves, and Turbulence; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Hansen, M.; Protachevicz, P.R.; Iarosz, K.C.; Caldas, I.L.; Batista, A.M.; Macau, E.E.N. The effect of time delay for synchronisation suppression in neuronal networks. Chaos Solit. Fractals 2022, 164, 112690. [Google Scholar] [CrossRef]
- Dura-Bernal, S.; Suter, B.A.; Gleeson, P.; Cantarelli, M.; Quintana, A.; Rodriguez, F.; Kedziora, D.J.; Chadderdon, F.L.; Kerr, C.C.; Neymotin, S.A.; et al. NetPyNE, a tool for data-driven multiscale modeling of brain circuits. eLife 2019, 8, e44494. [Google Scholar]
- Vijayan, S.; Hale, G.J.; Moore, C.I.; Brown, E.N.; Wilson, M. Activity in the barrel cortex during active behavior and sleep. J. Neurophysiol. 2010, 103, 2074–2084. [Google Scholar] [CrossRef]
- Borges, F.S.; Gabrick, E.C.; Protachevicz, P.R.; Higa, G.S.V.; Lameu, E.L.; Rodriguez, P.X.R.; Ferraz, M.S.A.; Szezech, J.D.; Batista, A.M.; Kihara, A.H. Intermittency properties in a temporal lobe epilepsy model. Epilepsy Behav. 2023, 139, 109072. [Google Scholar] [CrossRef]
- Alonso, L.M.; Marder, E. Visualization of currents in neural models with similar behavior and different conductance densities. eLife 2019, 8, e42722. [Google Scholar] [CrossRef]
- Eun, S.H.; Kim, H.D.; Eun, B.L.; Lee, I.K.; Chung, H.J.; Kim, J.S.; Kang, H.C.; Lee, Y.M.; Suh, E.S.; Kim, D.W.; et al. Comparative trial of low- and high-dose zonisamide as monotherapy for childhood epilepsy. Seizure 2011, 20, 558–563. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Y.; Cheng, J.; Tao, J. Ion channels in epilepsy: Blasting fuse for neuronal hyperexcitability. In Epilepsy—Advances in Diagnosis and Therapy; Al-Zwaini, I.J., Albadri, B.A.-H., Eds.; IntechOpen: London, UK, 2018; Chapter 10. [Google Scholar]
- Palmer, E.E. Potassium channel mutations in epilepsy. In The Oxford Handbook of Neuronal Ion Channels; Bhattacharjee, A., Ed.; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Chen, X.; Feng, Y.; Quinn, R.J.; Pountney, D.L.; Richardson, D.R.; Mellick, G.D.; Ma, L. Potassium Channels in Parkinson’s Disease: Potential Roles in Its Pathogenesis and Innovative Molecular Targets for Treatment. Pharmacol. Rev. 2023, 75, 758–788. [Google Scholar]
- Xu, J.-H.; Tang, F.-R. Voltage-dependent calcium channels, calcium binding proteins, and their interaction in the pathological process of epilepsy. Int. J. Mol. Sci. 2018, 19, 2735. [Google Scholar] [CrossRef]
- Jorge, B.S.; Campbell, C.M.; Miller, A.R.; Kearney, J.A. Voltage-gated potassium channel KCNV2 (Kv8.2) contributes to epilepsy susceptibility. Proc. Natl. Acad. Sci. USA 2011, 108, 5443–5448. [Google Scholar] [CrossRef] [PubMed]
- Zamponi, G.W.; Lory, P.; Perez-Reyes, E. Role of voltage-gate calcium channels in epilepsy. Neuroscience 2010, 460, 395–403. [Google Scholar]
- Zamponi, G.W.; Striessnig, J.; Koschak, A.; Dolphin, A.C. The physiology, and pharmacology of voltage-gated calcium channels and their future therapeutic potential. Pharmacol. Rev. 2015, 67, 821–870. [Google Scholar] [PubMed]
- Han, D.-Y.; Guan, B.-J.; Wang, Y.-J.; Hatzoglou, M.; Mu, T.-W. L-type calcium channel blockers enhance trafficking and function of epilepsy-associated α1(D219N) subunits of GABAA receptors. J. Am. Chem. Soc. 2015, 15, 2135–2148. [Google Scholar] [CrossRef] [PubMed]
- Köhling, R.; Wolfart, J. Potassium channels in Epilepsy. Cold Spring Harb. Perspect. Med. 2016, 6, a022871. [Google Scholar] [CrossRef] [PubMed]
- Passmore, G.M.; Reilly, J.M.; Thakur, M.; Keasberry, V.N.; Marsh, S.J.; Dickenson, A.H.; Brown, D.A. Functional significance of M-type potassium channels in nociceptive cutaneous sensory endings. Front. Mol. Neurosci. 2012, 5, 63. [Google Scholar] [CrossRef]
- Cooper, E.C. Potassium Channels (including KCNQ) and Epilepsy. In Jasper’s Basic Mechanisms of the Epilepsies, 4th ed.; Noebels, J.L., Avoli, M., Rogawski, M.A., Olsen, R., Delgado-Escueta, A.V., Eds.; National Center for Biotechnology Information (US): Bethesda, MD, USA, 2012. [Google Scholar]
- Humphries, E.S.A.; Dart, C. Neuronal and cardiovascular Potassium channels as therapeutic drug targets: Promise and pitfalls. J. Biomol. Screen. 2015, 20, 1055–1073. [Google Scholar]
- Niday, Z.; Tzingounis, A.V. Potassium channel gain of function in epilepsy: An unresolved paradox. Neuroscientist 2018, 24, 368–380. [Google Scholar]
- Villa, C.; Combi, R. Potassium channels and human epileptic phenotypes: An updated overview. Front. Cell. Neurosci. 2016, 10, 81. [Google Scholar] [CrossRef] [PubMed]
- McCoy, M.T.; Jayanthi, S.; Cadet, J.L. Potassium channels and their potential roles in substance use disorders. Int. J. Mol. Sci. 2021, 22, 1249. [Google Scholar] [CrossRef] [PubMed]
- Gao, K.; Lin, Z.; Wen, S.; Jiang, Y. Potassium channels and epilepsy. Acta Neurol. Scand. 2022, 146, 699–707. [Google Scholar] [CrossRef] [PubMed]
- Smart, S.L.; Lopantsev, V.; Zhang, C.L.; Robbins, C.A.; Wang, H.; Chiu, S.Y.; Schwartzkroin, P.A.; Messing, A.; Tempel, B.L. Deletion of the Kv1.1 Potassium channel causes epilepsy in mice. Neuron 1998, 20, 809–819. [Google Scholar] [CrossRef]
- Ågren, R.; Nilsson, J.; Århem, P. Closed and open state dependent block of potassium channels cause opposing effects on excitability—A computational approach. Sci. Rep. 2019, 9, 8175. [Google Scholar] [CrossRef]
- Rajakulendran, S.; Hanna, M.G. The role of calcium channels in epilepsy. Cold Spring Harb. Perspect. Med. 2016, 6, a022723. [Google Scholar] [CrossRef]
- Powell, K.L.; Cain, S.M.; Snutch, T.P.; O’Brien, T.J. Low threshold T-type calcium channels as targets for novel epilepsy treatments. Br. J. Clin. Pharmacol. 2013, 77, 729–739. [Google Scholar] [CrossRef]
- Roopa, B.; Janardhan, M.; Karunasree, P. Effect of calcium blocker as anticonvulsant and its potentiating effect when used along with sodium valproate in pentylenetetrazole induced seizures in Albino rats. Int. J. Basic Clin. Pharmacol. 2008, 7, 714. [Google Scholar]
- Willmore, L.J. Calcium antagonists and epilepsy. Mayo Clin. Proc. 1995, 80, 70–715. [Google Scholar] [CrossRef]
- Tringham, E.; Powell, K.L.; Cain, S.M.; Kuplast, K.; Mezeyoya, J.; Weerapura, M.; Eduljee, C.; Jiang, X.; Smith, P.; Morrison, J.-L.; et al. T-Type calcium channel blockers that attenuate thalamic burst firing and suppress absense seizures. Epilepsy 2012, 4, 121. [Google Scholar]
- Kulak, W.; Sobaniec, W.; Wojtal, K.; Czuczwar, S.J. Calcium modulation in epilepsy. Pol. J. Pharmacol. 2004, 56, 29–41. [Google Scholar] [PubMed]
- Kopecky, B.J.; Liang, R.; Bao, J. T-type calcium channel blockers as neuroprotective agents. Pflug. Arch. Eur. J. Physiol. 2014, 466, 757–765. [Google Scholar] [CrossRef] [PubMed]
- Cain, S.M.; Snutch, T.P. T-type calcium channels in burst-firing, network synchrony, and epilepsy. Biochim. Biophys. Acta 2018, 1828, 1572–1578. [Google Scholar] [CrossRef]
- El-Azab, M.F.; Moustafa, Y.M. Influence of calcium channel blockers on anticonvulsant and antinociceptive activities of valproic acid in pentylenetetrazole-kindled mice. Pharmacol. Rep. 2012, 64, 305–314. [Google Scholar] [CrossRef] [PubMed]
- Gardos, G. The function of calcium in the potassium permeability of human erythrocytes. Biochim. Biophys. Acta Bioenerg. 1958, 30, 653–654. [Google Scholar] [CrossRef] [PubMed]
- Hille, B. Ionic channels in excitable membranes. Current problems and biophysical approaches. Biophys. J. 1978, 22, 283–294. [Google Scholar] [CrossRef]
- Vergara, C.; Latorre, R.; Marrion, N.V.; Adelman, J.P. Calcium-activated potassium channels. Curr. Opin. Neurobiol. 1998, 8, 321–329. [Google Scholar] [CrossRef]
- Momin, A.; Cadiou, H.; Mason, A.; McNaughton, P.A. Role of the hyperpolarization-activated current Ih in somatosensory neurons. J. Physiol. 2008, 586, 5911–5929. [Google Scholar] [CrossRef]
- Stafstrom, C.E. Persistent sodium current and its role in epilepsy. Epilepsy Curr. 2007, 7, 15–22. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borges, F.S.; Protachevicz, P.R.; Souza, D.L.M.; Bittencourt, C.F.; Gabrick, E.C.; Bentivoglio, L.E.; Szezech, J.D., Jr.; Batista, A.M.; Caldas, I.L.; Dura-Bernal, S.; et al. The Roles of Potassium and Calcium Currents in the Bistable Firing Transition. Brain Sci. 2023, 13, 1347. https://doi.org/10.3390/brainsci13091347
Borges FS, Protachevicz PR, Souza DLM, Bittencourt CF, Gabrick EC, Bentivoglio LE, Szezech JD Jr., Batista AM, Caldas IL, Dura-Bernal S, et al. The Roles of Potassium and Calcium Currents in the Bistable Firing Transition. Brain Sciences. 2023; 13(9):1347. https://doi.org/10.3390/brainsci13091347
Chicago/Turabian StyleBorges, Fernando S., Paulo R. Protachevicz, Diogo L. M. Souza, Conrado F. Bittencourt, Enrique C. Gabrick, Lucas E. Bentivoglio, José D. Szezech, Jr., Antonio M. Batista, Iberê L. Caldas, Salvador Dura-Bernal, and et al. 2023. "The Roles of Potassium and Calcium Currents in the Bistable Firing Transition" Brain Sciences 13, no. 9: 1347. https://doi.org/10.3390/brainsci13091347
APA StyleBorges, F. S., Protachevicz, P. R., Souza, D. L. M., Bittencourt, C. F., Gabrick, E. C., Bentivoglio, L. E., Szezech, J. D., Jr., Batista, A. M., Caldas, I. L., Dura-Bernal, S., & Pena, R. F. O. (2023). The Roles of Potassium and Calcium Currents in the Bistable Firing Transition. Brain Sciences, 13(9), 1347. https://doi.org/10.3390/brainsci13091347





