Neurocognitive Assessment of Mathematics-Related Capacities in Neurosurgical Patients
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. General Surgical and Experimental Procedures
2.3. Psychophysical Tests
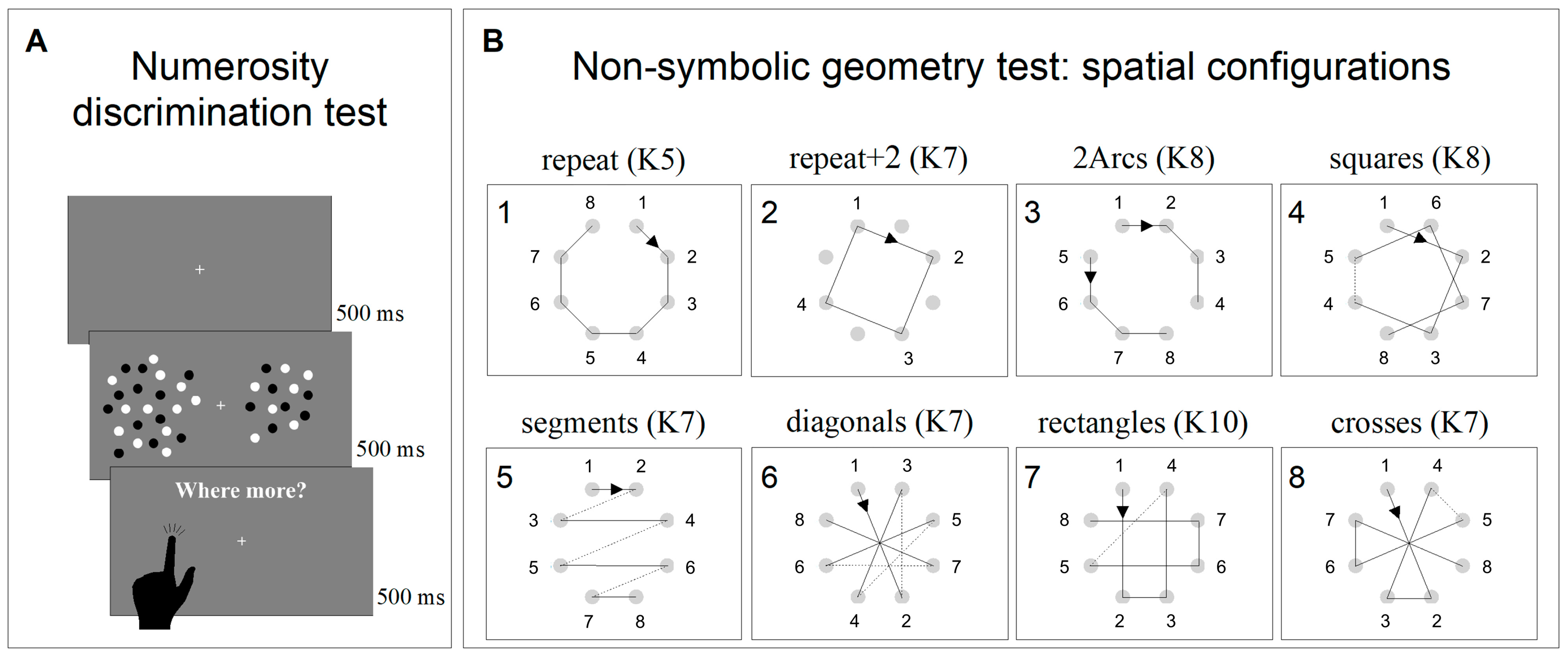
2.3.1. Non-Symbolic Numerosity Perception Test
2.3.2. Non-Symbolic Geometry Test
2.4. Data Analysis
3. Results
3.1. Neuropsychological Assessment
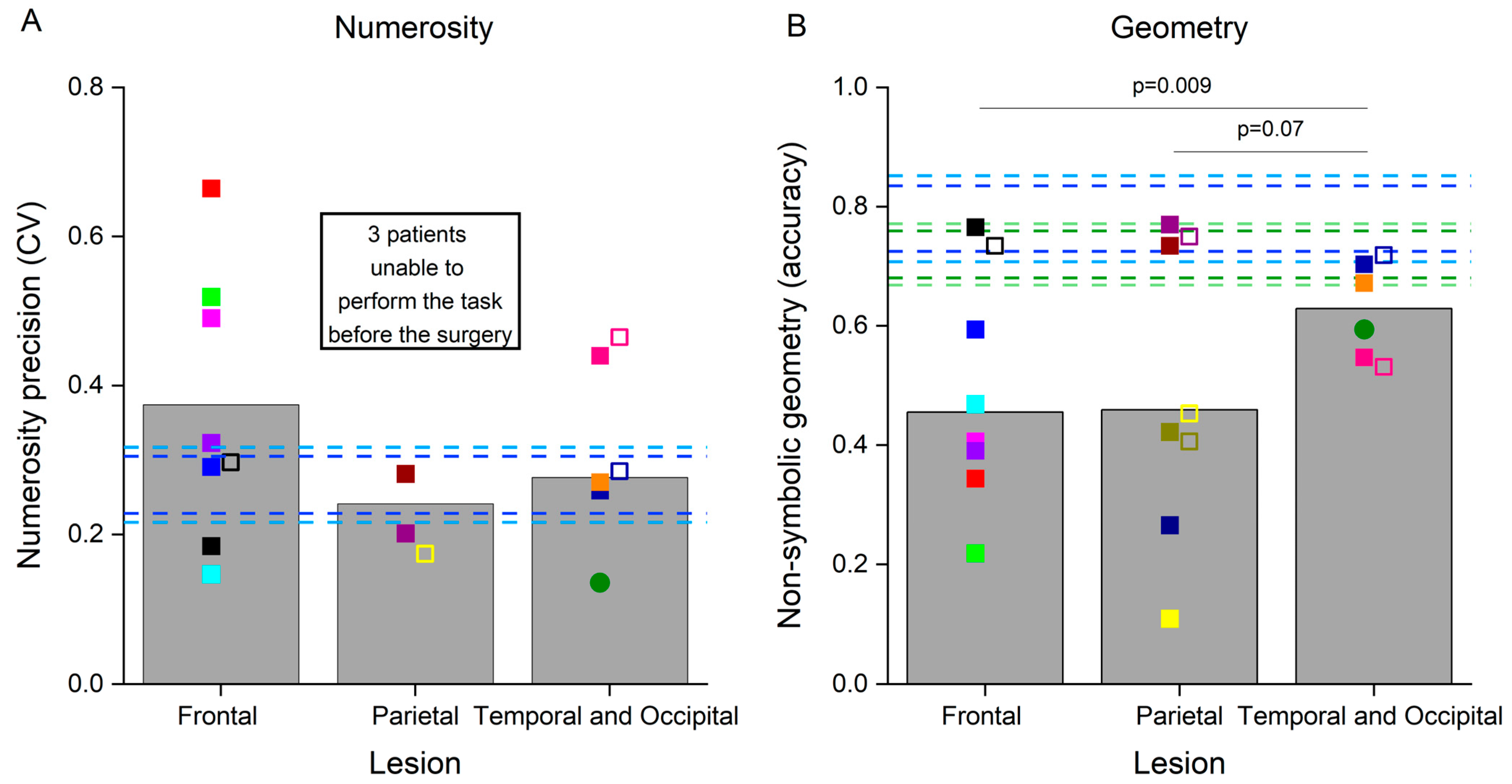
3.2. Non-Symbolic Numerosity and Non-Symbolic Geometry Tests
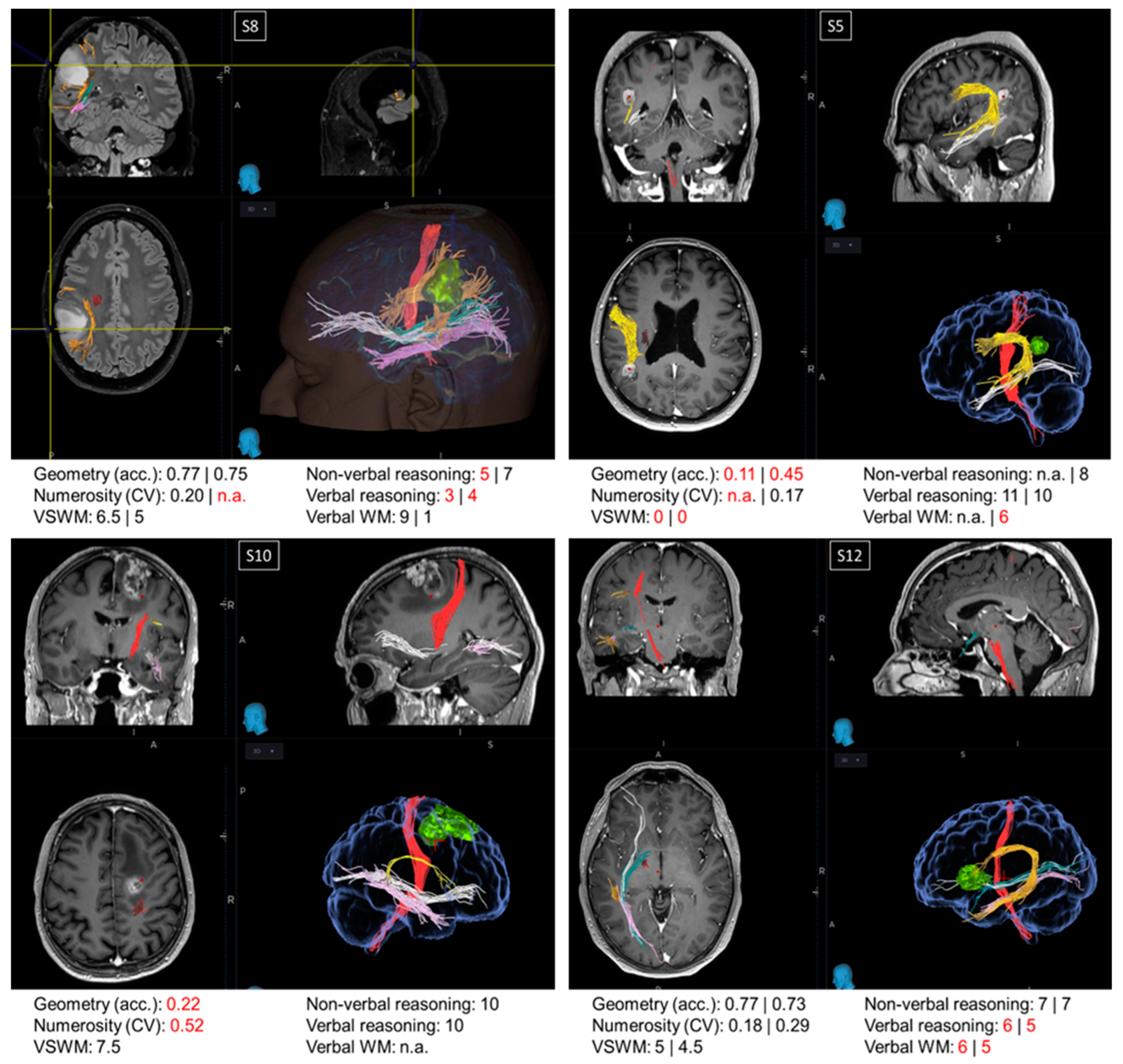
3.3. Single Cases
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brown, T.J.; Brennan, M.C.; Li, M.; Church, E.W.; Brandmeir, N.J.; Rakszawski, K.L.; Patel, A.S.; Rizk, E.B.; Suki, D.; Sawaya, R.; et al. Association of the Extent of Resection With Survival in Glioblastoma: A Systematic Review and Meta-Analysis. JAMA Oncol. 2016, 2, 1460. [Google Scholar] [CrossRef] [PubMed]
- Dadario, N.B.; Brahimaj, B.; Yeung, J.; Sughrue, M.E. Reducing the Cognitive Footprint of Brain Tumor Surgery. Front. Neurol. 2021, 12, 711646. [Google Scholar] [CrossRef] [PubMed]
- Duffau, H.; Mandonnet, E. The “Onco-Functional Balance” in Surgery for Diffuse Low-Grade Glioma: Integrating the Extent of Resection with Quality of Life. Acta Neurochir. 2013, 155, 951–957. [Google Scholar] [CrossRef] [PubMed]
- Hamer, R.P.; Jain, S.; Teo, C.; Loh, W.N.-H.; Chan, H.-M.; Yeo, T.T.; Teo, K. Optimizing the Onco-Functional Balance in Supratentorial Brain Tumour Surgery: A Single Institution’s Initial Experience with Intraoperative Cortico-Subcortical Mapping and Monitoring in Singapore. J. Clin. Neurosci. 2020, 79, 224–230. [Google Scholar] [CrossRef] [PubMed]
- Hervey-Jumper, S.L.; Berger, M.S. Maximizing Safe Resection of Low- and High-Grade Glioma. J. Neurooncol. 2016, 130, 269–282. [Google Scholar] [CrossRef] [PubMed]
- Mandonnet, E.; Duffau, H. An Attempt to Conceptualize the Individual Onco-Functional Balance: Why a Standardized Treatment Is an Illusion for Diffuse Low-Grade Glioma Patients. Crit. Rev. Oncol. Hematol. 2018, 122, 83–91. [Google Scholar] [CrossRef]
- Sanai, N.; Polley, M.-Y.; McDermott, M.W.; Parsa, A.T.; Berger, M.S. An Extent of Resection Threshold for Newly Diagnosed Glioblastomas: Clinical Article. J. Neurosurg. 2011, 115, 3–8. [Google Scholar] [CrossRef]
- Ille, S.; Sollmann, N.; Hauck, T.; Maurer, S.; Tanigawa, N.; Obermueller, T.; Negwer, C.; Droese, D.; Boeckh-Behrens, T.; Meyer, B.; et al. Impairment of Preoperative Language Mapping by Lesion Location: A Functional Magnetic Resonance Imaging, Navigated Transcranial Magnetic Stimulation, and Direct Cortical Stimulation Study. J. Neurosurg. 2015, 123, 314–324. [Google Scholar] [CrossRef]
- Ille, S.; Gempt, J.; Meyer, B.; Krieg, S.M. nTMS Guidance of Awake Surgery for Highly Eloquent Gliomas. Neurosurg. Focus 2018, 45, V9. [Google Scholar] [CrossRef]
- Krieg, S.M.; Lioumis, P.; Mäkelä, J.P.; Wilenius, J.; Karhu, J.; Hannula, H.; Savolainen, P.; Lucas, C.W.; Seidel, K.; Laakso, A.; et al. Protocol for Motor and Language Mapping by Navigated TMS in Patients and Healthy Volunteers; Workshop Report. Acta Neurochir. 2017, 159, 1187–1195. [Google Scholar] [CrossRef]
- Picht, T.; Krieg, S.M.; Sollmann, N.; Rösler, J.; Niraula, B.; Neuvonen, T.; Savolainen, P.; Lioumis, P.; Mäkelä, J.P.; Deletis, V.; et al. A Comparison of Language Mapping by Preoperative Navigated Transcranial Magnetic Stimulation and Direct Cortical Stimulation During Awake Surgery. Neurosurgery 2013, 72, 808–819. [Google Scholar] [CrossRef] [PubMed]
- Ruis, C. Monitoring Cognition during Awake Brain Surgery in Adults: A Systematic Review. J. Clin. Exp. Neuropsychol. 2018, 40, 1081–1104. [Google Scholar] [CrossRef] [PubMed]
- Duffau, H. Mapping the Connectome in Awake Surgery for Gliomas: An Update. J. Neurosurg. Sci. 2017, 61, 612–630. [Google Scholar] [CrossRef] [PubMed]
- Della Puppa, A.; De Pellegrin, S.; Lazzarini, A.; Gioffrè, G.; Rustemi, O.; Cagnin, A.; Scienza, R.; Semenza, C. Subcortical Mapping of Calculation Processing in the Right Parietal Lobe. J. Neurosurg. 2015, 122, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Della Puppa, A.; De Pellegrin, S.; Rossetto, M.; Rustemi, O.; Saladini, M.; Munari, M.; Scienza, R. Intraoperative Functional Mapping of Calculation in Parietal Surgery. New Insights and Clinical Implications. Acta Neurochir. 2015, 157, 971–977. [Google Scholar] [CrossRef]
- Semenza, C.; Salillas, E.; De Pallegrin, S.; Della Puppa, A. Balancing the 2 Hemispheres in Simple Calculation: Evidence From Direct Cortical Electrostimulation. Cereb. Cortex 2016, 27, 4806–4814. [Google Scholar] [CrossRef]
- Anobile, G.; Castaldi, E.; Turi, M.; Tinelli, F.; Burr, D. Numerosity but Not Texture-Density Discrimination Correlates with Math Ability in Children. Dev. Psychol. 2016, 52, 1206–1216. [Google Scholar] [CrossRef]
- Anobile, G.; Arrighi, R.; Castaldi, E.; Grassi, E.; Pedonese, L.; Moscoso, P.A.M.; Burr, D.C. Spatial but Not Temporal Numerosity Thresholds Correlate with Formal Math Skills in Children. Dev. Psychol. 2018, 54, 458–473. [Google Scholar] [CrossRef]
- Chen, Q.; Li, J. Association between Individual Differences in Non-Symbolic Number Acuity and Math Performance: A Meta-Analysis. Acta Psychol. 2014, 148, 163–172. [Google Scholar] [CrossRef]
- Halberda, J.; Feigenson, L. Developmental Change in the Acuity of the “Number Sense”: The Approximate Number System in 3-, 4-, 5-, and 6-Year-Olds and Adults. Dev. Psychol. 2008, 44, 1457–1465. [Google Scholar] [CrossRef]
- Libertus, M.E.; Feigenson, L.; Halberda, J. Preschool Acuity of the Approximate Number System Correlates with School Math Ability: Approximate Number System and Math Abilities. Dev. Sci. 2011, 14, 1292–1300. [Google Scholar] [CrossRef] [PubMed]
- Piazza, M. Neurocognitive Start-up Tools for Symbolic Number Representations. Trends Cogn. Sci. 2010, 14, 542–551. [Google Scholar] [CrossRef] [PubMed]
- Halberda, J.; Ly, R.; Wilmer, J.B.; Naiman, D.Q.; Germine, L. Number Sense across the Lifespan as Revealed by a Massive Internet-Based Sample. Proc. Natl. Acad. Sci. USA 2012, 109, 11116–11120. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Brannon, E.M. Training the Approximate Number System Improves Math Proficiency. Psychol. Sci. 2013, 24, 2013–2019. [Google Scholar] [CrossRef] [PubMed]
- Hyde, D.C.; Khanum, S.; Spelke, E.S. Brief Non-Symbolic, Approximate Number Practice Enhances Subsequent Exact Symbolic Arithmetic in Children. Cognition 2014, 131, 92–107. [Google Scholar] [CrossRef]
- Butterworth, B. Foundational Numerical Capacities and the Origins of Dyscalculia. Trends Cogn. Sci. 2010, 14, 534–541. [Google Scholar] [CrossRef] [PubMed]
- Piazza, M.; Facoetti, A.; Trussardi, A.N.; Berteletti, I.; Conte, S.; Lucangeli, D.; Dehaene, S.; Zorzi, M. Developmental Trajectory of Number Acuity Reveals a Severe Impairment in Developmental Dyscalculia. Cognition 2010, 116, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Mazzocco, M.M.M.; Feigenson, L.; Halberda, J. Impaired Acuity of the Approximate Number System Underlies Mathematical Learning Disability (Dyscalculia): Impaired Numerical Acuity Contributes to MLD. Child Dev. 2011, 82, 1224–1237. [Google Scholar] [CrossRef]
- Mejias, S.; Grégoire, J.; Noël, M.-P. Numerical Estimation in Adults with and without Developmental Dyscalculia. Learn. Individ. Differ. 2012, 22, 164–170. [Google Scholar] [CrossRef]
- Castaldi, E.; Turi, M.; Gassama, S.; Piazza, M.; Eger, E. Excessive Visual Crowding Effects in Developmental Dyscalculia. J. Vis. 2020, 20, 7. [Google Scholar] [CrossRef]
- Dehaene, S. The Number Sense: How the Mind Creates Mathematics; Oxford University Press: New York, NY, USA, 1997; ISBN 978-0-19-511004-3. [Google Scholar]
- Dehaene, S.; Piazza, M.; Pinel, P.; Cohen, L. Three Parietal Circuits for Number Processing. Cogn. Neuropsychol. 2003, 20, 487–506. [Google Scholar] [CrossRef] [PubMed]
- Arsalidou, M.; Taylor, M.J. Is 2+2=4? Meta-Analyses of Brain Areas Needed for Numbers and Calculations. NeuroImage 2011, 54, 2382–2393. [Google Scholar] [CrossRef]
- Eger, E. Neuronal Foundations of Human Numerical Representations. In Progress in Brain Research; Elsevier: Amsterdam, The Netherlands, 2016; Volume 227, pp. 1–27. ISBN 978-0-444-63698-0. [Google Scholar]
- Castaldi, E.; Vignaud, A.; Eger, E. Mapping Subcomponents of Numerical Cognition in Relation to Functional and Anatomical Landmarks of Human Parietal Cortex. NeuroImage 2020, 221, 117210. [Google Scholar] [CrossRef] [PubMed]
- Iuculano, T. Neurocognitive Accounts of Developmental Dyscalculia and Its Remediation. In Progress in Brain Research; Elsevier: Amsterdam, The Netherlands, 2016; Volume 227, pp. 305–333. ISBN 978-0-444-63698-0. [Google Scholar]
- Iuculano, T.; Menon, V. Development of Mathematical Reasoning. In Stevens’ Handbook of Experimental Psychology and Cognitive Neuroscience; John Wiley & Sons: New York, NY, USA, 2018; pp. 183–222. [Google Scholar]
- Castaldi, E.; Piazza, M.; Iuculano, T. Learning Disabilities: Developmental Dyscalculia. In Handbook of Clinical Neurology; Elsevier: Amsterdam, The Netherlands, 2020; Volume 174, pp. 61–75. ISBN 978-0-444-64148-9. [Google Scholar]
- Slater, A.; Morison, V.; Town, C.; Rose, D. Movement Perception and Identity Constancy in the New-Born Baby. Br. J. Dev. Psychol. 1985, 3, 211–220. [Google Scholar] [CrossRef]
- Lourenco, S.F.; Huttenlocher, J. The Representation of Geometric Cues in Infancy. Infancy 2008, 13, 103–127. [Google Scholar] [CrossRef]
- Dillon, M.R.; Izard, V.; Spelke, E.S. Infants’ Sensitivity to Shape Changes in 2D Visual Forms. Infancy 2020, 25, 618–639. [Google Scholar] [CrossRef]
- Dehaene, S.; Izard, V.; Pica, P.; Spelke, E. Core Knowledge of Geometry in an Amazonian Indigene Group. Science 2006, 311, 381–384. [Google Scholar] [CrossRef]
- Amalric, M.; Wang, L.; Pica, P.; Figueira, S.; Sigman, M.; Dehaene, S. The Language of Geometry: Fast Comprehension of Geometrical Primitives and Rules in Human Adults and Preschoolers. PLoS Comput. Biol. 2017, 13, e1005273. [Google Scholar] [CrossRef]
- Sablé-Meyer, M.; Fagot, J.; Caparos, S.; Van Kerkoerle, T.; Amalric, M.; Dehaene, S. Sensitivity to Geometric Shape Regularity in Humans and Baboons: A Putative Signature of Human Singularity. Proc. Natl. Acad. Sci. USA 2021, 118, e2023123118. [Google Scholar] [CrossRef]
- Castaldi, E.; Arrighi, R.; Cicchini, G.M.; Andolfi, A.; Maduli, G.; Burr, D.C.; Anobile, G. Perception of Geometric Sequences and Numerosity Both Predict Formal Geometric Competence in Primary School Children. Sci. Rep. 2021, 11, 14243. [Google Scholar] [CrossRef]
- Wang, L.; Amalric, M.; Fang, W.; Jiang, X.; Pallier, C.; Figueira, S.; Sigman, M.; Dehaene, S. Representation of Spatial Sequences Using Nested Rules in Human Prefrontal Cortex. NeuroImage 2019, 186, 245–255. [Google Scholar] [CrossRef] [PubMed]
- Amalric, M.; Dehaene, S. Origins of the Brain Networks for Advanced Mathematics in Expert Mathematicians. Proc. Natl. Acad. Sci. USA 2016, 113, 4909–4917. [Google Scholar] [CrossRef] [PubMed]
- Stupp, R.; Weller, M.; Belanger, K.; Bogdahn, U.; Ludwin, S.K.; Lacombe, D.; Mirimanoff, R.O. Radiotherapy plus Concomitant and Adjuvant Temozolomide for Glioblastoma. N. Engl. J. Med. 2005, 352, 987–996. [Google Scholar] [CrossRef] [PubMed]
- Brainard, D.H. The Psychophysics Toolbox. Spat. Vis. 1997, 10, 433–436. [Google Scholar] [CrossRef] [PubMed]
- Efron, B.T.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Medina, J.; Fischer-Baum, S. Single-Case Cognitive Neuropsychology in the Age of Big Data. Cogn. Neuropsychol. 2017, 34, 440–448. [Google Scholar] [CrossRef] [PubMed]
- Al Roumi, F.; Marti, S.; Wang, L.; Amalric, M.; Dehaene, S. Mental Compression of Spatial Sequences in Human Working Memory Using Numerical and Geometrical Primitives. Neuron 2021, 109, 2627–2639.e4. [Google Scholar] [CrossRef] [PubMed]
- Castaldi, E.; Piazza, M.; Dehaene, S.; Vignaud, A.; Eger, E. Attentional Amplification of Neural Codes for Number Independent of Other Quantities along the Dorsal Visual Stream. eLife 2019, 8, e45160. [Google Scholar] [CrossRef]
- Harvey, B.M.; Dumoulin, S.O. A Network of Topographic Numerosity Maps in Human Association Cortex. Nat. Hum. Behav. 2017, 1, 36. [Google Scholar] [CrossRef]
- Llana, T.; Fernandez-Baizan, C.; Mendez-Lopez, M.; Fidalgo, C.; Mendez, M. Functional Near-Infrared Spectroscopy in the Neuropsychological Assessment of Spatial Memory: A Systematic Review. Acta Psychol. 2022, 224, 103525. [Google Scholar] [CrossRef]
- Hofstetter, S.; Cai, Y.; Harvey, B.M.; Dumoulin, S.O. Topographic Maps Representing Haptic Numerosity Reveals Distinct Sensory Representations in Supramodal Networks. Nat. Commun. 2021, 12, 221. [Google Scholar] [CrossRef]
- Eger, E.; Pinel, P.; Dehaene, S.; Kleinschmidt, A. Spatially Invariant Coding of Numerical Information in Functionally Defined Subregions of Human Parietal Cortex. Cereb. Cortex 2015, 25, 1319–1329. [Google Scholar] [CrossRef] [PubMed]
- Bulthé, J.; De Smedt, B.; Op de Beeck, H.P. Format-Dependent Representations of Symbolic and Non-Symbolic Numbers in the Human Cortex as Revealed by Multi-Voxel Pattern Analyses. NeuroImage 2014, 87, 311–322. [Google Scholar] [CrossRef] [PubMed]
- Bulthé, J.; De Smedt, B.; Op de Beeck, H.P. Visual Number Beats Abstract Numerical Magnitude: Format-Dependent Representation of Arabic Digits and Dot Patterns in Human Parietal Cortex. J. Cogn. Neurosci. 2015, 27, 1376–1387. [Google Scholar] [CrossRef] [PubMed]
- DeWind, N.K.; Park, J.; Woldorff, M.G.; Brannon, E.M. Numerical Encoding in Early Visual Cortex. Cortex 2018, 114, 76–89. [Google Scholar] [CrossRef]
- Maldonado Moscoso, P.A.; Greenlee, M.W.; Anobile, G.; Arrighi, R.; Burr, D.C.; Castaldi, E. Groupitizing Modifies Neural Coding of Numerosity. Hum. Brain Mapp. 2022, 43, 915–928. [Google Scholar] [CrossRef]
- Karami, A.; Castaldi, E.; Eger, E.; Piazza, M. Neural Codes for Visual Numerosity Independent of Other Quantities Are Present Both in the Dorsal and in the Ventral Stream of the Human Brain. bioRxiv 2023. [Google Scholar] [CrossRef]
| Patient | Lesion Location and Size (mm) | Pathology | Age | Non-Verbal Reasoning | VSWM | Verbal Reasoning | Verbal WM | Numerosity (CV) | Geometry (Acc) | Geometry (Acc 1st Run) | Geometry (Acc 2nd Run) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | Right occipital lobe (23 × 17 × 20) | G | 55 | 4 | 5 | 9 | 9 | 0.14 | 0.59 | 0.62 | 0.57 |
| S2 | Left temporal gyrus (20 × 20 × 20) | Avm | 53 | 12 7 | 3.5 4 | 4 7 | 5 3 | 0.44 0.46 | 0.55 0.53 | 0.54 0.54 | 0.55 0.53 |
| S3 | Right middle temporal gyrus (9 × 9 × 9) | Ca | 39 | 8 1 | 4 4 | 3 2 | 6 6 | 0.26 0.28 | 0.70 0.72 | 0.67 0.79 | 0.72 0.68 |
| S4 | Left temporal–parietal junction (34 × 27 × 30) | G | 68 | 8 | 4.5 | 7 | 10 | 0.27 | 0.67 | 0.58 | 0.72 |
| S5 | Left AG (22 × 22 × 22) | Ca | 45 | n.a. 8 | 0 0 | 11 0 | n.a. 6 | n.a. 0.17 | 0.11 0.45 | 0.12 0.42 | 0.10 0.48 |
| S6 | Right parietal AG/SMG (34 × 28 × 25) | G | 68 | 7 7 | 4 4.5 | 13 13 | 13 10 | n.a. n.a. | 0.42 0.41 | 0.42 0.38 | 0.42 0.43 |
| S7 | Right parietal (42 × 40 × 30) | G | 55 | 5 | 4 | 3 | 5 | n.a. | 0.27 | 0.25 | 0.27 |
| S8 | Left parietal lobe (30 × 28 × 34) | O | 28 | 5 7 | 6.5 5 | 3 4 | 9 1 | 0.2 n.a. | 0.77 0.75 | 0.71 0.83 | 0.80 0.70 |
| S9 | Left parietal lobe (30 × 27 × 30) | M | 56 | 12 | 4.5 | 8 | 13 | 0.28 | 0.73 | 0.58 | 0.82 |
| S10 | Right frontal lobe (MFG/IFG) (40 × 29 × 36) | G | 64 | 10 | 7.5 | 10 | n.a. | 0.52 | 0.22 | 0.25 | 0.20 |
| S11 | Right SFG (10 × 10 × 10) | M | 46 | 7 | 5 | 10 | 11 | 0.15 | 0.47 | 0.5 | 0.45 |
| S12 | Left IFG (fronto-opercular) (10 × 12 × 10) | G | 54 | 77 | 5 4.5 | 6 5 | 6 5 | 0.18 0.29 | 0.77 0.73 | 0.79 0.75 | 0.75 0.73 |
| S13 | Right frontal lobe (61 × 40 × 40) | A | 58 | 3 | 5 | 8 | 10 | 0.29 | 0.59 | 0.62 | 0.57 |
| S14 | Left frontal lobe (MFG/IFG) (50 × 24 × 20) | Co | 29 | 4 | 4.5 | 1 | 4 | 0.66 | 0.34 | 0.33 | 0.35 |
| S15 | Left frontal lobe (SFG/MFG) (40 × 47 × 40) | G | 72 | 6 | 4.5 | 8 | 10 | 0.49 | 0.41 | 0.38 | 0.42 |
| S16 | Right temporal lobe (MTG) (15 × 20 × 15) | G | 67 | 9 | 5.5 | 12 | 9 | 0.32 | 0.39 | 0.29 | 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castaldi, E.; Bonaudo, C.; Maduli, G.; Anobile, G.; Pedone, A.; Capelli, F.; Arrighi, R.; Della Puppa, A. Neurocognitive Assessment of Mathematics-Related Capacities in Neurosurgical Patients. Brain Sci. 2024, 14, 69. https://doi.org/10.3390/brainsci14010069
Castaldi E, Bonaudo C, Maduli G, Anobile G, Pedone A, Capelli F, Arrighi R, Della Puppa A. Neurocognitive Assessment of Mathematics-Related Capacities in Neurosurgical Patients. Brain Sciences. 2024; 14(1):69. https://doi.org/10.3390/brainsci14010069
Chicago/Turabian StyleCastaldi, Elisa, Camilla Bonaudo, Giuseppe Maduli, Giovanni Anobile, Agnese Pedone, Federico Capelli, Roberto Arrighi, and Alessandro Della Puppa. 2024. "Neurocognitive Assessment of Mathematics-Related Capacities in Neurosurgical Patients" Brain Sciences 14, no. 1: 69. https://doi.org/10.3390/brainsci14010069
APA StyleCastaldi, E., Bonaudo, C., Maduli, G., Anobile, G., Pedone, A., Capelli, F., Arrighi, R., & Della Puppa, A. (2024). Neurocognitive Assessment of Mathematics-Related Capacities in Neurosurgical Patients. Brain Sciences, 14(1), 69. https://doi.org/10.3390/brainsci14010069






