Using Electroencephalogram-Extracted Nonlinear Complexity and Wavelet-Extracted Power Rhythm Features during the Performance of Demanding Cognitive Tasks (Aristotle’s Syllogisms) in Optimally Classifying Patients with Anorexia Nervosa
Abstract
:1. Introduction
1.1. The Main Aim of the Work
1.2. The Structure of Aristotle’s Syllogism and Its Relation to Cognitive Processes—Reasoning Starts with Premises, Which Can Be Statements, Perceptions, or Beliefs
1.3. Literature Review on Related Work
1.3.1. Literature Review on Aspects of Cognitive Function, Linear and Nonlinear EEG Features Extractions in AN
1.3.2. Feature Extraction and Selection Methods Used in EEG Classification Problems
1.3.3. Measurement of Brain’s Responses during Demanding Cognitive Tasks—The α, β, δ, θ Specific Frequency Bands (Rhythms)
1.3.4. EEG Rhythms α, β, δ, θ Specifically in AN
2. Materials and Methods
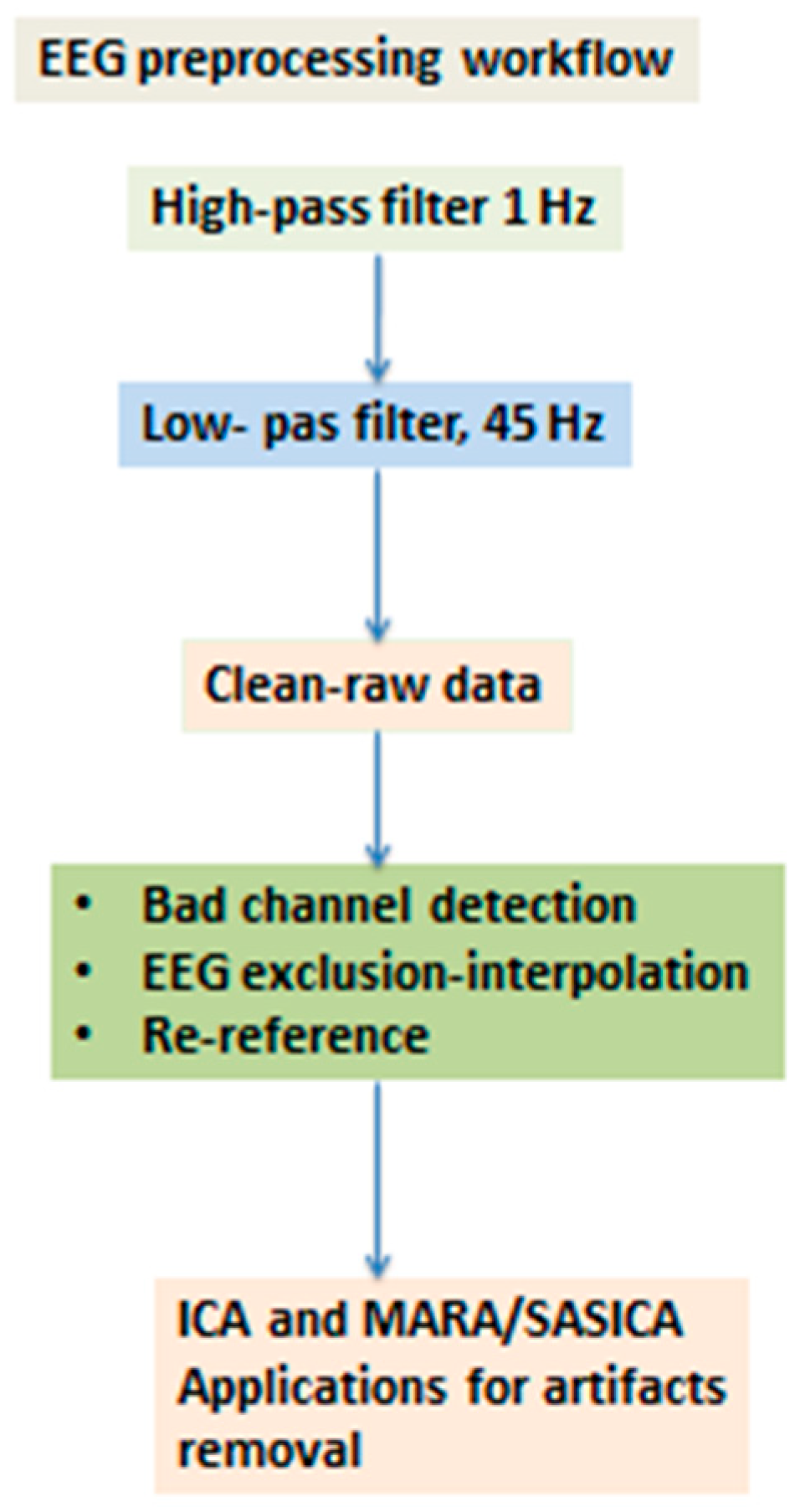
2.1. The Workflow
2.2. Participants and EEG Recordings
2.3. Cognitive Tasks Description in Aristotle’s Experiment
- All men are mortal. (MaP)
- Socrates is a man. (SaM)
- Socrates is mortal. (SaP)
- (All S is P)
- (Some S is P)
2.4. Approximate and Sample Entropy AppEn
2.5. Higuchi Fractal Dimension (HFD) Measure
- (a)
- Let an EEG epoch is s = {s(1), s(2), …, s(N)} of length N, then for each epoch’s sample i, we compute the absolute differences between values s(i) and s(I − k) (i.e., the samples at distance k), for k = 1, …, kmax.
- (b)
- We multiply each absolute difference by a normalization coefficient taking into consideration the different numbers of samples that are contained for each value of k. The coefficient is computed based on the starting point m = 1,…, k as well as on N, the total number of data points of an epoch.
- (c)
- Thus, the Lm(k) is estimated as:
2.5.1. Interpreting and Comparing AppEn and HFD
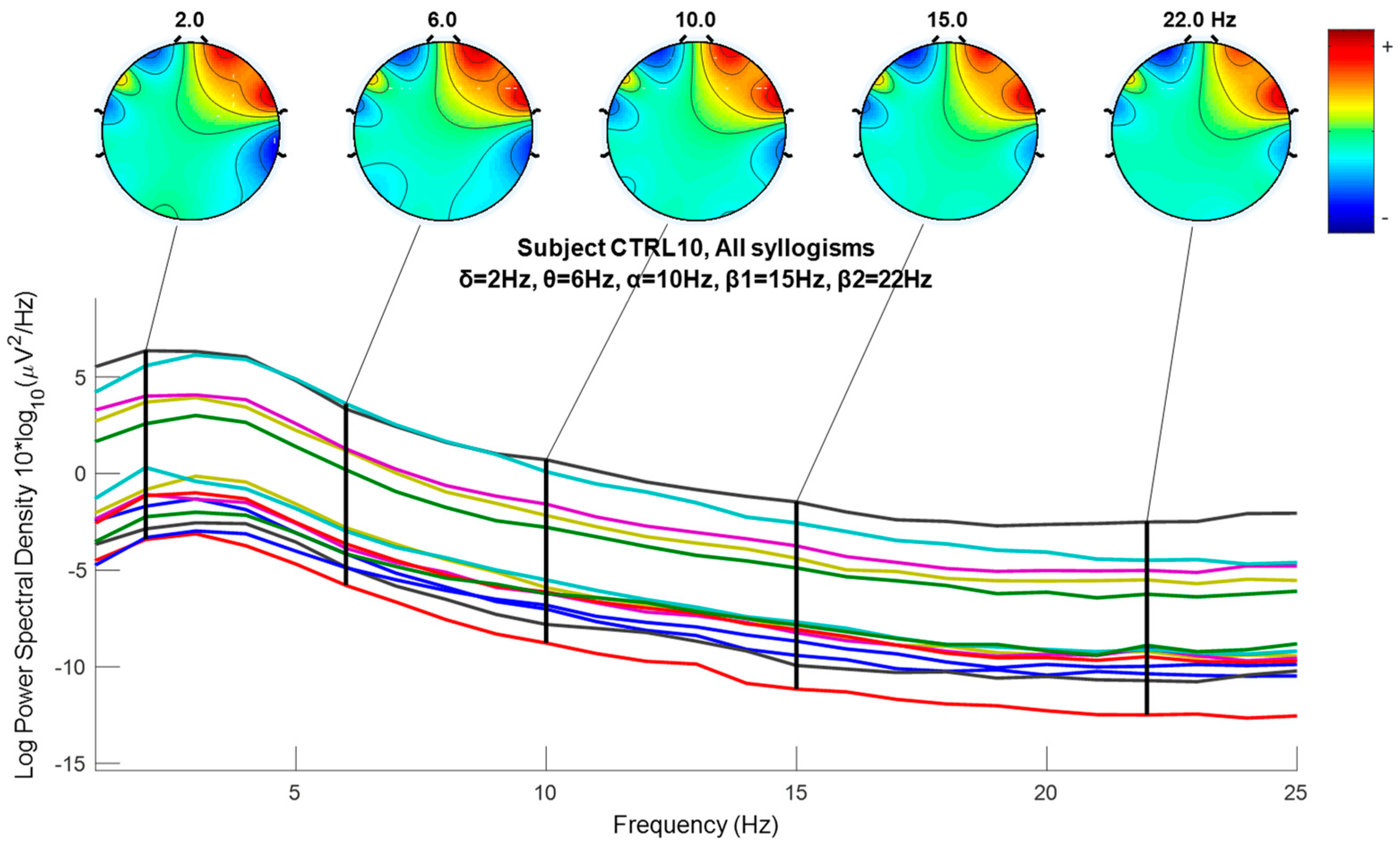
2.6. Wavelet Extracted EEG Power Rhythms (Waves, or Frequency Sub-Bands) as EEG Feature Potential Biomarker
2.7. Classification and Used Classifiers
- -
- Decision trees: Deep tree, medium tree, and shallow tree;
- -
- Support vector machines: Linear SVM, fine Gaussian SVM, medium Gaussian SVM, coarse Gaussian SVM, quadratic SVM, and cubic SVM;
- -
- Nearest neighbor classifiers: Fine kNN, medium kNN, coarse kNN, cosine kNN, cubic kNN, and weighted kNN;
- -
- Ensemble classifiers: Boosted trees (AdaBoost, RUSBoost), bagged trees, subspace kNN, and sub-space discriminant.
Evaluation of Classifier’s Performance
2.8. Assessing the Performance of Classifiers: The ROC (Receiver Operating Curve), the CM (Confusion Matrix), and the Parallel Coordinates (PC) Tools
3. Results
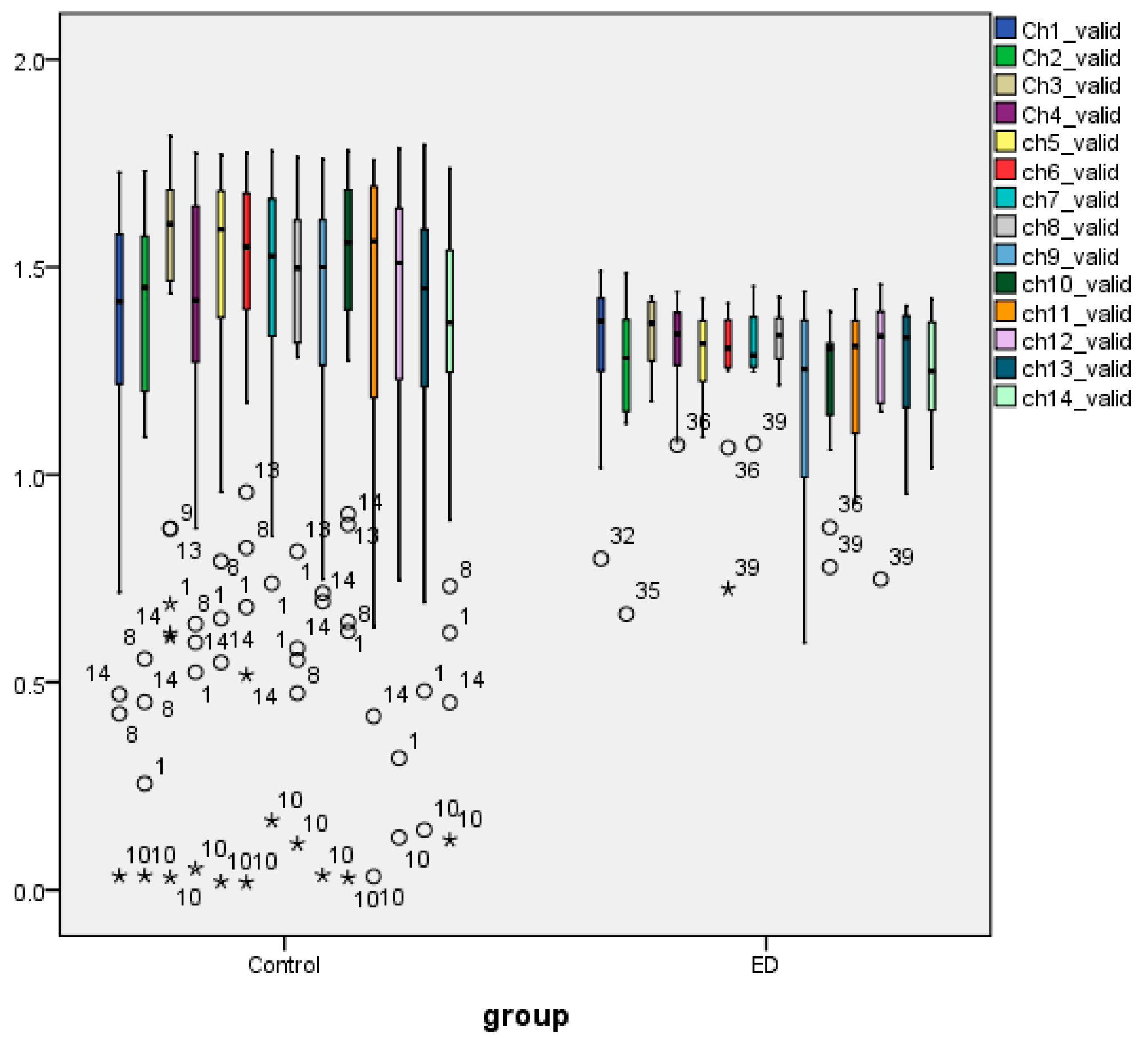
3.1. Statistical Analysis AppEn and HFD Features
3.2. Statistical and Correlational Results of Behavioral Data
3.2.1. Correctness:
3.2.2. Degree of Confidence (DoC):
3.2.3. Correlation Analysis of Behavioral and AppEn/Higuchi FD Values
3.2.4. Correlations of Behavioral Data (% Degree of Confidence-DoC and % Correctness) with AppEn and HFD (Spearman’s Rho, Nonparametric)
3.2.5. Independent Samples t-Tests of Behavioral Data (% Degree of Confidence, DoC and % Correctness)
3.3. MANOVA of Extracted Higuchi Fractal Dimension (HFD) Feature
3.4. Nonparametric Tests of Extracted AppEn Feature
3.5. Nonparametric Tests of EEG Extracted Power Rhythms Feature
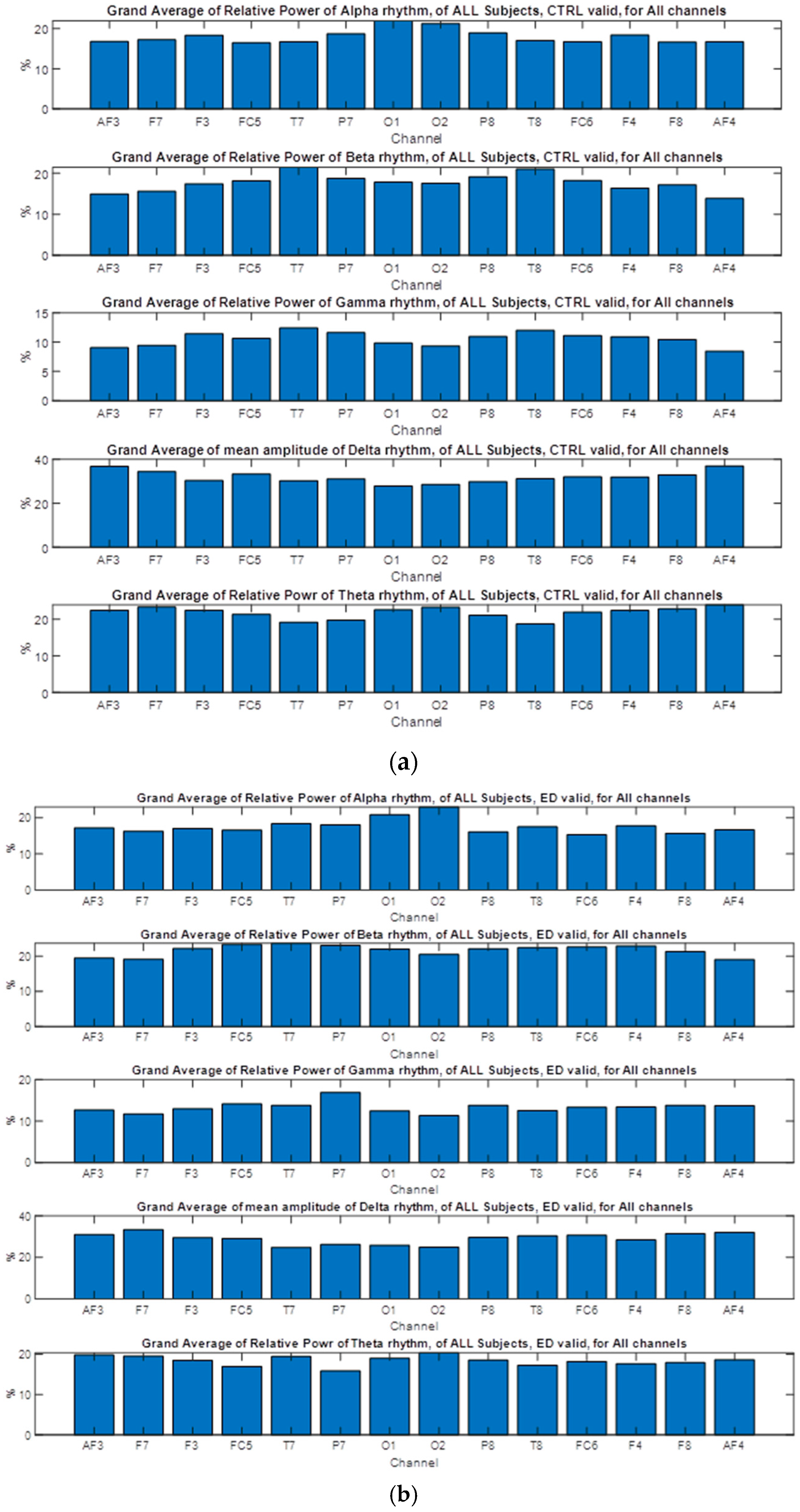
3.6. Nonparametric Tests of EEG Extracted Rhythms–Relative Power
3.6.1. Alpha Relative Power at Channels Level, Valid Syllogism
3.6.2. Alpha Relative Power for Invalid Syllogism
3.6.3. Alpha Relative Power for Paradox Syllogism
3.6.4. Beta Relative Power, Valid Syllogism
3.6.5. Beta Relative Power, Invalid and Paradox Syllogisms
3.6.6. Gamma Relative Power
3.6.7. Delta Relative Power
3.6.8. Theta Relative Power
- -
- No significant group effects were found for the Alpha AGMRP, in all syllogisms;
- -
- Significant group effects were found for the Beta AGMRP, in valid syllogisms;
- -
- No significant group effects were found for the Delta AGMRP, in all syllogisms;
- -
- No significant group effects were found for the Gamma AGMRP, in all syllogisms;
- -
- Significant group effects were found for the Theta AGMRP, in valid syllogisms.
3.7. Results of Classification
3.7.1. Classification Based on Higuchi and AppEn Features
3.7.2. Classification Based on the Extracted Features of Amplitude of EEG Rhythms
3.7.3. Classification Results of Relative Power of EEG Rhythms
4. Discussion
4.1. The findings from Our Study
4.2. The Contribution of Our Findings in the Existing Literature
5. Conclusions
6. Limitations
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| (a) | |||||
| Extracted Approximate Entropy (AppEn) Descriptive Features (Number of Data Analyzed: 2(Groups) × 31(Subjects) × 14(Channels) = 868) | Target Feature | ||||
| EEG Channels (electrodes) | Group | ||||
| Participant | Ch-1 | Ch-2 | … | Ch-14 | |
| CON-1 | AppEn(1,1) | AppEn(1,2) | … | AppEn(1,14) | CON |
| CON-2 | AppEn(2,1) | AppEn(2,2) | … | AppEn(2,14) | CON |
| … | … | … | … | ||
| CON-30 | AppEn(21,1) | AppEn(21,2) | … | AppEn(21,14) | CON |
| ED-1 | AppEn(1,1) | AppEn(1,2) | … | AppEn(1,14) | ED |
| ED-2 | AppEn(2,1) | AppEn(2,2) | … | AppEn(2,14) | ED |
| … | … | … | … | … | … |
| ED-31 | AppEn(21,1) | AppEn(21,2) | … | AppEn(21,14) | ED |
| (b) | |||||
| Extracted Higuchi Fractal Dimension (HFD) Descriptive Features (Number of data analyzed: 2(groups) × 31(subjects) × 14(channels) = 868) | Target Feature | ||||
| EEG Channels (electrodes) | Group | ||||
| Participant | Ch-1 | Ch-2 | … | Ch-14 | |
| CON-1 | HFD(1,1) | HFD(1,2) | … | HFD(1,14) | CON |
| CON-2 | HFD(2,1) | HFD(2,2) | … | HFD(2,14) | CON |
| … | … | … | … | ||
| CON-21 | HFD(21,1) | HFD(21,2) | … | HFD(21,14) | CON |
| ED-1 | HFD(1,1) | HFD(1,2) | … | HFD(1,14) | ED |
| ED-2 | HFD(2,1) | HFD(2,2) | … | HFD(2,14) | ED |
| … | … | … | … | … | |
| ED-21 | HFD(21,1) | HFD(21,2) | … | HFD(21,14) | ED |
| (c) | |||||
| Extracted EEG Rhythms (alpha, beta, gamma, delta, theta) Descriptive Features Number of data analyzed: 2(groups) × 31(subjects) × 4(Rhythms) × 14(channels) = 3472 | Target Feature | ||||
| EEG Channels (electrodes) | Group | ||||
| Participant | Ch-1 | Ch-2 | … | Ch-14 | |
| CON-1 | α(1,1) β(1,1) δ(1,1) θ(1,1) | α(1,2) β(1,2) δ(1,2) θ(1,2) | … | α(1,14) β(1,14) δ(1,14) θ(1,14) | CON |
| CON-2 | α(2,1) β(2,1) δ(2,1) θ(2,1) | α(2,2) β(2,2) δ(2,2) θ(2,2) | … | α(2,14) β(2,14) δ(2,14) θ(2,14) | CON |
| … | … | … | … | ||
| CON-31 | α(21,1) β(21,1) δ(21,1) θ(21,1) | α(21,2) β(21,2) δ(21,2) θ(21,2) | … | α(21,14) β(21,14) δ(21,14) θ(21,14) | CON |
| ED-1 | α(1,1) β(1, 1) δ(1, 1) θ(1, 1) | α(1,2) β(1,2) δ(1,2) θ(1,2) | … | α(1,14) β(1,14) δ(1,14) θ(1,14) | ED |
| ED-2 | α(2, 1) β(2, 1) δ(2, 1) θ(2, 1) | α(2,2) β(2,2) δ(2,2) θ(2,2) | … | α(2,14) β(2,14) δ(2,14) θ(2,14) | ED |
| … | … | … | … | … | |
| ED-31 | α(21,1) β(21,1) δ(21,1) θ(21,1) | α(21,2) β(21,2) δ(21,2) θ(21,2) | … | α(21,14) β(21,14) δ(21,14) θ(21,14) | ED |
| Brain Rhythm (Wave) | Frequency (HZ) | Amplitude (μV) | Brain Region | Associated Cognitive Activity |
|---|---|---|---|---|
| Delta (δ) | f <4 | 20–200 | Frontal Temporal Occipital | Waking state Deep sleep Sleeping adults Normal in infants |
| Theta (θ) | 4 ≤ f ≤ 7 | 20–100 | Temporal Occipital | -Locomotion -Sensory information -Consciousness slips towards drowsiness -unconscious material -deep meditation -creative inspiration -emotional studies -drowsiness -spatial memory processes Common in children and young adults than in older adults |
| Alpha (α) | 8 ≤ f ≤ 12 | 20–60 | Occipital | -mental fatigue -cognitive disorders -no attention condition -during dreaming -awake but relaxed -attenuation as signal of visual activity -semantic memory processes to any type of task -during visually presented simulation |
| Beta (β) | 13 ≤ f ≤ 29 | 2–30 | Frontal Central Parietal | -active attention -active thinking -focus on external world -solving concrete problems -panic states -is found in normal adults -drowsiness -sensory motor area -light sleep -REM sleep |
| Gamma (γ) | 30 ≤ f ≤ 64 | -Anterior temporal -posterial temporal -occipital sites | -Prominent during higher focus and concentration -imbalanced excitatory/inhibitory Activity in autism group |
References
- Papageorgiou, C.; Stachtea, X.; Papageorgiou, P.; Alexandridis, A.T.; Tsaltas, E.; Angelopoulos, E. Aristotle Meets Zeno: Psychophysiological Evidence. PLoS ONE 2016, 11, e0168067. [Google Scholar] [CrossRef] [PubMed]
- Hayes, B.K.; Heit, E. Inductive reasoning 2.0. WIREs Cogn. Sci. 2018, 9, e1459. [Google Scholar] [CrossRef] [PubMed]
- Brisson, J.; Markovits, H. Reasoning strategies and semantic memory effects in deductive reasoning. Mem. Cogn. 2020, 48, 920–930. [Google Scholar] [CrossRef]
- Sloman, S.A. The empirical case for two systems of reasoning. Psychol. Bull. 1996, 119, 3–22. [Google Scholar] [CrossRef]
- Janssen, E.M.; Velinga, S.B.; De Neys, W.; Van Gog, T. Recognizing biased reasoning: Conflict detection during decision-making and decision-evaluation. Acta Psychol. 2021, 217, 103322. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Rabavilas, A.D.; Stachtea, X.; Giannakakis, G.A.; Kyprianou, M.; Papadimitriou, G.N.; Stefanis, C.N. The interference of introversion-extraversion and depressive symptomatology with reasoning performance: A behavioural study. J. Psycholinguist. Res. 2012, 41, 129–139. [Google Scholar] [CrossRef] [PubMed]
- Lord, B.; John, A. Evaluating EEG complexity metrics as biomarkers for depression. Psychophysiology 2023, 60, e14274. [Google Scholar] [CrossRef]
- Jhonson-Laird, P.N.; Bara, B.G. Syllogistic inference. Cognition 1984, 16, 1–61. [Google Scholar] [CrossRef]
- Baddeley, A. Working Memory, Thought and Action; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Hattori, M. Probabilistic representation in syllogistic reasoning: A theory to integrate mental models and heuristics. Cognition 2016, 157, 296–320. [Google Scholar] [CrossRef]
- Halford, G.S.; Cowan, N.; Andrews, G. Separating cognitive capacity from knowledge: A new hypothesis. Trends Cognit. Sci. 2007, 11, 236–242. [Google Scholar] [CrossRef]
- Smith, R., Translator; Aristotle’s Prior Analytics; Hacket Publishing Company: Indianapolis, IN, USA; Cambridge, UK, 1989. [Google Scholar]
- Owen, O.F.; Kenyon, F.G.; Peters, F.H., Translators; Aristotle’s Organon; Complete Edition; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- De Neys, W. Dual processing in reasoning: Two systems but one reasoned. Psychol. Sci. 2006, 17, 428–433. [Google Scholar] [CrossRef] [PubMed]
- Goel, V. Anatomy of deductive reasoning. Trends Cognit. Sci. 2007, 11, 435–441. [Google Scholar] [CrossRef] [PubMed]
- Williams, C.C.; Kappen, M.; Hassall, C.D.; Wright, B.; Krigolson, O.E. Thinking theta and alpha: Mechanisms of intuitive and analytical reasoning. Neuroimage 2019, 189, 574–580. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, C.; Papageorgiou, P.; Stachtea, X.; Alexandridis, A.T.; Margariti, M.; Rizos, E.; Chrousos, G.; Tsaltas, E. Aristotelian vs. Paradoxical Reasoning Elicit Distinct N400 ERPs. Int. J. Clin. Med. Res. 2018, 5, 35–43. [Google Scholar]
- Papaodysseus, C.; Zannos, S.; Giannopoulos, F.; Arabadjis, D.; Rousopoulos, P.; Stachtea, X.; Papageorgiou, C. A new approach for the classification of event related potentials for valid and paradox reasoning. Biocybernet. Biomed. Eng. 2016, 36, 292–301. [Google Scholar] [CrossRef]
- Belekou, A.; Papageorgiou, C.; Karavasilis, E.; Tsaltas, E.; Kelekis, N.; Klein, C.; Smyrnis, N. Paradoxical Reasoning: An fMRI Study. Front. Psychol. 2022, 13, 850491. [Google Scholar] [CrossRef] [PubMed]
- Papaioannou, A.; Kalantzi, E.; Papageorgiou, C.; Korombili, K.; Bokou, A.; Pehlivanidis, A.; Papageorgiou, C.; Papaioannou, G. Differences in Performance of ASD and ADHD Subjects, Facing Cognitive Loads in an Innovative Reasoning Experiment. Brain Sci. 2021, 11, 1531. [Google Scholar] [CrossRef] [PubMed]
- Papaioannou, A.; Kalantzi, E.; Papageorgiou, C.; Korombili, K.; Bokou, A.; Pehlivanidis, A.; Papageorgiou, C.; Papaioannou, G. Complexity analysis of the brain activity in Autism Spectrum Disorder (ASD) and Attention Deficit Hyperactivity Disorder (ADHD) due to cognitive loads/demands induced by Aristotle’s type of syllogism/reasoning. A Power Spectral Density and multiscale entropy (MSE) analysis. Heliyon 2021, 7, e07984. [Google Scholar] [CrossRef]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders, 5th ed.; DSM-5; American Psychiatric Publishing: Arlington, VA, USA, 2013. [Google Scholar]
- Su, T.; Gong, J.; Tang, G.; Qiu, S.; Chen, P.; Chen, G.; Wang, J.; Huang, L.; Wang, Y. Structural and functional brain alterations in anorexia nervosa: A multimodal meta-analysis of neuroimaging studies. Human Brain Mapping 2021, 42, 5154–5169. [Google Scholar] [CrossRef]
- Brand-Gothelf, A.; Leor, S.; Apter, A.; Fennig, S. The impact of comorbid depressive and anxiety disorders on severity of anorexia nervosa in adolescent girls. J. Nerv. Ment. Dis. 2014, 202, 759–762. [Google Scholar] [CrossRef]
- Hatch, A.; Madden, S.; Kohn, M.R.; Clarke, S.; Touyz, S.; Gordon, E.; Williams, L.M. In first presentation adolescent anorexia nervosa, do cognitive markers of underweight status change with weight gain following a refeeding intervention? Int. J. Eat. Disord. 2010, 43, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Keifer, E.; Duff, K.; Beglinger, L.J.; Barstow, E.; Andersen, A.; Moser, D.J. Predictors of neuropsychological recovery in treatment for anorexia nervosa. Eat. Disord. 2010, 18, 302–317. [Google Scholar] [CrossRef] [PubMed]
- Lozano-Serra, E.; Andres-Perpiña, S.; Lázaro-García, L.; Castro-Fornieles, J. Adolescent anorexia nervosa: Cognitive performance after weight recovery. J. Psychosom. Res. 2014, 76, 6–11. [Google Scholar] [CrossRef] [PubMed]
- Moser, D.J.; Benjamin, M.L.; Bayless, J.D.; McDowell, B.D.; Paulsen, J.S.; Bowers, W.A.; Arndt, S.; Andersen, A.E. Neuropsychological functioning pretreatment and posttreatment in an inpatient eating disorders program. Int. J. Eat. Disord. 2003, 33, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Steinglass, J.E.; Dalack, M.; Foerde, K. The Promise of Neurobiological Research in Anorexia Nervosa. Curr. Opin. Psychiatry 2019, 32, 491–497. [Google Scholar] [CrossRef] [PubMed]
- Sato, Y.; Saito, N.; Utsumi, A.; Aizawa, E.; Shoji, T.; Izumiyama, M.; Mushiake, H.; Hongo, M.; Fukudo, S. Neural Basis of Impaired Cognitive Flexibility in Patients with Anorexia Nervosa. PLoS ONE 2013, 8, e61108. [Google Scholar] [CrossRef] [PubMed]
- Fuglset, T.S. Set-shifting, central coherence and decision-making in individuals recovered from anorexia nervosa: A systematic review. J. Eat. Disord. 2019, 7, 22. [Google Scholar] [CrossRef]
- Pietrini, F.; Castellini, G.; Ricca, V.; Polito, C.; Pupi, A.; Faravelli, C. Functional neuroimaging in anorexia nervosa: A clinical approach. Eur. Psychiatry 2011, 26, 176–182. [Google Scholar] [CrossRef]
- Kaufmann, L.K.; Hänggi, J.; Jäncke, L.; Baur, V.; Piccirelli, M.; Kollias, S.; Schnyder, U.; Martin-Soelch, C.; Milos, G. Age influences structural brain restoration during weight gain therapy in anorexia nervosa. Transnatl. Psychiatry 2020, 10, 126. [Google Scholar] [CrossRef]
- Mallorquí-Bagué, N.; Lozano-Madrid, M.; Testa, G.; Vintró-Alcaraz, C.; Sánchez, I.; Riesco, N.; Perales, J.C.; Navas, J.F.; Martínez-Zalacaín, I.; Megías, A.; et al. Clinical and Neurophysiological Correlates of Emotion and Food Craving Regulation in Patients with Anorexia Nervosa. J. Clin. Med. 2020, 9, 960. [Google Scholar] [CrossRef]
- Rylander, M.; Taylor, G.; Bennett, S.; Pierce, C.; Keniston, A.; Mehler, P.S. Evaluation of cognitive function in patients with severe anorexia nervosa before and after medical stabilization. J. Eat. Disord. 2020, 8, 35. [Google Scholar] [CrossRef] [PubMed]
- Seidel, M.; Brooker, H.; Lauenborg, K.; Wesnes, K.; Sjögren, M. Cognitive Function in Adults with Enduring Anorexia Nervosa. Nutrients 2021, 13, 859. [Google Scholar] [CrossRef] [PubMed]
- Tenconi, E.; Meregalli, V.; Buffa, A.; Collantoni, E.; Cavallaro, R.; Meneguzzo, P.; Favaro, A. Belief Inflexibility and Cognitive Bias in Anorexia Nervosa—The Role of the Bias against Disconfirmatory Evidence and Its Clinical and Neuropsychological Correlates. J. Clin. Med. 2023, 12, 1746. [Google Scholar] [CrossRef] [PubMed]
- Southgate, L.; Tchanturia, K.; Treasure, J. Information processing bias in anorexia nervosa. Psychiatry Res. 2008, 160, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Brockmeyer, T.; Febry, H.; Leiteritz-Rausch, A.; Wünsch-Leiteritz, W.; Leiteritz, A.; Friederich, H.C. Cognitive flexibility, central coherence, and quality of life in anorexia nervosa. J. Eat. Disord. 2022, 10, 22. [Google Scholar] [CrossRef] [PubMed]
- Collantoni, E.; Michelon, S.; Tenconi, E.; Degortes, D.; Titton, F.; Manara, R.; Clementi, M.; Pinato, C.; Forzan, M.; Cassina, M.; et al. Functional connectivity correlates of response inhibition impairment in anorexia nervosa. Psychiatry Res. Neuroimaging 2016, 247, 9–16. [Google Scholar] [CrossRef]
- Yue, L.; Tang, Y.; Kang, Q.; Wang, Q.; Wang, J.; Chen, J. Deficits in response inhibition on varied levels of demand load in anorexia nervosa: An event-related potentials study. Eat. Weight. Disord. 2020, 25, 231–240. [Google Scholar] [CrossRef]
- Kaye, W.H.; Fudge, J.L.; Paulus, M. New insights into symptoms and neurocircuit function of anorexia nervosa. Nat. Rev.-Neurosci. 2009, 10, 573–584. [Google Scholar] [CrossRef]
- Connan, F.; Campbell, I.; Katzman, M.; Lightman, S.; Treasure, J. A neurodevelopmental model for anorexia nervosa. Physiol. Behav. 2003, 79, 13–24. [Google Scholar] [CrossRef]
- Acharya, U.R.; Sree, S.V.; Alvin, A.P.C.; Yanti, R.; Suri, J.S. Application of non-linear and wavelet-based features for the automated identification of epileptic EEG signals. Int. J. Neural Syst. 2012, 22, 1250002. [Google Scholar] [CrossRef]
- Iasemidis, L.D.; Sackellares, J.C. The temporal evolution of the largest Lyapunov exponent on the human epileptic cortex. In Measuring Chaos in the Human Brain; Duke, D.W., Pritchard, W.S., Eds.; World Scientific: Singapore, 1991; pp. 49–82. [Google Scholar]
- Iasemidis, L.D.; Sackellares, J.C. Chaos theory and epilepsy. Neuroscientist 1996, 2, 118–126. [Google Scholar] [CrossRef]
- Güler, I.; Übeyli, E.D. Multiclass support vector machines for EEG signals classification. IEEE Trans. Inf. Technol. Biomed. 2007, 11, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Güler, N.F.; Übeyli, E.D.; Güler, I. Recurrent neural networks employing Lyapunov exponents for EEG signals classification. Exp. Syst. Appl. 2005, 29, 506–514. [Google Scholar] [CrossRef]
- Srinivasan, V.; Eswaran, C.; Sriraam, N. Approximate entropy-based epileptic EEG detection using artificial neural networks. IEEE Trans. Inf. Technol. Biomed. 2007, 11, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Vidaurre, C.; Krämer, N.; Blankertz, B.; Schlögl, A. Time domain parameters as a feature for EEG-based brain-computer interfaces. Neural Netw. 2009, 22, 1313–1319. [Google Scholar] [CrossRef]
- Lerner, D.E. Monitoring changing dynamics with correlation integrals: Case study of an epileptic seizure. Phys. D 1996, 97, 563–576. [Google Scholar] [CrossRef]
- Higuchi, T. Approach to an irregular time-series on the basis of the fractal theory. Phys. D 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Accardo, A.; Affinito, M.; Carrozzi, M.; Bouquet, F. Use of the fractal dimension for the analysis of electroencephalographic time series. Biol. Cybern. 1997, 77, 339–350. [Google Scholar]
- Finotello, F.; Scarpa, F.; Zanon, M. EEG signal features extraction based on fractal dimension. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 4154–4157. [Google Scholar]
- Hurst, H.E. Long-term storage of reservoirs: An experimental study. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Taghizadeh-Sarabi, M.; Daliri, M.R.; Niksirat, K.S. Decoding objects of basic categories from electroencephalographic signals using wavelet transform and support vector machines. Brain Topograph. 2015, 28, 33–46. [Google Scholar] [CrossRef]
- Hjorth, B. EEG analysis based on time domain properties. Electroencephalogr. Clin. Neurophysiol. 1970, 29, 306–310. [Google Scholar] [CrossRef] [PubMed]
- Kaushik, G.; Gaur, P.; Sharma, R.R.; Pachori, R.B. EEG signal seizure detection focused on Hjorth parameters from tunable Q-wavelet sub-bands. Biomed. Signal Process. Control 2022, 76, 103645. [Google Scholar] [CrossRef]
- Jelinek, H.F.; Cornforth, D.J.; Tarvainen, M.P.; Spence, I.; Russell, J. Decreased Sample Entropy to Orthostatic Challenge in Anorexia Nervosa. J. Metab. Synd. 2017, 6, 226. [Google Scholar] [CrossRef]
- De la Cruz, F.; Schumann, A.; Suttkus, S.; Helbing, N.; Bär, K.J. Dynamic changes in the central autonomic network of patients with anorexia nervosa. Eur. J. Neurosci. 2023, 57, 1597–1610. [Google Scholar] [CrossRef] [PubMed]
- Ferenets, R.; Lipping, T.; Anier, A.; Ville Jäntti, V.; Melto, S.; Hovilehto, S. Comparison of Entropy and Complexity Measures for the Assessment of Depth of Sedation. IEEE Trans. Biomed. Eng. 2006, 53, 1067–1077. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, B.; Amirfattahi, R. Comparison of Correlation Dimension and Fractal Dimension in Estimating BIS index. Wirel. Sens. Netw. 2010, 2, 67–73. [Google Scholar] [CrossRef]
- Van Gog, T.; Paas, F.; van Merriënboer, J.J.G. Effects of processoriented worked examples on troubleshooting transfer performance. Learn. Instruct. 2006, 16, 154–164. [Google Scholar] [CrossRef]
- Sweller, J. Element interactivity and intrinsic, extraneous, and germane cognitive load. Edu. Psychol. Rev. 2010, 22, 123–138. [Google Scholar] [CrossRef]
- Karkare, S.; Saha, G.; Bhattacharya, J. Investigating long-range correlation properties in EEG during complex cognitive tasks. Chaos Solitons Fractals 2009, 42, 2067–2073. [Google Scholar] [CrossRef]
- Amin, H.U.; Malik, A.S.; Badruddin, N.; Kamel, N.; Hussain, M. Effects of Stereoscopic 3D Display Technology on Event-related Potentials (ERPs). In Proceedings of the 7th International IEEE EMBS Conference on Neural Engineering, Montpellier, France, 22–24 April 2015; pp. 1084–1087. [Google Scholar]
- Stockwell, R.G. Why use the S transform? In Pseudo-Differential Operators: Partial Differential Equations and Time-Frequency Analysis; Fields Institute Communications Series; American Mathematical Society: Providence RI, USA, 2007; Volume 52, pp. 279–309. [Google Scholar]
- Hariharan, M.; Vijean, V.; Sindhu, R.; Divakar, P.; Saidatul, A.; Yaacob, S. Classification of mental tasks using stockwell transform. Comput. Elect. Eng. 2014, 40, 1741–1749. [Google Scholar] [CrossRef]
- Noshadi, S.; Abootalebi, V.; Sadeghi, M.T.; Shahvazian, M.S. Selection of an efficient feature space for EEG-based mental task discrimination. Biocybern. Biomed. Eng. 2014, 34, 159–168. [Google Scholar] [CrossRef]
- Lena, S.M.; Fiocco, A.J.; Leyenaar, J.K. The role of cognitive deficits in the development of eating disorders. Neuropsychol. Rev. 2004, 14, 99–113. [Google Scholar] [CrossRef]
- Duchesne, M.; Mattos, P.; Fontenelle, L.F.; Veiga, H.; Rizo, L.; Appolinario, J.C. Neuropsychology of eating disorders: A systematic review of the literature. Rev. Bras. Psiquiatr. 2004, 26, 107–117. [Google Scholar] [CrossRef]
- Vitousek, K.; Manke, F. Personality variables and disorders in anorexia nervosa and bulimia nervosa. J. Abnorm. Psychol. 1994, 103, 137–147. [Google Scholar] [CrossRef]
- Polivy, J.; Herman, C.P. Causes of eating disorders. Annu. Rev. Psychol. 2002, 53, 187–213. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Brockmeyer, T.; Hartmann, M.; Skunde, M.; Herzog, W.; Friederich, H.C. Set-shifting ability across the spectrum of eating disorders and in overweight and obesity: A systematic review and meta-analysis. Psychol. Med. 2014, 44, 3365–3385. [Google Scholar] [CrossRef] [PubMed]
- Lang, K.; Lopez, C.; Stahl, D.; Tchanturia, K.; Treasure, J. Central coherence in eating disorders: An updated systematic review and meta-analysis. World J. Biol. Psychiatry 2014, 15, 586–598. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.; Tchanturia, K.; Stahl, D.; Treasure, J. Central coherence in eating disorders: A systematic review. Psychol. Med. 2008, 38, 1393–1404. [Google Scholar] [CrossRef]
- Grebb, J.A.; Yingling, C.D.; Reus, V.I. Electrophysiologic abnormalities in patients with eating disorders. Compr. Psychiatry 1984, 25, 216–224. [Google Scholar] [CrossRef]
- Crisp, A.H.; Fenton, G.W.; Scotton, L. A controlled study of the EEG in anorexia nervosa. Br. J. Psychiatry 1968, 114, 1149–1160. [Google Scholar] [CrossRef]
- Rodriguez, G.; Babiloni, C.; Brugnolo, A.; Del Percio, C.; Cerro, F.; Gabrielli, F.; Girtler, N.; Nobili, F.; Murialdo, G.; Rossini, P.M.; et al. Cortical sources of awake scalp EEG in eating disorders. Clin. Neurophysiol. 2007, 118, 1213–1222. [Google Scholar] [CrossRef]
- Hatch, A.; Madden, S.; Kohn, M.R.; Clarke, S.; Touyz, S.; Gordon, E.; Williams, L.M. EEG in adolescent anorexia nervosa: Impact of refeeding and weight gain. Int. J. Eat. Disord. 2011, 44, 65–75. [Google Scholar] [CrossRef]
- Toth, E.; Tury, F.; Gati, A.; Weisz, J.; Kondakor, I.; Molnar, M. Effects of sweet and bitter gustatory stimuli in anorexia nervosa on EEG frequency spectra. Int. J. Psychophysiol. 2004, 52, 285–290. [Google Scholar] [CrossRef] [PubMed]
- Hestad, K.A.; Wieder, S.; Nilsen, C.B.; Indredavik, M.S.; Sand, S. Increased frontal electroencephalogram theta amplitude in patients with anorexia nervosa compared to healthy controls. Neuropsychiatr. Dis. Treat. 2016, 12, 2419–2423. [Google Scholar] [CrossRef] [PubMed]
- Debener, S.; Minow, F.; Emkes, R.; Gandras, K.; de Vos, M. How about taking a low-cost, small, and wireless EEG for a walk? Psychophysiology 2012, 49, 1617–1621. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, C.; Manios, E.; Tsaltas, E.; Koroboki, E.; Alevizaki, M.; Angelopoulos, E.; Dimopoulos, M.; Papageorgiou, C.; Zakopoulos, N. Brain Oscillations Elicited by the Cold Pressor Test: A Putative Index of Untreated Essential Hypertension. Int. J. Hypertens. 2017, 2017, 7247514. [Google Scholar] [CrossRef] [PubMed]
- Delorme, A.; Makeig, S. EEGLAB: An open-source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Winkler, I.; Haufe, S.; Tangerman, M. Automatic Classification of Artifactual ICA Components for Artifact Removal in EEG Signals. Behav. Brain Funct. 2011, 7, 30. [Google Scholar] [CrossRef]
- Chaumon, M.; Bishop, D.V.M.; Busch, N.A. A practical guide to the selection of independent components of the electroencephalogram for artifact correction. J. Neurosci. Methods 2015, 250, 47–63. [Google Scholar] [CrossRef]
- Ramirez, R.; Palencia-Lefler, M.; Giraldo, S.; Evamvakousis, Z. Musical neurofeedback for treating depression in elderly people. Front. Neurosci. 2015, 9, 354. [Google Scholar] [CrossRef]
- Delvin, K. The Language of Mathematics. Making the Invisible Visible; W. H. Freeman & Company: New York, NY, USA, 1998. [Google Scholar]
- Evans, J.S.B.T. In two minds: Dual-process accounts of reasoning. Trends Cogn. Sci. 2003, 7, 454–459. [Google Scholar] [CrossRef]
- Evans, J.S. Logic and human reasoning; An assessment of the deduction paradigm. Psychol. Bull. 2002, 128, 978–996. [Google Scholar] [CrossRef] [PubMed]
- Stephens, R.G.; Dunn, J.C.; Hayes, B.K.; Kalish, M.L. A test of two processes: The effect of training on deductive and inductive reasoning. Cognition 2020, 199, 104223. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Stachtea, X.; Papageorgiou, P.; Alexandridis, A.T.; Makris, G.; Chrousos, G.; Kosteletos, G. Gender-dependent variations in optical illusions: Evidence from N400 waveforms. Physiol. Meas. 2020, 41, 095006. [Google Scholar] [CrossRef] [PubMed]
- Bradley, M.M.; Lang, P.J. Measuring emotion: The self-assessment manikin and the semantic differential. J. Behav. Ther. Exp. Psychiatry 1994, 25, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [PubMed]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Characterization of strange attractors. Phys. Rev. Lett. 1983, 50, 346–349. [Google Scholar] [CrossRef]
- Klinkenberg, B. A review of methods used to determine the fractal dimension of linear features. Math. Geol. 1994, 26, 23–46. [Google Scholar] [CrossRef]
- Gowri, M.; Raj, C. EEG feature extraction using Daubechies wavelet and classification using neural network. Int. J. Pure Appl. Math. 2018, 119, 2585–2597. [Google Scholar]
- Jacob, J.E.; Nair, G.K.; Iype, T.; Cherian, A. Diagnosis of encephalopathy based on energies of EEG sub bands using discrete wavelet transform and support vector machine. Neurol. Res. Int. 2018, 1, 1613456. [Google Scholar]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Britton, J.W.; Frey, L.C.; Hopp, J.L.; Korb, P.; Koubeissi, M.Z.; Lievens, W.E.; Pestana-Knight, E.M.; Louis, E.K. Electroencephalography (EEG): An Introductory Text and Atlas of Normal and Abnormal Findings in Adults, Children, and Infants; American Epilepsy Society: Chicago, IL, USA, 2016. [Google Scholar]
- Jolliffe, J.L. Principal Component Analysis, 2nd ed.; Springer: New York, NY, USA, 2002; pp. 10–150. [Google Scholar]
- John, G.H.; Langley, P. Estimating Continuous Distributions in Bayesian Classifiers. arXiv 2013, arXiv:1302.4964. [Google Scholar]
- Kelleher, J.D.; Mac Namee, B.; D’Arcy, A. Fundamentals of Machine Learning for Predictive Data Analytics: Algorithms, Worked Examples, and Case Studies; The MIT press: Cambridge, MA, USA, 2015. [Google Scholar]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, MS, USA, 1995; pp. 116–160. [Google Scholar]
- Azuaje, F.; Witten, I.H.; Frank, E. Review of “Data Mining: Practical Learning Tools and Techniques” by Witten and Frank. Biomed. Eng. 2006, 5, 51. [Google Scholar]
- Cox, D.R. The regression analysis of binary sequences (with discussion). J. R. Stat. Soc. B 1958, 20, 215–242. [Google Scholar]
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (with discussion). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines, 3rd ed.; Pearson Education: Hoboken, NJ, USA, 2009; pp. 122–218. [Google Scholar]
- Quinlan, R. Programs for Machine Learning; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1993; pp. 17–45. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John Willey and Sons Inc.: New York, NY, USA, 1998. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Picard, R.; Cook, D. Cross-Validation of Regression Models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Kohavi, R.A. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann Publisher: San Francisco, CA, USA, 1995; Volume 2, pp. 1137–1143. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Burges, C.J.C. A tutorial for support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [CrossRef] [PubMed]
- Zou, K.H.; O’Malley, A.J.; Mauri, L. Receiver-Operating Characteristic Analysis for Evaluating Diagnostic Tests and Predictive Models. Circulation 2007, 115, 654–657. [Google Scholar] [CrossRef] [PubMed]
- Kakkos, I. Processing and Analysis of EEG Data Recordings with the Application of Machine Learning Methods. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 2021. [Google Scholar]
- Wang, L.; Zhang, M.; Zou, F.; Wu, X.; Wang, Y. Deductive-reasoning brain networks: A coordinate-based meta-analysis of the neural signatures in deductive reasoning. Brain Behav. 2020, 10, e01853. [Google Scholar] [CrossRef] [PubMed]
- Demos, J.N. Getting Started with Neurofeedback; Ww Norton & Co: New York, NY, USA, 2005. [Google Scholar]
- Blume, M.; Schmidt, R.; Hilbert, A. Abnormalities in the EEG power spectrum in bulimia nervosa, binge-eating disorder, and obesity: A systematic review. Eur. Eat. Disord. Rev. 2019, 27, 124–136. [Google Scholar] [CrossRef]
- Léonard, T.; Pepinà, C.; Bond, A.; Treasure, J. Assessment of Test-Meal Induced Autonomic Arousal in Anorexic, Bulimic and Control females. Eur. Eat. Disord. Rev. 1998, 6, 188–200. [Google Scholar] [CrossRef]
- Hilui, J.C.; David, I.A.; Daquer, A.F.C.; Duchesne, M.; Volchan, E.; Appolinario, J.C. A Systematic Review of Electrophysiological Findings in Binge-Purge Eating Disorders: A Window into Brain Dynamics. Front. Psychol. 2021, 12, 619780. [Google Scholar] [CrossRef] [PubMed]
- Salto, F.; Requena, C.; Alvarez-Merino, P.; Rodriguez, V.; Poza, J.; Hornero, R. Electrical analysis of logical complexity: An exploratory EEG study of logically valid/invalid deductive inference. Brain Inform. 2023, 10, 13. [Google Scholar] [CrossRef]
- Holliday, J.; Tchanturia, K.; Landau, S.; Collier, D.; Treasure, J. Is impaired set-shifting an endophenotype of anorexia nervosa? Am. J. Psychiatry 2005, 162, 2269–2275. [Google Scholar] [CrossRef]
- Tchanturia, K.; Morris, R.G.; Anderluh, M.B.; Collier, D.A.; Nikolaou, V.; Treasure, J. Set shifting in anorexia nervosa: An examination before and after weight gain, in full recovery and relationship to childhood and adult OCPD traits. J. Psychiatr. Res. 2004, 38, 545–552. [Google Scholar] [CrossRef]
- Wagner, A.; Ruf, M.; Braus, D.F.; Schmidt, M.H. Neuronal activity changes and body image distortion in anorexia nervosa. Neuroreport 2003, 14, 2193–2197. [Google Scholar] [CrossRef]
- Santerre, C.; Allen, J.J.B. Methods for studying the psychophysiology of emotion. In Emotion and Psychopathology: Bridging Affective and Clinical Science; Rottenberg, J., Johnson, S.L., Eds.; American Psychological Association: Washington, DC, USA, 2007; pp. 53–79. [Google Scholar]
- Finn, P.R.; Justus, A. Reduced EEG alpha power in the male and female offspring of alcoholics. Alcohol. Clin. Exp. Res. 1999, 23, 256–262. [Google Scholar] [CrossRef]
- Jensen, O.; Tesche, C.D. Frontal theta activity in humans increases with memory load in a working memory task. Eur. J. Neurosci. 2002, 15, 1395–1399. [Google Scholar] [CrossRef] [PubMed]
- Spalatro, A.V.; Marzolla, M.; Vighetti, S.; Daga, G.A.; Fassini, S.; Vitiello, B.; Amianto, F. The song of anorexia nervosa: A specific potential response to musical stimuli in affected participants. Eat. Weight. Disord.-Stud. Anorex. Bulim. Obes. 2021, 26, 807–816. [Google Scholar] [CrossRef] [PubMed]
- Jáuregui-Lobera, I. Electroencephalography in eating disorders. Neuropsychiatr. Dis. Treat. 2012, 8, 1–11. [Google Scholar] [CrossRef]
- Čukić, M.; Stokić, M.; Radenković, S.; Ljubisavljević, M.; Simić, S.; Savić, D. Nonlinear analysis of EEG complexity in episode and remission phase of recurrent depression. Int. J. Methods Psychiatr. Res. 2020, 29, e1816. [Google Scholar] [CrossRef] [PubMed]
- Baldock, E.; Tchanturia, K. Translating laboratory research into clinical practice: Foundations, functions and future of cognitive remediation therapy for anorexia nervosa. Therapy 2007, 4, 285–292. [Google Scholar] [CrossRef]






| Channel Index | Channel Name | Location |
|---|---|---|
| 1 | AF3 | Anterio-frontal, left |
| 2 | F7 | Frontal-temporal, left |
| 3 | F3 | Frontal, left |
| 4 | FC5 | Frontal-central, left |
| 5 | T7 | Temporal, left |
| 6 | P7 | Parietal, left |
| 7 | 01 | Occipital, left |
| 8 | 02 | Occipital, right |
| 9 | P8 | Parietal, right |
| 10 | T8 | Temporal, right |
| 11 | FC6 | Frontal-central, right |
| 12 | F4 | Frontal, right |
| 13 | F8 | Frontal-temporal, right |
| 14 | AF4 | Anterio-frontal, right |
| Syllogism | |
|---|---|
| Valid | Paradox |
| All humans are mortal. All Greeks are humans. All Greeks are mortal. | Achilles and the tortoise decided to race. The tortoise started 100 m ahead of Achilles as the latter is 100 times faster than the tortoise. Therefore, when Achilles will have advanced 100 m the tortoise will be 1 m ahead of him. When Achilles covers this 1 m, the tortoise will be 1/100 m ahead of him. When Achilles covers this 1/100 m the tortoise will be 1/10,000 m ahead etc. Therefore, the tortoise will always be ahead of Achilles. |
| Invalid | |
| Some photographers are humans. Some doctors are not humans. Hence, no doctor is photographer. | |
| EEG | Signal Characteristics | HFD | AppEn |
|---|---|---|---|
| 1. | Non-fractal but irregular: Irregular and complex but lacking self-similarity | Low | High |
| 2. | Fractal but predictable: Clear fractal properties, Predictable patterns | High | Low |
| 3. | Sensitivity to different types of complexity: -strong spatial self-similarity -lacking temporal irregularity | High | Low |
| MANOVA Multivariate Tests of HIGUCHI Estimations | ||||
|---|---|---|---|---|
| Effect: Group, Pillais Trace | ||||
| Syllogism | Value | F | Sig. (p-Value) | Partial Eta Squared |
| Valid | 0.573 | 2.395 | 0.028 | 0.573 |
| invalid | 0.320 | 0.840 | 0.624 | 0.320 |
| Paradox | 0.428 | 1.335 | 0.256 | 0.428 |
| HIGUCHI FD Analysis. MANOVA Results. Tests between Subjects Effects. F, p-Values, Partial Eta Squared (Using the Bonferroni Adjusted Alpha Value (p < 0.0035)) | |||
|---|---|---|---|
| CHANNEL | Valid | Invalid | Paradox |
| F, p-Value, η2 | F, p-Value, η2 | F, p-Value, η2 | |
| AF3 | 6.082, 0.018, 0.138 | 1.547, 0.221, 0.039 | 0.964, 0.332, 0.025 |
| F7 | 4.50, 0.040, 0.106 | 1.363, 0.250, 0.035 | 0.736, 0.396, 0.016 |
| F3 | 3.303, 0.077, 0.080 | 0.242, 0.625, 0.006 | 0.299, 0.588, 0.008 |
| FC5 | 5.422, 0.025, 0.125 | 0.238, 0.628, 0.006 | 0.135, 0.715, 0.004 |
| T7 | 0.746, 0.393, 0.019 | 0.010, 0.922, 0.000 | 0.014, 0.906, 0.000 |
| P7 | 2.840, 0.100, 0.070 | 0.156, 0.695, 0.004 | 0.376, 0.544, 0.010 |
| O1 | 5.566, 0, 024, 0.128 | 0.710, 0.374, 0.021 | 0.186, 0.669, 0.005 |
| O2 | 5.029, 0.031, 0.117 | 0.244, 0.624, 0.006 | 0.136, 0.712, 0.004 |
| P8 | 3.136, 0.085, 0.076 | 0.172, 0.681, 0.004 | 0.148, 0.702, 0.004 |
| T8 | 1.039, 0.315, 0.027 | 0.522, 0.474, 0.014 | 1.899, 0.176, 0.048 |
| FC6 | 2.294, 0.138, 0.057 | 0.330, 0.596, 0.009 | 0.003, 0.957, 0.000 |
| F4 | 8.227, 0.007, 0.178 | 0.199, 0.658, 0.005 | 0.156, 0.695, 0.004 |
| F8 | 5.413, 0.025, 0.125 | 1.791, 0.189, 0.045 | 0.231, 0.634, 0.006 |
| AF4 | 13.776, 0.001, 0.266 | 3.300, 0.077, 0.080 | 4.379, 0.043, 0.103 |
| HFD, One-Way ANOVA, Syllogism: Valid | ||||
|---|---|---|---|---|
| Channel | Healthy Controls Mean (SE) | AN Mean (SE) | F-Stats | p-Value |
| Ch1 | 1.647 (0.021) | 1.737 (0.026) | 6.082 | 0.018 * |
| Ch2 | 1.658 (0.019) | 1.730 (0.022) | 4.541 | 0.040 * |
| Ch3 | 1.683 (0.022) | 1.754 (0.028) | 3.303 | 0.077 |
| Ch4 | 1.690 (0.021) | 1.774 (0.025) | 5.422 | 0.025 * |
| Ch5 | 1.730 (0.025) | 1.768 (0.027) | 0.746 | 0.393 |
| Ch6 | 1.701 (0.023) | 1.769 (0.025) | 2.840 | 0.100 |
| Ch7 | 1.665 (0.022) | 1.753 (0.024) | 5.566 | 0.024 * |
| Ch8 | 1.655 (0.019) | 1.733 (0.027) | 5.029 | 0.031 |
| Ch9 | 1.696 (0.018) | 1.758 (0.030) | 3.136 | 0.085 |
| Ch10 | 1.719 (0.022) | 1.759 (0.031) | 1.039 | 0.315 |
| Ch11 | 1.684 (0.022) | 1.744 (0.030) | 2.294 | 0.138 |
| Ch12 | 1.675 (0.020) | 1.773 (0.022) | 8.227 | 0.007 * |
| Ch13 | 1.674 (0.023) | 1.767 (0.028) | 5.413 | 0.025 * |
| Ch14 | 1.625 (0.018) | 1.746 (0.025) | 13.77 | 0.001 ** |
| HFD, One-Way ANOVA, Syllogism: Invalid | ||||
|---|---|---|---|---|
| Channel | Healthy Controls Mean (SE) | AN Mean (SE) | F-Stats | p-Value |
| Ch1 | 1.671 (0.017) | 1.716 (0.036) | 1.547 | 0.221 |
| Ch2 | 1.676 (0.017) | 1.715 (0.034) | 1.363 | 0.250 |
| Ch3 | 1.700 (0.017) | 1.718 (0.034) | 0.242 | 0.625 |
| Ch4 | 1.706 (0.018) | 1.725 (0.037) | 0.238 | 0.628 |
| Ch5 | 1.755 (0.020) | 1.759 (0.035) | 0.010 | 0.922 |
| Ch6 | 1.732 (0.017) | 1.745 (0.030) | 0.156 | 0.695 |
| Ch7 | 1.694 (0.019) | 1.728 (0.033) | 0.810 | 0.374 |
| Ch8 | 1.697 (0.016) | 1.714 (0.037) | 0.244 | 0.624 |
| Ch9 | 1.720 (0.019) | 1.734 (0.041) | 0.172 | 0.681 |
| Ch10 | 1.747 (0.020) | 1.717 (0.040) | 0.522 | 0.474 |
| Ch11 | 1.705 (0.018) | 1.727 (0.037) | 0.330 | 0.569 |
| Ch12 | 1.698 (0.018) | 1.713 (0.027) | 0.199 | 0.658 |
| Ch13 | 1.695 (0.017) | 1.739 (0.029) | 1.791 | 0.189 |
| Ch14 | 1.648 (0.017) | 1.709 (0.031) | 3.300 | 0.077 |
| HFD, One-Way ANOVA, Syllogism: Paradox | ||||
|---|---|---|---|---|
| Channel | Healthy Controls Mean (SE) | AN Mean (SE) | F-Stats | p-Value |
| Ch1 | 1.678 (0.018) | 1.713 (0.034) | 0.964 | 0.332 |
| Ch2 | 1.687 (0.018) | 1.716 (0.026) | 0.736 | 0.396 |
| Ch3 | 1.713 (0.018) | 1.732 (0.029) | 0.299 | 0.588 |
| Ch4 | 1.729 (0.016) | 1.742 (0.034) | 0.135 | 0.715 |
| Ch5 | 1.763 (0.018) | 1.759 (0.032) | 0.014 | 0.906 |
| Ch6 | 1.731 (0.017) | 1.751 (0.025) | 0.376 | 0.544 |
| Ch7 | 1.705 (0.019) | 1.720 (0.025) | 0.186 | 0.669 |
| Ch8 | 1.692 (0.017) | 1.680 (0.030) | 0.138 | 0.712 |
| Ch9 | 1.733 (0.018) | 1.719 (0.032) | 0.148 | 0.702 |
| Ch10 | 1.767 (0.018) | 1.716 (0.036) | 1.899 | 0.176 |
| Ch11 | 1.718 (0.020) | 1.716 (0.034) | 0.003 | 0.957 |
| Ch12 | 1.723 (0.017) | 1.736 (0.033) | 0.156 | 0.695 |
| Ch13 | 1.719 (0.018) | 1.736 (0.034) | 0.231 | 0.634 |
| Ch14 | 1.657 (0.017) | 1.723 (0.025) | 4.379 | 0.043 * |
| HFD, One-Way ANOVA, All Channels | ||||||
|---|---|---|---|---|---|---|
| Sum of Squares | df | Mean Square | F | Sig. | ||
| Mean valid Higuchi | Between groups Within groups Total | 0.049 0.354 0.403 | 1 38 39 | 0.049 0.009 | 5.219 | 0.028 |
| Mean invalid Higuchi | Between groups Within groups Total | 0.004 0.318 0.323 | 1 38 39 | 0.004 0.008 | 0.510 | 0.479 |
| Mean paradox Higuchi | Between groups Within groups Total | 0.001 0.287 0.288 | 1 38 39 | 0.001 0.008 | 0.114 | 0.737 |
| Channel Index | Channel Name | Valid | Invalid | Paradox |
|---|---|---|---|---|
| 1 | AF3 | ns | s | ns |
| 2 | F7 | ns | s | ns |
| 3 | F3 | s | s | s |
| 4 | FC5 | ns | s | s |
| 5 | T7 | s | s | s |
| 6 | P7 | s | s | s |
| 7 | O1 | s | s | s |
| 8 | O2 | s | s | s |
| 9 | P8 | s | s | s |
| 10 | T8 | s | s | s |
| 11 | FC6 | s | s | ns |
| 12 | F4 | s | s | s |
| 13 | F8 | s | s | s |
| 14 | AF4 | ns | s | ns |
| Alpha (α) (8–13 Hz) | Beta (β) (13–30 Hz) | Delta (δ) (1–4 Hz) | Theta (θ) (4–8 Hz) | |
|---|---|---|---|---|
| Valid | - | AF3, F3 FC5, FC6 | - | - |
| Invalid | P8 | AF3, P7 | - | F7, FC6, AF4 |
| Paradox | F7, T8 FC6, AF4 | O2 | T7 | - |
| Channel | X2 | df | p |
|---|---|---|---|
| 1 (AF3) | 4.654 | 1 | 0.031 |
| 3 (F3) | 4.183 | 1 | 0.041 |
| 4 (FC5) | 4.776 | 1 | 0.029 |
| 7 (O1) | 4.069 | 1 | 0.044 |
| 12 (F4) | 5.278 | 1 | 0.022 |
| 14 (AF4) | 5.941 | 1 | 0.015 |
| (a) | ||||
| Valid Case | Ch3 (F3) | Ch4 (FC5) | Ch12 (F4) | Ch14 (AF4) |
| X2 | 4.899 | 3.957 | 5.941 | 7.693 |
| df | 1 | 1 | 1 | 1 |
| p | 0.027 | 0.047 | 0.015 | 0.006 |
| (b) | ||||
| Invalid Case | Ch1 (AF3) | Ch4 (FC5) | Ch11 (FC6) | Ch13 (F8) |
| X2 | 4.268 | 3.680 | 5.031 | 4.770 |
| df | 1 | 1 | 1 | 1 |
| p | 0.039 | 0.055 (partial) | 0.025 | 0.029 |
| (a) | ||||||||||
| Valid | Invalid | Paradox | ||||||||
| EEG Wave RP | Channel Level Analysis | Brain’s Total Activation Analysis | Channel Level Analysis | Brain’s Total Activation Analysis | Channel Level Analysis | Brain’s Total Activation Analysis | ||||
| alpha | No | No | No | No | No | No | ||||
| beta | Yes AF3, F3 FC5, O1 F4, AF4 | Yes | No | No | No | No | ||||
| gamma | Yes AF4 | No | No | No | No | No | ||||
| delta | No | No | No | No | No | No | ||||
| theta | Yes F3, FC5 F4, AF4 | Yes | Yes AF3, FC5 FC6, F8 | No | No | No | ||||
| (b) | ||||||||||
| Alpha | Beta | Delta | Gamma | Theta | ||||||
| CTRL | AN | CTRL | AN | CTRL | AN | CTRL | AN | CTRL | AN | |
| Valid | 18.013 | 17.864 | 17.658 | 22.23 | 31.96 | 27.90 | 10.54 | 13.73 | 21.81 | 18.25 |
| Invalid | 17.849 | 18.204 | 18.345 | 19.77 | 30.36 | 32.19 | 11.07 | 11.54 | 22.35 | 18.28 |
| Paradox | 17.65 | 19.11 | 19.11 | 18.54 | 30.09 | 32.00 | 12.91 | 11.08 | 20.20 | 19.33 |
| (a) Without PCA | |||||
| Feature (Measure) | Syllogism | Best Classification Model | Accuracy, % | Area Under Curve (AUC) | OOPROC (Sensitivity, Specificity) |
| Higuchi FD | Valid | SVM (Linear) SVM (Medium Gaussian) Ensemble (subspace Disc) | 66.7 66.7 66.7 | 0.83 0.56 0.58 | (0.33, 0.67) (0.33, 0.67) (0.50, 0.83) |
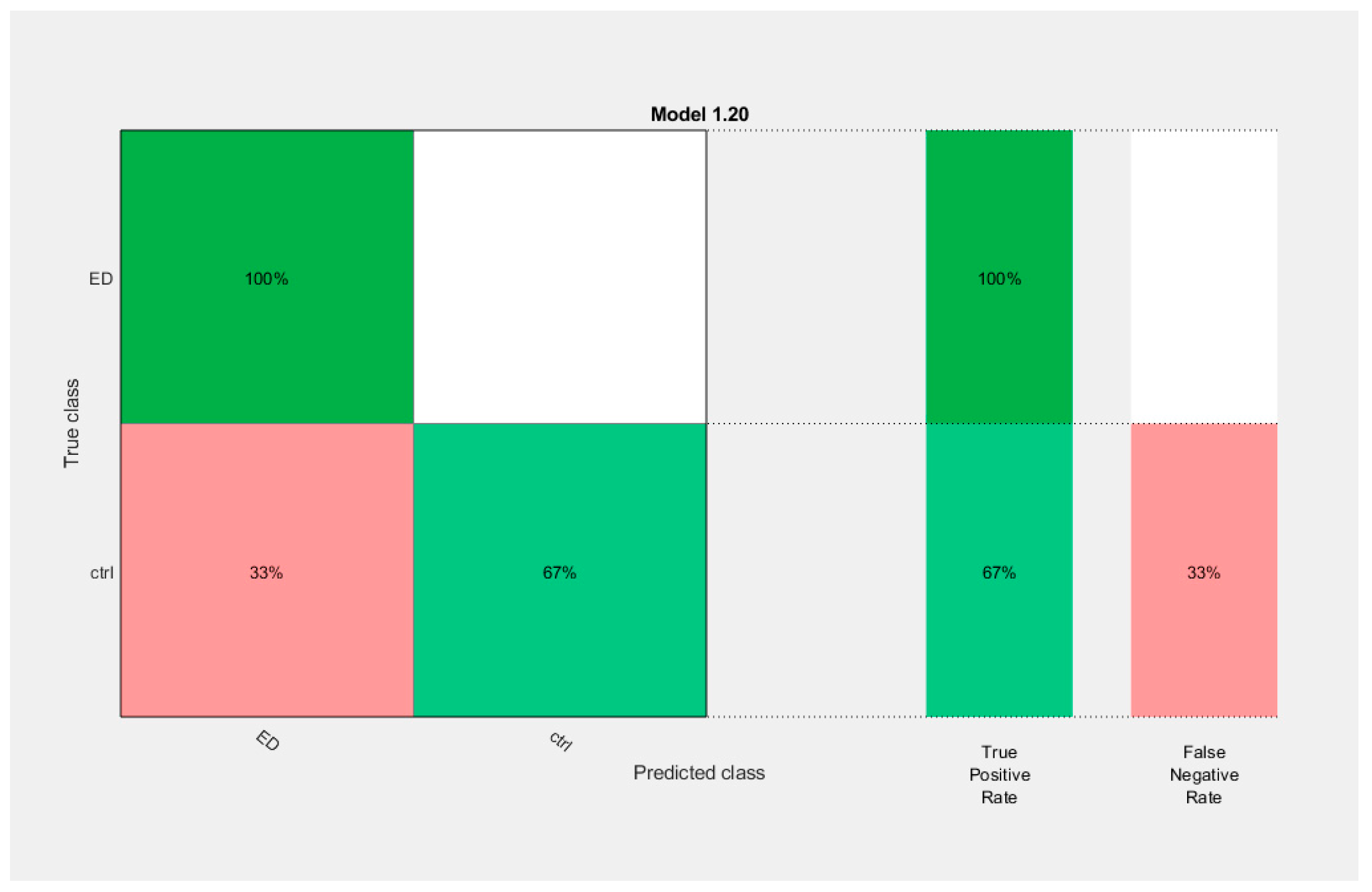
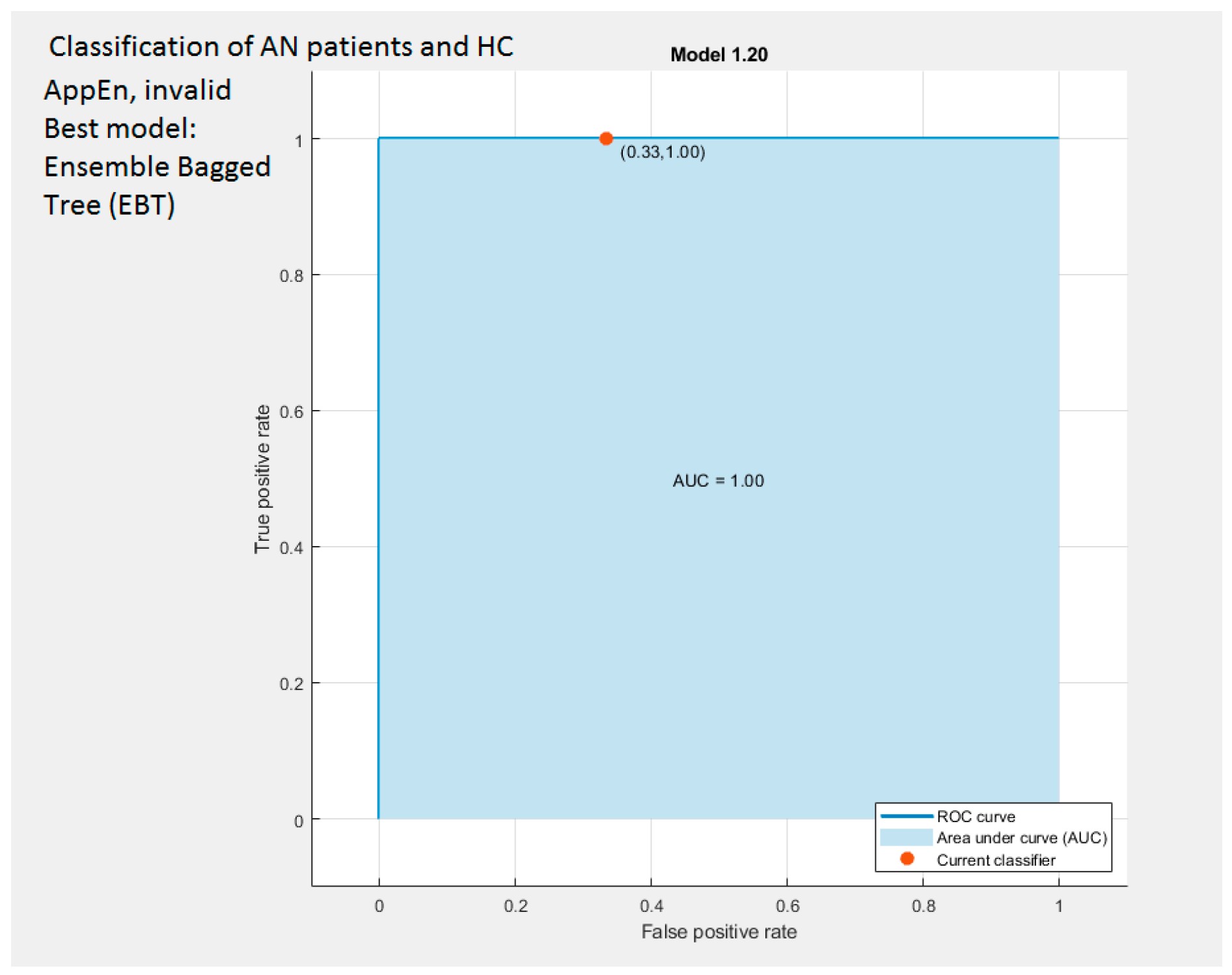
| AppEn | Invalid | Ensemble (Bagged Trees, BT) | 83.3 | ||
| (b) With PCA | |||||
| Feature (Measure) | Syllogism | Best Classification Model | Accuracy, % | Area Under Curve (AUC) | OOPROC (Sensitivity, Specificity) |
| Higuchi FD | Valid | Linear Discriminant (*) Logistic Regression (*) KNN (Fine) (*) | 75 75 75 | 0.78 0.76 0.75 | (0.33, 0.83) (0.33, 0.83) (0.33, 0.83) |
| AppEn | Invalid | Ensemble (Bagged Trees, BT) | 83.3 | ||
| (a) Without PCA | |||||
| Rhythm | Syllogism | Best Classification Model | Accuracy, % | Area Under Curve (AUC) | OOPROC (Sensitivity, Specificity) |
| Alpha | Valid | SVM fine Gaus. Linear Discriminant | 83.3 66.7 | 0.59 0.69 | (0.00, 0.50) (0.38, 0.75) |
| Theta | Invalid | SVM Cubic KNN Fine KNN weighted | 75 75 66.7 | 0.69 0.75 0.58 | (0.50, 1.00) (0.50, 1.00) (0.67, 1.00) |
| (b) With PCA | |||||
| Rhythm | Syllogism | Best Classification Model | Accuracy, % | Area Under Curve (AUC) | OOPROC (Sensitivity, Specificity) |
| Alpha | Valid | SVM fine Gaus. KNN | 83.3 66.7 | 0.50 0.50 | (0.00, 0.50) (0.25, 0.50) |
| Theta | Invalid | KNN SVM Quadrat SVM cubic | 75 66.7 66.7 | 0.75 0.78 0.83 | (0.50, 1.00) (0.67, 1.00) (0.67, 1.00) |
| Valid | Invalid | Paradox | ||||
|---|---|---|---|---|---|---|
| EEG Rhythm (Wave) | Model | Accuracy % | Model | Accuracy % | Model | Accuracy % |
| Alpha Relative Power | Fine Tree | 75.6 no split 70.0 split | SVM Coarse Logistic regression | 70 no split. 55 split | SVM Linear Ensemble BT | 75.6 no split 85 split |
| Beta Relative Power | SVM Ensemble subspace Discr. | 70.7 no split 85.0 split | SVM SVM (cubic) | 75.0 no split 70.0 split | SVM fine Gaussian SVM cubic | 68.3 no split 75.0 split |
| Delta Relative Power | Ensemble BT Logistic Regression | 78.0 no split 60.0 split | SVM Fine Gaussian Ensemble subspace KNN | 70.0 no split 90.0 split | SVM Quadrat. Ensemble BT | 70.7 no split 75 split |
| Gamma Relative Power | KNN (cubic) SVM (linear) | 73.2 no split 85.0 split | SVM Gaussian SVM Cubic | 70.0 no split 65.0 split | Linear Discr. LD Logistic Regr. | 73.3 no split 65.0 split |
| Theta Relative Power | SVM linear KNN weighted | 68.3 no split 80.0 split | SVM fine Gaussian SVM Coarse Gaussian | 70.0 no split 70.0 split | KNN weighted SVM Quadratic | 70.7 no split 75.0 split |
| Grand Mean AppEn | Grand Mean HFD | |||||
|---|---|---|---|---|---|---|
| Group | Valid | Invalid | Paradox | Valid | Invalid | Paradox |
| Healthy Controls | 1.371 | 1.482 | 1.389 | 1.679 | 1.703 | 1.715 |
| AN Patients | 1.259 | 1.210 | 1.283 | 1.755 | 1.726 | 1.726 |
| Comparison | AppEnAN < AppEnHC | Same ** | same | HFDAN > HFDHC | same | same |
| Result * | Not normal | Not normal | Not normal | Normal | Normal | Normal |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karavia, A.; Papaioannou, A.; Michopoulos, I.; Papageorgiou, P.C.; Papaioannou, G.; Gonidakis, F.; Papageorgiou, C.C. Using Electroencephalogram-Extracted Nonlinear Complexity and Wavelet-Extracted Power Rhythm Features during the Performance of Demanding Cognitive Tasks (Aristotle’s Syllogisms) in Optimally Classifying Patients with Anorexia Nervosa. Brain Sci. 2024, 14, 251. https://doi.org/10.3390/brainsci14030251
Karavia A, Papaioannou A, Michopoulos I, Papageorgiou PC, Papaioannou G, Gonidakis F, Papageorgiou CC. Using Electroencephalogram-Extracted Nonlinear Complexity and Wavelet-Extracted Power Rhythm Features during the Performance of Demanding Cognitive Tasks (Aristotle’s Syllogisms) in Optimally Classifying Patients with Anorexia Nervosa. Brain Sciences. 2024; 14(3):251. https://doi.org/10.3390/brainsci14030251
Chicago/Turabian StyleKaravia, Anna, Anastasia Papaioannou, Ioannis Michopoulos, Panos C. Papageorgiou, George Papaioannou, Fragiskos Gonidakis, and Charalabos C. Papageorgiou. 2024. "Using Electroencephalogram-Extracted Nonlinear Complexity and Wavelet-Extracted Power Rhythm Features during the Performance of Demanding Cognitive Tasks (Aristotle’s Syllogisms) in Optimally Classifying Patients with Anorexia Nervosa" Brain Sciences 14, no. 3: 251. https://doi.org/10.3390/brainsci14030251
APA StyleKaravia, A., Papaioannou, A., Michopoulos, I., Papageorgiou, P. C., Papaioannou, G., Gonidakis, F., & Papageorgiou, C. C. (2024). Using Electroencephalogram-Extracted Nonlinear Complexity and Wavelet-Extracted Power Rhythm Features during the Performance of Demanding Cognitive Tasks (Aristotle’s Syllogisms) in Optimally Classifying Patients with Anorexia Nervosa. Brain Sciences, 14(3), 251. https://doi.org/10.3390/brainsci14030251






