Prediction of Antioxidant Capacity of Thiolate–Disulfide Systems Using Species-Specific Basicity Values
Abstract
:1. Introduction
1.1. Basis of Oxidative Stress and Antioxidant Pathways
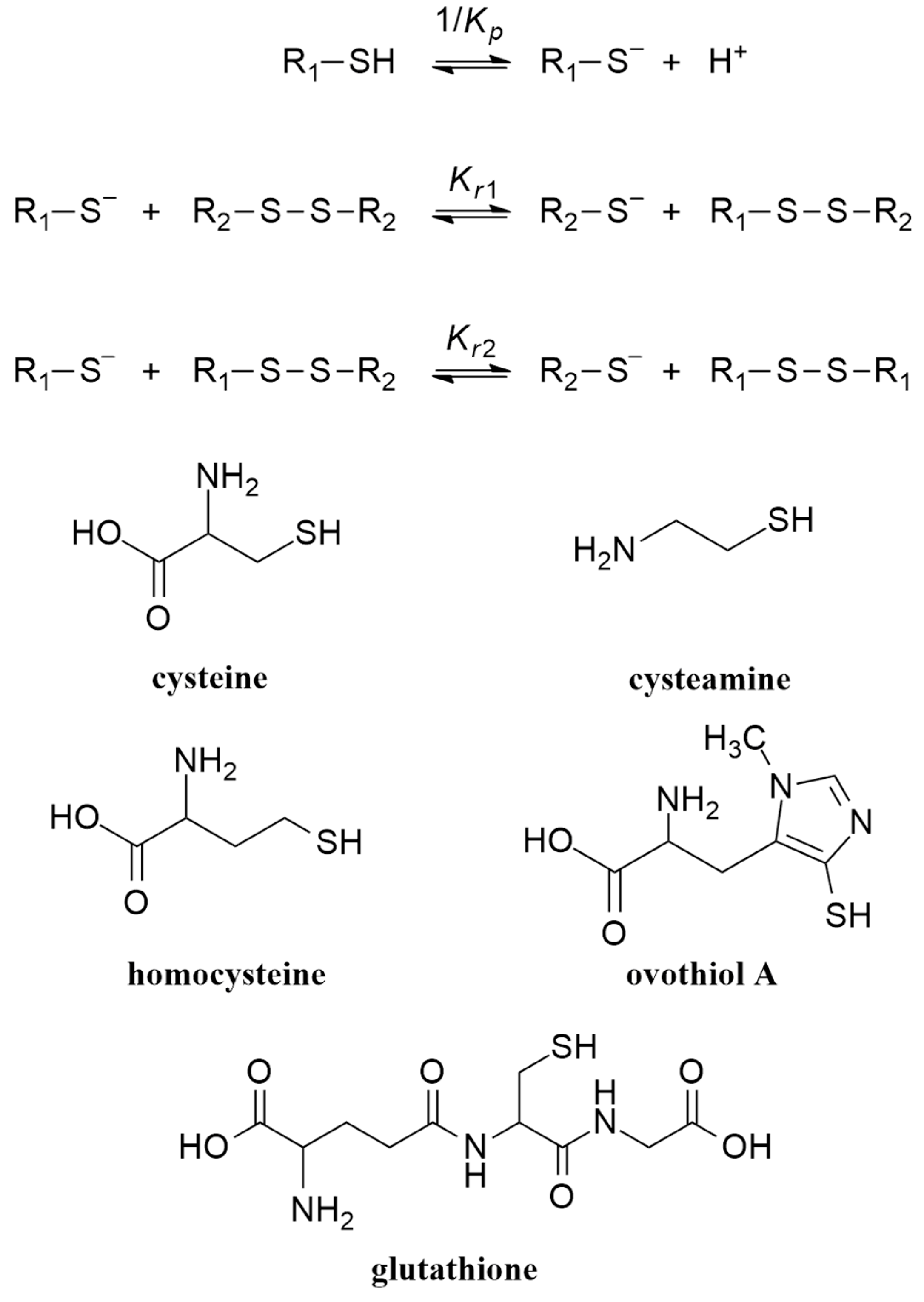
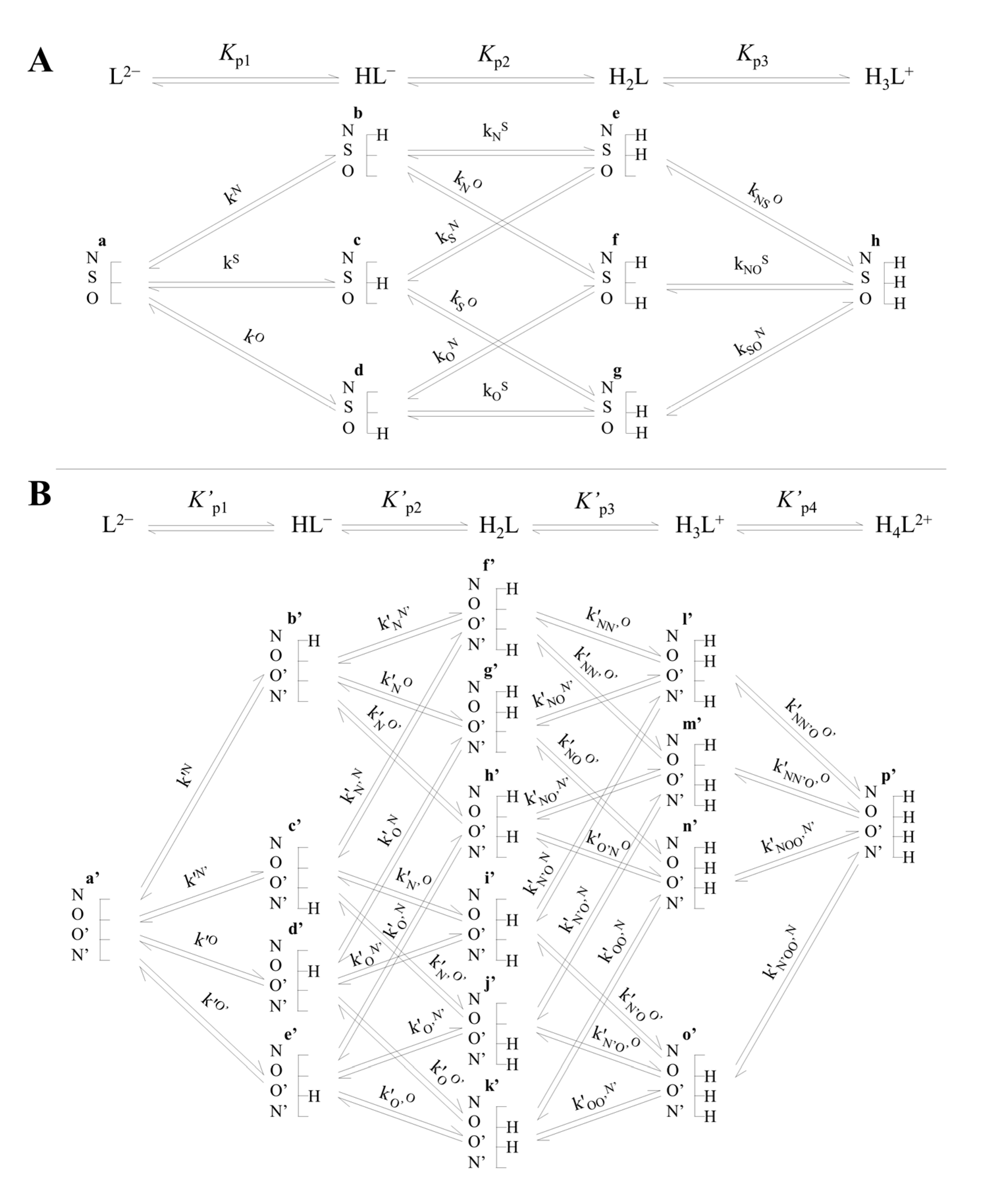
1.2. Thiol–Disulfide (Selenol–Diselenide) Systems and Their Species-Specific Acid–Base and Redox Equilibria
2. Materials and Methods
2.1. Data Collection
2.2. Statistical Analysis and Mathematical Calculations
3. Results
3.1. Relationship between Acid–Base and Redox Characteristics
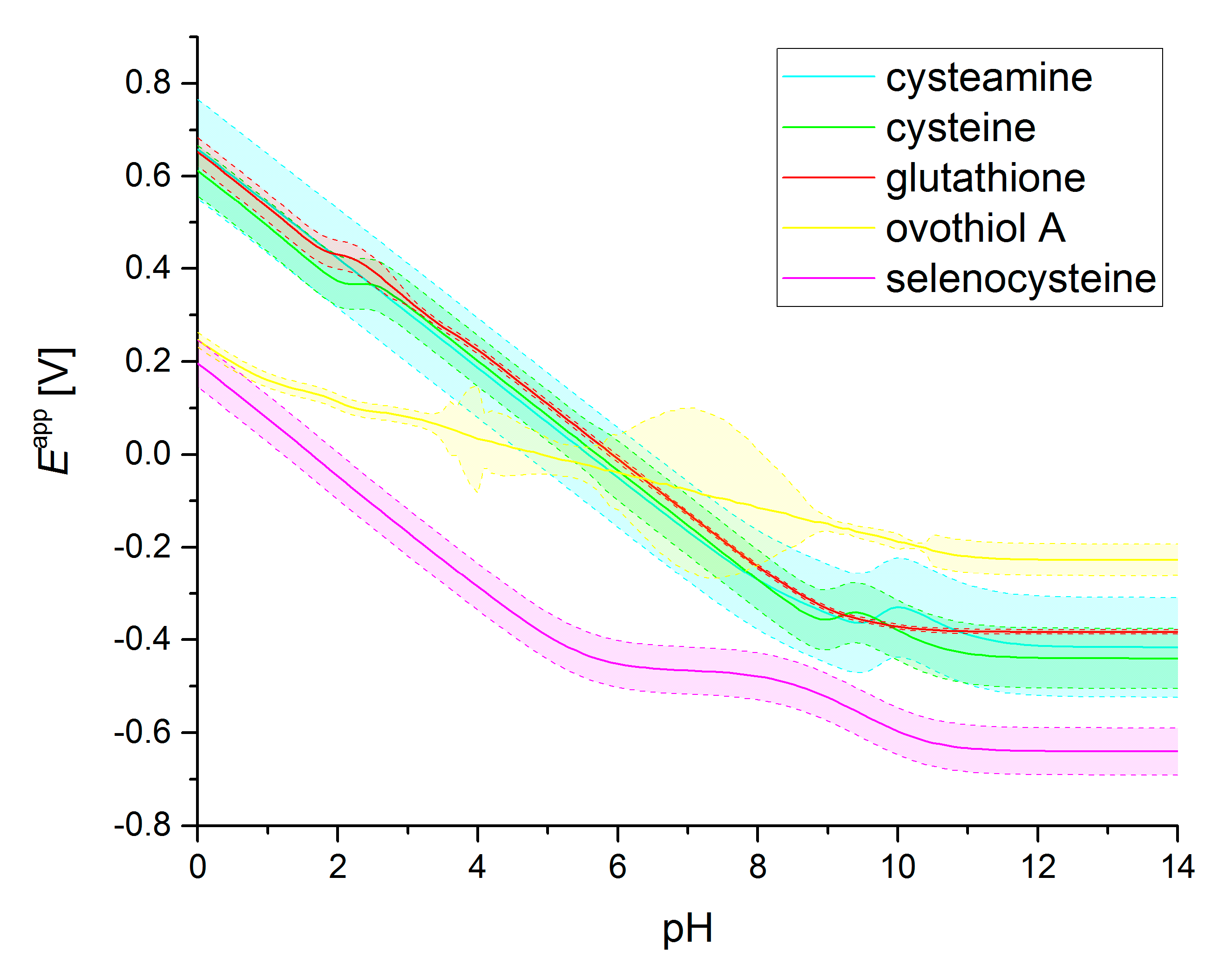
3.2. Standard Redox Potential pH Profiles
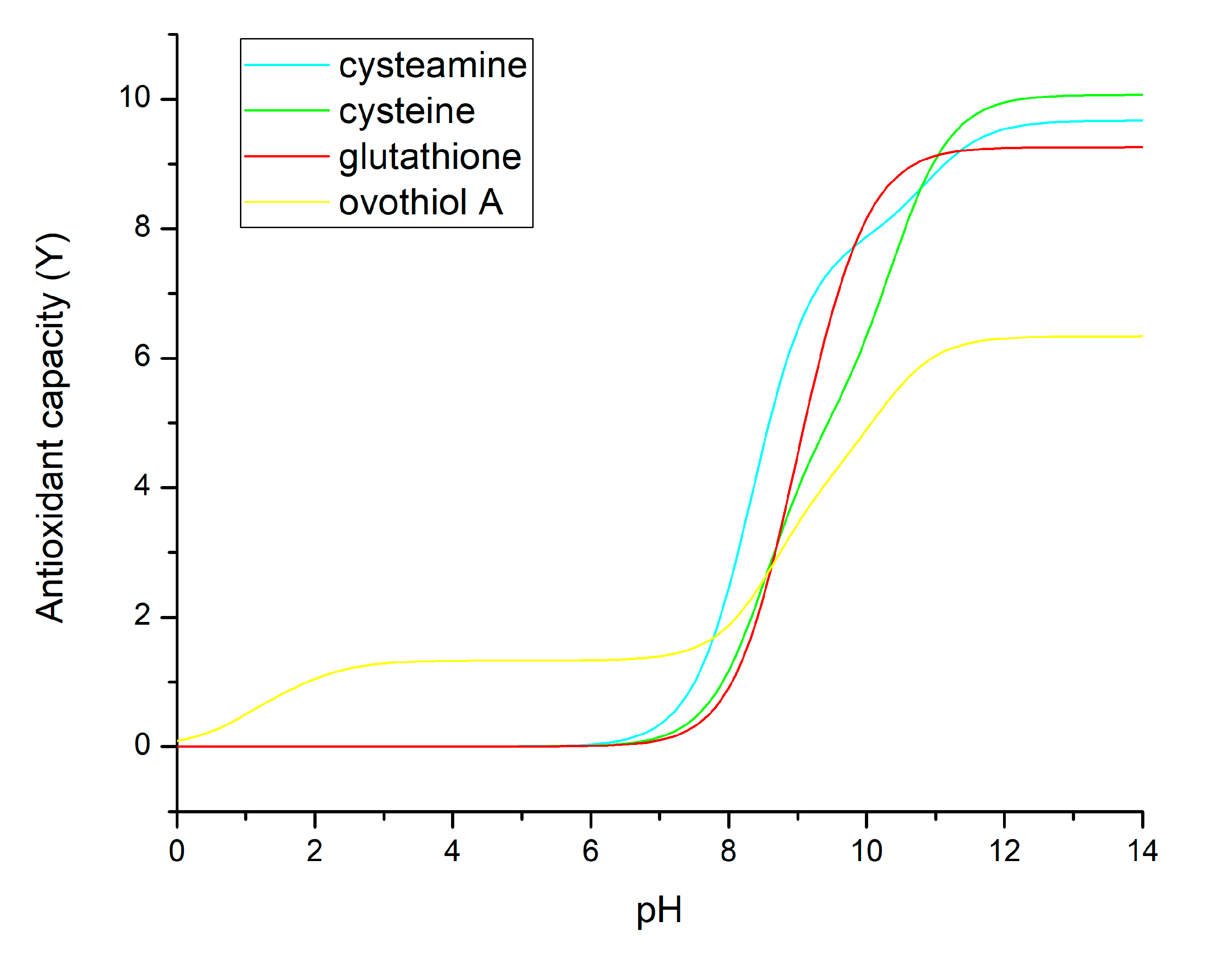
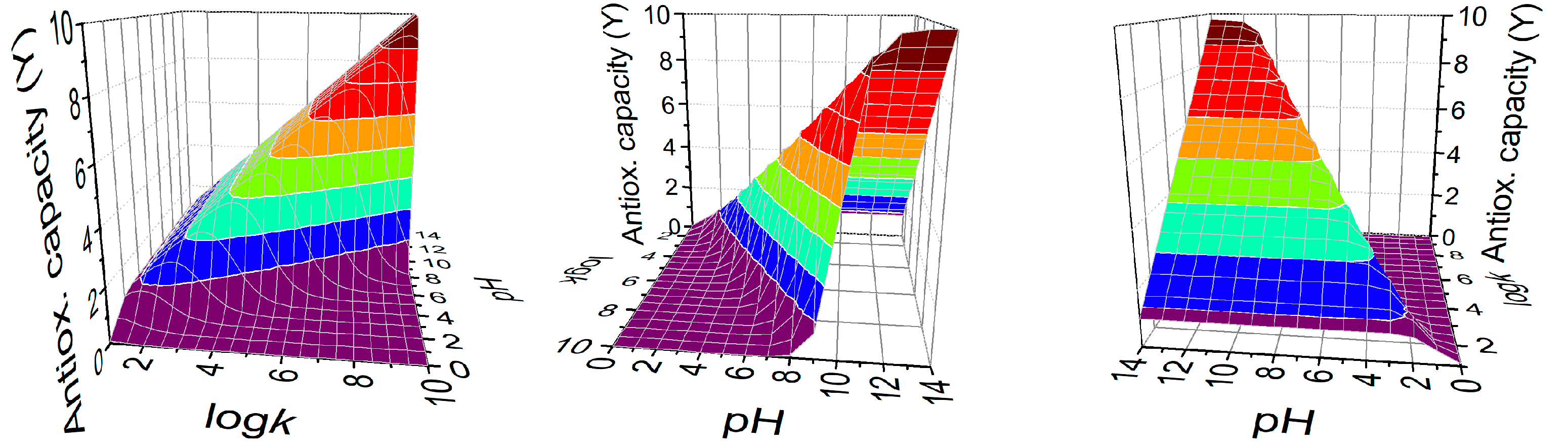
3.3. Antioxidant Capacities Directly from Thiolate Basicities
3.4. Designing for Optimal Antioxidant Capacity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Villamena, F.A. Molecular Basis of Oxidative Stress: Chemistry, Mechanisms, and Disease Pathogenesis; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-0-470-57218-4. [Google Scholar]
- Pizzino, G.; Irrera, N.; Cucinotta, M.; Pallio, G.; Mannino, F.; Arcoraci, V.; Squadrito, F.; Altavilla, D.; Bitto, A. Oxidative Stress: Harms and Benefits for Human Health. Oxid. Med. Cell. Longev. 2017, 2017, 8416763. [Google Scholar] [CrossRef]
- Forman, H.J.; Zhang, H. Targeting Oxidative Stress in Disease: Promise and Limitations of Antioxidant Therapy. Nat. Rev. Drug Discov. 2021, 20, 689–709. [Google Scholar] [CrossRef] [PubMed]
- Nagy, P. Kinetics and Mechanisms of Thiol–Disulfide Exchange Covering Direct Substitution and Thiol Oxidation-Mediated Pathways. Antioxid. Redox Signal. 2013, 18, 1623–1641. [Google Scholar] [CrossRef] [PubMed]
- Ho, H.; Cheng, M.; Chiu, D.T. Glucose-6-Phosphate Dehydrogenase—From Oxidative Stress to Cellular Functions and Degenerative Diseases. Redox Rep. 2007, 12, 109–118. [Google Scholar] [CrossRef] [PubMed]
- Losada-Barreiro, S.; Sezgin-Bayindir, Z.; Paiva-Martins, F.; Bravo-Díaz, C. Biochemistry of Antioxidants: Mechanisms and Pharmaceutical Applications. Biomedicines 2022, 10, 3051. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Lee, T.-H. Antioxidant Enzymes as Redox-Based Biomarkers: A Brief Review. BMB Rep. 2015, 48, 200–208. [Google Scholar] [CrossRef] [PubMed]
- Huchzermeyer, B.; Menghani, E.; Khardia, P.; Shilu, A. Metabolic Pathway of Natural Antioxidants, Antioxidant Enzymes and ROS Providence. Antioxidants 2022, 11, 761. [Google Scholar] [CrossRef]
- Gulcin, İ. Antioxidants and Antioxidant Methods: An Updated Overview. Arch. Toxicol. 2020, 94, 651–715. [Google Scholar] [CrossRef]
- Karademir, S.E.; Ozyurek, M.; Ercag, E.; Guclu, K.; Apak, R. The Cupric Ion Reducing Antioxidant Capacity and Polyphenolic Content of Some Herbal Teas. Int. J. Food Sci. Nutr. 2006, 57, 292–304. [Google Scholar]
- Alam, M.N.; Bristi, N.J.; Rafiquzzaman, M. Review on in Vivo and in Vitro Methods Evaluation of Antioxidant Activity. Saudi Pharm. J. 2013, 21, 143–152. [Google Scholar] [CrossRef]
- Ulrich, K.; Jakob, U. The Role of Thiols in Antioxidant Systems. Free. Radic. Biol. Med. 2019, 140, 14–27. [Google Scholar] [CrossRef] [PubMed]
- Ganguly, P.; Alam, S.F. Role of Homocysteine in the Development of Cardiovascular Disease. Nutr. J. 2015, 14, 6. [Google Scholar] [CrossRef] [PubMed]
- Aoyama, K.; Nakaki, T. Glutathione in Cellular Redox Homeostasis: Association with the Excitatory Amino Acid Carrier 1 (EAAC1). Molecules 2015, 20, 8742–8758. [Google Scholar] [CrossRef] [PubMed]
- Castellano, I.; Migliaccio, O.; D’Aniello, S.; Merlino, A.; Napolitano, A.; Palumbo, A. Shedding Light on Ovothiol Biosynthesis in Marine Metazoans. Sci. Rep. 2016, 6, 21506. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Orgován, G.; Hosztafi, S.; Noszál, B. The Complete Microspeciation of Ovothiol A, the Smallest Octafarious Antioxidant Biomolecule. Anal. Bioanal. Chem. 2014, 406, 2377–2387. [Google Scholar] [CrossRef]
- Osik, N.A.; Zelentsova, E.A.; Tsentalovich, Y.P. Kinetic Studies of Antioxidant Properties of Ovothiol A. Antioxidants 2021, 10, 1470. [Google Scholar] [CrossRef] [PubMed]
- Whitesides, G.M.; Lilburn, J.E.; Szajewski, R.P. Rates of Thiol-Disulfide Interchange Reactions between Mono- and Dithiols and Ellman’s Reagent. J. Org. Chem. 1977, 42, 332–338. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Noszál, B. Species-Specific Standard Redox Potential of Thiol-Disulfide Systems: A Key Parameter to Develop Agents against Oxidative Stress. Sci. Rep. 2016, 6, 37596. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Noszál, B. The Species- and Site-Specific Acid–Base Properties of Biological Thiols and Their Homodisulfides. J. Pharm. Biomed. Anal. 2014, 95, 184–192. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Noszál, B. Species-Specific Thiol-Disulfide Equilibrium Constants of Ovothiol A and Penicillamine with Glutathione. RSC Adv. 2016, 6, 26757–26764. [Google Scholar] [CrossRef]
- Bjerrum, N. Dissoziationskonstanten von Mehrbasischen Säuren Und Ihre Anwendung Zur Berechnung Molekularer Dimensionen. Z. Phys. Chem. 1923, 106U, 219–242. [Google Scholar] [CrossRef]
- Pálla, T.; Mirzahosseini, A.; Noszál, B. Properties of Selenolate-Diselenide Redox Equilibria in View of Their Thiolate-Disulfide Counterparts. Antioxidants 2023, 12, 822. [Google Scholar] [CrossRef] [PubMed]
- Pahari, S.; Sun, L.; Alexov, E. PKAD: A Database of Experimentally Measured pKa Values of Ionizable Groups in Proteins. Database 2019, 2019, baz024. [Google Scholar] [CrossRef] [PubMed]
- Keire, D.A.; Strauss, E.; Guo, W.; Noszal, B.; Rabenstein, D.L. Kinetics and Equilibria of Thiol/Disulfide Interchange Reactions of Selected Biological Thiols and Related Molecules with Oxidized Glutathione. J. Org. Chem. 1992, 57, 123–127. [Google Scholar] [CrossRef]
- Sharma, S.V.; Van Laer, K.; Messens, J.; Hamilton, C.J. Thiol Redox and pKa Properties of Mycothiol, the Predominant Low-Molecular-Weight Thiol Cofactor in the Actinomycetes. ChemBioChem 2016, 17, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Castellano, I.; Seebeck, F.P. On Ovothiol Biosynthesis and Biological Roles: From Life in the Ocean to Therapeutic Potential. Nat. Prod. Rep. 2018, 35, 1241–1250. [Google Scholar] [CrossRef]
- Pálla, T.; Mirzahosseini, A.; Noszál, B. Species-Specific, pH-Independent, Standard Redox Potential of Selenocysteine and Selenocysteamine. Antioxidants 2020, 9, 465. [Google Scholar] [CrossRef]
- Noszal, B. Group Constant: A Measure of Submolecular Basicity. J. Phys. Chem. 1986, 90, 4104–4110. [Google Scholar] [CrossRef]
- Noszál, B.; Szakács, Z. Microscopic Protonation Equilibria of Oxidized Glutathione. J. Phys. Chem. B 2003, 107, 5074–5080. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Somlyay, M.; Noszál, B. The Comprehensive Acid–Base Characterization of Glutathione. Chem. Phys. Lett. 2015, 622, 50–56. [Google Scholar] [CrossRef]
- Mirzahosseini, A.; Orgován, G.; Tóth, G.; Hosztafi, S.; Noszál, B. The Complete Microspeciation of Ovothiol A Disulfide: A Hexabasic Symmetric Biomolecule. J. Pharm. Biomed. Anal. 2015, 107, 209–216. [Google Scholar] [CrossRef] [PubMed]
- Pálla, T.; Mirzahosseini, A.; Noszál, B. The Species-Specific Acid-Base and Multinuclear Magnetic Resonance Properties of Selenocysteamine, Selenocysteine, and Their Homodiselenides. Chem. Phys. Lett. 2020, 741, 137076. [Google Scholar] [CrossRef]
- Inoue, T.; Kirchhoff, J.R. Electrochemical Detection of Thiols with a Coenzyme Pyrroloquinoline Quinone Modified Electrode. Anal. Chem. 2000, 72, 5755–5760. [Google Scholar] [CrossRef] [PubMed]
- Marjanovic, B.; Simic, M.G.; Jovanovic, S.V. Heterocyclic Thiols as Antioxidants: Why Ovothiol C Is a Better Antioxidant than Ergothioneine. Free. Radic. Biol. Med. 1995, 18, 679–685. [Google Scholar] [CrossRef]

| Protein Name | PDB ID | Res ID | logk | E° [V] (95% CI) |
|---|---|---|---|---|
| Alpha-1-antitrypsin | 1QLP | 232 | 6.86 | −0.247 (−0.253; −0.241) |
| Hydroperoxide reductase c | 4MA9 | 46 | 5.94 | −0.191 (−0.198; −0.185) |
| Human DJ-1 | 1P5F | 106 | 5.4 | −0.159 (−0.166; −0.152) |
| Creatine kinase | 1I0E | 283 | 5.6 | −0.171 (−0.177; −0.164) |
| O6-Alkylguanine-DNA alkyltransferase | 1EH6 | 145 | 5.3 | −0.153 (−0.160; −0.145) |
| Tyrosine phosphatase 1b | 2HNP | 215 | 5.57 | −0.169 (−0.176; −0.162) |
| Papaya protease omega | 1PPO | 25 | 2.88 | −0.006 (−0.017; 0.005) |
| Yersinia protein tyrosine phosphatase | 1YPT | 403 | 4.67 | −0.114 (−0.123; −0.106) |
| Cathepsin B | 1THE | 29 | 3.6 | −0.050 (−0.060; −0.040) |
| DsbA protein | 1DSB | 30 | 3.5 | −0.044 (−0.054; −0.033) |
| Thioredoxin | 2TRX | 32 | 7.1 | −0.261 (−0.267; −0.256) |
| 2TRX | 35 | 9.9 | −0.431 (−0.438; −0.423) | |
| Disulfide isomerase | 1MEK | 36 | 4.5 | −0.104 (−0.113; −0.096) |
| Ubiquitin conjugating enzyme | 1JBB | 87 | 11.1 | −0.504 (−0.513; −0.494) |
| Ubiquitin-conjugating enzyme 2B | 1JAS | 88 | 10.2 | −0.449 (−0.457; −0.441) |
| Human thioredoxin | 1ERT | 32 | 6.3 | −0.213 (−0.219; −0.207) |
| Glutaredoxin | 1EGO | 11 | 5.5 | −0.165 (−0.172; −0.158) |
| 1EGO | 14 | 10.5 | −0.467 (−0.476; −0.459) | |
| Acyl-coenzyme A binding protein | 1NTI | 86 | 9.9 | −0.431 (−0.438; −0.423) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pálla, T.; Noszál, B.; Mirzahosseini, A. Prediction of Antioxidant Capacity of Thiolate–Disulfide Systems Using Species-Specific Basicity Values. Antioxidants 2024, 13, 1053. https://doi.org/10.3390/antiox13091053
Pálla T, Noszál B, Mirzahosseini A. Prediction of Antioxidant Capacity of Thiolate–Disulfide Systems Using Species-Specific Basicity Values. Antioxidants. 2024; 13(9):1053. https://doi.org/10.3390/antiox13091053
Chicago/Turabian StylePálla, Tamás, Béla Noszál, and Arash Mirzahosseini. 2024. "Prediction of Antioxidant Capacity of Thiolate–Disulfide Systems Using Species-Specific Basicity Values" Antioxidants 13, no. 9: 1053. https://doi.org/10.3390/antiox13091053
APA StylePálla, T., Noszál, B., & Mirzahosseini, A. (2024). Prediction of Antioxidant Capacity of Thiolate–Disulfide Systems Using Species-Specific Basicity Values. Antioxidants, 13(9), 1053. https://doi.org/10.3390/antiox13091053






