A Novel Approach to Obtain Vaccine Effectiveness Continuous Profiles. Example Case: COVID-19 in Elderly Mexicans
Abstract
:1. Introduction
2. Methods
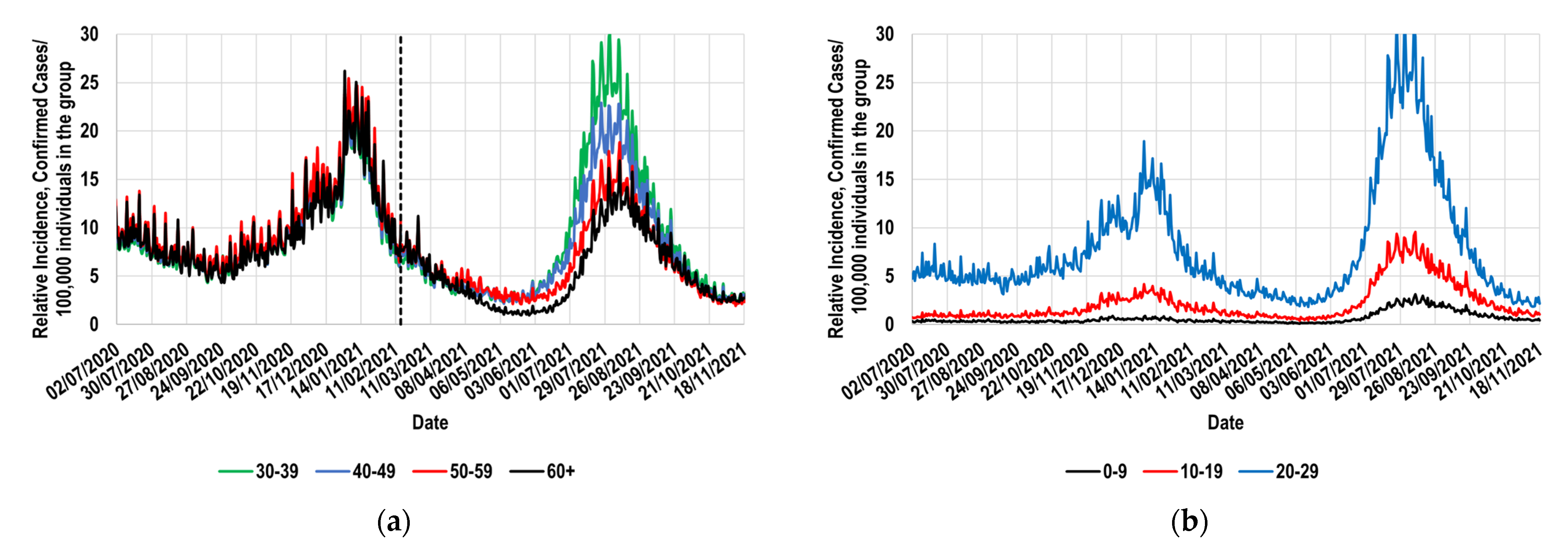
2.1. Relative Incidence of Confirmed Total Cases for the Interest Population Groups
2.2. Identification of a Suitable Reference Group and Its Behavior during the Study Period
2.3. The Beneficial Effect of Vaccines against Symptomatic Disease
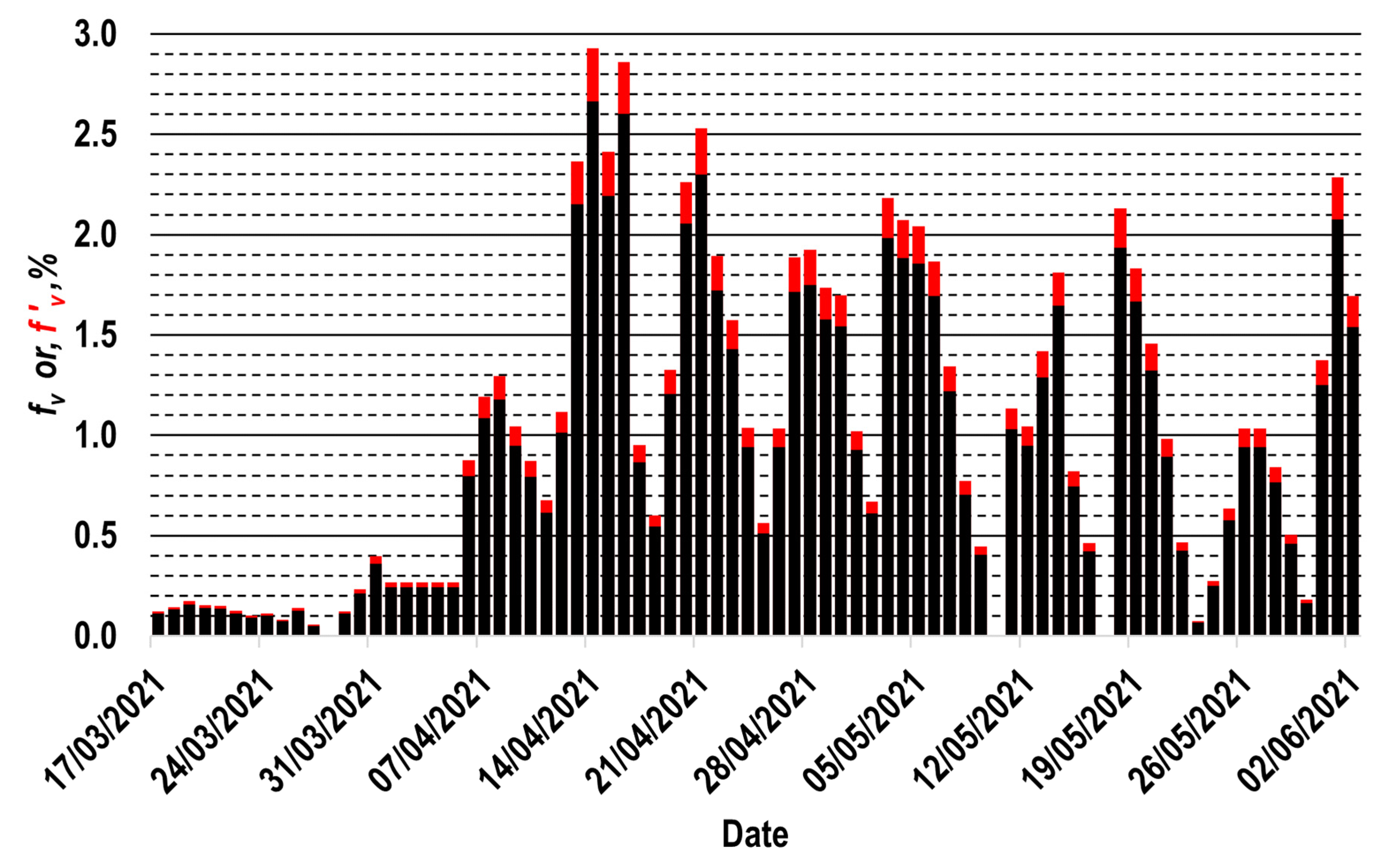
2.4. Vaccination Profile for the Interest Population Group
2.5. The Relationship between the Vaccine Effectiveness Profile ( Profile), the Beneficial Effect Profile ( Profile) and the Vaccination Profile
3. Results
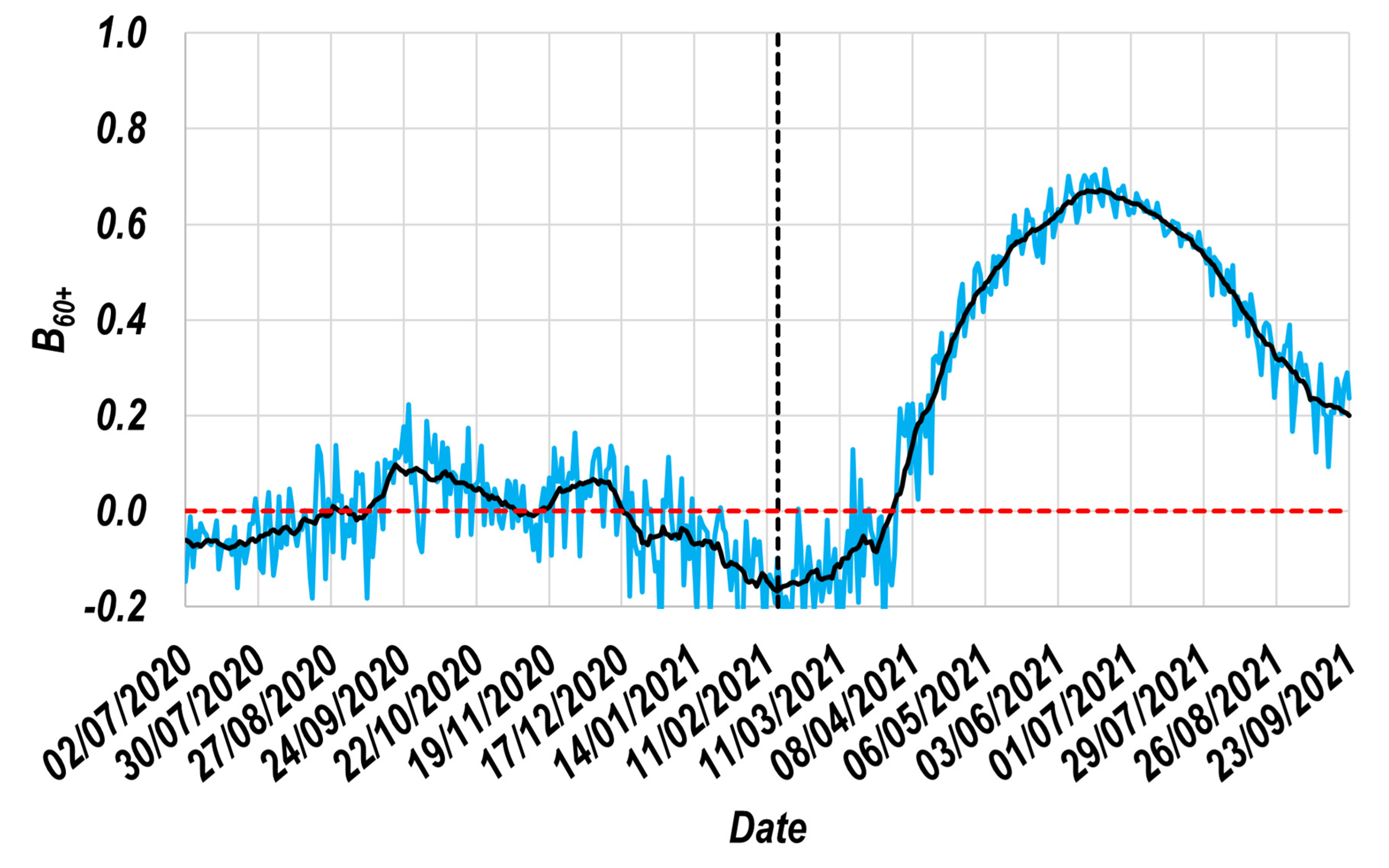
3.1. The Resulting Beneficial Effect Profile ( Profile)
3.2. The Resulting Vaccine Effectiveness Profile ( Profile)
- Maximum value of the profile ( value);
- Number of days prior to the application of the second dose during which the first dose effects are perceptible in the group ();
- Time interval during which the daily value of is greater than 0.8 ();
- Time interval during which the daily value of is greater than 0.5 ();
- Minimum number of days after completing the vaccination scheme required for the daily value of to decrease to values less than 0.1 ().
3.3. Comparison with Previous Reports
4. Discussion
- (1)
- The availability of the mDBs containing realistic information about the symptom onset dates of many thousands of confirmed cases (for this work’s example, more than half a million confirmed cases were considered), as well as the number of individuals vaccinated each day in the study group. It is essential to recognize that the obtainable results are as realistic as the used information. In Mexico, during the study period, the COVID-19 tests, the registration of confirmed cases, and the vaccination campaigns were entirely controlled by the country’s leading health authorities; this could favor minor or slight imprecisions in data.
- (2)
- The assignation of a reference group; for this study, the 30–39 group was selected. During a long period, the reference group must have exhibited daily values of its relative incidence that were similar to those shown by the study group. Figure 1a and Figure 3 demonstrate that the Mexican 30–39 group fulfilled such a condition for at least 37 weeks. It would be expected that population groups in which the recommendation to socially isolate was successfully implemented would not fulfill this condition. Therefore, its fulfillment must not be assumed, and it must be corroborated with real-world data. To illustrate these exceptions, consider the case of the Mexican students, who continued their education remotely during the study period. This strategy is expected to have significantly contributed to the decrease in relative incidence among younger Mexicans (<30 years old). Thus, the proposed methodology must not be applied to such population groups.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| WHO | World Health Organization |
| Vaccine effectiveness | |
| Beneficial effect induced by the administrated vaccines | |
| Percentage of the population daily vaccinated (registered in real-time) | |
| Percentage of the population daily vaccinated (considering a possible underestimation of 10% concerning the values) | |
| Relative Incidence | |
| Vaccinated group (expressed as a superscript) | |
| Unvaccinated group (expressed as a superscript) | |
| Totality of a group (expressed as a superscript) | |
| Confirmed Cases | |
| Population of a group | |
| mDB | massive Database |
| Reference group | |
| Group of 60 or more years old (expressed as a subscript) | |
| Reference group (expressed as a subscript) | |
| Group of 30 to 39 years old (expressed as a subscript) | |
| A specific date for which an affirmation is valid (expressed as a superscript) | |
| time elapsed since the completion of the vaccination scheme (expressed as a superscript) | |
| Maximum value of the profile | |
| Number of days prior to the application of the second dose during which the first dose effects are perceptible in the group | |
| Time interval during which the daily value of is greater than 0.8 | |
| Time interval during which the daily value of is greater than 0.5 | |
| Minimum number of days after completing the vaccination scheme required for the daily value of to decrease to values less than 0.1. | |
| Confidence Interval |
References
- Pifarré i Arolas, H.; Acosta, E.; López-Casasnovas, G.; Lo, A.; Nicodemo, C.; Riffe, T.; Myrskylä, M. Years of life lost to COVID-19 in 81 countries. Sci. Rep. 2021, 11, 3504. [Google Scholar] [CrossRef] [PubMed]
- Carrera-Hueso, F.J.; Álvarez-Arroyo, L.; Poquet-Jornet, J.E.; Vázquez-Ferreiro, P.; Martínez-Gonzalbez, R.; El-Qutob, D.; Ramón-Barrios, M.A.; Martínez-Martínez, F.; Poveda-Andrés, J.L.; Crespo-Palomo, C. Hospitalization budget impact during the COVID-19 pandemic in Spain. Health Econ. Rev. 2021, 11, 43. [Google Scholar] [CrossRef] [PubMed]
- Mishra, N.P.; Das, S.S.; Yadav, S.; Khan, W.; Afzal, M.; Alarifi, A.; Kenawy, E.-R.; Ansari, M.T.; Hasnain, M.S.; Nayak, A.K. Global impacts of pre- and post-COVID-19 pandemic: Focus on socio-economic consequences. Sens. Int. 2020, 1, 100042. [Google Scholar] [CrossRef] [PubMed]
- Nicola, M.; Alsafi, Z.; Sohrabi, C.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, M.; Agha, R. The socio-economic implications of the coronavirus pandemic (COVID-19): A review. Int. J. Sur. 2020, 78, 185–193. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-C.; Chen, C.-S.; Chan, Y.-J. The outbreak of COVID-19: An overview. J. Chin. Med. Assoc. 2020, 83, 217–220. [Google Scholar] [CrossRef] [PubMed]
- Fadda, M.; Albanese, E.; Suggs, L.S. When a COVID-19 vaccine is ready, will we all be ready for it? Int. J. Public Health 2020, 65, 711–712. [Google Scholar] [CrossRef] [PubMed]
- Coronavirus Disease (COVID-19): COVID-19 Vaccines. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/covid-19-vaccines (accessed on 4 February 2023).
- Status of COVID-19 Vaccines within WHO EUL/PQ Evaluation Process. Available online: https://extranet.who.int/pqweb/sites/default/files/documents/Status_COVID_VAX_07July2022.pdf (accessed on 4 February 2023).
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and efficacy of the BNT162b2 mRNA COVID-19 vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef]
- Falsey, A.R.; Sobieszczyk, M.E.; Hirsch, I.; Sproule, S.; Robb, M.L.; Corey, L.; Neuzil, K.M.; Hahn, W.; Hunt, J.; Mulligan, M.J.; et al. Phase 3 safety and efficacy of AZD1222 (ChAdOx1 nCoV-19) COVID-19 vaccine. N. Engl. J. Med. 2021, 385, 2348–2360. [Google Scholar] [CrossRef]
- Sadoff, J.; Gray, G.; Vandebosch, A.; Cárdenas, V.; Shukarev, G.; Grinsztejn, B.; Goepfert, P.A.; Truyers, C.; Fennema, H.; Spiessens, B.; et al. Safety and efficacy of single-dose Ad26.COV2.S vaccine against COVID-19. N. Engl. J. Med. 2021, 384, 2187–2201. [Google Scholar] [CrossRef]
- El Sahly, H.M.; Baden, L.R.; Essink, B.; Doblecki-Lewis, S.; Martin, J.M.; Anderson, E.J.; Campbell, T.B.; Clark, J.; Jackson, L.A.; Fichtenbaum, C.J.; et al. Efficacy of the mRNA-1273 SARS-CoV-2 vaccine at completion of blinded phase. N. Engl. J. Med. 2021, 385, 1774–1785. [Google Scholar] [CrossRef]
- Tanriover, M.D.; Doğanay, H.L.; Akova, M.; Güner, H.R.; Azap, A.; Akhan, S.; Köse, Ş.; Erdinç, F.Ş.; Akalın, E.H.; Tabak, Ö.F.; et al. Efficacy and safety of an inactivated whole-virion SARS-CoV-2 vaccine (CoronaVac): Interim results of a double-blind, randomised, placebo-controlled, phase 3 trial in Turkey. Lancet 2021, 398, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Ella, R.; Reddy, S.; Blackwelder, W.; Potdar, V.; Yadav, P.; Sarangi, V.; Aileni, V.K.; Kanungo, S.; Rai, S.; Reddy, P.; et al. Efficacy, safety, and lot-to-lot immunogenicity of an inactivated SARS-CoV-2 vaccine (BBV152): Interim results of a randomised, double-blind, controlled, phase 3 trial. Lancet 2021, 398, 2173–2184. [Google Scholar] [CrossRef] [PubMed]
- Heath, P.T.; Galiza, E.P.; Baxter, D.N.; Boffito, M.; Browne, D.; Burns, F.; Chadwick, D.R.; Clark, R.; Cosgrove, C.; Galloway, J.; et al. Safety and efficacy of NVX-CoV2373 COVID-19 vaccine. N. Engl. J. Med. 2021, 385, 1172–1183. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.-Y.; Gu, Y.; Wheeler, B.; Young, H.; Holloway, S.; Sunny, S.-K.; Moore, Z.; Zeng, D. Effectiveness of Covid-19 vaccines over a 9-month period in North Carolina. N. Engl. J. Med. 2022, 386, 933–941. [Google Scholar] [CrossRef] [PubMed]
- Chemaitelly, H.; Tang, P.; Hasan, M.R.; AlMukdad, S.; Yassine, H.M.; Benslimane, F.M.; Al Khatib, H.A.; Coyle, P.; Ayoub, H.H.; Al Kanaani, Z.; et al. Waning of BNT162b2 vaccine protection against SARS-CoV-2 infection in Qatar. N. Engl. J. Med. 2021, 385, e83. [Google Scholar] [CrossRef]
- Tartof, S.Y.; Slezak, J.M.; Fischer, H.; Hong, V.; Ackerson, B.K.; Ranasinghe, O.N.; Frankland, T.B.; Ogun, O.A.; Zamparo, J.M.; Gray, S.; et al. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study. Lancet 2021, 398, 1407–1416. [Google Scholar] [CrossRef]
- Goldberg, Y.; Mandel, M.; Bar-On, Y.M.; Bodenheimer, O.; Freedman, L.; Haas, E.J.; Milo, R.; Alroy-Preis, S.; Ash, N.; Huppert, A. Waning immunity after the BNT162b2 vaccine in Israel. N. Engl. J. Med. 2021, 385, e85. [Google Scholar] [CrossRef]
- Mizrahi, B.; Lotan, R.; Kalkstein, N.; Peretz, A.; Perez, G.; Ben-Tov, A.; Chodick, G.; Gazit, S.; Patalon, T. Correlation of SARS-CoV-2-breakthrough infections to time-from-vaccine. Nat. Commun. 2021, 12, 6379. [Google Scholar] [CrossRef] [PubMed]
- Pegu, A.; O‘Connell, S.E.; Schmidt, S.D.; O‘Dell, S.; Talana, C.A.; Lai, L.; Albert, J.; Anderson, E.; Bennett, H.; Corbett, K.S.; et al. Durability of mRNA-1273 vaccine–induced antibodies against SARS-CoV-2 variants. Science 2021, 373, 1372–1377. [Google Scholar] [CrossRef]
- van Gils, M.J.; Lavell, A.; van der Straten, K.; Appelman, B.; Bontjer, I.; Poniman, M.; Burger, J.A.; Oomen, M.; Bouhuijs, J.H.; van Vught, L.A.; et al. Antibody responses against SARS-CoV-2 variants induced by four different SARS-CoV-2 vaccines in health care workers in the Netherlands: A prospective cohort study. PLoS Med. 2022, 19, e1003991. [Google Scholar] [CrossRef]
- Suthar, M.S.; Arunachalam, P.S.; Hu, M.; Reis, N.; Trisal, M.; Raeber, O.; Chinthrajah, S.; Davis-Gardner, M.E.; Manning, K.; Mudvari, P.; et al. Durability of immune responses to the BNT162b2 mRNA vaccine. Med 2022, 3, 25–27. [Google Scholar] [CrossRef] [PubMed]
- Levin, E.G.; Lustig, Y.; Cohen, C.; Fluss, R.; Indenbaum, V.; Amit, S.; Doolman, R.; Asraf, K.; Mendelson, E.; Ziv, A.; et al. Waning immune humoral response to BNT162b2 COVID-19 vaccine over 6 months. N. Engl. J. Med. 2021, 385, e84. [Google Scholar] [CrossRef] [PubMed]
- Coronavirus (COVID-19) Vaccinations. Available online: https://ourworldindata.org/covid-vaccinations (accessed on 4 February 2023).
- Wouters, O.J.; Shadlen, K.C.; Salcher-Konrad, M.; Pollard, A.J.; Larson, H.J.; Teerawattananon, Y.; Jit, M. Challenges in ensuring global access to COVID-19 vaccines: Production, affordability, allocation, and deployment. Lancet 2021, 397, 1023–1034. [Google Scholar] [CrossRef] [PubMed]
- Vaccine Equity. Available online: https://www.who.int/campaigns/vaccine-equity (accessed on 4 February 2023).
- Alaran, A.J.; Adebisi, Y.A.; Badmos, A.; Khalid-Salako, F.; Gaya, S.K.; Ilesanmi, E.B.; Olaoye, D.Q.; Bamisaiye, A.; Lucero-Prisno, D.E. Uneven power dynamics must be levelled in COVID-19 vaccines access and distribution. Public Health Pract. 2021, 2, 100096. [Google Scholar] [CrossRef]
- Choi, E.M. COVID-19 vaccines for low-and middle-income countries. Trans. R. Soc. Tropical Med. Hyg. 2021, 115, 447–456. [Google Scholar] [CrossRef]
- Makoni, M. Tanzania refuses COVID-19 vaccines. Lancet 2021, 397, 566. [Google Scholar] [CrossRef]
- Sallam, M. COVID-19 vaccine hesitancy worldwide: A concise systematic review of vaccine acceptance rates. Vaccines 2021, 9, 160. [Google Scholar] [CrossRef]
- Adnan; Ali, A.; ur Rahmamn, M.; Shah, Z.; Kumam, P. Investigation of a time-fractional COVID-19 mathematical model with singular kernel. Adv. Contin. Discret. Model. 2022, 2022, 34. [Google Scholar] [CrossRef]
- Abadin Zafar, Z.U.; Ali, N.; Inc, M.; Shah, Z.; Younas, S. Mathematical modeling of corona virus (COVID-19) and stability analysis. Comput. Methods Biomech. Biomed. Eng. 2022, 0, 1–20. [Google Scholar] [CrossRef]
- Leung, K.; Wu, J.T.; Leung, G.M. Effects of adjusting public health, travel, and social measures during the roll-out of COVID-19 vaccination: A modelling study. Lancet Public Health 2021, 6, e674–e682. [Google Scholar] [CrossRef]
- Matrajt, L.; Eaton, J.; Leung, T.; Brown, E.R. Vaccine optimization for COVID-19: Who to vaccinate first? Sci. Adv. 2021, 7, eabf1374. [Google Scholar] [CrossRef] [PubMed]
- Jentsch, P.C.; Anand, M.; Bauch, C.T. Prioritising COVID-19 vaccination in changing social and epidemiological landscapes: A mathematical modelling study. Lancet Infect. Dis. 2021, 21, 1097–1106. [Google Scholar] [CrossRef]
- Hogan, A.B.; Winskill, P.; Watson, O.J.; Walker, P.G.T.; Whittaker, C.; Baguelin, M.; Brazeau, N.F.; Charles, G.D.; Gaythorpe, K.A.M.; Hamlet, A.; et al. Within-country age-based prioritisation, global allocation, and public health impact of a vaccine against SARS-CoV-2: A mathematical modelling analysis. Vaccine 2021, 39, 2995–3006. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sandmann, F.G.; Barnard, R.C.; Pearson, C.A.B.; Pastore, R.; Pebody, R.; Flasche, S.; Jit, M. Optimising health and economic impacts of COVID-19 vaccine prioritisation strategies in the WHO European Region: A mathematical modelling study. Lancet Reg. Health Eur. 2022, 12, 100267. [Google Scholar] [CrossRef] [PubMed]
- Evaluation of COVID-19 Vaccine Effectiveness. Available online: https://www.who.int/publications/i/item/WHO-2019-nCoV-vaccine_effectiveness-measurement-2021.1 (accessed on 4 February 2023).
- Datos Abiertos Dirección General de Epidemiología. Available online: https://www.gob.mx/salud/documentos/datos-abiertos-152127 (accessed on 4 February 2023).
- Datos Abiertos. Available online: https://datosabiertos.salud.gob.mx/gobmx/salud/datos_abiertos/historicos/2021/12/datos_abiertos_covid19_25.12.2021.zip (accessed on 4 February 2023).
- Calendario de Vacunación. Available online: http://vacunacovid.gob.mx/wordpress/calendario-vacunacion/ (accessed on 4 February 2023).
- Población. Available online: https://www.inegi.org.mx/temas/estructura/ (accessed on 4 February 2023).
- Presentaciones de las Conferencias de Prensa 2021. Available online: https://www.gob.mx/salud/documentos/presentaciones-de-las-conferencias-de-prensa-2021 (accessed on 4 February 2023).
- Plan Nacional de Vacunación en la Ciudad de México. Available online: https://www.salud.cdmx.gob.mx/storage/app/uploads/public/613/cbc/f21/613cbcf21e670863591851.pdf (accessed on 4 February 2023).
- COVID-19 MÉXICO Comunicado Técnico Diario. Available online: https://www.gob.mx/cms/uploads/attachment/file/680207/2021.11.04_17h00_ComunicadoTecnicoDiario_Covid19__4_.pdf (accessed on 4 February 2023).
- Hyndman, R.J. Moving averages. In International Encyclopedia of Statistical Science, 1st ed.; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 866–869. [Google Scholar]
- Vaccine Efficacy, Effectiveness and Protection. Available online: https://www.who.int/news-room/feature-stories/detail/vaccine-efficacy-effectiveness-and-protection (accessed on 4 February 2023).
- Coronavirus (COVID-19) Deaths. Available online: https://ourworldindata.org/covid-deaths (accessed on 4 February 2023).
- Define and Solve a Problem by Using Solver. Available online: https://support.microsoft.com/en-us/office/define-and-solve-a-problem-by-using-solver-5d1a388f-079d-43ac-a7eb-f63e45925040 (accessed on 4 February 2023).
- Yu, D.C.; Fagan, J.E.; Foote, B.; Aly, A.A. An optimal load flow study by the generalized reduced gradient approach. Electr. Power Syst. Res. 1986, 10, 47–53. [Google Scholar] [CrossRef]
- Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. Revue française d’automatique, informatique, recherche opérationnelle. Rech. Opérationnelle 1974, 3, 73–103. Available online: http://www.numdam.org/item/?id=RO_1974__8_3_73_0 (accessed on 14 March 2023). [CrossRef] [Green Version]
- Facó, J.L.D. A generalized reduced gradient algorithm for solving large-scale discrete-time nonlinear optimal control problems. IFAC Proc. 1989, 22, 45–50. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Sánchez, Ó.A.; González-Ortiz, L.J.; Sánchez-Peña, M.J.; Gutiérrez-Pulido, H.; Cervantes, O.; Márquez-Sandoval, F.; Hernández-Bello, J.; Casillas, N.; Muñoz-Valle, J.F. A Novel Approach to Obtain Vaccine Effectiveness Continuous Profiles. Example Case: COVID-19 in Elderly Mexicans. Vaccines 2023, 11, 719. https://doi.org/10.3390/vaccines11040719
González-Sánchez ÓA, González-Ortiz LJ, Sánchez-Peña MJ, Gutiérrez-Pulido H, Cervantes O, Márquez-Sandoval F, Hernández-Bello J, Casillas N, Muñoz-Valle JF. A Novel Approach to Obtain Vaccine Effectiveness Continuous Profiles. Example Case: COVID-19 in Elderly Mexicans. Vaccines. 2023; 11(4):719. https://doi.org/10.3390/vaccines11040719
Chicago/Turabian StyleGonzález-Sánchez, Óscar A., Luis J. González-Ortiz, M. Judith Sánchez-Peña, Humberto Gutiérrez-Pulido, Oscar Cervantes, Fabiola Márquez-Sandoval, Jorge Hernández-Bello, Norberto Casillas, and José Francisco Muñoz-Valle. 2023. "A Novel Approach to Obtain Vaccine Effectiveness Continuous Profiles. Example Case: COVID-19 in Elderly Mexicans" Vaccines 11, no. 4: 719. https://doi.org/10.3390/vaccines11040719
APA StyleGonzález-Sánchez, Ó. A., González-Ortiz, L. J., Sánchez-Peña, M. J., Gutiérrez-Pulido, H., Cervantes, O., Márquez-Sandoval, F., Hernández-Bello, J., Casillas, N., & Muñoz-Valle, J. F. (2023). A Novel Approach to Obtain Vaccine Effectiveness Continuous Profiles. Example Case: COVID-19 in Elderly Mexicans. Vaccines, 11(4), 719. https://doi.org/10.3390/vaccines11040719







