The Impact of Serotype Cross-Protection on Vaccine Trials: DENVax as a Case Study
Abstract
1. Introduction
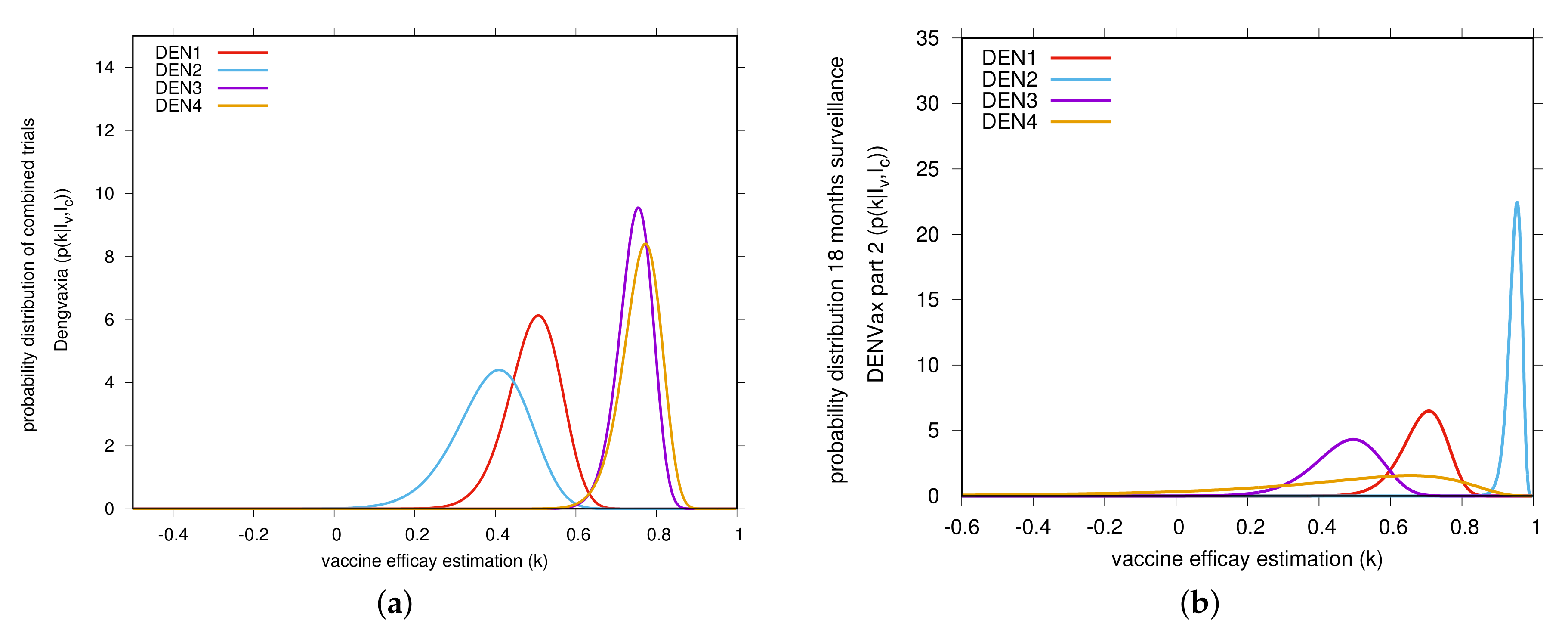
2. Results
3. Discussion
4. Materials and Methods
4.1. Linear Infection Model
4.2. Modeling Vaccine Trials with the Linear Infection Model
5. Bayesian Analysis
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Halstead, S.B. Antibody-dependent Enhancement of Infection: A Mechanism for Indirect Virus Entry into Cells. In Cellular Receptors for Animal Viruses; Cold Spring Harbor Laboratory Press: New York, NY, USA, 1994; Chapter 25; pp. 493–516. ISBN 0-87969-429-7. [Google Scholar]
- Dejnirattisai, W.; Jumnainsong, A.; Onsirisakul, N.; Fitton, P.; Vasanawathana, S.; Limpitikul, W.; Puttikhunt, C.; Edwards, C.; Duangchinda, T.; Supasa, S.; et al. Cross-Reacting Antibodies Enhance Dengue Virus Infection in Humans. Science 2010, 328, 745–748. [Google Scholar] [CrossRef] [PubMed]
- Halstead, S.B. Dengue antibody-dependent enhancement: Knowns and unknowns. Microbiol. Spectrum. 2014, 2, AID-0022-2014. [Google Scholar]
- Katzelnick, L.C.; Gresh, L.; Halloran, M.E.; Mercado, J.C.; Kuan, G.; Gordon, A.; Balmaseda, A.; Harris, E. Antibody-dependent enhancement of severe dengue disease in humans. Science 2017, 358, 929–932. [Google Scholar] [CrossRef] [PubMed]
- Capeding, M.R.; Tran, N.H.; Hadinegoro, R.S.; MuhammadIsmail, H.I.H.J.; Chotpitayasunondh, T.; Chua, M.N.; Luong, C.Q.; Rusmil, K.; Wirawan, D.N.; Nallusamy, R.; et al. Clinical efficacy and safety of a novel tetravalent dengue vaccine in healthy children in Asia: A phase 3, randomised, observer-masked, placebo-controlled trial. Lancet 2014, 384, 1358–1365. [Google Scholar] [CrossRef]
- Villar, L.; Dayan, G.H.; Arredondo-García, J.L.; Rivera, D.M.; Cunha, R.; Deseda, C.; Reynales, H.; Costa, M.S.; Morales-Ramírez, J.O.; Carrasquilla, G.; et al. Efficacy of a tetravalent dengue vaccine in children in Latin America. N. Engl. J. Med. 2015, 372, 113–123. [Google Scholar] [CrossRef]
- Hadinegoro, S.R.; Arredondo-García, J.L.; Capeding, M.R.; Deseda, C.; Chotpitayasunondh, T.; Dietze, R.; Ismail, H.I.H.M.; Reynales, H.; Limkittikul, K.; Rivera-Medina, D.M.; et al. Efficacy and long term safety of a dengue vaccine in regions of endemic disease. N. Engl. J. Med. 2015, 373, 1195–1206. [Google Scholar] [CrossRef]
- Biswal, S.; Reynales, H.; Saez-Llorens, X.; Lopez, P.; Borja-Tabora, C.; Kosalaraksa, P.; Sirivichayakul, C.; Watanaveeradej, V.; Rivera, L.; Espinoza, F.; et al. Efficacy of a Tetravalent Dengue Vaccine in Healthy Children and Adolescents. N. Engl. J. Med. 2019, 381, 2009–2019. [Google Scholar] [CrossRef]
- Biswal, S.; Borja-Tabora, C.; Martinez Vargas, L.; Velásquez, H.; Alera, M.T.; Sierr, V.; Rodriguez-Arenales, E.J.; Yu, D.; Wickramasinghe, V.P.; Moreira, E.D., Jr.; et al. Efficacy of a tetravalent dengue vaccine in healthy children aged 4–16 years: A randomised, placebo-controlled, phase 3 trial. Lancet 2020, 395, 1423–1433. [Google Scholar] [CrossRef]
- Kallas, E.G.; Precioso, A.R.; Palacio, R.; Thomé, B.; Braga, P.E.; Vanni, T.; Campos, L.M.A.; Ferrari, L.; Mondini, G.; Salomão, M.D.; et al. Safety and immunogenicity of the tetravalent, live-attenuated dengue vaccine Butantan-DV in adults in Brazil: A two-step, double-blind, randomised placebo-controlled phase 2 trial. Lancet Infect. Dis. 2020, 20, 839–850. [Google Scholar] [CrossRef]
- Aguiar, M.; Stollenwerk, N.; Halstead, S.B. The risks behind Dengvaxia recommendation. Lancet Infect. Dis. 2016, 16, 882–883. [Google Scholar] [CrossRef]
- Halstead, S.B.; Russell, P.K. Protective and Immunological Behavior of Yellow Fever Dengue Chimeric Vaccine. Vaccine 2016, 34, 1643–1647. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, M.; Stollenwerk, N.; Halstead, S.B. The impact of the newly licensed dengue vaccine in endemic countries. PLoS Negl. Trop. Dis. 2016, 10, e0005179. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization Strategic Advisory Group of Experts (SAGE) on Immunization. Background Paper on Dengue Vaccines Prepared by the SAGE Working Group on Dengue Vaccines and the WHO Secretariat. 2016. Available online: http://www.who.int/immunization/sage/meetings/2016/april/1_Background_Paper_Dengue_Vaccines_2016_03_17.pdf? (accessed on 2 April 2016).
- Aguiar, M.; Stollenwerk, N. Dengvaxia efficacy dependency on serostatus: A closer look at more recent data. Clin. Infect. Dis. 2018, 66, 641–642. [Google Scholar] [CrossRef] [PubMed]
- Aguiar, M.; Stollenwerk, N. Dengvaxia: Age as surrogate for serostatus. Lancet Infect. Dis. 2018, 18, 245. [Google Scholar] [CrossRef]
- Sanofi Updates Information on Dengue Vaccine. Available online: https://www.sanofi.com/en/media-room/press-releases/2017/2017-11-29-17-36-30 (accessed on 29 November 2017).
- World Health Organization. Revised SAGE Recommendation on Use of Dengue Vaccine. 2018. Available online: https://www.who.int/immunization/diseases/dengue/revised_SAGE_recommendations_dengue_vaccines_apr2018/en/ (accessed on 19 April 2018).
- Halstead, S.B.; Katzelnick, L.C.; Russell, P.K.; Markoff, L.; Aguiar, M.; Dans, L.R.; Dans, A.L. Ethics of a partially effective dengue vaccine: Lessons from the Philippines. Vaccine 2020, 38, 5572–5576. [Google Scholar] [CrossRef]
- Aguiar, M. Dengue vaccination: A more ethical approach is needed. Lancet 2018, 391, 1769–1770. [Google Scholar] [CrossRef]
- Aguiar, M.; Mateus, L.; Stollenwerk, N. The currently best estimate for worldwide dengue vaccine efficacy. AIP Conf. Proc. 2016, 1738, 390014. [Google Scholar]
- Sabin, A.B. Research on dengue during World War II. Am. J. Trop. Med. Hyg. 1952, 1, 30–50. [Google Scholar] [CrossRef]
- Anderson, K.B.; Gibbons, R.V.; Cummings, D.A.; Nisalak, A.; Green, S.; Libraty, D.H.; Jarman, R.G.; Srikiatkhachorn, A.; Mammen, M.P.; Darunee, B.; et al. A Shorter Time Interval Between First and Second Dengue Infections Is Associated With Protection From Clinical Illness in a School-based Cohort in Thailand. J. Infect. Dis. 2013, 209, 360–368. [Google Scholar] [CrossRef]
- Stollenwerk, N.; Jansen, V. Population Biology and Criticality: From Critical Birth—Death Processes to Self-Organized Criticality in Mutation Pathogen Systems; Imperial College Press; World Scientific: London, UK, 2011. [Google Scholar]
- Stollenwerk, N.; Aguiar, M.; Ballesteros, S.; Boto, J.; Kooi, B.; Mateus, L. Dynamic noise, chaos and parameter estimation in population biology. R. Soc. Interface Focus 2012, 2, 156–169. [Google Scholar] [CrossRef] [PubMed]
- Mateus, L.; Stollenwerk, N.; Zambrini, J.C. Stochastic Models in Population Biology: From Dynamic Noise to Bayesian Description and Model Comparison for Given Data Sets. Int. J. Comput. Math. 2013, 90, 2161–2173. [Google Scholar] [CrossRef]
- Mateus, L.; Masoero, D.; Rocha, F.; Aguiar, M.; Skwara, U.; Ghaffari, P.; Zambrini, J.C.; Stollenwerk, N. Epidemiological models in semiclassical approximation: An analytically solvable model as test case. In Proceedings of the 14th International Conference on Computational and Mathematical Methods in Science and Engineering, CMMSE 2014, Cadiz, Spain, 3–7 July 2014; ISBN 978-84-616-9216-3. [Google Scholar]


| Part 1 Efficacy Data of the TAK-003 Phase 3 Trial | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| section A | section B | ||||||||
| Seropositive at baseline (82.2%) | Seronegative at baseline (74.9%) | Overall (seropositive and seronegative) | |||||||
| vaccine efficacy | |||||||||
| Dengue Serotype | Vaccinated | Control | Estimated vaccine | Vaccinated | Control | Estimated Vaccine | Vaccinated | Control | Estimated vaccine |
| () | () | efficacy and 95% | () | () | efficacy and 95% | ( 12,700) | () | efficacy and 95% | |
| Dengue cases | Dengue cases | Confidence Interval | Dengue cases | Dengue cases | Confidence Interval | Dengue cases | Dengue cases | Confidence Interval | |
| ALL | 41 | 110 | 20 | 39 | 61 | 149 | |||
| [] | [] | [] | |||||||
| 7 | 17 | 9 | 13 | 16 | 30 | ||||
| [] | [] | [] | |||||||
| 3 | 42 | 0 | 22 | 3 | 64 | ||||
| [] | [] | ||||||||
| 28 | 47 | 11 | 4 | 39 | 51 | ||||
| [] | [] | [] | |||||||
| 3 | 4 | 0 | 0 | inconclusive | 3 | 4 | |||
| [] | [] | ||||||||
| Part 2 Efficacy Data of the TAK-003 Phase 3 Trial | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| section A | section B | ||||||||
| Seropositive at baseline (82.2%) | Seronegative at baseline (74.9%) | Overall (seropositive and seronegative) | |||||||
| vaccine efficacy | |||||||||
| Dengue Serotype | Vaccinated | Control | Estimated vaccine | Vaccinated | Control | Estimated Vaccine | Vaccinated | Control | Estimated vaccine |
| () | () | efficacy and 95% | () | () | efficacy and 95% | ( 12,700) | () | efficacy and 95% | |
| Dengue cases | Dengue cases | Confidence Interval | Dengue cases | Dengue cases | Confidence Interval | Dengue cases | Dengue cases | Confidence Interval | |
| ALL | 75 | 150 | 39 | 56 | 114 | 206 | |||
| [] | [] | [] | |||||||
| 21 | 37 | 17 | 25 | 38 | 62 | ||||
| [] | [] | [] | |||||||
| 7 | 54 | 1 | 26 | 8 | 80 | ||||
| [] | [] | [] | |||||||
| 43 | 54 | 20 | 6 | 63 | 60 | ||||
| [] | [] | [] | |||||||
| 4 | 5 | 1 | 0 | inconclusive | 5 | 5 | |||
| [] | [] | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguiar, M.; Stollenwerk, N. The Impact of Serotype Cross-Protection on Vaccine Trials: DENVax as a Case Study. Vaccines 2020, 8, 674. https://doi.org/10.3390/vaccines8040674
Aguiar M, Stollenwerk N. The Impact of Serotype Cross-Protection on Vaccine Trials: DENVax as a Case Study. Vaccines. 2020; 8(4):674. https://doi.org/10.3390/vaccines8040674
Chicago/Turabian StyleAguiar, Maíra, and Nico Stollenwerk. 2020. "The Impact of Serotype Cross-Protection on Vaccine Trials: DENVax as a Case Study" Vaccines 8, no. 4: 674. https://doi.org/10.3390/vaccines8040674
APA StyleAguiar, M., & Stollenwerk, N. (2020). The Impact of Serotype Cross-Protection on Vaccine Trials: DENVax as a Case Study. Vaccines, 8(4), 674. https://doi.org/10.3390/vaccines8040674




