Could a New COVID-19 Mutant Strain Undermine Vaccination Efforts? A Mathematical Modelling Approach for Estimating the Spread of B.1.1.7 Using Ontario, Canada, as a Case Study
Abstract
1. Introduction
2. Methods
- Reporting is relatively consistent.
- The total population in a region is constant.
- All severe cases are reported.
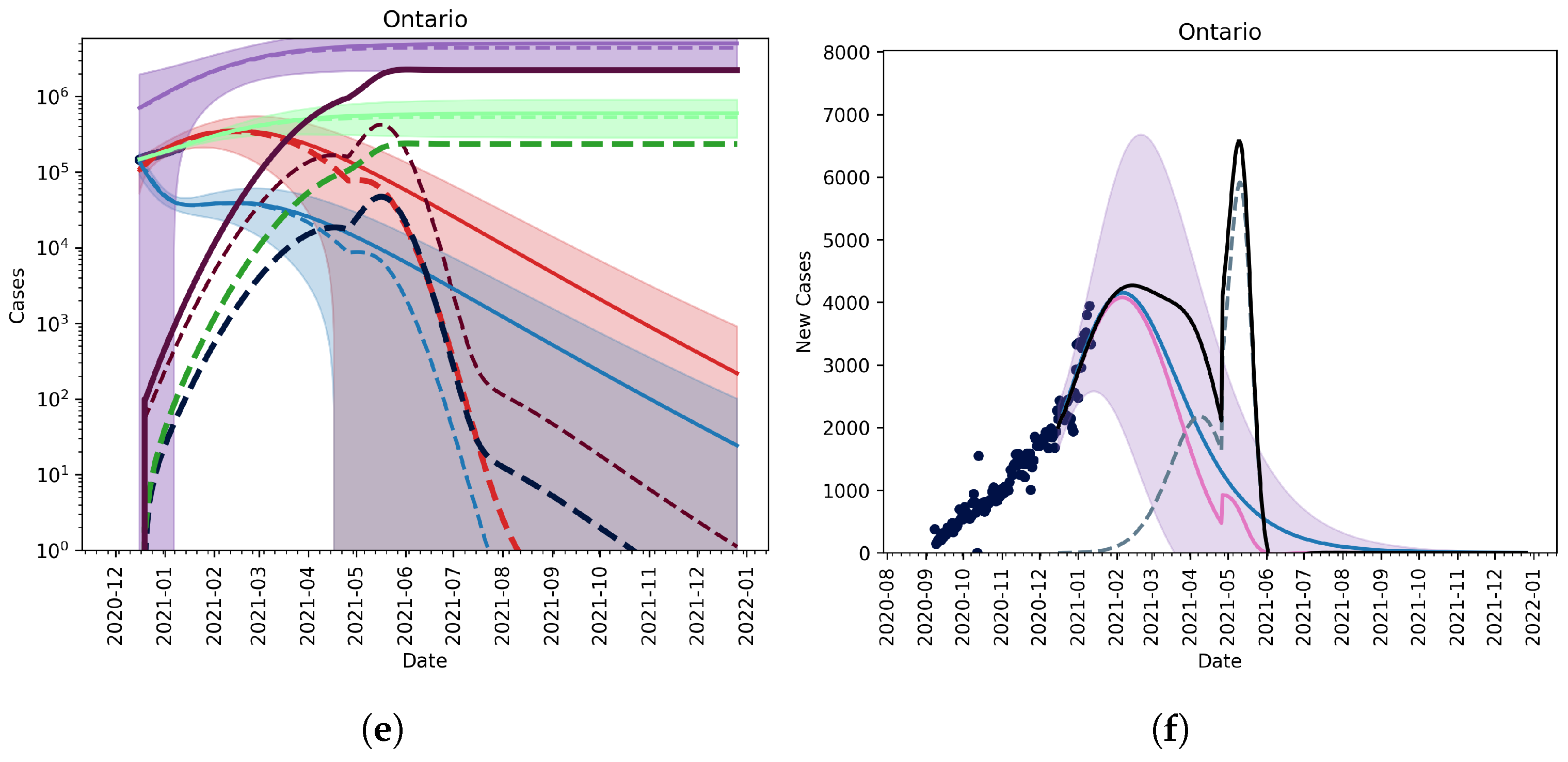
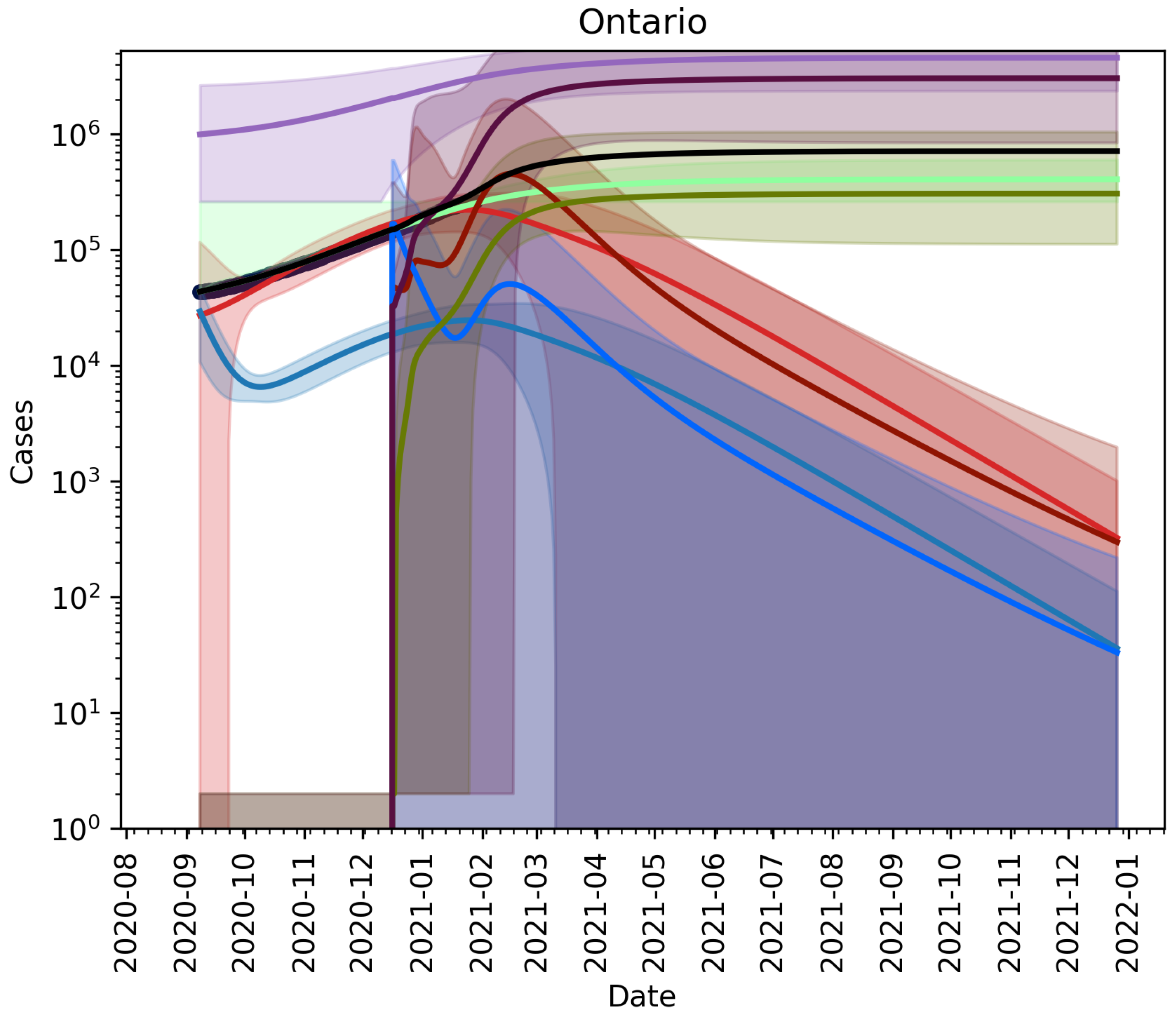
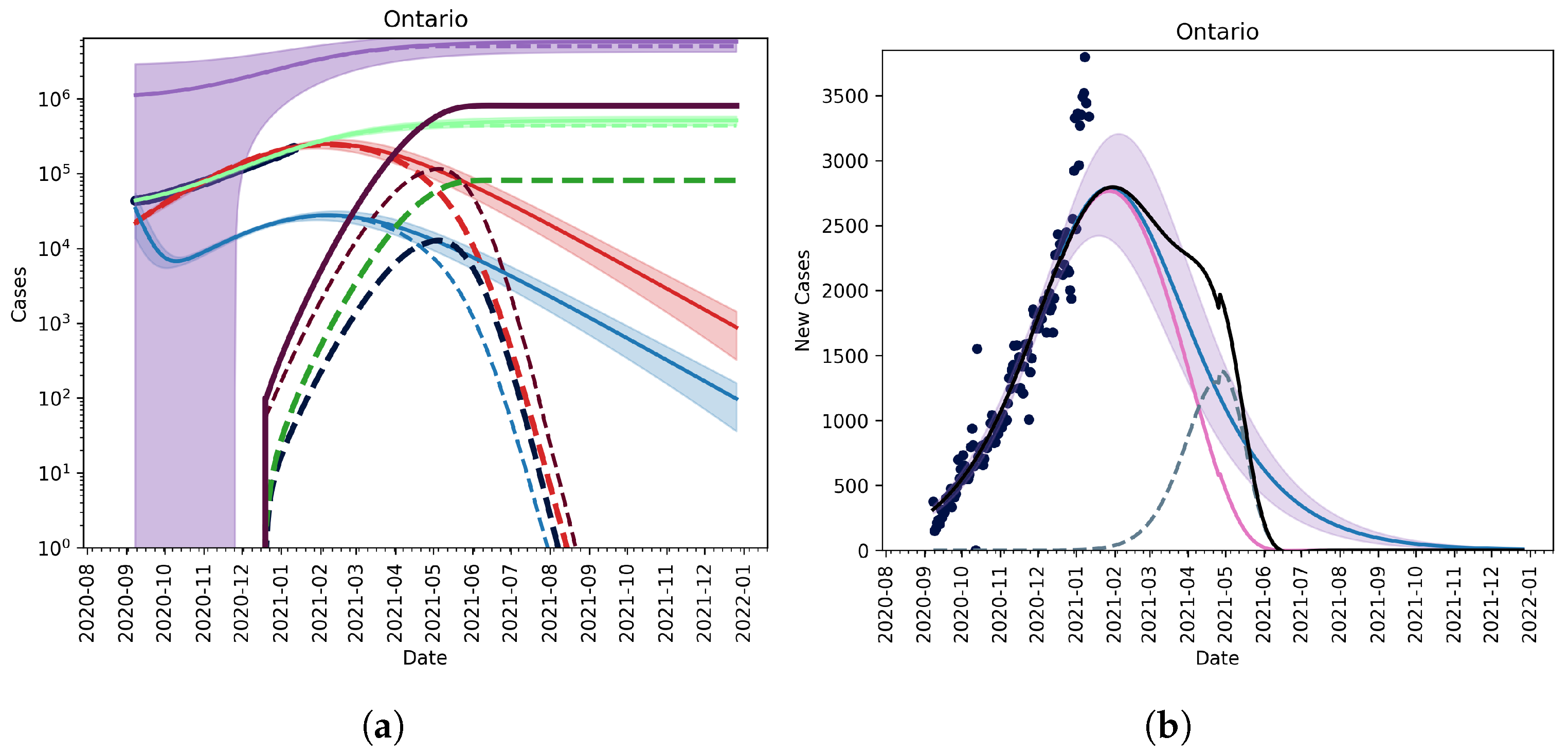
3. Results
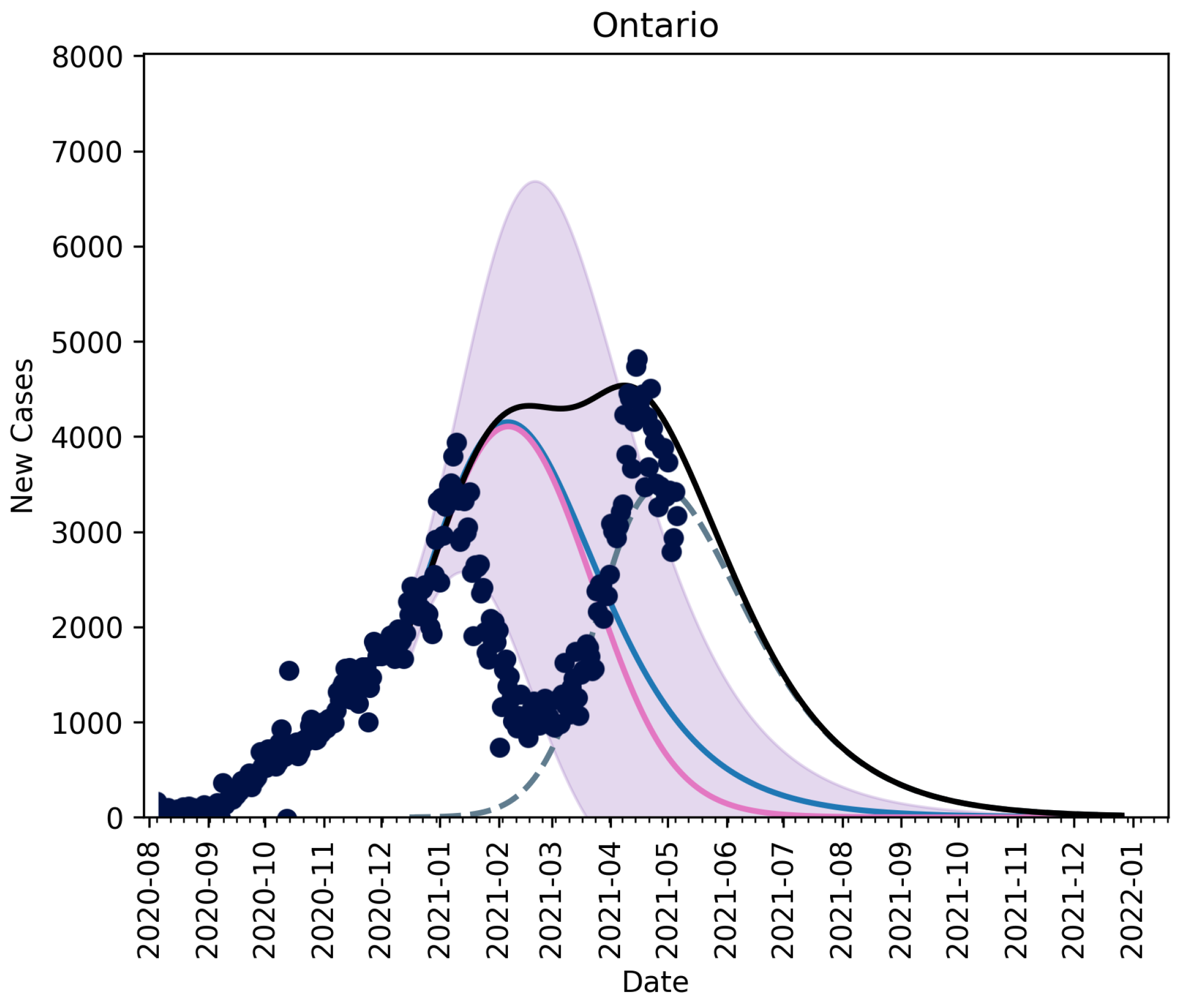
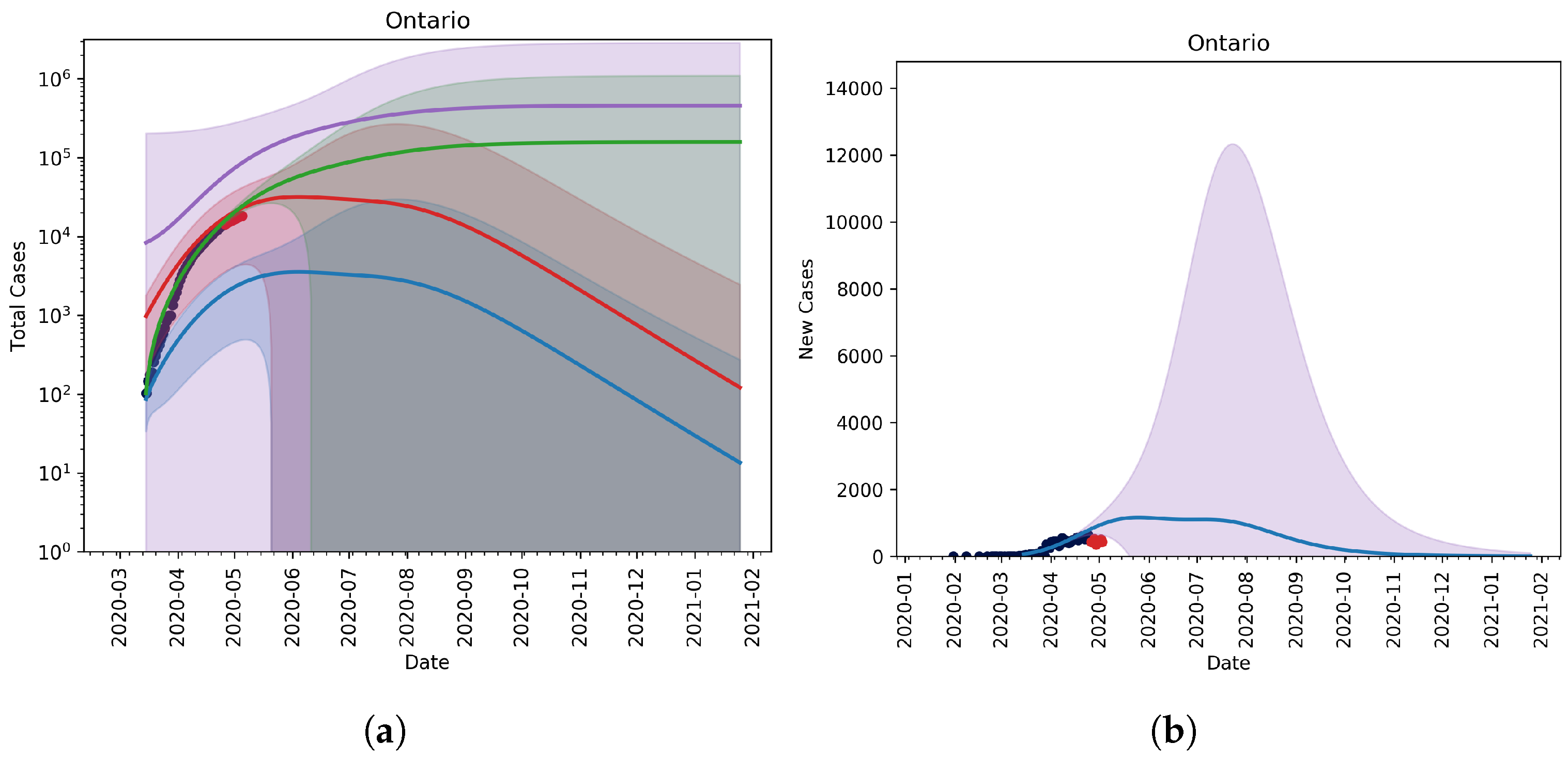
3.1. Scenario-Based Extrapolation from First Known Cases of B.1.1.7 Variant in Ontario
No Vaccination, No Relaxation
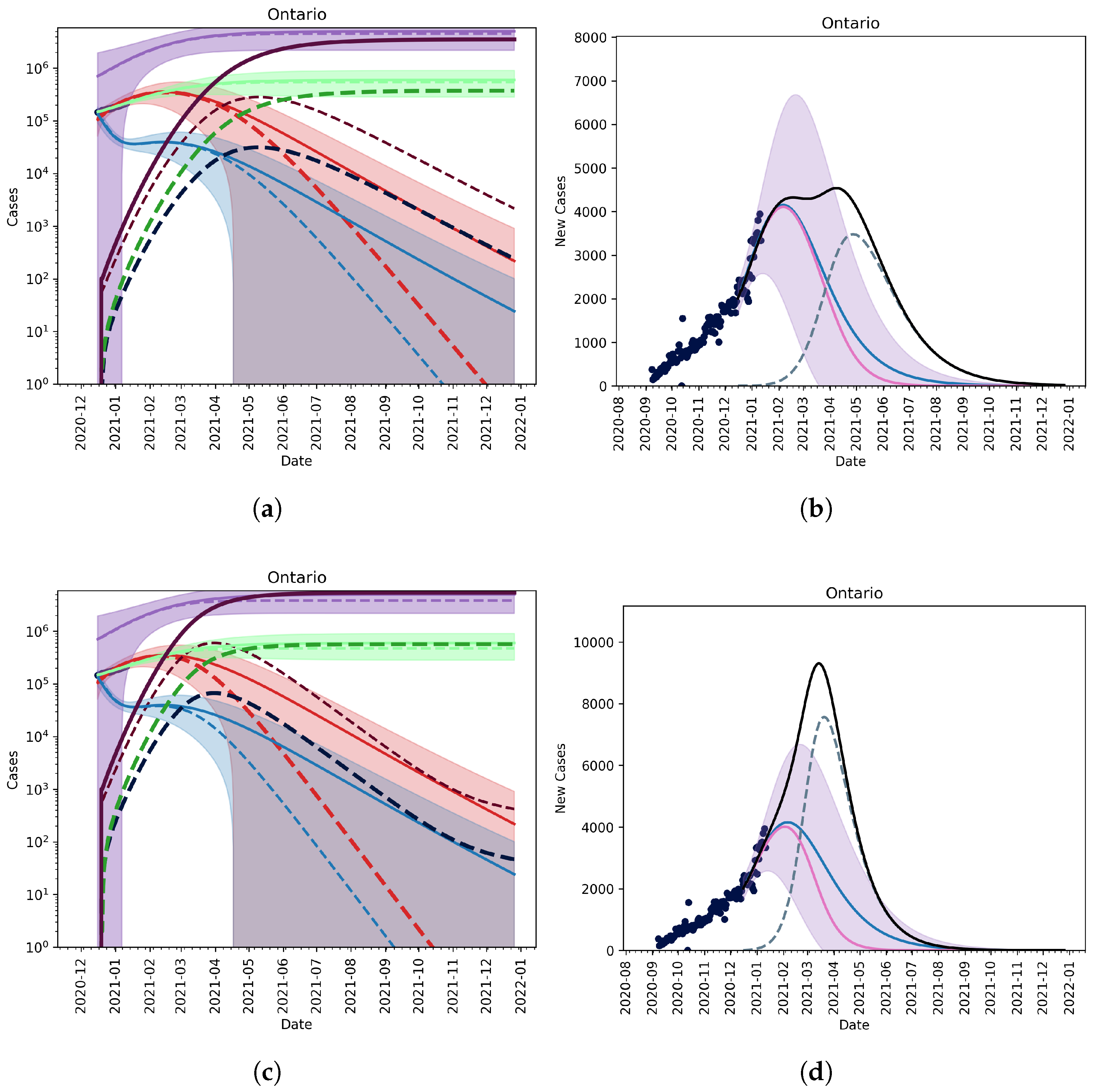
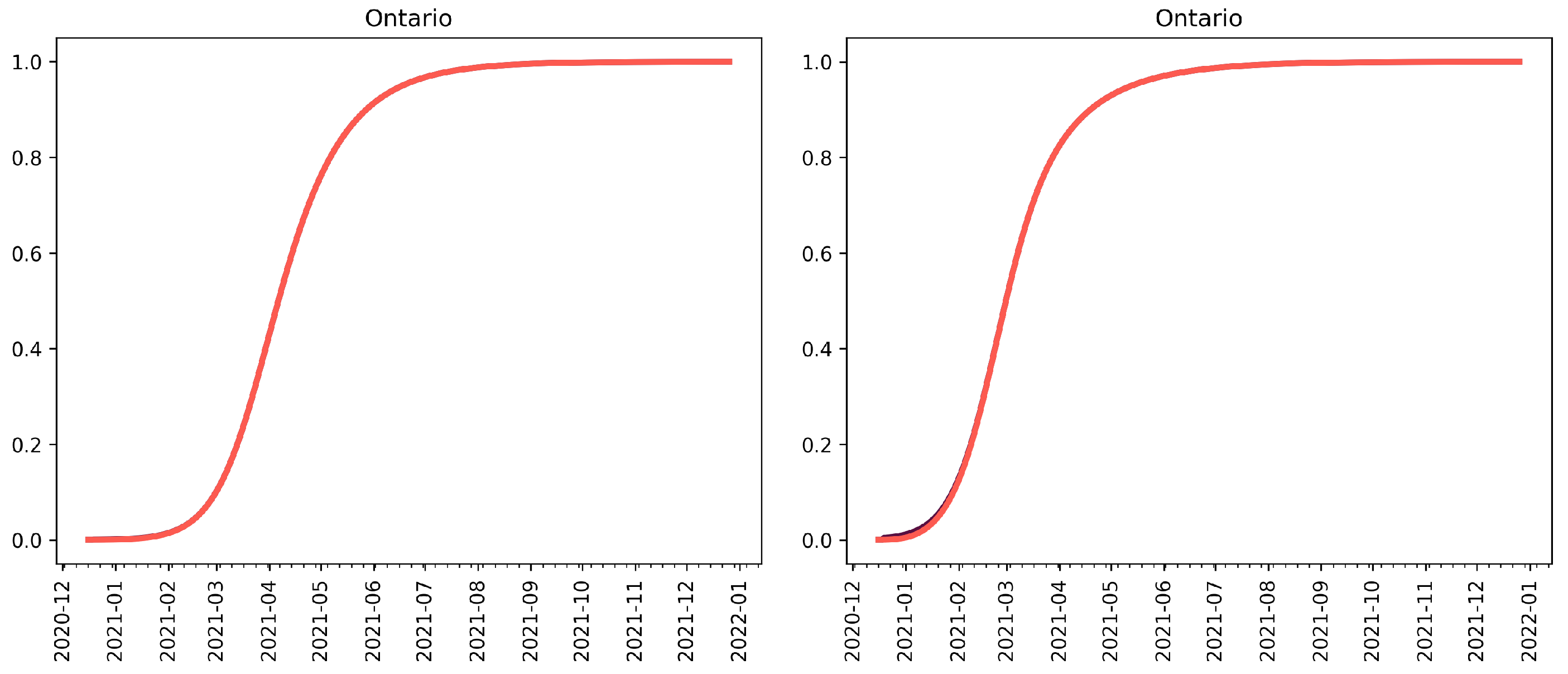
3.2. Extension to Vaccination and Relaxation
3.2.1. Vaccination without Relaxation
3.2.2. Vaccination and Relaxation
3.2.3. Fitting an Unknown Mutant
3.2.4. Christmas as an Anomaly
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Heesterbeek, H.; Anderson, R.M.; Andreasen, V.; Bansal, S.; De Angelis, D.; Dye, C.; Eames, K.T.; Edmunds, W.J.; Frost, S.D.; Funk, S.; et al. Modeling infectious disease dynamics in the complex landscape of global health. Science 2015, 347, aaa4339. [Google Scholar] [CrossRef] [PubMed]
- Stern, A.; Andino, R. Viral evolution: It is all about mutations. In Viral Pathogenesis; Elsevier: Amsterdam, The Netherlands, 2016; pp. 233–240. [Google Scholar]
- Bonhoeffer, S.; Nowak, M.A. Intra-host versus inter-host selection: Viral strategies of immune function impairment. Proc. Natl. Acad. Sci. USA 1994, 91, 8062–8066. [Google Scholar] [CrossRef]
- Martins, N.E.; Faria, V.G.; Teixeira, L.; Magalhães, S.; Sucena, É. Host adaptation is contingent upon the infection route taken by pathogens. PLoS Pathog. 2013, 9, e1003601. [Google Scholar] [CrossRef] [PubMed]
- Duffy, S. Why are rna virus mutation rates so damn high? PLoS Biol. 2018, 16, e3000003. [Google Scholar] [CrossRef] [PubMed]
- Binder, S.; Levitt, A.M.; Sacks, J.J.; Hughes, J.M. Emerging infectious diseases: Public health issues for the 21st century. Science 1999, 284, 1311–1313. [Google Scholar] [CrossRef]
- Burch, C.L.; Chao, L. Evolvability of an rna virus is determined by its mutational neighbourhood. Nature 2000, 406, 625–628. [Google Scholar] [CrossRef]
- Arenas, M.; Araujo, N.M.; Branco, C.; Castelhano, N.; Castro-Nallar, E.; Pérez-Losada, M. Mutation and recombination in pathogen evolution: Relevance, methods and controversies. Infect. Genet. Evol. 2018, 63, 295–306. [Google Scholar] [CrossRef] [PubMed]
- Cobey, S. Pathogen evolution and the immunological niche. Ann. N. Y. Acad. Sci. 2014, 1320, 1. [Google Scholar] [CrossRef] [PubMed]
- MacLean, R.C.; Hall, A.R.; Perron, G.G.; Buckling, A. The evolution of antibiotic resistance: Insight into the roles of molecular mechanisms of resistance and treatment context. Discov. Med. 2010, 10, 112–118. [Google Scholar]
- Hu, B.; Guo, H.; Zhou, P.; Shi, Z.-L. Characteristics of sars-cov-2 and covid-19. Nat. Rev. Microbiol. 2020, 19, 141–154. [Google Scholar] [CrossRef]
- Duhon, J.; Bragazzi, N.; Kong, J.D. The impact of non-pharmaceutical interventions, demographic, social, and climatic factors on the initial growth rate of covid-19: A cross-country study. Sci. Total Environ. 2021, 760, 144325. [Google Scholar] [CrossRef] [PubMed]
- Alam, I.; Radovanovic, A.; Incitti, R.; Kamau, A.A.; Alarawi, M.; Azhar, E.O.; Gojobori, T. Covmt: An interactive sars-cov-2 mutation tracker, with a focus on critical variants. Lancet Infect. Dis. 2021, 21, 602. [Google Scholar] [CrossRef]
- Phan, T. Genetic diversity and evolution of sars-cov-2. Infect. Genet. Evol. 2020, 81, 104260. [Google Scholar] [CrossRef]
- Pachetti, M.; Marini, B.; Giudici, F.; Benedetti, F.; Angeletti, S.; Ciccozzi, M.; Masciovecchio, C.; Ippodrino, R.; Zella, D. Impact of lockdown on covid-19 case fatality rate and viral mutations spread in 7 countries in europe and north america. J. Transl. Med. 2020, 18, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Epidemiological Update: Occurrence of Variants of Sars-Cov-2 in the Americas. 20 January 2021. Available online: https:www.tinyurl.com/mlqzzc6k (accessed on 2 February 2021).
- Betti, M.I.; Heffernan, J.M. A simple model for fitting mild, severe, and known cases during an epidemic with an application to the current sars-cov-2 pandemic. Infect. Dis. Model. 2021, 6, 313–323. [Google Scholar] [PubMed]
- Public Health Ontario. Covid-19 uk Variant voc-202012/01—What We Know So Far; Technical Report; Public Health Ontario: Toronto, ON, Canada, 2020. [Google Scholar]
- Korber, B.; Fischer, W.M.; Gnanakaran, S.; Yoon, H.; Theiler, J.; Abfalterer, W.; Hengartner, N.; Giorgi, E.E.; Bhattacharya, T.; Foley, B.; et al. Tracking changes in sars-cov-2 spike: Evidence that d614g increases infectivity of the covid-19 virus. Cell 2020, 182, 812–827. [Google Scholar] [CrossRef] [PubMed]
- Office of the Premier. Ontario Delivers First Covid-19 Vaccine in the Country. 2020. Available online: https://tinyurl.com/1suzwju8 (accessed on 2 February 2021).
- Betti, M.; Bragazzi, N.L.; Heffernan, J.; Kong, J.; Raad, A. Integrated vaccination and non-pharmaceutical interventions based strategies in ontario, canada, as a case study: A mathematical modeling study. medRxiv 2021. [Google Scholar] [CrossRef]
- Canada’s Covid-19 Immunization Plan. Available online: https://www.canada.ca/en/public-health/services/diseases/2019-novel-coronavirus-infection/canadas-reponse/canadas-covid-19-immunization-plan.html#a8 (accessed on 2 February 2021).
- Duong, D. What’s Important to Know about the New Covid-19 Variants? CMAJ 2021, 193, E141–E142. [Google Scholar] [CrossRef]
- Koyama, T.; Weeraratne, D.; Snowdon, J.L.; Parida, L. Emergence of drift variants that may affect covid-19 vaccine development and antibody treatment. Pathogens 2020, 9, 324. [Google Scholar] [CrossRef] [PubMed]
- Mahase, E. Covid-19: What New Variants Are Emerging and How Are They Being Investigated? BMJ 2021, 372. [Google Scholar] [CrossRef]
- CDC. New Variants of the Virus that Causes Covid-19. 2021. Available online: https://www.cdc.gov/coronavirus/2019-ncov/transmission/variant.html (accessed on 2 February 2021).
- Van Oosterhout, C.; Hall, N.; Ly, H.; Tyler, K.M. Covid-19 Evolution during the Pandemic–Implications of New Sars-Cov-2 Variants on Disease Control and Public Health Policies. Virulence 2021, 12, 507–508. [Google Scholar] [CrossRef] [PubMed]
- Emergencies Preparedness, Response: Sars-Cov-2 Variants. Available online: https://www.who.int/csr/don/31-december-2020-sars-cov2-variants/en/. (accessed on 2 February 2021).
- Rambaut, A.; Holmes, E.C.; O’Toole, Á.; Hill, V.; McCrone, J.T.; Ruis, C.; du Plessis, L.; Pybus, O.G. A dynamic nomenclature proposal for sars-cov-2 lineages to assist genomic epidemiology. Nat. Microbiol. 2020, 5, 1403–1407. [Google Scholar] [CrossRef] [PubMed]
- Government of Canada. Travel Restrictions in Canada. 2021. Available online: https://travel.gc.ca/travel-covid/travel-restrictions (accessed on 2 February 2021).


| Parameter | Fitted Value |
|---|---|
| p | |
| r | |
| k | |
| d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Betti, M.; Bragazzi, N.; Heffernan, J.; Kong, J.; Raad, A. Could a New COVID-19 Mutant Strain Undermine Vaccination Efforts? A Mathematical Modelling Approach for Estimating the Spread of B.1.1.7 Using Ontario, Canada, as a Case Study. Vaccines 2021, 9, 592. https://doi.org/10.3390/vaccines9060592
Betti M, Bragazzi N, Heffernan J, Kong J, Raad A. Could a New COVID-19 Mutant Strain Undermine Vaccination Efforts? A Mathematical Modelling Approach for Estimating the Spread of B.1.1.7 Using Ontario, Canada, as a Case Study. Vaccines. 2021; 9(6):592. https://doi.org/10.3390/vaccines9060592
Chicago/Turabian StyleBetti, Mattew, Nicola Bragazzi, Jane Heffernan, Jude Kong, and Angie Raad. 2021. "Could a New COVID-19 Mutant Strain Undermine Vaccination Efforts? A Mathematical Modelling Approach for Estimating the Spread of B.1.1.7 Using Ontario, Canada, as a Case Study" Vaccines 9, no. 6: 592. https://doi.org/10.3390/vaccines9060592
APA StyleBetti, M., Bragazzi, N., Heffernan, J., Kong, J., & Raad, A. (2021). Could a New COVID-19 Mutant Strain Undermine Vaccination Efforts? A Mathematical Modelling Approach for Estimating the Spread of B.1.1.7 Using Ontario, Canada, as a Case Study. Vaccines, 9(6), 592. https://doi.org/10.3390/vaccines9060592







