Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Membranes
2.2. Reagents
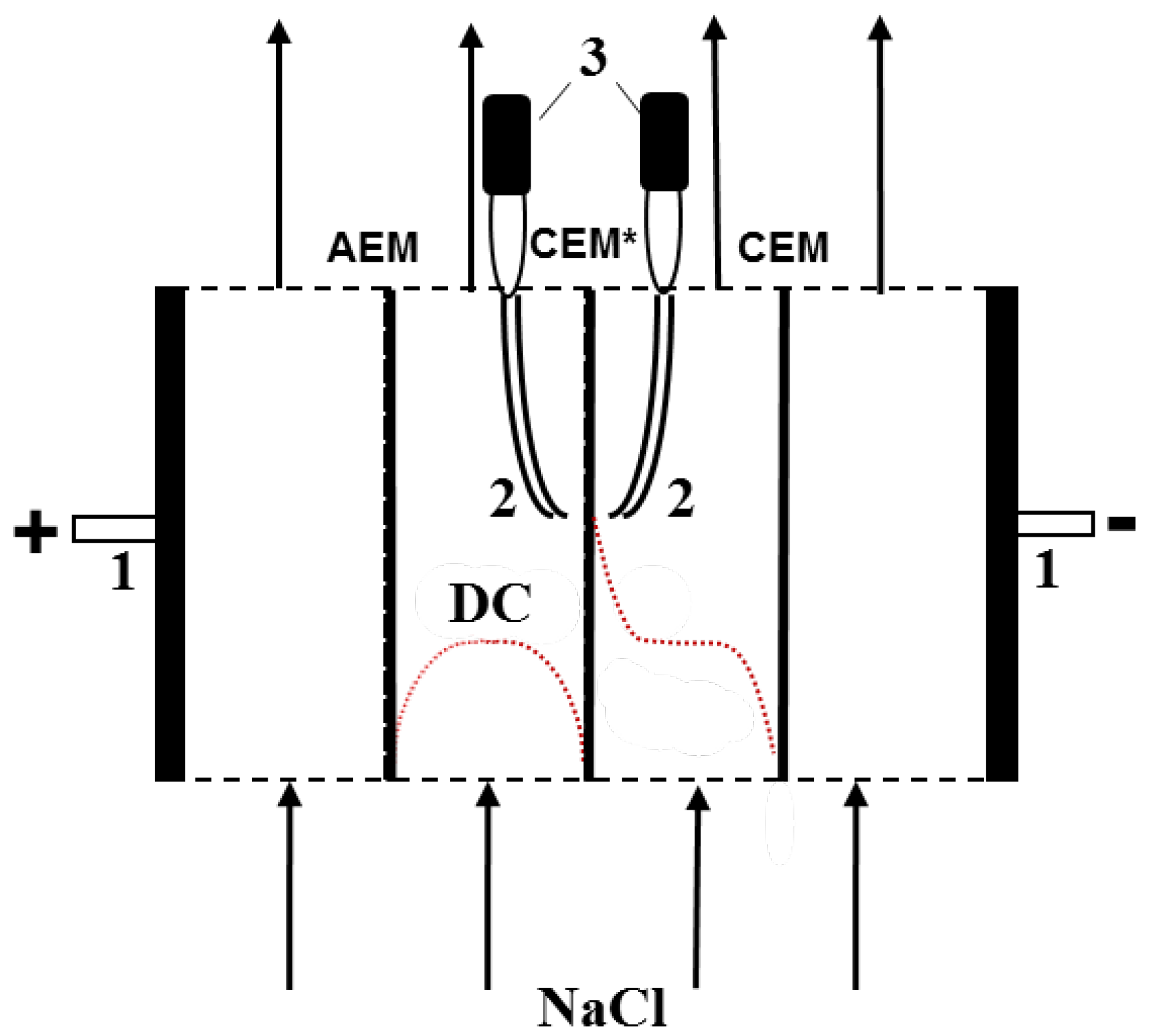
2.3. Methods of Membrane Characterization
3. Results
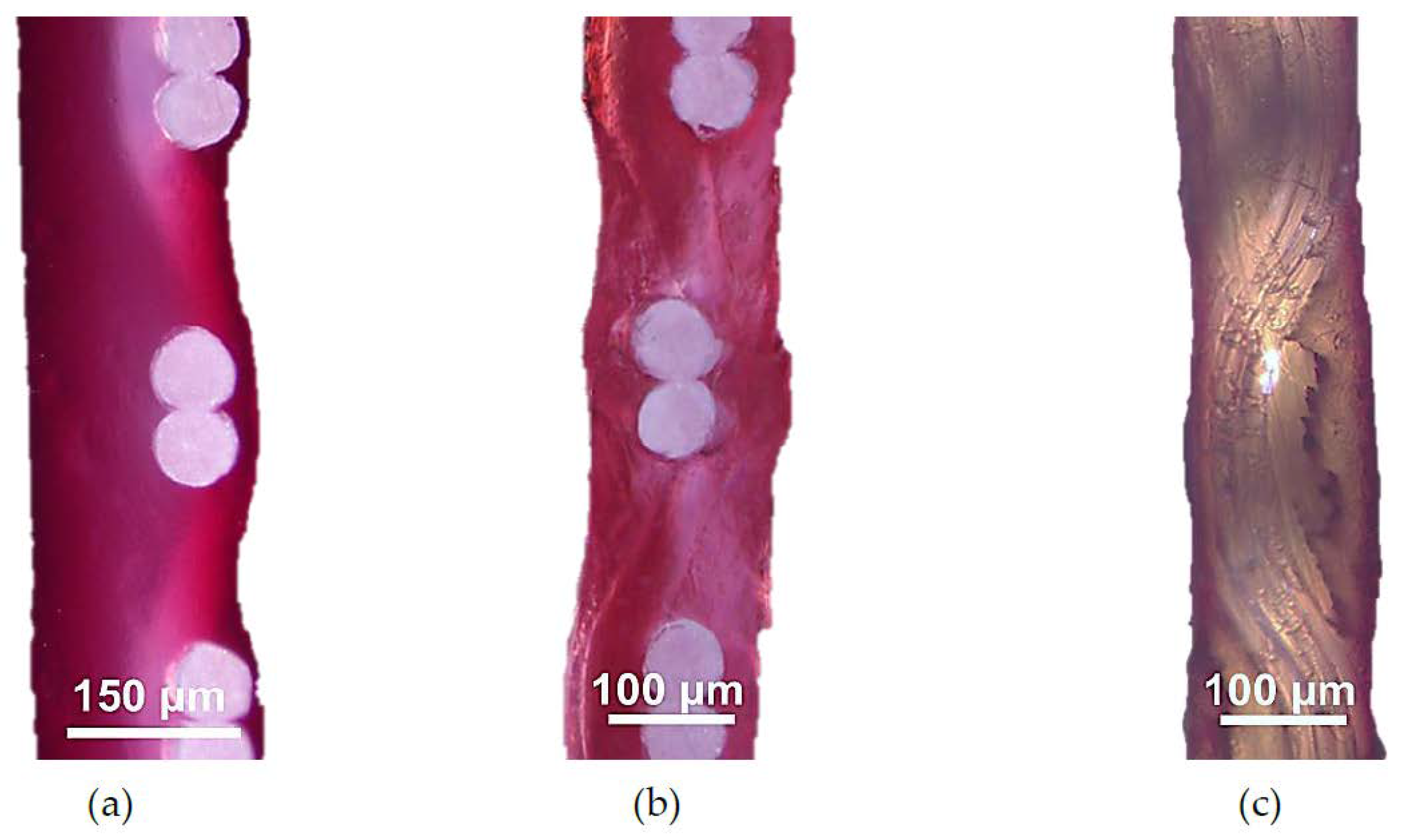
3.1. Structural Characteristics of the Investigated Membranes
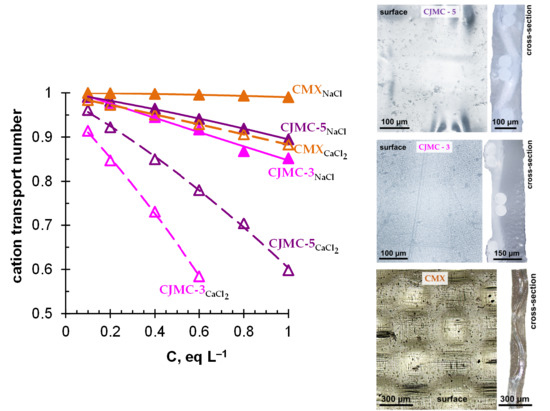
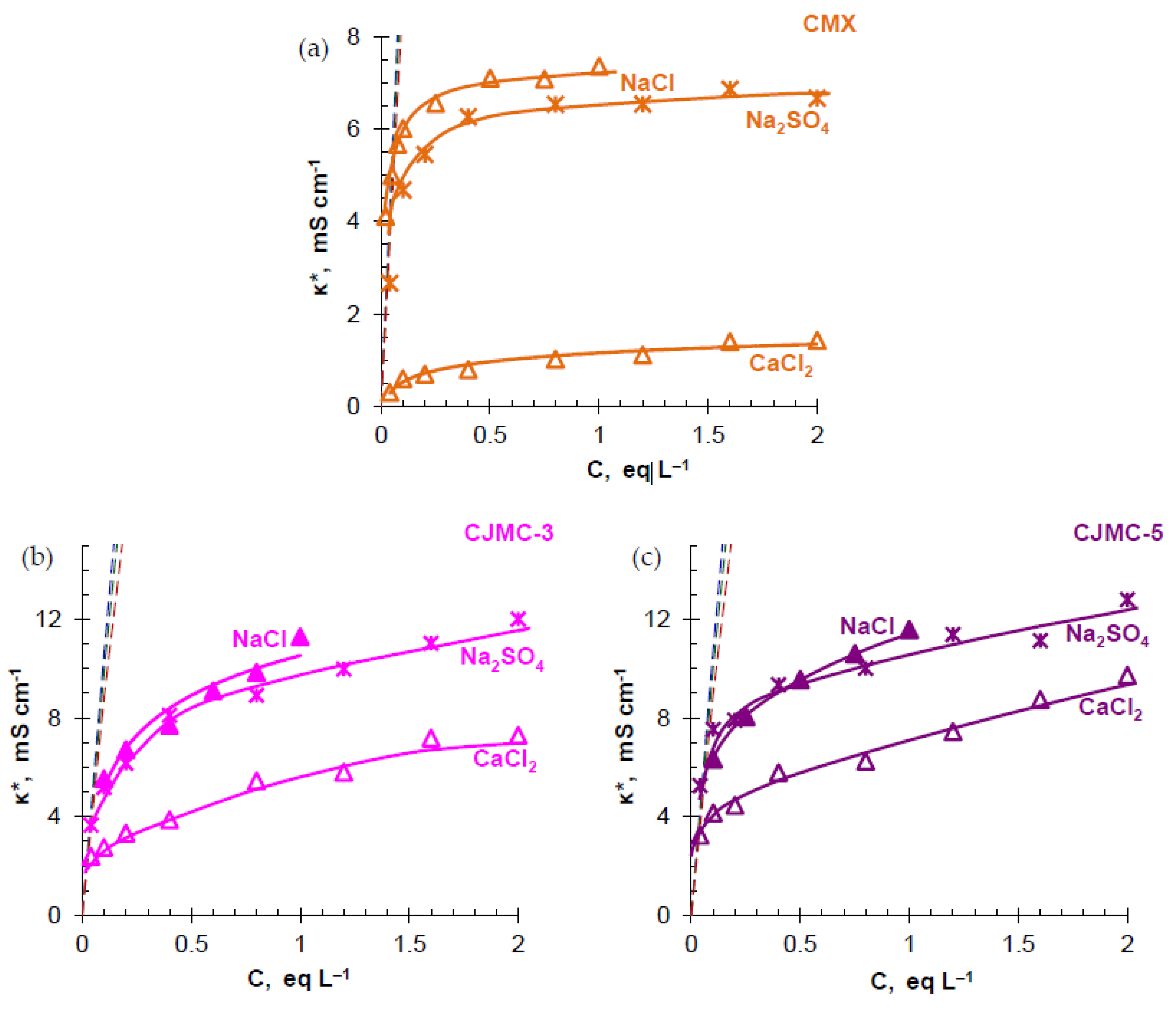
3.2. Transport Characteristics
3.3. Current Voltage Curves and Water Splitting Rate
3.4. Fouling with Aromatic Macromolecular Substances
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CEM | cation-exchange membranes | integral diffusion permeability coefficient of a membrane (cm2 s−1) | |
| molar concentration of the counterion in the solution at the entrance to the desalination compartment (mmol cm−3) | differential (or local) diffusion permeability coefficient (cm2 s−1) | ||
| concentration at the isoconductivity point (meq cm−3). | PVC | polyvinyl chloride | |
| CVC | current–voltage curve | PVDF | polyvinylidene fluoride |
| electrolyte diffusion coefficient (m2 s−1) | total exchange capacity (mmol g−1) | ||
| diffusion coefficient of a counterion in the gel phase (m2 s−1) | ion-exchange capacity of the gel phase (mmol cm−3 wet gel) | ||
| membrane thickness (cm) | the gas constant (J K−1 mol−1) | ||
| DC | desalination channel/compartment | system resistance at low currents (Ohm·cm2) | |
| potential difference between two reversible to the anion electrodes separated by the membrane under study (V) | RO | reverse osmosis | |
| ED | electrodialysis | working area of a membrane (cm2) | |
| Faraday constant (C mol−1) | SSS | sodium 4-styrenesulfonate | |
| volume fraction of the gel phase | temperature (K) | ||
| volume fraction of the electroneutral solution | electromigration transport number of the counterion in the solution | ||
| potential drop (V) | effective transport number of the counterion in a membrane | ||
| intermembrane distance (cm) | “true” transport number of the counterion | ||
| electric current density ( mA cm−2) | “apparent” transport number of the counterion | ||
| experimental value of limiting current | transport numbers of the coion in a membrane | ||
| theoretical value of limiting current | TDS | total dissolved solid (mol L−1) | |
| IEM | ion-exchange membrane | water transport number (mol H2O/F) | |
| flux density of an electrolyte (mmol cm−2 s−1) | average linear flow rate of the electrolyte solution (cm s−1) | ||
| electrical conductivity of a membrane (mS cm−1) | water content (%, gH2O/gdry) | ||
| electrical conductivity of the gel phase (mS cm−1) | charge number of the counterion | ||
| length of the membrane working area (cm) | charge number of the coion | ||
| molality of a solution (mmol g−1) |
References
- Zhang, C.; Ma, J.; Waite, T.D. Ammonia-rich solution production from wastewaters using chemical-free flow-electrode capacitive deionization. ACS Sustain. Chem. Eng. 2019, 7, 6480–6485. [Google Scholar] [CrossRef]
- Kuntke, P.; Rodrigues, M.; Sleutels, T.; Saakes, M.; Hamelers, H.V.M.; Buisman, C.J.N. Energy-efficient ammonia recovery in an up-scaled hydrogen gas recycling electrochemical system. ACS Sustain. Chem. Eng. 2018, 6, 7638–7644. [Google Scholar] [CrossRef]
- Trifi, I.M.; Trifi, B.; Ben Ayed, S.; Hamrouni, B. Removal of phosphate by Donnan dialysis coupled with adsorption onto calcium alginate beads. Water Sci. Technol. 2019, 80, 117–125. [Google Scholar] [CrossRef] [PubMed]
- Kozmai, A.; Goleva, E.; Vasil’eva, V.; Nikonenko, V.; Pismenskaya, N. Neutralization dialysis for phenylalanine and mineral salt separation. Simple theory and experiment. Membranes 2019, 9, 171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Merle, G.; Wessling, M.; Nijmeijer, K. Anion exchange membranes for alkaline fuel cells: A review. J. Membr. Sci. 2011, 377, 1–35. [Google Scholar] [CrossRef]
- Kraytsberg, A.; Ein-Eli, Y. Review of advanced materials for proton exchange membrane fuel cells. Energy Fuels 2014, 28, 7303–7330. [Google Scholar] [CrossRef]
- Su, L.; Ajo-Franklin, C.M. Reaching full potential: Bioelectrochemical systems for storing renewable energy in chemical bonds. Curr. Opin. Biotech. 2019, 57, 66–72. [Google Scholar] [CrossRef]
- Kuntke, P.; Sleutels, T.H.J.A.; Rodríguez Arredondo, M.; Georg, S.; Barbosa, S.G.; ter Heijne, A.; Hamelers, H.V.M.; Buisman, C.J.N. (Bio)electrochemical ammonia recovery: Progress and perspectives. Appl. Microbiol. Biotechnol. 2018, 102, 3865–3878. [Google Scholar] [CrossRef] [Green Version]
- Tadimeti, J.G.D.; Chandra, A.; Chattopadhyay, S. Optimum concentrate stream concentration in CaCl2 removal from sugar solution using electrodialysis. Chem. Eng. Process Technol. 2015, 6, 1000216. [Google Scholar]
- Tanaka, Y. Ion-exchange membrane electrodialysis for saline water desalination and its application to seawater concentration. Ind. Eng. Chem. Res. 2011, 50, 7494–7503. [Google Scholar] [CrossRef]
- Rezvani, F.; Sarrafzadeh, M.-H.; Ebrahimi, S.; Oh, H.-M. Nitrate removal from drinking water with a focus on biological methods: A review. Environ. Sci. Pollut. Res. 2019, 26, 1124–1141. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Pinoy, L.; Meesschaert, B.; Van der Bruggen, B. Separation of small organic ions from salts by ion-exchange membrane in electrodialysis. AIChE J. 2011, 57, 2070–2078. [Google Scholar] [CrossRef]
- Perera, M.K.; Englehardt, J.D.; Dvorak, A.C. Technologies for recovering nutrients from wastewater: A critical review. Environ. Eng. Sci. 2019, 36, 511–529. [Google Scholar] [CrossRef]
- Ward, A.J.; Arola, K.; Thompson Brewster, E.; Mehta, C.M.; Batstone, D.J. Nutrient recovery from wastewater through pilot scale electrodialysis. Water Res. 2018, 135, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Abou-Shady, A. Recycling of polluted wastewater for agriculture purpose using electrodialysis: Perspective for large scale application. Chem. Eng. Trans. 2017, 323, 1–18. [Google Scholar] [CrossRef]
- Khramtsov, A.G.; Blinov, A.V.; Blinova, A.A.; Serov, A.V.; Blinova, A.A. Influence of the whey type on composition and properties of its mineralizates. Foods Raw Mater. 2017, 5, 30–40. [Google Scholar] [CrossRef]
- El Rayess, Y.; Mietton-Peuchot, M. Membrane Technologies in Wine Industry: An Overview. Crit. Rev. Food Sci. Nutr. 2016, 56, 2005–2020. [Google Scholar] [CrossRef]
- Serre, E.; Rozoy, E.; Pedneault, K.; Lacour, S.; Bazinet, L. Deacidification of cranberry juice by electrodialysis: Impact of membrane types and configurations on acid migration and juice physicochemical characteristics. Sep. Purif. Technol. 2016, 163, 228–237. [Google Scholar] [CrossRef]
- Fidaleo, M.; Moresi, M.; Cammaroto, A.; Ladrange, N.; Nardi, R. Soy sauce desalting by electrodialysis. J. Food Eng. 2012, 110, 175–181. [Google Scholar] [CrossRef]
- Liu, M.; Liu, D.; Fang, T.; Chen, J. Electrodialysis technology application in reducing salt concentration of abalone visceral fish sauce. J. Chin. Inst. Food Sci. Technol. 2016, 16, 115–123. [Google Scholar]
- Kim, M.-S.; Na, J.-G.; Lee, M.-K.; Ryu, H.; Chang, Y.-K.; Triolo, J.M.; Yun, Y.-M.; Kim, D.-H. More value from food waste: Lactic acid and biogas recovery. Water Res. 2016, 96, 208–216. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Shon, H.K.; Gray, S.R.; Elimelech, M. Membrane-based processes for wastewater nutrient recovery: Technology, challenges, and future direction. Water Res. 2016, 89, 210–221. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghyselbrecht, K.; Van Houtte, E.; Pinoy, L.; Verbauwhede, J.; Van der Bruggen, B.; Meesschaert, B. Treatment of RO concentrate by means of a combination of a willow field and electrodialysis. Resour. Conserv. Recycl. 2012, 65, 116–123. [Google Scholar] [CrossRef]
- Hoshino, T. Preliminary studies of lithium recovery technology from seawater by electrodialysis using ionic liquid membrane. Desalination 2013, 317, 11–16. [Google Scholar] [CrossRef]
- Sun, Y.; Guo, X.; Hu, S.; Xiang, X. Highly efficient extraction of lithium from salt lake brine by LiAl-layered double hydroxides as lithium-ion-selective capturing material. J. Energy Chem. 2019, 34, 80–87. [Google Scholar] [CrossRef] [Green Version]
- Iizuka, A.; Yamashita, Y.; Nagasawa, H.; Yamasaki, A.; Yanagisawa, Y. Separation of lithium and cobalt from waste lithium-ion batteries via bipolar membrane electrodialysis coupled with chelation. Sep. Purif. Technol. 2013, 113, 33–41. [Google Scholar] [CrossRef]
- Zhang, Y.-F.; Liu, L.; Du, J.; Fu, R.; Van der Bruggen, B.; Zhang, Y. Fracsis: Ion fractionation and metathesis by a NF-ED integrated system to improve water recovery. J. Membr. Sci. 2017, 523, 385–393. [Google Scholar] [CrossRef]
- Jaroszek, H.; Dydo, P. Potassium nitrate synthesis by electrodialysis-metathesis: The effect of membrane type. J. Membr. Sci. 2018, 549, 28–37. [Google Scholar] [CrossRef]
- Han, X.; Yan, X.; Wang, X.; Ran, J.; Wu, C.; Zhang, X. Preparation of chloride-free potash fertilizers by electrodialysis metathesis. Sep. Purif. Technol. 2018, 191, 144–152. [Google Scholar] [CrossRef]
- Nie, X.-Y.; Sun, S.-Y.; Sun, Z.; Song, X.; Yu, J.-G. Ion-fractionation of lithium ions from magnesium ions by electrodialysis using monovalent selective ion-exchange membranes. Desalination 2017, 403, 128–135. [Google Scholar] [CrossRef]
- Mikhaylin, S.; Bazinet, L. Fouling on ion-exchange membranes: Classification, characterization and strategies of prevention and control. Adv. Colloid Interface Sci. 2016, 229, 34–56. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Wang, H.; Xu, T.-W.; Xu, Z.-L. Polymeric Membranes. In Membrane-Based Separations in Metallurgy, 1st ed.; Lan, Y.J., Li, N., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 297–334. ISBN 978-0-12-803410-1. [Google Scholar]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion exchange membranes: New developments and applications. J. Membr. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Pawlowski, S.; Crespo, J.G.; Velizarov, S. Profiled ion exchange membranes: A comprehensible review. Int. J. Mol. Sci. 2019, 20, 165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Zhang, Z.; Jiang, C.; Xu, T. Recovery of gamma-aminobutyric acid (GABA) from reaction mixtures containing salt by electrodialysis. Sep. Purif. Technol. 2016, 170, 353–359. [Google Scholar] [CrossRef]
- Wei, X.; Wang, Y.; Yan, H.; Wu, K.; Xu, T. Purification of methylsulfonylmethane from mixtures containing salt by conventional electrodialysis. Membranes 2020, 10, 23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Website of Hefei ChemJoy Polymer Materials Co., Ltd. Available online: http://www.cj-membrane.com/display/369191.html (accessed on 4 July 2020).
- Gao, H.; Zhang, B.; Tong, X.; Chen, Y. Monovalent-anion selective and antifouling polyelectrolytes multilayer anion exchange membrane for reverse electrodialysis. J. Membr. Sci. 2018, 567, 68–75. [Google Scholar] [CrossRef]
- Yan, H.; Wang, Y.; Wu, L.; Shehzad, M.A.; Jiang, C.; Fu, R.; Liu, Z.; Xu, T. Multistage-batch electrodialysis to concentrate high-salinity solutions: Process optimisation, water transport, and energy consumption. J. Membr. Sci. 2019, 570–571, 245–257. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, Q.; Zhang, Y.; Li, Y.; Wang, Y.; Xu, T. Separation of methionine from the mixture with sodium carbonate using bipolar membrane electrodialysis. J. Membr. Sci. 2016, 498, 48–56. [Google Scholar] [CrossRef]
- Wang, Y.; Li, W.; Xu, T. Electrodialysis for cleaner separation and purification of sarcosine. CIESC J. 2014, 66, 3137–3143. [Google Scholar]
- Wang, Y.; Pan, S.; Xu, T. Electrodialysis for production of xylitol from acid hydrolysis method. CIESC J. 2014, 66, 3529–3534. [Google Scholar]
- Li, C.; Ge, S.; Li, W.; Zhang, Z.; She, S.; Huang, L.; Wang, Y. Desalting of papermaking tobacco sheet extract using selective electrodialysis. Membr. Water Treat. 2017, 8, 381–393. [Google Scholar] [CrossRef]
- Sarapulova, V.; Shkorkina, I.; Mareev, S.; Pismenskaya, N.; Kononenko, N.; Larchet, C.; Dammak, L.; Nikonenko, V. Transport characteristics of Fujifilm ion-exchange membranes as compared to homogeneous membranes AMX and CMX and to heterogeneous membranes MK-40 and MA-41. Membranes 2019, 9, 84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, T. Ion exchange membranes: State of their development and perspective. J. Membr. Sci. 2005, 263, 1–29. [Google Scholar] [CrossRef]
- Molau, G.E. Heterogeneous ion-exchange membranes. J. Membr. Sci. 1981, 8, 309–330. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Pokhidnia, E.V.; Pourcelly, G.; Nikonenko, V.V. Can the electrochemical performance of heterogeneous ion-exchange membranes be better than that of homogeneous membranes? J. Membr. Sci. 2018, 566, 54–68. [Google Scholar] [CrossRef]
- Lin, X.; Liang, X.; Poynton, S.D.; Varcoe, J.R.; Ong, A.L.; Ran, J.; Li, Y.; Li, Q.; Xu, T. Novel alkaline anion exchange membranes containing pendant benzimidazolium groups for alkaline fuel cells. J. Membr. Sci. 2013, 443, 193–200. [Google Scholar] [CrossRef]
- Zhou, J.; Kuang, H.; Zhuang, W.; Chen, Y.; Liu, D.; Ying, H.; Wu, J. Application of electrodialysis to extract 5′-ribonucleotides from hydrolysate: Efficient decolorization and membrane fouling. RSC Adv. 2018, 8, 29115–29128. [Google Scholar] [CrossRef] [Green Version]
- Yan, H.; Wang, Y.; Xu, T. Developing ion exchange membrane for treating high salinity water using electrodialysis. In Proceedings of the 5th International Conferences on Sustainable Chemical Product and Process Engineering (SCPPE), Tianjin, China, 30 June–3 July 2019. [Google Scholar]
- Mizutani, Y.; Yamane, R.; Ihara, H.; Motomura, H. Studies of ion exchange membranes. xvi. the preparation of ion exchange membranes by the “paste method”. Bull. Chem. Soc. Jpn. 1963, 36, 361–366. [Google Scholar] [CrossRef] [Green Version]
- Hori, Y.; Nakatani, T.; Mizutani, Y. Morphology of ion exchange membranes. J. Electron. Microsc. 1986, 35, 220–226. [Google Scholar] [CrossRef]
- Meng, D.; Zhao, Q.; Pan, X.; Zhang, T. Preparation of La2O3 by ion-exchange membrane electrolysis of LaCl3 aqueous solution. J. Rare Earths 2019, 37, 1009–1014. [Google Scholar] [CrossRef]
- Długołęcki, P.; Anet, B.; Metz, S.J.; Nijmeijer, K.; Wessling, M. Transport limitations in ion exchange membranes at low salt concentrations. J. Membr. Sci. 2010, 346, 163–171. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs. structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef] [PubMed]
- Nagarale, R.K.; Gohil, G.S.; Shahi, V.K. Recent developments on ion-exchange membranes and electro-membrane processes. Adv. Colloid Interface Sci. 2006, 119, 97–130. [Google Scholar] [CrossRef] [PubMed]
- Belashova, E.D.; Melnik, N.A.; Pismenskaya, N.D.; Shevtsova, K.A.; Nebavsky, A.V.; Lebedev, K.A.; Nikonenko, V.V. Overlimiting mass transfer through cation-exchange membranes modified by Nafion film and carbon nanotubes. Electrochim. Acta 2012, 59, 412–423. [Google Scholar] [CrossRef]
- Lteif, R.; Dammak, L.; Larchet, C.; Auclair, B. Conductivité électrique membranaire: Étude de l’effet de la concentration, de la nature de l’électrolyte et de la structure membranaire. Eur. Polym. J. 1999, 35, 1187–1195. [Google Scholar] [CrossRef]
- Karpenko, L.V.; Demina, O.A.; Dvorkina, G.A.; Parshikov, S.B.; Larchet, C.; Auclair, B.; Berezina, N.P. Comparative study of methods used for the determination of electroconductivity of ion-exchange membranes. Russ. J. Electrochem. 2001, 37, 287–293. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nevakshenova, E.E.; Nikonenko, V.V. Using a single set of structural and kinetic parameters of the microheterogeneous model to describe the sorption and kinetic properties of ion-exchange membranes. Pet. Chem. 2018, 58, 465–473. [Google Scholar] [CrossRef]
- Gnusin, N.P.; Berezina, N.P.; Shudrenko, A.A.; Ivina, A.P. Electrolyte diffusion across ion-exchange membranes. Russ. J. Phys. Chem. A 1994, 68, 506–510. [Google Scholar]
- Larchet, C.; Dammak, L.; Auclair, B.; Parchikov, S.; Nikonenko, V. A simplified procedure for ion-exchange membrane characterisation. New J. Chem. 2004, 28, 1260. [Google Scholar] [CrossRef]
- Volodina, E.; Pismenskaya, N.; Nikonenko, V.; Larchet, C.; Pourcelly, G. Ion transfer across ion-exchange membranes with homogeneous and heterogeneous surfaces. J. Colloid Interface Sci. 2005, 285, 247–258. [Google Scholar] [CrossRef] [PubMed]
- Rösler, H.-W.; Maletzki, F.; Staude, E. Ion transfer across electrodialysis membranes in the overlimiting current range: Chronopotentiometric studies. J. Membr. Sci. 1992, 72, 171–179. [Google Scholar] [CrossRef]
- Newman, J.S. Electrochemical Systems, 3rd ed.; Prentice-Hall international series in the physical and chemical engineering sciences; Prentice-Hall: Englewood Cliffs, NY, USA, 2004; ISBN 978-0-13-248922-5. [Google Scholar]
- Mareev, S.A.; Butylskii, D.Y.; Pismenskaya, N.D.; Larchet, C.; Dammak, L.; Nikonenko, V.V. Geometric heterogeneity of homogeneous ion-exchange Neosepta membranes. J. Membr. Sci. 2018, 563, 768–776. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Pismenskaya, N.D.; Akberova, E.M.; Nebavskaya, K.A. Effect of thermochemical treatment on the surface morphology and hydrophobicity of heterogeneous ion-exchange membranes. Russ. J. Phys. Chem. A 2014, 88, 1293–1299. [Google Scholar] [CrossRef]
- Titorova, V.; Sabbatovskiy, K.; Sarapulova, V.; Kirichenko, E.; Sobolev, V.; Kirichenko, K. Characterization of MK-40 membrane modified by layers of cation exchange and anion exchange polyelectrolytes. Membranes 2020, 10, 20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gnusin, N.P.; Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A. Transport structural parameters to characterize ion exchange membranes. J. Membr. Sci. 2004, 243, 301–310. [Google Scholar] [CrossRef]
- Helfferich, F.G. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962; ASIN: B0000CLGWI. [Google Scholar]
- Sarapulova, V.V.; Titorova, V.D.; Nikonenko, V.V.; Pismenskaya, N.D. Transport characteristics of homogeneous and heterogeneous ion-exchange membranes in sodium chloride, calcium chloride, and sodium sulfate solutions. Membr. Membr. Technol. 2019, 1, 168–182. [Google Scholar] [CrossRef]
- Demina, O.A.; Kononenko, N.A.; Falina, I.V.; Demin, A.V. Theoretical estimation of differential coefficients of ion-exchange membrane diffusion permeability. Colloid J. 2017, 79, 317–327. [Google Scholar] [CrossRef]
- Filippov, A.N.; Kononenko, N.A.; Demina, O.A. Diffusion of electrolytes of different natures through the cation-exchange membrane. Colloid J. 2017, 79, 556–566. [Google Scholar] [CrossRef]
- Zhu, S.; Kingsbury, R.S.; Call, D.F.; Coronell, O. Impact of solution composition on the resistance of ion exchange membranes. J. Membr. Sci. 2018, 554, 39–47. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Freeman, B.D. Equilibrium ion partitioning between aqueous salt solutions and inhomogeneous ion exchange membranes. Desalination 2018, 446, 31–41. [Google Scholar] [CrossRef]
- Geise, G.M.; Freeman, B.D.; Paul, D.R. Comparison of the permeation of MgCl2 versus NaCl in highly charged sulfonated polymer membranes. In Modern Applications in Membrane Science and Technology; Escobar, I., Van der Bruggen, B., Eds.; American Chemical Society, Oxford University Press: Washington, DC, USA, 2011; Volume 1078, pp. 239–245. ISBN 978-0-8412-2618-0. [Google Scholar]
- Geise, G.M.; Paul, D.R.; Freeman, B.D. Fundamental water and salt transport properties of polymeric materials. Prog. Polym. Sci. 2014, 39, 1–42. [Google Scholar] [CrossRef]
- Luo, T.; Abdu, S.; Wessling, M. Selectivity of ion exchange membranes: A review. J. Membr. Sci. 2018, 555, 429–454. [Google Scholar] [CrossRef]
- Rard, J.A.; Miller, D.G. The mutual diffusion coefficients of NaCl-H2O and CaCl2-H2O at 25 °C from Rayleigh interferometry. J. Solut. Chem. 1979, 8, 701–716. [Google Scholar] [CrossRef]
- Kozmai, A.E.; Nikonenko, V.V.; Zyryanova, S.; Pismenskaya, N.D.; Dammak, L. A simple model for the response of an anion-exchange membrane to variation in concentration and pH of bathing solution. J. Membr. Sci. 2018, 567, 127–138. [Google Scholar] [CrossRef]
- Drioli, E.; Giorno, L.; Fontananova, E. Comprehensive Membrane Science and Engineering; Elsevier Science: Amsterdam, The Netherlands, 2017; ISBN 978-0-444-53204-6. [Google Scholar]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Lakshminaraynaiah, N. Transport. Phenomena in Membranes; Academic Press: New York, NY, USA; London, UK, 1969. [Google Scholar]
- Larchet, C.; Auclair, B.; Nikonenko, V. Approximate evaluation of water transport number in ion-exchange membranes. Electrochim. Acta 2004, 49, 1711–1717. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, A.; Zhang, X.; Xu, T. The concentration, resistance, and potential distribution across a cation exchange membrane in 1:2 (Na2SO4) type aqueous solution. Desalination 2012, 284, 106–115. [Google Scholar] [CrossRef]
- Pham, S.V.; Kwon, H.; Kim, B.; White, J.K.; Lim, G.; Han, J. Helical vortex formation in three-dimensional electrochemical systems with ion-selective membranes. Phys. Rev. E 2016, 93, 033114. [Google Scholar] [CrossRef] [Green Version]
- Mishchuk, N.A. Concentration polarization of interface and non-linear electrokinetic phenomena. J. Colloid Interface Sci. 2010, 160, 16–39. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B. Electro-osmotically induced convection at a permselective membrane. Phys. Rev. E 2000, 62, 2238–2251. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, I.; Zaltzman, B. Equilibrium electroconvective instability. Phys. Rev. Lett. 2015, 114, 114502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nikonenko, V.V.; Mareev, S.A.; Pis’menskaya, N.D.; Uzdenova, A.M.; Kovalenko, A.V.; Urtenov, M.K.; Pourcelly, G. Effect of electroconvection and its use in intensifying the mass transfer in electrodialysis (Review). Russ. J. Electrochem. 2017, 53, 1122–1144. [Google Scholar] [CrossRef]
- Andersen, M.B.; Wang, K.M.; Schiffbauer, J.; Mani, A. Confinement effects on electroconvective instability: General. Electrophoresis 2017, 38, 702–711. [Google Scholar] [CrossRef]
- Rubinstein, I.; Zaltzman, B.; Pundik, T. Ion-exchange funneling in thin-film coating modification of heterogeneous electrodialysis membranes. Phys. Rev. E 2002, 65, 041507. [Google Scholar] [CrossRef]
- Mishchuk, N.A. Polarization of systems with complex geometry. Curr. Opin. Colloid Interface Sci. 2013, 18, 137–148. [Google Scholar] [CrossRef]
- Chang, H.-C.; Demekhin, E.A.; Shelistov, V.S. Competition between Dukhin’s and Rubinstein’s electrokinetic modes. Phys. Rev. E 2012, 86, 046319. [Google Scholar] [CrossRef] [Green Version]
- Green, Y.; Park, S.; Yossifon, G. Bridging the gap between an isolated nanochannel and a communicating multipore heterogeneous membrane. Phys. Rev. E 2015, 91, 011002. [Google Scholar] [CrossRef] [Green Version]
- Belova, E.I.; Lopatkova, G.Y.; Pismenskaya, N.D.; Nikonenko, V.V.; Larchet, C.; Pourcelly, G. Effect of anion-exchange membrane surface properties on mechanisms of overlimiting mass transfer. J. Phys. Chem. B 2006, 110, 13458–13469. [Google Scholar] [CrossRef]
- Slouka, Z.; Senapati, S.; Yan, Y.; Chang, H.-C. Charge inversion, water splitting, and vortex suppression due to DNA sorption on ion-selective membranes and their ion-current signatures. Langmuir 2013, 29, 8275–8283. [Google Scholar] [CrossRef]
- Vobecká, L.; Belloň, T.; Slouka, Z. Behavior of embedded cation-exchange particles in a DC electric field. Int. J. Mol. Sci. 2019, 20, 3579. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, M.-S.; Choi, Y.-J.; Moon, S.-H. Effects of charge density on water splitting at cation-exchange membrane surface in the over-limiting current region. Korean J. Chem. Eng. 2004, 21, 221–229. [Google Scholar] [CrossRef]
- Nikonenko, V.; Urtenov, M.; Mareev, S.; Pourcelly, G. Mathematical modeling of the effect of water splitting on ion transfer in the depleted diffusion layer near an ion-exchange membrane. Membranes 2020, 10, 22. [Google Scholar] [CrossRef] [Green Version]
- Sarapulova, V.; Nevakshenova, E.; Nebavskaya, X.; Kozmai, A.; Aleshkina, D.; Pourcelly, G.; Nikonenko, V.; Pismenskaya, N. Characterization of bulk and surface properties of anion-exchange membranes in initial stages of fouling by red wine. J. Membr. Sci. 2018, 559, 170–182. [Google Scholar] [CrossRef]
- Lam Quoc, A.; Lamarche, F.; Makhlouf, J. Acceleration of pH variation in cloudy apple juice using electrodialysis with bipolar membranes. J. Agric. Food Chem. 2000, 48, 2160–2166. [Google Scholar] [CrossRef]
- Bazinet, L.; Doyen, A. Antioxidants, mechanisms, and recovery by membrane processes. Crit. Rev. Food Sci. Nutr. 2017, 57, 677–700. [Google Scholar] [CrossRef] [PubMed]
- Bdiri, M.; Dammak, L.; Larchet, C.; Hellal, F.; Porozhnyy, M.; Nevakshenova, E.; Pismenskaya, N.; Nikonenko, V. Characterization and cleaning of anion-exchange membranes used in electrodialysis of polyphenol-containing food industry solutions; comparison with cation-exchange membranes. Sep. Purif. Technol. 2019, 210, 636–650. [Google Scholar] [CrossRef]
- Lindstrand, V.; Sundström, G.; Jönsson, A.-S. Fouling of electrodialysis membranes by organic substances. Desalination 2000, 128, 91–102. [Google Scholar] [CrossRef]
- Tanaka, N.; Nagase, M.; Higa, M. Organic fouling behavior of commercially available hydrocarbon-based anion-exchange membranes by various organic-fouling substances. Desalination 2012, 296, 81–86. [Google Scholar] [CrossRef]
- Garcia-Vasquez, W.; Dammak, L.; Larchet, C.; Nikonenko, V.; Grande, D. Effects of acid–base cleaning procedure on structure and properties of anion-exchange membranes used in electrodialysis. J. Membr. Sci. 2016, 507, 12–23. [Google Scholar] [CrossRef]
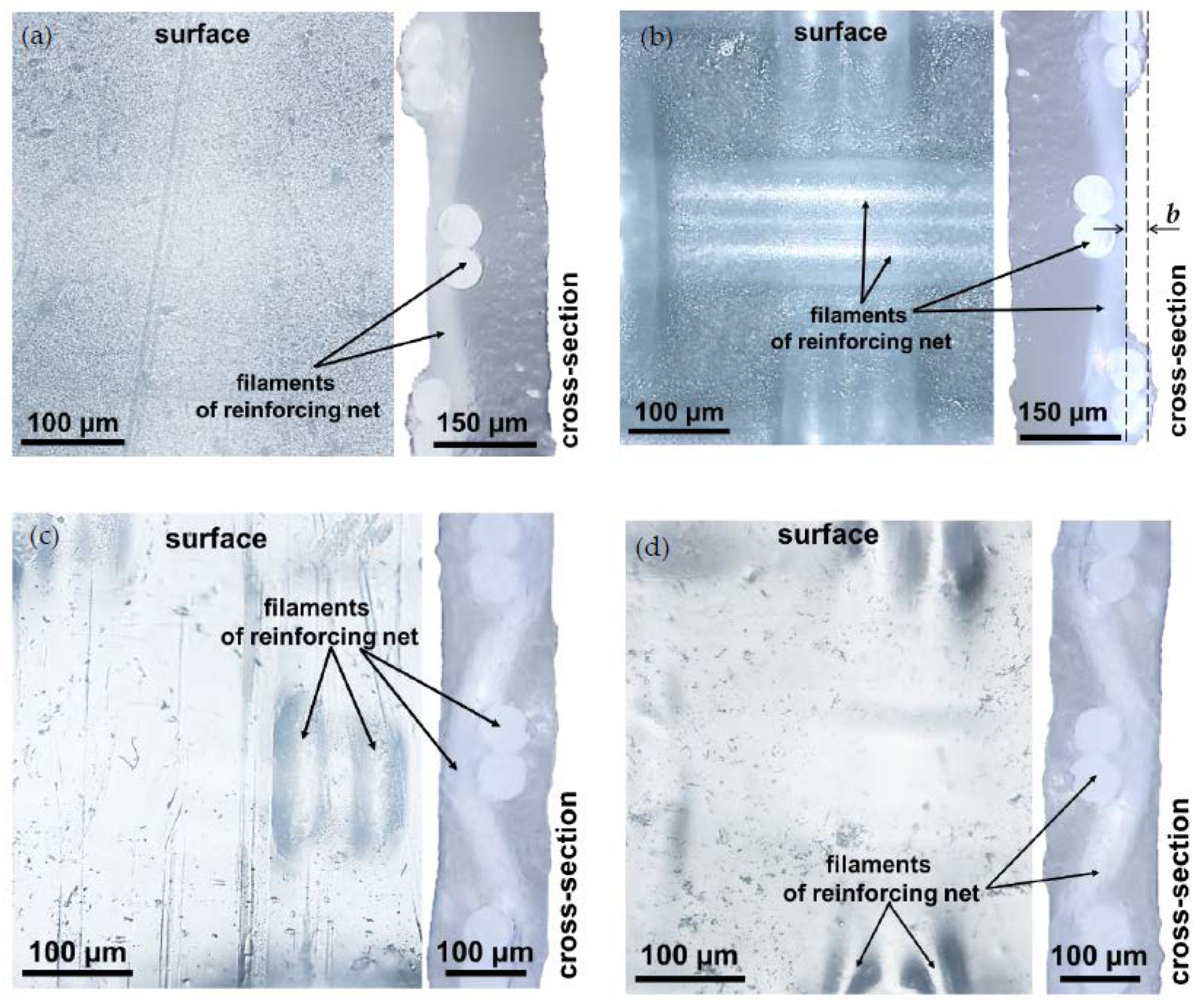





| Membranes | Thickness (sw) 1, μm | Exchange Capacity (sw), mmol g−1 | Water Content, gH2O/gdry, % | Water Content, mol H2O/mol Functional Groups | Resistance 2 (Ohm cm2) |
|---|---|---|---|---|---|
| CJMC-3 | 185 ± 5 190 ± 20 [37] 170 ± 0.01 [53] | 0.63 ± 0.05 0.80–1.0 [37] 0.80–1.0 [53] | 44 ± 3 40–45 [37] 35–45 [53] | 27 ± 1 | 2.2 ± 0.3 3.0 ± 0.5 [37] 2.5–3.5 [53] |
| CJMC-5 | 140 ± 3 140 ± 3 3 | 0.57 ± 0.07 1.00–1.20 3 | 32 ± 5 25–27 3 | 23 ± 1 | 1.4 ± 0.2 2.0–2.5 3 |
| CMX [44] | 170 ± 5 164 [54] | 1.61 ± 0.05 1.62 [54] | 28 ± 3 18 [54] | 8 ± 1 9 [28] | 2.6 ± 0.3 2.91 [54] |
| Membranes | , mS cm−1 | , mmol cm−3sw gel | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NaCl | CaCl2 | Na2SO4 | NaCl | CaCl2 | Na2SO4 | ||||
| CMX | 5.5 ± 0.2 6.7 [71] | 0.3 ± 0.3 | 4.9 ± 0.3 | 1.8 ± 0.2 | 0.11 | 0.22 | 0.11 | 2 | 37 |
| CJMC-3 | 3.9 ± 0.3 | 1.3 ± 0.3 | 3.7 ± 0.3 | 0.9 ± 0.2 | 0.33 | 0.38 | 0.35 | 2 | 6 |
| CJMC-5 | 5.2 ± 0.3 | 2.4 ± 0.3 | 4.8 ± 0.3 | 0.8 ± 0.2 | 0.28 | 0.33 | 0.32 | 2 | 2 |
| Membranes | tw mol H2O/F | ||
|---|---|---|---|
| CJMC-3 | 0.982 (0.15 M NaCl) | 0.94 1 [37] | 16 |
| CJMC-5 | 0.989 (0.15 M NaCl) | 0.96 1 | 11 |
| CMX | 0.997 (0.25 M NaCl) | 0.98 2 [87] | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarapulova, V.; Pismenskaya, N.; Butylskii, D.; Titorova, V.; Wang, Y.; Xu, T.; Zhang, Y.; Nikonenko, V. Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membranes 2020, 10, 165. https://doi.org/10.3390/membranes10080165
Sarapulova V, Pismenskaya N, Butylskii D, Titorova V, Wang Y, Xu T, Zhang Y, Nikonenko V. Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membranes. 2020; 10(8):165. https://doi.org/10.3390/membranes10080165
Chicago/Turabian StyleSarapulova, Veronika, Natalia Pismenskaya, Dmitrii Butylskii, Valentina Titorova, Yaoming Wang, Tongwen Xu, Yang Zhang, and Victor Nikonenko. 2020. "Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions" Membranes 10, no. 8: 165. https://doi.org/10.3390/membranes10080165
APA StyleSarapulova, V., Pismenskaya, N., Butylskii, D., Titorova, V., Wang, Y., Xu, T., Zhang, Y., & Nikonenko, V. (2020). Transport and Electrochemical Characteristics of CJMCED Homogeneous Cation Exchange Membranes in Sodium Chloride, Calcium Chloride, and Sodium Sulfate Solutions. Membranes, 10(8), 165. https://doi.org/10.3390/membranes10080165