The Role of Sulphonic and Phosphoric Pendant Groups on the Diffusion of Monovalent Ions in Polyelectrolyte Membranes: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Molecular Dynamics Simulations
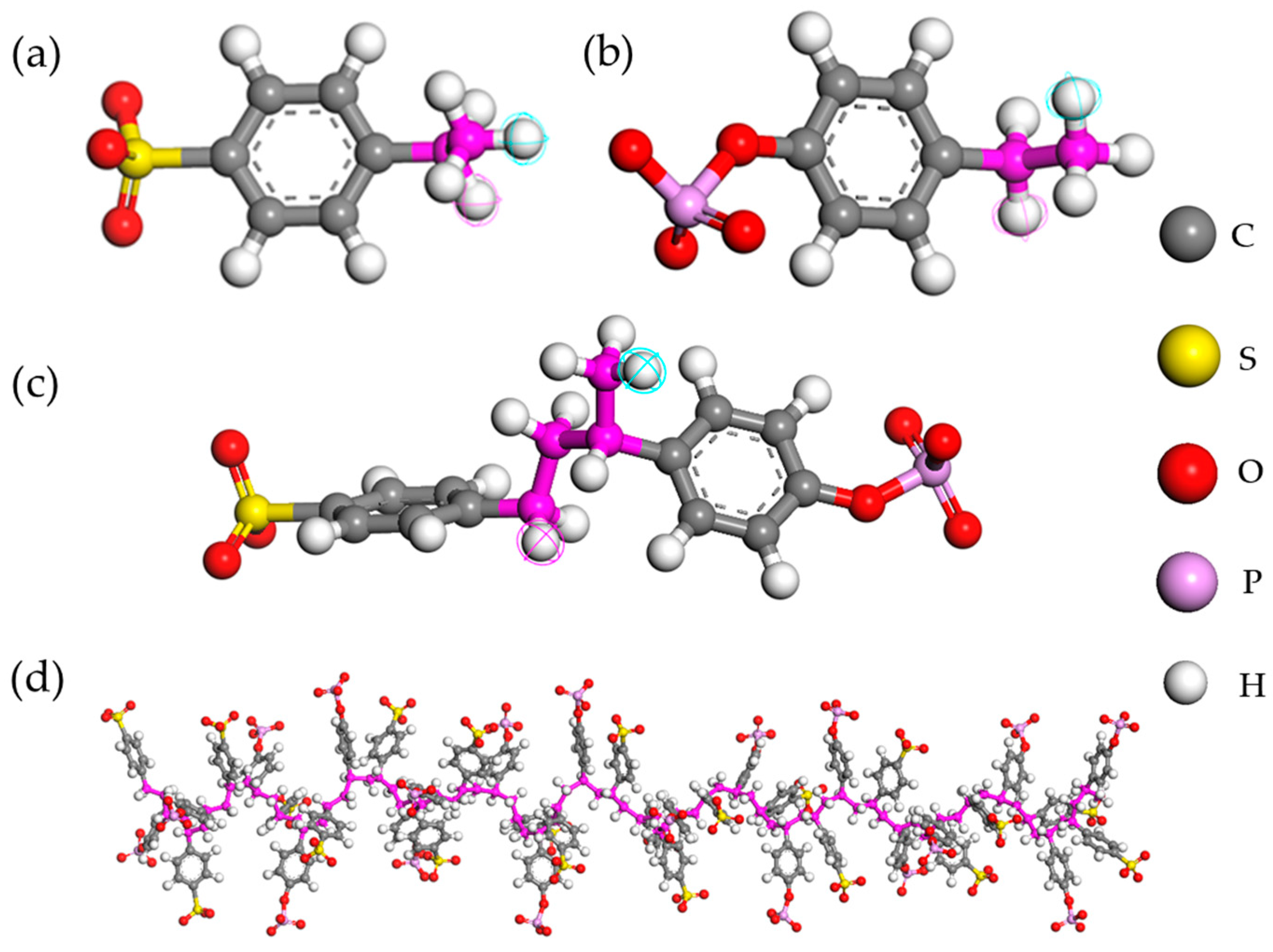
2.1. Model
2.2. Construction of Polyelectrolyte–Aqueous System
2.3. Molecular Dynamics Simulations
3. Results and Discussion
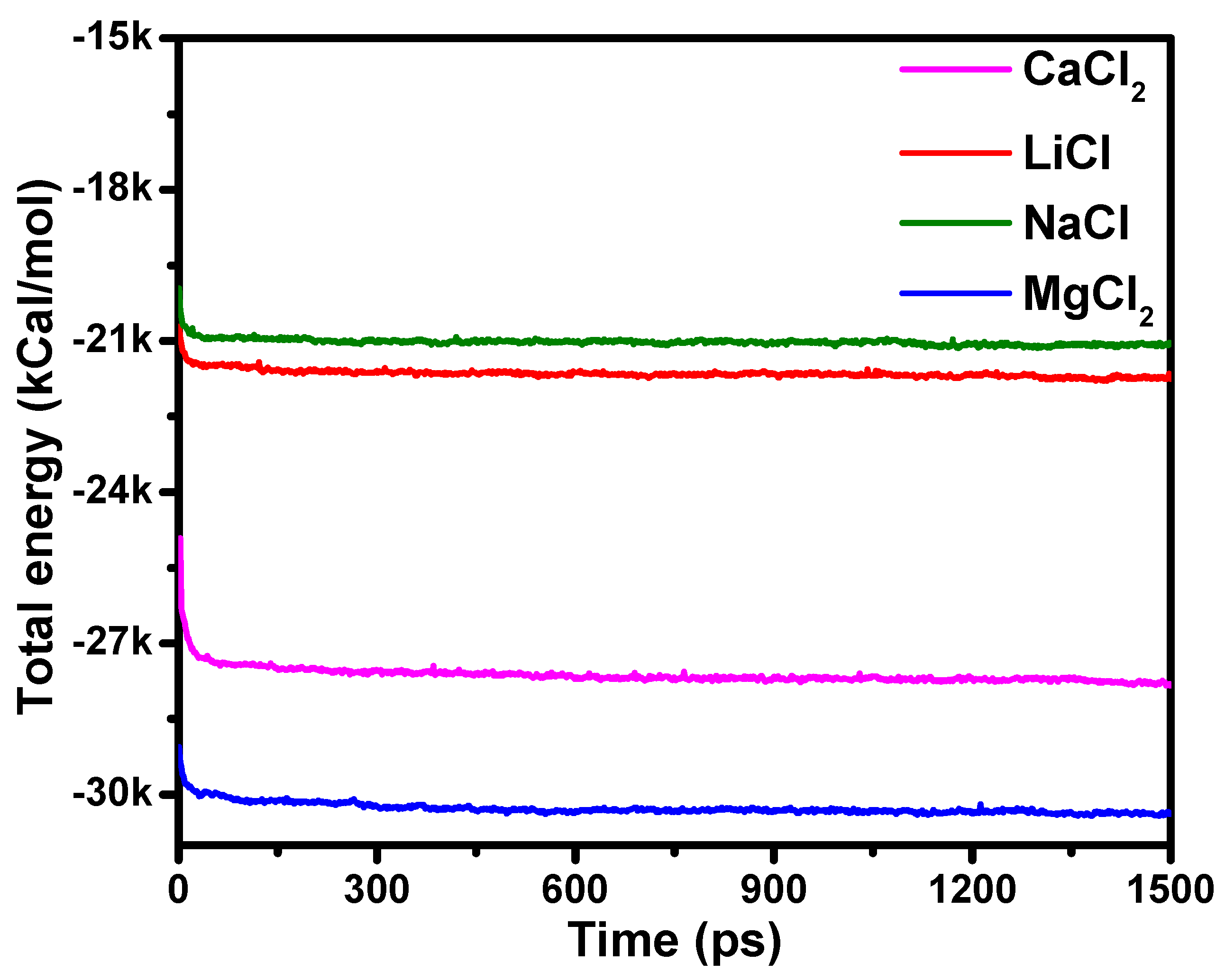
3.1. The Role of the Fixed-Charged Groups
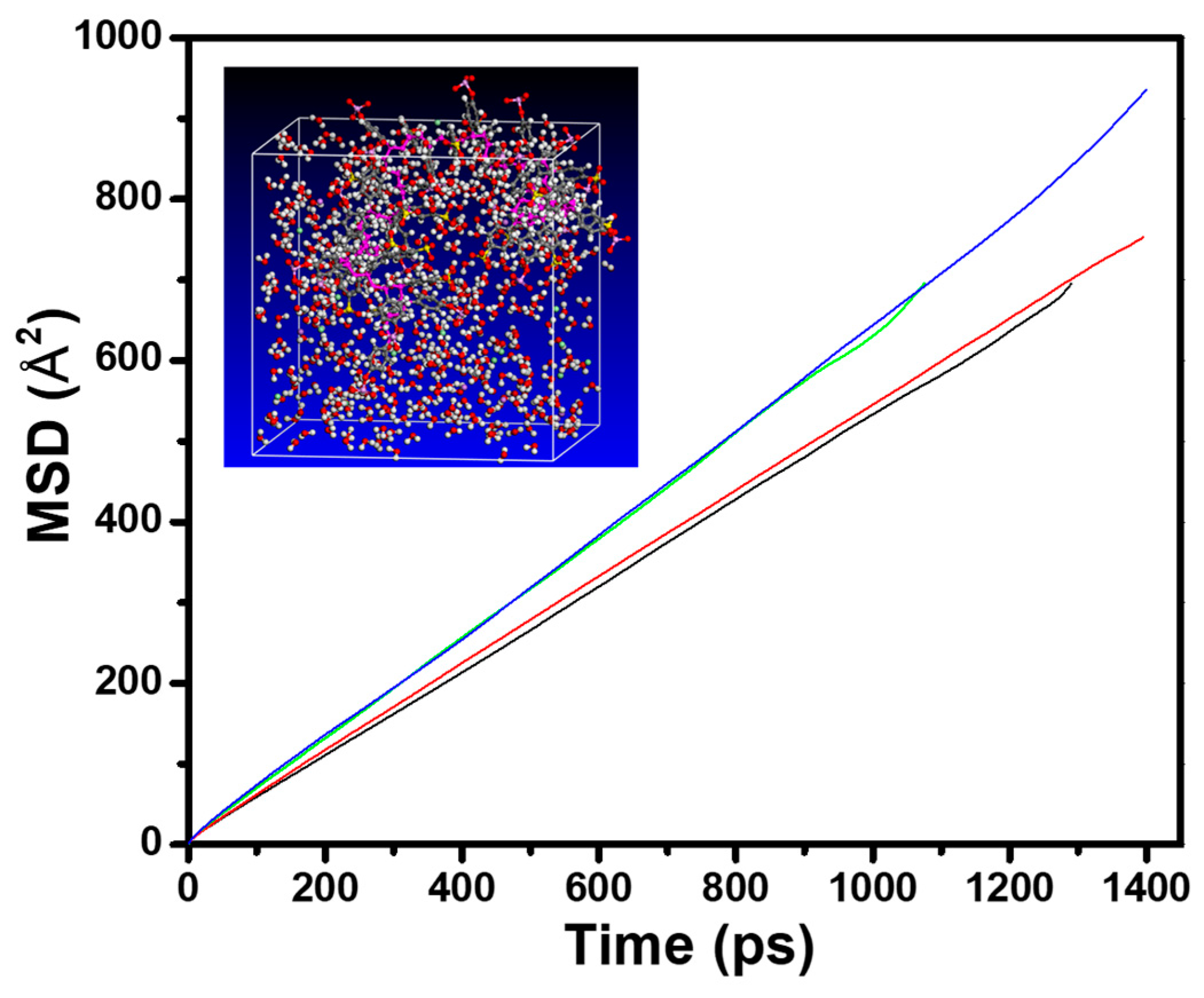
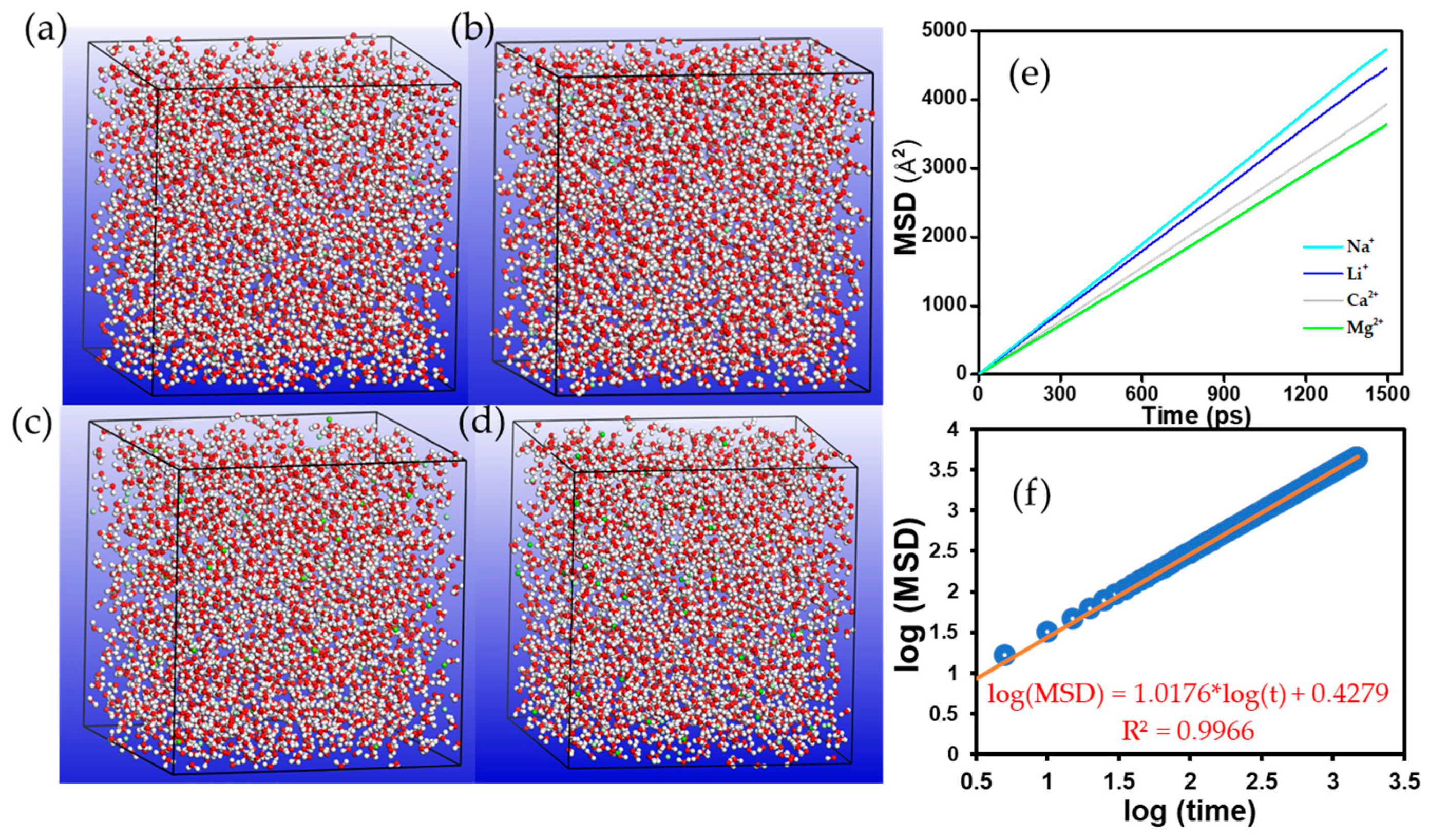
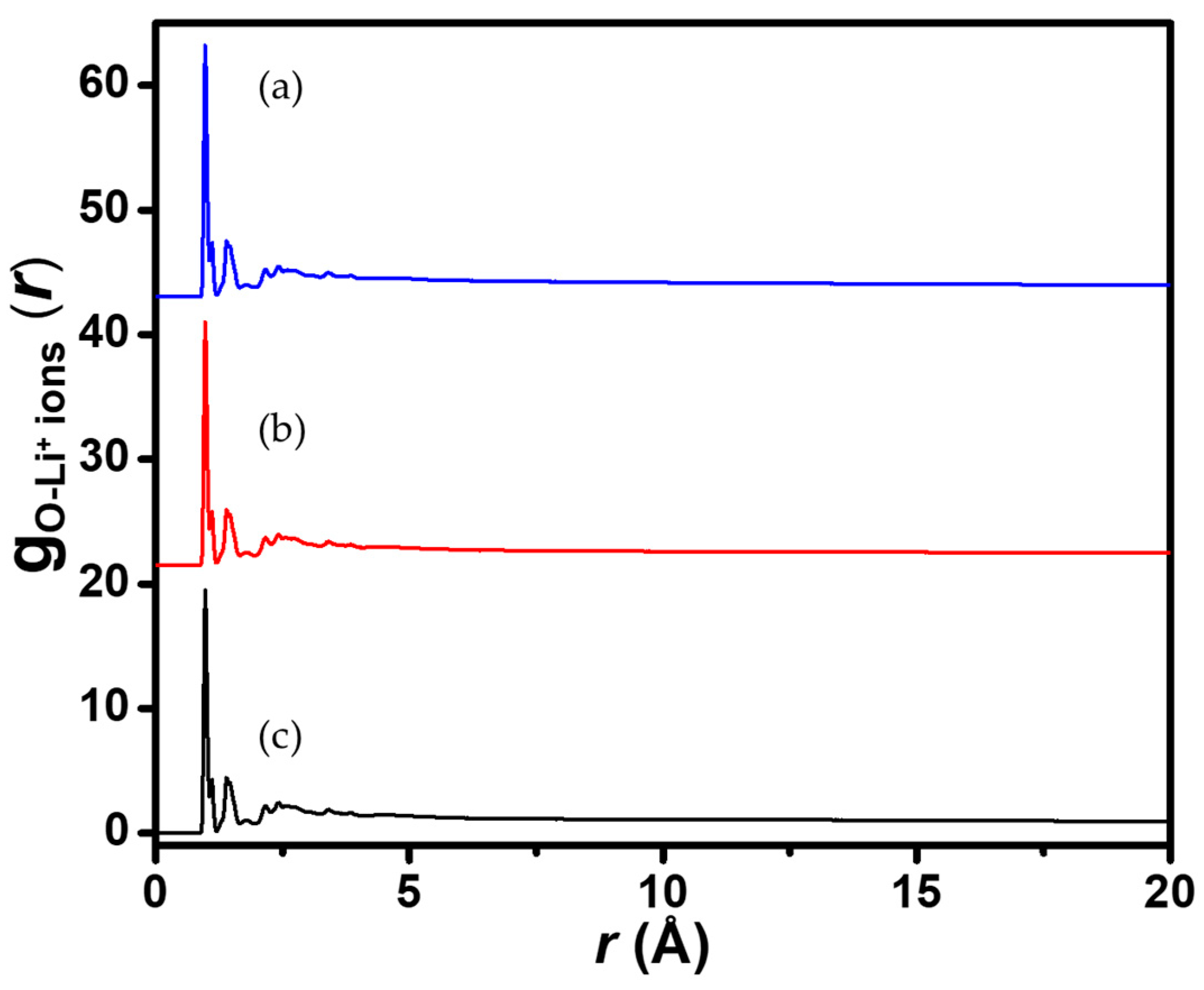
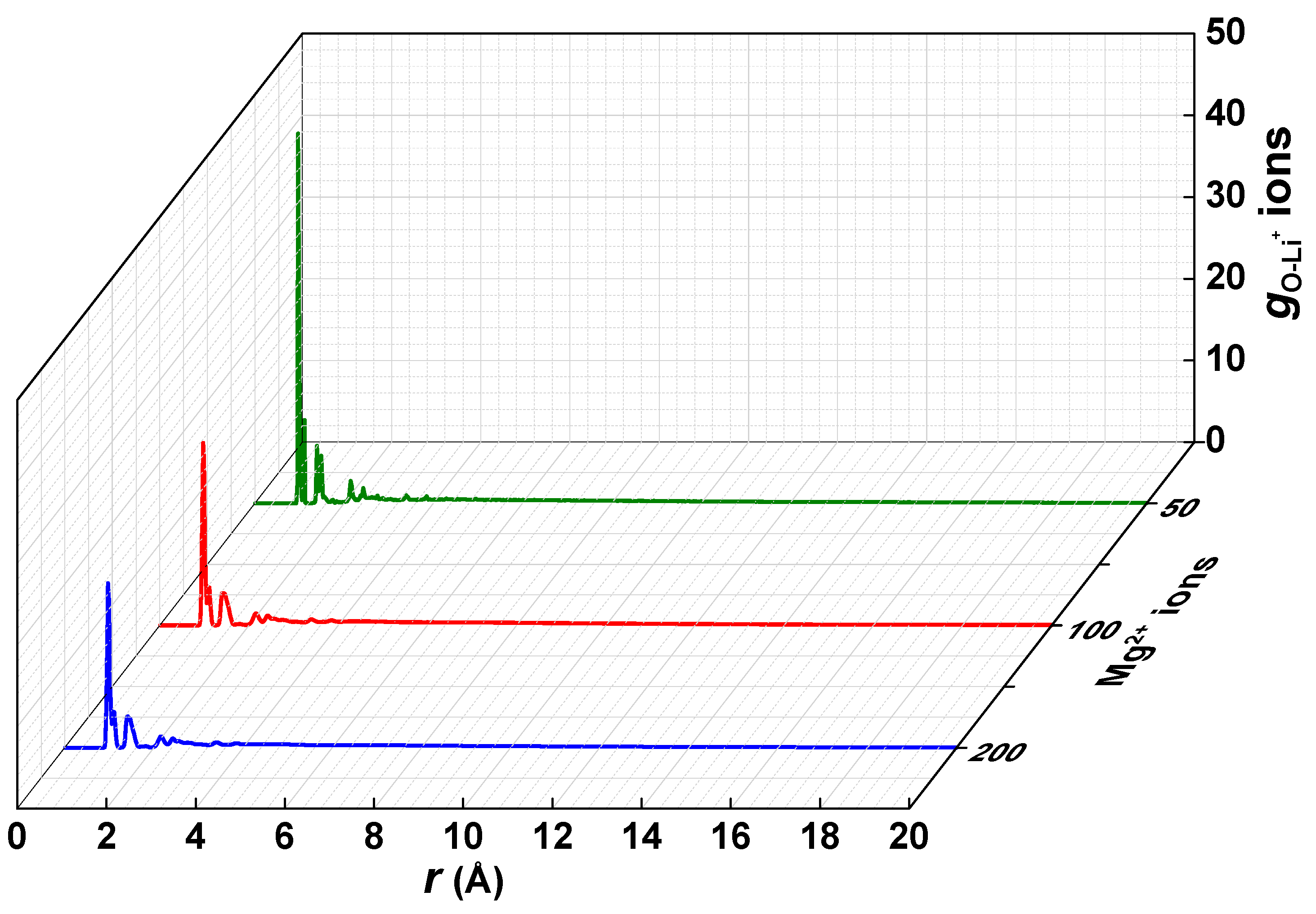
3.2. Diffusion of Counterions in Aqueous Media
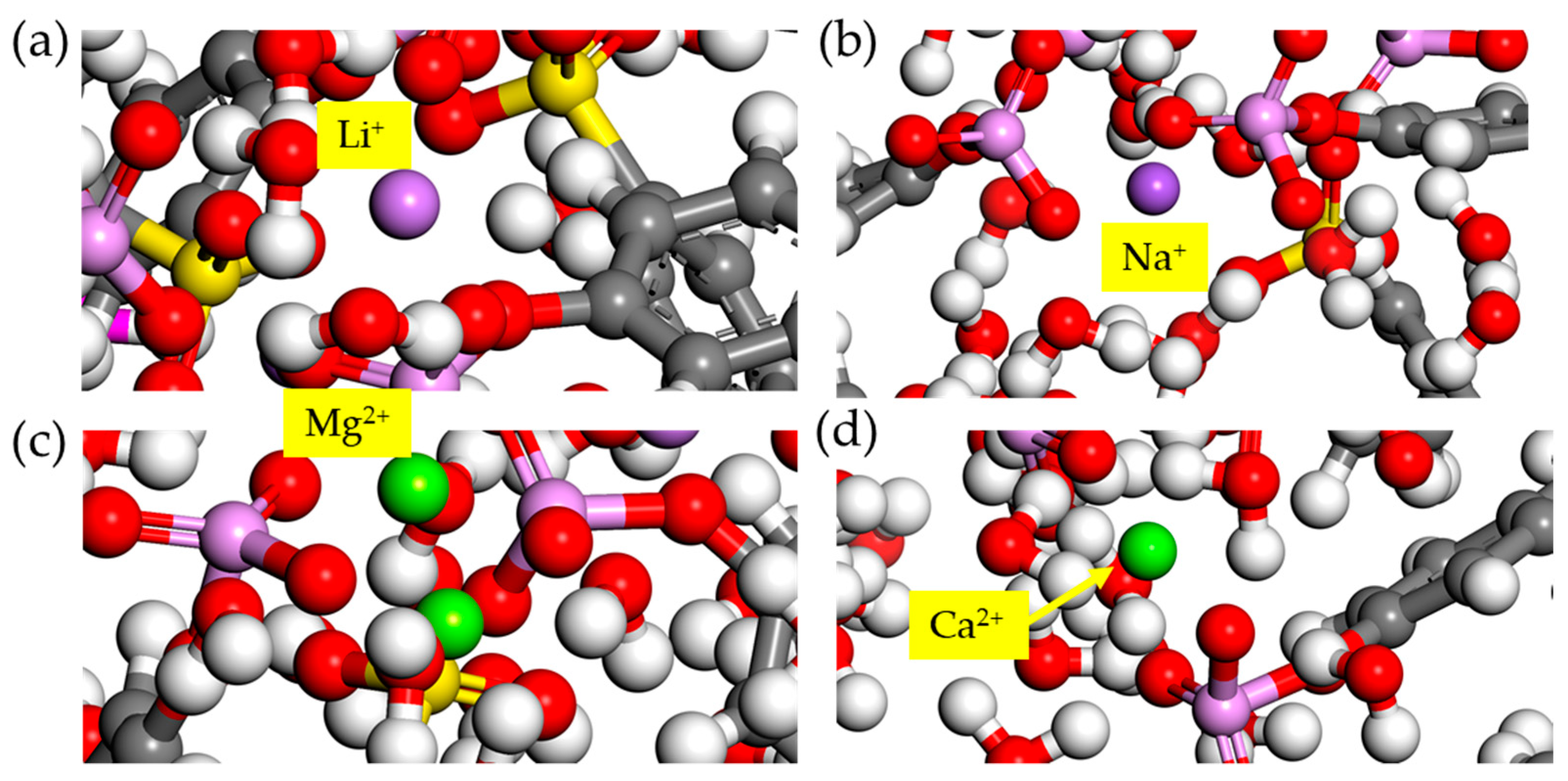
3.3. Interaction of Co-Existing Ions with the Polyelectrolyte Chain
3.4. Interaction of the Polyelectrolyte Chain with Mg2+/Li+ Ions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dutta, D.; Kumari, A.; Panda, R.; Jha, S.; Gupta, D.; Goel, S.; Jha, M.K. Close loop separation process for the recovery of Co, Cu, Mn, Fe and Li from spent lithium-ion batteries. Sep. Purif. Technol. 2018, 200, 327–334. [Google Scholar] [CrossRef]
- Zhang, W.; Xu, C.; He, W.; Li, G.; Huang, J. A review on management of spent lithium ion batteries and strategy for resource recycling of all components from them. Waste Manag. Res. 2018, 36, 99–112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, Y.; Zhu, M.; Yao, Y.; Wang, H.; Tong, B.; Zhao, Z. A novel approach for the selective extraction of Li+ from the leaching solution of spent lithium-ion batteries using benzo-15-crown-5 ether as extractant. Sep. Purif. Technol. 2020, 237, 116325. [Google Scholar] [CrossRef]
- Ikram, R.; Mohamed Jan, B.; Atif Pervez, S.; Papadakis, V.M.; Ahmad, W.; Bushra, R.; Kenanakis, G.; Rana, M. Recent Advancements of N-Doped Graphene for Rechargeable Batteries: A Review. Crystals 2020, 10, 1080. [Google Scholar] [CrossRef]
- Mun, S.C.; Won, J.H. Manufacturing Processes of Microporous Polyolefin Separators for Lithium-Ion Batteries and Correlations between Mechanical and Physical Properties. Crystals 2021, 11, 1013. [Google Scholar] [CrossRef]
- Dang, H.; Li, N.; Chang, Z.; Wang, B.; Zhan, Y.; Wu, X.; Liu, W.; Ali, S.; Li, H.; Guo, J.; et al. Lithium leaching via calcium chloride roasting from simulated pyrometallurgical slag of spent lithium ion battery. Sep. Purif. Technol. 2020, 233, 116025. [Google Scholar] [CrossRef]
- Zhang, X.; Han, A.; Yang, Y. Review on the production of high-purity lithium metal. J. Mater. Chem. 2020, 8, 22455–22466. [Google Scholar] [CrossRef]
- Sato, Y. Electrowinning of Metallic Lithium from Molten Salts. ECS Proc. Vol. 2002, 2002, 771. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Y.; Xing, G.; Tang, Y. Building High Power Density of Sodium-Ion Batteries: Importance of Multidimensional Diffusion Pathways in Cathode Materials. Front. Chem. 2020, 8, 152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pandit, B.; Rondiya, S.R.; Dzade, N.Y.; Shaikh, S.F.; Kumar, N.; Goda, E.S.; Al-Kahtani, A.A.; Mane, R.S.; Mathur, S.; Salunkhe, R.R. High Stability and Long Cycle Life of Rechargeable Sodium-Ion Battery Using Manganese Oxide Cathode: A Combined Density Functional Theory (DFT) and Experimental Study. ACS Appl. Mater. Interfaces 2021, 13, 11433–11441. [Google Scholar] [CrossRef]
- Abraham, K.M. How Comparable Are Sodium-Ion Batteries to Lithium-Ion Counterparts? ACS Energy Lett. 2020, 5, 3544–3547. [Google Scholar] [CrossRef]
- Strathmann, H. Electrodialysis, a mature technology with a multitude of new applications. Desalination 2010, 264, 268–288. [Google Scholar] [CrossRef]
- Sadrzadeh, M.; Mohammadi, T. Sea water desalination using electrodialysis. Desalination 2008, 221, 440–447. [Google Scholar] [CrossRef]
- Gurreri, L.; Tamburini, A.; Cipollina, A.; Micale, G. Electrodialysis Applications in Wastewater Treatment for Environmental Protection and Resources Recovery: A Systematic Review on Progress and Perspectives. Membranes 2020, 10, 146. [Google Scholar] [CrossRef] [PubMed]
- Ying, J.; Luo, M.; Jin, Y.; Yu, J. Selective separation of lithium from high Mg/Li ratio brine using single-stage and multi-stage selective electrodialysis processes. Desalination 2020, 492, 114621. [Google Scholar] [CrossRef]
- Nie, X.-Y.; Sun, S.-Y.; Sun, Z.; Song, X.; Yu, J.-G. Ion-fractionation of lithium ions from magnesium ions by electrodialysis using monovalent selective ion-exchange membranes. Desalination 2017, 403, 128–135. [Google Scholar] [CrossRef]
- Nie, X.-Y.; Sun, S.-Y.; Song, X.; Yu, J.-G. Further investigation into lithium recovery from salt lake brines with different feed characteristics by electrodialysis. J. Membr. Sci. 2017, 530, 185–191. [Google Scholar] [CrossRef]
- Nagarale, R.K.; Gohil, G.S.; Shahi, V.K. Recent developments on ion-exchange membranes and electro-membrane processes. Adv. Colloid Interface Sci. 2006, 119, 97–130. [Google Scholar] [CrossRef]
- Ran, J.; Wu, L.; He, Y.; Yang, Z.; Wang, Y.; Jiang, C.; Ge, L.; Bakangura, E.; Xu, T. Ion exchange membranes: New developments and applications. J. Membr. Sci. 2017, 522, 267–291. [Google Scholar] [CrossRef]
- Ling, C.; Liang, X.; Fan, F.; Yang, Z. Diffusion behavior of the model diesel components in different polymer membranes by molecular dynamic simulation. Chem. Eng. Sci. 2012, 84, 292–302. [Google Scholar] [CrossRef]
- Chang, K.-S.; Chung, Y.-C.; Yang, T.-H.; Lue, S.J.; Tung, K.-L.; Lin, Y.-F. Free volume and alcohol transport properties of PDMS membranes: Insights of nano-structure and interfacial affinity from molecular modeling. J. Membr. Sci. 2012, 417, 119–130. [Google Scholar] [CrossRef]
- Carrillo, J.-M.Y.; Dobrynin, A.V. Molecular Dynamics Simulations of Polyelectrolyte Adsorption. Langmuir 2007, 23, 2472–2482. [Google Scholar] [CrossRef]
- Zhu, Y.-L.; Lu, Z.-Y.; Milano, G.; Shi, A.-C.; Sun, Z.-Y. Hybrid particle–field molecular dynamics simulation for polyelectrolyte systems. Phys. Chem. Chem. Phys. 2016, 18, 9799–9808. [Google Scholar] [CrossRef]
- Winkler, R.G.; Gold, M.; Reineker, P. Collapse of Polyelectrolyte Macromolecules by Counterion Condensation and Ion Pair Formation: A Molecular Dynamics Simulation Study. Phys. Rev. Lett. 1998, 80, 3731–3734. [Google Scholar] [CrossRef]
- Stevens, M.J.; Kremer, K. Form factor of salt-free linear polyelectrolytes. Macromolecules 1993, 26, 4717–4719. [Google Scholar] [CrossRef]
- Stevens, M.J.; Kremer, K. The nature of flexible linear polyelectrolytes in salt free solution: A molecular dynamics study. J. Chem. Phys. 1995, 103, 1669–1690. [Google Scholar] [CrossRef]
- Liu, S.; Muthukumar, M. Langevin dynamics simulation of counterion distribution around isolated flexible polyelectrolyte chains. J. Chem. Phys. 2002, 116, 9975–9982. [Google Scholar] [CrossRef]
- Konieczny, M.; Likos, C.N.; Löwen, H. Soft effective interactions between weakly charged polyelectrolyte chains. J. Chem. Phys. 2004, 121, 4913–4924. [Google Scholar] [CrossRef] [Green Version]
- Molnar, F.; Rieger, J. “Like-Charge Attraction” between Anionic Polyelectrolytes: Molecular Dynamics Simulations. Langmuir 2005, 21, 786–789. [Google Scholar] [CrossRef] [PubMed]
- Ju, S.P.; Lee, W.J.; Huang, C.I.; Cheng, W.Z.; Chung, Y.T. Structure and dynamics of water surrounding the poly(methacrylic acid): A molecular dynamics study. J. Chem. Phys. 2007, 126, 224901. [Google Scholar] [CrossRef] [PubMed]
- Chung, Y.T.; Huang, C.I. Ion condensation behavior and dynamics of water molecules surrounding the sodium poly(methacrylic acid) chain in water: A molecular dynamics study. J. Chem. Phys. 2012, 136, 124903. [Google Scholar] [CrossRef]
- Sun, S.-Y.; Nie, X.-Y.; Huang, J.; Yu, J.-G. Molecular simulation of diffusion behavior of counterions within polyelectrolyte membranes used in electrodialysis. J. Membr. Sci. 2020, 595, 117528. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model. 2016, 22, 47. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, M.; Alam, M.P.; Chakravarty, C. Thermodynamic, Diffusional, and Structural Anomalies in Rigid-Body Water Models. J. Phys. Chem. 2011, 115, 6935–6945. [Google Scholar] [CrossRef]
- Ahlström, P.; Wallqvist, A.; Engström, S.; Jönsson, B. A molecular dynamics study of polarizable water. Mol. Phys. 1989, 68, 563–581. [Google Scholar] [CrossRef]
- Israelachvili, J.N. (Ed.) 4-Interactions Involving Polar Molecules. In Intermolecular and Surface Forces, 3rd ed.; Academic Press: San Diego, CA, USA, 2011; pp. 71–90. [Google Scholar]
- Weaver, J.H.; Frederikse, H.P.R. Crc Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 1977. [Google Scholar]
- Ruan, Y.; Zhu, Y.; Zhang, Y.; Gao, Q.; Lu, X.; Lu, L. Molecular Dynamics Study of Mg2+/Li+ Separation via Biomimetic Graphene-Based Nanopores: The Role of Dehydration in Second Shell. Langmuir 2016, 32, 13778–13786. [Google Scholar] [CrossRef]
- Zhu, Y.; Ruan, Y.; Zhang, Y.; Chen, Y.; Lu, X.; Lu, L. Mg2+-Channel-Inspired Nanopores for Mg2+/Li+ Separation: The Effect of Coordination on the Ionic Hydration Microstructures. Langmuir 2017, 33, 9201–9210. [Google Scholar] [CrossRef]
- Wu, H.; Lin, Y.; Feng, W.; Liu, T.; Wang, L.; Yao, H.; Wang, X. A novel nanofiltration membrane with [MimAP][Tf2N] ionic liquid for utilization of lithium from brines with high Mg2+/Li+ ratio. J. Membr. Sci. 2020, 603, 117997. [Google Scholar] [CrossRef]
- Xu, W.; Liu, D.; He, L.; Zhao, Z. A Comprehensive Membrane Process for Preparing Lithium Carbonate from High Mg/Li Brine. Membranes 2020, 10, 371. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Lin, S.; Yu, J. Lithium recovery from ultrahigh Mg2+/Li+ ratio brine using a novel granulated Li/Al-LDHs adsorbent. Sep. Purif. Technol. 2021, 256, 117780. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulazeez, I.; Salhi, B.; Baig, N.; Peng, Q. The Role of Sulphonic and Phosphoric Pendant Groups on the Diffusion of Monovalent Ions in Polyelectrolyte Membranes: A Molecular Dynamics Study. Membranes 2021, 11, 940. https://doi.org/10.3390/membranes11120940
Abdulazeez I, Salhi B, Baig N, Peng Q. The Role of Sulphonic and Phosphoric Pendant Groups on the Diffusion of Monovalent Ions in Polyelectrolyte Membranes: A Molecular Dynamics Study. Membranes. 2021; 11(12):940. https://doi.org/10.3390/membranes11120940
Chicago/Turabian StyleAbdulazeez, Ismail, Billel Salhi, Nadeem Baig, and Qing Peng. 2021. "The Role of Sulphonic and Phosphoric Pendant Groups on the Diffusion of Monovalent Ions in Polyelectrolyte Membranes: A Molecular Dynamics Study" Membranes 11, no. 12: 940. https://doi.org/10.3390/membranes11120940
APA StyleAbdulazeez, I., Salhi, B., Baig, N., & Peng, Q. (2021). The Role of Sulphonic and Phosphoric Pendant Groups on the Diffusion of Monovalent Ions in Polyelectrolyte Membranes: A Molecular Dynamics Study. Membranes, 11(12), 940. https://doi.org/10.3390/membranes11120940